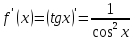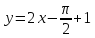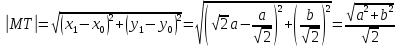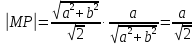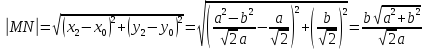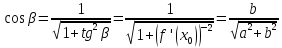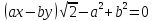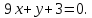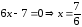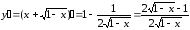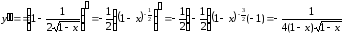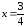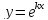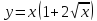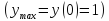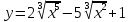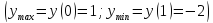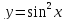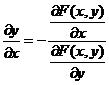Рассмотрим
кривую, уравнение которой имеет вид
Уравнение
касательной к данной кривой в точке
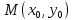

Нормалью
к кривой в данной точке называется
прямая, проходящая через данную точку,
перпендикулярную к касательной в этой
точке.
Уравнение
нормали к данной кривой в точке


Длина
отрезка касательной, заключенного между
точкой касания и осью абсцисс называется
длиной
касательной,
проекция этого отрезка на ось абсцисс
называется подкасательной.
Длина
отрезка нормали, заключенного между
точкой касания и осью абсцисс называется
длиной
нормали,проекция
этого отрезка на ось абсцисс называется
поднормалью.
Пример
17
Написать
уравнения касательной и нормали к кривой


Решение:
Найдем
значение функции в точке

Найдем
производную заданной функции в точке
Уравнение
касательной найдем по формуле (34):
Уравнение
нормали найдем по формуле (35):
Ответ:
Уравнение
касательной :
Уравнение
нормали :
Пример
18
Написать
уравнения касательной и нормали, длины
касательной и подкасательной, длины
нормали и поднормали для эллипса
в
точке

для которой
Решение:
Найдем

параметрически по формуле (10):
Найдем
координаты точки касания

и значение производной в точке касания

Уравнение
касательной найдем по формуле (34):
Найдем
координаты


касательной с осью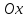
Длина
касательной равна длине отрезка

Согласно
определению, подкасательная

Где
угол
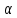
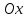

равный
Таким
образом, подкасательная

Уравнение
нормали найдем по формуле (35):
Найдем
координаты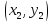

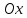
Длина
нормали равна длине отрезка

Согласно
определению, поднормаль
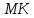
Где
угол

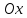

Поэтому,
поднормаль
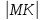
Ответ:
Уравнение
касательной :
Уравнение
нормали :
Длина
касательной

подкасательная
Длина
нормали

Задания
7. Написать
уравнения касательной и нормали:
1. К параболе в точке, абсцисса которой

2.
К окружности

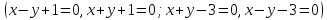
3.
К циклоиде


4.
В каких точках кривой

а)
оси Оx; б) прямой

10.
Промежутки монотонности функции.
Экстремумы функции.
Условие
монотонности функции:
Для
того, чтобы дифференцируемая на


чтобы во всех точках, принадлежащих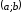

Для
того, чтобы дифференцируемая на

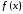
чтобы во всех точках, принадлежащих
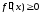
Промежутки,
на которых производная функции сохраняет
определенный знак, называются промежутками
монотонности
функции
Пример
19
Найти
промежутки монотонности функции

Решение:
Найдем
производную функции
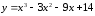
Найдем
промежутки знакопостоянства полученной
производной. Для этого
разложим полученный
квадратный трехчлен на множители:

Исследуем
знак полученного выражения, используя
метод интервалов.
Таким
образом, получаем согласно (36), (37),что
заданная функция возрастает на

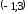
Ответ:
Заданная
функция

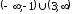

Определение
Функция


максимум (минимум),
если существует такая окрестность
точки

что для всех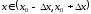
(
Локальный
минимум или максимум функции

экстремумом.
Необходимое
условие существования экстремума.
Пусть
функция
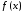
точки
Если функция
в точке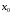
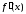

Точка

точкой
функции

если производная

Достаточные
условия наличия экстремума в критической
точке
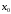
Пусть
точка

Первое
достаточное условие экстремума:
Пусть
функция




Точка

при переходе через
производная
функции меняет знак с плюса на минус.
Точка

переходе через
производная
функции меняет знак с минуса на плюс.
Пример
20
Найти
экстремумы функции

Решение:
Найдем
производную заданной функции
Приравнивая
в полученной производной к нулю числитель
и знаменатель, найдем критические точки:
Исследуем
знак производной, используя метод
интервалов.

Из
рисунка видно, что при переходе через
точку

минус. Следовательно, в точке
локальный максимум.
При
переходе через точку

плюс.
Следовательно,
в точке

локальный минимум.
При
переходе через точку

критическая точка
функции.
Ответ:

локальный максимум,
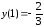
локальный минимум.
Второе
достаточное условие экстремума:
Если
первые
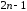

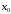
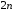
производная функции



причем,
если
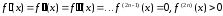
(38)
то
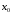
минимум
если

(39)
то
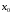
максимум.
Пример
21
Найти
экстремумы функции, пользуясь второй
производной

Решение:
ОДЗ:

Найдем
первую производную заданной функции
Найдем
критические точки функции:
Точку

определена только в левой окрестности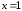
Найдем
вторую производную
Находим
Таким
образом, на основании (39) делаем вывод
о том, что при

Ответ:

локальный максимум.
Задания
8.
Исследовать
на возростание и убывание функции:
|
1. |
2. |
3. |
|
4. |
5. |
6. |
Исследовать
на экстремумы функции:
|
7. |
|
|
|
8. |
|
|
|
9. |
|
|
|
10. |
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Найдем производную, дифференцируя функцию $ y(x) $ по переменной $ x $:
$$ (x^2)’_x+ (2xy^2)’_x + (3y^4)’_x = (6)’_x $$
Учитывая, что $ y^2 $ и $ y^4 $ сложные функции продолжаем:
$$ 2x + 2y^2 + 4xyy’ + 12y^3 y’ = 0 $$
Выражаем $ y’ $ из полученного уравнения:
$$ 4xyy’ + 12y^3 y’ = -2x — 2y^2 $$
Выносим $ y’ $ за скобки:
$$ y'(4xy + 12y^3) = -2x — 2y^2 $$
Делим обе части уравнения на выражение $ 4xy+12y^3 $:
$$ y’ = -frac{2x+2y^2}{4xy + 12y^3} = -frac{x+y^2}{2xy+6y^3} $$
Теперь вычисляем значение $ y’ $:
$$ y’ = -frac{1 + (-1)^2}{2cdot 1 cdot (-1) + 6cdot (-1)^3} = -frac{2}{-8} = frac{1}{4} $$
Зная, что $ y’ = frac{1}{4} $ и $ y(x_0) = y(1) = -1 $ составляем уравнения касательной и нормали к кривой в точке $ M(1;-1) $.
Получаем уравнение касательной:
$$ y — (-1) = frac{1}{4} (x — 1) $$
Записываем в красивой форме:
$$ y = frac{1}{4} x — frac{3}{4} $$
Получаем уравнение нормали:
$$ y — (-1) = -frac{1}{frac{1}{4}} (x — 1) $$
Раскрываем скобки и записываем в красивой форме, полученное уравнение:
$$ y+1 = -4(x-1) $$
$$ y = -4x + 3 $$
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Назначение сервиса. Данный сервис предназначен для нахождения уравнения нормали к кривой. Решение оформляется в формате Word. Для получения уравнения необходимо выбрать вид заданной функции.
Функция задана в явном виде
Функция задана в неявном виде
Функция задана в параметрическом виде
Пример
Задание №1
Найти уравнение нормали к параболе y = 1/2*x2 в точке (-2;2).
Решение находим с помощью калькулятора.
Запишем уравнения нормали в общем виде:
По условию задачи x0 = -2, тогда y0 = 2
Теперь найдем производную:
y’ = (1/2•x2)’ = x
следовательно:
f'(-2) = -2 = -2
В результате имеем:
или
yk = 1/2•x+3
Задание №2
Написать уравнения нормали к кривой y2-1/2*x3-8 в точке M0(0;2).
Решение.
Поскольку функция задана в неявном виде, то производную ищем по формуле:
Для нашей функции:
Тогда:
или
следовательно:
Fx‘(0;2) = 3/4•02/2 = 0
В результате имеем:
или
x = 0
Задание №3
Написать уравнения нормали к эллипсу, заданному в параметрической форме: x = 5*sqrt(2)*cos(t);y = 3*sqrt(2)*sin(t) в точке M0(-5;3).
Решение.
Запишем уравнения нормали в для функции, заданной в параметрической форме:
(x — x0)x’ + (y — y0)y’ = 0
Данной точке M0(-5;3) соответствует значение t = 3/4•π
Для нашей функции:
следовательно:
Вывод уравнения нормали к графику функции
Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Замечание 1
Нормаль — это прямая, которая образует с касательной к графику функции угол в $90°$.
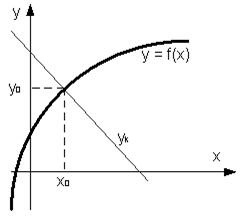
Рисунок 1. Нормальный перпендикуляр к графику касательной. Автор24 — интернет-биржа студенческих работ
В связи с тем, что нормаль перпендикулярна к касательной, её угловой коэффициент будет величиной, обратной к угловому коэффициенту касательной:
$k_{норм}=- frac{1}{k_{к}}= -1 frac{1}{f’(x_0)}$.
Пользуясь полученным выводом, запишем уравнение нормали к графику функции:
$y – y_0 = — frac{1}{f’(x_0)} cdot (x – x_0) left(1right) $, здесь $x_0$ и $y_0$ — координаты точки для которой строится искомая линия, при этом производная в этой точке $f’(x_0) ≠ 0$.
Порядок действий при поиске уравнения нормальной прямой если задана координата $x_0$:
- Вычисляется, чему равен нулевой игрек $y(x_0)$ для функции.
- Затем нужно определить производную.
- Нужно высчитать затем, чему равен $f’(x)$ в точке $x_0$, найденное значение — коэффициент касательной.
- Все найденные значения подставляются в формулу $(1)$.
Напомним также как выглядит само уравнение касательной:
$y – y_0 = f’(x_0) cdot (x – x_0)$.
Пример 1
Найдите уравнение нормали для функции $y=x^2$ в точке $x_0=2$.
Решение:
Производная данной функции составит $y’(x) = 2x$, затем найдём, чему равен наш подопытный кролик-функция в заданной точке $y_0= x^2 = 2^2 = 4$.
Теперь нужно высчитать производную функции в точке $x_0$: $y’(2) = 2 x = 2 cdot 2= 4$.
Все полученные значения расставляем по своим местам в формулу $(1)$:
$y-4=-frac{1}{4} cdot (x – 2)$
Уравнение нормали найдено.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 07.05.2023

Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Уравнение нормали
Определение и уравнение нормали
Уравнение нормали имеет вид:
В случае параметрического задания функции нормаль задается уравнением:
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |