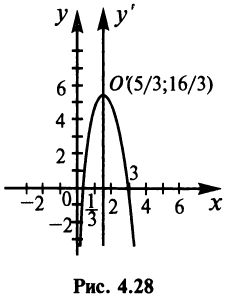
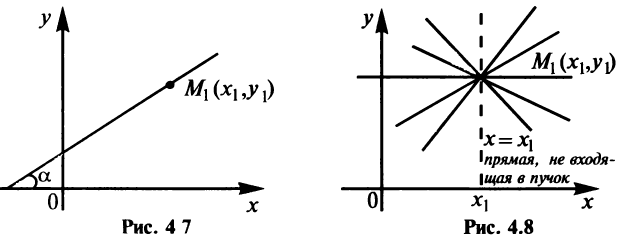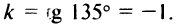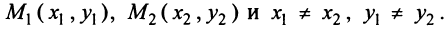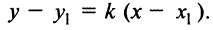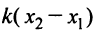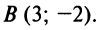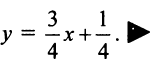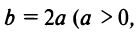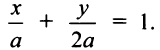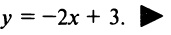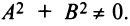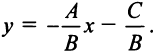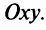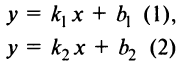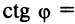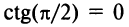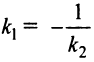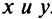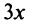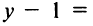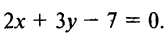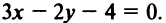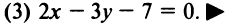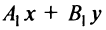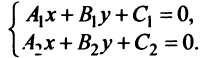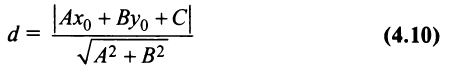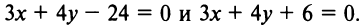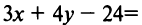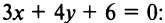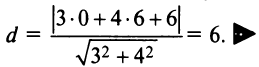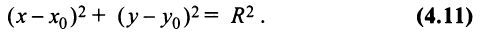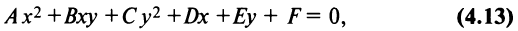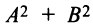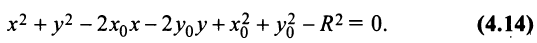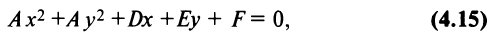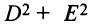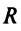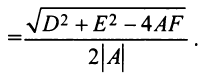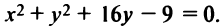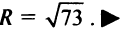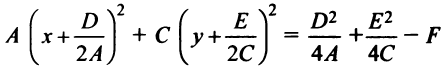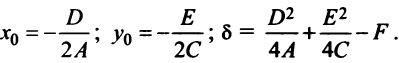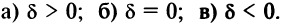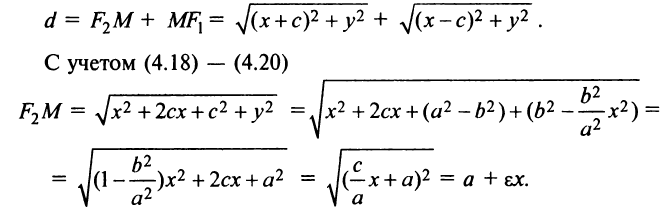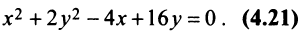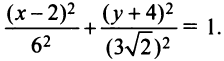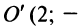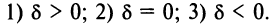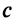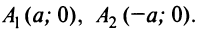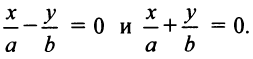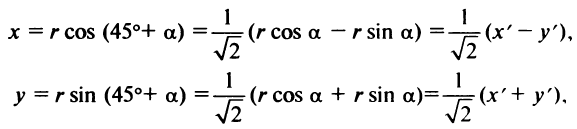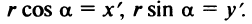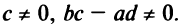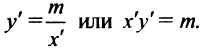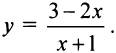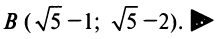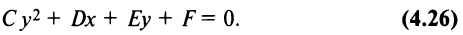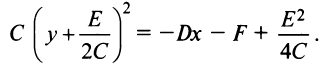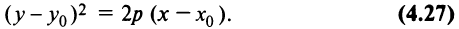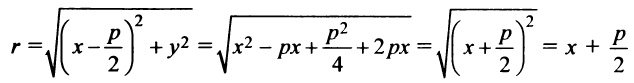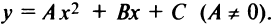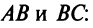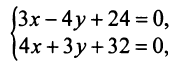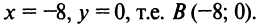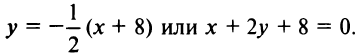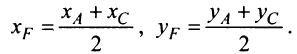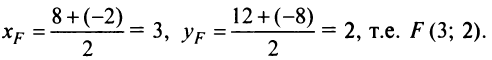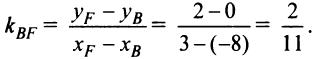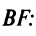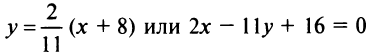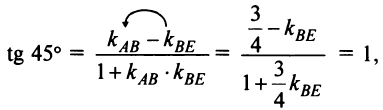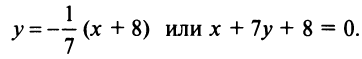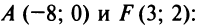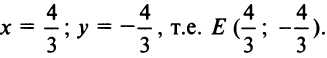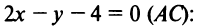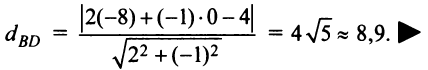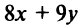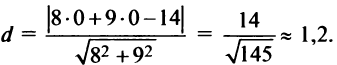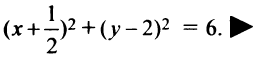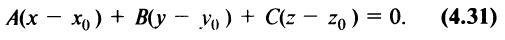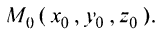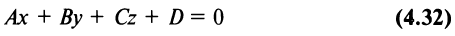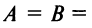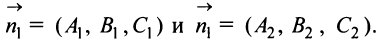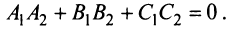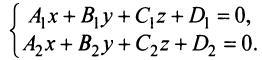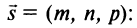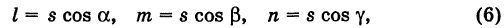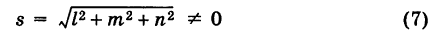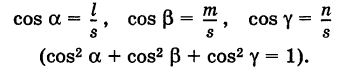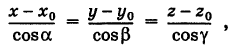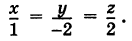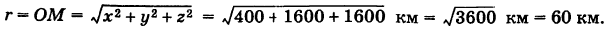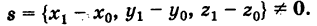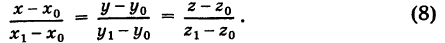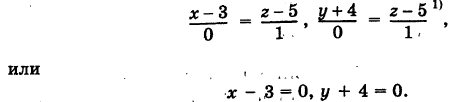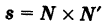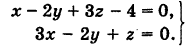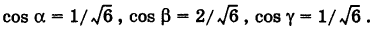Урок 5
оПределение уравнения линии.
Примеры на отыскание множеств точек.
оПределение уравнения линии.
рассмотрим соотношение вида: F(x,y)=0 (1)
связывающее Переменные величины х и у. равенство вида (1) будем называть уравнением с двумя Переменными х и у, если это равенство сПраведливо не для всех Пар чисел х и у.
Примеры уравнений: 2х+3у=0, х 2 +у 2 -25=0.
если равенство (1) сПраведливо для всех Пар чисел х и у, то оно называется т ождеством .
Примеры тождеств: (х+у) 2 — х 2 -2ху -у 2 =0, (х-у)(х+у) — х 2 +у 2 =0.
уравнение (1) будем называть уравнением множества точек (х;у), если этому уравнению удовлетворяют координаты х и у любой точки множества и не удовлетворяют координатам никакой точки, не Принадлежащей этому множеству.
важным Понятием аналитической геометрии является Понятие уравнения линии. Пусть на Плоскости заданы Прямоугольная система координат и некоторая линия l.
оПределение. уравнение (1) называется уравнением линии l (в заданной системе координат), если этому уравнению удовлетворяют координаты х и у любой точки, лежащей на линии l , и не удовлетворяют координаты никакой точки, не лежащей на этой линии.
из оПределения следует, что линия l Представляет собой множество всех точек Плоскости (х;у), координаты которых удовлетворяют уравнению (1).
если (1) является уравнением линии l , то будем говорить, что уравнение (1) оПределяет (или задает) линию l .
Понятие уравнения линии дает возможность сводить геометрические задачи к алгебраическим. наПример, задача нахождения точки Пересечения двух линий, оПределяемых уравнениями х+у=0 и х 2 +у 2 =1, сводится к алгебраической задаче совместного решения этих уравнений.
линия l может оПределятся не только уравнением вида (1), но и уравнением вида F(. )=0, содержащим Полярные координаты.
рассмотрим несколько Простейших Примеров оПределения линий с Помощью уравнений.
1) х — у=0 . заПисав это уравнение в виде у=х, заключаем, что множество точек, координаты которых удовлетворяют данному уравнению, Представляет собой биссектрису Первого и третьего координатных углов. это и есть линия, оПределенная данным уравнением.
2) х 2 — у 2 =0. Представив уравнение в виде (х-у)(х+у)=0, заключаем, что множество точек, координаты которых удовлетворяют данному уравнению, — это две Прямые, содержащие биссектрисы четырех координатных углов. (см рисунок — гиПерссылка)
3) х 2 +у 2 =0. множество точек, координаты которых удовлетворяют этому уравнению, состоит из одной точки (0;0). в данном случае уравнение оПределяет, как говорят, вырожденную линию.
4) х 2 +у 2 +1=0. так как При любых х и у числа х 2 и у 2 неотрицательны, то х 2 +у 2 +1>0. значит, нет ни одной точки, координаты которой удовлетворяют данному уравнению, т.е. никакого геометрического образа на Плоскости данное уравнение не оПределяет. оно оПределяет «Пустое» множество точек.
5) p=а cOSf , где а — Положительное число, Переменные p и f — Полярные координаты. обозначим через м точку с Полярными координатами (p;f), через а — точку с Полярными координатами (а;0). если p=а cOSf , где 0
6) p=аf , где а — Положительное число, p и f — Полярные координаты. обозначим через м точку с Полярными координатами (p;f). если p=0, то и f=0. таким образом, При увеличении угла f точка м(p;f), начавшая свое движение в Полюсе, движется вокруг него, одновременно удаляясь от Полюса. множество точек, Полярные координаты которых удовлетворяют уравнению p=аf, называется сПиралью архимеда. При этом ПредПолагается, чтоf? может Принимать любые неотрицательные значения.
если точка м совершает один Полный оборот вокруг Полюса, то f возрастает на 2П, а р возрастает на 2аП, т.е. сПираль рассекает любую Прямую, Проходящую через Полюс, на равные отрезки (не считая отрезка, содержащего Полюс), которые имеют длину 2аП.
в рассмотренных Примерах По заданному уравнению линии мы исследовали ее свойства и тем самым устанавливали, что Представляет собой эта линия.
рассмотрим теПерь обратную задачу для заданного (какими-то его свойствами) множества точек, т.е. для заданной линии l , требуется найти его уравнение F (х;у)=0.
Примеры на отыскание множеств точек.
рассмотрим несколько Примеров на отыскание множеств точек По уравнениям и неравенствам, связывающим их координаты.
Пример 1. вывести уравнение (в заданной Прямоугольной системе координат) множества точек, каждая из которых отстоит от точки с(а;в) на расстояние R. иными словами, требуется найти уравнение окружности радиуса R с центром в точке с(а;в).
решение. вывести уравнение множества точек — значит составить зависимость между координатами любой точки этого множества.
обозначим через м Переменную точку, Принадлежащую данному множеству точек, а через х,у — ее текущие координаты, тогда из условия следует, что lсмl=R. Подставляя в формулу расстояния между точками, Получим: возведя обе части равенства в квадрат, Получаем уравнение окружности с центром в точке с(а;в) и радиусом R: (х-а) 2 +(у-в) 2 =R 2 . оно встречается во многих геометрических задачах. Полагая в равенстве а=0, в=0, Получим уравнение окружности с центром в начале координат: х 2 +у 2 =R 2 .
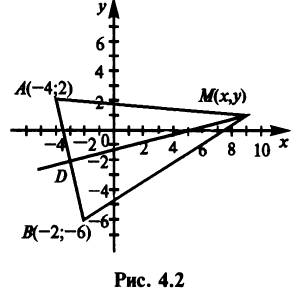
Пример 2. найти уравнение множества точек, равноудаленных от точек а(1;1) и в(3;3).
решение. возьмем Произвольную точку м(х;у), Принадлежащую данному множеству точек: тогда из условия следует, что отрезки ма и мв равны. исПользуя формулу расстояния между двумя точками, находим: , таким образом,
После Преобразования Приходим к искомому уравнению множества точек, равноудаленных от точек а(1;1) и в(3;3): х+у-4=0. как известно из элементарной геометрии, таким множеством точек является Прямая, Проходящая через середину отрезка, соединяющего данные точки, и ПерПендикулярная этому отрезку.
- даны точки о(2;-2), а(2;2), в(2;-1), с(3;-3), м(5;-5) и к(3;-2). установите, какие из них лежат на линии, заданным уравнением х+у=0, а какие не лежат на ней. (ответ: точки о, с и м лежат на линии, а точки а, в и к не лежат на ней)
- даны точки а(1;п / 3), в(2;0), с(2;п / 4), м(v3;п / 6) и к(1;2?п3). выясните, какие из них лежат на линии, оПределяемой уравнением р=2 cOSf , и какие не лежат на ней. (ответ: точки а, в и м — лежат на данной линии, точки с и к — не лежат на ней. уравнение оПределяет окружность с диаметром ов)
- составьте уравнение линии, По которой движется точка м(х;у), равноудаленная от точек а(0;2) и в(4;-2). (ответ: х-у-2=0)
- составьте уравнение линии, расстояние каждой точки которой от точки а(0;0,25) равно расстоянию этой же точки от Прямой у=-0,25. (ответ: у=х 2 )
- найдите уравнение множества точек, сумма расстояний каждой из которых от точек а(2;0) и в(-2;0) равна 2v5. (ответ: 0,2х 2 +у 2 =1)
- найдите уравнение множества точек, равноудаленных от точки а(2;2) и оси ох. (ответ: у=0,25х 2 -х+2)
- найдите уравнение множества точек, равноудаленных от оси оу и точки а(4;0). (ответ: у 2 =8х-16)
- составьте уравнение линии, оПисываемой серединой отрезка с длиной, равной D , один из концов которого Перемещается По оси абсцисс, а другой конец — По оси ординат. (ответ: х 2 +у 2 =0,25 D 3 )
Автор: Вяликова Мария Владимировна — учитель математики и информатики высшей квалификационной категории МАОУ Пролетарская СОШ Новгородского района Новгородской области
Множество точек на плоскости
Пример №1 . Составить уравнение множества точек на плоскости, равноудаленных от точек A(1;2) и B(-2;0).
Решение
Пусть точка М принадлежит искомому множеству точек, тогда МА=МВ. Так как
то
После возведения левой и правой частей в квадрат и упрощений получим:
(x-1) 2 + (y-2) 2 = (x + 2) 2 + y 2
x 2 — 2x + 1 + y 2 — 4y + 4 = x 2 + 4x + 4 + y 2
или
— 6x — 4y + 1 = 0
Ответ: — 6x — 4y + 1 = 0.
Пример №2 .
Составить уравнение множества точек на плоскости, отношение расстояний которых от точки A(1;-2) и от прямой x=1 равно 1 /2.
Решение
Из условия следует, что для любой точки M(x;y) искомого множества справедливо соотношение MA:MB = 1 /2. Так как:
то
или
Возведя левую и правую части в квадрат и упрощая, получим:
4(x — 1) 2 + 4(y + 2) 2 = |x — 1| 2
т.е.
4(x 2 — 2x + 1) + 4(y 2 + 4y + 4) = x 2 — 2x + 1
или
3x 2 + 4y 2 — 6x +16y +19 = 0
Ответ: 3x 2 + 4y 2 — 6x +16y +19 = 0.
Пример №3 . Составить уравнение линий, если расстояние каждой ее точки А(2,0) относится к расстоянию до прямой 5x+8=0 как 5:4 .
Решение. Выражаем x = -8/5. λ=5/4. Подставляем данные в задание №2.
Пример №4 . Составить уравнение линии, каждая точка которой равноудалена от прямой x+6=0 и от начала координат.
Примечание. Здесь x=-6 , λ=1.
Составить уравнения множества точек равноудаленных от точки и прямой
Задание
Составить уравнение множества точек плоскости, равноудалённых от точки F (7; 3) и от прямой x — 2y = 11
Решение
Расстояние от точки А(x1, y1) до прямой Ax + By + C = 0 равно длине перпендикуляра, опущенного из этой точки на прямую.
Она определяется по формуле
d1 = (Ax1 + By1 + C)/(A^2 + B^2)^0.5 = (x1 — 2y1 — 11)/(5^0.5)
Расстояние d2 между точками A(x1, y1) и B(x2, y2) плоскости определяется по формуле
d2 = ((x2 — x1)^2 + (y2 — y1)^2)^0.5
Из условия равноудалённости следует, что d1 = d2
(x1 — 2y1 — 11)/(5^0.5) = ((x2 — x1)^2 + (y2 — y1)^2)^0.5
Нужно возвести обе части в квадрат и привести подобные слагаемые
Получается квадратное уравнение, то есть геометрическим местом точек равноудалённых от заданной точи и прямой является парабола.
http://math.semestr.ru/line/points.php
http://www.andreyolegovich.ru/edu/mathematics/9/039.php
Лекция 12.
Уравнение ГМТ. Уравнения прямой в
плоскости
Вопросы:
-
Уравнение множества точек. Общее
уравнение. Параметрические уравнения. -
Направляющий вектор прямой. Векторное
уравнение прямой. Уравнение прямой в
форме определителя. -
Каноническое уравнение прямой.
Параметрические уравнения прямой. -
Уравнение прямой, проходящей через
две точки. -
Общее уравнение прямой. Исследование
общего уравнения прямой. -
Уравнение прямой в отрезках.
-
Уравнение прямой, заданной точкой и
перпендикулярным (ортогональным)
вектором. -
Уравнение прямой с угловым коэффициентом.
-
Нормированное и Нормальное уравнение
прямой. -
Взаимное расположение двух прямых
на плоскости: условия параллельности
и совпадения двух прямых. Условие
перпендикулярности двух прямых. -
Вычисление угла между двумя прямыми.
-
Вычисление расстояния от точки до
прямой.
Положение точки
в плоскости чаще всего описывается в
декартовой прямоугольной системе
координат парой чисел М(x;y).
Описание линии, в
частности прямой, можно было бы строить
путем описания каждой ее точки, однако
это очень затруднительно ввиду того,
что точек бесконечно много.
Если имеем уравнение
,
(12.1)
то все точки
разбиваются на два класса: 1) точки,
координаты которых удовлетворяют
уравнению, 2) точки, координаты которых
не удовлетворяют уравнению. Точки
первого класса образуют множество F,
а уравнение (1) называется уравнением
множества точек F.
Если уравнение
(1) – многочлен первого и второго порядка,
например,
или
,
то такие множества – объект изучения
аналитической геометрии. Если уравнение
(1) – многочлен произвольного порядка
степени, большей второй, то такие
множества – объект изучения алгебраической
геометрии. Если уравнение (1) – любая
другая функция, то такие множества –
объект изучения дифференциальной
геометрии.
Уравнение
называется также неявным
уравнением. Если уравнение (12.1) можно
разрешить относительно одной координаты,
например, у,
, (12.2)
где х
– независимое переменное, у
– зависимое, то множество называется
графиком функции, а уравнение (12.2) –
явным
уравнением. Если обе координаты х
и у
задаются с помощью вспомогательного
переменного – параметра t
(или нескольких
параметров),
(12.3)
то уравнения (12.3)
называются параметрическими
уравнениями множества F.
Уравнение прямой
связывает между собой координаты точки,
принадлежащей прямой. Из курса планиметрии
известно, что через две точки плоскости
можно провести единственную прямую
(аксиома планиметрии). На языке алгебры
это означает, что, записать уравнение
прямой можно, зная координаты двух ее
точек, т.е. два условия. Если же известна
только одна точка прямой, то для
составления уравнения требуется задать
еще одно условие, например, вектор,
параллельный прямой. В этом случае можно
записать уравнение прямой, называемое
каноническим,
а также параметрические уравнения. Если
кроме точки искомой прямой известен
вектор, перпендикулярный прямой, то
можно записать общее
уравнение.
Если известны отрезки, отсекаемые прямой
на осях координат, то можно записать
так называемое уравнение
«в
отрезках».
Если в
прямоугольной системе координат известен
отрезок, отсекаемый на оси ординат
(начальная ордината) и угол наклона
(тангенс угла наклона) прямой к оси
абсцисс, получим уравнение
с
угловым коэффициентом.
Если известен угол между перпендикуляром
к прямой и осью абсцисс, расстояние от
начала координат до прямой, можно
записать нормальное
(нормированное)
уравнение. Все уравнения получаются из
наглядных геометрических соображений.
2. Уравнения прямой в аффинной системе координат
2.1. Уравнение прямой, проходящей через данную точку параллельно данному вектору
Дано: М0(х0;у0),
,
причем
.
Составить уравнение
l
/ l
М0,
l
||
/
Решение.
Определение
1.
Вектор, отличный
от нулевого, параллельный искомой
прямой, называется направляющим
вектором прямой.
Точка плоскости
М
принадлежит прямой l,
если координаты точки удовлетворяют
уравнению прямой. На языке векторов это
означает, что, где бы ни лежала точка М
на прямой l,
вектор
коллинеарен вектору
.
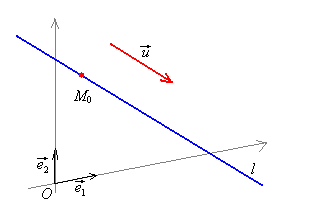
||
,
или,
=t
.
(12.4)
Откуда
Получили
векторное уравнение
прямой:
(12.5)
Откуда
(12.6)
– параметрические
уравнения прямой, где t
– параметр.
Условие коллинеарности
векторов: координаты
,
пропорциональны. Если
,
,
то.
(12.7)
Это уравнение
связывает координаты точки М0,
вектора
и произвольной точки М
прямой l.
Оно называется каноническим
уравнением прямой.
Условие коллинеарности
векторов
,
можно записать в форме определителя,
используя свойство: определитель с
пропорциональными строками равен нулю,
т.е.
(12.8)
Это уравнение
прямой в форме определителя.
Откуда
, (12.9)
Коэффициенты m
и n
одновременно не обращаются в нуль, т.к.
.
Из уравнения (12.9) вытекают следствия:
-
Если l
||
(1;0)
, то уравнение примет вид
(прямая параллельна оси Ох).
-
Если l
||
(0;1)
, то уравнение примет вид
(прямая
параллельна оси Оу). -
Если прямая не
параллельная осям, тогда выразим
:
, (12.10)
где
– угловой коэффициент прямой в данной
системе координат.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Общие уравнения геометрических мест точек
Уравнением множества точек (уравнением г.м.т.) координатной плоскости называется равенство, связывающее координаты точек, верное для координат точек, принадлежащих множеству
, и неверное для координат точек, не принадлежащих
. Например, уравнение множества в аффинной системе координат
имеет вид:
(3.1)
в частности, в прямоугольной системе координат , а в полярной системе координат
(3.2)
где и
— некоторые функции двух аргументов.
Уравнения (3.1), (3.2) представляют собой аналитическую запись функциональной зависимости между координатами точек на плоскости, образующих геометрическое место точек. В частных случаях одна из координат может быть выражена через другую, т.е. одна координата задается как явная функция другой координаты. Тогда получается уравнение, разрешенное относительно этой координаты, например:
Заметим, что уравнениями вида в прямоугольной системе координат
могут быть заданы графики элементарных функций: степенных, тригонометрических, показательных, логарифмических.
Пример 3.1. Изобразить на координатной плоскости (в прямоугольной системе координат) множества точек, координаты которых удовлетворяют следующим уравнениям:
Решение. а) Уравнению удовлетворяют только те точки плоскости, у которых равны абсциссы и ординаты
. Эти точки лежат на биссектрисах
и
координатных углов (рис. 3.1, а).
б) Разлагая левую часть уравнения на множители, получаем уравнение , которое равносильно совокупности уравнений
Первому уравнению отвечают биссектрисы нечетных координатных углов, второму — биссектрисы четных координатных углов. Следовательно, заданному уравнению удовлетворяют только те точки, которые принадлежат хотя бы одной из указанных биссектрис (рис. 3.1, 6).
в) Уравнение равносильно системе уравнений
которая определяет единственную точку (начало координат) на плоскости (рис. 3.1, в).
г) Выражение есть квадрат расстояния от точки
до начала координат. Поэтому уравнению
(или
) удовлетворяют только те точки, которые удалены от точки
на расстояние, равное 1. Это множество точек является окружностью с центром в начале координат и радиусом 1 (рис.3.1,г).
д) Уравнению удовлетворяет каждая точка с неположительной абсциссой. Следовательно, множество решений этого уравнения представляет собой полуплоскость
, ограниченную осью ординат (рис.3.1,д).
е) Уравнение не имеет действительных решений, поэтому на координатной плоскости нет точек, удовлетворяющих этому уравнению.
Пример 3.2. На координатной плоскости (в прямоугольной системе координат) отмечены точки
и
. Вывести уравнения заданных множеств:
а) прямой (рис.3.2,а);
б) серединного перпендикуляра к отрезку (рис.3.2,б);
в) окружности с диаметром (рис.3.2,в).
Решение. а) Точка принадлежит прямой
тогда и только тогда, когда ее радиус-вектор
удовлетворяет условию
, где
— некоторое действительное число (см. Применение векторов в задачах). Записывая это векторное равенство в координатной форме, получаем
Исключая параметр из этой системы (например, подставляя во второе уравнение
), приходим к уравнению
или
.
б) Пусть произвольная точка плоскости. Эта точка принадлежит серединному перпендикуляру к отрезку
тогда и только тогда, когда
. Записывая это равенство в координатной форме, получаем
Возводя в квадрат и приводя подобные члены, приходим к уравнению .
в) Найдем радиус заданной окружности:
и координаты центра окружности — середины отрезка
, так как
. По определению точка
принадлежит этой окружности тогда и только тогда, когда
. Записывая это равенство в координатной форме, получаем
Возводя в квадрат и перенося все члены в левую часть равенства, получаем .
Пример 3.3. Изобразить на плоскости в полярной системе координат множества точек, координаты которых удовлетворяют следующим уравнениям:
а) (спираль Архимеда);
б) (кардиоида);
в) (лемниската Бернулли).
Решение. а) Построение выполняется по точкам при . Далее учитывается, что при каждом полном обороте полярный радиус увеличивается на
(рис.3.3-1).
б) Построение выполняется по точкам при , а затем продолжается симметрично полярной оси, так как замена
на
не изменяет уравнения (рис.3.3-2,а).
в) Построение выполняется по точкам при , а затем продолжается симметрично полярной оси и полюса
(рис.3.3-2,б).
Уравнения пересечений и объединений геометрических мест точек
Рассмотрим основные операции с множествами точек на координатной плоскости, заданными своими уравнениями.
Пусть множества и
в аффинной системе координат
заданы общими уравнениями
и
соответственно.
Пересечение множеств
и
состоит из точек, координаты которых удовлетворяют системе уравнений
Можно составить одно уравнение, равносильное этой системе, например:
Объединение множеств
и
состоит из точек, координаты которых удовлетворяют совокупности уравнений
равносильной одному уравнению, например:
.
Включение с алгебраической точки зрения означает, что уравнение
является следствием уравнения
, то есть
Равенство означает, что уравнения
и
равносильны (эквивалентны), то есть
В частности, равносильные уравнения, описывающие одно и то же геометрическое место точек, получаются при тождественных алгебраических преобразованиях равенств, например, при умножении обеих частей уравнения на отличное от нуля число, при приведении подобных членов, при переносе членов из одной части уравнения в другую с изменением знака на противоположный и т.п.
Полученные соотношения, сводящие операции с множествами на плоскости к алгебраическим операциям с уравнениями этих геометрических мест точек, не зависят от выбора системы координат. Например, в прямоугольной системе координат аналогичные соотношения получаем, полагая
и
, а в полярной системе координат
при
и
.
Параметрические уравнения геометрических мест точек
Функциональная зависимость между координатами точек плоскости, например в прямоугольной системе координат , может быть задана в параметрической форме, в которой обе координаты выражаются в виде функций вспомогательной переменной, называемой параметром:
(3.3)
где — параметр, принимающий действительные значения. Систему (3.3) называют параметрическим уравнением геометрического места точек.
Пример 3.4. Изобразить на координатной плоскости (в прямоугольной системе координат) множества точек, координаты которых удовлетворяют следующим параметрическим уравнениям:
Решение. 1) Исключим из заданной системы уравнений параметр . Возведя обе части каждого уравнения в квадрат и сложив почленно результаты, получим уравнение окружности
(см. пример 3.1 ,г). Параметром
служит величина угла поворота радиус-вектора изображающей точки, измеряемого от положительного направления оси абсцисс (рис.3.4,а).
2) Уравнения задают циклоиду — линию, которую описывает точка, принадлежащая окружности при качении этой окружности (без проскальзывания) по прямой (оси абсцисс). Построение одной арки циклоиды выполняется по точкам при . Затем эта арка «переносится» вдоль оси абсцисс (рис.3.4,б). Параметром
служит величина угла поворота радиуса катящейся окружности.
3) Уравнения задают астроиду (гипоциклоиду) — линию, которую описывает точка, принадлежащая окружности при качении этой окружности (без проскальзывания) по другой неподвижной окружности, касаясь ее внутренним образом. Астроида и обе окружности изображены на рис.3.4,в (астроида полужирной линией, неподвижная окружность сплошной, а подвижная — штриховой). Построение выполняется по точкам при , а затем продолжается симметрично координатным осям.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Содержание:
Множества:
Под множеством X = {х, х х», …} понимается собрание (совокупность) некоторых элементов х, х х’ … . Если х есть элемент множества X, то пишут х € X (читается: х принадлежит X); если у не является элементом множества X, то пишут у t X (читается: у не принадлежит множеству X).
Пример:
X — множество всех студентов в данной аудитории.
Пример:
Х = {1,2, 3, …} — множество натуральных чисел.
Удобно ввести понятие пустого множества
Пример:
Множество трехголовых людей пусто.
Множества X и X’ считаются равными, т. е. X = X’, если они состоят из одних и тех же элементов.
Определение: Множество У, состоящее из части элементов множества X или совпадающее с ним, называется подмножеством множества X; в этом случае пишут
Условились считать, что пустое множество есть подмножество любого множества.
Если множества изображать «логическими фигурами», то соотношению (1) соответствует рис. 10.
Если под символом V понимать «для любого», то соотношение (1) эквивалентно следующему:
где стрелка 
Пример:
Пусть X — множество всех студентов первого курса, У — множество студенток первого курса. Очевидно,
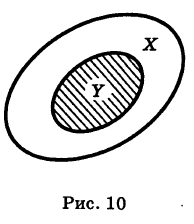
Определение: Под объединением (суммой) двух множеств X и Y понимается множество X U У (U — знак объединения), состоящее из всех элементов, принадлежащих хотя бы одному из данных множеств, т. е. входящих или в X, или в У, или в X и в У одновременно (рис. 11).
Аналогично определяется объединение большего числа множеств. Так, под объединением X U У U Z трех множеств понимается множество всех элементов, принадлежащих хотя бы одному из множеств X, У, Z. Логически знак объединения множеств соответствует союзу «или» (соединительному).
Например: {1, 2, 3} U {2, 3, 4} — {1, 2, 3, 4}.
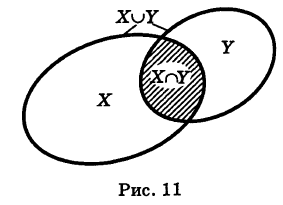
Определение: Под пересечением (произведением) двух множеств X и У понимается множество 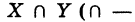
Таким образом, знак пересечения множеств логически соответствует союзу «и». Если множества X и У не имеют общих элементов, то их пересечение пусто:
Аналогично определяется пересечение большего числа множеств. Так, под пересечением 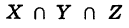
Например: {1, 2, 3} 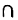
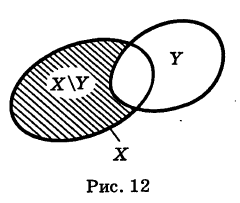
Определение: Для множеств X и У под их разностью ХУ понимается множество, содержащее все элементы множества X, не входящие в множество У (рис. 12).
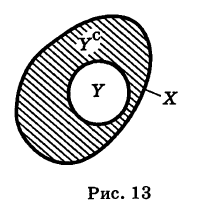
Если У X, то множество Ус = ХУ называется дополнением множества У до множества X (рис. 13).
Очевидно, 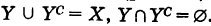
Например: {1, 2, 3}{2, 3, 4} = {1}.
Метод координат на плоскости
Раздел математики, занимающийся изучением свойств геометрических фигур с помощью алгебры, носит название аналитической геометрии, а использование для этой цели координат называется методом координат.
Выше мы применили метод координат для решения ряда важных, но частных задач. Теперь мы приступим к систематическому изложению того, как в аналитической геометрии решается общая задача, состоящая в исследовании методами математического анализа формы, расположения и свойств данной линии.
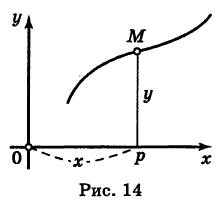
Пусть мы имеем некоторую линию на плоскости (рис. 14). Координаты х и у точки М, лежащей на этой линии, не могут быть вполне произвольными; они должны быть подчинены известным ограничениям, обусловленным геометрическими свойствами данной линии. Тот факт, что числа х и у являются координатами точки, лежащей на данной линии, аналитически записывается в виде некоторого уравнения. Это уравнение называется уравнением линии на плоскости.
Сущность метода координат на плоскости заключается в том, что всякой плоской линии сопоставляется ее уравнение1*, а затем свойства этой линии изучаются путем аналитического исследования соответствующего уравнения.
Линия как множество точек
Линия на плоскости обычно задается как множество точек, обладающих некоторыми геометрическими свойствами, исключительно им присущими.
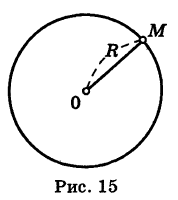
Пример:
Окружность радиуса R (рис. 15) есть множество всех точек плоскости, удаленных на расстояние R от некоторой ее точки О (центр окружности).
Иными словами, на окружности расположены те и только те точки, расстояние которых от центра окружности равно ее радиусу.
Пример:
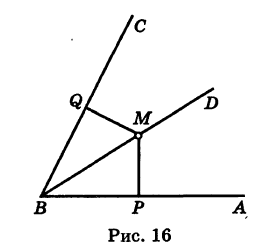
Биссектриса угла ABC (рис. 16) есть множество всех точек, лежащих внутри угла и равноудаленных от его сторон. Этим утверждается, что: 1) для каждой точки М, лежащей на биссектрисе BZ), длины перпендикуляров MP и MQ, опущенных соответственно на стороны ВА и ВС угла, равны между собой: MP = MQ, и 2) всякая точка, находящаяся внутри угла ABC и не лежащая на его биссектрисе, будет ближе к одной стороне угла, чем к другой.
Уравнение линии на плоскости
Сформулируем теперь точнее определение уравнения линии1* на плоскости.
Определение: Уравнением линии (уравнением кривой) на плоскости Оху называется уравнение, которому удовлетворяют координаты х и у каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
Таким образом, для того чтобы установить, что данное уравнение является уравнением некоторой линии К, необходимо и достаточно: 1) доказать, что координаты .любой точки, лежащей на линии К у удовлетворяют этому уравнению, и 2) доказать, обратно, что если координаты некоторой точки удовлетворяют этому уравнению, то точка обязательно лежит на линии К.
Отсюда уже автоматически будет следовать, что: 1′) если координаты какой-нибудь точки не удовлетворяют данному уравнению, то точка эта не лежит на линии К, и 2′) если точка не лежит на линии К, то ее координаты не удовлетворяют данному уравнению.
Если точка М (*, у) передвигается по линии К, то ее координаты х и у, изменяясь, все время удовлетворяют уравнению этой кривой. Поэтому координаты точки М (х, у) называются текущими координатами точки линии К.
На плоскости Оху текущие координаты точки М данной кривой К обычно обозначаются через х и у, причем первая из них есть абсцисса точки М, а вторая — ее ордината. Однако, если это целесообразно, текущие координаты точки М можно обозначать.
Линию мы часто будем называть кривой независимо от того, прямолинейна она или не прямолинейна любыми буквами, например М (X, У) или М 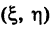
у = 2х и У = 2Х,
где точки N (х, у) и N (X, У) расположены на плоскости Оху, представляют собой уравнение одной и той же прямой на этой плоскости.
Основное понятие аналитической геометрии — уравнение линии — поясним на ряде примеров.
Пример:
Составить уравнение окружности данного радиуса R с центром в начале координат.
Решение:
Возьмем на окружности (рис. 17) произвольную точку М (х, у) и соединим ее с центром О. По определению окружности имеем ОМ = R,
т. е. 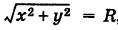
Уравнение (1) связывает между собой координаты х и у каждой точки данной окружности. Обратно, если координаты точки М (х, у) удовлетворяют уравнению (1), то, очевидно, ОМ = R и, следовательно, эта точка лежит на нашей окружности. Таким образом, уравнение (1) представляет собой уравнение окружности радиуса R с центром в начале координат.
Пример:
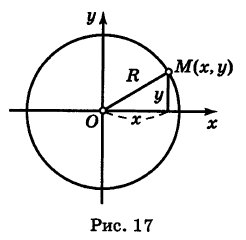
Составить уравнения биссектрис координатных углов.
Решение:
Рассмотрим сначала биссектрису I и III координатных углов (рис. 18, а). Возьмем на ней произвольную точку М (х, у). Если точка М лежит в I квадранте, то абсцисса и ордината ее обе положительны и равны между собой (по свойству биссектрисы). Если же точка М (jc, у) лежит в III квадранте, то абсцисса и ордината будут обе отрицательны, а модули их равны, поэтому будут равны и координаты хм у этой точки. Следовательно, в обоих случаях имеем
Обратно, если координаты х и у какой-нибудь точки М (х, у) удовлетворяют уравнению (2), то эта точка, очевидно, лежит на биссектрисе
I и III координатных углов. Поэтому уравнение (2) представляет собой уравнение биссектрисы I и III координатных углов.
Рассмотрим теперь биссектрису II и IV координатных углов (рис. 18, б). Возьмем на ней произвольную точку N (х, у). В каком бы квадранте — II или IV — ни была расположена эта точка, координаты ее х и у равны по модулю и отличаются знаками.
Следовательно, в обоих случаях имеем
Обратно, если для какой-нибудь точки N (,х, у) выполнено уравнение (3), то эта точка, очевидно, лежит на биссектрисе II и IV координатных углов. Таким образом, уравнение (3) есть уравнение биссектрисы II и IV координатных углов.
Пример:
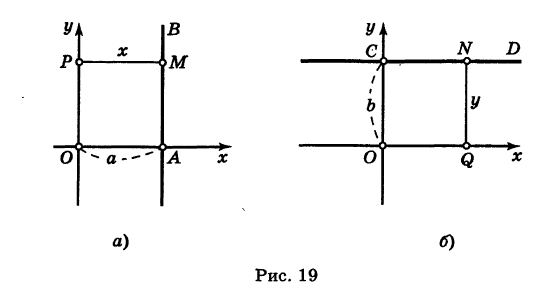
Составить уравнение прямой, параллельной оси ординат.
Решение:
Пусть прямая АВ || О у и пусть отрезок OA = а (рис. 19, а). Тогда для любой точки М (х, у) прямой АВ ее абсцисса х равна а:
х = а. (4)
Обратно, если абсцисса некоторой точки М (х, у) равна а, то эта точка лежит на прямой АВ.
Таким образом, уравнение (4) представляет собой уравнение прямой, параллельной оси Оу и отстоящей от нее на расстоянии, равном числовому значению а; при этом если прямая расположена справа от оси Оу, то а положительно; если же прямая расположена слева от оси Оу, то а отрицательно.
В частности, при а = 0 получаем уравнение оси ординат: х = 0.
Пример:
Составить уравнение прямой, параллельной оси абсцисс.
Решение:
Совершенно аналогично, если прямая CD || Ох и ОС = Ь (рис. 19, б), то ее уравнение будет
при этом если прямая CD расположена выше оси Оху то Ъ положительно, если же прямая CD расположена ниже оси Ох, то b отрицательно.
В частности, при b = 0 получаем уравнение оси абсцисс: у = 0.
Пример:
Найти линию, расстояние точек которой от точки В (12, 16) в два раза больше, чем от точки А (3, 4).
Решение:
Если М (х, у) — произвольная точка искомой линии, то согласно условию задачи имеем
Чтобы составить уравнение этой линии, надо выразить AM и ВМ через координаты х и у точки М. На основании формулы расстояния между двумя точками имеем
откуда, согласно соотношению (5),
Это и есть уравнение искомой линии.
Но в таком виде трудно судить, какую линию представляет это уравнение, поэтому упростим его. Возведя обе части в квадрат и раскрыв скобки, получим
или после несложных преобразований имеем равносильное уравнение
Сравнивая полученное уравнение с уравнением (1), мы видим, что искомая линия является окружностью радиуса 10 с центром в начале координат.
Построение линии по ее уравнению
Если переменные х и у связаны некоторым уравнением, то множество точек М (х, у), координаты которых удовлетворяют этому уравнению, представляет собой, вообще говоря, некоторую линию на плоскости (геометрический образ уравнения).
В частных случаях эта линия может вырождаться в одну или несколько точек. Возможны также случаи, когда уравнению не соответствует никакое множество точек.
Например, уравнению
соответствует единственная точка (1, 2), так как этому уравнению удовлетворяет единственная пара значений: х = 1 и у = 2.
Уравнению
не соответствует никакое множество точек, так как этому уравнению нельзя удовлетворить никакими действительными значениями x и у.
Зная уравнение линии, можно по точкам построить эту линию.
Пример:
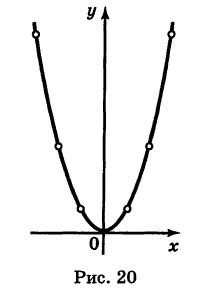
Построить линию, выражаемую уравнением
(обычно говорят короче: построить линию у = х2).
Решение:
Давая абсциссе х в уравнении (1) числовые значения и вычисляя соответствующие значения ординаты у, получим следующую таблицу:
Нанося соответствующие точки на плоскость, мы видим, что конфигурация этих точек определяет начертание некоторой линии; при этом чем гуще построена сеть точек, тем отчетливее выступает ее контур. Соединяя построенные точки линией, характер которой учитывает положение промежуточных точек1*, мы и получаем линию, определяемую данным уравнением (1) (рис. 20). Эта линия называется параболой.
Некоторые элементарные задачи с решением
Если известно уравнение линии, то легко могут быть решены простейшие задачи, связанные с расположением этой линии на плоскости.
Задача 1. Заданы уравнение линии К и координаты точки М (а, Ь). Определить, лежит точка М на линии К или нет.
Иными словами, требуется узнать, проходит линия К через точку М или не проходит.
На основании понятия уравнения линии получаем правило:
чтобы определить, лежит ли точка М на данной линии К, нужно в уравнение этой линии подставить координаты нашей точки. Если при этом уравнение удовлетворится (т. е. в результате подстановки получится тождество), то точка лежит на линии; в противном случае, если координаты точки не удовлетворяют уравнению линии, данная точка не лежит на линии.
Для того чтобы иметь возможность судить о положении промежуточных точек линии, мы должны предварительно изучить общие свойства уравнения этой линии (подробнее см. в гл. XI).
В частном случае линия проходит через начало координат тогда и только тогда, когда уравнение линии удовлетворяется при х = 0 и у — 0.
Пример:
Дана окружность
Определить, лежат ли на ней точки М (-3, 4) и N (4, -2).
Решение:
Подставляя координаты точки М в уравнение (1), получаем тождество
Следовательно, точка М лежит на данной окружности.
Аналогично, подставляя координаты точки N в уравнение (1), будем иметь
Следовательно, точка N не лежит на данной окружности.
Задача 2. Найти точку пересечения двух линий, заданных своими уравнениями.
Точка пересечения одновременно находится как на первой линии, так и на второй. Следовательно, координаты этой точки удовлетворяют уравнениям обеих линий. Отсюда получаем правило:
чтобы найти координаты точки пересечения двух линий, достаточно совместно решить систему их уравнений.
Если эта система не имеет действительных решений, то линии не пересекаются.
Пример:
Найти точки пересечения параболы у = х2 и прямой у — 4.
Решение:
Решая систему
получаем две точки пересечения: А (-2, 4) и В (2, 4).
Задача 3. Найти точки пересечения данной линии с осями координат.
Эта задача является частным случаем задачи 2. Учитывая, что уравнение оси Ох есть у = 0, получаем правило: ‘
чтобы найти абсциссы точек пересечения данной линии с осью Ох, в уравнении этой линии нужно положить у = 0 и решить полученное уравнение относительно х.
Аналогично, так как уравнение оси Оу есть х — 0, то получаем правило:
чтобы найти ординаты точек пересечения данной линии с осью Оу, нужно в уравнении этой линии положить д: = 0 и решить полученное уравнение относительно у.
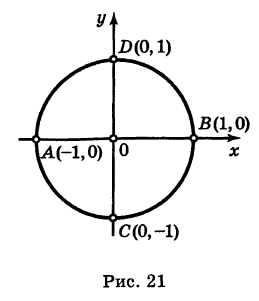
Пример:
Найти точки пересечения окружности 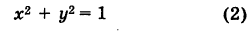
Решение:
Полагая у = 0 в уравнении (2), получаем х2= 1, т. е. х1 = -1 и х2 = 1. Отсюда находим две точки пересечения данной окружности с осью Ох (рис. 21): А (-1, 0) и В (1, 0).
Аналогично, полагая х = 0 в уравнении (2), получаем у2 = 1, т. е. ух = -1 и у2 = 1. Следовательно, имеются две точки пересечения данной окружности с осью Оу (рис. 21): С (0, -1) и D (0, 1).
Две основные задачи аналитической геометрии на плоскости
Резюмируя содержание этой главы, можно сказать, что всякой линии на плоскости соответствует некоторое уравнение между текущими координатами (х, у) точки этой линии. Наоборот, всякому уравнению между х и г/, где х и у — координаты точки на плоскости, соответствует, вообще говоря, некоторая линия, свойства которой вполне определяются данным уравнением.
Отсюда, естественно, возникают две основные задачи аналитической геометрии на плоскости.
Задача 1 .Дана линия, рассматриваемая как множество точек. Составить уравнение этой линии.
Задача 2. Дано уравнение некоторой линии. Изучить по этому уравнению ее геометрические свойства (форму и расположение).
Алгебраические линии
Определение: Линия называется линией (или кривой) n-го порядка(п = 1, 2,…), если она определяется уравнением п-й степени относительно текущих прямоугольных координат.
Такие линии называются алгебраическими. Например, линии
являются кривыми соответственно первого, второго и третьего порядков.
Общий вид кривых первого порядка есть
Ах + By + С = О,
где коэффициенты А и Б не равны нулю одновременно, т. е. 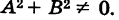
Общий вид кривых второго порядка следующий:
где коэффициенты А, Б и С не равны нулю одновременно, т. е.
Заметим, что не всякому уравнению второго порядка соответствует действительная кривая. Например, уравнению 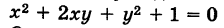
В следующих главах мы подробно изучим кривую первого порядка (прямую линию) и рассмотрим важнейшие представители кривых второго порядка (окружность, эллипс, гипербола, парабола).
Уравнение кривой n-го порядка может быть записано в следующем виде:
где хотя бы один из старших коэффициентов apqt т. е. таких, что p + q = п, отличен от нуля (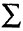
Отметим важное свойство: порядок кривой (1) не зависит от выбора прямоугольной системы координат.
Действительно, выбирая другую систему прямоугольных координат О’х’уна основании формул перехода имеем
где 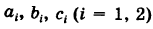
Отсюда уравнение кривой (1) в новых координатах О’х’у’ будет иметь вид
где п’ — порядок преобразованной кривой. Очевидно, что п’ < п. Аналогично, исходя из уравнения (3) и совершая обратный переход от координат х’, у’ к координатам х, у, получим уравнение (1), в котором п < п, следовательно,
Определение уравнения линии на плоскости
Уравнение линии является важнейшим понятием аналитической геометрии.
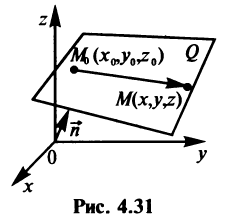
Пусть мы имеем на плоскости некоторую линию (кривую) (рис. 4.1). Координаты 
Определение. Уравнением линии (кривой) на плоскости 
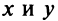
В общем случае уравнение линии может быть записано в виде 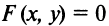
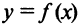
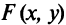
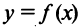
Если точка 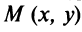
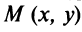
Пример:
Найти уравнение множества точек, равноудаленных от точек
Решение:
Расстояние между двумя точками 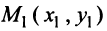
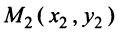
Если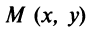
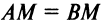
Возведя обе части уравнения в квадрат, получим после преобразований уравнение 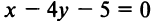
Очевидно, это уравнение прямой 
Любую линию в принципе можно выразить соответствующим уравнением (хотя на практике это не всегда просто сделать). Однако не всякое уравнение определяет на плоскости некоторую линию.
Например, уравнение 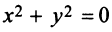
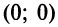
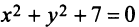
Чтобы убедиться, лежит ли точка 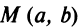
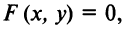
Уравнение прямой
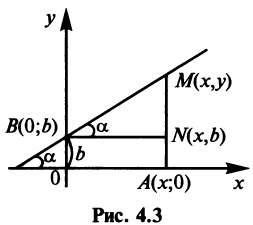
Пусть прямая пересекает ось 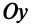
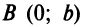
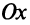
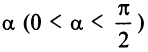
Возьмем на прямой произвольную точку 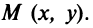
Введем угловой коэффициент прямой 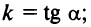
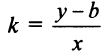
Можно показать, что формула (4.2) остается справедливой и для случая
Итак, мы доказали, что координаты каждой точки прямой удовлетворяют уравнению (4.2). Нетрудно показать, что координаты любой точки, не лежащей на прямой, не удовлетворяют уравнению (4.2).
Уравнение (4.2) называется уравнением прямой с угловым коэффициентом.
Рассмотрим частные случаи уравнения (4.2).
- Если
то получаем
— уравнение прямой, проходящей через начало координат и образующей при
острый угол
с осью
а при
— тупой угол (см. рис. 4.4). В частности, уравнение биссектрисы I и III координатных углов имеет вид
(так как
), а уравнение биссектрисы II и IV координатных углов
- Если
, то
, и уравнение прямой, параллельной оси
, имеет вид
, а самой оси
— вид
(см. рис. 4.5).
- Если
, то прямая перпендикулярна оси
(см.рис. 4.6) и
— не существует, т.е. вертикальная прямая не имеет углового коэффициента. Предположим, что эта прямая отсекает на оси
отрезок, равный
Очевидно, что уравнение такой прямой
(так как абсцисса любой точки прямой равна а), а уравнение оси
есть
.
Уравнение прямой, проходящей через данную точку в данном направлении
Пусть прямая проходит через точку 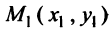
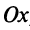
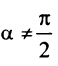
Так как точка 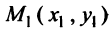
Вычитая равенство (4.3) из равенства (4.2), получим уравнение искомой прямой
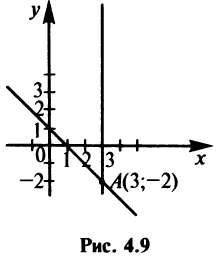
Уравнение пучка прямых. Если в уравнении (4.4) 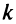
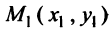
Пример:
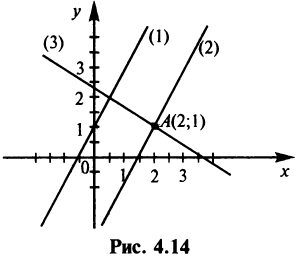
Составить уравнение прямой проходящей через точку А (3;-2): а) под углом 135° к оси 
Решение:
1. а) угловой коэффициент прямой
Уравнение прямой, проходящей через точку А (3; -2) (см. рис. 4.9), по формуле (4.4) имеет вид у + 2 = -1 (х —3) или у = -х + 1
б) Уравнение прямой, параллельной оси 
2. Уравнение пучка прямых, проходящих через точку А (3;-2), имеет вид
у + 2 = к (х -3).
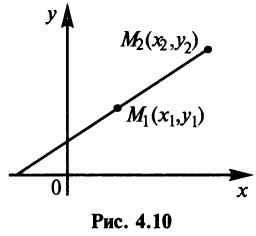
Уравнение прямой, проходящей через две данные точки
Пусть даны две точки
Для составления уравнения прямой 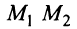
Так как точка 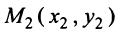
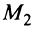
и найдем угловой коэффициент прямой
Теперь уравнение искомой прямой примет вид
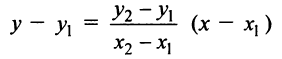
Пример:
Составить уравнение прямой, проходящей через точки 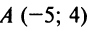
Решение:
По уравнению (4.6): 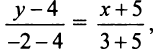
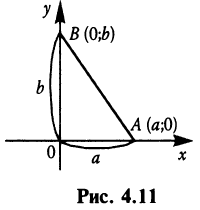
Уравнение прямой в отрезках
Найдем уравнение прямой по заданным отрезкам 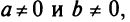
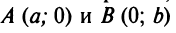
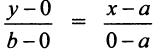
Уравнение (4.7) называется уравнением прямой в отрезках.
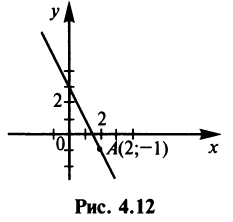
Пример:
Составить уравнение прямой, проходящей через точку А (2; —1), если эта прямая отсекает от положительной полуоси 
Решение:
По условию 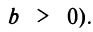
Так как точка А (2; —1) лежит на прямой, то ее координаты удовлетворяют этому уравнению, т.е. 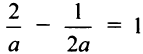
Итак, уравнение искомой прямой имеет вид 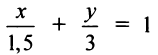
Общее уравнение прямой и его исследование
Рассмотрим уравнение первой степени с двумя переменными в общем виде
в котором коэффициенты 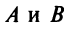
1. Пусть 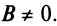
Обозначим 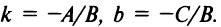
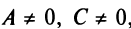
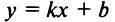
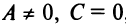
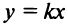
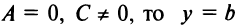
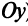
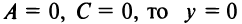
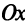
2.Пусть 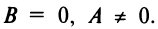
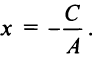
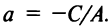
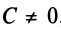
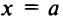
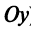
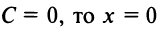
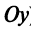
Таким образом, при любых значениях коэффициентов 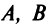
Уравнение (4.8) называется общим уравнением прямой. Заметим, что в отличие от уравнения пучка прямых (4.4) общее уравнение (4.8) включает и уравнение любой вертикальной прямой, параллельной оси 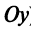
Угол между двумя прямыми
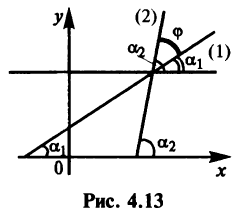
Пусть заданы две прямые
и требуется определить угол 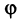
Из рис. 4.13 видно, что 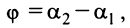
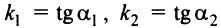
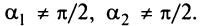
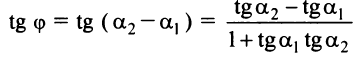
где стрелка означает, что угол 
Условия параллельности и перпендикулярности прямых
Если прямые 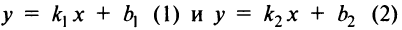
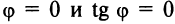
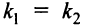
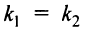
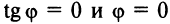
Если прямые перпендикулярны, то 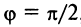
или 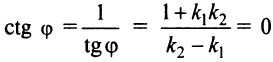
или 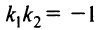
Если прямые заданы общими уравнениями 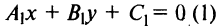
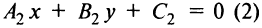
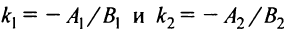

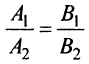
Условие перпендикулярности прямых 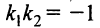
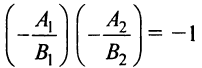
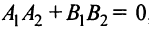
Пример:
Составить уравнения двух прямых, проходящих через точку 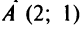
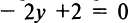
Решение:
Уравнение пучка прямых, проходящих через точку 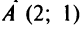
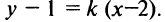
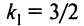
в виде 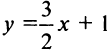
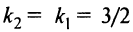
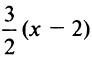
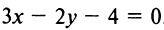
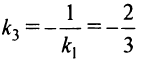
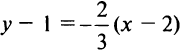
Задачу можно решить и другим способом. Прямая 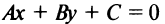
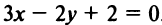
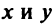
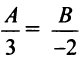
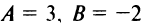
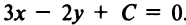
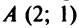
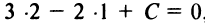
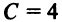
Уравнение прямой, перпендикулярной данной 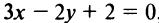
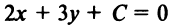
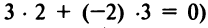
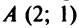
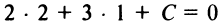
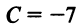
Точка пересечения прямых
Пусть даны две прямые 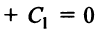
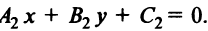
Если прямые не параллельны, т.е.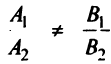
Расстояние от точки до прямой
Пусть даны точка 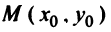
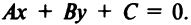
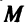
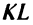
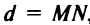
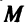
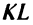
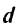
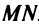
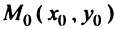
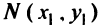
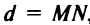
(доказательстю формулы (4.10) опускаем).
Пример:
Найти расстояние между параллельными прямыми
Решение:
Возьмем на одной из прямых, например прямой 
Тогда искомое расстояние равно расстоянию от точки 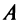
Окружность, эллипс и линия
Изучение кривых второго порядка, описываемых уравнениями второй степени с двумя переменными, начнем с окружности.
Пусть дана окружность радиуса 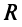
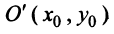
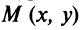
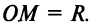
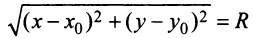
Итак, координаты каждой точки окружности 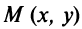
Уравнение (4.11) называется нормальным уравнением окружности. В частности, уравнение окружности с центром в начале координат 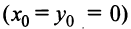
Рассмотрим уравнение второй степени с двумя переменными в общем виде
в котором 
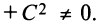
Чтобы уравнения (4.13) и (4.14) представляли одну и ту же линию, коэффициент 
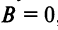
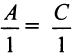
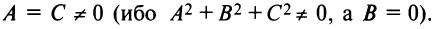
называемое общим уравнением окружности.
Поделив обе части уравнения на 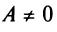
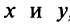
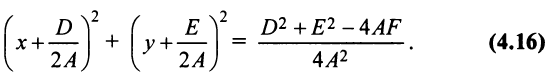
1)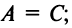
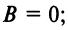
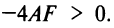
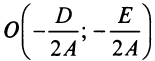
Пример:
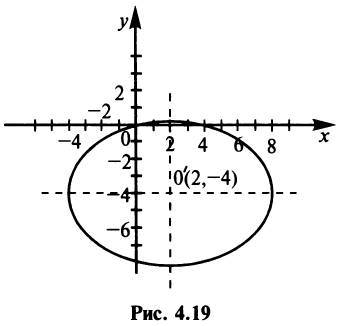
Найти координаты центра и радиус окружности
Решение:
Дополнив члены, содержащие 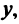
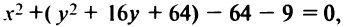
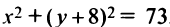
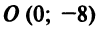
Рассмотрим уравнение кривой второго порядка (4.13), в котором по-прежнему будем полагать 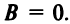
или
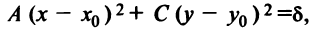
Будем предполагать для простоты исследования, что центр кривой находится в начале координат, т.е. 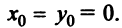
Кривая второго порядка (4.17) называется эллипсом (точнее кривой эллиптического типа), если коэффициенты 
Для определенности будем полагать, что 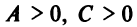
Возможны три случая:
Очевидно, что в третьем случае (при 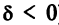
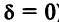
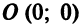
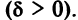
называется каноническим уравнением эллипса с полуосями 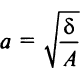
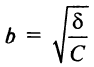
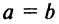
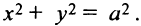
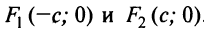
его эксцентриситетом. Эксцентриситет характеризует форму эллипса. Очевидно, что 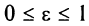
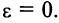
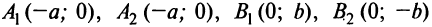
Найдем сумму расстояний от любой точки эллипса 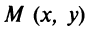
Аналогично можно получить, что 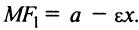
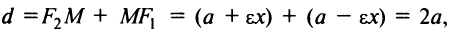
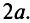
- Заказать решение задач по высшей математике
Пример:
Определить вид и расположение кривой
Решение:
Так как 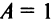
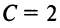
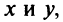
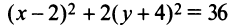
Следовательно, кривая (4.21) представляет эллипс с полуосями 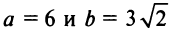
Гипербола и парабола
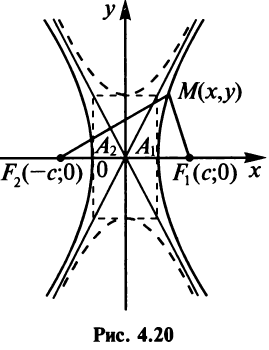
Кривая второго порядка (4.17) называется гиперболой (точнее кривой гиперболического типа), если коэффициенты 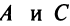
Пусть для определенности 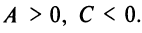
В первом случае (при 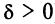
где 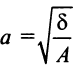
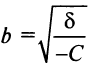
Фокусы гиперболы — точки 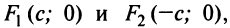
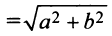
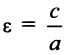
Можно показать (аналогично тому, как мы поступали при исследовании эллипса), что для любой точки гиперболы абсолютная величина разности ее расстояний до фокусов есть величина постоянная, равная 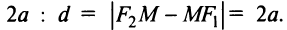
Перепишем уравнение гиперболы (4.21) в виде
При достаточно больших 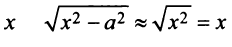
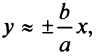

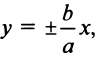
Для равносторонней гиперболы 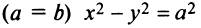
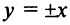
Во втором случае (при 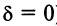
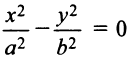
В третьем случае (при 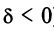
с полуосями 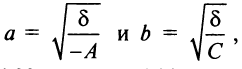
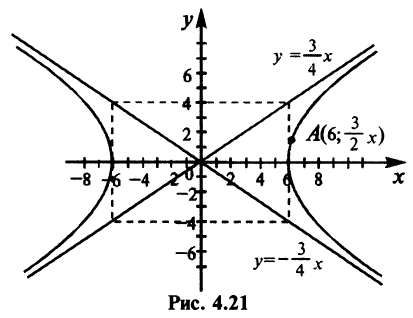
Пример:
Написать уравнение гиперболы с асимптотами 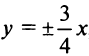
Решение:
Так как точка (6; 3/2) лежит на гиперболе, то ее координаты должны удовлетворять уравнению (4.22) 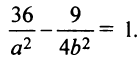
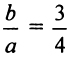
асимптоты гиперболы 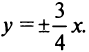
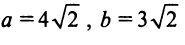
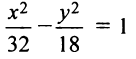
Рассмотрим обратную пропорциональную зависимость, задаваемую уравнением 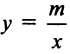
Выбрав в качестве новых осей 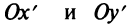
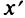
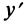
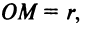
так как из 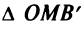
Теперь уравнение (4.24) в новой системе координат 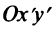
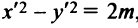
При 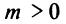
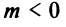
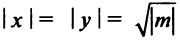
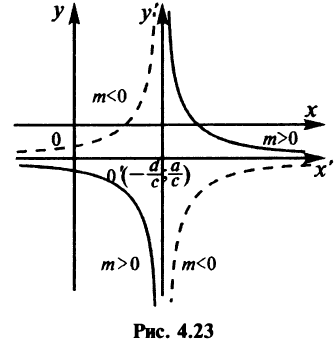
Рассмотрим график дробно-линейной функции
где
Преобразуя (4.25), получим
Введем новые координаты
Обозначим 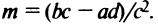
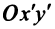
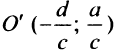
Итак, график дробно-линейной функции (4.25) есть равносторонняя гипербола с асимптотами 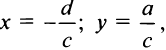
Пример:
Найти координаты центра, вершин и уравнения асимптот гиперболы
Решение:
Преобразуем уравнение, выделив целую часть дробно-линейной функции:
или 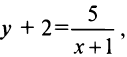
Полагая 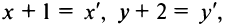
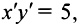
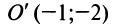
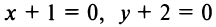
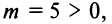
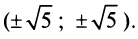
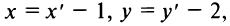
Пусть в уравнении кривой второго порядка (4.13)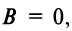
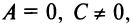
Пусть также 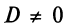
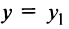
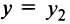
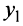
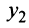
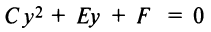
Полагая 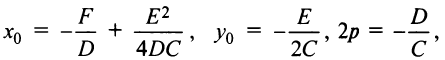
Кривая (4.27) называется параболой, а точка 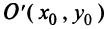
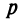
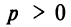
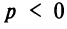
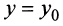
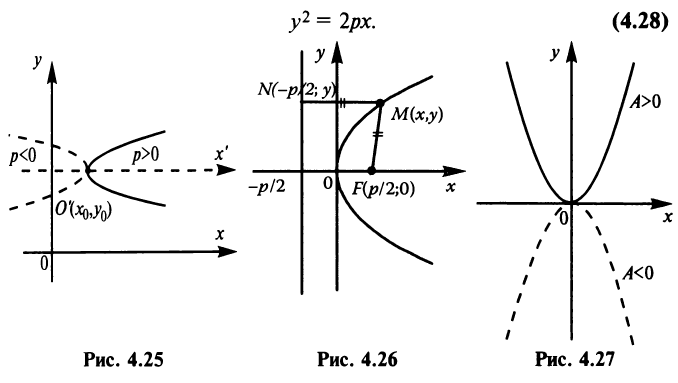
Если вершина параболы находится в начале координат, то уравнение (4.27) принимает вид
Точка 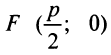
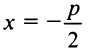
Для произвольной точки 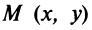
(так как 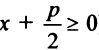
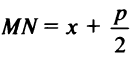
Таким образом, парабола представляет множество всех точек плоскости, равноотстоящих от данной тонки (фокуса) 
Если в уравнении (4.28) поменять местами 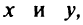
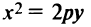
обычно записывают в виде 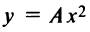
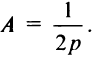
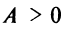
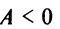
Отсюда 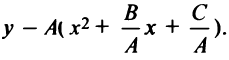
в скобках, до полного квадрата, получим
Обозначив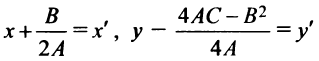
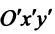
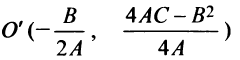
Таким образом, график квадратного трехчлена 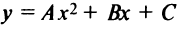
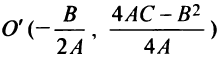
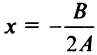
Пример:
Построить кривую
Решение:
Вынося коэффициент при 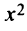
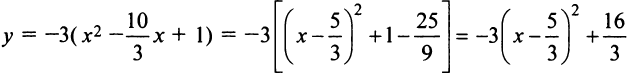
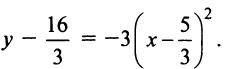
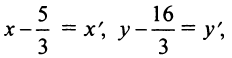
Таким образом, заданная кривая есть парабола с вершиной в точке 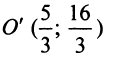
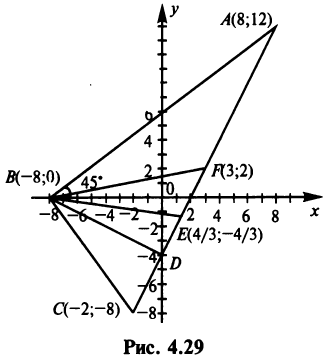
Пример:
Даны уравнения сторон треугольника
Составить уравнение высоты, медианы и биссектрисы, проведенных из вершины 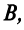
Решение:
1. Найдем координаты вершин треугольника, решив соответствующие системы уравнений сторон. Так, координаты вершины 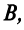
откуда
Аналогично находим координаты вершин 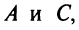
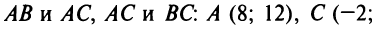
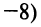
2. Пучок прямых, проходящих через точку 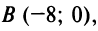
Из уравнения прямой 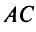
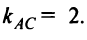
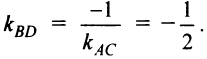
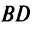
3. Из школьного курса математики известно, что координаты середины отрезка равны полусуммам соответствующих координат его концов, т.е.
Поэтому
По формуле (4.5) угловой коэффициент
Подставляя 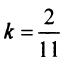
(уравнение 
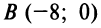
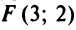
4. Из уравнений прямых 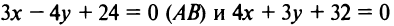
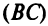
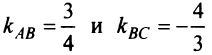
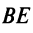
откуда 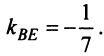
(Если «не заметить», что 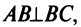
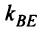
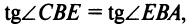
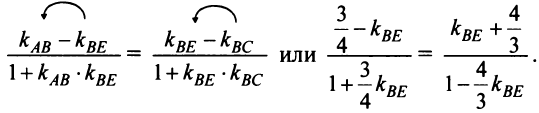
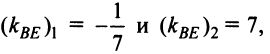
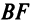
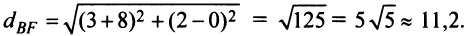
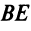
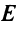
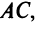
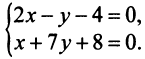
Теперь по формуле (3.5)
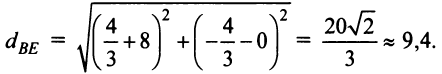
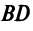
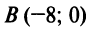
Пример:
Найти расстояние от начала координат до прямой, проходящей через центр гиперболы 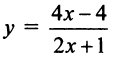
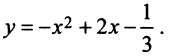
Решение:
1. В уравнении гиперболы выделим целую часть; получим
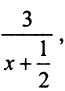
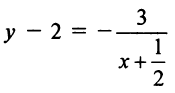
Полагая 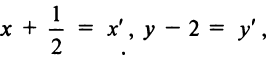
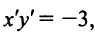
2. Выделив полный квадрат, представим уравнение параболы в виде
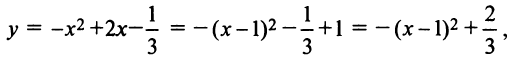
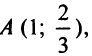
3. Составляем уравнение прямой 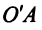
4. Находим расстояние от точки 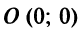
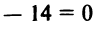
5. Очевидно, что центр искомой окружности должен совпасть с центром гиперболы 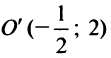
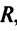
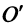
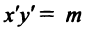
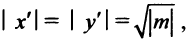
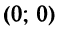
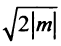
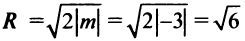
Понятие об уравнении плоскости и прямой в пространстве
Общее уравнение плоскости. Пусть плоскость 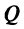
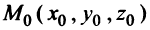
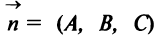
Этими условиями определяется единственная плоскость в пространстве 
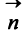
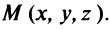
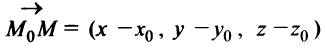
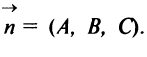
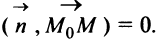
Уравнение (4.31) представляет уравнение плоскости, перпендикулярной данному вектору 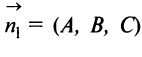
Уравнение плоскости, записанное в виде
(где 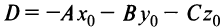
Можно доказать, что всякое уравнение первой степени с тремя переменными есть уравнение плоскости.
Если 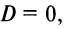
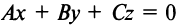
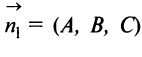
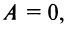
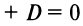
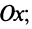
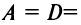
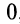
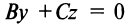
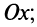
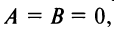
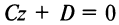
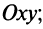
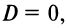
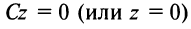
Условия параллельности и перпендикулярности плоскостей определяются условиями коллинеарности и перпендикулярности нормальных векторов
Условием параллельности двух плоскостей является пропорциональность коэффициентов при одноименных переменных
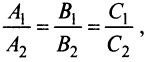
Прямая в пространстве может быть задана как линия пересечения двух плоскостей, т.е. как множество точек, удовлетворяющих системе
Если прямая параллельна вектору
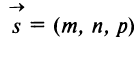
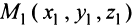
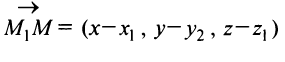
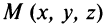
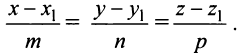
Эти уравнения называются каноническими уравнениями прямой линии в пространстве.
Уравнения прямой линии в пространстве
Прямая в пространстве однозначно определяется точкой 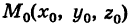
Пусть 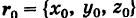
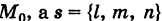
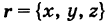
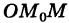
Так как векторы 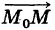
где 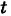
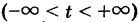
(t — параметр).
Проецируя равенство (3) на координатные оси, будем иметь параметрические уравнения прямой линии в пространстве
Если из уравнений (4) исключить параметр то получим так называемые канонические уравнения прямой линии в пространстве
Система (5) содержит два уравнения, например при 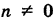
Эти уравнения представляют собой уравнения двух плоскостей, пересечением которых является данная прямая. Заметим, что первое уравнение не содержит координаты у, а второе — координаты х. Следовательно, первая плоскость параллельна оси Оу, а вторая параллельна оси Ох, т.е. эти плоскости являются плоскостями, проецирующими нашу прямую на координатную плоскость Oxz и соответственно на координатную плоскость Oyz.
Числа 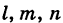
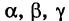
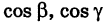
где
— длина вектора s. Отсюда получаем
Таким образом, направляющие коэффициенты прямой пропорциональны соответствующим направляющим косинусам этой прямой.
Уравнения прямой (5) можно записать в стандартном виде
где 
Пример:
Уравнения движения ракеты 
Какова траектория ракеты? На каком расстоянии будет находиться ракета М от точки старта О (0, 0, 0) через 10 с?
Решение:
Исключая из данных уравнений время получим уравнения траектории 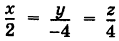
Таким образом, траектория представляет собой прямую линию, проходящую через начало координат.
При f = 10 с имеем х = 20, у = -40, z = 40 и
Пример:
Написать уравнения прямой, проходящей через две несовпадающие точки 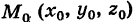
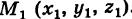
Следовательно, на основании (5) имеем
Пример:
Написать уравнения прямой, проходящей через точку 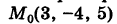
Решение:
Очевидно, имеем 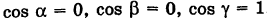
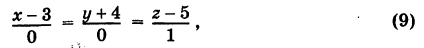
Направляющий вектор прямой (9) есть {0, 0, 1}, т.е. эта прямая перпендикулярна осям Ох и Оу.
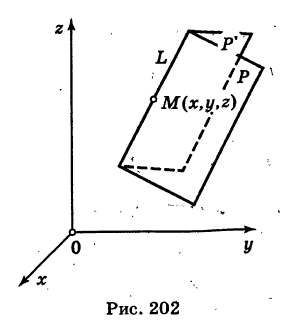
Прямую L в пространстве можно задать также как линию пересечения двух плоскостей Р и Р’ (рис. 202):
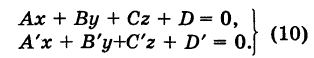
Предполагается, что плоскости не параллельны и не сливаются. Векторы 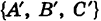
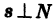
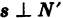
(х — знак векторного произведения.
Пример:
Определить направляющие косинусы прямой
Решение:
Имеем 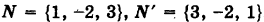
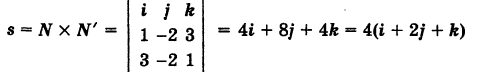
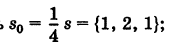
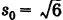
- Функции нескольких переменных
- Комплексные числ
- Координаты на прямой
- Координаты на плоскости
- Числовые ряды
- Знакопеременные ряды
- Степенные ряды
- Элементы матричного анализа

Ответ или решение1
Никитина Валентина
- Допустим, что точка М на координатной плоскости Оху с координатами х (абсцисса) и у (ордината) принадлежит множеству точек, равноудаленных от оси Oy и точки F(4;0). Очевидно, что точка М(х; у) удалена от оси Оу на расстоянии, равного абсциссе этой точки, то есть на х.
- Расстояние МF найдём по формуле вычисления расстояния между двумя точками. Итак, это расстояние равно √((х – 4)² + у²). По условию задания, х = √((х – 4)² + у²). Это равенство является искомым уравнением. Не забывая о том, что значение арифметического корня всегда неотрицательно, возводим в квадрат обе части полученного уравнения и раскроем скобки в правой части. Тогда, имеем: х² = х² — 8 * х + 16 + у², откуда 8 * х = у² + 16.
- Последнее уравнение, как известно, является уравнением параболы.
Ответ: 8 * х = у² + 16.

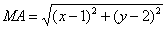
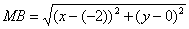
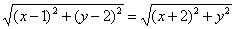
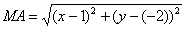
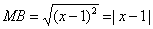
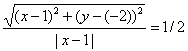
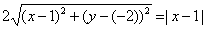

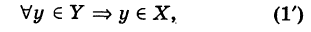
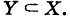
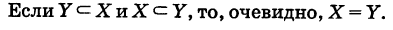
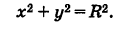


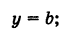

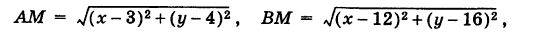
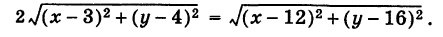
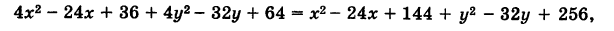
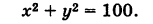
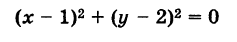
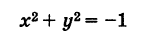



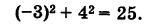
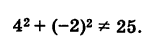
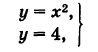
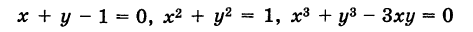
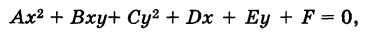
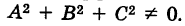
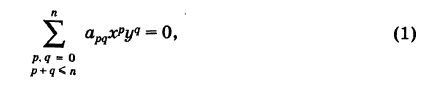
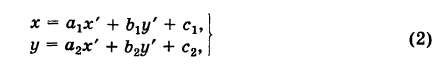
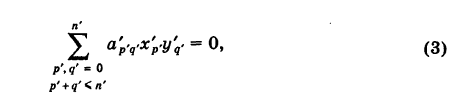
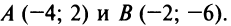
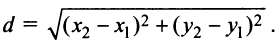
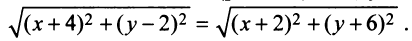
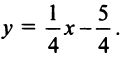
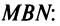
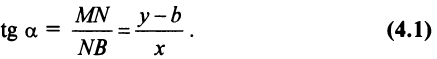

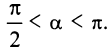
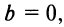 то получаем
то получаем 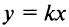 — уравнение прямой, проходящей через начало координат и образующей при
— уравнение прямой, проходящей через начало координат и образующей при 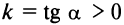 острый угол
острый угол 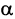 с осью
с осью 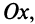 а при
а при 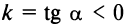 — тупой угол (см. рис. 4.4). В частности, уравнение биссектрисы I и III координатных углов имеет вид
— тупой угол (см. рис. 4.4). В частности, уравнение биссектрисы I и III координатных углов имеет вид 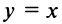 (так как
(так как 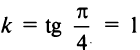 ), а уравнение биссектрисы II и IV координатных углов
), а уравнение биссектрисы II и IV координатных углов 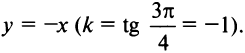
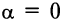 , то
, то 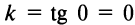 , и уравнение прямой, параллельной оси
, и уравнение прямой, параллельной оси 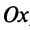 , имеет вид
, имеет вид 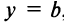 , а самой оси
, а самой оси 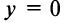 (см. рис. 4.5).
(см. рис. 4.5).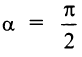 , то прямая перпендикулярна оси
, то прямая перпендикулярна оси 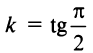 — не существует, т.е. вертикальная прямая не имеет углового коэффициента. Предположим, что эта прямая отсекает на оси
— не существует, т.е. вертикальная прямая не имеет углового коэффициента. Предположим, что эта прямая отсекает на оси 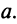 Очевидно, что уравнение такой прямой
Очевидно, что уравнение такой прямой 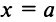 (так как абсцисса любой точки прямой равна а), а уравнение оси
(так как абсцисса любой точки прямой равна а), а уравнение оси 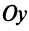 есть
есть 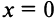 .
.