Как найти уравнение касательной для функции - Autoru.top

п.1. Уравнение касательной

Рассмотрим кривую (y=f(x)).
Выберем на ней точку A с координатами ((x_0,y_0)), проведем касательную AB в этой точке.

Как было показано в §42 данного справочника, угловой коэффициент касательной равен производной от функции f в точке (x_0): $$ k=f'(x_0) $$ Уравнение прямой AB, проведенной через две точки: ((y_B-y_A)=k(x_B-x_A)).
Для (A(x_0,y_0), B(x,y)) получаем: begin{gather*} (y-y_0)=k(x-x_0)\ y=k(x-x_0)+y_0\ y=f'(x_0)(x-x_0)+f(x_0) end{gather*}

Уравнение касательной к кривой (y=f(x)) в точке (x_0) имеет вид: $$ y=f'(x_0)(x-x_0)+f(x_0) $$ при условии, что производная (f'(x_0)=aneinfty) — существует и конечна.

Чтобы записать уравнение касательной с угловым коэффициентом в виде (y=kx+b), нужно раскрыть скобки и привести подобные: $$ y=f'(x_0)(x-x_0)+f(x_0)=underbrace{f'(x_0)}_{=k}x+underbrace{f(x_0)-f'(x_0)cdot x_0}_{=b} $$

Уравнение касательной с угловым коэффициентом: begin{gather*} y=kx+b\ k=f'(x_0), b=f(x_0)-f'(x_0)cdot x_0 end{gather*}

п.2. Алгоритм построения касательной

На входе: уравнение кривой (y=f(x)), абсцисса точки касания (x_0).
Шаг 1. Найти значение функции в точке касания (f(x_0))
Шаг 2. Найти общее уравнение производной (f’ (x))
Шаг 3. Найти значение производной в точке касания (f'(x_0 ))
Шаг 4. Записать уравнение касательной (y=f’ (x_0)(x-x_0)+f(x_0)), привести его к виду (y=kx+b)
На выходе: уравнение касательной в виде (y=kx+b)

Например:

Пусть (f(x)=x^2+3).
Найдем касательную к этой параболе в точке (x_0=1).

(f(x_0)=1^2+3=4 )
(f'(x)=2x )
(f'(x_0)=2cdot 1=2)
Уравнение касательной: $$ y=2(x-1)+4=2x-2+4=2x+2 $$ Ответ: (y=2x+2)

п.3. Вертикальная касательная

В случае, если производная (f'(x_0)=pminfty) — существует, но бесконечна, в точке (x_0) проходит вертикальная касательная (x=x_0).

Внимание!

Не путайте вертикальные касательные с вертикальными асимптотами.
Вертикальная асимптота проходит через точку разрыва 2-го рода (x_0notin D), в которой функция не определена и производная не существует. График функции приближается к асимптоте на бесконечности, но у них никогда не бывает общих точек.
А вертикальная касательная проходит через точку (x_0in D), входящую в область определения. График функции и касательная имеют одну общую точку ((x_0,y_0)).

Вертикальные касательные характерны для радикалов вида (y=sqrt[n]{x}).

Например:

Пусть (f(x)=sqrt[5]{x-1}+1).
Найдем касательную к этой кривой в точке (x_0=1).

(f(x_0)=sqrt[5]{1-1}+1=1)
(f'(x)=frac15(x-1)^{frac15-1}+0=frac15(x-1)^{-frac45}=frac{1}{5(x-1)^{frac45}} )
(f'(x_0)=frac{1}{5(1-1)^{frac45}}=frac10=+infty)
В точке (x_0) проходит вертикальная касательная.
Её уравнение: (x=1)
Ответ: (y=2x+2)

п.4. Примеры

Пример 1. Для функции (f(x)=2x^2+4x)
a) напишите уравнения касательных, проведенных к графику функции в точках его пересечения с осью OX.

Находим точки пересечения, решаем уравнение: $$ 2x^2+4x=0Rightarrow 2x(x+2)=0Rightarrow left[ begin{array}{l} x=0\ x=-2 end{array} right. $$ Две точки на оси: (0;0) и (-2;0).
Касательная в точке (x_0=0): begin{gather*} f(x_0)=0, f'(x)=4x+4\ f'(x_0)=4cdot 0+4=4\ y=4(x-0)+0=4x end{gather*} Касательная в точке (x_0=-2): begin{gather*} f(x_0)=0, f'(x)=4x+4\ f'(x_0)=4cdot (-2)+4=-4\ y=-4(x+2)+0=-4x-8 end{gather*}

б) Найдите, в какой точке касательная образует с положительным направлением оси OX угол 45°. Напишите уравнение этой касательной.

Общее уравнение касательной: (f'(x)=4x+4)
По условию (f'(x_0)=tgalpha=tg45^circ=1)
Решаем уравнение: $$ 4x_0+4=1Rightarrow 4x_0=-3Rightarrow x_0=-frac34 $$ Точка касания (x_0=-frac34) begin{gather*} f(x_0)=2cdotleft(-frac34right)^2+4cdotleft(-frac34right)=frac98-3=-frac{15}{8} end{gather*} Уравнение касательной: begin{gather*} y=1cdotleft(x+frac34right)-frac{15}{8}=x-frac98 end{gather*}

в) найдите, в какой точке касательная будет параллельна прямой (2x+y-6=0). Напишите уравнение этой касательной.

Найдем угловой коэффициент заданной прямой: (y=-2x+6Rightarrow k=-2).
Касательная должна быть параллельной, значит, её угловой коэффициент тоже (k=-2). Получаем уравнение: begin{gather*} f'(x_0)=-2\ 4x_0+4=-2Rightarrow 4x_0=-6Rightarrow x_0=-frac32 end{gather*} Точка касания (x_0=-frac32) begin{gather*} f(x_0)=2cdotleft(-frac32right)^2+4cdotleft(-frac32right)=\ =frac92-6=-frac32 end{gather*} Уравнение касательной: begin{gather*} y=-2cdotleft(x+frac32right)-frac32=-2x-frac92 end{gather*} Или, в каноническом виде: begin{gather*} 2x+y+frac92=0 end{gather*}

г) в какой точке функции можно провести горизонтальную касательную? Напишите уравнение этой касательной.

У горизонтальной прямой (k=0).
Получаем уравнение: (f'(x_0)=0). begin{gather*} 4x_0+4=0Rightarrow 4x_0=-4Rightarrow x_0=-1 end{gather*} Точка касания (x_0=-1) begin{gather*} f(x_0)=2cdot(-1)^2+4cdot(-1)=-2 end{gather*} Уравнение касательной: begin{gather*} y=0cdot(x+1)-2=-2 end{gather*}

Ответ: а) (y=4x) и (y=-4x-8); б) (y=x-frac98); в) (2x+y+frac92=0); г) (y=-2)

Пример 2. Напишите уравнение касательной к графику функции в заданной точке:
a) ( f(x)=frac5x+frac x5, x_0=4 ) begin{gather*} f(x_0)=frac54+frac45=frac{25+16}{20}=frac{41}{20}\ f'(x)=left(frac5xright)’+left(frac x5right)’=-frac{5}{x^2}+frac15=frac{-25+x^2}{5x^2}=frac{x^2-25}{5x^2}\ f'(x_0)=frac{4^2-25}{5cdot 4^2}=-frac{9}{80} end{gather*} Уравнение касательной: $$ y=-frac{9}{80}(x-4)+frac{41}{20}=-frac{9}{80}x+frac{9}{20}+frac{41}{20}=-frac{9}{80}x+2,5 $$
б) ( f(x)=frac{x^2+5}{3-x}, x_0=2 ) begin{gather*} f(x_0)=frac{2^2+5}{3-2}=frac91=9\ f'(x)=frac{(x^2+5)'(3-x)-(x^2+5)(3-x)’}{(3-x)^2}=frac{2x(3-x)+(x^2+5)}{(3-x)^2}=\ =frac{6x-2x^2+x^2+5}{(3-x)^2}=frac{-x^2+6x+5}{(3-x)^2}\ f'(x_0)=frac{-2^2+6cdot 2+5}{(3-2)^2}=13 end{gather*} Уравнение касательной: $$ y=13(x-2)+9=13x-26+9=13x-17 $$

Пример 3*. Найдите точку, в которой касательная к графику функции (f(x)=frac{x^2+2}{x+3}-x) перпендикулярна прямой (y=11x+3). Напишите уравнение этой касательной.

Угловой коэффициент данной прямой (k_1=11).
Угловой коэффициент перпендикулярной прямой (k_2=-frac{1}{k_1}=-frac{1}{11}) begin{gather*} f'(x)=left(frac{x^2+2}{x+3}right)’-x’=frac{2x(x+3)-(x^2+2)cdot 1}{(x+3)^2}-1=frac{2x^2+6x-x^2-2-(x+3)^2}{(x+3)^2}=\ =frac{x^2+6x-2-x^2-6x-9}{(x+3)^2}=- frac{11}{(x+3)^2} end{gather*} В точке касания: begin{gather*} f'(x_0)=k_2Rightarrow=-frac{11}{(x+3)^2}=-frac{1}{11}Rightarrow (x+3)^2=121Rightarrow (x+3)^2-11^2=0Rightarrow\ Rightarrow (x+14)(x+8)=0Rightarrow left[ begin{array}{l} x=-14\ x=8 end{array} right. end{gather*}
Уравнение касательной при (x_0=-14) begin{gather*} f(x_0)=frac{(-14)^2+2}{-14+3}+14=frac{198}{-11}+14=-18+14=-4\ y=-frac{1}{11}(x+14)-4=-frac{x+58}{11} end{gather*} Уравнение касательной при (x_0=8) begin{gather*} f(x_0)=frac{8^2+2}{8+3}-8=frac{66}{11}-8=-2\ y=-frac{1}{11}(x-8)-2=-frac{x+14}{11} end{gather*}
Ответ: точка касания (-14;-4), уравнение (y=-frac{x+58}{11})
и точка касания (8;-2), уравнение (-frac{x+14}{11})

Пример 4*. Найдите уравнения общих касательных к параболам (y=x^2-5x+6) и (y=x^2+x+1). Укажите точки касания.

Найдем производные функций: begin{gather*} f_1′(x)=2x-5, f_2′(x)=2x+1 end{gather*} Пусть a – абсцисса точки касания для первой параболы, b — для второй.
Запишем уравнения касательных (g_1(x)) и (g_2(x)) через эти переменные. begin{gather*} g_1(x)=f_1′(a)(x-a)+f_1(a)=(2a-5)(x-a)+a^2-5a+6=\ =(2a-5)x-2a^2+5a+a^2-5a+6=(2a-5)x+(6-a^2)\ \ g_2(x)=f_2′(b)(x-b)+f_2(b)=(2b+1)(x-b)+b^2+b+1=\ =(2b+1)x-2b^2-b+b^2+b+1=(2b+1)x+(1-b^2) end{gather*} Для общей касательной должны быть равны угловые коэффициенты и свободные члены. Получаем систему уравнений: begin{gather*} begin{cases} 2a-5=2b+1\ 6-a^2=1-b^2 end{cases} Rightarrow begin{cases} 2(a-b)=6\ a^2-b^2=5 end{cases} Rightarrow begin{cases} a-b=3\ (a-b)(a+b)=5 end{cases} Rightarrow begin{cases} a-b=3\ a+b=frac53 end{cases} Rightarrow \ Rightarrow begin{cases} 2a=3+frac53\ 2b=frac53-3 end{cases} Rightarrow begin{cases} a=frac73\ b=-frac23 end{cases} end{gather*} Находим угловой коэффициент и свободный член из любого из двух уравнений касательных: $$ k=2a-5=2cdotfrac73-5=-frac13, b=6-a^2=6-frac{49}{9}=frac59 $$ Уравнение общей касательной: $$ y=-frac x3+frac59 $$
Точки касания: begin{gather*} a=frac73, f_1(a)=left(frac73right)^2-5cdotfrac73+6=frac{49}{9}-frac{35}{3}+6=frac{49-105+54}{9}=-frac29\ b=-frac23, f_2(b)=left(-frac23right)^2-frac23+1=frac49-frac23+1frac{4-6+9}{9}=frac79 end{gather*}
Ответ: касательная (y=-frac x3+frac59); точки касания (left(frac73;-frac29right)) и (left(-frac23;frac79right))

Пример 5*. Докажите, что кривая (y=x^4+3x^2+2x) не пересекается с прямой (y=2x-1), и найдите расстояние между их ближайшими точками.

Решим уравнение: (x^4+3x^2+2x=2x-1) begin{gather*} x^4+3x^2+1=0Rightarrow D=3^2-4=5Rightarrow x^2=frac{-3pmsqrt{5}}{2} end{gather*} Оба корня отрицательные, а квадрат не может быть отрицательным числом.
Значит, (xinvarnothing) — решений нет, кривая и прямая не пересекаются.
Что и требовалось доказать.

Чтобы найти расстояние, необходимо построить касательную к кривой с тем же угловым коэффициентом (k=2), то и y данной прямой. Тогда искомым расстоянием будет расстояние от точки касания до прямой (y=2x-1).
Строим уравнение касательной. По условию: (f'(x)=4x^3+6x+2=2) begin{gather*} 4x^3+6x=0Rightarrow 2x(2x^2+3)=0Rightarrow left[ begin{array}{l} x=0\ 2x^2+3=0 end{array} right. Rightarrow left[ begin{array}{l} x=0\ x^2=-frac32 end{array} right. Rightarrow left[ begin{array}{l} x=0\ xinvarnothing end{array} right. Rightarrow x=0 end{gather*} Точка касания (x_0=0, y_0=0^4+3cdot 0^2+2cdot 0=0).
Уравнение касательной: (y=2(x-0)+0=2x)

Ищем расстояние между двумя параллельными прямыми:
(y=2x) и (y=2x-1).
Перпендикуляр из точки (0;0) на прямую (y=2x-1) имеет угловой коэффициент (k=-frac12), его уравнение: (y=-frac12 x+b). Т.к. точка (0;0) принадлежит этому перпендикуляру, он проходит через начало координат и (b=0).

Уравнение перпендикуляра: (y=-frac x2).
Находим точку пересечения прямой (y=2x-1) и перпендикуляра (y=-frac x2): begin{gather*} 2x-1=-frac x2Rightarrow 2,5x=1Rightarrow x=0,4; y=-frac{0,4}{2}=-0,2 end{gather*} Точка пересечения A(0,4;-0,2).
Находим расстояние (OA=sqrt{0,4^2+(-0,2)^2}=0,2sqrt{2^2+1^2}=frac{sqrt{5}}{5})
Ответ: (frac{sqrt{5}}{5})

Источник

Уравнение касательной к графику функции

2 апреля 2011

Пусть дана функция f, которая в некоторой точке x₀ имеет конечную производную f (x₀). Тогда прямая, проходящая через точку (x₀; f (x₀)), имеющая угловой коэффициент f ’(x₀), называется касательной.

А что будет, если производная в точке x₀ не существует? Возможны два варианта:

Касательная к графику тоже не существует. Классический пример — функция y = |x| в точке (0; 0).
Касательная становится вертикальной. Это верно, к примеру, для функции y = arcsin x в точке (1; π/2).

Уравнение касательной

Всякая невертикальная прямая задается уравнением вида y = kx + b, где k — угловой коэффициент. Касательная — не исключение, и чтобы составить ее уравнение в некоторой точке x₀, достаточно знать значение функции и производной в этой точке.

Итак, пусть дана функция y = f (x), которая имеет производную y = f ’(x) на отрезке [a; b]. Тогда в любой точке x₀ ∈ (a; b) к графику этой функции можно провести касательную, которая задается уравнением:

y = f ’(x₀) · (x − x₀) + f (x₀)

Здесь f ’(x₀) — значение производной в точке x₀, а f (x₀) — значение самой функции.

Задача. Дана функция y = x³. Составить уравнение касательной к графику этой функции в точке x₀ = 2.

Уравнение касательной: y = f ’(x₀) · (x − x₀) + f(x₀). Точка x₀ = 2 нам дана, а вот значения f (x₀) и f ’(x₀) придется вычислять.

Для начала найдем значение функции. Тут все легко: f (x₀) = f (2) = 2³ = 8;
Теперь найдем производную: f ’(x) = (x³)’ = 3x²;
Подставляем в производную x₀ = 2: f ’(x₀) = f ’(2) = 3 · 2² = 12;
Итого получаем: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.
Это и есть уравнение касательной.

Задача. Составить уравнение касательной к графику функции f (x) = 2sin x + 5 в точке x₀ = π/2.

В этот раз не будем подробно расписывать каждое действие — укажем лишь ключевые шаги. Имеем:

f (x₀) = f (π/2) = 2sin (π/2) + 5 = 2 + 5 = 7;
f ’(x) = (2sin x + 5)’ = 2cos x;
f ’(x₀) = f ’(π/2) = 2cos (π/2) = 0;

Уравнение касательной:

y = 0 · (x − π/2) + 7 ⇒ y = 7

В последнем случае прямая оказалась горизонтальной, т.к. ее угловой коэффициент k = 0. Ничего страшного в этом нет — просто мы наткнулись на точку экстремума.

Смотрите также:

Правила вычисления производных
Вводный урок по вычислению производных степенной функции
Что такое логарифм
Тест к уроку «Площади многоугольников без координатной сетки» (легкий)
Текстовые задачи про рельсы
Задача B4: Семья из трех человек едет из Москвы в Нижний Новгород

Источник

Геометрический смысл производной

Если плохо разбираешься в производной, то вот тебе полноценный гид по ней, с текстом, примерами и вебинарами: «Производная функции – геометрический смысл и правила дифференцирования»!

Рассмотрим график какой-то функции ( y=fleft( x right)):

Выберем на линии графика некую точку ( A). Пусть ее абсцисса ( {{x}_{0}}), тогда ордината равна ( fleft( {{x}_{0}} right)).

Затем выберем близкую к точке ( A) точку ( B) с абсциссой ( {{x}_{0}}+Delta x); ее ордината – это ( fleft( {{x}_{0}}+Delta x right)):

Проведем прямую через эти точки. Она называется секущей (прямо как в геометрии).

Обозначим угол наклона прямой к оси ( Ox) как ( alpha ).

Как и в тригонометрии, этот угол отсчитывается от положительного направления оси абсцисс против часовой стрелки.

Какие значения может принимать угол ( alpha )?

Как ни наклоняй эту прямую, все равно одна половина будет торчать вверх. Поэтому максимально возможный угол – ( 180{}^circ ), а минимально возможный – ( 0{}^circ ).

Значит, ( alpha in left[ 0{}^circ ;180{}^circ right)). Угол ( 180{}^circ ) не включается, поскольку положение прямой в этом случае в точности совпадает с ( 0{}^circ ), а логичнее выбирать меньший угол.

Возьмем на рисунке такую точку ( C), чтобы прямая ( AC) была параллельна оси абсцисс, а ( BC) – ординат:

grafik funktsii nahozhdenie kasatelnoj s pomoshyu proizvodnoj

По рисунку видно, что ( AC=Delta x), а ( BC=Delta f).

Тогда отношение приращений:

( frac{Delta f}{Delta x}=frac{BC}{AC}={tg}alpha )

(так как ( angle C=90{}^circ ), то ( triangle ABC) – прямоугольный).

Давай теперь уменьшать ( Delta x).

Тогда точка ( B) будет приближаться к точке ( A). Когда ( Delta x) станет бесконечно малым ( left( Delta xto 0 right)), отношение ( frac{Delta f}{Delta x}) станет равно производной функции в точке ( {{x}_{0}}).

Что же при этом станет с секущей?

Точка ( B) будет бесконечно близка к точке ( A), так что их можно будет считать одной и той же точкой.

Но прямая, имеющая с кривой только одну общую точку – это ни что иное, как касательная (в данном случае это условие выполняется только на небольшом участке – вблизи точки ( A), но этого достаточно).

Говорят, что при этом секущая занимает предельное положение.

Угол наклона секущей к оси ( displaystyle Ox) назовем ( varphi ). Тогда получится, что производная

( {f}’left( {{x}_{0}} right)underset{Delta xto 0}{mathop{=}},frac{Delta f}{Delta x}= {tg}varphi ),

то есть

Производная равна тангенсу угла наклона касательной к графику функции в данной точке

Поскольку касательная – это прямая, давай теперь вспомним уравнение прямой:

( y=kx+b).

За что отвечает коэффициент ( displaystyle k)? За наклон прямой. Он так и называется: угловой коэффициент.

Что это значит? А то, что равен он тангенсу угла между прямой и осью ( displaystyle Ox)!

То есть вот что получается:

( {f}’left( {{x}_{0}} right)= {tg}varphi =k).

Но мы получили это правило, рассматривая возрастающую функцию. А что изменится, если функция будет убывающей?

Посмотрим: Теперь углы ( alpha ) и ( displaystyle varphi ) тупые. А приращение функции ( Delta f) – отрицательное.

Снова рассмотрим ( triangle ABC): ( angle B=180{}^circ -alpha text{ }Rightarrow text{ } {tg}angle B=- {tg}alpha ).

С другой стороны, ( {tg}angle B=frac{AC}{BC}=frac{-Delta f}{Delta x}).

Получаем: ( frac{-Delta f}{Delta x}=- {tg}alpha text{ }Rightarrow text{ }frac{Delta f}{Delta x}= {tg}alpha ), то есть все, как и в прошлый раз.

Снова устремим точку ( displaystyle B) к точке ( displaystyle A), и секущая ( displaystyle AB) примет предельное положение, то есть превратится в касательную к графику функции в точке ( displaystyle A).

Итак, сформулируем окончательно полученное правило:

Производная функции в данной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или (что то же самое) угловому коэффициенту этой касательной:

( {f}’left( {{x}_{0}} right)= {tg}varphi =k)

nahozhdenie kasatelnoj k grafiku funktsii

Это и есть геометрический смысл производной.

Окей, все это интересно, но зачем оно нам? Вот пример:

На рисунке изображен график функции ( displaystyle y=mathsf{f}left( x right)) и касательная к нему в точке с абсциссой ( {{x}_{0}}).

Найдите значение производной функции ( displaystyle mathsf{f}left( x right)) в точке ( {{x}_{0}}).

nahozhdenie kasatelnoj k grafiku funktsii 2

Решение.

Как мы недавно выяснили, значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс:

( displaystyle f’left( x right)=k= {tg}varphi).

Значит, для нахождения значения производной нам нужно найти тангенс угла наклона касательной.

На рисунке у нас отмечено две точки, лежащие на касательной, координаты которых нам известны. Так давай достроим прямоугольный треугольник, проходящий через эти точки, и найдем тангенс угла наклона касательной!

Угол наклона касательной к оси ( displaystyle Ox) – это ( displaystyle angle BAC). Найдем тангенс этого угла:

( displaystyle {tg}angle BAC=frac{BC}{AC}=frac{6}{5}=1,2).

Таким образом, производная функции ( displaystyle mathsf{f}left( x right)) в точке ( {{x}_{0}}) равна ( displaystyle 1,2).

Ответ: ( displaystyle 1,2).

Теперь попробуй сам.

Уравнение касательной к графику функций

А сейчас сосредоточимся на произвольных касательных.

Предположим, у нас есть какая-то функция, например, ( fleft( x right)=left( {{x}^{2}}+2 right)). Мы нарисовали ее график и хотим провести касательную к нему в какой-нибудь точке ( {{x}_{0}}). Например, в точке ( {{x}_{0}}=2).

Берем линейку, пристраиваем ее к графику и чертим:

Что мы знаем об этой прямой? Что самое важное нужно знать о прямой на координатной плоскости?

Поскольку прямая – это изображение линейной функции, очень удобно было бы знать ее уравнение. То есть коэффициенты ( k) и ( b) в уравнении

( y=kx+b).

Но ведь ( k) мы уже знаем! Это угловой коэффициент касательной, который равен производной функции в этой точке:

( k={f}’left( {{x}_{0}} right)).

В нашем примере будет так:

( {f}’left( x right)={{left( {{x}^{2}}+2 right)}^{prime }}=2x;)

( k={f}’left( {{x}_{0}} right)={f}’left( 2 right)=2cdot 2=4.)

Теперь остается найти ( b) . Это проще простого: ведь ( b) – значение ( y) при ( displaystyle x=0).

Графически ( b) – это координата пересечения прямой с осью ординат (ведь ( displaystyle x=0) во всех точках оси ( displaystyle Oy)):

Проведём ( BCparallel Ox) (так, что ( triangle ABC) – прямоугольный).

Тогда ( angle ABC=alpha )(тому самому углу между касательной и осью абсцисс). Чему равны ( displaystyle AC) и ( displaystyle BC)?

По рисунку явно видно, что ( BC={{x}_{0}}), а ( AC=fleft( {{x}_{0}} right)-b). Тогда получаем:

( {f}’left( {{x}_{0}} right)= {tg}alpha =frac{AC}{BC}=frac{fleft( {{x}_{0}} right)-b}{{{x}_{0}}}text{ }Rightarrow text{ }b=fleft( {{x}_{0}} right)-{{x}_{0}}cdot {f}’left( {{x}_{0}} right)).

Соединяем все полученные формулы в уравнение прямой:

( y=kx+b={f}’left( {{x}_{0}} right)cdot x+fleft( {{x}_{0}} right)-{{x}_{0}}cdot {f}’left( {{x}_{0}} right);)

( y={f}’left( {{x}_{0}} right)cdot left( x-{{x}_{0}} right)+fleft( {{x}_{0}} right))

Это и есть уравнение касательной к графику функции ( fleft( x right)) в точке ( {{x}_{0}}).

Пример:

Найди уравнение касательной к графику функции ( fleft( x right)={{x}^{2}}-2x+3) в точке ( {{x}_{0}}=3).

Решение:

На этом примере выработаем простой…

Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике

ЕГЭ №7. Производная функции — геометрический смысл, дифференцирование

На этом видео мы вспомним, что такое функция и её график, научимся искать производную некоторых функций, например, такой: y = 2×3 – 3×2 + x + 5.

Мы разберём от А до Я все 7 типов задач, которые могут попасться в задаче №7 из ЕГЭ. Узнаем, на какие 3 фразы в условии задачи нужно обратить особое внимание, чтобы с лёгкостью решить задачу и не потерять баллы на ровном месте.

Разберём все возможные ошибки, которые можно допустить в этих задачах. Мы поймём, что многие из этих задач решаются обычным подсчётом клеточек на графике! Главное – не перепутать, что нужно считать.

P.S. Не забудьте потом посмотреть родственную тему: «Интегралы на ЕГЭ. Первообразные элементарных функций».

Источник

В этой статье мы разберем все типы задач на нахождение уравнения касательной.

Вспомним геометрический смысл производной: если к графику функции y=f(x) в точке x_0 проведена касательная, то коэффициент наклона касательной (равный тангенсу угла между касательной и положительным направлением оси ) равен производной функции в точке x_0 .

$k=tg{alpha}=f^{prime}(x_0)$

Возьмем на касательной произвольную точку с координатами ( x;y) :

И рассмотрим прямоугольный треугольник 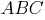ABC :

В этом треугольнике $tg{alpha}={BC}/{AB}={y-f(x_0)}/{x-x_0}=f{prime}(x_0)$

Отсюда ${y-f(x_0)}= f{prime}(x_0)(x-x_0)$

Или

$y=f(x_0)+ f{prime}(x_0)(x-x_0)$

Это и есть уравнение касательной, проведенной к графику функции y=f(x) в точке x_0 .

Чтобы написать уравнение касательной, нам достаточно знать уравнение функции и точку, в которой проведена касательная. Тогда мы сможем найти f(x_0) и $f{prime}(x_0)$ .

Есть три основных типа задач на составление уравнения касательной.

1. Дана точка касания x_0

2. Дан коэффициент наклона касательной, то есть значение производной функции y=f(x) в точке x_0 .

3. Даны координаты точки, через которую проведена касательная, но которая не является точкой касания.

Рассмотрим каждый тип задач.

1. Написать уравнение касательной к графику функции в точке x_0=1 .

а) Найдем значение функции в точке x_0=1 .

б) Найдем значение производной в точке x_0=1 . Сначала найдем производную функции y=f(x)

$f{prime}(x)=3x^2-4x$

$f{prime}(1)=3*1^2-4*1=-1$

Подставим найденные значения в уравнение касательной:

Раскроем скобки в правой части уравнения. Получим: y=-x+3

Ответ: y=-x+3 .

2. Найти абсциссы точек, в которых касательные к графику функции $y={1/4}x^4-{8/3}x^3 +{{15}/2}x^2$ параллельны оси абсцисс.

Если касательная параллельна оси абсцисс, следовательно угол между касательной и положительным направлением оси равен нулю, следовательно тангенс угла наклона касательной равен нулю. Значит, значение производной функции $y={1/4}x^4-{8/3}x^3 +{{15}/2}x^2$ в точках касания равно нулю.

а) Найдем производную функции $y={1/4}x^4-{8/3}x^3 +{{15}/2}x^2$ .

$y{prime}=x^3-8x^2+15x$

б) Приравняем производную к нулю и найдем значения , в которых касательная параллельна оси :

Приравняем каждый множитель к нулю, получим:

Ответ: 0;3;5

3. Написать уравнения касательных к графику функции , параллельных прямой y=-x+3 .

Касательная параллельна прямой y=-x+3 . Коэффициент наклона этой прямой равен -1. Так как касательная параллельна этой прямой, следовательно, коэффициент наклона касательной тоже равен -1. То есть мы знаем коэффициент наклона касательной, а, тем самым, значение производной в точке касания.

Это второй тип задач на нахождение уравнения касательной.

Итак, у нас дана функция и значение производной в точке касания.

а) Найдем точки, в которых производная функции равна -1.

Сначала найдем уравнение производной.

Нам нужно найти производную дроби.

$({u/v})^{prime}={u{prime}v-v{prime}u}/{v^2}$

$y{prime}={(3x-4){prime}(2x-3)-(2x-3){prime}(3x-4)}/{(2x-3)^2}={3(2x-3)-2(3x-4)}/{(2x-3)^2}={-1}/{(2x-3)^2}$

Приравняем производную к числу -1.

${-1}/{(2x-3)^2}=-1$

2x-3=1 или 2x-3=-1

x_0=2 или x_0=1

б) Найдем уравнение касательной к графику функции в точке x_0=2 .

Найдем значение функции в точке x_0=2 .

(по условию)

Подставим эти значения в уравнение касательной:

б) Найдем уравнение касательной к графику функции в точке x_0=1 .

Найдем значение функции в точке x_0=1 .

(по условию).

Подставим эти значения в уравнение касательной:

Ответ:

4. Написать уравнение касательной к кривой $y=sqrt{8-x^2}$ , проходящей через точку A(3,1)

Сначала проверим, не является ли точка A(3,1) точкой касания. Если точка является точкой касания, то она принадлежит графику функции, и её координаты должны удовлетворять уравнению функции. Подставим координаты точки A(3,1) в уравнение функции.

$1<>sqrt{8-3^2}$ . Мы получили под корнем отрицательное число, равенство не верно, и точка A(3,1) не принадлежит графику функции и не является точкой касания.

Это последний тип задач на нахождение уравнения касательной. Первым делом нам нужно найти абсциссу точки касания.

Найдем значение x_0 .

Пусть x_0 — точка касания. Точка A(3,1) принадлежит касательной к графику функции $y=sqrt{8-x^2}$ . Если мы подставим координаты этой точки в уравнение касательной, то получим верное равенство:

$1=f(x_0)+ f{prime}(x_0)(3-x_0)$ .

Значение функции $y=sqrt{8-x^2}$ в точке x_0 равно $f(x_0)= sqrt{8-{x_0}^2}$ .

Найдем значение производной функции $y=sqrt{8-x^2}$ в точке x_0 .

Сначала найдем производную функции $y=sqrt{8-x^2}$ . Это сложная функция.

$f{prime}(x)={1/{2sqrt{8-x^2}}}*(8-x^2){prime}={{-2x}/{2sqrt{8-x^2}}}$

Производная в точке x_0 равна $f{prime}(x_0)={-2{x_0}}/{2sqrt{8-{x_0}^2}}$ .

Подставим выражения для f(x_0) и $f{prime}(x_0)$ в уравнение касательной. Получим уравнение относительно x_0 :

$1=sqrt{8-{x_0}^2}+{-2{x_0}}/{2sqrt{8-{x_0}^2}}(3-x_0)$

Решим это уравнение.

Сократим числитель и знаменатель дроби на 2:

$1=sqrt{8-{x_0}^2}+{-{x_0}}/{sqrt{8-{x_0}^2}}(3-x_0)$

Приведем правую часть уравнения к общему знаменателю. Получим:

$1={8-{x_0}^2-{x_0}(3-x_0)}/{sqrt{8-{x_0}^2}}$

Упростим числитель дроби и умножим обе части на ${sqrt{8-{x_0}^2}}$ — это выражение строго больше нуля.

Получим уравнение

${8-3x_0}={sqrt{8-{x_0}^2}}$

Это иррациональное уравнение.

Решим его. Для этого возведем обе части в квадрат и перейдем к системе.

$delim{lbrace}{matrix{2}{1}{{64-48{x_0}+9{x_0}^2=8-{x_0}^2} {8-3x_0>=0} }}{ }$

Решим первое уравнение.

$10{x_0}^2-48x_0+56=0$

$5{x_0}^2-24x_0+28=0$

Решим квадратное уравнение, получим

x_0=2 или x_0=2,8

Второй корень не удовлетворяет условию , следовательно, у нас только одна точка касания и её абсцисса равна .

Напишем уравнение касательной к кривой $y=sqrt{8-x^2}$ в точке x_0=2 . Для этого подставим значение x_0=2 в уравнение $y=sqrt{8-{x_0}^2}+{-2{x_0}}/{2sqrt{8-{x_0}^2}}(x-x_0)$ — мы его уже записывали.

Получим:

$y=sqrt{8-{2}^2}-{2*{2}}/{2sqrt{8-{(2)}^2}}(x-2)$

Ответ: y=-x+4
И.В. Фельдман, репетитор по математике.

Источник

Решение уравнения касательной через график производной функции

Содержание:

Геометрический смысл производной функции в точке
Уравнение касательной к графику функций
Алгоритм составления уравнения касательной к графику функции
Примеры решения задач

Геометрический смысл производной функции в точке

Производная функции, имеющей вид f(x), в некой точк (x_0) является пределом отношения приращения функции (Delta f=f(x_0+Delta x)-f(x_0)) к приращению аргумента (Delta x), если (Delta xrightarrow 0), и данный предел существует.

Вывод формулы имеет следующий вид:

(f'(x_0)=lim_{Delta xrightarrow 0}frac{f(x_0+Delta x)-f(x_0)}{Delta x})

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Графически производную можно изобразить в виде кривой таким образом:

График

Источник: egemaximum.ru

Разберем типичный пример в доказательство определению. Попробуем найти производную записанным ранее методом ((x^2+1)):

((x^2+1)’=lim_{Delta xrightarrow 0}frac{((x+Delta x)^2+1)-(x^2+1)}{Delta x}=lim_{Delta xrightarrow 0}frac{x^2+2xDelta x+Delta x^2-x^2}{Delta x}= lim_{Delta xrightarrow 0}frac{Delta x(2x+Delta x)}{Delta x}=2x)

Согласно историческим фактам, одновременно с написанием работы Ньютона по изучению процессов в физике и формулировке понятия производной Лейбницем было введено определение производной с помощью геометрических закономерностей. Узнать, в чем состоит геометрический смысл производной, можно с помощью исследования графика функции y=f(x) на плоскости:

исследования графика функции y=f(x) на плоскости

Источник: math24.biz

В качестве обозначения точки (х0), соответствующей значению заданной функции, используем Р. Затем построим некую секущую, которая будет пересекать точки Р и Р1. Предположим, что полученный угол, образованный положительным направлением оси абсцисс Х и построенной секущей, равен (beta).

Результатом наших действий является геометрическая фигура под названием прямоугольный треугольник, катеты которого соответствуют переменным (triangle x) и (triangle y). Введем обозначения:

(triangle x) обозначает приращение аргумента функции;
(triangle y ) является приращением функции непосредственно.

Приращение функции относится к приращению аргумента, как тангенс угла, образованный секущей и положительным направлением оси абсцисс:

(frac{triangle x}{triangle y}=tg beta)

Когда значение (triangle x) стремится к нулю, точка Р1 на изображенном графике смещается в сторону точки Р. Положение секущей в таком случае меняется по отношению к графику.

Секущая занимает предельное положение в виде прямой, когда приращение стремится к нулю. Точки Р и Р1 на данной прямой будут совмещены. Рассматриваемая прямая является касательной к графику в точке Р.

Запишем следующее соотношение:

(tgbeta rightarrow tgalpha, если triangle xrightarrow 0)

Геометрический смысл производной: производная функции в точке обладает значением, численно равным тангенсу угла наклона касательной к функции в рассматриваемой точке.

Известным фактом является то, что какая-либо прямая обладает уравнением, которое можно записать в общем виде:

(y=k cdot x+b)

В уравнении касательной к функции в некой точке Р коэффициент k определяется, как значение производной в точке х0:

(lim_{triangle x rightarrow 0}frac{triangle x}{triangle y}=tg alpha = k)

В процессе решения практических заданий нередко можно встретить примеры, где требуется использовать геометрический смысл производной. Одной из подобных задач является изучение графически заданной функции в сравнении с графиком производной искомой функции.

Уравнение касательной к графику функций

Представим, что имеется некая функция (y=f(x)). Отметим на ее графике точку (x_o). Если провести касательную, пересекающую данную точку, то ее можно задать с помощью следующего уравнения:

(Large{y_k=f(x_o)+f'(x_o)(x-x_o)})

В результате угловой коэффициент касательной будет определен по формуле:

(k=f'(x_o))

В качестве наглядного примера изобразим график по исходным данным:

Источник: shkolkovo.net

Определение таких значений для k и b, при которых прямая (y_k=kx+b) играет роль касательной к функции (y=f(x)), заключается в решении одной из следующих систем:

(Large{begin{cases} k=f'(x_o)\ b=f(x_o)-f'(x_o)cdot x_oend{cases}})

(Large{begin{cases} k=f'(x_o)\ f(x_o)=y_k(x_o)end{cases}})

Алгоритм составления уравнения касательной к графику функции

Составить уравнение, с помощью которого задана касательная к графику функции, несложно. Нужно лишь следовать следующему алгоритму и выполнять действия в таком порядке:

Рассчитать значение ( fleft( {{x}_{0}} right).)
Записать формулу производной функции ({f}’left( x right).)
Определить значение ({f}’left( {{x}_{0}} right).)
Выполнить подстановку ({{x}_{0}},text{ }fleft( {{x}_{0}} right)) и ({f}’left( {{x}_{0}} right) )в формулу уравнения касательной (y={f}’left( {{x}_{0}} right)cdot left( x-{{x}_{0}} right)+fleft( {{x}_{0}} right).)

Рассмотрим конкретный пример. Попробуем составить уравнение касательной к функции (fleft( x right)={{x}^{2}}-2x+3.) Выполним действия последовательно, руководствуясь записанным ранее алгоритмом:

(fleft( x right)={{x}^{2}}-2x+3, {{x}_{0}}=3)

(fleft( {{x}_{0}} right)=fleft( 3 right)={{3}^{2}}-2cdot 3+3=6)

({f}’left( x right)={{left( {{x}^{2}}-2x+3 right)}^{prime }}=2{x} -2)

({f}’left( {{x}_{0}} right)={f}’left( 3 right)=2cdot 3-2=4)

(begin{array}{l}y={f}’left( {{x}_{0}} right)cdot left( x-{{x}_{0}} right)+fleft( {{x}_{0}} right)=\text{ }=4left( x-3 right)+6=4{x} -12+6=4{x} -6end{array})

Примеры решения задач

Задача 1

Функция ( y=mathsf{f}left( x right)) изображена графически. На этом же правильном графике построена касательная в точке, абсцисса которой равна ({x}_{0}.)

Задача 1

Требуется определить значения производной функции (mathsf{f}left( x right)), которые она принимает в точке ({{x}_{0}}.)

Решение

Согласно определению значения производной в точке касания, запишем:

(f’left( x right)=k= {tg}varphi)

Заметим, что для вычисления значения производной требуется определить тангенс угла наклона касательной. Воспользуемся координатами пары точек, которые принадлежат касательной на графике, чтобы построить прямоугольный треугольник. Угол наклона касательной к оси абсцисс равен (angle BAC). Определим тангенс рассматриваемого угла:

( {tg}angle BAC=frac{BC}{AC}=frac{6}{5}=1,2.)

В результате значение производной функции (mathsf{f}left( x right)) в точке ({{x}_{0}}) соответствует 1,2.

Ответ: 1,2.

Задача 2

Дана некая функция (y=frac{1}{3}x^3-4x+1). Требуется записать уравнение касательной к графику этой функции в точке (x_0=3.)

Решение

(f'(x)=x^2-4)

(f'(3)=3^2-4=5)

(f(3)=frac{1}{3}cdot 3^3-4cdot 3+1=9-12+1=-2.)

В таком случае:

(y_k=f'(x_0)(x-x_0)+f(x_0))

(y_k=5(x-3)-2)

(y_k=5x-17)

Ответ: (y=5x-17.)

Задача 3

Изображено два графика функций:

(f(x)=x^2+2x-3)

(ay+5x+6a=0)

Нужно вычислить все значения, которые принимает параметр а при пересечении рассматриваемых графиков только в одной точке.

Решение

Функция (f(x)) на графике будет иметь вид параболы, пересекающей ось абсцисс в следующих точках:

x=-3

x=1

Данная парабола имеет одну точку пересечения с осью ординат:

y=-3

Если зафиксировать а, то при каждом таком значении (ay+5x+6a=0) будет иметь вид прямой:

если a=0, то прямая x=0 с единственной точкой пересечения с f(x), соответствующей (0;-3);
если (ane 0,) то получается пучок прямых (y=-dfrac{5}{a}x-6), пересекающих точку (0;-6).

В результате графики обладают единственной общей точкой при таких значениях a, при которых прямая y будет касаться параболы. Касание в точке (x_o) возможно при следующих условиях:

(begin{cases} f'(x_o)=-dfrac{5}{a}\ f(x_o)=y(x_o) end{cases} Rightarrow begin{cases} x_o=-dfrac{5}{2a}-1\ 8a^2-20a-25=0 end{cases} Rightarrow a=dfrac{5}{4}(1 pm sqrt3))

Задача 3

Источник: shkolkovo.net

Ответ: (ain Big{ dfrac{5}{4}(1-sqrt3); 0; dfrac{5}{4}(1+sqrt3)Big}.)

Задача 4

Имеется некое уравнение:

(dfrac{1}{3}x^3+2x^2-dfrac{88}{3}=a(x+8))

Требуется определить все вероятные значения, которыми обладает параметр а, определяющие для данного уравнения единственное решение.

Решение

Проанализируем функцию и пучок, состоящий из прямых:

(f(x)=dfrac{1}{3}x^3+2x^2-dfrac{88}{3})

(y=a(x+8))

Точка максимума равна:

(f'(x)=x^2+4x Rightarrow x=-4=x_{max})

Точка минимума равна:

(x=0=x_{min})

Запишем следующие соотношения:

(f(x_{max})=-dfrac{56}{3})

(f(x_{min})=-dfrac{88}{3})

Каждая из прямых (y=ax+8a) пересекает точку (-8;0). Выявим такие случаи, при которых прямая у будет касаться графика функции f(x) в точке касания (x_o.) Подберем под заданные условия значения параметра:

(begin{cases} f'(x_o)=a\ f(x_o)=y(x_o) end{cases} Rightarrow begin{cases} x_o^2+4x_o=a\ 2x_o^3+30x_o^2+96x_o+88=0 end{cases}Rightarrow begin{cases} x_o^2+4x_o=a\ (x_o+2)^2(x_o+11)=0 end{cases} Rightarrow left[ begin{gathered} begin{aligned} &begin{cases} x_o=-2\ a=-4 end{cases}\ &begin{cases} x_o=-11\ a=77 end{cases} end{aligned} end{gathered} right.)

В результате уравнение ( f(x)=y) обладает только одним значением, когда параметр а имеет значения, при которых прямые y проходят в заштрихованных участках. Отметим, что граничный случай a=77 является посторонним.

Задача 4

Источник: shkolkovo.net

График в уменьшенном масштабе:

График в уменьшенном масштабе

Источник: shkolkovo.net

Таким образом:

(ain (-infty; 77))

Ответ: (ain (-infty; 77).)

Задача 5

Записана система:

(begin{cases} sqrt{(x-a)^2+y^2}+sqrt{x^2+(y+a)^2}=|asqrt2|\ x^2+y^2leqslant 18 end{cases})

Нужно найти такие значения параметра а, при которых данная система обладает только одним решением.

Решение

С помощью первого из уравнений системы можно построить отрезок BC, где B(a;0), C(0;-a), при условии, что a≠0. Представим, что (A(x;y)). В таком случае:

(begin{aligned} &BA=sqrt{(x-a)^2+y^2}\[1ex] &AC=sqrt{x^2+(y+a)^2}\[1ex] &BC=sqrt{(a-0)^2+(0+a)^2}=|asqrt2| end{aligned})

Запишем первое из уравнений, как:

BA+AC=BC

Заметим, с помощью этого уравнения можно задать множество точек А, принадлежащих отрезку ВС. Если а=0, то рассматриваемое уравнение задает только одну точку O(0;0).

С помощью второго неравенства можно изобразить окружность, центр которой находится в точке O(0;0), а ее радиус равен (R=3sqrt2.)

Система будет иметь лишь одно решение при параметре а≠0 — в том случае, когда отрезок касается окружности:

если a>0, отрезок BC располагается в 4 четверти;
если a<0, отрезок ВС располагается во 2 четверти.

Вариант с нулевым значением (а=0) также подходит под условия задачи, так как точка О лежит на окружности.

Задача 5

Источник: shkolkovo.net

Когда a>0, получим:

(BO=CO=|a|=a)

(OK=3sqrt2), является радиусом, проведенным в точку касания.

В таком случае:

(dfrac12cdot OBcdot OC=S_{triangle OBC}=dfrac12cdot OKcdot BC quadRightarrowquad acdot a=3sqrt2cdot asqrt2 quadRightarrowquad a=6.)

Когда a<0, получим:

(BO=CO=|a|=-a)

В таком случае:

(dfrac12cdot OBcdot OC=S_{triangle OBC}=dfrac12cdot OKcdot BC quadRightarrowquad -acdot (-a)=3sqrt2cdot (-asqrt2) quadRightarrowquad a=-6.)

Ответ: (ain {-6;0;6}.)

Источник

п.1. Уравнение касательной

п.2. Алгоритм построения касательной

п.3. Вертикальная касательная

п.4. Примеры

Уравнение касательной к графику функции

Уравнение касательной

Геометрический смысл производной

Уравнение касательной к графику функций

Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике

ЕГЭ №7. Производная функции — геометрический смысл, дифференцирование

Решение уравнения касательной через график производной функции

Геометрический смысл производной функции в точке

Уравнение касательной к графику функций

Алгоритм составления уравнения касательной к графику функции

Примеры решения задач

Не пропустите также: