Что такое номинальное напряжение и как его найти
Содержание
- 1 О терминологии
- 2 Как определяется НП
- 3 Примеры расчётов
- 3.1 Пример 1
- 3.2 Пример 2
- 3.3 Пример 3
- 4 Видео по теме
Непосредственное применение закона Ома для вычисления напряжения U возможно только для простой электрической сети (преимущественно постоянного тока). В большинстве прочих ситуаций перед расчётом необходимо уточнить, о каком именно U пойдёт речь, каков тип потребителя и в какой сети он функционирует. Особенно много путаницы возникает с терминами «среднее номинальное напряжение» и «номинальное допускаемое напряжение».
О терминологии
Базу энергетической системы составляют трехфазные сети, в которых используются 2 типа напряжений:
- Линейное, присутствующее между двумя жилами электрического кабеля.
- Фазное напряжение проявляется в ходе измерений потенциала между нулевым проводом и находящимся под током.
Если подключение к электросети происходит по схеме «треугольник», то линейные и фазные напряжения имеют одинаковые значения. Если же подсоединение производится с помощью «звезды», количественные показатели линейного напряжения становятся выше фазного в 1.733. Значение напряжения, присутствующего в трехфазной сети, записывают в виде дроби, например, 220/380. Числитель обозначает фазную, а знаменатель линейную величину.
В электротехнике часто приходится иметь дело со следующими тремя обозначениями, связанными с электрооборудованием и системой питания:
- Номинальное (линейное) напряжение сети или системы электрического питания.
- Номинальное напряжение отдельной единицы оборудования.
- Рабочее или допустимое напряжение.
Первое для сети переменного тока определяется как предельное значение данного параметра, присвоенное электрической цепи или системе для обозначения её класса. Такую характеристику часто обозначают как системное напряжение Uc. Например, для России действует следующий ряд Uc, соответствующий нормам ГОСТ Р 57382–2017: 110→330→500→750 кВ. При этом минимальное значение Uc не может быть меньше 6 кВ (ГОСТ 721–77).
Принятое в конкретном регионе значение номинального напряжения системы определяется пиковой потребляемой мощностью и протяжённостью линий электропередачи. При проектировании любого электрооборудования разработчик в первую очередь учитывает условия той системы, в которой будет работать это оборудование.
Производители электрооборудования в обязательном порядке указывают на своих устройствах главные характеристики: силу тока в А, мощность в Вт, а также номинальное фазное напряжение, являющееся базисным в стандартизованном ряду потенциалов. Для зон безопасности обычно принимается допуск ± 10 % или выше.
Однако номинальное напряжение не является точным рабочим показателем для работающего оборудования. Оно представляет собой значение параметра, по которому электрическое устройство названо или упоминается. Таким образом, фактическое напряжение, при котором работает устройство, может отличаться от номинального в пределах диапазона, обеспечивающего удовлетворительную работу оборудования.
Поэтому на практике рассматриваемый параметр чаще используется в качестве эталона для описания фактических возможностей электрических устройств и систем. Он характеризует возможности той сети, к которой может быть подключено устройство с сохранением условий для его безопасной и надёжной работы. Следовательно, допустимо рассматривать данный показатель лишь как приблизительную оценку уровня работы конкретной электрической системы. Предельные значения выбираются таким образом, чтобы они находились в границах диапазона номинального напряжения.
Следует отметить, что реальная разница между входным и номинальным Uc всегда присутствует, но она не должна превышать допуск безопасности. С другой стороны, расхождение между этими параметрами должно быть достаточно большим, чтобы можно было легко подкорректировать изменение номинального напряжения в линии электропередачи.
Рабочее напряжение — это фактическое значение характеристик питания, которое подаётся на клеммы оборудования. Параметр измеряется при помощи таких приборов как вольтметры, мультиметры. Если разница показателей, измеренных в ходе тестирования, выходит за пределы заявленного диапазона, то работоспособность этой единицы оборудования не будет обеспечена.
Как определяется НП
Проще всего дело обстоит с выяснением данного номинала применительно к электрооборудованию. Например, для однофазного асинхронного двигателя на паспортной табличке указано, что значение данного показателя составляет 240 В ± 10 %. Это означает, что двигатель может безопасно работать в диапазоне от 216 В до 264 В. Учитывается, что паспортная мощность двигателя и прочие проектные характеристики соответствуют нормам стандарта.
Чтобы рассчитать номинальные напряжения сложных или составных электрических сетей, поступают иначе. Например, если нужно выяснить указанный параметр для региональной сети электропотребления, каждая из составляющих которой рассчитана на собственные, различающиеся от ветви к ветви параметры, используют следующую последовательность действий:
- Пользуясь законом Ома для составной цепи, определяем значение номинального напряжения на выходе.
- Если мощность потребителей неизвестна, но зато есть фактическое значение Uф, то искомый параметр для каждого i-того потребителя определяется по формуле:
- Полученные значения Рi складываются.
При проведении таких расчётов необходимо различать номинал на каждом i-том элементе. Первый из параметров является предельным значением, которое может непрерывно подаваться к потребителю. Он применяется только к тем характеристикам сопротивления, которые лежат в области выше допустимой.
При вычислении номинального напряжения с помощью формулы Ома следует принимать во внимание то, что конечный результат может оказаться слишком высоким. Это может привести к выходу из строя элемента при длительном воздействии на него повышенной разности потенциалов. Поэтому итог расчётов сравнивается с максимальным (критическим) значением сопротивления, которое разрешено для данного элемента. Меньшее значение и будет действительным, указываемым отдельно для каждой серии и типоразмера изделия.
Примеры расчётов
Рассмотрим несколько примеров расчета номинального напряжения
Пример 1
Для номинальной мощности энергопотребителя в 1 Вт и его сопротивлении 100 кОм нужно определить номинал Uном, приняв, что верхняя граница параметра (Umax) равна 200 В.
Воспользовавшись формулой закона Ома для участка цепи, получим:
Однако максимально допустимое Umax на элементе только 200 В, поэтому подавать на элемент 316 В нельзя. Отсюда следует, что Uном = 200 В.
Пример 2
В стабильном режиме эксплуатации энергосистема выдаёт 11 кВ с допустимым колебанием ± 10 %. Какими будут наибольшие колебания, при которых такая система ещё сохранит свою работоспособность?
С учётом ранее указанного допуска безопасности 11 кВ ± 10 % данные значения будут составлять от 9.9 кВ до 12.1 кВ.
Пример 3
Автоматический выключатель, установленный для обслуживания энергосистемы 132 кВ, должен сохранять свою работоспособность в диапазоне Uном ±10 %. Следовательно, потенциал, подаваемый на автоматический выключатель, может находиться в пределах, не превышающих 118.8 … 145.2 кВ.
Образец более сложного расчёта
Определить номинальный ток генератора мощностью 48000 Вт при напряжении 110 В, учитывая, что Uном = 220 В, угол сдвига между фазами cosφ = 0.85. Обмотки трёхфазной схемы генератора соединены звездой. Расстояние между смежными пазами в статоре соответствует паспортной мощности двигателя.
Сначала находим фазное напряжение при соединении в звезду:
Определяем значение полной номинальной мощности генератора:
Искомое значение номинального тока генератора:
Поскольку расчётное фазное напряжение больше фактического, то длительная работоспособность генератора полностью обеспечится. Все прочие параметры системы следует рассчитывать с учетом тока Iн не менее 150 А.
Описанная методика действий с определёнными эксплуатационными факторами электрооборудования и энергосистем позволяет уточнять условия надёжной работы устройств, не допускать перегрузки их отдельных элементов, осуществлять более точный подбор типоразмеров трансформаторов, генераторов, электродвигателей и прочего электрооборудования.
Видео по теме
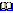 |
Учебник «Онлайн Электрик» | > |  |
Содержание |  Расчет | Пример | Расчет | Пример | Источники | Источники | 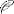 Теория Теория |
Выбор номинального напряжения линии электропередачи по эмпирическим формулам
При
проектировании развития электрической сети одновременно с разработкой вопроса о
конфигурации электрической сети решается вопрос о выборе ее номинального
значения. Выбор напряжения осуществляется из шкалы номинальных значений, установленных
[32], [33].
Номинальное напряжение UНОМ зависит от многих факторов, поэтому
задача его выбора не может иметь однозначного решения. При проектировании
электрических сетей используется несколько подходов. Одним из таких подходов
является выбор UНОМ по эмпирическим формулам:
а)
Формула Стилла
|
UНОМ ≈ 4,34 |
(1) |
где
L – длина линии,
км; Р – активная мощность, кВт;
Область
применения формулы (1) определяется условиями L ≤ 250 км, Р ≤ 60 МВт.
б)
Формула Залесского А.М.
|
UНОМ = |
(2) |
Область
применения формулы (2) определяется условиями L ≤ 1000 км, Р > 60 МВт.
в)
Формула Илларионова
|
UНОМ = |
(3) |
Формула (3) используется для
напряжения 35¸1150 кВ и принципиально правильно
отражает необходимость все более высоких номинальных напряжений с увеличением
протяженности линии, особенно при P>1000 МВт.
г)
Эмпирическая формула зависимости напряжения от передаваемой мощности и
протяженности линии:
|
UНОМ = |
(4) |
С
учетом условий использования формул (1)-(4) из ряда стандартных напряжений [32], [33]
выбирается ближайшее сечение. Результат расчета напряжения по эмпирическим
формулам является ориентировочным. В общем случае выбор номинального напряжения
сети является задачей технико-экономического сравнения различных вариантов.
[Пример]
Описание:
В разделе сайта представлены эмпирические формулы для выбора номинального напряжения линии электропередачи.
Ключевые слова:
Выбор номинального напряжения линии электропередачи по эмпирическим формулам, формула Стиля, Формула Залесского А.М., Формула Илларионова, эмпирическая формаула зависимости напряжения от передаваемой мощности и протяженности линии
| Библиографическая ссылка на ресурс «Онлайн Электрик»: |
|
Алюнов, А.Н. Онлайн Электрик : Интерактивные расчеты систем электроснабжения / А. Н. Алюнов. – Москва : Всероссийский научно-технический информационный центр, 2010. – EDN XXFLYN. |
Номинальной (установленной) мощностью эдектроприемника, называют мощность, на которую он рассчитан для длительного потребления электроэнергии из сети при номинальном напряжении и продолжительном номинальном режиме работы. Приводится на заводской табличке или в паспорте электроприемника. Там же указываются и другие технические параметры: род тока, номинальное напряжение Uном, частота, число фаз, коэффициент полезного действия, Т ном, коэффициент мощности при номинальной нагрузке cos ф и пр.
Номинальная мощность электродвигателей — это полезная механическая мощность на валу рн, выраженная в кВт. Для плавильных электропечей и сварочных установок — это полная мощность питающих их трансформаторов SH, выраженная в кВА. Для двигателей — генераторов, выпрямителей и преобразователей частоты принимается номинальная мощность генератора, выпрямителя и преобразователя (на вторичной стороне) в кВт или кВА.
Установленной мощностью для печей сопротивления, ванн электролиза, источников света является мощность, потребляемая этими электроприемниками из сети в кВт при номинальном напряжении.
Для электроприемников с повторно-кратковременным режимом работы за установленную принимается мощность рн, приведенная к продолжительному режиму, по выражениям:
Ниже видео о номинальной мощности электродинамиков:
Формула напряжения в физике — это представление электрической потенциальной энергии на единицу заряда. Если ток был размещен в определенном месте, напряжение указывает на ее потенциальную энергию в этой точке. Другими словами, это измерение силы, содержащейся в электрическом поле или цепи в данной точке. Он равен работе, которую нужно было бы выполнить за единицу заряда против электрического поля, чтобы переместить его из одной точки в другую.
Напряжение является скалярной величиной, у него нет направления. Закон Ома гласит, что интенсивность равна текущему временному сопротивлению.
Сопротивление
Формула механической мощности — средняя и мгновенная мощность
Любой проводник в цепи препятствует прохождению через себя тока. Данная характеристика определяет такую физическую величину, как сопротивление. Исходя из величины сопротивления, все вещества относят к проводникам или изоляторам. Точная граница весьма расплывчата, поэтому при некоторых условиях некоторые вещества можно отнести как к изоляторам, так и к проводникам. Участок электросхемы может иметь элемент с определенным значением величины, который именуется резистор.
Резисторы различных типов
Для переменного тока
Нужно понимать, что закон не применим напрямую к переменным цепям, например, с катушками индуктивности, конденсаторами или линиям передач. Закон может использоваться только для чисто резистивных цепей переменного тока без каких-либо изменений. В цепи RLC противодействие току является импедансом Z, который образует комбинацию двух ортогональных частей сопротивления.
Переменный ток
Im=Vm/Z
В этом случае Vm связано с Im с помощью константы пропорциональности Z (импеданса) и константы пропорциональности R. Для чисто резистивных линий, где (Z = R).
Vm = ImZ и Vm = ImR
Z — это общее сопротивление участка к переменному току, состоящее из реальной части — сопротивления и мнимой — реактивности.
Формула ее определяется теоремой Пифагора, поскольку угол Ф зависит от реактивной составляющей.
Интегральная форма
Взаимосвязь параметров электрической цепи
Все параметры любой электрической цепи строго взаимосвязаны, поэтому в любой момент времени можно точно определить величину любого из них, зная остальные.
К сведению. Основополагающий закон, по которому производится большинство расчетов, – закон Ома, согласно которому сила тока обратно пропорциональна его сопротивлению и прямо пропорциональна приложенной разности потенциалов.
Формула напряжения тока закона Ома выглядит следующим образом:
I=U/R.
Так, цепь с большим напряжением пропускает больший ток, а при одинаковом напряжении ампераж будет больше там, где меньше сопротивление.
Принятые обозначения в формуле расчета напряжения и тока понятны во всем мире:
- I – сила тока;
- U – напряжение;
- R – сопротивление.
Путем простейшего математического преобразования находится формула расчета сопротивления через силу тока и напряжение.
Кроме закона Ома, используется формула расчета мощности:
P=U∙I.
Символом P здесь обозначена мощность тока.
Любая схема может содержать участки, где имеется последовательное соединение, или есть элемент, подключенный параллельно. Расчеты при этом усложняются, но базовые формулы остаются одинаковыми.
Закон Ома для неоднородного участка цепи
Физическая величина, равная отношению работы сторонних сил Aст при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой (ЭДС) источника Eэдс:
$ E_{эдс} = {A_{cт}over q} $ (1).
Таким образом, ЭДС равна работе, совершаемой сторонними силами при перемещении единичного положительного заряда. При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа электростатического поля равна нулю, а работа сторонних сил равна сумме всех ЭДС, действующих в этой цепи.
Работа электростатических сил по перемещению единичного заряда равна разности потенциалов $ Δφ = φ_1 – φ_2 $ между начальной и конечной точками 1 и 2 неоднородного участка. Работа сторонних сил равна, по определению, электродвижущей силе Eэдс, действующей на данном участке. Поэтому полная работа равна:
$ U_п = φ_1 – φ_2 + E_{эдc} $ (2).
Величина Uп называется напряжением на участке цепи 1–2. В случае однородного участка напряжение равно разности потенциалов:
$ U_п = φ_1 – φ_2 $ (3).
Немецкий исследователь Георг Симон Ом в начале XIX века установил, что сила тока I, текущего по однородному проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:
$ I = {U over R} $ (4).
Рис. 2. Портрет Георга Ома.
Величина R — это электрическое сопротивление. Уравнение (4) выражает закон Ома для однородного участка цепи. Для участка цепи, содержащего ЭДС, закон Ома записывается в следующем виде:
$ U_п = I * R = φ_1 – φ_2 + E_{эдс} = Δ φ_{12} + E_{эдс}$ (5).
Данное уравнение называется обобщенным законом Ома для неоднородного участка цепи.
Как работает закон в реальной жизни
Используя совместно формулу расчета мощности и закон Ома, можно производить вычисления, не зная одной из величин. Самый простой пример – для лампы накаливания известны только ее мощность и напряжение. Применяя приведенные выше формулы, можно легко определить параметры нити накаливания и ток через нее.
Сила тока формула через мощность:
I=P/U;
Сопротивление:
R=U/I.
Такой же результат можно найти из мощности, не прибегая к промежуточным расчетам:
R=U2/P.
Аналогично можно вычислить любую величину, зная только две из них. Для упрощения преобразований имеется мнемоническое отображение формул, позволяющее находить любые величины.
Внимательно посмотрев на формулы, можно заметить, что, если уменьшить напряжение на лампе в два раза, ожидаемая мощность не снизится аналогично в два раза, а в четыре, согласно формуле:
P=U2/R.
Это довольно распространенная ошибка среди далеких от электротехники людей, которые неправильно соотносят мощность и напряжение, а также их действие на остальные параметры.
Кстати. Сила тока, найденная через сопротивление и напряжение, справедлива как для постоянного, так и для переменного тока, если в ней не используются такие элементы, как конденсатор или индуктивность.
Облегчить расчеты можно, используя онлайн калькулятор.
Определение через разложение электрического поля
Используя приведенное выше понятие, потенциал не находится на одном месте, когда магнитные поля меняются со временем. В физике иногда полезно обобщать электрическое значение, рассматривая только консервативную часть поля. Это делается с помощью следующего разложения, используемого в электродинамике.
В показанной выше формуле Е — индуцированный — вращательное электрическое поле, обусловленное изменяющимися во времени магнитными фонами. В этом случае сила между точками всегда определяется однозначно.
Пример с обычной водой
Существуют вещества, которые можно отнести одновременно к проводникам и изоляторам. Самый простой пример – обыкновенная вода. Дистиллированная вода является хорошим изолятором, но наличие в ней практически любых примесей делает ее проводником. Особенно это относится к солям различных металлов. При растворении в воде соли диссоциируются на ионы, их наличие – прямой повод для возникновения тока. Чем больше концентрация солей, тем меньшим сопротивлением будет обладать вода.
Для наглядности можно взять дистиллированную воду для приготовления электролита для автомобильных аккумуляторных батарей. Опустив щупы омметра в воду, можно увидеть, что его показания велики. Добавление всего нескольких кристаллов поваренной соли через некоторое время вызывает резкое уменьшение сопротивления, которое будет тем меньше, чем больше соли перейдет в раствор.
Различные используемые величины
Кроме основных величин: вольт, ампер, ом, ватт, используют кратные, большие или меньшие. Для обозначений применяют соответствующие приставки:
- Кило – 1000;
- Мега – 1000000;
- Гига – 1000000000;
- Милли – 0.001.
Таким образом, получается:
- Киловольт (кВ) – тысяча вольт;
- Мегаватт (Мвт) – миллион ватт;
- Миллиом (мОм) – одна тысячная Ом;
- Гигаватт (ГВт) – тысяча мегаватт или миллиард ватт.
Как найти напряжение
Формула нахождения напряжения как разности потенциалов в электрическом поле:
U=ϕA-ϕB, где ϕAи ϕB – потенциалы в точках А и В, соответственно.
Также можно записать напряжение как работу по переносу единицы заряда из точки А в точку В в электрическом поле:
U=A/q, где q – величина заряда.
Работа тем больше, чем выше напряженность электрического поля Е, то есть сила, действующая на неподвижный заряд.
Потенциальную энергию заряда в электростатическом поле называют электростатический потенциал.
Единицы измерения в формуле
Вам будет интересно:Антиклиналь + синклиналь – это складчатые горы
В формуле, определяющей напряжение, значением СИ является вольт. Таким образом, что 1В = 1 джоуль/кулон. Вольт назван в честь итальянского физика Алессандро Вольта, который изобрел химическую батарею.
Это означает, что в формуле напряжения в физике один кулон заряда получит один джоуль потенциальной энергии, когда он будет перемещен между двумя точками, где разность электрических потенциалов составляет один вольт. При напряжении 12, один кулон заряда получит 12 джоулей потенциальной энергии.
Батарея на шесть вольт имеет потенциал для одного кулона заряда, чтобы получить шесть джоулей потенциальной энергии между двумя местоположениями. Батарея на девять вольт имеет потенциал для одного кулона заряда, чтобы получить девять джоулей потенциальной энергии.
Гидравлическая аналогия
Чтобы легче усвоить законы электрических цепей, можно представить себе аналогию с гидравлической системой, в которой соединение насоса и трубопроводов образует замкнутую систему. Для этого нужны следующие соответствия:
- Источник питания – насос;
- Проводники – трубы;
- Электроток – движение воды.
Без особых усилий становится понятнее, что чем меньше диаметр труб, тем медленнее по ним движется вода. Чем мощнее насос, тем большее количество воды он способен перекачать. При одинаковой мощности насоса уменьшение диаметра труб приведет к снижению потока воды.
Измерительные приборы
Для измерения параметров электрических цепей служат измерительные приборы:
- Вольтметр;
- Амперметр;
- Омметр.
Наиболее часто используется класс комбинированных устройств, в которых переключателем выбирается измеряемая величина – ампервольтомметры или авометры.
Формулы, примеры решения задач: ТОЭ | Электрические машины | Высшая математика | Теоретическая механика
- Электрический ток, плотность тока, электрическое напряжение, энергия при протекании тока, мощность электрического тока
- Электрический ток
Электрический ток — это явление упорядоченного движения электрических зарядов. За направление электрического тока принимается направление движения положительных зарядов.
Формула электрического тока:
Электрический ток измеряется в амперах. СИ: А.
Электрический ток обозначается латинскими буквами i или I. Символом i(t) обозначается «мгновенное» значение тока, т.е. ток произвольного вида в любой момент времени. В частном случае он может быть постоянным или переменным.
Прописной латинской буквой I обозначается, как правило, постоянное значение тока.
В любом участке неразветвленной электрической цепи протекает одинаковый по величине ток, который прямо пропорционален напряжению на концах участка и обратно пропорционален его сопротивлению. Величина тока определяется по закону Ома:
1) для цепи постоянного тока
2) для цепи переменного тока,
где U — напряжение, В;
R — омическое сопротивление, Ом;
Z — полное сопротивление, Ом.
Омическое сопротивление проводника:
,
где l — длина проводника, м;
s — поперечное сечение, мм2;
ρ — удельное сопротивление, (Ом · мм2) / м.
Зависимость омического сопротивления от температуры:
Rt = R20 [1 + α(t — 20°)],
где R20 — сопротивление при 20°C, Ом;
Rt — сопротивление при t°C, Ом;
α — температурный коэффициент сопротивления.
Полное сопротивление цепи переменного тока:
,
где— активное сопротивление, Ом;
— индуктивное сопротивление, Ом;
— индуктивность, Гн;
— емкостное сопротивление, Ом;
— ёмкость, Ф.
Активное сопротивление больше омического сопротивления R:
,
где— коэффициент, учитывающий увеличение сопротивления при переменном токе, зависящий от: частоты тока; магнитных свойств, проводимости и диаметра проводника.
При промышленной частоте, для нестальных проводников, принимаюти считают
.
- Плотность тока
Плотность тока (j) — это сила тока, рассчитанная на единицу площади поперечного сечения (s).
Для равномерного распределения плотности тока и сонаправленности её с нормалью к поверхности, через которую протекает ток, формула плотности тока принимает вид:,
где I — сила тока через поперечное сечение проводника площадью s.
СИ: А/м2 - Электрическое напряжение
При протекании тока, как и при всяком перемещении зарядов, происходит процесс преобразования энергии. Электрическое напряжение — количество энергии, которое необходимо затратить на перемещение единицы заряда из одной точки в другую.
Формула электрического напряжения:
Электрическое напряжение обозначается латинской буквой u. Символом u(t) обозначается «мгновенное» значение напряжения, а прописной латинской буквой U обозначается, как правило, постоянное напряжение.
Электрическое напряжение измеряется в вольтах. СИ: В. - Энергия при протекании электрического тока
Формула энергии, при протекании электрического тока:
СИ: Дж - Мощность при протекании электрического тока
Формула мощности, при протекании электрического тока:
СИ: Вт.
- Электрическая цепь
- Электрическая цепь — это совокупность устройств, предназначенных для протекания по ним электрического тока.
Эти устройства называются элементами цепи. - Источники электрической энергии — устройства, преобразующие различные виды энергии, например механическую или химическую, в энергию электрического тока.
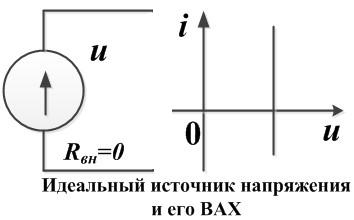
- Идеальный источник напряжения — источник, напряжение на зажимах которого не зависит от величины протекающего через него тока.
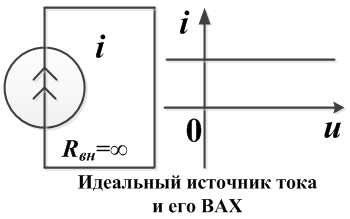
Внутреннее сопротивление идеального источника напряжения можно условно принять равным нулю. - Идеальный источник тока — источник, величина протекающего тока через который не зависит от напряжения на его зажимах.
Внутреннее сопротивление такого источника можно условно принять равным бесконечности. - Приемник — это устройство, потребляющее энергию или преобразующее электрическую энергию в другие виды энергии.
- Двухполюсник — это цепь, имеющая два зажима для подключения (полюса).
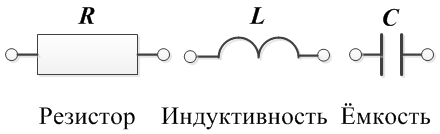
- Идеальный R-элемент (резистивный элемент, резистор) — это такой пассивный элемент цепи, в котором происходит необратимый процесс преобразования электрической энергии в тепловую.
Основной параметр резистора — это его сопротивление.
Сопротивление измеряется в омах. СИ: Ом
Проводимость — это обратная величина по отношению к сопротивлению..
Измеряется проводимость в сименсах. СИ: См.
Формула мощности R-элемента:.
Формула энергии R-элемента:
.
- Идеальный С-элемент (емкостной элемент, или конденсатор) — это такой пассивный элемент цепи, в котором происходит процесс преобразования энергии электрического тока в энергию электрического поля и наоборот. В идеальном C-элементе потери энергии отсутствуют.
Формула ёмкости:
. Примеры: задача 1, задача 2.
Ток в ёмкости:
Напряжения на ёмкости:
.
Закон коммутации для емкостного элемента. При токе конечной амплитуды заряд на C-элементе не может измениться скачком:.
.
При неизменной ёмкости, напряжение на емкостном элементе не может измениться скачком:.
Мощность C-элемента:.
При p > 0 — энергия запасается, при p < 0 — энергия возвращается в источник.
Энергия C-элемента:
, или
.
Если к моменту времени, энергия равна 0, то
Емкость измеряется в фарадах. СИ: Ф. - Идеальный L-элемент (индуктивный элемент или катушка индуктивности) — это такой пассивный элемент цени, в котором происходит процесс преобразования энергии электрического тока в энергию магнитного поля и наоборот. В идеальном L-элементе потери энергии отсутствуют.
Для линейного L-элемента формула индуктивности (L) имеет вид:
,
где— потокосцепление.
Индуктивность обозначается буквойи играет роль коэффициента пропорциональности между потоком
и током
.
Напряжение на индуктивном элементе:
.
Ток в индуктивном элементе:
.
Закон коммутации для индуктивного элемента. При напряжении конечной амплитуды, потокосцепление не может измениться скачком:.
.
При неизменной индуктивности ток в индуктивном элементе не может измениться скачком:.
Мощность L-элемента:.
При p > 0 — энергия запасается, при p < 0 — энергия возвращается в источник.
Энергия L-элемента:
, или
.
Если к моменту времени, энергия равна 0, то
Индуктивность измеряется в генри. СИ: Гн
Пример: задача 3. - R, L, C — основные пассивные двухполюсные элементы электрических цепей.
- Основные законы электрических цепей
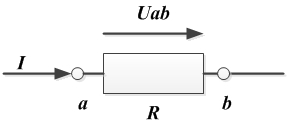
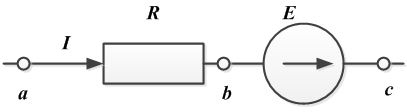
- Закон Ома для участка цепи, не содержащего источник ЭДС.
Закон Ома для участка цепи, не содержащего источник ЭДС, устанавливает связь между током и напряжением на этом участке.
Применительно к данному рисунку, математическое выражение закона Ома имеет вид:
, или
Формулируется это равенство так: при неизменном сопротивлении проводника напряжение на нем пропорционально току в проводнике. - Закон Ома для участка цепи, содержащего источник ЭДС
Для схемы
.
Для схемы
.
В общем случае
.
- Закон Джоуля-Ленца. Энергия, выделяемая на сопротивлении R при протекании по нему тока I, пропорциональна произведению квадрата силы тока и величины сопротивления:
- Законы Кирхгофа.
Топология (строение) цепи.
Электрическая схема — графическое изображение электрической цепи.
Ветвь ‐ участок цепи, содержащий один или несколько последовательно соединенных элементов и заключенный между двумя узлами.
Узел ‐ точка цепи, где сходится не менее трех ветвей. Узлы нумеруют произвольно, как правило, арабской цифрой. На схеме узел может быть обозначен точкой, а может и не быть обозначен. Как правило, не обозначают те узлы, расположение которых очевидно (т‐образные соединения). Если пересекающиеся ветви образуют узел, то он обозначается точкой. Если в месте пересечения ветвей точки нет, то и узла нет (провода лежат друг на друге).
Контур – замкнутый путь, проходящий по нескольким ветвям. Контуры независимы, если отличаются хотя бы одной ветвью. Контура обозначают стрелкой с указанным направлением обхода и римской цифрой. Направление обхода выбирают произвольно. Независимых контуров в схеме может быть много, при этом не все эти контура необходимы для составления достаточного для решения задачи количества уравнений.
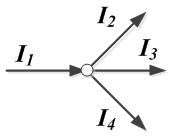
Первый закон Кирхгофа:
1) алгебраическая сумма токов, подтекающих к любому узлу схемы, равна нулю:
;
2) сумма подтекающих к любому узлу токов равна сумме утекающих от узла токов:
. Пример 1. Первый закон Кирхгофа.
Второй закон Кирхгофа:
1) алгебраическая сумма падений напряжения в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль того же контура:
2) алгебраическая сумма напряжений (не падений напряжения!) вдоль любого замкнутого контура равна нулю:
. Пример 2. Второй закон Кирхгофа.
- Матричная форма записи уравнений Кирхгофа:
,
где А, В — квадратные матрицы коэффициентов при токах и напряжениях порядка p х p (p — число ветвей схемы; q — число узлов схемы);
I, E — матрицы-столбцы неизвестных токов и заданных ЭДС
Элементами матрицы А являются коэффициенты при токах в левой части уравнений, составленных по первому и второму законам Кирхгофа. Первыестроки матрицы А содержат коэффициенты при токах в уравнениях, составленных по первому закону Кирхгофа, и имеют элементы +1, -1, 0 в зависимости от того, с каким знаком входит данный ток в уравнение.
Элементы следующихстрок матрицы А равны значениям сопротивлении при соответствующих токах в уравнениях, составленных по второму закону Кирхгофа, с соответствующим знаком. Элементы матрицы В равны коэффициентам при ЭДС в правой части уравнений, составленных по законам Кирхгофа. Первые
строки матрицы имеют нулевые элементы, так как ЭДС в правой части уравнений, записанных по первому закону Кирхгофа, отсутствуют. Остальные
строки содержат элементы +1, -1 в зависимости от того, с каким знаком входит ЭДС в уравнение, и 0, если ЭДС в уравнения не входит.
Общее решение уравнений, составленных по законам Кирхгофа:
,
где— матрица проводимостей.
.
Токи в каждой ветви:
;
;
.
- Режимы работы электрических цепей
- Номинальный режим работы элемента электрической цепи — это режим, при котором он работает с номинальными параметрами.
- Согласованный режим — это режим, при котором мощность, отдаваемая источником или потребляемая приемником, имеет максимальное значение. Такое значение получается при определенном соотношении (согласовании) параметров электрической цепи.
- Режим холостого хода — это такой режим, при котором через источник или приемник не протекает электрический ток. При этом источник не отдает энергию во внешнюю часть цепи, а приемник не потребляет ее. Для двигателя это будет режим без механической нагрузки навалу.
- Режим короткого замыкания — это режим, возникающий при соединении между собой разноименных зажимов источника или пассивного элемента, а также участка электрической цепи, находящегося под напряжением.
- Электрические цепи постоянного тока
- Если ток постоянный, то отсутствует явление самоиндукции и напряжение на катушке индуктивности равно нулю:
, так как
- Постоянный ток через емкость не проходит.
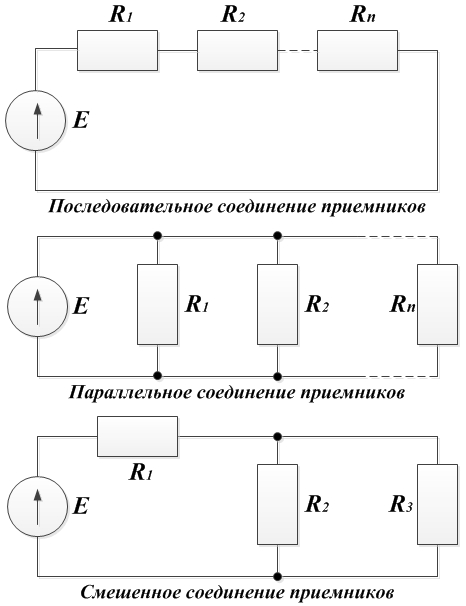
- Простая цепь постоянного тока — это цепь с одним источником при последовательном, параллельном или смешанном соединение приемников.
При последовательном соединении приемников:
I×Rэкв;
Rэкв=ΣRi.
При параллельном соединении приемников напряжение на всех приемниках одинаково.
По закону Ома токи в каждой ветви:
.
По первому закону Кирхгофа общий ток:
E×Gэкв;
Gэкв=G1+G2+…+Gn; Rэкв=1/Gэкв.
При смешанном соединении:
Rэкв=.
- Метод контурных токов.
Метод основан на применении второго закона Кирхгофа и позволяет сократить при расчете сложных систем число решаемых уравнений.
Во взаимно независимых контурах, где для каждого контура хотя бы одна ветвь входит только в этот контур, рассматривают условные контурные токи во всех ветвях контура.
Контурные токи, в отличие от токов ветвей, имеют следующие индексы:или
Уравнения составляют по второму закону Кирхгофа для контурных токов.
Токи ветвей выражают через контурные токи по первому закону Кирхгофа.
Число выбираемых контуров и число решаемых уравнений равно числу уравнений, составляемых по второму закону Кирхгофа:.
Сумма сопротивлений всех резистивных элементов каждого контура со знаком плюс является коэффициентом при токе контура, имеет следующие индексы:или
Знак коэффициента при токе смежных контуров зависит от совпадения или несовпадения направления смежных контурных токов. ЭДС входят в уравнение со знаком плюс, если направления ЭДС и направление тока контура совпадают. Пример 3. Метод контурных токов. - Метод узловых потенциалов.
Метод основан на применении первого закона Кирхгофа и позволяет сократить число решаемых уравнений при нахождении неизвестных токов до. При составлении уравнений потенциал одного из узлов схемы принимают равным нулю, а токи ветвей выражают через неизвестные потенциалы остальных
узлов схемы и для них записывают уравнения по первому закону Кирхгофа. Решение системы
уравнений позволяет определить неизвестные потенциалы, а через них найти токи ветвей.
Приследует отдавать предпочтение методу узловых потенциалов.
- Формула двух узлов:
.
Пример 4. Метод узловых потенциалов. - Метод пропорциональных величии.
Метод применяют для нахождения неизвестных токов при цепочечном соединении резистивных элементов в электрических цепях с одним источником. Токи и напряжения, а также и известную ЭДС цепи выражают через ток самой удаленной от источника ветви. Задача сводится к решению одного уравнения с одним неизвестным. - Баланс мощностей
На основании закона сохранения энергии мощность, развиваемая источниками электрической энергии, должна быть равна мощности преобразования в цепи электрической энергии в другие виды энергии:
.
— сумма мощностей, развиваемых источниками;
— сумма мощностей всех приемников и необратимых преобразований энергии внутри источников.
Баланс мощностей составляют, чтобы проверить правильность найденного решения. При этом сравнивают мощность, внесенную в цепь источниками энергии с мощностью, затрачиваемой потребителями.
Формула мощности для одного резистора:
Суммарная мощность потребителей:
PП=
Мощность источников:
Pист = PE + PJ,
где PE = ±EI — мощность источника ЭДС (определятся умножением его ЭДС на ток, протекающий в данной ветви. Ток берут со знаком, полученным в результате расчета. Минус перед произведением ставят, если направление тока и ЭДС не совпадают на схеме);
PJ = JUJ — мощность источника тока (определятся умножением тока источника на падение напряжения на нем).
Для определения UJ выбирают любой контур, который включал бы в себя источник тока. Обозначают падение UJ на схеме против тока источника, и записывают контурное уравнение. Все величины, кроме UJ, в данном уравнении уже известны, что позволяет рассчитать падение напряжения UJ.
Сравнение мощностей: Pист = PП. Если равенство соблюдено, значит, баланс сошелся и расчет токов верен. - Алгоритм расчета цепи по законам Кирхгофа
- Топология цепи.
- Определяем общее число ветвей p*.
- Определяем число ветвей с источниками тока pит. Токи в данных ветвях считаем известными и равными токам источников.
- Определяем число ветвей с неизвестными токами: p*‐pит
- Находим количество узлов q.
- Находим число уравнений, составляемых по первому закону Кирхгофа:
.
- Находим число уравнений, составляемых по второму закону Кирхгофа:
.
- Произвольно наносим на схему номера и направления неизвестных токов.
- Произвольно наносим на схему номера узлов.
- Составляем узловые уравнения для произвольно выбранных узлов (по первому закону).
- Обозначаем на схеме контура и выбираем направления их обхода.
- Количество обозначаемых контуров равно количеству уравнений, составляемых по второму закону Кирхгофа. При этом ни один из контуров не должен включать в себя ветвь с источником тока.
- Составляем контурные уравнения для выбранных контуров (по второму закону).
- Объединяем составленные уравнения в систему. Известные величины переносим в правую часть уравнений. Коэффициенты при искомых токах вносим в матрицу А (левые части уравнений)(о матрицах читаем здесь). Заполняем матрицу F, занося в нее правые части уравнений.
- Решаем полученную систему уравнений (примеры решения систем уравнений).
- Проверяем правильность решения составлением баланса мощностей.
Пример: задача 4.
- Электрические цепи переменного тока
- Электрическая цепь синусоидального тока — это электрическая цепь, в которой ЭДС, напряжения и и токи, изменяющиеся по синусоидальному закону:
- Переменный ток — это ток, периодически меняющийся по величине и направлению и характеризующийся амплитудой, периодом, частотой и фазой.
- Амплитуда переменного тока — это наибольшее значение, положительное или отрицательное, принимаемое переменным током.
- Период — это время, в течение которого происходит полное колебание тока в проводнике.
- Частота — это величина, обратная периоду.
- Фаза — это угол
или
, стоящий под знаком синуса. Фаза характеризует состояние переменного тока с течением времени. При t=0 фаза называется начальной.
- Периодический режим:
. К такому режиму может быть отнесен и синусоидальный:
,
где— амплитуда;
— начальная фаза;
— угловая скорость вращения ротора генератора.
При f = 50 Гцрад/с.
- Синусоидальный ток — это ток изменяющийся во времени по синусоидальному закону:
.
- Среднее значение синусоидального тока (ЭДС, напряжение), формула:
,
то есть среднее значение синусоидального тока составляетот амплитудного. Аналогично,
.
- Действующее значение синусоидального тока (ЭДС, напряжение), формула:
. Аналогично,
.
- Количество теплоты, выделенное за один период синусоидальным током, формула:
.
Действующее значение синусоидального тока I численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты,что и синусоидальный ток.
=R×Iпост2×T или Iпост=I=
- Коэффициент амплитуды синусоидального тока (κa) — это отношение амплитуды синусоидального тока к действующему значению синусоидального тока:
.
- Коэффициент формы синусоидального тока (κф) — это отношение действующего значения синусоидального тока к среднему за пол периода значению синусоидального тока:
κф=.
Для несинусоидальных периодических токов κa≠, κф≠1,11. Это отклонение косвенно свидетельствует о том, насколько несинусоидальный ток отличается от синусоидального.
- Резонансные явления в электрических цепях
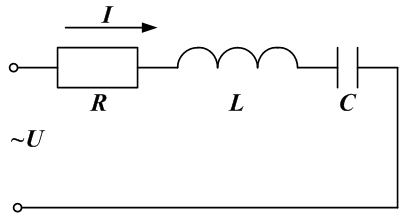
- Резонанс напряжений.
Резонансом в электрических цепях называется режим участка электрической цепи, содержащей индуктивный и емкостной элементы, при котором разность фаз между напряжением и током равна нулю.
Режим резонанса может быть получен при изменении частоты ω питающего напряжения или изменением параметров L и C.
При последовательном соединении возникает резонанс напряжения.
Ток в схеме равен:
При совпадении вектора тока с вектором напряжения по фазе:
где— резонансная частота напряжения, определяемая из условия
Тогда
Волновое или характеристическое сопротивление последовательного контура:
Добротность контура — это отношение напряжения на индуктивности или емкости к напряжению на входе в режиме резонанса:
Добротность контура представляет собой коэффициент усиления по напряжению:
ULрез=IрезXрез=
В промышленных сетях резонанс напряжений является аварийным режимом, так как увеличение напряжения на конденсаторе может привести к его пробою, а рост тока — к нагреву проводов и изоляции. - Резонанс токов.
Резонанс токов может возникнуть при параллельном соединении реактивных элементов в цепях переменного тока. В этом случае:где
тогда
При резонансной частоте реактивные составляющие проводимости могут сравниться по модулю и суммарная проводимость будет минимальной. При этом общее сопротивление становится максимальным, общий ток минимальным, вектор тока совпадает с вектором напряжения. Такое явление называется резонансом токов.
Волновая проводимость:.
При g << bL ток в ветви с индуктивностью значительно больше общего тока, поэтому такое явление называется резонансом токов.
Резонансная частота:
ω*=
Из формулы следует:
1) резонансная частота зависит от параметров не только реактивных сопротивлений, но и активных;
2) резонанс возможен, если RL и RC больше или меньше ρ, в противном случае частота будет мнимой величиной и резонанс не возможен;
3) если RL = RC = ρ, то частота будет иметь неопределенное значение, что означает возможность существования резонанса на любой частоте при совпадении фаз напряжения питания и общего тока;
4) при RL = RC << ρ резонансная частота напряжения равна резонансной частоте тока.
Энергетические процессы в цепи при резонансе токов аналогичны процессам при резонансе напряжений.
Реактивная мощность при резонансе токов равна нулю. Подробно, реактивная мощность рассмотрена здесь.
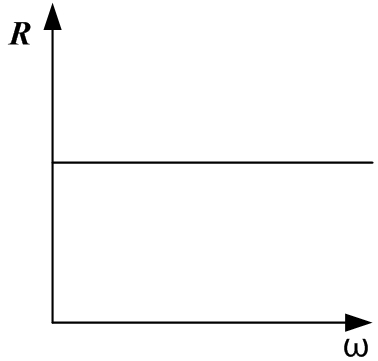
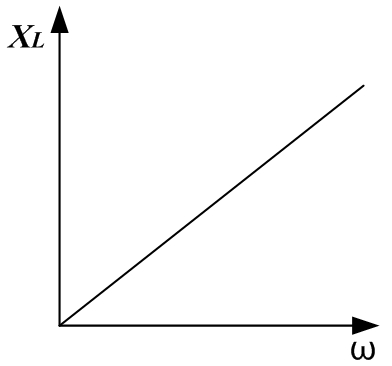
Идеальное активное сопротивление не зависит от частоты, индуктивное сопротивление линейно зависит от частоты, емкостное сопротивление зависит от частоты по гиперболическому закону:

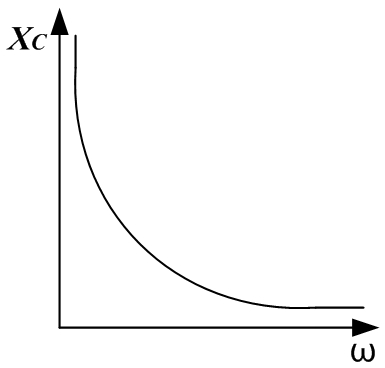














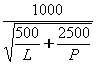 .
.











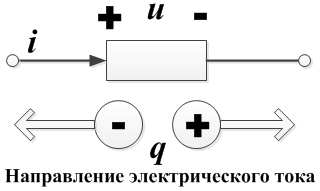

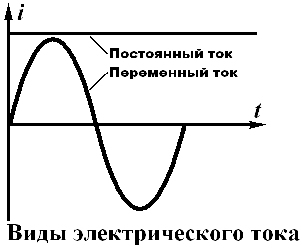

 ,
, ,
, ,
, — активное сопротивление, Ом;
— активное сопротивление, Ом; — индуктивное сопротивление, Ом;
— индуктивное сопротивление, Ом; — индуктивность, Гн;
— индуктивность, Гн; — емкостное сопротивление, Ом;
— емкостное сопротивление, Ом; — ёмкость, Ф.
— ёмкость, Ф. ,
, — коэффициент, учитывающий увеличение сопротивления при переменном токе, зависящий от: частоты тока; магнитных свойств, проводимости и диаметра проводника.
— коэффициент, учитывающий увеличение сопротивления при переменном токе, зависящий от: частоты тока; магнитных свойств, проводимости и диаметра проводника. и считают
и считают  .
. .
. ,
,



 .
. .
. .
. . Примеры: задача 1, задача 2.
. Примеры: задача 1, задача 2.
 .
. .
. .
. .
. .
. , или
, или .
. , энергия равна 0, то
, энергия равна 0, то
 ,
, — потокосцепление.
— потокосцепление. .
. .
. .
. .
. .
. .
.
 , или
, или 
 .
.
 .
. .
.
 ;
;
 . Пример 1. Первый закон Кирхгофа.
. Пример 1. Первый закон Кирхгофа.
 . Пример 2. Второй закон Кирхгофа.
. Пример 2. Второй закон Кирхгофа. ,
, строки матрицы А содержат коэффициенты при токах в уравнениях, составленных по первому закону Кирхгофа, и имеют элементы +1, -1, 0 в зависимости от того, с каким знаком входит данный ток в уравнение.
строки матрицы А содержат коэффициенты при токах в уравнениях, составленных по первому закону Кирхгофа, и имеют элементы +1, -1, 0 в зависимости от того, с каким знаком входит данный ток в уравнение. строк матрицы А равны значениям сопротивлении при соответствующих токах в уравнениях, составленных по второму закону Кирхгофа, с соответствующим знаком. Элементы матрицы В равны коэффициентам при ЭДС в правой части уравнений, составленных по законам Кирхгофа. Первые
строк матрицы А равны значениям сопротивлении при соответствующих токах в уравнениях, составленных по второму закону Кирхгофа, с соответствующим знаком. Элементы матрицы В равны коэффициентам при ЭДС в правой части уравнений, составленных по законам Кирхгофа. Первые  ,
, — матрица проводимостей.
— матрица проводимостей. .
. ;
; ;
;
 .
. , так как
, так как 
 I×Rэкв;
I×Rэкв; .
. E×Gэкв;
E×Gэкв; .
. или
или 
 .
. или
или 
 следует отдавать предпочтение методу узловых потенциалов.
следует отдавать предпочтение методу узловых потенциалов. .
. .
. — сумма мощностей, развиваемых источниками;
— сумма мощностей, развиваемых источниками; — сумма мощностей всех приемников и необратимых преобразований энергии внутри источников.
— сумма мощностей всех приемников и необратимых преобразований энергии внутри источников.

 .
.
 или
или  , стоящий под знаком синуса. Фаза характеризует состояние переменного тока с течением времени. При t=0 фаза называется начальной.
, стоящий под знаком синуса. Фаза характеризует состояние переменного тока с течением времени. При t=0 фаза называется начальной. . К такому режиму может быть отнесен и синусоидальный:
. К такому режиму может быть отнесен и синусоидальный: ,
, — амплитуда;
— амплитуда; — начальная фаза;
— начальная фаза; — угловая скорость вращения ротора генератора.
— угловая скорость вращения ротора генератора. рад/с.
рад/с. .
. ,
, от амплитудного. Аналогично,
от амплитудного. Аналогично, .
. . Аналогично,
. Аналогично, .
. .
. =R×Iпост2×T или Iпост=I=
=R×Iпост2×T или Iпост=I=
 .
. .
. , κф≠1,11. Это отклонение косвенно свидетельствует о том, насколько несинусоидальный ток отличается от синусоидального.
, κф≠1,11. Это отклонение косвенно свидетельствует о том, насколько несинусоидальный ток отличается от синусоидального. .
.




 — резонансная частота напряжения, определяемая из условия
— резонансная частота напряжения, определяемая из условия




 где
где


 .
.