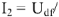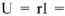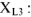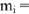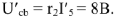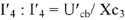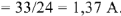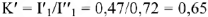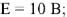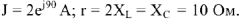Достаточно сложным и чаще всего не изучаемым аспектом темы переменный ток является метод построения векторных диаграмм. Анализируя вынужденные электромагнитные колебания, мы уже обсудили сдвиг тока и напряжения на реактивных сопротивлениях (катушка индуктивности и конденсатор) по сравнению с активным сопротивлением (резистор). Тогда одним из задаваемых вопросов задачи является вопрос о направлении суммарного тока или напряжения в данный конкретный момент времени. Для ответа на этот вопрос и используется метод построения векторных диаграмм.
Векторная диаграмма — это изображение гармонически изменяющихся величин (текущего тока и напряжения) в виде векторов на плоскости.
Рис. 1. Векторная диаграмма
Построение векторных диаграмм происходит в прямоугольной декартовой системе координат. Построение начинается с проведения вектора, численно равного амплитудному значению тока в цепи. Данный вектор сонаправим в осью ОХ (рис. 1.1).
Т.к. напряжение на активном сопротивлении находится в одной фазе с током, то вектор амплитуды напряжения сонаправлен с вектором тока (рис. 1.2. красный).
На катушке напряжение опережает ток, поэтому отложим вектор амплитуды напряжения на катушке () вверх под углом
относительно вектора тока (рис. 1.2. синий).
На конденсаторе напряжение отстаёт от тока, поэтому отложим вектор амплитуды напряжения на конденсаторе () вниз под углом
относительно вектора тока (рис. 1.2. зелёный).
Угол , используемый в логике построений, используется в случае идеальности контура и катушки.
Для построения общего вектора напряжения достаточно векторно сложить напряжения:
(1)
Проще всего сначала найти вектор-сумму (т.к. они расположены вдоль одной прямой). В нашем случае, эти вектора разнонаправлены, найдём
(рис. 1.3. жёлтый).
И последнее, осталось сложить получившийся вектор с вектором для получения значения полного напряжения в цепи (рис. 1.4. оранжевый). Для получения модуля вектора воспользуемся теоремой Пифагора, т.к. вектора находятся под прямым углом. Тогда:
(2)
- где
Угол — угол между вектором силы тока и полного напряжения называется сдвигом фаз между колебаниями силы тока и напряжения. Данный параметр можно найти и исходя из параметров системы:
(3)
- где
Вывод: задачи на данную тематику касаются поиска сдвига фаз между колебаниями силы тока и напряжения через график (рис. 1.4) или через соотношение (3), а также поиска полного напряжения в цепи также через график (рис. 1.4) или через соотношение (2).
Угол сдвига фаз между током и напряжением
Начальные фазы электромагнитных синусоидальных колебаний первичного и вторичного напряжения, с частотой одинаковой величины, могут существенно различаться на некоторый угол сдвига фаз (угол φ). Переменные величины могут неоднократно в течение определенного периода некоторого времени изменяются с определенной частотой. Если электрические процессы имеют неизменный характер, а сдвиг фаз равен нулю, это свидетельствует о синхронизме источников величин переменного напряжения, например, трансформаторов. Сдвиг фазы служит определяющим фактором коэффициента мощности в электрических сетях переменного тока.
Угол сдвига фаз находится при необходимости, тогда, если один из сигналов является опорным, а второй сигнал с фазой в самом начале совпадает с углом сдвига фаз.
Измерение угла сдвига фаз производится прибором, в котором присутствует нормированная погрешность.
Фазометр может производить измерение угла сдвига в границах от 0 о до 360 о в некоторых случаях от -180 о С до +180 о С, а диапазон измеряемых частот сигналов может колебаться от 20Гц до 20 ГГц. Измерение гарантируется в том случае если напряжение входного сигнала равно от 1 мВ до 100 В, если же напряжение входного сигнала превышает эти границы точность измерения не гарантируется.
Что такое фаза, фазовый угол и сдвиг фаз
Говоря о переменном токе, часто оперируют такими терминами как «фаза», «фазовый угол», «сдвиг фаз». Обычно это касается синусоидального переменного или пульсирующего тока (полученного путем выпрямления синусоидального тока).
Поскольку периодическое изменение ЭДС в сети или тока в цепи — это гармонический колебательный процесс
, то и функция, описывающая данный процесс, — гармоническая, то есть синус или косинус, в зависимости от начального состояния колебательной системы.
Аргументом функции в данном случае является как раз фаза, то есть положение колеблющейся величины (тока или напряжения) в каждый рассматриваемый момент времени относительно момента начала колебаний. А сама функция принимает значение колеблющейся величины, в этот же момент времени.
Чтобы лучше понять значения термина «фаза», обратимся к графику зависимости напряжения в однофазной сети переменного тока от времени. Здесь мы видим что, напряжение изменяется от некоторого максимального значения Um до -Um, периодически проходя чрез ноль.
В процессе изменения, напряжение принимает множество значений в каждый момент времени, периодически (спустя период времени Т) возвращаясь к тому значению, с которого начиналось наблюдение за данным напряжением.
Можно сказать, что в любой момент времени напряжение находится в определенной фазе, которая зависит от нескольких факторов: от времени t, прошедшего от начала колебаний, от угловой частоты, и от начальной фазы. То что стоит в скобках — полная фаза колебаний в текущий момент времени t. Пси — начальная фаза.
Фазовый угол
Начальную фазу называют в электротехнике еще начальным фазовым углом
, поскольку фаза измеряется в радианах или в градусах, как и все обычные геометрические углы. Пределы изменения фазы лежат в интервале от 0 до 360 градусов или от 0 до 2*пи радиан.
На приведенном выше рисунке видно, что в момент начала наблюдения за переменным напряжением U, его значение не было нулем, то есть фаза уже успела в данном примере отклониться от нуля на некоторый угол Пси, равный около 30 градусов или пи/6 радиан — это и есть начальный фазовый угол.
В составе аргумента синусоидальной функции, Пси является константной, поскольку данный угол определяется в начале наблюдения за изменяющимся напряжением, и потом уже в принципе не изменяется. Однако его наличие определяет общий сдвиг синусоидальной кривой относительно начала координат.
По ходу дальнейшего колебания напряжения, текущий фазовый угол изменяется, вместе с ним изменяется и напряжение.
Для синусоидальной функции, если полный фазовый угол (полная фаза с учетом начальной фазы) равен нулю, 180 градусам (пи радиан) или 360 градусам (2*пи радиан), то напряжение принимает нулевое значение, а если фазовый угол принимает значение 90 градусов (пи/2 радиан) или 270 градусов (3*пи/2 радиан) то в такие моменты напряжение максимально отклонено от нуля.
Фазовый сдвиг
Обычно в ходе электротехнических измерений в цепях переменного синусоидального тока (напряжения), наблюдение ведут одновременно и за током и за напряжением в исследуемой цепи. Тогда графики тока и напряжения изображают на общей координатной плоскости.
В этом случае частота изменения тока и напряжения идентичны, но различны, если смотреть на графики, их начальные фазы. В этом случае говорят о фазовом сдвиге между током и напряжением, то есть о разности их начальных фазовых углов.
Иными словами фазовый сдвиг определяет то, на сколько одна синусоида смещена во времени относительно другой. Фазовый сдвиг, как и фазовый угол, измеряется в градусах или радианах. По фазе опережает тот синус, период которого начинается раньше, а отстает по фазе тот, чей период начинается позже. Фазовый сдвиг обозначают обычно буквой Фи.
Методы измерения угла сдвига фаз
Существует несколько способов измерения угла сдвига фаз, это:
- Использование двухлучевого или двухканального осциллографа.
- Компенсационный метод основан на сравнении измеряемого фазового сдвига, с фазовым сдвигом, который предоставляется образцовым фазовращателем.
- Суммарно-разностный метод, он заключается в использовании гармонических или сформированных прямоугольных сигналов.
- Преобразование сдвига фаз во временном интервале.
Как измеряется угол сдвига фаз осциллографом
Осциллографический способ можно отнести к самому простейшему с погрешностью в районе 5 о . Определение сдвига осуществляется при помощи осциллограмм. Существует четыре осциллографических метода:
- Применение линейной развертки.
- Метод эллипса.
- Метод круговой развертки.
- Использование яркостных меток.
Определение угла сдвига фаз зависит от характера нагрузки. При определении фазного сдвига в первичной и вторичной цепях трансформатора, углы могут считаться равными и практически не отличаются друг от друга.
Угол сдвига фаз напряжений, измеряемый по эталонному источнику частоты и при использовании измерительного органа лает возможность обеспечить точность всех последующих измерений. Фазные напряжения и угол сдвига фаз зависят от нагрузки, так симметричная нагрузка обуславливает равенство фазного напряжения , токов нагрузки и угол фазного сдвига, также будет равна нагрузка по потребляемой мощности на всех фазах электроустановки.
Угол сдвига фаз между током и напряжением в несимметричных трехфазных цепях не равны друг другу. Для того чтобы вычислить угол сдвига фаз (угол φ) в цепь включают последовательно присоединенные сопротивления (резисторы), индуктивности и конденсаторы (емкости).
Рис. №1. Последовательное соединение сопротивления, индуктивности и емкости для вычисления угла сдвига фаз. В этом контуре протекает переменный ток, который способствует возникновению ЭДС.
Рис. №2. Схема проведения опыта по определению сдвига фаз между током и напряжением. Слева показаны схемы подключения конденсаторов, катушек индуктивности и резисторов, справа показаны результаты опыта.
Из результатов опыта можно определить, что сдвиг фаз между напряжением и током служит при определении нагрузки и не может зависеть от переменных величины тока и напряжения в электрической сети.
Как вывод, можно сказать, что:
- Составляющие элементы комплексного сопротивления, такие как резистор и емкость, а также проводимость не будут взаимообратными величинами.
- Отсутствие одного из элементов делает резистивные и реактивные значения, которые входят в состав комплексного сопротивления и проводимости и делают их величинами взаимообратными.
- Реактивные величины в комплексном сопротивлении и проводимости используются с противоположным знаком.
Угол сдвига фаз между напряжением и током всегда выражается, как главный аргументированный фактор комплексного сопротивления φ.
Источник
Урок 43-2 (продолжение) Переменный ток
Рассмотрим по отдельности случаи подключения внешнего источника переменного тока к резистру с сопротивлением R
, конденсатору емкости
C
и катушки индуктивности
L
. Во всех трех случаях напряжения на резисторе, конденсаторе и катушке равны напряжению источника переменного тока.
1. Резистор в цепи переменного тока
Сопротивление R называют активным, потому что цепь с таким сопротивлением поглощает энергию.
Активное сопротивление — устройство, в котором энергия электрического тока необратимо преобразуется в другие виды энергии (внутреннюю, механическую)
Пусть напряжение в цепи меняется по закону: u = Umcos ωt ,
тогда сила тока меняется по закону: i = u/R = IRcosωt
u – мгновенное значение напряжения;
i – мгновенное значение силы тока;
IR
— амплитуда тока, протекающего через резистор.
Связь между амплитудами тока и напряжения на резисторе выражается соотношением RIR
=
UR
Колебания силы тока совпадают по фазе с колебаниями напряжения. (т.е. фазовый сдвиг между током и напряжением на резисторе равен нулю).
2. Конденсатор в цепи переменного тока
При включении конденсатора в цепь постоянного напряжения сила тока равна нулю, а при включении конденсатора в цепь переменного напряжения сила тока не равна нулю. Следовательно, конденсатор в цепи переменного напряжения создает сопротивление меньше, чем в цепи постоянного тока.
Соотношение между амплитудами тока IC
и напряжения
Ток опережает по фазе напряжение на угол π/2.
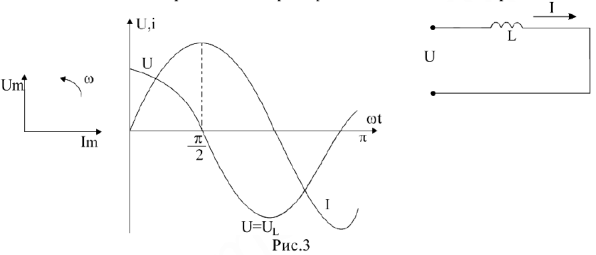
3. Катушка в цепи переменного тока
В катушке, включенной в цепь переменного напряжения, сила тока меньше силы тока в цепи постоянного напряжения для той же катушки. Следовательно, катушка в цепи переменного напряжения создает большее сопротивление, чем в цепи постоянного напряжения.
Соотношение между амплитудами тока IL
и напряжения
UL
:
Ток отстает по фазе от напряжения на угол π/2.
Теперь можно построить векторную диаграмму для последовательного RLC-контура, в котором происходят вынужденные колебания на частоте ω. Поскольку ток, протекающий через последовательно соединенные участки цепи, один и тот же, векторную диаграмму удобно строить относительно вектора, изображающего колебания тока в цепи. Амплитуду тока обозначим через I
. Фаза тока принимается равной нулю. Это вполне допустимо, так как физический интерес представляют не абсолютные значения фаз, а относительные фазовые сдвиги.
Векторная диаграмма на рисунке построена для случая, когда или В этом случае напряжение внешнего источника опережает по фазе ток, текущий в цепи, на некоторый угол φ.
Векторная диаграмма для последовательной RLC-цепи
Из рисунка видно, что
Из выражения для I
видно, что амплитуда тока принимает максимальное значение при условии
Явление возрастания амплитуды колебаний тока при совпадении частоты ω внешнего источника с собственной частотой ω электрической цепи называется электрическим резонансом
. При резонансе
Сдвиг фаз φ между приложенным напряжением и током в цепи при резонансе обращается в нуль. Резонанс в последовательной RLC-цепи называется резонансом напряжений
. Аналогичным образом с помощью векторной диаграммы можно исследовать явление резонанса при параллельном соединении элементов
R
,
L
и
C
(так называемый
резонанс токов
).
При последовательном резонансе (ω = ω) амплитуды UC
и
UL
напряжений на конденсаторе и катушке резко возрастают:
Рисунок иллюстрирует явление резонанса в последовательном электрическом контуре. На рисунке графически изображена зависимость отношения амплитуды UC
напряжения на конденсаторе к амплитуде напряжения источника от его частоты ω. Кривые на рисунке называются
резонансными кривыми
.
Источник
Сдвиг фаз переменного тока и напряжения
Мощность постоянного тока, как мы уже знаем, равна произведению напряжения на силу тока. Но при постоянном токе направления тока и напряжения всегда совпадают. При переменном же токе совпадение направлений тока и напряжения имеет место только в случае отсутствия в цепи тока конденсаторов и катушек индуктивности.
Для этого случая формула мощности
остается справедливой.
На рисунке 1 представлена кривая изменения мгновенных значений мощности для этого случая (направление тока и напряжения совпадают). Обратим внимание на то обстоятельство, что направления векторов напряжения и тока в этом случае совпадают, то есть фазы тока и напряжения всегда одинаковы.
Рисунок 1. Сдвиг фаз тока и напряжения. Сдвига фаз нет, мощность все время положительная.
При наличии в цепи переменного тока конденсатора или катушки индуктивности, фазы тока и напряжения совпадать не будут.
О причинах этого несовпадения читайте в моем учебники для емкостной цепи и для индуктивной цепи, а сейчас установим, как будет оно влиять на величину мощности переменного тока.
Представим себе, что при начале вращения радиусы-векторы тока и напряжения имеют различные направления. Так как оба вектора вращаются с одинаковой скоростью, то угол между ними будет оставаться неизменным во все время их вращения. На рисунке 2 изображен случай отставания вектора тока Im от вектора напряжения Um на угол в 45°.
Рисунок 2. Сдвиг фаз тока и напряжения. Фазы тока и напряжения сдвинуты на 45, мощность в некоторые периоды времени становиться отрицательной.
Рассмотрим, как будут изменяйся при этом ток и напряжение. Из построенных синусоид тока и напряжения видно, что когда напряжение проходит через ноль, ток имеет отрицательное значение.
Затем напряжение достигает своей наибольшей величины и начинает уже убывать, а ток хотя и становится положительным, но еще не достигает наибольшей величины и продолжает возрастать. Напряжение изменило свое направление, а ток все еще течет в прежнем направлении и т. д. Фаза тока все время запаздывает по сравнению с фазой напряжения. Между фазами напряжения и тока существует постоянный сдвиг, называемый сдвигом фаз.
Действительно, если мы посмотрим на рисунок 2, то заметим, что синусоида тока сдвинута вправо относительно синусоиды напряжения. Так как по горизонтальной оси мы откладываем градусы поворота, то и сдвиг фаз можно измерять в градусах. Нетрудно заметить, что сдвиг фаз в точности равен углу между радиусами-векторами тока и напряжения.
Вследствие отставания фазы тока от фазы напряжения его направление в некоторые моменты не будет совпадать с направлением напряжения. В эти моменты мощность тока будет отрицательной, так как произведение положительной величины на отрицательную величину всегда будет отрицательным. Эта значит, что внешняя электрическая цепь в эти моменты становится не потребителем электрической энергии, а источником ее. Некоторое количество энергии, поступившей в цепь во время части периода, когда мощность была положительной, возвращается источнику энергии в ту часть периода, когда мощность отрицательна.
Чем больше сдвиг фаз, тем продолжительнее становятся части периода, в течение которых мощность делается отрицательной, тем, следовательно, меньше будет средняя мощность тока.
При сдвиге фаз в 90° мощность в течение одной четверти периода будет положительной, а в течение другой четверти периода — отрицательной. Следовательно, средняя мощность тока будет равна нулю, и ток не будет производить никакой работы (рисунок 3).
Рисунок 3. Сдвиг фаз тока и напряжения. Фазы тока и напряжения сдвинуты на 90, мощность в течении одной четвери периода положительна, а в течении другой отрицательна. В среднем мощьноть равна нулю.
Теперь ясно, что мощность переменного тока при наличии сдвига фаз будет меньше произведения эффективных значений тока и напряжения, т. е. формулы
в этом случае будут неверны
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Векторная диаграмма токов и напряжений
Процессы, протекающие в электроцепи переменного тока с активным сопротивлением и реактивной индуктивностью, можно наглядно выразить в графическом виде.
Статья даст описание, что такое векторные диаграммы, где и для чего они используются. Также будет описана временная диаграмма и ее назначение. В конце будет дан пример построения простой диаграммы для электроцепи с последовательным соединением элементов.
Определение
Векторная диаграмма токов и напряжений — это геометрическое изображение всех процессов, величин и амплитуд синусоидального тока. Все имеющиеся величины располагаются на плоскости в виде векторов.
Построение векторной диаграммы использует физика и электротехника. Благодаря созданию такой диаграммы можно значительно упростить выполняемые расчеты, а так же в наглядном и доступном виде отобразить происходящие процессы.
Метод векторных диаграмм позволяет также увидеть в цепи переменного тока возникающие короткие и межфазовые замыкания, а также вычислить возможные потери мощности.
Обычно такая диаграмма строится вместе с временной. Временная диаграмма — это графическое изображение входа и выхода в электрической цепи. Временные диаграммы помогают определить временной промежуток между началом, протеканием и окончанием сигнала. Например, при нажатии на кнопку возникает сигнал, который поступает к приемнику и запускает процесс его работы.
Временные диаграммы также применимы к синусоидальной электрической цепи, так как этот ток имеет начальную точку отсчета (включение питания) и время движения от источника тока к потребителю. Такие диаграммы представляют собой график, на котором изображается начальная точка отсчета, вектор времени и углы смещения фаз.
Разновидности
Разобравшись, что такое и для чего применяется векторная диаграмма, нужно узнать какие разновидности построения существуют. Они отличаются по характеру построения и типу. По характеру бывают:
- Точными. Векторная точная диаграмма — это отображение выполненного численного расчета в соответствующем масштабе. С помощью нее определяют параметры фаз и амплитудные значения строго геометрическим способом.
- Качественные. Такие гистограммы строят для наблюдения взаимосвязи между электровеличинами без использования числовых характеристик. Такой способ позволяет экспериментировать с различными параметрами и моделировать процессы в электроцепях.
Векторную диаграмму токов можно построить 2 разными способами:
- Круговым. В ее принципе лежит вектор, который описывает изменение характеристик путем образования круга или полукруга на плоскости. При таком варианте учитывается направление движения с учетом направления положения вектора.
- Линейным. Такой векторной диаграмме при изменении характеристик направление изменяется строго прямолинейно.
Оба построения могут использоваться для расчета характеристик переменного тока в цепи с сопротивлением и индуктивностью.
Построение
Построение простых векторных диаграмм будет рассмотрено в данном разделе. Для примера можно взять простую цепь с несколькими элементами и их значениями. Такая схема подразумевает последовательное соединение элементов между собой. Цепь состоит из катушки индуктивности, конденсатора и активного сопротивления. Параметры каждого элемента цепи приведены ниже.
- Катушка индуктивности UL с напряжением 15 вольт. Ток в индуктивном сопротивлении имеет сдвиг фазы 90°.
- Конденсатор UC с напряжением 20 вольт и опережением на 90 градусов.
- Напряжение резистора UR 10 вольт, его направление совпадает с током I.
- Сила тока в цепи I равняется 3 ампера.
Далее можно сделать простую диаграмму, которая поможет определить напряжение для всей схемы.
- Отложить на плоскости I в виде горизонтальной линии с масштабом 1 A/см (масштаб может быть любым, главное — выполнять все элементы диаграммы одного типа в одном масштабе). Сам ток равен 3 ампера, поэтому его длина будет равна 3 см.
- Теперь необходимо отложить вертикальный вектор UL в масштабе 5 В/см. Он отображает напряжение катушки индуктивности и равен 15 вольт. Его длина на плоскости составит в данном масштабе так же 3 см.
- Далее нужно графически обозначить вектор напряжения активного сопротивления. Его точка отсчета располагается на окончании вертикального вектора UL. Для принятого масштаба 5 В/см ему соответствует вектор длиной 2 см. Линия должна быть строго параллельна горизонтальному вектору I.
- Теперь нужно отобразить на данной диаграмме напряжение конденсатора UC. Его началом будет конечная точка вектора UR, а конец данного вектора будет расположен ниже горизонтального вектора I. В масштабе 5 В/см ему соответствует вектор длиной 4 см.
- Чтобы определить соответствующее такой схеме общение напряжение U надо будет сделать следующее. Начало вектора расположено в принятой точке отсчета, а конец его будет расположен в конечной точке вектора UC.
Поэтому если есть схема с последовательным соединением элементов, то всегда можно довольно просто построить векторную диаграмму и рассчитать общее напряжение для такой схемы.
Способ 2
Построение векторных диаграмм с учетом всех известных значений для цепи переменного тока с последовательным соединением конденсатора, резистора и катушки индуктивности. При таком построении нам так же известно напряжение самой цепи. Цепь состоит из:
- Резистора UR;
- Конденсатора UC;
- Катушки UL.
Далее надо:
- На плоскости Im откладывается вектор UR (резистор). Его направление точно совпадает с током, поэтому это будет горизонтальная линия.
- От точки отсчета откладывается вниз вектор UC (конденсатор). Вектор откладывается под углом 90 градусов вниз, так как он имеет указанное ранее опережение 90°.
- От этой же точки отсчета откладывается вектор UL (катушка индуктивности). Ее значение откладывается ровно на 90 градусов вертикально, так как есть сдвиг фазы на 90 градусов.
Данная диаграмма может использоваться для контроля и расчета влияния всех известных параметров цепи и элементов, а также их взаимосвязи между собой.
- Показать результат сложения вектора UL и UC.
- При увеличении величины сопротивления определить разницу между напряжением и сопротивлением можно, используя новый вектор Um.
- Кроме того можно определить угол сдвига фазы φ в цепи.
Основное преимущество векторной диаграммы заключается в следующем — простое и быстрое сложение, вычитание двух параметров во время расчета электрических цепей.
Понятие о векторах и векторных диаграммах также подразумевает расчет цепи питания трехфазной сети, подключенной по методу звезды. Она строится с учетом сразу 3 отложенных векторов от 0 оси ординат. Такое построение определяет вектор от источника тока к приемнику. Строится вектор со следующими значениями:
- На оси ОХ откладываются настоящие значения величин, а на оси OY мнимые значения.
- Угловая величина обозначается как W.
- Также присутствует сам вектор Im и угол сдвига фаз φ.
Далее нужно сделать:
- На плоскости выбрать точку отсчета.
- От нее отложить вектор Im, учитывая угол сдвига фаз равный 90°.
- Длина вектора Im равна значению его напряжения и откладывается в выбранном масштабе.
Таким же образом на плоскость накладываются еще две прямые линии. Общая диаграмма покажет симметричность фаз или их сдвиг при появлении короткого замыкания. Такая диаграмма может стать примером для расчета напряжения, тока или нагрузки на каждую фазу с моделированием различных параметров.
Заключение
Векторные диаграммы сложны в понимании при расчете сложных цепей, с большим количеством сопротивлений и индуктивностью. Также, при расчете стоит учитывать тип соединения всех элементов, симметрию цепи и основные ее значения.
Видео по теме
Как построить векторную диаграмму токов и напряжений
Расчеты в цепях с синусоидальными напряжениями и токами упрощаются, если вместо синусоид оперировать с их изображениями — вращающимися векторами (рис. 1).
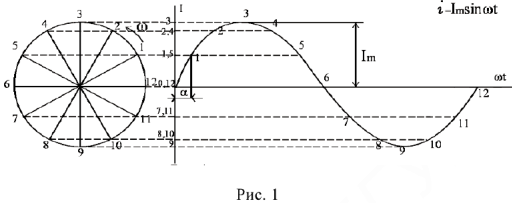
Проекция конца вектора на ось координат совершает синусоидальные колебания : каждое мгновенное значение тока, соответствующее моменту времени 
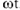
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Таким образом, синусоидальная функция условно представляется вектором, длина которого определяется максимальным или действующим ее значением, а направление — ее начальной фазой; положительная начальная фаза откладывается от горизонтальной оси в сторону вращения векторов (против часовой стрелки). Векторы токов и напряжений, вращаясь с одной и той же
угловой скоростью 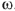
Алгебраическому суммированию синусоид, т.е. суммированию их мгновенных значений, соответствуют геометрические действия над изображающими их векторами. Применение в этой форме законов Кирхгофа даст возможность путем построения векторных диаграмм достаточно просто и наглядно рассчитывать электрические цепи. Приступая к графическому расчету пеней переменного тока, следует помнить, что физические процессы на участках цепи с сопротивлением, индуктивностью, емкостью весьма различны.
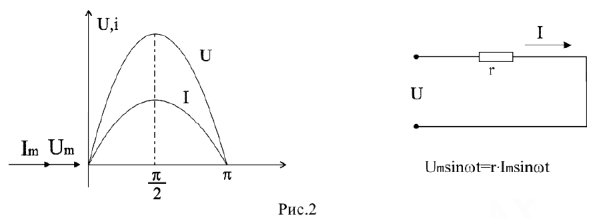
Соответственно вектор тока и вектор напряжения имеют одно направление.
В индуктивном элементе ток отстает от напряжения на 
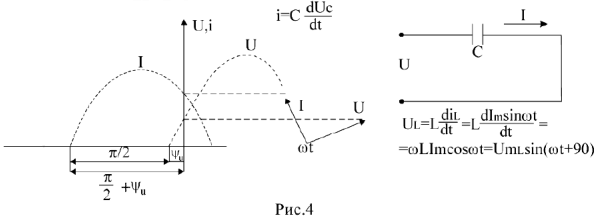
В емкостном элементе в активном сопротивлении ток и напряжение совпадают по фазе (рис.2), ток опережает напряжение на 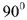
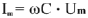
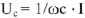
Рассмотрим расчет разветвленных электрических цепей с помощью векторных диаграмм.
Графоаналитический метод расчета
К оглавлению…
Графоаналитический метод расчета — это совокупность графического метода и метода пропорционального пересчета. Метод основан на том, что в линейной цепи токи пропорциональны напряжениям, векторная диаграмма напряжений и токов, рассчитанная и построенная для одного значения питающего цепь напряжения, сохранит свой вид при изменении величины этого напряжения, на диаграмме при этом изменятся лишь масштабы напряжений и токов.
Пример №1.
Для цепи (рис.5) известны параметры
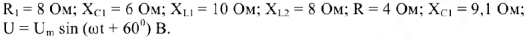
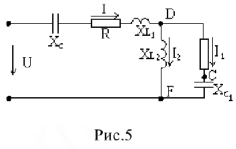
Требуется определить действующее значение токов ветвей, напряжений на участках цепи, начальные фазы токов и напряжений.
Построение векторной диаграммы начинается с наиболее удаленного источника элемента цепи, как говорят, с «конца» схемы. Принимаем масштабы для тока 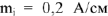
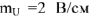
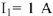
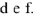
Падение напряжения на емкостном сопротивлении равно по величине 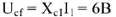
Падение напряжения на 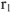
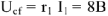
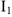
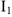
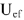
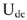
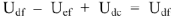
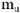
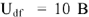
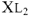
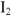
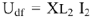
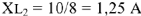
Для узла 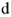
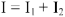
Определив величину тока 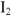
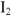
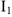
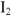
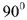
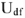
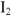
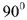
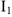

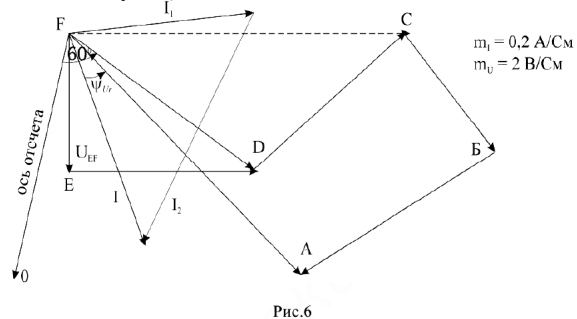
Запишем и графически решим уравнение по второму закону Кирхгофа для контура 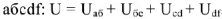
Перейдем к построению этого уравнения. Примем конец вектора 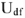
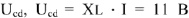

Принимаем конец вектора 
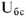
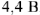


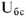
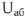
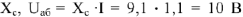
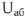
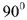

Если теперь соединим начало координат (точку 
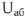
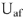
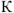
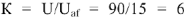
Входное напряжение имеет начальную фазу 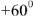
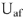
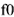

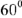
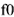
Пользуясь векторной диаграммой, можно записать мгновенные значения всех рассчитанных величин. Например, ток во второй ветви:
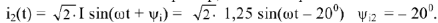
Напряжение участка 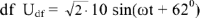
Построенная в такой последовательности векторная диаграмма напряжений носит название топографической.
Топографическая диаграмма
Топографические диаграммы представляют собой диаграммы комплексных потенциалов, причем каждой точке схемы соответствует определенная точка на топографической диаграмме.
Топографическая диаграмма позволяет измерить величину и начальную фазу напряжения любого участка цепи, не участвующею в расчете. Например,
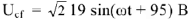
В действующее значение напряжения между точками 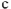

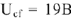
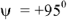
Рассмотрим пример построения топографической диаграммы на комплексной плоскости.
Пример №2.
Дана цепь (рис.7), её параметры:
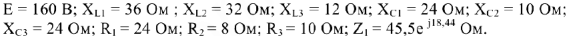
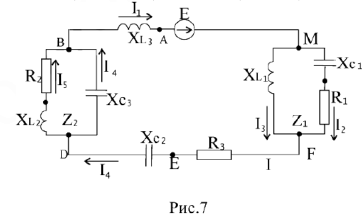
Комплексным методом рассчитаем токи цепи:
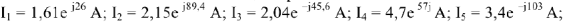
Строим на векторной плоскости диаграмму токов в масштабе 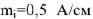
Тогда точка 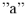
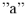
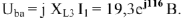
Строим вектор 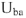
Из точки 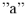
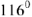
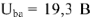
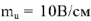
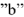
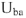
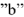
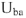
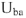
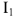
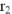
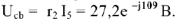
По полученному выражению из точки 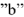
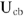
Контроль построения: вектор 
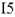
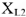
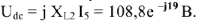
Из точки 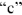
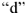
Контроль построения: вектор 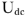
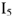
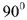
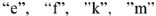
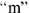
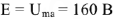
Пользуясь топографической диаграммой, легко определить напряжения между любыми точками цепи. Например, комплекс напряжения 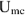
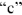
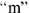
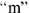
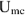
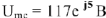
ПримсрЗ. Рассмотрим расчет цепи на рис.7 графоаналитическим методом
Зададимся условным значением тока 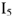
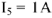
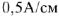
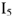
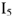
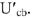
В масштабе 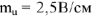
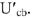
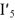
Вычислив напряжение 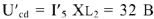
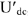
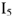
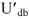
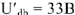
Из конца вектора тока 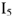
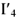
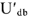
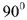
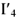
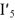
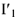
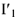
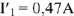
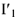
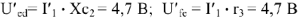
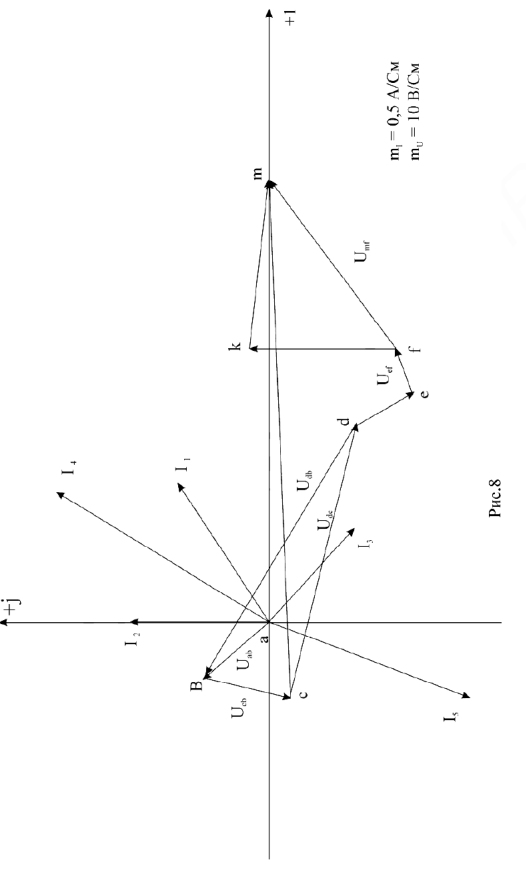
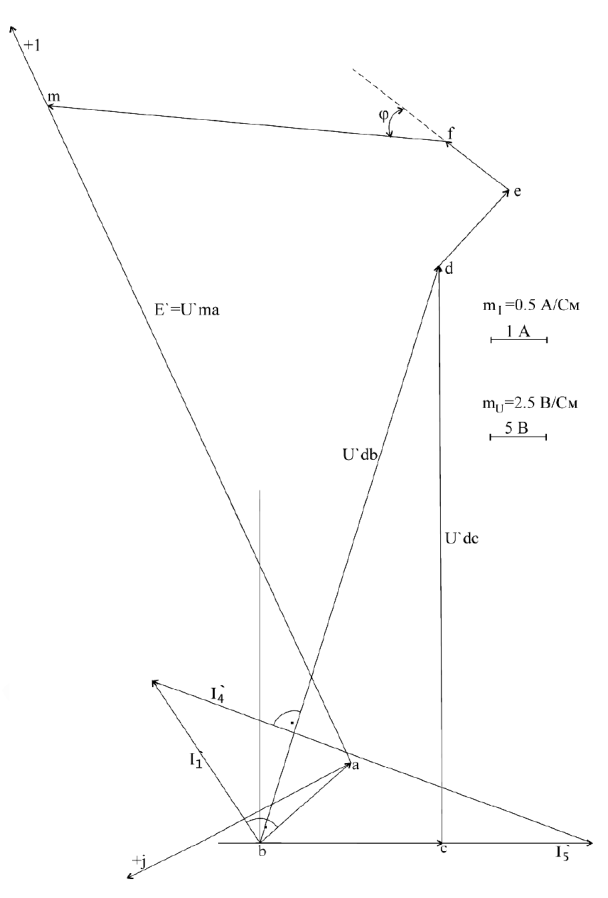
Рис.9
Из точки 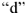
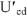
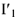
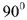
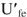
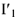
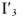
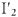
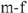
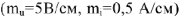
Тогда
С учетом фазовых соотношений между током 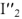
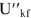
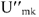
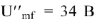
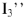
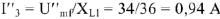
Построив вектор 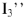
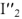
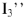
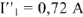
Чтобы привести диаграмму на рис.10 в соответствие с найденными ранее значениями тока 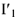
Умножая длины всех векторов на рис.10 на коэффициент 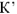
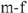
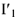
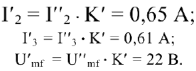
Измеряем угол 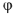
Под углом 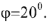
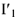
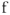
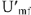
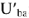
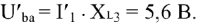
Поскольку напряжение 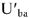
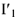
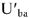
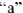
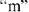
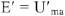
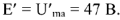
Векторная диаграмма на рис.9 является также и топографической диаграммой. ЭДС 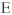
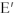
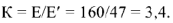
Поскольку рассчитываемая цепь линейна, то напряжения и токи, вызываемые ЭДС 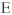
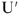
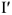
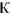
Таким образом

Чтобы измерить начальные фазы токов и напряжений, следует на рис.9 выбрать такую систему координат, в которой ЭДС 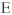
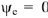
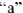
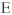
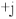
Рассмотрим пример построения векторной диаграммы по известным токам и напряжениям (действующие значения напряжений и токов получены экспериментально). В этом случае при помощи векторной диаграммы можно решить обратную задачу расчета цепи: но токам и напряжениям цепи определить эквивалентные параметры двухполюсников, составляющих цепь.
Пример №3.
Дана цепь (рис.11), известны показания измерительных приборов. Найдем параметры двухполюсника, эквивалентного данной схеме.
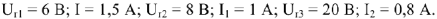
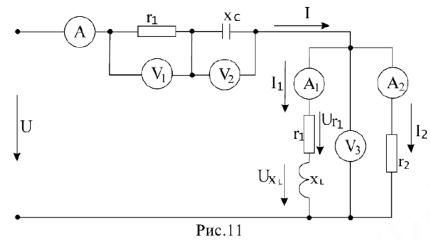
Для данной схемы можно составить три уравнения по законам Кирхгофа:
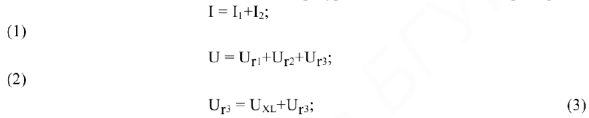
Решим эти уравнения графически. Построение диаграммы следует начать с построения вектора 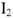
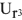
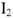
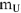
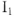
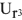
Используя показания амперметров 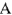
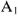
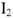
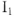
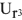
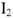
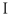
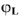
Далее достраивается диаграмма напряжений: напряжения 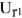
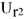
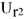
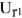
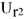
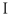
Замыкающий вектор на диаграмме напряжений соединяет начало построения и конец вектора 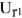
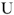
Теперь с помощью треугольников напряжений (сопротивлений), токов (проводимостсй), построенных для какого-либо участка цепи или для всей цепи можно найти сопротивления, проводимости и параметры двухполюсника.
Определим эквивалентные параметры всей цени заданной схемы (см. рис.11) 
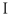
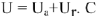
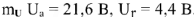
Векторная диаграмма сложной электрической цепи
Векторная диаграмма для сложной электрической цепи может быть построена только после расчета этой цепи; строится она на комплексной плоскости по известным комплексам токов всех ветвей и комплексам напряжений на каждом элементе цепи. Пример 5. Заданы источники энергии, сопротивления схемы
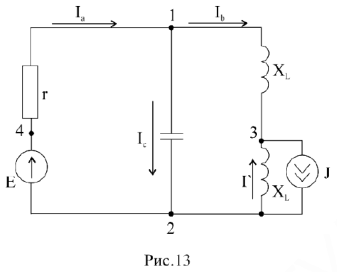
В результате расчета определены токи в ветвях:
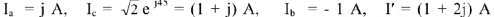
и падения напряжений на каждом элементе схемы:
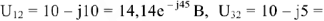
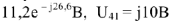
Для построения векторной диаграммы составим уравнение по первому и второму законам Кирхгофа в общем виде и в численном выражении:
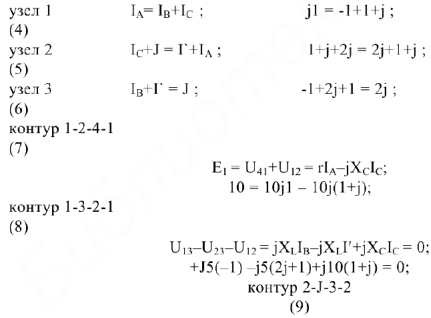
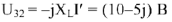
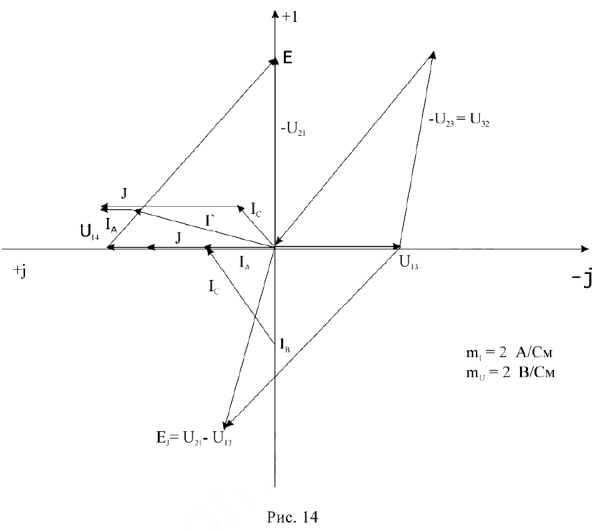
Приступим к построению уравнения (4). В выбранном масштабе токов 
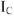
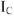
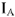
Построена векторная диаграмма токов, отображающая уравнение (4). Для узла 2 графически решаем уравнение (5); из начала координат строим комплекс тока 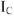
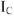
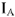
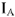
- Перейдем к построению двух независимых уравнений второго закона Кирхгофа (7 и 8).
Из начала координат строим комплекс напряжения 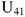
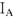
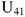
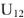
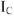
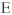
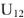
Комплекс ЭДС 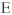
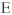
Для контура 1-3-2-1 строится комплекс напряжения 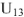
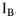
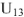
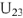
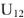
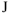
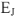
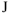
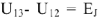
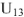
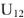
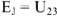
Возможно эти дополнительные страницы вам будут полезны:
- Предмет электротехника
- Решение задач по электротехнике
- Помощь по электротехнике
- Заказать работу по электротехнике
- Контрольная работа по электротехнике