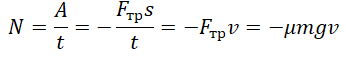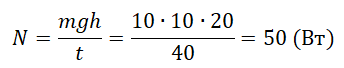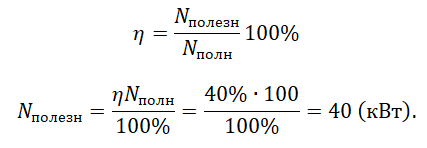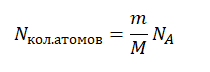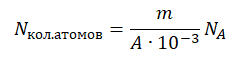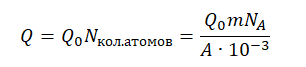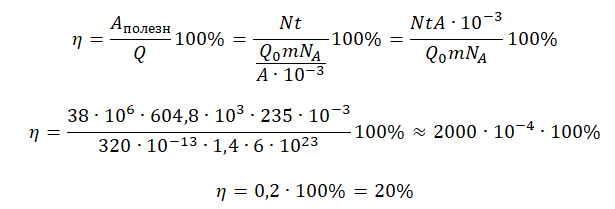Угол между векторами.
Формула вычисления угла между векторами
| cos α = | a · b |
| | a |·| b | |
Примеры задач на вычисление угла между векторами
Примеры вычисления угла между векторами для плоских задачи
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 3 2 = √ 16 + 9 = √ 25 = 5
Найдем угол между векторами:
| cos α = | a · b | = | 24 | = | 24 | = 0.96 |
| | a | · | b | | 5 · 5 | 25 |
Решение: Найдем скалярное произведение векторов:
a · b = 5 · 7 + 1 · 5 = 35 + 5 = 40.
Найдем модули векторов:
| a | = √ 7 2 + 1 2 = √ 49 + 1 = √ 50 = 5√ 2
| b | = √ 5 2 + 5 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
| cos α = | a · b | = | 40 | = | 40 | = | 4 | = 0.8 |
| | a | · | b | | 5√ 2 · 5√ 2 | 50 | 5 |
Примеры вычисления угла между векторами для пространственных задач
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 + 0 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 4 2 + 2 2 = √ 16 + 16 + 4 = √ 36 = 6
Найдем угол между векторами:
| cos α = | a · b | = | 28 | = | 14 |
| | a | · | b | | 5 · 6 | 15 |
Решение: Найдем скалярное произведение векторов:
a · b = 1 · 5 + 0 · 5 + 3 · 0 = 5.
Найдем модули векторов:
| a | = √ 1 2 + 0 2 + 3 2 = √ 1 + 9 = √ 10
| b | = √ 5 2 + 5 2 + 0 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
cos α = a · b | a | · | b | = 5 √ 10 · 5√ 2 = 1 2√ 5 = √ 5 10 = 0.1√ 5
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Нахождение угла между векторами
Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.
Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →
Углом между векторами a → и b → называется угол между лучами О А и О В .
Полученный угол будем обозначать следующим образом: a → , b → ^
Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.
a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.
Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.
Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.
Нахождение угла между векторами
Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.
Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .
Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:
cos a → , b → ^ = a → , b → a → · b →
Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.
Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно — 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.
Решение
Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = — 9 3 · 6 = — 1 2 ,
Теперь определим угол между векторами: a → , b → ^ = a r c cos ( — 1 2 ) = 3 π 4
Ответ: cos a → , b → ^ = — 1 2 , a → , b → ^ = 3 π 4
Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.
Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:
cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2
А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2
Исходные данные: векторы a → = ( 2 , 0 , — 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.
Решение
- Для решения задачи можем сразу применить формулу:
cos a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 2 2 + 0 2 + ( — 1 ) 2 · 1 2 + 2 2 + 3 2 = — 1 70 ⇒ a → , b → ^ = a r c cos ( — 1 70 ) = — a r c cos 1 70
- Также можно определить угол по формуле:
cos a → , b → ^ = ( a → , b → ) a → · b → ,
но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( — 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 = — 1 cos a → , b → ^ = a → , b → ^ a → · b → = — 1 5 · 14 = — 1 70 ⇒ a → , b → ^ = — a r c cos 1 70
Ответ: a → , b → ^ = — a r c cos 1 70
Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.
Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , — 1 ) , B ( 3 , 2 ) , C ( 7 , — 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .
Решение
Найдем координаты векторов по координатам заданных точек A C → = ( 7 — 2 , — 2 — ( — 1 ) ) = ( 5 , — 1 ) B C → = ( 7 — 3 , — 2 — 2 ) = ( 4 , — 4 )
Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( — 1 ) · ( — 4 ) 5 2 + ( — 1 ) 2 · 4 2 + ( — 4 ) 2 = 24 26 · 32 = 3 13
Ответ: cos A C → , B C → ^ = 3 13
Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:
A B 2 = O A 2 + O B 2 — 2 · O A · O B · cos ( ∠ A O B ) ,
b → — a → 2 = a → + b → — 2 · a → · b → · cos ( a → , b → ) ^
и отсюда выведем формулу косинуса угла:
cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 — b → — a → 2 a → · b →
Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.
Хотя указанный способ имеет место быть, все же чаще применяют формулу:
Как найти угол между векторами
Чтобы найти угол ( phi ) между векторами, вы должны сначала найти косинус угла, а затем из него найти арккосинус, то есть:
( phi=arccos (cos phi) )
Косинус угла между векторами равен скалярному произведению этих векторов, деленному на произведение их длин. Если векторы заданы на плоскости и имеют координаты ( overline=left(a_ ; a_right), overline=left(b_ ; b_right) ) , то косинус между ними рассчитывается по формуле:
ПРИМЕРЫ РАСЧЕТА УГЛОВ МЕЖДУ ВЕКТОРАМИ
Задание: Найти угол ( phi ) между векторами ( overline=(1 ; 3) quad<и>quad overline=(4 ; 2) )
Решение: Сначала по формуле
найти косинус угла между заданными векторами:
Тогда требуемый угол ( phi=arccos left(frac<sqrt<2>><2>right)=45^ <circ>)
Решение: Сначала находим косинус угла между заданными векторами, для этого используем формулу
Подставляя координаты векторов ( overline overline ) , получим
http://zaochnik.com/spravochnik/matematika/vektory/nahozhdenie-ugla-mezhdu-vektorami-primery-i-reshen/
http://www.homework.ru/spravochnik/kak-najti-ugol-mezhdu-vektorami/
Направление равнодействующей для сил приложенных к одной точке, формула
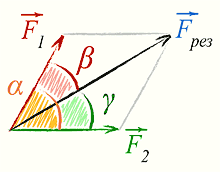 |
Величина равнодействующей двух сил приложенных к одной точке определяется правилом параллелограмма. А Направление равнодействующей определяется по формулам: |
[ sin(β) = frac{F_2}{F_{рез}} sin(α) ]
[ sin(γ) = frac{F_1}{F_{рез}} sin(α) ]
Вычислить, найти углы, направление равнодействующей для сил приложенных к одной точке по формулам (1)
Copyright © FXYZ.ru, 2007 — 2023.
Мобильная β версия | полная
Сила — это одно из важных понятий в физике. Она является причиной изменения состояния любых объектов. В данной статье рассмотрим, что собой представляет эта величина, какие силы бывают, а также покажем, как находить проекцию силы на ось и на плоскость.
Сила и ее физический смысл
В физике сила — это векторная величина, которая показывает изменение количества движения тела за единицу времени. Данное определение полагает силу динамической характеристикой. С точки зрения же статики сила в физике — это мера упругой или пластической деформации тел.
Международная система СИ выражает силу в ньютонах (Н). Что такое 1 ньютон, проще всего понять на примере второго закона классической механики. Математическая запись его следующая:
F¯ = m*a¯
Здесь F¯ — некоторая внешняя сила, действующая на тело массой m, и приводящая к ускорению a¯. Из формулы следует количественное определение одного ньютона: 1 Н — это такая сила, которая приводит к изменению скорости тела массой 1 кг на 1 м/с за каждую секунду.


Примерами динамического проявления силы являются ускорение автомобиля или свободно падающего тела в гравитационном земном поле.
Статическое проявление силы, как было отмечено, связано с явлениями деформации. Здесь следует привести следующие формулы:
F = P*S
F = -k*x
Первое выражение связывает силу F с давлением P, которое она оказывает на некоторую площадку S. Через эту формулу 1 Н можно определить как давление в 1 паскаль, прилагаемое к площадке 1 м2. Например, столб атмосферного воздуха на уровне моря давит на площадку 1 м2 с силой 105 Н!
Второе выражение является классической формой записи закона Гука. Например, растяжение или сжатие пружины на линейную величину x приводит к возникновению противодействующей силы F (в выражении k — коэффициент пропорциональности).
Какие силы бывают
Выше уже было показано, что силы могут быть статические и динамические. Здесь скажем, что помимо этой их особенности, они могут быть силами контакта или дальнодействующие. Например, сила трения, реакции опоры — это контактные силы. Причина их появления заключается в справедливости принципа Паули. Последний гласит, что два электрона не могут занимать одно и то же состояние. Именно поэтому прикосновение двух атомов приводит к их отталкиванию.
Дальнодействующие силы появляются в результате взаимодействия тел через некоторое поле-носитель. Например, такими являются сила гравитации или электромагнитное взаимодействие. Обе силы имеют бесконечный радиус действия, однако, их интенсивность падает, как квадрат расстояния (законы Кулона и всемирного тяготения).

Сила — векторная величина
Разобравшись со смыслом рассматриваемой физической величины, можно перейти к изучению вопроса проекции силы на ось. В первую очередь заметим, что данная величина является векторной, то есть она характеризуется модулем и направлением. Покажем, как рассчитывать модуль силы и ее направление.
Известно, что любой вектор можно задать однозначно в данной системе координат, если известны значения координат его начала и конца. Предположим, что имеется некоторый направленный отрезок MN¯. Тогда его направление и модуль можно определить с помощью следующих выражений:
MN¯ = (x2-x1; y2-y1; z2-z1);
|MN¯| = √((x2-x1)2 + (y2-y1)2 + (z2-z1)2).
Здесь координаты с индексами 2 соответствуют точке N, с индексами 1 — точке M. Вектор MN¯ направлен из M в N.
Для общности мы показали, как находить модуль и координаты (направление) вектора в трехмерном пространстве. Аналогичные формулы без третьей координаты справедливы для случая на плоскости.
Таким образом, модуль силы — это ее абсолютная величина, выраженная в ньютонах. С точки зрения геометрии, модуль — это длина направленного отрезка.
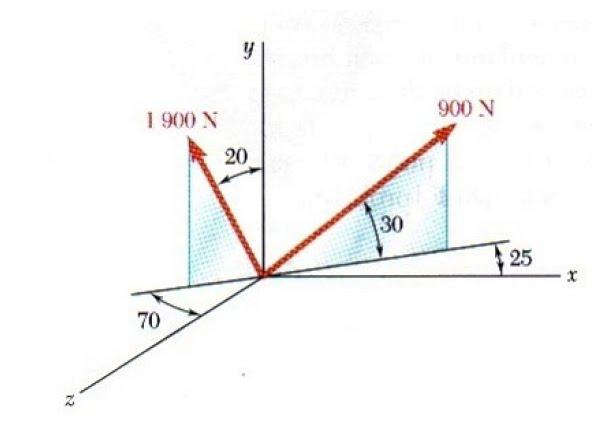
Что такое проекция силы на ось?
Речь о проекциях направленных отрезков на координатные оси и плоскости удобнее всего вести, если предварительно расположить соответствующий вектор в начале координат, то есть в точке (0; 0; 0). Предположим, что у нас имеется некоторый вектор силы F¯. Поместим его начало в точку (0; 0; 0), тогда координаты вектора можно записать так:
F¯ = ((x1 — 0); (y1 — 0); (z1 — 0)) = (x1; y1; z1).
Вектор F¯ показывает направление силы в пространстве в данной координатной системе. Теперь проведем перпендикулярные отрезки из конца F¯ к каждой из осей. Расстояние от точки пересечения перпендикуляра с соответствующей осью до начала координат называется проекцией силы на ось. Не трудно догадаться, что в случае с силой F¯ ее проекции на оси x, y и z будут равны x1, y1 и z1, соответственно. Заметим, что эти координаты показывают модули проекций силы (длину отрезков).
Углы между силой и ее проекциями на координатные оси
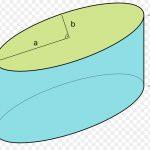
Вычисление этих углов не является сложной задачей. Все, что требуется для ее решения, — это знание свойств тригонометрических функций и умение применять теорему Пифагора.
Например, определим угол между направлением силы и ее проекцией на ось x. Соответствующий прямоугольный треугольник будет образован гипотенузой (вектор F¯) и катетом (отрезок x1). Второй катет — это дистанция от конца вектора F¯ до оси x. Угол α между F¯ и осью x вычисляется по формуле:
α = arccos(|x1|/|F¯|) = arccos(x1/√(x12+y12+z12)).
Как видим, для определения угла между осью и вектором необходимо и достаточно знать координаты конца направленного отрезка.
Для углов с другими осями (y и z) можно записать аналогичные выражения:
β = arccos(|y1|/|F¯|) = arccos(y1/√(x12+y12+z12));
γ = arccos(|z1|/|F¯|) = arccos(z1/√(x12+y12+z12)).
Заметим, что во всех формулах стоят модули в числители, что исключает появление тупых углов. Между силой и ее осевыми проекциями углы всегда меньше или равны 90o.
Сила и ее проекции на плоскости координат
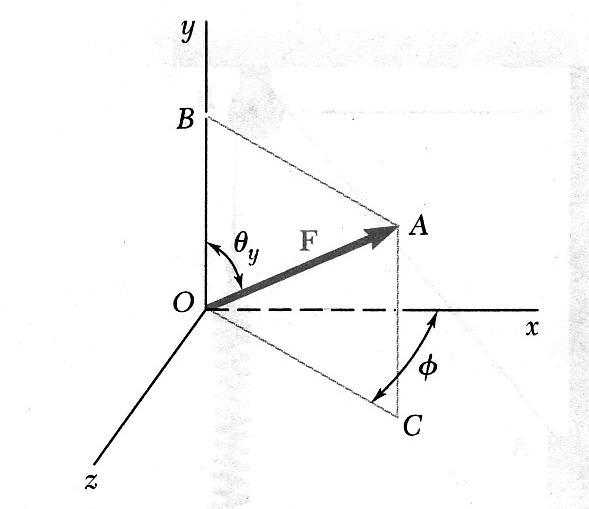
Определение проекции силы на плоскость не отличается от такового для оси, только в данном случае перпендикуляр следует опускать не на ось, а на плоскость.
В случае пространственной прямоугольной системы координат мы имеем три взаимно перпендикулярные плоскости xy (горизонтальная), yz (фронтальная вертикальная), xz (боковая вертикальная). Точки пересечения опущенных из конца вектора перпендикуляров к названным плоскостям равны:
(x1; y1; 0) для xy;
(x1; 0 ; z1) для xz;
(0 ; y1; z1) для zy.
Если каждую из отмеченных точек соединить с началом координат, то мы получим проекцию силы F¯ на соответствующую плоскость. Чему равен модуль силы, мы знаем. Чтобы найти модуль каждой проекции, необходимо применить теорему Пифагора. Обозначим проекции на плоскости как Fxy, Fxz и Fzy. Тогда для их модулей будут справедливы равенства:
Fxy = √(x12+y12);
Fxz = √(x12+ z12);
Fzy = √(y12+ z12).
Углы между проекциями на плоскость и вектором силы
В пункте выше были приведены формулы для модулей проекций на плоскость рассматриваемого вектора F¯. Эти проекции вместе с отрезком F¯ и расстоянием от его конца до плоскости образуют прямоугольные треугольники. Поэтому, как и в случае с проекциями на ось, можно воспользоваться определением тригонометрических функций, чтобы вычислить рассматриваемые углы. Можно записать следующие равенства:
α = arccos(Fxy /|F¯|) = arccos(√(x12+y12) /√(x12+y12+z12));
β = arccos(Fxz/|F¯|) = arccos(√(x12+z12)/√(x12+y12+z12));
γ = arccos(Fzy/|F¯|) = arccos(√(y12+z12)/√(x12+y12+z12)).
Важно понимать, что угол между направлением силы F¯ и соответствующей ее проекцией на плоскость равен углу между F¯ и этой плоскостью. Если рассматривать эту задачу с точки зрения геометрии, то можно сказать, что направленный отрезок F¯ является наклонной по отношению к плоскостям xy, xz и zy.
Где используются проекции сил?
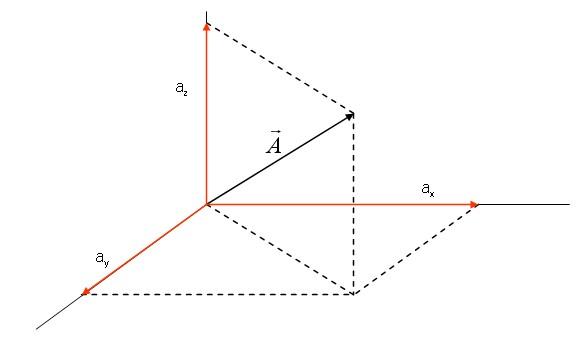
Приведенные формулы для проекций силы на оси координат и на плоскости представляют не только теоретический интерес. Они часто используются при решении физических задач. Сам процесс нахождения проекций называется разложением силы на ее составляющие. Последние представляют собой вектора, сумма которых должна дать исходный вектор силы. В общем случае можно разложить силу на произвольные составляющие, однако, для решения задач удобно пользоваться именно проекциями на перпендикулярные оси и плоскости.
Задачи, где применяются понятие проекций сил, могут быть самыми разными. Например, тот же второй закон Ньютона предполагает, что внешняя сила F¯, действующая на тело, должна быть направлена так же, как вектор скорости v¯. Если их направления различаются на некоторый угол тогда, чтобы равенство оставалось справедливым, подставлять в него следует уже не саму силу F¯, а ее проекцию на направление v¯.
Далее приведем пару примеров, где покажем, как пользоваться записанными формулами.
Задача на определение проекций силы на плоскости и на оси координат
Предположим, что имеется некоторая сила F¯, которая представлена вектором, имеющим следующие координаты конца и начала:
(2; 0; 1);
(-1; 4; -1).
Необходимо определить модуль силы, а также все ее проекции на координатные оси и плоскости и углы между F¯ и каждой ее проекцией.
Начнем решать задачу с вычисления координат вектора F¯. Имеем:
F¯ = (-1; 4; -1) — (2; 0; 1) = (-3; 4; -2).
Тогда модуль силы будет равен:
|F¯| = √(9 + 16 + 4) = √29 ≈ 5,385 Н.
Проекции на оси координат равны соответствующим координатам вектора F¯. Рассчитаем углы между ними и направлением F¯. Имеем:
α = arccos(|-3 |/5,385) ≈ 56,14o;
β = arccos(|4|/5,385) ≈ 42,03o;
γ = arccos(|-2|/5,385) ≈ 68,20o.
Поскольку координаты вектора F¯ известны, можно рассчитать модули проекций силы на плоскости координат. Пользуясь приведенными выше формулами, получаем:
Fxy = √(9 +16 ) = 5 Н;
Fxz = √(9 + 4 ) = 3,606 Н;
Fzy = √(16 + 4 ) = 4,472 Н.
Наконец, остается вычислить углы между найденными проекциями на плоскость и вектором силы. Имеем:
α = arccos(Fxy /|F¯|) = arccos(5/5,385) ≈ 21,8o;
β = arccos(Fxz/|F¯|) = arccos(3,606/5,385) ≈ 48,0o;
γ = arccos(Fzy/|F¯|) = arccos(4,472/5,385) ≈ 33,9o.
Таким образом, вектор F¯ ближе всего наклонен к координатной плоскости xy.
Задача со скользящим бруском по наклонной плоскости

Теперь решим физическую задачу, где необходимо будет применить концепцию проекции силы. Пусть дана деревянная наклонная плоскость. Угол ее наклона к горизонту равен 45o. На плоскости находится деревянный брусок, имеющий массу 3 кг. Необходимо определить, с каким ускорением будет перемещаться этот брусок по плоскости вниз, если известно, что коэффициент трения скольжения равен 0,7.
Для начала составим уравнение движения тела. Поскольку на него будут действовать всего две силы (проекция силы тяжести на плоскость и сила трения), то уравнение примет вид:
Fg — Ff = m*a =>
a = (Fg — Ff)/m.
Здесь Fg, Ff — проекция силы тяжести и сила трения, соответственно. То есть задача сводится к вычислению их значений.
Поскольку угол, под которым плоскость наклонена к горизонту, равен 45o, то несложно показать, что проекция силы тяжести Fg вдоль поверхности плоскости будет равна:
Fg = m*g*sin(45o) = 3*9,81/√2 ≈ 20,81 Н.
Эта проекция силы стремится вывести из состояния покоя деревянный брусок и придать ему ускорение.
Согласно определению, сила трения скольжения равна:
Ff = μ*N
Где μ = 0,7 (см. условие задачи). Сила реакции опоры N равна проекции силы тяжести на ось, перпендикулярную наклонной плоскости, то есть:
N = m*g*cos(45o)
Тогда сила трения равна:
Ff = μ*m*g*cos(45o) = 0,7*3*9,81/√2 ≈ 14,57 Н.
Подставляем найденные силы в уравнение движения, получаем:
a = (Fg — Ff)/m = (20,81 — 14,57)/3 = 2,08 м/с2.
Таким образом, брусок будет спускаться по наклонной плоскости, увеличивая за каждую секунду свою скорость на 2,08 м/с.
Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:
Работа силы
В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.
Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).
Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:
Важно!
Механическая работа совершается, если:
- На тело действует сила.
- Под действием этой силы тело перемещается.
- Угол между вектором силы и вектором перемещения не равен 90 градусам (потому что косинус прямого угла равен нулю).
Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.
Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.
Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:
Работа различных сил
Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.
| Работа силы тяжести |
Модуль силы тяжести: Fтяж = mg Работа силы тяжести: A = mgs cosα |
| Работа силы трения скольжения |
Модуль силы трения скольжения: Fтр = μN = μmg Работа силы трения скольжения: A = μmgs cosα |
| Работа силы упругости |
Модуль силы упругости: Fупр = kx Работа силы упругости: |
Работа силы упругости
Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):
Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:
s = x1 – x2
Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:
Работы силы трения покоя
Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.
Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.
A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)
Знак работы силы
Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:
- Если α = 0о, то cosα = 1.
- Если 0о < α < 90o, то cosα > 0.
- Если α = 90о, то cosα = 0.
- Если 90о < α < 180o, то cosα < 0.
- Если α = 180о, то cosα = –1.
Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180о). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0о). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.
Геометрический смысл работы
Графическое определение
Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.
A = Sфиг
Мощность
Определение
Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:
Рассмотрим частные случаи определения мощности в таблице.
Мощность при равномерном прямолинейном движении тела |
Работа при равномерном прямолинейном движении определяется формулой: A = Fтs Fт — сила тяги, s — перемещение тела под действием этой силы. Отсюда мощность равна: |
Мощность при равномерном подъеме груза |
Когда груз поднимается, совершается работа, по модулю равная работе силе тяжести. За перемещение в этом случае можно взять высоту. Поэтому: |
Мгновенная мощность при неравномерном движении |
Выше мы уже получили, что мощность при постоянной скорости равна произведению этой скорости на силу тяги. Но если скорость постоянно меняется, можно вычислить мгновенную мощность. Она равна произведению силы тяги на мгновенную скорость: |
Мощность силы трения при равномерном движении по горизонтали |
Мощность силы трения отрицательна так же, как и работа. Это связано с тем, что угол между векторами силы трения и перемещения равен 180о (косинус равен –1). Учтем, что сила трения скольжения равна произведению силы нормальной реакции опоры на коэффициент трения: |
Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?
Коэффициент полезного действия
Не вся работа, совершаемая телами, может быть полезной. В реальном мире на тела действует несколько сил, препятствующих совершению работы другой силой. К примеру, чтобы переместить груз на некоторое расстояние, нужно совершить работу гораздо большую, чем можно получить при расчете по формулам выше.
Определения:
- Работа затраченная — полная работа силы, совершенной над телом (или телом).
- Работа полезная — часть полной работы силы, которая вызывает непосредственно перемещение тела.
- Коэффициент полезного действия (КПД) — процентное отношение полезной работы к работе затраченной. КПД обозначается буквой «эта» — η. Единицы измерения эта величина не имеет. Она показывает эффективность работы механизма или другой системы, совершающей работу, в процентах.
КПД определяется формулой:
Работа может определяться как произведение мощности на время, в течение которого совершалась работа:
A = Nt
Поэтому формулу для вычисления КПД можно записать в следующем виде:
Частые случаи определения КПД рассмотрим в таблице ниже:
Устройство |
Работа полезная и полная |
КПД |
| Неподвижный блок, рычаг |
Aполезн = mgh Асоверш. |
 |
| Наклонная плоскость |
Aполезн = mgh Асоверш. = Fl l — совершенный путь (длина наклонной плоскости). |
 |
Пример №4. Определите полезную мощность двигателя, если его КПД равен 40%, а его мощность по паспорту равна 100 кВт.
В данном случае необязательно переводить единицы измерения в СИ. Но в таком случае ответ мы тоже получим в кВт. Из этой формулы выразим полезную мощность:
Задание EF17557
Какую мощность развивает сила тяги трактора, перемещая прицеп со скоростью 18 км/ч, если она составляет 16,5 кН?
Ответ:
а) 916 Вт
б) 3300 Вт
в) 82500 Вт
г) 297000 Вт
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать формулу для расчета мощности.
3.Выполнить общее решение задачи.
4.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Сила тяги, перемещающая прицеп, равна: Fт = 16,5 кН.
• Скорость перемещения прицепа под действием силы тяги: v = 18 км/ч.
Переведем единицы измерения в СИ:
16,5 кН = 16,5∙103 Н
18 км/ч = 18000/3600 м/с = 5 м/с
Мощность равна отношению работы ко времени, в течение которого эта работа совершалась:
N=At
Но работа равна произведению силы, перемещения и косинуса угла между векторами силы и перемещения. В данном случае будем считать, что угол равен нулю, следовательно косинус — единице. Тогда работа равна:
A = Fs
Тогда мощность равна:
N=Fst=Fv=16,5·103·5=82500 (Вт)
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17574
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
Время движения |
Ускорение |
Модуль работы силы трения |
Алгоритм решения
1.Установить наличие и характер зависимости кинематических характеристик движения от массы тела.
2.Вывести формулу для модуля работы силы трения.
3.Установить, как изменится модуль работы силы трения при уменьшении массы тела вдвое.
Решение
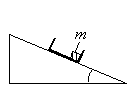
При скольжении с наклонной плоскости происходит равноускоренное движение. Положение тела в любой момент времени при таком движении можно определить с помощью кинематических уравнений:
x=xo+v0xt+axt22
y=yo+v0yt+ayt22
Из этих уравнений видно, что ускорение и время никак не зависят от массы тела. Следовательно, при уменьшении массы тела в 2 раза его время движения и ускорение не изменятся.
Чтобы выразить модуль работы силы трения, выберем такую систему отсчета, чтобы вектор силы трения был расположен вдоль оси Ox.Тогда сила трения будет равна:
Fтр = μmg
Известно, что работа определяется формулой:
A = Fs cosα
Тогда работа силы трения равна:
A = μmgs cosα
Вектор силы трения всегда направлен противоположно вектору перемещения. Поэтому косинус угла между ними равен –1. Но нас интересует только модуль работы. Поэтому будем считать, что он равен:
A = μmgs
Модуль работы силы трения и масса тела зависят прямо пропорционально. Следовательно, если массу тела уменьшить вдвое, то и модуль работы силы трения уменьшится вдвое.
Поэтому правильная последовательность цифр в ответе: 332.
Ответ: 332
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18646
В первой серии опытов брусок перемещают при помощи нити равномерно и прямолинейно вверх по наклонной плоскости. Во второй серии опытов на бруске закрепили груз, не меняя прочих условий.
Как изменятся при переходе от первой серии опытов ко второй сила натяжения нити и коэффициент трения между бруском и плоскостью?
Для каждой величины определите соответствующий характер её изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
| Сила натяжения нити | Коэффициент трения |
Алгоритм решения
- Определить, какая величина изменилась во второй серии опытов.
- Определить, как зависит от этой величины сила натяжения нити.
- Определить, как зависит от этой величины коэффициент трения.
Решение
Когда к бруску подвесили груз, увеличилась масса. Когда тело на нити перемещается вверх прямолинейно и равномерно, сила натяжения нити определяется модулем силы тяжести:
T = mg
Эта формула показывает, что сила натяжения нити и масса тела зависят прямо пропорционально. Если, добавив к бруску груз, масса увеличится, то сила натяжения нити тоже увеличится.
Коэффициент трения — это величина, которая зависит только от материалов и типа поверхности. Поэтому увеличение массы тела на него никак не повлияют.
Верная последовательность цифр в ответе: 13.
Ответ: 13
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18271
Определите коэффициент полезного действия атомной электростанции, расходующей за неделю уран-235 23592U массой 1,4 кг, если её мощность равна 38 МВт. При делении одного ядра урана-235 выделяется энергия 200 МэВ.
Алгоритм решения
1.Записать исходные данные и перевести их в СИ.
2.Записать формулу для определения КПД атомной электростанции.
3.Решить задачу в общем виде.
4.Подставить известные данные и вычислить искомую величину.
5.Массовое число: A = 235.
6.Зарядовое число: Z = 92.
Решение
Запишем исходные данные:
• Энергия, выделяемая при делении одного ядра урана-235: Q0 = 200 МэВ.
• Масса урана-235: m = 1,4 кг.
• Время, в течение которого происходит деление: t = 1 неделя.
• Мощность атомной электростанции: N = 38 МВт.
Переведем все единицы измерения в СИ:
1 эВ = 1,6∙10–19 Дж
200 МэВ = 200∙106∙1,6∙10–19 Дж = 320∙10–13 Дж
1 неделя = 7∙24∙60∙60 с = 604,8∙103 с
38 МВт = 38∙106 Вт
КПД атомной электростанции есть отношение полезной работы к выделенной за это же время энергии:
η=AполезнQ100%
Полезную работу мы можем вычислить по формуле:
A=Nt
Выделенное количество теплоты мы можем рассчитать, вычислив количество атомов, содержащихся в 1,4 кг урана-235 и умножив их на энергию, выделяемую при делении одного такого атома.
Количество атомов равно произведению количество молей на постоянную Авогадро:
Nкол.атомов = νNA
Количество молей равно отношения массы вещества к его молярной массе, следовательно:
Молярная масса численно равна массовому числу в граммах на моль. Следовательно:
M = A (г/моль) = A∙10–3 (кг/моль)
Отсюда количество атомов равно:
Энергия, выделенная всеми атомами, равна:
Теперь можем вычислить КПД:
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 12k
Содержание:
- Система сходящихся сил
- Равнодействующая системы сходящихся сил
- Разложение силы по заданным направлениям
- Разложение силы по двум заданным направлениям
- Разложение силы по трем заданным направлениям
- Проекция силы на ось и плоскость
- Аналитический способ определения равнодействующей
- Условия и уравнения равновесия системы сходящихся сил
- Геометрическое условие равновесия
- Аналитические условия равновесия. Уравнения равновесия
- Методика решения задач на равновесие
- Примеры решения задач на равновесие под действием системы сходящихся сил
- Система сходящихся сил и решение задач
- Условия равновесия системы совпадающих сил
- Геометрический метод решения задач
- Аналитический метод решения задач
- Проекция силы на ось и на плоскость
- Аналитические условия равновесия системы совпадающих сил
- Образец выполнения и решения задач на темы С2
- Система сходящихся сил на плоскости
- Геометрическое условие равновесия системы сходящихся сил
- Геометрический метод решения задач
- Аналитические условия равновесия системы сходящихся сил
- Примеры решения задач на тему: Система сходящихся сил
Система сходящихся сил — это такая система сил, действующих на абсолютно твёрдое тело, в которой линии действия всех сил пересекаются в одной точке. Такая система сил является на плоскости статически определимой, если число неизвестных сил в ней не больше двух.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Система сходящихся сил
Определение:
Система сил, линии действия которых пересекаются в одной точке, называется системой сходящихся сил. Системы сходящихся сил могут быть плоскими и пространственными.
Нехай на тверде тіло діє система збіжних сил
Используя теорему 1.1, § 1.3, перенесем силы вдоль линий их действия в точку В и получим эквивалентную систему сил, приложенных к твердому телу в одной точке (рис. 2.1, б), которую еще называют пучком.
Равнодействующая системы сходящихся сил
Силы, приложенные в одной точке твердого тела, можно добавлять, используя аксиому о параллелограмм сил. Пусть к телу в точке О приложена система n сходящихся сил 
Найдем равнодействующую 


(индекс в обозначении равнодействующей соответствует количеству положительных сил).
К равнодействующей 

Составим равнодействующую 


Как видно из рис. 2.2, б, построение параллелограммов сил эквивалентна построении векторного многоугольника сил. Для системы сил, изображенной на рис. 2.2, б, векторный многоугольник сил построим следующим образом: к концу вектора 






Замыкающая сторона силового многоугольника, которая направлена против его обхода, определяет равнодействующую как по величине, так и по направлению (Рис. 2.2, б). Определение равнодействующей системы сходящихся сил по правилу параллелограмма или силового многоугольника называется геометрическим способом определения равнодействующей.
В случае плоской системы сходящихся сил силовой многоугольник используется для графического определения равнодействующей. Изображая силы в определенном масштабе, величину равнодействующей силы определим непосредственным измерением ее на чертеже. Геометрический способ определения равнодействующей используется в графостатици.
Разложение силы по заданным направлениям
Разложить данную силу на несколько составляющих — значит найти такую систему нескольких сил, для которых данная сила равнодействующей. Эта задача является
неопределенной и имеет однозначное решение лишь при задании дополнительных условий. Такими дополнительными условиями могут, например, быть: 1) задания двух направлений, вдоль которых должны действовать составляющие силы; 2) задания
модулей обеих составляющих сил; 3) задания модуля одной составляющей силы и
направление второй. Рассмотрим два частных случая.
Разложение силы по двум заданным направлениям
Задача сводится к построению такого параллелограмма, у которого сила, которая разлагается, является диагональю, а стороны параллельны заданным направлениям. Например, на рис. 2.3, а, показано, что сила 




Разложение силы по трем заданным направлениям
Если заданные направления АВ, АС и АD не лежащих в одной плоскости, то задача является определенной и сводится к построению такого параллелепипеда, в которого диагональ является заданной силой 

Проекция силы на ось и плоскость
Аналитический способ решения задач статики основывается на понятии о проекции силы на ось. Проекция силы на ось является алгебраическая величина, равная произведению модуля силы на косинус угла между положительным направлением оси и силой (Рис. 2.4)
Отметим, что:
Проекцией силы 

соединяет проекции начала и конца вектора 
В отличие от проекции силы на ось, проекция силы на плоскость является векторной величиной. Она характеризуется не только своим модулем, но и направлением в плоскости Oxу. Модуль проекции силы на плоскость

где θ — угол между направлением силы 
в которой эта ось лежит, а потом найденную проекцию на плоскость спроектировать на эту ось.
Например, в случае, изображенном на рис. 2.5, таким способом найдем, что:
При решении многих задач механики удобно задавать силу через ее проекции на оси прямоугольной декартовой системы координат (рис. 2.6):





Аналитический способ определения равнодействующей
Кроме геометрического существует еще и аналитический способ определения равнодействующей системы сходящихся сил. Если равенство (2.1) спроектируем на оси
декартовой системы координат (рис. 2.2, а), то получим:
где 



Итак, проекция равнодействующей системы сходящихся сил на эту ось равна алгебраической сумме проекций составляющих сил на эту же ось.
Поскольку формулы (2.7) определяют проекции равнодействующей на три взаимно перпендикулярные оси, то модуль и направление равнодействующей 
Условия и уравнения равновесия системы сходящихся сил
По определению уравновешенной системы сил имеем
а для системы сходящихся сил (см. § 2.2) получили
Сравнивая эквивалентности (а) и (б), получим векторное условие равновесия: для равновесия системы сходящихся сил необходимо и достаточно, чтобы ее равнодействующая была равна нулю:
Векторное равенство (2.9) является необходимым и достаточным условием равновесия
системы сходящихся сил. Условия, которым при этом должны удовлетворять самые силы, можно выразить в геометрической или аналитической форме.
Геометрическое условие равновесия
Как известно, равнодействующая — это замыкающая сторона силового многоугольника (рис. 2.2, б). Условие (2.9) будет выполняться только тогда, когда конец последней силы совместится с началом первой силы при построении силового многоугольника, то есть когда силовой многоугольник будет замкнутым. Необходимым и достаточным условием равновесия системы сходящихся сил есть замкнутость ее силового многоугольника (рис. 2.2, в).
Аналитические условия равновесия. Уравнения равновесия
Аналитические условия равновесия системы сходящихся сил вытекают из условия (2.9), согласно которой модуль равнодействующей равна нулю. Используя формулу (2.8), получаем
Это означает, что для равновесия системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на три взаимно перпендикулярные
оси равны нулю.
Равенства (2.10) называются аналитическими условиями равновесия системы сходящихся сил.
Для случая плоской системы сходящихся сил будем иметь:
Итак, задачи на равновесие системы сходящихся сил можно решать двумя способами — геометрически и аналитически. Первый способ удобен для плоской системы сходящихся сил.
Аналитические условия равновесия (2.10) или (2.11), расписаны для конкретной задачи, в которые входят неизвестные параметры, реакции связей, активные силы, расстояния, углы и т.д., называются уравнениями равновесия.
При решении задач статики реакции связей всегда есть неизвестными величинами. Для их определения используют условия равновесия той или другой системы сил.
Задачи, в которых число неизвестных величин равно числу уравнений равновесия, в которые они входят, называются статически определенными. Системы, для которых это имеет место, называются статически определенными.
Задачи, в которых число неизвестных величин больше, чем число уравнений равновесия, в которые входят эти величины, называются статически неопределенными. Системы, для которых это имеет место, называются статически неопределенными.
Методика решения задач на равновесие
Все задачи на равновесие желательно решать по такой методике.
1. Следуя масштаба, сделать четкий схематический рисунок к задачи.
2. Выбрать объект равновесия. Последним может быть точка, тело или
система тел, к которым приложено заданные и неизвестные силы. Если заданы
силы действуют на одно тело, а неизвестные — на второе, то необходимо рассматривать
равновесие системы тел в целом или последовательно равновесие каждого тела.
3. Изобразить на рисунке все заданные силы, приложенные к объекту равновесия.
4. Условно освободить объект равновесия от наложенных связей, а их действие заменить реакциями связей. Изобразить на рисунке реакции связей.
5. Выяснить, какая система сил действует на объект равновесия и условия равновесия рационально использовать.
6. В соответствии с условиями равновесия составить уравнение равновесия или выполнить соответствующие графические построения.
7. Решить уравнение равновесия, найти неизвестные величины и проанализировать полученные результаты.
Все расчеты в процессе решения задачи рекомендуется выполнять в общем виде, а числовые значения подставлять только в конечные алгебраические выражения.
Примеры решения задач на равновесие под действием системы сходящихся сил
Задача 2.1. Однородная горизонтальная балка, вес которой
Решение. Объектом равновесия выберем балку АВ, на которую действует одна заданная сила
Мысленно освободимся от связей. Линия действия реакции 




Балка находится в равновесии под действием трех сходящихся сил 





Поскольку в 


Задача 2.2. Вертикальный стояк подъемного крана опирается на подпятник A и подшипник В (рис. 2.8, а). В точке С действует вертикальная нагрузка Р = 20 кН. Высота стояка АВ равна 2 м, вылет стрелы крана — 4 м. Найти опорные реакции при условии, что кран находится в
равновесии.
Решение. Рассмотрим равновесие крана. На него действует заданная сила






замкнутый силовой треугольник (рис. 2.8, в). Видим, что треугольник сил подобен треугольника АВD (рис. 2.8, б). С подобия треугольников записываем отношение соответствующих сторон:
откуда определяем величины реакции связей 
Задачи 2.1, 2.2 могут быть решены аналитическим способом, с использованием условий равновесия произвольной плоской системы сил (см. раздел 6).
Задача 2.3. Груз Р весом 2 кН содержится в равновесии лебедкой D с помощью каната, перекинутого через блок B (рис 2.9, а). пренебрегая трением на блоке, определить усилия в стержнях AB и CВ, считая, что крепления в точках A, B и С — шарнирные. Углы показано на рис. 2.9, а. Размерами блока и весом стержней пренебречь.
Решение. Объект равновесия выбираем блок B, который рассматриваем как точку. К нему приложена заданная сила тяжести груза 
то есть реакции стержней будут направлены вдоль их осей.
Стержень АВ является растянутый, поэтому его реакция 
точки А, стрижень ВС — сжат, и его реакция 
пренебрегаем, то
На блок В действует система сходящихся сил, расположенных в плоскости рисунка. Для решения задачи используем аналитические условия равновесия. Для этого выберем систему координат с началом в точке В (рис. 2.9, б) и запишем два уравнения равновесия (2.11):
Решим эти уравнения и определим неизвестные величины:
Анализируя полученные результаты, мы видим, что усилия 

Задача 2.4. Найти усилия, возникающие в стержнях АВ, АС и AD (рис. 2.10) под действием
силы 


Решение. Объект равновесия выберем узел А. На него действуют заданные силы 



На узел А действует пространственная система сходящихся сил. Выберем систему координат с началом в точке О и запишем уравнение равновесия (2.10):
Решим полученную систему уравнений и определим неизвестные величины усилий в стержнях:
Полученные результаты свидетельствуют о том, что стержни АВ и АС работают на растяжение, а стержень АD — на сжатие.
Система сходящихся сил и решение задач
Система сходящихся сил — это такая система сил, действующих на абсолютно твёрдое тело, в которой линии действия всех сил пересекаются в одной точке. Такая система сил является на плоскости статически определимой, если число неизвестных сил в ней не больше двух.
Условия равновесия системы совпадающих сил
Совпадающими называются силы, линии действия которых
пересекаются в одной точке.
Если все силы по линиям их действия перенести в эту точку, то получим эквивалентную систему сил, которая приложена к одной точке. Равнодействующая 

Поскольку система смежных сил может быть заменена одной силой (равнодействующей), то необходимым и достаточным условием равновесия тела под действием системы совпадающих сил является равенство нуля этого равнодействующего:
Геометрически это уравнение означает, что в построенном многоугольнике конец последнего вектора совпадает с началом первого, то есть многоугольник представляет
собой замкнутую фигуру.
В случае, когда на тело действуют три уравновешенные совпадающие силы, силовой (векторный) многоугольник сводится к силовому треугольнику. Решение задачи на равновесие в этом случае сводится к нахождению сторон треугольника с помощью тригонометрических формул.
Теорема о трех непараллельных силах. Если тело находится в равновесии под действием трех непараллельных сил, то линии действия этих сил обязательно пересекаются в одной точке и лежат в одной плоскости, то есть силы образуют плоскую систему совпадающих сил.
Теорема о трех силах облегчает решение задачи на равновесие твердого тела в том случае, когда направление одной из сил неизвестно. Найдя точку пересечения линий действий двух сил, направления которых известны, можно определить направление линии действия третьей силы, поскольку она должна проходить через точку приложения этой силы и точку пересечения линий действий первых двух сил.
Геометрический метод решения задач
Непосредственное использование сил многоугольника для решение задач статики сводится к геометрическому построению в масштабе векторного многоугольника с
дальнейшим определением неизвестных элементов с помощью тригонометрических формул. При решении задач на равновесие твердого тела геометрическим методом рекомендуется соблюдать следующий порядок:
1. Выделить объект равновесия;
2. Показать на чертежах точки примера и направления активных сил, действующих на объект равновесия;
3. Выяснить характер связей и возможные направления их реакций;
4. Построить замкнутый силовой многоугольник (построение надо начинать с силы, которая известна как по модулю, так и по направлению);
5. Из силового многоугольника найти неизвестные величины.
Аналитический метод решения задач
Аналитический метод решения задачи рекомендуется использовать в тех случаях, когда требуется определить скорости точек для большого числа положений плоской фигуры.
Проекция силы на ось и на плоскость
Общим способом определения модуля и направления равнодействующей является аналитический, который тоже следует из условия (C2.1) и базируется на аналитическом методе обозначения силы.
Аналитический метод обозначения силы заключается в том, что, выбрав некоторую прямоугольную систему координат 

Алгебраические значения длин направленных отрезков 

проекциями силы на оси 


Если





Модуль и направление силы по известным проекциям на
три взаимно перпендикулярные оси 

При определении проекции силы на ось возможны 4 случаи (рис.C2.2).
1. Вектор силы образует острый угол 

2. Вектор силы образует с положительным направлением оси тупой угол (рис.С2.2, б). В этом случае проекция силы на ось отрицательная и по модулю равна:
3. Вектор силы образует прямой угол с осью 
4. Сила параллельна к координатной оси. В этом случая сила проецируется на ось в натуральную величину со знаком плюс, когда ее направление совпадает с положительным направлением оси (рис.С2.2, г), и со знаком минус в противоположном случае (рис.С2.2, д):
В некоторых случаях для нахождения проекции силы на ось удобнее сначала найти ее проекцию на плоскость, в которой лежит эта ось, а уже затем спроектировать найденную проекцию на нужную ось.
Например, в случае, что изображен на рис. 2.3, сначала лучше спроектировать
силу 





Аналитические условия равновесия системы совпадающих сил
Пусть силы 

Если тело под действием заданной системы сил находится в равновесии, то 

Таким образом, для равновесия пространственной системы совпадающих сил необходимо и достаточно, чтобы сумма проекций этих сил на каждую из трех
координатных осей равнялась нулю.
При решении задачи аналитическим способом до трех первых пунктов, приведенных в разделе С2.2, надо добавить следующие:
4. Выбрать декартовую систему координат
5. Составить уравнение равновесия твердого тела в проекциях на оси координат;
6. Решить полученную систему уравнений равновесия и найти неизвестные величины.
Образец выполнения и решения задач на темы С2
Задача 1
Задано:
Определить: натяжение 

Решение.
Центр шарнира точка В находится в равновесии под действием сил натяжения нитей



(п. С1.4, задача 1).
Таким образом, точка В находится в равновесии под действием трех сил, лежащих в одной плоскости и линии действия которых пересекаются в одной точке.
Величину и направление реакции 

Для решения уравнения (1) построим силовой (векторный) треугольник (рис.2).
Для этого из произвольной точки Р (полюса) отложим вектор 
нам известна. Поскольку векторный треугольник должен быть замкнутым, то с начала этого вектора проведем направление 

Векторы 

Определив углы треугольника, можно записать теорему синусов:
Отсюда получим:
Ответ:
Задача 2
Задано:
Определить: натяжение нити 


Решение. Шарнир D находится в равновесии под действием силы тяжести 



Реакции 

Все силы приложены к одной точке D и для определение неизвестных реакций можно воспользоваться аналитическими условиями равновесия системы совпадающих сил.
С точкой О свяжем пространственную систему координат, направив ось перпендикулярно плоскости АВС, а оси 

Спроектировав все силы на оси выбранной системы координат, достанем:
Из уравнения (1) находим:
Выразим из уравнения (2) натяжение нити и 
Откуда:
Если при решении задачи какая-то из реакций приобретает отрицательное значение, то это означает, что направление этой реакции надо изменить на противоположное. Тогда, действительное направление реакций 

Ответ:
Система сходящихся сил на плоскости
Система сходящихся сил на плоскости — это такая система сил, действующих на абсолютно твёрдое тело, в которой линии действия всех сил пересекаются в одной точке. Такая система сил является на плоскости статически определимой, если число неизвестных сил в ней не больше двух.
Геометрическое условие равновесия системы сходящихся сил
Сходящимися называются силы, линии действия которых пересекаются в одной точке (рис.2.1, а).
Если перенести все силы вдоль линии их действия в эту точку, получим эквивалентную систему сил, приложенных к одной точке.
Равнодействующая 

на прилагаемых силах, то есть равнодействующая 
Поскольку система сходящихся сил может быть заменена одной силой — равнодействующей, то необходимым и достаточным условием равновесия тела под действием системы сходящих сил является равенство нулю этой равнодействующей:
Геометрически это условие состоит в том, чтобы конец последнего вектора совпадал с началом первого в векторном (силовом) многоугольнике, построенном из сил системы, то есть силы должны образовывать замкнутый многоугольник.
Если тело находится в равновесии под действием трех сходящихся сил, то силовой многоугольник сводится к силовому треугольнику. Решения же задачи о равновесии в этом случае требует нахождения неизвестных элементов треугольника с помощью тригонометрических формул или измерений.
При решении задач на равновесие тела под действием трех сил часто приходится пользоваться теоремой о трех силах:
Если тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил обязательно пересекаются в одной точке, то есть силы образуют сходящуюся систему сил.
Теорема о трех непараллельных силах облегчает решение задач на равновесие твердого тела в тех случаях, когда направление одной из трех сил неизвестное. Определив точку пересечения линий действия двух сил, направление которых известно, можно указать направление линии действия третьей силы, поскольку она должна пройти через точку приложения этой силы и точку пересечения линий действия первых двух сил.
Геометрический метод решения задач
Непосредственное использование многоугольника сил при решение задач статики приводит к геометрическим построениям с последующим определением неизвестных элементов с помощью, например, формул тригонометрии.
При решении задач на равновесие твердого тела геометрическим методом рекомендуется придерживаться следующего порядка:
- Выделить объект, который будет рассматриваться в равновесии.
- Установить и показать на схеме активные силы, действующие на тело.
- Выяснить характер связей и установить направления их реакций.
- Построить замкнутый силовой многоугольник (построение надо начинать с сил, известных по модулю и по направлению).
- Из силового многоугольника определить неизвестные силы.
Аналитические условия равновесия системы сходящихся сил
Наиболее общим способом определения модуля и направления равнодействующей является аналитический, который базируется на аналитическом определении силы.
Если выбрать некоторую прямоугольную систему координатных осей 



Алгебраические значения длин направленных отрезков 





Если 



Модуль и направление силы по известным проекциям на взаимно перпендикулярные оси 

При определении проекции силы на ось возможны следующие случаи (рис.2.3):
Рис. 2.3
1. Сила образует острый угол 
2. Сила образует с положительным направлением оси тупой угол (рис.2.3, б). В этом случае ее проекция на координатную ось имеет отрицательный знак и равна
3. Сила образует прямой угол 
4. Сила параллельна координатной оси (рис.2.3, г, д). В этом случае сила проецируется в натуральную величину и проекция положительна, если ее направление совпадает с положительным направлением оси (рис.2.3, г), и отрицательная, если направление силы совпадает с отрицательным направлением оси (рис.2.3, д).
Если силы 

Поскольку модуль равнодействующей определяется по формуле
то тело под действием системы сходящихся сил будет находиться в равновесии, когда 


Таким образом, для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы суммы проекций всех этих сил на каждую из координатных осей равнялись нулю.
При решении задач аналитическим способом нужно выполнить три первых пункта, указанные в параграфе 2.2, а затем следующие:
4. Выбрать декартову систему координат 
5. Составить уравнения равновесия твердого тела в проекциях на эти оси координат.
6. Решить систему составленных уравнений и определить неизвестные величины.
Примеры решения задач на тему: Система сходящихся сил
Задача № 1
Идеальный стержень 



Определить натяжение нити 

Решение. Рассмотрим равновесие узла 









Величину и направление усилия 


Согласно записанному векторному уравнению построим силовой треугольник.
Для этого с произвольной точки 









Найти неизвестные величины можно или померив соответствующие стороны силового треугольника, или, по известным углам треугольника из теоремы синусов:
Откуда:
Ответ:
Задача № 2
Нить с двумя телами на концах 








Определить вес тел 

Решение. Сначала выясним, равновесие какого объекта надо рассмотреть при решении задачи. По условию задачи нужно определить вес тела 







Поскольку прямые 




Таким образом, на объект равновесия, точку 








Составим уравнение равновесия. Для этого, выберем систему координат 

Для проекций на ось 
Знак проекции 





Сумма проекций всех сил на ось 
Проекции сил 



С учетом численных значений тригонометрических функций и величины 
Найдя из первого уравнения:
и подставив во второе, получим:
Ответ:
Задача № 3
Однородный стержень 




Определить величину и направление реакции 
Решение. Задачу решим геометрическим и аналитическим способами, используя теорему о равновесии тела под действием 3-х сил.
Рассмотрим равновесие стержня 



Направление натяжения троса 






Найдем точку пересечения линий действия силы тяжести 



На рис.2.7 









Соответственно, отрезок 

Таким образом
После определения направления реакции 
Запишем геометрическое условие равновесия системы сил, действующих на стержень 
Согласно записанному векторному уравнению построим замкнутый силовой треугольник (рис.2.8).
Для этого из произвольной точки 






Проведенные прямые пересекаются в точке 



Из силового треугольника находим:
Решим задачу аналитическим способом. Для этого выберем прямоугольную систему координат 
Из первого уравнения выразим 
Отсюда получим:
Ответ:
Балка 



Определить реакции опор 

Решение. Рассмотрим равновесие балки 







Для определения направления реакции 






С рис.2.10 видно, что 

Теперь перейдем к определению величин реакций опор.
Составим уравнение равновесия сил в проекциях на оси выбранной системы координат 
С учетом числовых значений:
В результате получим:
Ответ:
Перейдем к определению реакций опор балки 
В этом случае, реакция 






Определим угол 


Составим уравнение равновесия для системы сил, действующей на балку:
С учетом числовых данных:
Добавив уравнение получим:
Подставив значение 

Ответ:
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки