1. Найдите углы треугольника KLM, если угол LKM = 36 градусов.
1. Найдите углы треугольника KLM, если угол LKM = 36 градусов. В ответ запишите все номера вероятных ответов. 2. Какой из треугольников с данными сторонами существует? а) 3; 4; 5 б) 2; 3; 6 в) 6; 7; 14 г) 4; 5; 9. 3. В равнобедренном треугольнике одна сторона равна 9 см, а другая — 20 см. Какая из обозначенных величин может являться третьей стороной?
- Нагуманов-Шайхулла Генка
- Геометрия 2019-10-04 23:12:28 2 1
Задание 1.
Сумма углов треугольника 180, отсюда:
180=lt;LKM+lt;KLM+lt;LMK.
lt;KLM+lt;LMK=180-lt;LKM=180-36=144.
Градусная мера угла больше нуля, если брать только целые числа то минимум 1, выходит
lt;KLM=(1-143).
lt;LMK=(1-143).
То есть хоть какой из их может быть в предлах от 1 до 143.
Ответ:lt;LMK и lt;KLM лежат в границах от 1 до 143.
Задание 2.
Признаком существования треугольника является условие, что сумма 2-ух сторон его больше третей.
а) 3; 4; 5.
3+4gt;5.
3+5gt;4.
4+5gt;3.
Треугольник существует.
б) 2; 3; 6.
2+3lt;6.
Треугольник не существует.
в) 6; 7; 14.
6+7lt;14.
Треугольник не существует.
г) 4; 5; 9.
4+5=9.
Треугольник не существует.
Задание 3.
Признаком существования треугольника является условие, что сумма 2-ух сторон его больше третей.
Если третья сторона =9 см, то признак не соблюдается, означает 3-я сторона равна 20 см.
Ответ: 3-я сторона 20 см.
Найдите косинус угла М треугольника КСМ, если К(1; 7), С (-2; 4), М(2; 0).
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,285
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,101
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем 
 |
(1) |
 |
(2) |
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

Пример 1. Известны стороны треугольника ABC: 

Решение. Из формул (1) и (2) находим:
И, наконец, находим угол C:
Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
Найдем сторону c используя теорему косинусов:


Далее, из формулы

 . . |
(3) |
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:

Пример 2. Известны две стороны треугольника ABC: 

Решение. Иcпользуя теорму косинусов найдем сторону c:

Из формулы (3) найдем cosA:

Поскольку уже нам известны два угла то находим третий:
Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
Так как, уже известны два угла, то можно найти третий:

Далее, для находждения сторон b и c воспользуемся тероемой синусов:
Пример 3. Известна одна сторона треугольника ABC: 

Решение. Поскольку известны два угла, то легко можно найти третий угол С:
Найдем сторону b. Из теоремы синусов имеем:
Найдем сторону с. Из теоремы синусов имеем:
http://www.soloby.ru/701407/%D0%BD%D0%B0%D0%B9%D0%B4%D0%B8%D1%82%D0%B5-%D0%BA%D0%BE%D1%81%D0%B8%D0%BD%D1%83%D1%81-%D1%83%D0%B3%D0%BB%D0%B0-%D0%BC-%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%B0-%D0%BA%D1%81%D0%BC-%D0%B5%D1%81%D0%BB%D0%B8-%D0%BA-1-7-%D1%81-2-4-%D0%BC-2-0
http://matworld.ru/geometry/reshenie-treugolnikov.php
Сумма углов треугольника равна (180°).
Доказательство
Рассмотрим произвольный треугольник (KLM) и докажем, что
∠
(K) (+)
∠
(L) (+)
∠
(M =)
180°
.
1. Через вершину (L) параллельно стороне (KM) проведём прямую (a).
2. При пересечении параллельных прямых (a) и (KM) секущей (KL), углы, которые обозначаются (1), будут накрест лежащими углами, а углы, обозначенные (2) — это накрест лежащие углы при пересечении этих же параллельных прямых секущей (ML).
Очевидно, сумма углов (1), (2) и (3) равна развёрнутому углу с вершиной (L), т. е.
∠
(1) (+)
∠
(2) (+)
∠
(3 =)
180°
, или
∠
(K) (+)
∠
(L) (+)
∠
(M =)
180°
.
Теорема доказана.
Следствия из теоремы о сумме углов треугольника
Следствие 1. Сумма острых углов прямоугольного треугольника равна
90°
.
Следствие 2. В равнобедренном прямоугольном треугольнике каждый острый угол равен
45°
.
Следствие 3. В равностороннем треугольнике каждый угол равен
60°
.
Следствие 4. В любом треугольнике либо все углы острые, либо два угла острые, а третий — тупой или прямой.
Следствие 5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Доказательство
Из равенств
∠
(KML) (+)
∠
(BML=)
180°
и
∠
(K) (+)
∠
(L) (+)
∠
(KML =)
180°
получаем, что
∠
(BML =)
∠
(K) (+)
∠
(L).
Остроугольный, прямоугольный и тупоугольный треугольники
Как гласит четвёртое следствие из теоремы о сумме углов треугольника, можно выделить три вида треугольников в зависимости от углов.
У треугольника (KLM) все углы острые.
У треугольника (KMN) угол (K = 90)
°
.
У прямоугольного треугольника сторона, лежащая против прямого угла, называется гипотенузой, а две остальные стороны — катетами.
На рисунке (MN) — гипотенуза, (MK) и (KN) — катеты.
У треугольника (KLM) один угол тупой.
Вы отправили работу на проверку эксперту. Укажите номер телефона на него придет СМС
Отправить
Незнайка → ЕГЭ → Математика → Профильная → Вариант 14 → Задание 6
Задание № 4968
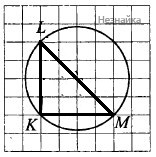
Найдите угол КLM. Ответ дайте в градусах.
Показать ответ
Комментарий:
LM- диаметр,вписанный в окружность треугольник, у которого одна из сторон является диаметром — прямоугольный, а наш еще и равнобедренный => ∠L=45
Ответ: 45
Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.
2 302 833
Уже готовятся к ЕГЭ, ОГЭ и ВПР.
Присоединяйся!
Мы ничего не публикуем от вашего имени
Ответ:
∠ L = 24, ∠ K = 78°, ∠ M = 78°
Объяснение:
∠ KNL = 180 — ∠ KNM = 180 — 63 = 117°
Обозначим ∠ NKM = x, тогда ∠LKM = ∠ LMK = 2x
∠ KNL — внешний по отношению к ΔNKM, он равен сумме двух других углов, не смежных с ним. Составим уравнение:
117 = х + 2х
117 = 3х
х = 39°
∠LKM = ∠ LMK = 78°
∠ KLM = 180 — 78 — 78 = 24°
Приложения:

7
Помогите срочно !!!!!
Найдите углы треугольника КLM.
1 ответ:
0
0
1)угол М=180-125=55 градусов
2)LK=MK, значит, треугольник LMK-равнобедренный
3)угол K=углу М(треугольник LMK-равнобед.)=55 градусов
4)угол L=180-(55+55)=70 градусов
Читайте также
Пусть О-точка пересечения диагоналей АС и ВД параллелограмма АВСД. После всех построений рассмотрим треуг.BOF и ЕОД. угол BOF=углу EOД, т.к. они вертикальные; угол FBO = углу OДE -т.к. они накрест лежащие; сторона ВО=стороне ОД, т.к. О-точка пересечения диагоналей делит сторону ВД пополам. отсюда следует, что треуг.BOF = труг. ОЕД по стороне и двум прилежащим углам. значит BF=ЕД=3см
АД=АЕ+ЕД=5+3=8см АД=ВС=8см
Р=2*АД+2*АВ 28=2*8+2*АВ 2*АВ=28-16=12 АВ=12/2=6см
Ответ: АД=ВС=8см АВ=СД=6см
Сумма углов треугольника = 180°
∠1 = х
∠2 = 3х
∠3 = 6х
х + 3х + 6х = 180
10х = 180
х = 180/10
х = 18° ← ∠1
∠2 = 3х = 3 * 18 = 54°
∠3 = 6х = 6 * 18 = 108°
Ответ: 18°, 54°, 108°
Дуга — это часть окружности,
ее длина зависит от радиуса и
от центрального угла, опирающегося на эту дугу…
длина окружности C = 2*π*R
длина дуги в 1° —это 360 часть длины окружности
длина дуги в 45° —в 45 раз больше
длина оставшейся от окружности (большей) дуги в (360-45) раз больше
большая дуга АВ имеет длину 2*π*R*315 / 360 = 133
2*π*R = 133*360 / 315 = 133*8 / 7 = 19*8
отсюда можно найти радиус (но в данной задаче этого можно и не делать)))
меньшая дуга АВ имеет длину 2*π*R*45 / 360 = 19*8*45 / 360 = 19
Острые — 6, 10
Вертикальные — 2 и 12, 4 и 5, 9 и 11, 7 и 8.
Прямые — 1, 2, 12, 3, 4, 5
Накрест лежащие — 2 и 5, 11 и 8, 11 и 12, 5 и 7, 7 и 9, 4 и 12, 2 и 9, 4 и 8.
тупые — 11, 9, 7, 8
односторонние — 2 и 3, 12 и 10, 11 и 6
смежные — 1 и 12, 1 и 2, 3 и 4, 3 и 5, 10 и 11, 10 и 9, 6 и 8, 6 и 7
соотвественные — 8 и 9, 7 и 11, 6 и 10, 1 и 3, 2 и 4, 5 и 12, 1 и 10, 12 и 9, 2 и 11, 3 и 6, 5 и 8, 4 и 7.
Отрезки касательных, проведенных к окружности из одной точки, равны, т.е. АВ=АС. ОВ=ОС как радиусы, сторона АО — общая, следовательно треуг-ки АВО=АСО. Теперь рассмотрим треуг-ник АВС. Он равнобедренный с углом ВАС=30*2=60, следовательно треуг. АВС равносторонний, АВ=АС=ВС=5см.
Ответ: ВС=5см.