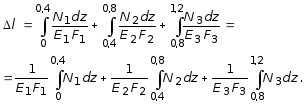Рассмотрим
однородный стержень с одним концом,
жестко заделанным, и другим — свободным,
к которому приложена центральная
продольная сила Р
(рис. 2.2). До нагружения стержня его
длина равнялась l -после
нагружения она стала равной l + Dl
(рис. 2.2). Величину Dl
называют абсолютным удлинением стержня.
Рис. 2.2
Если
в нагруженном стержне напряженное
состояние является однородным, т.е. все
участки стержня находятся в одинаковых
условиях, деформация e
остается одной и той же по длине стержня
и равной

Если
же по длине стержня возникает неоднородное
напряженное состояние, то для
определения его абсолютного удлинения
необходимо рассмотреть бесконечно
малый элемент длиной dz
(рис. 2.2). При растяжении он увеличит
свою длину на величину D dz
и его деформация составит:
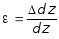
В
пределах малых деформаций при простом
растяжении или сжатии закон Гука
записывается в следующем виде:
s = E e . (2.3)
Величина
Е
представляет собой коэффициент
пропорциональности, называемый
модулем упругости материала первого
рода. Из совместного рассмотрения
уравнений (2.2) и (2.3) получим:
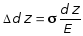
откуда
с учетом того, что
и
,
окончательно
получим:
. (2.4)
Если
стержень изготовлен из однородного
изотропного материала с Е = const,
имеет постоянное поперечное сечение
F = const
и нагружен по концам силой Р,
то из (2.4) получим
. (2.5)
При
решении многих практических задач
возникает необходимость, наряду с
удлинениями, обусловленными действием
механических нагрузок, учитывать
также удлинения, вызванные температурным
воздействием. В этом случае пользуются
принципом независимости действия
сил, и полные деформации рассматривают
как сумму силовой и температурной
деформаций:
, (2.6)
где
a — коэффициент
температурного расширения материала;
t -перепад
температуры тела. Для однородного
стержня, нагруженного по концам
продольными силами Р
и равномерно нагретого по длине, получим:

2.3. Пример расчета (задача № 1)
Для
стального бруса квадратного сечения
сжатого силой Р
с учетом собственного веса при исходных
данных приведенных ниже, требуется
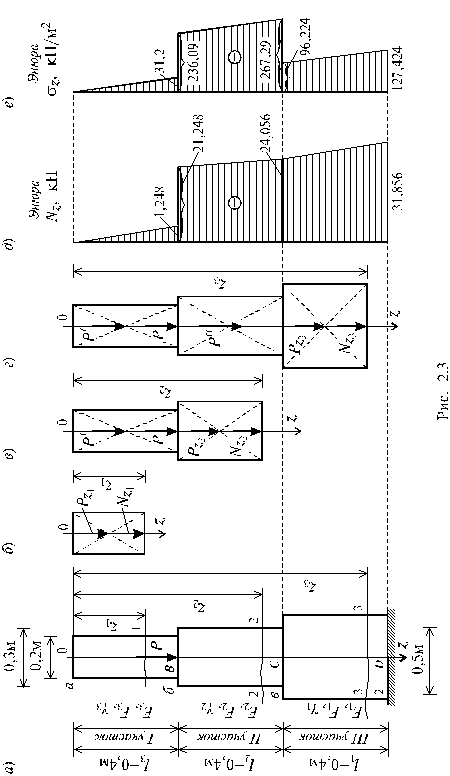
(рис. 2.3, а):
1. Определить
количество расчетных участков;
2. Составить
аналитические выражения для нормальных
сил Nz ,
нормальных напряжений sz
и вычислить их значения для каждого
из участков с учетом их собственных
весов;
3. Построить
эпюры Nz
и sz
;
4. Вычислить
перемещение верхнего конца колонны от
действия силы Р
и собственного веса.
Исходные данные: Р = 20 кН;
l1 = l2 = l3 = 0,4 м;
модуль упругости стали Е = 2,1×108 кН/м2;
F1 = 4×10-2 м2;
F2 = 9×10-2 м2;
F3 = 25×10-2 м2;
g = 78
кН/м3
.
Решение
1. Определение
количества участков.
Так как нормальная сила Nz
зависит от величин внешних сил, в данном
случае включающих в себя и собственный
вес колонны, а последний, в свою очередь,
от размеров поперечного сечения Fi
и
объемного веса g,
то границами участков следует назначать
те сечения, в которых приложены внешние
сосредоточенные силы и где происходит
скачкообразное изменение площади
поперечного сечения или объемного
веса материалов конструкций.
Исходя
из вышесказанного, учитывая g
= const,
брус будет иметь три участка:
1 участок — от
0 до сечения В
(где приложена сила Р);
2 участок — от
сечения
В
до сечения
С;
3 участок — от
сечения
С
до сечения
D.
Следует
заметить, что при определении нормальных
напряжений используются те же участки.
-
Составить
аналитические выражения для нормальных
сил Nz,
нормальных напряжений sz
и вычислить их значения для каждого
из участков, с учетом их собственных
весов.
Для
этого воспользуемся методом сечений.
1 участок
(0 — В)
0 £ z1 £ 0,4
м.
Проведя
сечение 1 — 1
на расстоянии z1
от
начала координат (точка 0), рассмотрим
равновесие верхней части. При этом, к
рассматриваемой части прикладываются
в центре ее тяжести собственный вес
и нормальная сила
,
заменяющую действие отброшенной
нижней части бруса на верхнюю
рассматриваемую (рис. 2.3,б).
Составив уравнение равновесия
рассматриваемой верхней части колонны
по оси z ,
получим:
.
В
свою очередь, собственный вес верхней
части колонны определяется следующим
образом:

Тогда
выражение для нормальной силы будет
иметь вид:
кН,
а
для нормальных напряжений
:
кН/м2.
Так
как,
и
линейно
зависят отz1 ,
то для построения их графиков (эпюр)
достаточно определить значения этих
величин на границах участка, т.е.

z1 = 0

z1 = 0,4 м кН;
кН/м2.
Знаки
минус при
и
указывают
на то, что принятое направление для
этих величин не совпадает с действительным,
т. к. в принятой схеме продольная сила
не растягивает, а сжимает первый участок.

участок (В — С)
0,4 м £ z2 £ 0,8
м.
Аналогично
предыдущему проводим сечение 2-2
на расстоянии z2
(рис. 2.3, в).
Для верхней части составляем уравнение
равновесия åz = 0 .
В
это уравнение войдут: собственный вес
первого участка Р1 =
= g F1 l1;
собственный вес отсеченной части второго
участка

сосредоточенная силаР
= 20 кН, а также сила
.
Тогда
уравнение равновесия примет вид:
Р1 + + P +
= 0,
отсюда
= —P — g F1 l1 —
= -20 — 78×4×10-2×0,4 — 78×9×10-2
(z2 -0,4) =
= -7,02×(z2 + 2,62678)
кН.
Учитывая
постоянство площади поперечного сечения
на втором участке, выражение для
нормального напряжения может быть
записано таким образом:
êÍ/ì2.
Вычислим
значения ординат
и
в граничных сечениях второго участка:

z2 = 0,4 м кН,
кН/м2;

z2 = 0,8 м кН,
кН/м2.

участок (С — D)
0,8 м £ z3 £
1,2 м.
Составив
уравнение равновесия åz = 0
(рис. 2.3, г)
для верхней части бруса, получим:
Р1 + Р2 + + P +
= 0,
откуда
= —P — g F1 l1 — g F2 l2 — g F3 (z3 — l1 — l2)
= -20 — 78×4×10-2×0,4 —
— 78×9×10-2 ×0,4 — 78×25×10-2 (z3 — 0,8) = -19,5×(z3 + 0,43364)
кН.
Выражение
для напряжения:
кН/м2.
Вычислим
значения ординат
и
в граничных сечениях третьего участка:

z3
= 0,8 м (0,8) =-19,5 (0,8 + 0,43364) = -24,056
кН,
(0,8) =-78 (0,8 + 0,43364) = -96,224кН/м2;

z3
= 1,2 м (1,2) =-19,5 (1,2 + 0,43364) = -31,856
кН,
кН/м2.
3. Построение
эпюр Nz
и sz
По причине линейной зависимости
нормальной силы и напряжений от координаты
z
для построения их эпюр достаточно
значений Nz
и
sz
в
граничных сечениях каждого из участков
(см. рис. 2.3, д, е).
Необходимым условием правильности
построения этих графиков является
выполнение следующих требований:
— скачок
в эпюре Nz
должен находиться в точке приложения
сосредоточенного усилия и быть равным
по величине значению этой силы;
— скачки
в эпюре sz
должны
совпадать с точками приложения внешней
силы Р
и изменения площади поперечного сечения
колонны.
После
анализа полученных эпюр (рис. 2.3, д, е)
легко можно убедиться, что построения
выполнены правильно.
4. Вычисление
перемещения верхнего конца колонны
от действия всех сил.
Полное перемещение согласно закону
Гука может быть вычислено по формуле

В
данном случае это выражение принимает
следующий вид:
Так
как величины определенных интегралов
равны площадям, очерченным соответствующими
подынтегральными функциями, то для
вычисления перемещений Dli
достаточно
вычислить площади эпюры Nz
на
каждом из этих участков и разделить их
на Ei
Fi
.
Следовательно,
м.
Соседние файлы в папке 1
- #
- #
- #
25.04.2014747.01 Кб42П1.DOC
- #
- #
- #
- #
- #
Примеры решения задач по сопротивлению материалов
На этой странице приведен еще один пример решения задачи по Сопромату, где необходимо найти внутренние усилия, напряжения и линейные удлинения на участках и в сечениях бруса, нагруженного продольной силой и собственным весом.
Результаты расчетов оформлены эпюрами продольных сил, напряжений и удлинений бруса.
Студентам технических специальностей ВУЗов в качестве методической помощи предлагаются к скачиванию готовые варианты контрольных работ по сопромату (прикладной механике). Представленные задания и примеры их решения предназначены, в частности, для учащихся Алтайского Государственного технического университета.
Варианты контрольных работ можно скачать в формате Word для ознакомления с порядком решения заданий, или для распечатывания и защиты (при совпадении вариантов).
***
Расчет стержня
Условие задачи:
Стержень, жестко закрепленный одним концом, состоящий из трех участков длиной l1…l3, и площадью А1…А3, находится под действием собственного веса и силы F, приложенной на координате lF (см. рис. 1).
Материал стрежня – сталь Ст.3.
Требуется:
Построить эпюры продольных сил N, нормальных напряжений σ и перемещений δ.
Исходные данные:
- l1 = 1,1 м;
- l2 = 1,0 м;
- l3 = 0,9 м;
- А1 = 40 см2;
- А2 = 20 см2;
- А3 = 25 см2;
- F = 70 кН;
- lF = l1 + l2;
- Опора расположена вверху.
Справочная информация:
Удельный вес стали Ст.3: γ = (77…79)×103 Н/м3.
Для расчетов принимаем удельный вес равным γ = 78×103 Н/м3.
Модуль продольной упругости (модуль Юнга) для стали Ст.3: Е = 2×1011 Н/м2.
Указания:
Собственный вес стержня можно представить в виде распределенной нагрузки q1 = γ×А1.
Ось z, направление силы F и нумерацию участков вести от опоры.
Решение задачи:
1. Вычерчиваем схему стержня в соответствии с исходными данными.
2. Расчет ведем от свободного конца стержня, т. е. с III-го участка.
Рассекаем стержень на силовом участке и отбрасываем часть стержня, содержащую опору (верхнюю часть).
Составляем уравнения для нахождения продольной силы N, нормального напряжения σ и удлинения стержня ∆l на силовом участке III:
2.1. Поскольку сила F на участке III не действует, то продольная сила на этом участке представлена только весом стержня, который увеличивается по мере удаления от плоскости 3-3. При этом зависимость величины продольной силы F от координаты z3 будет прямо пропорциональной, поскольку изменяется только координата, а площадь сечения А3 и плотность стали γ остается неизменной по всему участку.
Уравнение для продольной силы на участке:
N = q3×z3 = γ×А1×z3,
где
q3 – вес стержня, представленный в виде распределенной нагрузки (Н/м);
z3 – координата рассматриваемого сечения стержня по оси z (м);
А3 – площадь сечения участка III (м2);
γ – удельный вес материала стержня (для стали Ст.3 — γ = 78×103 Н/м3).
Тогда в сечении 3-3 продольная сила будет равна нулю (т. к. и координата и вес равны нулю), а в сечении 2-2 (верхнем сечении участка III) продольная сила определится по формуле:
N3 = q3×z3 = l3× γ×А3 = 0,9×78×103×25×10-4 = 175,5 Н.
2.2. Нормальное напряжение на силовом участке III определяем, как отношение продольной силы к площади участка в каждом рассматриваемом сечении стержня:
σ3 = N3/А3.
Тогда в сечении 3-3 нормальное напряжение будет равно нулю (т. к. продольная сила равна нулю), а в сечении 2-2 (со стороны участка III) определится по формуле:
σ3 = N3/А3 = 175,5/25×10-4 =70222,2 Па или σ3 ≈0,07 МПа.
2.3. Удлинение бруса на участке III определяем по закону Гука, с учетом изменяющегося по координате z веса стержня:
∆l3 = ∫[N3/(E×A3)]dz,
где Е – модуль продольной упругости стали; Е = 2×1011 Н/м2.
Удлинение изменяется по линейной зависимости от нижнего сечения (3-3) до верхнего сечения (2-2) участка, при этом в сечении 3-3 оно будет равно нулю, поскольку продольная сила N3 в этом сечении равна нулю, а в сечении 2-2 удлинение будет равно:
∆l3 = ∫[N3/(E×A3)]dz = ∫[(А3×γ×z3)/(Е×А3)]dz = (γ×l32)/2E =
= 78×103×0,81)/(2×2×1011) ≈ 0,000000158 м или ∆l3 ≈ 0,000158 мм.
3. Проводим расчет продольных сил, нормальных напряжений и удлинений стержня на участках II и I, учитывая, что к сечению 2-2 участка II приложена продольная сила F, которая по отношению к участкам II и I является растягивающей (т. е. положительной).
3.1. Продольная сила на участках II и I будет равна:
В начале участка II:
N21 = F + N3 = 70000 + 175,5 = 70175,5 Н или N21 ≈ 70,175 кН.
В конце участка II и в начале участка I:
N22 = N11 = N21 + q2×z2 = N21 + l2× γ×А2 =
= 70175,5 + (1,0×78×103×20×10-4) =70331,5 Н или N22 = N11 ≈ 70,33 кН.
В конце участка I:
N12 = N11 + q1×z1 = F + l1× γ×А1 = 70331,5 + (1,1×78×103×40×10-4) =70674,7 Н или N12 ≈ 70,67 кН.
3.2. Нормальное напряжение на участках II и I:
В начале участка II:
σ21 = N12 /А2 = 70175/20×10-4 = 35087500 Па или σ21 ≈ 35,09 МПа.
В конце участка II:
σ22 = N22/А2 = 70331,5 /20×10-4 = 35 165 750 Па или σ22 ≈ 35,16 МПа.
В начале участка I:
σ11 = N11/А1 = 70331,5 /40×10-4 = 17 582 875 Па или σ11 ≈ 17,58 МПа.
В конце участка I:
σ12 = N12/А1 = 70674,7 /40×10-4 = 17668675 Па или σ12 ≈ 17,7 МПа.
3.3. Удлинение стержня на участках II и I:
∆l2 = (γ×l22)/2E + (N×l2/E×A2) =
= 78×103×1)/(2×2×1011) + (70156×1/2×1011×20×10-4) ≈ 0,00017851 м или ∆l2 ≈ 0,1785 мм.
∆l1 = (γ×l12)/2E + (N×l1/E×A1) =
= (78×103×1,21)/(2×2×1011) + (70343×1,1/2×1011×40×10-4) ≈ 0,0000991 м или ∆l1 ≈ 0,0991 мм.
4. Определяем перемещения сечений стержня:
- δ0-0 = 0 мм;
- δ1-1 = ∆l1 = 0,0991 мм;
- δ2-2 = ∆l1 + ∆l2 = 0,0991 + 0,1785 = 0,2776 мм;
- δ3-3 = ∆l1 + ∆l2 + ∆l3 = 0,0991 + 0,1785 + 0,000158 = 0,2777 мм.
5. Результаты расчетов сводим в Таблицу 1, и строим эпюры продольных сил, нормальных напряжений и перемещений (см. рис. 1).
Таблица 1. Значения продольной силы, нормального напряжения и удлинения стержня по сечениям силовых участков.
|
Участок |
Границы |
Продольная |
Нормальное напряжение, |
Перемещение |
|
III |
начало |
0 |
0 |
0,2777 |
| конец |
0,1755 |
0,07 |
0,2776 |
|
|
II |
начало |
70,175 |
35,09 |
0,2776 |
| конец |
70,33 |
35,16 |
0,0991 |
|
|
I |
начало |
70,33 |
17,58 |
0,0991 |
| конец |
70,67 |
17,70 |
0 |
***
Пример расчета вала на скручивание
Контрольная по сопромату для ВУЗов
При растяжении возникает удлинение стержня – разница между длиной стержня до и после погрузки. Эта величина еще называется абсолютной деформацией.
$Delta l = l-l_0$
Как показывают опыты, удлинение зависят от значения продольной силы, от площади сечения и от длины стержня.
При этом отмечено, что при увеличении силы или длины стержня удлинения увеличивается пропорционально.
При изменении площади удлинения, наоборот, обратно пропорционально площади сечения. Есть
$Delta l = frac{N l}{E A}$,
где Е — определенный коэффициент пропорциональности.
Записав по другому, получим
$frac{N}{A} = frac{Delta l}{l} E$
Введем следующее понятие.
Относительная деформация (относительное удлинение) – отношение удлинения к начальной длине стержня.
$epsilon=frac{Delta l}{l}$
Тогда, учтя что N/A = $sigma$, получим зависимость между напряжениями и относительными деформациями

Закон Гука — утверждение, согласно которому деформация, возникающая в материале, пропорциональна напряжений. Открытый закон в 1660 году английским ученым Робертом Гуком.
Величина E называется модуль упругости (модуль Юнга). Это величина, характеризующая свойства материала сопротивляться растяжению или сжатию. Назван в честь английского физика XIX века Томаса Юнга.
Модуль упругости численно равен напряжению, которые могли бы возникнуть при единичных относительных деформациях (при $epsilon$ = 1).