Как найти токи методом двух узлов

При расчете токов методом двух узлов
вначале определяют напряжение между
узлами, а затем по закону Ома для участка
цепи находят токи в ветвях. Для схемы
(рис. 6) заданы параметры элементов:

r₁= 2 Ом,r₀₁= 0,5 Ом,

E₁= 100 В,r₂= 4 Ом,

E₂= 40 В, r₃= 5 Ом,

E₄= 10 В,r₄= 20
Ом.

Рис. 6

Определить токи во всех ветвях методом
двух узлов.

Порядок расчета:

А.Выбираем условное положительное
направление напряжения, например, от
узла «a» к «b»,aего величину определяем
по формуле:

.

ЭДС, направленные к узлу с большим
потенциалом «a» (Е₁,
Е₂), входят в формулу U_abсо
знаком «плюс». Полученное при расчете
положительное значение U_abпоказывает, что истинное направление
U_abсовпадает с условно положительным.

Б.Выбираем условно положительное
направление тока в ветви. При выбранном
направлении U_abпотенциал узла «а»
выше потенциала узла «b»
Поэтому направление тока пассивной
ветви выбираем совпадающим с направлением
U_ab. Токи активных
ветвей возьмем направленными от узла
«b» к узлу «а».

В.Определяем токи в ветвях по закону
Ома:

;

;

;

.

Знак «минус» тока показывает, что его
истинное направление в ветви противоположно
выбранному.

Источник ЭДС работает в режиме генератора
(разряд аккумулятора), если положительное
направление тока в ветви совпадает с
положительным направлением ЭДС этой
ветви. Если же положительные направления
тока в ветви и источника ЭДС не совпадают,
то ЭДС работает в режиме двигателя
(заряд аккумулятора).

Если в одну из ветвей схемы с двумя
узлами включен идеальный источник ЭДС,
внутреннее сопротивление которого
равно нулю, то узловое напряжение
определяется только величиной этой
ЭДС.

3. Символический метод расчета цепей синусоидального тока

Сущность метода состоит в том, что для
упрощения расчета цепей синусоидального
тока переходят от уравнений для мгновенных
значений, являвшихся по сути
интегро-дифференциальными уравнениями,
к алгебраическим уравнениям в комплексной
форме. Расчет цепи удобнее вести для
комплексных действующих величин
синусоидальных токов и напряжений.

Для
схемы (рис. 10) заданы следующие параметры:

r1 = 4,5 Ом, r2 = 5 Ом, r3 = 2,7 Ом,
X1 = 3 Ом,

X2 = 1,5 Ом, X3 = 4,5 Ом, X4 = 3,5 Ом,

U= 14,76 В, Ψ_U= 54,37.

Рис. 7

Для заданной схемы определить токи в
ветвях, записать баланс активных и
реактивных мощностей, записать мгновенное
значение тока и построить в масштабе
топографическую диаграмму.

Порядок расчета:

А.Определяем комплексные сопротивления
каждой ветви

,

,

.

Б.Определяем комплексное сопротивление
разветвленного участка «ас»:

В.Определяем комплексное сопротивление
всей цепи:

=₁+_ac= 4,5 + j3 + 3,29 –j1,13 = 7,79 + j1,87
= 7,95e^j13,57ْ .

Г.Записываем приложенное напряжение
в комплексной форме и определяем ток
I₁ в неразветвленной части
цепи:

A.

Д.Определяем напряжение на
разветвленном участке «ас»:

_ac=_1ac=3,48e^-j19ْ
=6,46e^j21,8=(6+j2,4)В.

Е.Определяем токи в остальных
ветвях:

A,

A.

Ж. Записываем мгновенное значение
тока i₃по его комплексному
действующему значению=1,23ej^80,8ْ
А.

Комплексная амплитуда тока
==1,23e^j80,8ْ
,

А.

З.
Комплексную мощность всей цепи определяем
как
=P±jQ,

где
=14,76e^j54.37ْ
В,
İ₁=1,85e^j40,8ْ

А,
=1,85e^—j40,8
ْ
А,
=14.76e^j54,37ْ
1,85e^—j40,8ْ
=
=27,3e^j13,57ْ
=
(26,5+j6,4)ВА.

И.
По закону сохранения энергии активная
мощность всей цепи равна сумме активных
мощностей всех n
активных сопротивлений, входящих в
цепь:
=4,51,85²+51,2²+2,71,23²=26,52
Вт.

К.
По закону сохранения энергии реактивная
мощность всей цепи равна алгебраической
сумме мощностей всех m
реактивных сопротивлений, входящих в
цепь (X_k>0,
если сопротивление индуктивное и X_k<0,
если емкостное):
=31,852+(3,51,5)1,22+(4,5)1,232+

+6,43
Вт.

Баланс активных и реактивных мощностей
сходится:

P=26,5≈26,52Вт Q=6,4≈6,43 Вт.

Л.Топографическая диаграмма — это
векторная диаграмма цепи, в которой
каждой точке электрической схемы
соответствует точка на топо­графической
диаграмме (рис. 8).

Это достигается тем, что векторы
напряжений на отдельных элемента х
схемы строятся в той последовательности,
в которой они расположены в схеме
(обходим схему в направлении тока).

Для построения топографической диаграммы
определяем напряжения на всех элементах
цепи.

U_r1 =
I₁ R₁
= 1,85 
4,5 = 8,34 В U_r3 =
I₃ r₃
= 1,23 
2,7 = 3,32 В

U_X1 =
I₁ X₁
= 1,85 
3 = 5,55 В U_X3
= I₃
X₃ =
1,23 
4,5 =5,54 В

U_r2 =
I₂ R₂
= 1,2 5
= 6 В I1 = 1,85 А

U_X2 =
I₂ X₂
= 1,2 
1,5 = 1,8 В I2 = 1,2 А

U_X4
=I₂ X₄
= 1,23,5 = 4,2 ВI3 = 1,23 А.

М.
Выбираем масштабы по току и напряжению
μ_I =
0,25 А/см, μ_U
= 1 В/см.
Построениетопографической диаграммы
начинаем с разветвленного участка цепи,
а именно ее второй ветви, содержащей
большее число элементов. Из т. «а»,
отложив в произвольном направлении токI₂, строим векторы_X2,_r2,_X4,
ориентируя их соответствующим образом
относительно тока I₂. Векторная
сумма этих трех напряжений даст величину
вектора_ас.
Аналогичным образом строим напряжение_аспо току третьей ветвиI₃.
Совместим эти две диаграммы с помощью
циркуля и линейки (по общему для них
вектору_ас).

Отсюда определим положение векторов
тока I₂иI₃относительно друг друга. Определяем
ток в неразветвленной цепи по уравнению
₁=₂+₃.
Затем из т. «c», ориентируя вектора
напряжений_X1и_r1относительно вектора тока
₁,
строим вектор напряжения_ab,
равный в масштабе величине приложенного
напряжения:

U
=
abμu
= 14,9 см1В/см=14,9
В≈14,76 В.

Построенную топографическую диаграмму
помещаем на комплексную плос­кость,
отложив под углом –Ψ_u =54,37°
от вектора приложенного напряжения
положительную ось вещественных чисел
(при –Ψ_u<0 – угол откладываем по
часовой стрелке, приΨ>0против). Если
величины углов между векторами токов
и положительной осью вещественных чисел
равны соответственно аргументам
комплексных действующих значений токов
I₁, I₂, иI₃,
то расчет цепи и построение топографической
диаграммы верны.

Рис. 8

З А Д А Н И Е 1

МЕТОДЫ РАСЧЕТА ЦЕПЕЙ ПОСТОЯННОГО ТОКА

Задача 1

Расчет разветвленной цепи с одним
источником электроэнергии.

По данным табл. 1, 2, 3 определить ток
в неразветвленной части цепи и ветви,
указанной в табл.1.

Рис. 9

Задача 2

По
данным табл. 4 определить количество
уравнений, необходимое и достаточное
для определения токов во всех ветвях
схемы по законам Кирхгофа. Составить
эти уравнения в общем виде.

Рис. 10

Задача 3а

Пользуясь методом узлового напряжения,
определить значения и направления всех
токов в ветвях схемы по данным табл. 5,
6, 7. Составить численный баланс мощностей.

Рис. 11

Задача 3b

Пользуясь методом контур­ных токов,
определить зна­чения и направления
всех токов в ветвях схемы по данным
табл. 5, 6, 7. Соста­вить численный баланс
мощностей.

Рис. 12

Задача 3c

Пользуясь методом наложения, определить
значения и направления всех токов в
ветвях схемы по данным табл. 5, 6, 7.
Составить численный баланс мощностей.

Рис. 13

Пример определения данных по варианту
задания

Задача 1

табл. 1 табл. 2 табл 3

табл. 4 Задача 2

табл. 5 табл. 6 табл. 7

Задача 3

З А Д А Н И Е 2

МЕТОДЫ РАСЧЕТА ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА

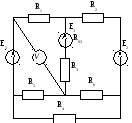
Задача 1.Для электрической цепи,
схема которой изображена на рис. 14 – 63
по заданным в табл. 8 сопротивлениям и
Э.Д.С. выполнить следующее:

1. составить систему уравнений, необходимых
   для определения токов по первому и
   второму законам Кирхгофа;

2. найти все токи, пользуясь методом
   контурных токов;

3. проверить правильность решения,
   применив метод узлового напряжения;
   предварительно упростить схему, заменив
   треугольник сопротивлений R₄,R₅иR₆эквивалентной звездой, начертить
   расчетную схему с эквивалентной звездой
   и показать на ней токи;

4. определить ток в резисторе R₆методом эквивалентного генератора;

5. определить показание вольтметра и
   составить баланс мощностей для заданной
   схемы;

6. построить в масштабе потенциальную
   диаграмму для внешнего контура.

Рис. 14
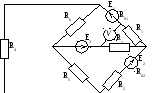
Рис. 15

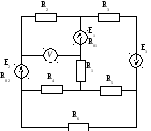
Рис. 16
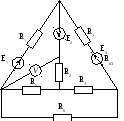
Рис. 17

Рис. 18 Рис. 19

Рис. 20
Рис. 21

Рис. 22
Рис. 23

Рис. 24 Рис. 25

Рис. 26 Рис. 27

Рис. 28
Рис. 29

Рис. 30 Рис. 31

Рис. 32
Рис. 33

Рис. 34 Рис. 35

Рис. 36
Рис. 37

Рис. 38 Рис. 39

Рис. 40 Рис. 41

Рис. 42
Рис. 43

Рис.44
Рис. 45

Рис. 46 Рис. 47

Рис.48 Рис. 49

Рис. 50 Рис. 51

Рис. 52 Рис. 53

Рис. 54 Рис. 55

Рис. 56 Рис. 57

E₃

Рис. 58 Рис. 59

Рис. 60 Рис. 61

Рис. 62 Рис. 63

З А Д А Н И Е 3

СИМВОЛИЧЕСКИЙ МЕТОД РАСЧЕТА ЦЕПИ
СИНУСОИДАЛЬНОГО ТОКА

По данным табл. 9, 10, 11 рассчитать
токи в ветвях заданной цепи приf= 50 Гц. Используя данные расчета, записать
мгновенное значение указанной в табл.
9 величины. Составить баланс мощностей.
В масштабе построить топографическую
диаграмму.

Пример определения данных по варианту
задания:

табл. 9табл.10табл.11

Таблица 6

Таблица 7

Таблица
8

Окончание табл.8

Таблица 9 Вариант Цепь не содержит элементов Определить мгн. значение указанной величины 1 r1 UL1 2 r2 UL2 3 r3 UL3 4 L1 i1 5 L2 i2 6 L3 i3 7 C1 UC2 8 C2 UC3 9 C3 UC1 10 L1,C2 UL2 11 L2,C1 UL1 12 L3,C2 UL2 13 L2,C3 UR1 14 L1,r2 UR3 15 L2,r3 i1 16 L3,r1 i2 17 C1,r1 i3 18 C2,r3 UR2 19 C3,r1 UL1 20 C1 i1 21 C2 i2 22 C3 i3 23 L1 UC1 24 L2 UL1 25 L3 UR1

Таблица 10 Вариант U, В Ψْu 1 110 15 2 150 -20 3 100 45 4 80 -50 5 70 18 6 60 -45 7 200 -15 8 220 60 9 160 30 10 180 -90 11 100 70 12 80 45 13 120 24 14 90 -80 15 60 25 16 70 -40 17 85 50 18 90 17 19 200 20 20 100 -20 21 140 35 22 120 90 23 110 25 24 140 -30 25 150 -15

Таблица 11

Наиболее простым методом расчета электрической цепи с двумя узлами – является метод узлового напряжения или метод двух узлов.

Важно отличать метод узлового напряжения (метод двух узлов) от метода узловых напряжений.

Содержание

• Методика расчёта
• Пример решения задач методом двух узлов
• Онлайн программа для расчета электрических цепей постоянного тока методом двух узлов.

Метод узлового напряжения (двух узлов)

Определим разность потенциалов между двумя узлами цепи А и B.

Найдём потенциал точки А, перемещаясь по первой ветви от узла B до А.

Исходя из выражения (1) можно записать:

Выразим ток первой ветви

где r₁ и g₁ – сопротивление и проводимость первой ветви соответственно.

Аналогично составляются уравнения для оставшихся ветвей.

По первому закону Кирхгофа запишем уравнение для узла B

Подставим в вышеуказанное уравнение выражения токов (2-5).

Раскрыв скобки, находим узловое напряжение U:

Общее выражение узлового напряжения

Исходя из вышеизложенного, узловое напряжение равно отношению алгебраической суммы произведений ЭДС на проводимости соответствующих ветвей к сумме проводимостей всех ветвей. ЭДС направленная к узлу A, записывается со знаком «+», если в противоположную сторону, то со знаком «-».

Давайте рассмотрим применения метода на конкретном примере.

Пример решения задач методом двух узлов (метод узлового напряжения)

У нас есть бесплатная онлайн программа для расчета электрических цепей методом двух узлов.

Пример. Электрическая цепь постоянного тока представлена на рисунке 2. Определить токи в ветвях методом двух узлов, если ЭДС источников равна E1 = 40 В, E2 = 50 В, E3 = 10 В, а сопротивления r1 = 10 Ом, r2 = 20 Ом, r3 = 15 Ом, r4 = 12 Ом.

Порядок расчёта:

1. Так как действительные направления токов до расчёта цепи нам неизвестны — произвольно указываем направления токов в ветвях, например, как на Рисунке 3.

1. Определим проводимость ветвей.

1. Найдем напряжение U_AВ. Для этого воспользуемся формулой 6.

В числителе записываем произведения ЭДС на проводимости соответствующих ветвей, причем ЭДС направленная к узлу A, записывается со знаком «+», если в противоположную сторону, то со знаком «-».

В знаменателе указываем сумму проводимостей всех ветвей:

Подставляем раннее найденные значения проводимостей и значения ЭДС указанные в условии задачи:

1. Определим токи в ветвях. С учетом направления ЭДС

Подставляем численные значения

Токи I₃ и I₄ получились с отрицательными значениями, следовательно их направление противоположно ранее принятому.

Правильность решения можно проверить при помощи баланса мощностей.

Так же для себя правильность решения задачи можно проверить выполнением первого закона Кирхгофа, а именно:

С учетом погрешности, условие выполняется.

Бесплатная онлайн программа.

Содержание:

1. Расчет сложных электрических цепей методом двух узлов
2. Пример задачи с решением 1.
3. Пример задачи с решением 2.

Расчет сложных электрических цепей методом двух узлов

Метод двух узлов применяется в тех случаях, если схема имеет два узла и ряд параллельных ветвей между ними. Для нахождения неизвестных токов составляют уравнения по закону Ома:

где — ток -й ветви;

— ЭДС -й ветви;

— узловое напряжение;

— сопротивление -й ветви;

— проводимость -й ветви, .

ЭДС и напряжение берутся со знаком «+», если их направления совпадают с направлением тока рассматриваемой ветви.

Величина находится по формуле

В этой формуле берется со знаком плюс «+», если ее направление противоположно направлению , и со знаком минус «-», если их направления совпадают.

Пример задачи с решением 1.

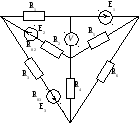
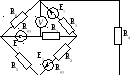
Составить необходимые уравнения для определения значений токов в ветвях схемы (рисунок 2.2), используя метод двух узлов.

Рисунок 2.2 — Электрическая цепь к примеру расчёта .методом двух узлов

Решение

По закону Ома токи в ветвях:

где

Напряжение между двумя узлами

Рассмотрим применение различных методов на задачах 1 и 2.

Возможно вам будут полезны данные страницы:

Пример задачи с решением 2.

В электрической цепи включены два источника переменного напряжения: (рисунок 4.1). Задачу решить методом контурных токов, методом непосредственного применения законов Кирхгофа и методом узлового напряжения. Осуществить моделирование работы схемы в среде Multisim.

Определить токи в ветвях, если ;

Рисунок 4.1 — Цепь переменного тока с двумя источниками питания к задаче 1

Решение

Метод контурных токов.

Определим значение реактивных сопротивлений элементов:

Рассчитаем полные сопротивления отдельных ветвей в комплексной форме:

Тогда исходная схема для решения методом контурных токов преобразуется к виду, представленному на рисунке 4.2.

Рисунок 4.2 — Цепь переменною тока с двумя источниками питания к задаче 1 для решения методом контурных токов

Определим значения ЭДС источников в комплексной форме:

Система уравнений для определения контурных токов

где

Таким образом,

Находим значение контурных токов:

где

Найти решение системы уравнений в комплексной форме можно, воспользовавшись Калькулятором (рисунок 4.3).

Рисунок 4.3 — Программа Калькулятор для решения системы уравнений

Токи в ветвях:

Модель электрической цепи в среде Multisim приведена на рисунке 4.4. Действующие значения токов соответствуют расчётным.

Рисунок 4.4 — Модель цепи переменною тока в Multisim с двумя источниками питания к задаче 1

Комплексные мощности источников ЭДС:

Здесь

Комплексные мощности нагрузки

Небольшие расхождения в полученных значениях мощностей объясняются округлением величин при расчете.

Метод непосредственного применения законов Кирхгофа.

Преобразуем заданные комплексные величины из алгебраической формы в показательную:

Записываем уравнение по первому закону Кирхгофа для узла а:

Записываем уравнения по второму закону Кирхгофа:

Объединив уравнения (4.1)-(4.3), получим

В уравнения (4.4) и (4.5) подставляем значения заданных величин:

Решаем уравнения (4.6) и (4.7), используя определители:

Метод узлового напряжения (метод двух узлов).

Размечаем схему применительно к методу узлового напряжения (рисунок 4.5).

Рисунок 4.5 — Цепь переменного тока с двумя источниками питания к задаче 1 для решения методом двух узлов

Находим комплексные проводимости полных сопротивлений ветвей:

Рассчитываем комплексное межузловое напряжение:

Определяем токи в ветвях:

Главная
→
Примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
1 Методы расчета электрических цепей при постоянных токах и напряжениях
→
1.4 Метод узловых потенциалов. Метод узлового напряжения (метод двух узлов)

1.4 Метод узловых потенциалов. Метод узлового напряжения (метод двух узлов)

Методы и примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
1 Методы расчета электрических цепей при постоянных токах и напряжениях

1.4 Метод узловых потенциалов. Метод узлового напряжения (метод двух узлов)

В методе узловых потенциалов за вспомогательные расчетные величины принимают потенциалы узлов схемы. При этом потенциалом одного из узлов задаются, обычно считая его равным нулю (заземляют). Этот узел называют опорным узлом. Затем для каждого узла схемы, кроме опорного узла, составляют систему уравнений методом узловых потенциалов. По найденным потенциалам узлов находят токи ветвей по обобщенному закону Ома (закону Ома для ветви с ЭДС).

Отметим, что метод узловых потенциалов без предварительного преобразования схемы не применим к схемам с взаимной индукцией.

Для схем, содержащих несколько ветвей только с идеальными источниками ЭДС (без пассивных элементов), не имеющих общего узла нужно применять особые способы составления системы уравнений метода узловых потенциалов.

Для схем, содержащих несколько ветвей только с идеальными источниками ЭДС (без пассивных элементов), имеющих общий узел, этот общий узел принимают за опорный узел (заземляют). Тогда потенциалы узлов, соединенных этими идеальными источниками ЭДС без пассивных элементов с опорным узлом, равны ЭДС этих идеальных источников (+E, если идеальный источник ЭДС направлен от опорного узла и –E в противном случае).

Метод двух узлов является частным случаем метода узловых потенциалов. Он применяется для определения токов в ветвях схемы с двумя узлами и произвольным числом параллельных активных и пассивных ветвей.

Решение задач методом узловых потенциалов и методом двух узлов

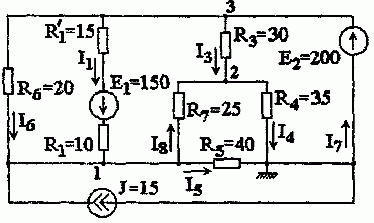
Задача 1.4.1 Рассчитать цепь рис. 1.4.1 методом узловых, потенциалов.

Рис. 1.4.1

Решение. В рассматриваемой схеме четыре узла. Заземлим узел 4 (опорный узел)

φ 4 =0.

Тогда

φ 3 = φ 4 + E 2 =200  B.

Необходимо найти потенциалы узлов 1 и 2. Составим систему уравнений по методу узловых потенциалов для узлов 1 и 2.

Рассматривая узел 1, получим

φ 1 ⋅ g 11 − φ 2 ⋅ g 12 − φ 3 ⋅ g 13 =J+ E 1 R 1 + R ′ 1

или

φ 1 ⋅ g 11 − φ 2 ⋅ g 12 =J+ E 1 R 1 + R ′ 1 + E 1 ⋅ g 13 .

В правой части этого уравнения оба слагаемых учтены со знаком плюс, так как J и E₁ направлены к узлу 1.

Рассматривая узел 2 (правая часть уравнения равна нулю, так как в ветвях, подсоединенных к узлу 2, нет источников энергии), получим

Индивидуалка Лиза (25 лет) т.8 929 529-57-81 Москва, метро Полянка. газификатор — вся актуальная информация на нашем сайте.

− φ 1 ⋅ g 21 + φ 2 ⋅ g 22 − φ 3 ⋅ g 23 =0

или

− φ 1 ⋅ g 21 + φ 2 ⋅ g 22 = E 2 ⋅ g 23 .

Найдем собственную проводимость первого узла

g 11 = 1 R 6 + 1 R 1 + R ′ 1 + 1 R ИТ + 1 R 2 + 1 R 5 = 1 20 + 1 25 + 1 25 + 1 40 =0,155  См.

Проводимость ветви с идеальным источником тока равна нулю, так как внутреннее сопротивление идеального источника тока R_ИТ равно бесконечности.

Собственная проводимость узла 2

g 22 = 1 R 2 + 1 R 3 + 1 R 4 = 1 25 + 1 30 + 1 35 =0,102  См.

Взаимные проводимости между узлами

g 13 = 1 R 6 + 1 R 1 + R ′ 1 = 1 20 + 1 25 =0,09  См; g 21 = g 12 = 1 R 2 = 1 25 =0,04  См; g 23 = 1 R 3 = 1 30 =0,033  См.

Подставив в уравнения известные величины, получим

{ φ 1 ⋅0,155− φ 2 ⋅0,04=39 − φ 1 ⋅0,04+ φ 2 ⋅0,102=6,6

Для решения этой системы используем метод определителей. Главный определитель системы

Δ=| 0,155 −0,04 −0,04 0,102 |=0,01421.

Частные определители

Δ 1 =| 39 −0,04 6,6 0,102 |=4,242; Δ 2 =| 0,155 39 −0,04 6,6 |=2,583.

Находим потенциалы узлов

φ 1 = Δ 1 Δ = 4,242 0,01421 =298,6   В;    φ 2 = Δ 2 Δ = 2,583 0,01421 =181,8   В.

Определяем токи в ветвях (положительные направления токов в ветвях с ЭДС выбираем по направлению ЭДС, в остальных ветвях произвольно)

I 1 = φ 3 − φ 1 + E 1 R 1 + R ′ 1 = 200−298,6+150 10+15 =2,056  А.

В числителе этого выражения от потенциала узла 3, из которого вытекает ток I₁, вычитается потенциал узла 1, к которому ток подтекает. Если ЭДС ветви совпадает (не совпадает) с выбранным направлением тока, то она учитывается со знаком плюс (минус). В знаменателе выражения учитываются сопротивления ветви.

Аналогично определяем другие токи (направления токов указаны на схеме рис. 1.4.1)

I 1 = φ 3 − φ 1 R 6 = 200−298,6 20 =−4,93  А; I 2 = φ 1 − φ 2 R 2 = 298,6−181,8 25 =4,67  А; I 3 = φ 3 − φ 2 R 3 = 200−181,8 30 =0,607  А; I 4 = φ 2 − φ 4 R 4 = 181,8−0 35 =5,194  А.

Для определения тока в ветви с идеальной ЭДС зададимся направлением тока I₇. По первому закону Кирхгофа для узла 3 составим уравнение

− I 7 + I 3 + I 1 + I 6 =0.

Откуда

I 7 = I 3 + I 1 + I 6 =0,607+2,056−4,98=−2,317  A.

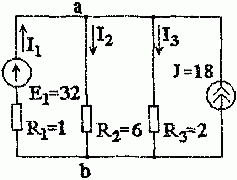
Задача 1.4.2 Определить токи в схеме рис. 1.4.2 методом узлового напряжения.

Рис. 1.4.2

Решение

1 Находим напряжение между двумя узлами по методу двух узлов

U ab = φ a − φ b = E 1 ⋅ g 1 +J g 1 + g 2 + g 3 = 32⋅ 1 1 +18 1 1 + 1 6 + 1 2 =30   B.

При составлении этого уравнения по методу двух узлов в числителе необходимо брать произведение ЭДС на проводимость своей ветви со знаком плюс, если ЭДС направлена к узлу a, и минус — если направлена от узла a к узлу b.

Аналогичное правило определяет и знаки токов источников тока.

2 Находим токи по закону Ома (по закону Ома для ветви с ЭДС)

I 1 = E 1 + φ b − φ a R 1 = E 1 − U ab R 1 = 32−30 1 =2  А; I 2 = U ab R 2 = 30 6 =5  А; I 3 = U ab R 3 = 30 2 =15  А.

Правильность решения проверим по первому закону Кирхгофа

I 1 − I 2 + I 3 +J=0; 2−5−15+18=0.

Метод узловых потенциалов в статье ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА. Основные положения и соотношения. Упражнения и задачи

опорный узел,
метод двух узлов,
метод узловых напряжений,
метод узловых потенциалов,
собственная проводимость,
взаимная проводимость