Как найти точку принадлежащую прямой призме - Autoru.top

Пересечение прямой с призмой

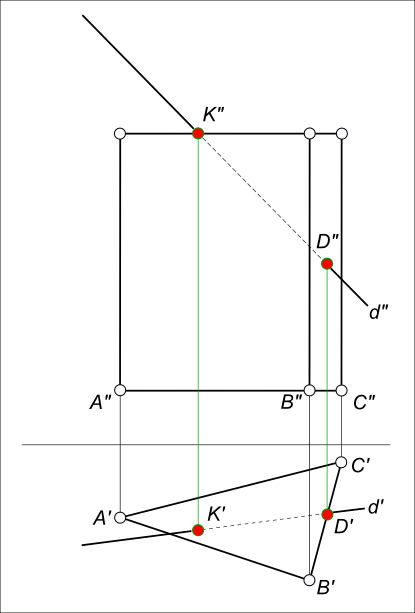
Построить пересечение прямой с призмой: d ∩ ABC

Пересечение прямой с призмой

Из чертежа видно что:
— ребра призмы перпендикулярны горизонтальной плоскости проекций H, на этом основании боковые грани призмы ABC занимают проецирующее положение к H;
— основания призмы проецируются на фронтальную плоскость проекции V в прямые линии, на этом основании основания призмы ABC занимают проецирующее положение к V.

Используем это чтобы построить пересечение прямой с призмой:
— пересечение боковой грани призмы BC с прямой d = D` и затем по линии связи D»;
— пересечение верхнего основания призмы с прямой d = K» и затем по линии связи K`.

Пересечение прямой с призмой: d ∩ ABC

Пересечение прямой с призмой

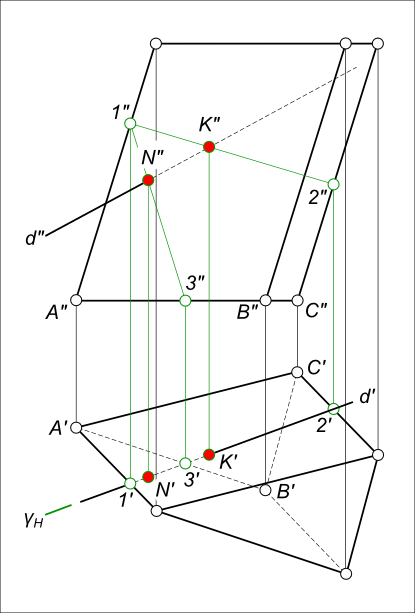
Здесь прямая d и призма ABC занимают общее положение, поэтому искать точки пересечения будем, применяя алгоритм пересечения прямой с плоскостью:

— Заключаем прямую d в вспомогательную горизонтально-проецирующую плоскость γ;
— Находим точки пересечения этой плоскости с боковыми ребрами призмы A, C и с ребром основания призмы AB — точки 1, 2 и 3 соответственно:
— γ_H ∩ ребро A` = 1` ⇒ 1″;
— γ_H ∩ ребро C` = 2` ⇒ 2″;
— γ_H ∩ ребро A`B` = 3` ⇒ 3″;
— Соединив полученные точки прямыми линиями, находим их точки пересечения с прямой d и в то же время с гранями призмы:
— 1″-2″ ∩ d» = K» ⇒ K`;
— 1″-3″ ∩ d» = N» ⇒ N`.

Определение видимости для горизонтальной плоскости проекций производим с помощью конкурирующих точек:
— в точке 1` имеет место пересечение ребра A` и прямой d`, перемещаясь вверх по линии связи точки 1 находим, что соответствующая ей точка прямой d» находится ниже соответствующей ей точка ребра A», а это означает что на горизонтальной плоскости проекций видима точка принадлежащая ребру A`;
— в точке 2` имеет место пересечение ребра C` и прямой d`, перемещаясь вверх по линии связи точки 2 находим, что соответствующая ей точка прямой d» находится выше соответствующей ей точка ребра C», а это означает что на горизонтальной плоскости проекций видима точка принадлежащая прямой d`

Определение видимости для фронтальной плоскости проекций производим аналогично.

Источник

9 декабря, 2013 Анна Веселова

Здравствуйте! Сегодня мы научимся создавать ассоциативный чертеж по готовой 3d модели призмы и пирамиды. Их мы построили на уроке по 3d моделированию

Урок 2. Создаем 3d модели призмы, пирамиды, цилиндра и конуса. Или как создать четыре 3d модели за 10 минут.

Также на этом уроке вы узнаете, как находить проекции точек на чертежах призмы и пирамиды.

Создаем ассоциативный чертеж по 3d модели

Для того, чтобы создать ассоциативный чертеж выполним следующее: создаем чертеж→на компактной панели выбираем кнопку

панель стандартные виды

«Вид»→ ниже выбираем «Стандартные виды»→в открывшемся окне выбираем файл с 3d моделью (расширение .m3d)

выбираем 3d модель призмы

→ на панели свойств, вкладка «схема» подбираем количество видов и расстояние между ними→жмем на поле чертежа и все, три проекции призмы или пирамиды готовы.

схема видов чертежа

Остается только вставить изометрию и оформить чертеж по ГОСТу.

Чтобы вставить изометрию открываем файл с 3d моделью призмы (пирамиды) и пересохраняем ее как рисунок в формате .png.

сохраняем модель в формате рисунка

Возвращаемся к созданию ассоциативного чертежа. В строке главного меню жмем на вкладку «Вставка»→ «Рисунок»→ в открывшемся окне выбираем рисунок с призмой (пирамидой)→ вставляем рисунок в чертеж.

вставляем рисунок в чертеж

Как найти проекции точек на пирамиде и призме?

Как найти проекции точек на призме?

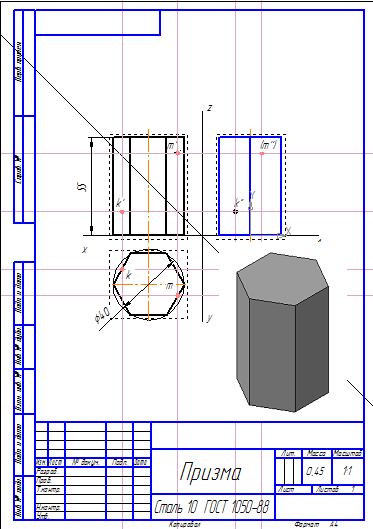
В задании на построение геометрических тел требуется найти недостающие проекции точек К и М (задачник Мироновой Р.С., стр. 65).

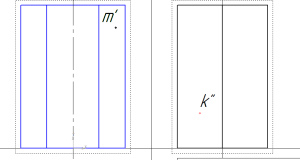
проекции точек на призме

Найдем проекции точек на призме.

Задана фронтальная проекция точки М – m’ и профильная проекция точки К – k’’.

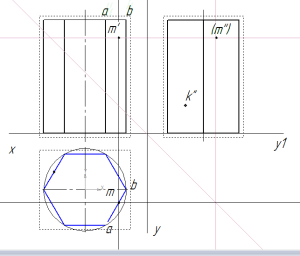
Найдем горизонтальную проекцию точки m. Для этого построим вспомогательную прямую через точку m’ до пересечения с горизонтальной проекцией призмы.

находим проекции точек на призме

Как видно из рисунка, точка m’ принадлежит грани ab. Поэтому горизонтальная проекция m будет находиться в месте пересечения вспомогательной прямой с гранью ab на горизонтальной проекции призмы.

Профильную проекцию находят с по линиям связи, построенным из m’ и m. Так как на профильной проекции призмы точку m’’ не видно, она взята в скобки.

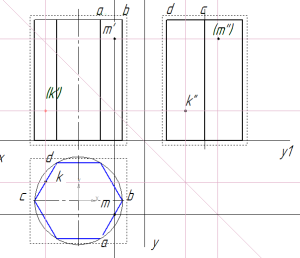
Для того, чтобы найти недостающие проекции точки К поступаем аналогично.

строим горизонтальную и фронтальную проекции точек

По линиям связи находим горизонтальную проекцию k, принадлежащую грани cd. Фронтальную проекцию (k’) также строим по линиям связи.

Как найти проекции точек на пирамиде?

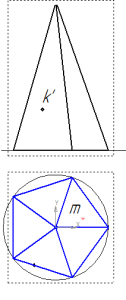
Точка М на пирамиде задана горизонтальной проекцией m, точка К – фронтальной проекцией k’.

точки на пирамиде

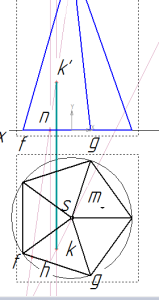
строим горизонтальную проекцию точки

Начнем с нахождения горизонтальной проекции k. Для этого через вершину пирамиды и k’ проводим вспомогательную прямую. Затем через полученную точку n проводим линию связи до пересечения с гранью fg. Через полученную точку h и вершину s проводим еще одну вспомогательную прямую.

И по линии связи опускаемся из точки k’ до пересечения с этой прямой hs. Горизонтальная проекция k найдена.

Профильную проекцию k’’ находим по линиям связи без дополнительных построений.

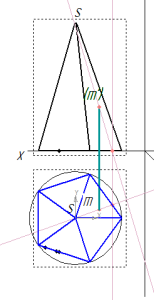
Фронтальную проекцию m’ находим аналогично построению горизонтальной проекции k. Описывать процесс не буду. Вот вам рисунок.

строим фронтальную проекцию точки М

Профильную проекцию m’’ найти особого труда не составит, все по тем же линиям связи.

Таким образом находят проекции точек на пирамиде и призме.

Чтобы лучше все уяснить посмотрите видеоурок.

Скачать чертежи бесплатно можно здесь

Теперь-то вы точно сможете быстро создать ассоциативный чертеж и найти по указанию преподавателя проекции точек на пирамиде или призме.

The following two tabs change content below.

Bio
Latest Posts

Рада приветствовать Вас в своем блоге! Я создала его с целью помочь всем желающим освоить программу Компас 3d. Мы пройдем весь путь от азов черчения до создания серьезных сборок. Присоединяйтесь!

Понравился материал? Подпишись на обновления!

Вы можете пропустить чтение записи и оставить комментарий. Размещение ссылок запрещено.

Источник

Точка принадлежит
поверхности, если она находится на линии
этой поверхности. План решения задачи
на принадлежность точки поверхности
включает:

определение
вида заданной поверхности;
выбор
графически простой для построения на
чертеже линии поверхности, проходящей
через заданную точку (прямая или
окружность);
построение
проекций этой линии на чертеже;
построение
искомых проекций точки.

Для лучшего
представления и понимания эпюр каждой
поверхности сопровождается наглядным
изображением, а стрелкой указывается
направление взгляда (фронтальная
проекция – вид спереди).

Точки и линии на поверхности призмы

Рассмотрим
построение точки и линии на поверхности
прямой призмы.

очки и линии на поверхности пирамиды

S₂

остроить профильную проекцию
пирамиды и недостающие проекции точки
и прямой.

m₂

В₂

E₂

C₂(G₂)

D₂(F₂)

А₁

В₁

С₁

D₁

E₁

G₁

F₁

S₁

m₁

очки и линии на поверхности цилиндра

Построить профильную
проекцию цилиндра и недостающие проекции
точки и прямой.

очки и линии на поверхности конуса

Построить профильную
проекцию конуса и недостающие проекции
точки и прямой.

Точки и линии
на поверхности сферы

остроение проекций точек на сфере
понятно из построения точкиF,
заданной на фронтальной проекции сферы.
Горизонтальная проекцияF₁точкиFнайдена с
помощью параллели, проходящей через
точку F
(F₂).
На горизонтальной проекции радиус
параллелиR_F,
проведенный из центра сферы, пересекается
с линией связи от фронтальной проекцииF₂точки
F. Для построения
профильной проекцииF₃точки F
необходимо замерить координатуyточкиF (у_F).

Построить
недостающие проекции точек и обозначить
их на наглядном изображении.

Точки и линии на поверхности тора

остроение проекций точек на торе
понятно из построения точкиА
(через параллель с
радиусом R_А),
заданной на фронтальной проекции тора

Построить недостающие
проекции точек и обозначить их на
наглядном изображении.

Лекция
№ 5

СЕЧЕНИЕ
ПОВЕРХНОСТЕЙ ПРОЕЦИРУЮЩИМИ

ПЛОСКОСТЯМИ

1. Сечение
многогранников проецирующими плоскостями
(призма, пирамида). 2. Сечение поверхностей
вращения проецирующими плоскостями
(цилиндр, конус, сфера).

1
СЕЧЕНИЕ МНОГОГРАННИКОВ ПРОЕЦИРУЮЩИМИ

ПЛОСКОСТЯМИ

лоскость пересекает многогранник
по плоским многоугольникам. Для построения
многоугольника необходимо найти его
вершины (точки пересечения плоскости
с ребрами и гранями).

Призма

Пирамида

2
СЕЧЕНИЕ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ
ПРОЕЦИРУЮЩИМИ ПЛОСКОСТЯМИ

При построении
точек сечения применяется способ
построения точек по принадлежности.

Сечение
цилиндра

Любая плоскость
может пересекать поверхность прямого
кругового цилиндра:

по
окружности,
если плоскость
сечения перпендикулярна его образующим
(рис. 63), такоесечение называется
нормальным;
по двум
образующим,
если секущая
плоскость
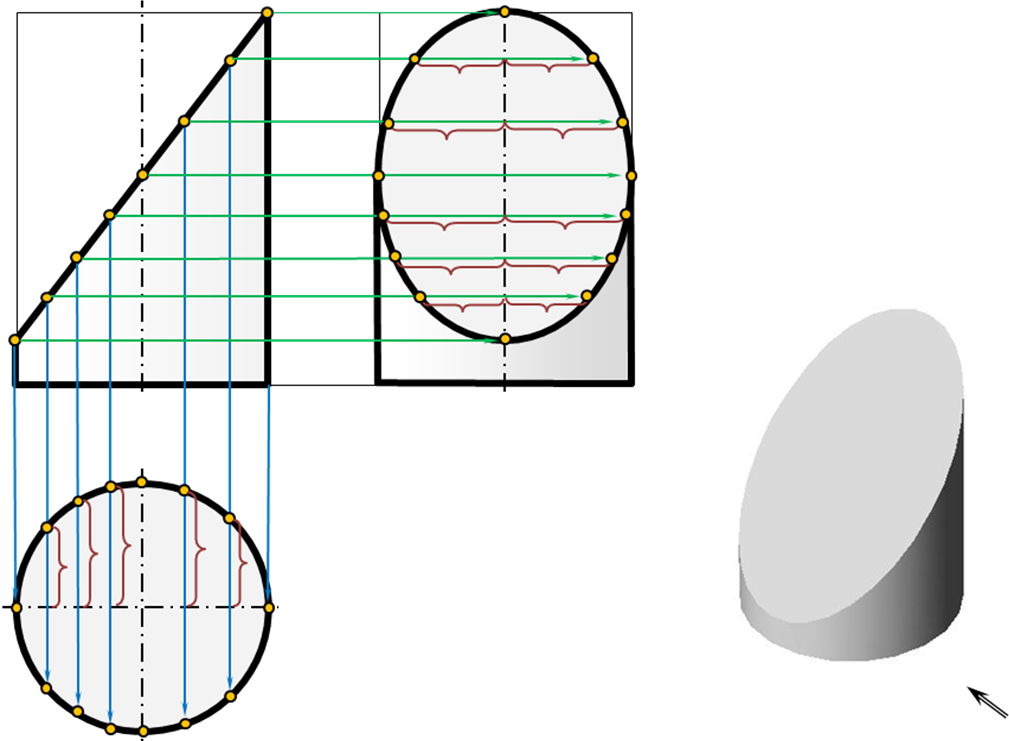
параллельна оси цилиндра (рис. 64);по эллипсу, если секущая
плоскостьнаклонена
к оси цилиндра и пересекает все
его образующие (построить три проекции
цилиндра).

Сечение конуса

Конус
является геометрическим
телом, которое может
иметь в сечении пять различных фигур:

треугольник,
если
секущая плоскость
пересекает конус через вершину по
двум образующим (рис. 65, а, б);

окружность,
если секущая
плоскость
параллельна основанию или перпендикулярна
оси, а конус прямой круговой
(рис. 66);

эллипс,
если
секущая плоскость пересекает
все образующие конуса под
некоторым углом к основанию конуса
(рис. 67);

параболу,
если
секущая плоскость параллельна
одной из образующих конуса
(рис. 68);

гиперболу,
если секущая
плоскость параллельна
оси конуса или параллельна
двум его образующим (рис. 69).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

←Метод координат

Задача 1

Задача 2

Задача 3

Задача1:

Основанием призмы АВСА₁В₁С₁ является правильный треугольник АВС со стороной 6. Боковое ребро АА₁ призмы равно 6 и образует со сторонами АВ и АС углы по 60⁰.
Определите:

а) угол между прямыми АА₁ и СВ₁;
б) расстояние от точки B₁ до плоскости А₁СВ;

Наша заданная призма не прямая, а наклонная, так как ребро АА₁ не перпендикулярно основанию. Это обстоятельство в значительной степени усложняет решение задачи Две боковые грани у нее не привычные прямоугольники, а ромбы со стороной, равной 6. Почему? Потому что боковые ребра у призмы параллельны, а в нашей задаче они еще и равны ребрам основания призмы. Третья боковая грань — прямоугольник, а в данной задаче — квадрат, так как все ребра призмы равны.

Конечно же ее, эту задачу, можно решить геометрически, что мы и сделаем, частично.

а) Угол между скрещивающимися прямыми АА₁и СВ₁определяется при помощи построения прямой, параллельной одной из скрещивающихся и пересекающих вторую из скрещивающихся прямых. В данной задаче это вообще несложно, так как прямая АА₁ параллельна плоскости СВ₁С₁ . Ну, и расстояние между прямыми находим построением дополнительной плоскости МАА₁.

Рассмотрим плоскость СВ₁С₁. Эта плоскость параллельна АА₁, так как прямые ${AA_1} parallel {CC_1} parallel {BB_1}$ . Это квадрат по условию, а следовательно, ${AA_1} parallel {M M_1}$ . Тогда угол между прямыми будет $widehat{( AA_1) (CB_1)}$ = ∠M₁OB₁ = 45°.

Кстати, представьте, что вам требуется найти угол между прямыми АС₁ и А₁В. В этом случае найти эти значения геометрически не так уж и просто. Как и определение расстояния от точки до плоскости.

Мы же пойдем другим путем, присоединим к нашей призме систему координат, определим координаты узловых точек и найдем, все что нужно по координатам прямых и плоскостей. (Кликните, чтобы увеличить чертеж).

Чтобы сделать рисунок более понятным, я закрасила грани и основания разным цветом. Предлагаю посмотреть на призму в проекциях на координатные плоскости, как бы со всех сторон. Соответственно на рисунке 1 смотрим на плоскость х0у, на рисунке 2 — z0y, а на рисунках 3 и 4 — плоскость z0x слева и справа от призмы.

Переходим к расчету координат узловых точек. Вспомним, что наша призма состоит их двух треугольников (основания призмы), двух ромбов (боковые грани) и квадрата (третья боковая грань). Чтобы определиться, насколько отстоит верхнее основание от нижнего, нам необходимо выяснить положение точки А₁.

Боковая грань АА₁С₁С — ромб углом 60⁰, а следовательно, его диагональ равна стороне. А это значит, что точка А₁ равноудалена от точек А и С. Точно также можно рассмотреть грань АА₁В₁В.

Получается, что точка А₁ равноудалена от точек А, В и С. А это значит, что координаты х и у можно определить по чертежу. Фактически, на чертеже представлена проекция нашей призмы на плоскость хОу. Учитывая, что треугольник ΔАВС правильный, и сторона его равна 6, можно сказать, что проекция точки А₁ — центр описанной окружности, а АА₁ — ее радиус. Найду его по теореме синусов, а вы можете и по-другому, вариантов много.

$[frac{a}{sin A} = frac{b}{sin B} = frac{c}{sin C} = 2R]$

$[AA_1 = frac{6}{2sin 60^0} = frac{3cdot2}{sqrt3} = 2sqrt3]$

Координата z для нижнего основания призмы равна 0, а для верхнего определяем его из рисунка2, где АА₁ — гипотенуза треугольника, а высота (она же координата z) — катет. Координата $z = sqrt{6^2 - (2sqrt3)^2} = 2sqrt6$

Итак, точки и их координаты: Нижнее основание

В верхнем основании каждая точка сдвигается на вдоль оси Ох, и координата

Переходим к следующему вопросу

б) По координатам узловых точек будем искать расстояние от вершины призмы до плоскости. Расстояние от точки В₁ до плоскости А₁СВ определим по формуле

$[rho = frac{left|{Ax_b + By_b + Cz_ba +D}right|}{sqrt{A^2 + B^2 + C^2}}]$

Осталась «самая ерунда» — найти эти самые A, B, C и D. Ну что ж, ищем.

Для этого составляем и решаем систему уравнений, основываясь на точках плоскости: .

$[begin{Bmatrix}{Acdot 0 +Bcdot(2sqrt3) + Ccdot(2sqrt6) + 1 = 0}\{Acdot (-3) +Bcdot(3sqrt3) + Ccdot 0 + 1 = 0}\{Acdot 3 +Bcdot(3sqrt3) + Ccdot(0) + 1 = 0}]$

$[begin{Bmatrix}{0 +{2sqrt3}B + {2sqrt6}C + 1 = 0}\{-3 A +{3sqrt3}B + 0 + 1 = 0}\{ 3A +{3sqrt3}B + 0 + 1 = 0}]$

Складываем второе и третье уравнение, получаем: $B = - frac{2}{6sqrt3} = - frac{sqrt3}{9}$

Из второго уравнения: $3A = 3sqrt3 B + 1 = 3sqrt3 cdot(-frac{sqrt3}{9}) + 1 = 0$ ,

Из первого уравнения:

Подставляем В и находим С : $2sqrt6 C = -2sqrt3 (- frac{sqrt3}{9}) -1 = frac{2}{3} - 1 = -frac{1}{3}$

$[C = -frac{1}{3cdot2sqrt6 } = - frac{sqrt6}{36}]$

(Кстати, уравнение нашей плоскости будет $0cdot x - frac{sqrt3}{9} y - frac{sqrt6}{36} z + 1 = 0$ . )

Теперь ищем расстояние от точки до плоскости:

$[rho = frac{left|{0cdot(-3) + (- frac{sqrt3}{9})cdot{5sqrt3} + ( - frac{sqrt6}{36}){2sqrt6} +1}right|}{sqrt{0^2 + (- frac{sqrt3}{9})^2 + ( - frac{sqrt6}{36})^2}}]$

Ответ: 45º,

Задача2 (вариант Ларина №272):

Дан куб АВСDА₁В₁С₁D₁ c ребром 2.

а) Докажите, что плоскости A₁BD и B₁D₁C параллельны
б) Найдите расстояние между плоскостями A₁BD и B₁D₁C.

С первым пунктом все просто: Плоскости параллельны, потому что пересекающиеся прямые их попарно параллельны.

Переходим к пункту б). Координаты точек будут

Составляем систему уравнения плоскости с координатами точек, через которые она проходит, чтобы определить коэффициенты А B, C и D:

$[begin{Bmatrix}{Acdot 0 +Bcdot 0 + Ccdot2 + 1 = 0}\{Acdot 2 +Bcdot 2 + Ccdot2 + 1 = 0}\{Acdot 0 +Bcdot 2 + Ccdot0 + 1 = 0}]$

$[begin{Bmatrix}{ 0 +0 + 2C + 1 = 0}\{2A +2B + 2C+ 1 = 0}\{ 0 +2B + 0 + 1 = 0}]$

Получаем: $B = -frac{1}{2}$ , $C = -frac{1}{2}$ , $A = frac{1}{2}$

Уравнение плоскости B₁D₁C будет $frac{1}{2}x -frac{1}{2}y - frac{1}{2}z+ 1 = 0$

Домножим на 2, чтобы избавиться от дробей

Получается, что у первого уравнения . Но если плоскости параллельны, а они у нас параллельны, их уравнения имеют одинаковые коэффициенты А, В, и С, но разные D. Ищем Для этого подставляем в уравнение плоскости B₁D₁C вместо D=1 , будет

, а вместо x, y, z — координаты точки, например, A₁( 2; 0; 2 ), принадлежащей плоскости A₁BD. Получим

Получается, что

Подставляем в формулу для определения расстояния между параллельными плоскостями

$[rho = frac{left |{D_1 -D_2 }right |}{sqrt{A^2 + B^2 + C^2}}]$

$[rho = frac{left |{2-0 }right |}{sqrt{1^2 + (-1)^2 + (-1)^2}} = frac{2}{sqrt3} = frac{2sqrt3}{3}]$

Ответ: $frac{2sqrt3}{3}$

Задача 3→

Источник

На этой странице вы узнаете

Чем упаковка стикеров похожа на призму?
Как можно попасть в призму в реальной жизни?
Как сложить игральные кости из листа бумаги?
Как найти объем воды в аквариуме?

Слышали такое выражение «смотреть сквозь призму чего-либо»? Оно значит ситуацию, в которой мы воспринимаем что-либо под влиянием каких-то убеждений или представлений. Замысловато, конечно… Возможно, потому что и сама призма — непростое понятие. Давайте разберемся с ней с точки зрения математики.

Определение призмы

Многие из нас пользуются стикерами. Для записи своих дел, для закладок, для пометок при ведении конспектов. Даже если мы ими не пользуемся, то наверняка видели их в магазинах или у родственников и друзей.

Один такой стикер можно принять за плоскость. Теперь вспомним, как выглядит упаковка с ними. Много-много стикеров накладываются друг на друга и получается небольшая объемная фигура, сверху и снизу которой лежат два абсолютно одинаковых листа. При этом сразу заметим, что нижний и верхний стикеры будут параллельны друг другу.

На самом деле, упаковка со стикерами является не чем иным, как призмой!

Призма — это многогранник, в котором две грани являются равными многоугольниками и лежат в параллельных плоскостях, а все остальные — параллелограммами.

Чем упаковка стикеров похожа на призму?

Упаковка стикеров является объемной фигурой, в основаниях которой лежат равные прямоугольники. А боковые стороны упаковки являются параллелограммом. Таким образом, упаковка стикеров полностью соответствует определению призмы.

Определение может показаться немного запутанным, но в нем нет ничего страшного. Разберемся, поближе взглянув на составные призмы.

Строение призмы

Представим себе обычную коробку. Ее дно и крышка равны между собой и лежат в параллельных плоскостях. Это и есть равные многоугольники. Также их называют основаниями призмы.

Посмотрим на стенки коробки. Они являются параллелограммами, просто с прямыми углами. Подробнее про параллелограммы можно прочитать в статье «Параллелограмм». Эти параллелограммы называются боковыми гранями призмы.

Возьмем линейку и измерим расстояние между основаниями призмы. Для этого из любой точки одного основания проведем перпендикуляр к другому.

Подробнее про расстояния между плоскостями можно узнать в статьях «Углы в пространстве» и «Расстояния между фигурами».

Может возникнуть вопрос, что мы сейчас нашли? Мы нашли высоту призмы.

Высота призмы — перпендикуляр, опущенный из любой точки одного основания на другое основание призмы.

В задачах намного удобнее опускать перпендикуляр не из произвольной точки, а из вершины призмы.

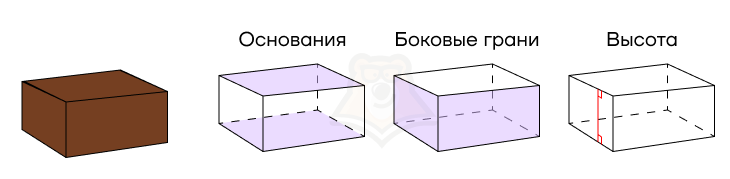
Рассмотрим элементы призмы.

Ребро — это линия пересечения двух плоскостей.

Представим, что вместо картонных стенок в нашей коробке ткань, которую нам нужно натянуть на каркас так, чтобы коробка не изменилась. В этом случае все прямые этого каркаса и будут ребрами.

Ребра бывают двух видов:

ребра оснований,
боковые ребра.

Отличить их также легко: ребра основания являются стороной многоугольника, который в нем лежит, в то время как боковые ребра не принадлежат основаниям.

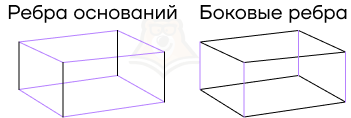
У боковых ребер есть одно очень важное свойство: они равны между собой и параллельны.

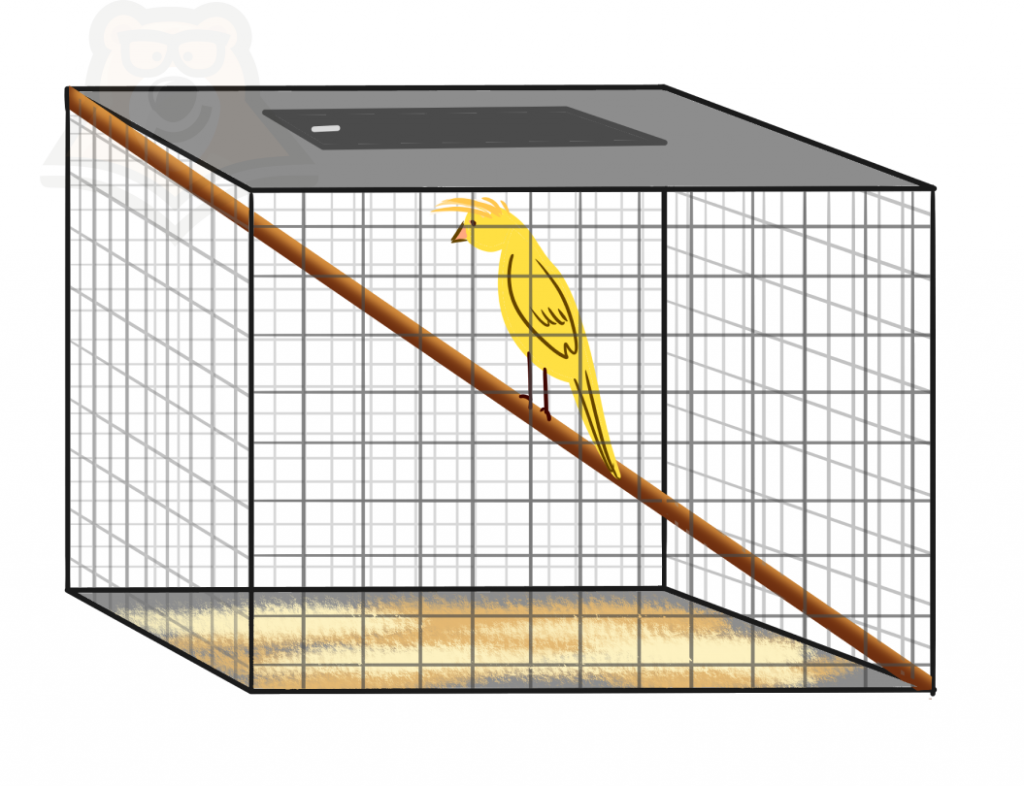
Диагональ призмы — отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.

Например, мы можем взять клетку попугая и от угла до угла сделать ему жердочку, чтобы птичке было весело жить. Эта жердочка и будет диагональю призмы.

Виды призм

Вернемся к рассуждениям о том, чем упаковка стикеров похожа на призму. Например, куб и параллелепипед будут отличаться. А если в основании призмы будет лежать треугольник или шестиугольник? Или двадцатиугольник? Разделим призмы на несколько видов.

Мы рассмотрим две классификации.

В первом случае будем рассматривать призмы по фигурам, которые лежат в основании. В многоугольнике может быть множество сторон, а значит, и в основании призмы может быть треугольник, четырехугольник, шестиугольник, десятиугольник и так далее.

В зависимости от фигуры в основании призмы могут называться по-разному. Вот три основных, которые чаще всего встречаются при решении заданий:

треугольная призма,

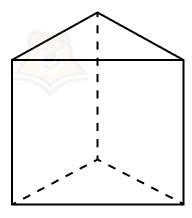
четырехугольная призма,

шестиугольная призма.

Аналогичным образом можно дать название любой призме, например, десятиугольная призма или стоугольная призма.

В определении призмы сказано, что в боковых гранях лежат параллелограммы. До этого мы чертили только прямоугольники, но в боковых гранях могут лежать не только они.

С этим связана вторая классификация призм. По этому признаку призмы делятся всего на два вида:

прямые,
наклонные.

Разберемся в них чуть подробнее.

Прямая призма — призма, боковые ребра которой перпендикулярны основаниям.

В этом случае боковые ребра и ребра оснований действительно образовывают прямоугольник.

Наклонная призма — призма, боковые ребра которой находятся под углом к основаниям.

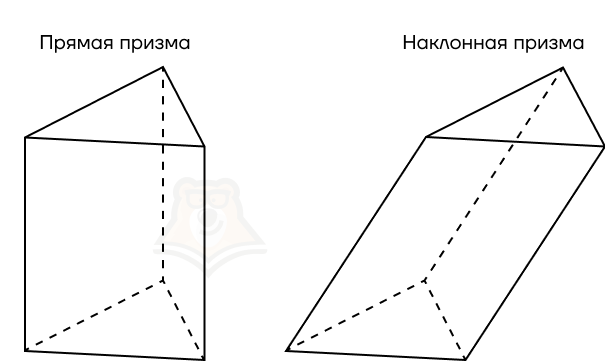
Где мы можем найти прямые и наклонные призмы? Оказывается, в архитектуре. Обычный жилой дом типовой застройки будет прямой призмой. А вот примером наклонной призмы может служить комплекс зданий “Ворота Европы” в Мадриде.

Чуть подробнее остановимся на прямых призмах. Они встречаются достаточно часто и обладают несколькими важными свойствами.

Посмотрите на свою комнату. Если по плану квартиры она будет многоугольником, то вы как бы сидите в призме. Теперь ответим на вопрос: как найти высоту комнаты?

Простой ответ: померить по стене. А если посмотреть на угол, то можно заметить, что ребро призмы совпадает с высотой. Таким образом, мы получаем первое свойство прямых призм.

Свойство 1. Высота прямой призмы совпадает с её боковым ребром.

Посмотрим на стены комнаты, на их форму. Они все являются прямоугольниками, верно?

Свойство 2. Все боковые грани прямой призмы — прямоугольники.

Как можно попасть в призму в реальной жизни?

Многие комнаты и помещения, особенно в типовой застройке, обладают формой призмы. Сидя в комнате, в классе, в столовой, даже в автобусе — мы как бы находимся внутри большой призмы.

Если мы в основании прямой призмы разместим правильный многоугольник, у нас получится правильная призма.

Правильная призма — прямая призма, в основании которой лежит правильный многоугольник.

Например, в правильной треугольной призме будет лежать равносторонний треугольник, а в правильной шестиугольной призме — правильный шестиугольник.

Определение параллелепипеда

Еще одной разновидностью прямоугольной призмы является параллелепипед.

Параллелепипед — это четырехугольная призма, все грани которой являются параллелограммами.

Параллелепипеды встречаются повсюду: коробки, мебель, комнаты, здания, склады, магазины. Поэтому изучить их не составит труда.

Свойство параллелепипеда, видимое невооруженным глазом: противоположные грани параллелепипеда равны. Как пример, вспомним ту же комнату: потолок и пол равны, так же как и стены, находящиеся напротив друг друга.

Нельзя не упомянуть про одно очень важное свойство параллелепипеда:

Все его диагонали пересекаются в одной точке и этой точкой делятся пополам. Это свойство справедливо для всех видов параллелепипеда.

Какие бывают параллелепипеды?

Параллелепипеды также бывают прямыми и наклонными. В этих случаях все определения такие же, как и для всех остальных призм.

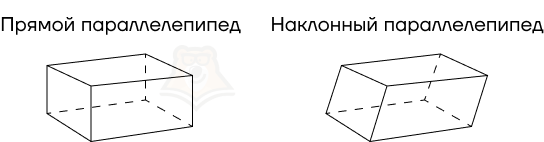
Прямой параллелепипед

Рассмотрим несколько интересных свойств прямого параллелепипеда.

1 свойство. Боковые ребра прямого параллелепипеда перпендикулярны основаниям.

2 свойство. Высота прямоугольного параллелепипеда равна длине его бокового ребра.

3 свойство. Боковые грани, которые лежат напротив друг друга, равны между собой и являются прямоугольниками.

Прямые параллелепипеды можно разделить еще на два вида:

Прямой параллелепипед: в основании лежит параллелограмм;

Прямоугольный параллелепипед: в основании лежит прямоугольник.

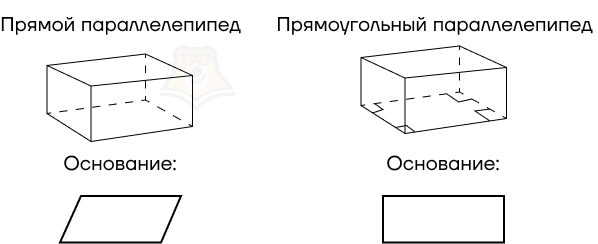
Рассмотрим свойства прямоугольного параллелепипеда.

1 свойство. Все грани прямоугольного параллелепипеда являются прямоугольниками.

2 свойство. Все углы в прямоугольном параллелепипеде, образованные двумя гранями, равны 90°.

3 свойство. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин его ширины, длины и высоты.

Таким образом, мы получаем важную формулу для параллелепипеда.

d² = a² + b² + c²

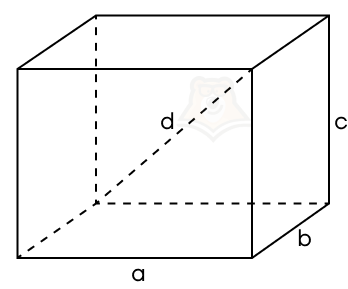
Пример 1. Дан прямоугольный параллелепипед. Два ребра, выходящие из одной его вершины, равны (sqrt{35}) и (sqrt{46}). Диагональ параллелепипеда равна 15. Найдите третье ребро параллелепипеда.

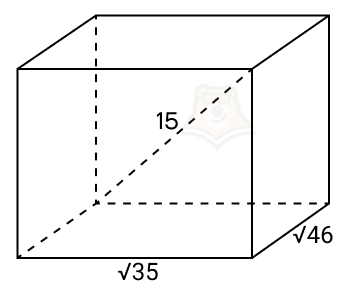
Решение. Пусть третье ребро параллелепипеда равняется х. Получаем уравнение:

(15^2 = (sqrt{35})^2 + (sqrt{46})^2 + x^2)
225 = 35 + 46 + x²
x² = 144
x = 12

Ответ: 12.

У прямоугольного параллелепипеда существует еще несколько видов. Прямоугольные параллелепипеды делятся на:

Произвольный прямоугольный параллелепипед. В основании может лежать прямоугольник.

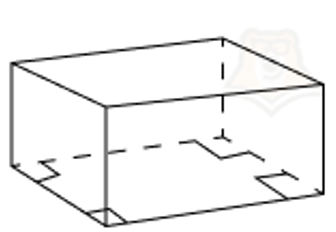
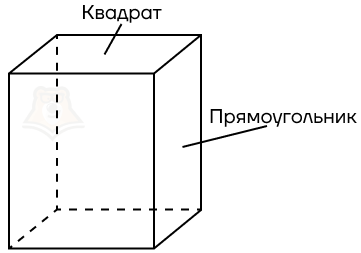
Правильный прямоугольный параллелепипед. В основании лежит правильный четырехугольник, то есть квадрат.
При этом боковые ребра не равны ребрам основания. Следовательно, в основаниях будут лежать квадраты, а в боковых гранях прямоугольники.

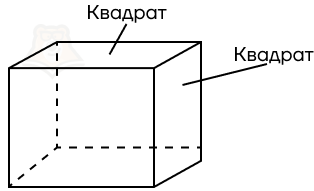
Куб. В основании лежит квадрат, а боковые ребра равны ребрам основания.
В кубе все ребра равны, а все его грани будут квадратом.

Таким образом, мы рассмотрели все виды параллелепипеда.

Формулы для призмы

Однако ни одна задача не может быть решена без формул. Поэтому необходимо рассмотреть несколько основных формул, которые могут встретиться не только в задачах, но и в жизни.

Немного вспомним моделирование, а именно развертку кубика. Мы знаем, что из листа бумаги без труда можно сложить кубик, если правильно его вычертить.

Как сложить игральные кости из листа бумаги?

Задумали вы вечером сыграть с семьей или друзьями в настольную игру. Но вот незадача: игральные кости опять куда-то запропастились. Не беда.Достаточно вычертить на листе бумаги несколько квадратов, вырезать получившуюся фигуру, согнуть по ребрам и склеить между собой с помощью клея. В итоге получатся кубики для игры.

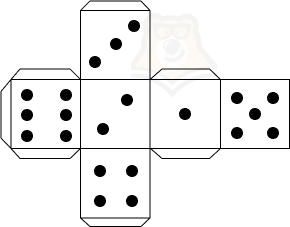
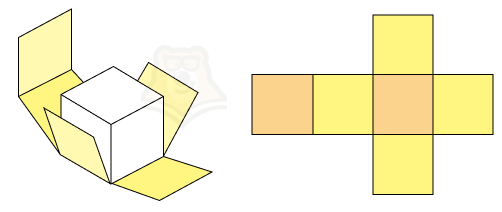
На рисунке оранжевым показаны основания, а желтым боковые грани нашего будущего кубика. А теперь представим, что нам нужно найти площадь боковой поверхности. Как это сделать?

Нужно найти площади желтых квадратиков и сложить их.

Площадь боковой поверхности призмы — сумма площадей всех боковых ее граней.

Единой формулы тут нет, поскольку призмы могут очень сильно отличаться друг от друга. В произвольных призмах придется считать площадь каждой боковой грани, а уже после их складывать.

Но есть один фокус! Правда, он работает только для прямой призмы. Если по условию дана прямая призма, то можно воспользоваться формулой

S_бок. = P * h

В этой формуле Р — периметр основания, h — высота призмы, которая совпадает с высотой боковой грани.

Пример 1. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равняется 2, а высота 10.

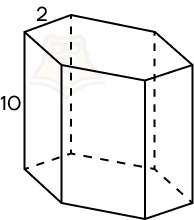
Решение.

Шаг 1. Поскольку правильная призма по определению прямая, мы можем воспользоваться формулой S = Ph.

Шаг 2. В основании правильной призмы лежит правильный шестиугольник, следовательно, периметр основания будет равен 6 * 2 = 12.

Шаг 3. Осталось найти только площадь боковой поверхности. Подставляем данные в формулу и получаем: S = 12 * 10 = 120.

Ответ: 120.

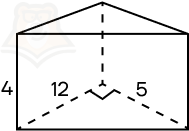
Пример 2. Дана прямая треугольная призма, в основании которой лежит прямоугольный треугольник с катетами 12 и 5. Высота призмы равна 13. Найдите площадь ее боковой поверхности.

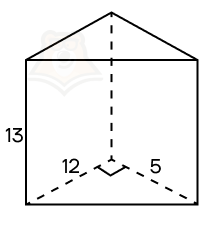
Решение.

Шаг 1. Поскольку призма прямая, можно воспользоваться формулой S = Ph.

Шаг 2. Найдем периметр основания. Для этого необходимо найти гипотенузу треугольника. Воспользуемся теоремой Пифагора: (sqrt{12^2 + 5^2} = sqrt{144 + 25} = sqrt{169} = 13).

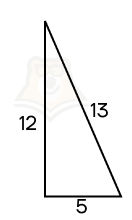
Шаг 3. Найдем периметр основания: P = 12 + 5 + 13 = 30.

Шаг 4. Осталось найти только площадь боковой поверхности. Подставляем данные в формулу и получаем: S = 30 * 13 = 390.

Ответ: 390.

Мы научились находить площадь боковой поверхности. А как найти всю площадь призмы? Вспомним нашу развертку с кубиком. Чтобы найти всю площадь кубика, нужно найти площадь всех квадратов, из которых он состоит. То есть и площадь боковой поверхности, и площадь оснований.

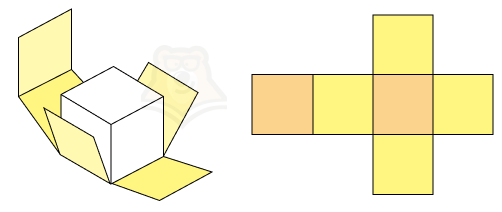
Площадь полной поверхности призмы — сумма площадей всех граней.

Следовательно, нам нужно сложить площади всех боковых граней и дважды площадь основания. Получаем следующую формулу.

S = S_бок + 2S_осн

Вспомним обычный хлеб, черный или белый. Его форма очень приближена к параллелепипеду. Тогда его корочка будет площадью полной поверхности параллелепипеда. А все что внутри, то есть мякиш, можно принять за объем.

Пример 3. Дана прямая призма, в основании которой лежит ромб с диагоналями 12 и 16. Боковое ребро призмы равно 25. Найдите площадь поверхности призмы.

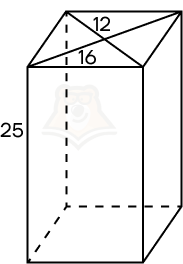
Решение.

Шаг 1. Найдем площадь основания. Площадь ромба можно найти по формуле (frac{1}{2} * D_1 * D_2). Следовательно, площадь ромба равна (frac{1}{2} * 12 * 16 = 96).

Шаг 2. Заметим, что диагонали ромба образуют четыре равных прямоугольных треугольника. Следовательно, чтобы найти сторону ромба, достаточно рассмотреть прямоугольный треугольник с катетами 6 и 8. По теореме Пифагора сторона ромба будет равна (sqrt{6^2 + 8^2} = sqrt{36 + 64} = sqrt{100} = 10).

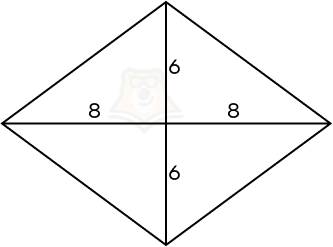
Шаг 3. Периметр ромба будет равен 4 * 10 = 40. Тогда площадь боковой поверхности равна 40 * 25 = 1000.

Шаг 4. Площадь полной поверхности будет равняться 1000 + 2 * 96 = 1000 + 192 = 1192.

Ответ: 1192

Пример 4. Площадь поверхности правильной четырехугольной призмы равняется 1980. Сторона основания равна 5. Найдите боковое ребро этой призмы.

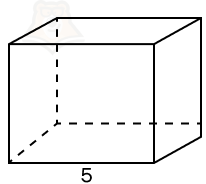
Решение.

Шаг 1. Воспользуемся формулой S = S_бок + 2S_осн. Площадь основания будет равняться площади квадрата, то есть 5 * 5 = 25.

Шаг 2. Подставим известные величины в формулу:

1980 = S_бок + 2 * 25
S_бок = 1930

Шаг 3. Площадь боковой поверхности равна произведению периметра основания на высоту призмы. Периметр равен 5 * 4 = 20. Тогда получаем уравнение:

20h = 1930
h = 96,5

Шаг 4. Поскольку по условию дана правильная призма, то высота совпадает с боковым ребром. Следовательно, боковое ребро равняется 96,5.

Ответ: 96,5.

Теперь рассмотрим, как найти объем призмы. Допустим, мы налили в прямоугольный аквариум немного воды. Как определить, сколько воды мы налили?

Для этого достаточно воспользоваться формулой объема призмы.

V = S_осн. * h

Эта формула общая, однако для каждой призмы она может принять свой вид в зависимости от того, какую формулу нужно использовать для поиска площади основания или высоты.

Например, чтобы найти объем воды в аквариуме, необходимо длину умножить на ширину и на высоту, а значит формула принимает вид V = abh.

Как найти объем воды в аквариуме?

Для этого достаточно перемножить ширину, длину аквариума и высоту воды. Тем самым мы найдем объем призмы, форму которой принимает вода в аквариуме.

Пример 5. Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 12 и 15. Боковое ребро призмы равно 4. Найдите объем этой призмы.

Решение.

Шаг 1. Для начала найдем площадь основания. В этом случае мы можем воспользоваться формулой (frac{1}{2}ab). Площадь равна (frac{1}{2} * 12 * 15 = 90).

Шаг 2. Воспользуемся формулой объема призмы и подставим известные величины:

V = 90 * 4 = 360.

Ответ: 360.

Пример 6. Дан сосуд, в основании которого лежит правильный треугольник. В этот сосуд налили 3000 см³ воды. Высота жидкости оказалась равной 10 см. После этого в сосуд опустили шарик и высота изменилась с 10 см на 14 см. Найдите объем шарика.

Решение. Немного вспомним физику, а именно тот факт, что объем вытесненной жидкости равен объему тела. Значит, чтобы найти объем шарика, необходимо найти насколько изменился объем воды.

Шаг 1. Найдем площадь основания сосуда. Для этого немного преобразуем формулу объема:
(S = frac{V}{h})
Тогда:
(S = frac{3000}{10} = 300)

Шаг 2. А теперь найдем объем после того, как в воду погрузили шарик. Он будет равен 300 * 14 = 4200.

Шаг 3. Объем вытесненной жидкости равен 4200 — 3000 = 1200.

Ответ: 1200.

Мы рассмотрели основные формулы, которые применяются для решения задач. Стоит заметить, что они универсальны, и в каждой задаче их рационально преобразовывать под ситуацию.

Фактчек

Призма — это многогранник, в котором две грани являются равными многоугольниками и лежат в параллельных плоскостях, а все остальные — параллелограммами. Равные многоугольники называются основаниями призмы, а остальные стороны — боковыми гранями. В призме есть ребра — линии пересечения двух ее граней. Ребра как бы образуют каркас призмы.
Призмы можно разделить на несколько видов по тому, какая фигура лежит в основании: треугольник, четырехугольник, шестиугольник или любой другой многоугольник. Призмы бывают прямые и наклонные. В прямых призмах боковые ребра перпендикулярны основанию, а в наклонных — нет. Правильная призма — прямая призма, в основании которой лежит правильный многоугольник.
Параллелепипед — это четырехугольная призма, все грани которой являются параллелограммами. Параллелепипеды бывают наклонными и прямыми. Прямые параллелепипеды включают в себя прямоугольные параллелепипеды, которые, в свою очередь, делятся на произвольные, правильные и кубы.
В призме можно найти площадь боковой поверхности, площадь полной поверхности и объем. Для каждого из этих случаев необходимо пользоваться формулами.

Проверь себя

Задание 1.
Что такое диагональ призмы?

Отрезок, соединяющий две соседние вершины в призме.
Отрезок, соединяющий противоположные углы в боковой грани призмы.
Отрезок, соединяющий противоположные углы в основании призмы.
Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.

Задание 2.
Что такое прямая призма?

Призма, боковые ребра которой перпендикулярны основаниям.
Призма, боковые ребра которой расположены под острым углом относительно основания.
Призма, боковые ребра которой расположены под тупым углом относительно основания.
Призма, в основании которой лежит прямоугольник.

Задание 3.
Как найти высоту прямой призмы?

Высоту нужно найти с помощью оснований.
Высота совпадает с боковым ребром.
Необходимо найти расстояние между двумя вершинами, не принадлежащими одной грани.
В прямой призме невозможно найти высоту.

Задание 4.
Какая фигура лежит в основании прямоугольного параллелепипеда?

Параллелограмм с острыми углами.
Ромб с острыми углами.
Трапеция.
Прямоугольник.

Задание 5.
Как найти площадь полной поверхности призмы?

Нужно найти сумму площадей всех боковых граней.
Нужно сложить площадь боковой поверхности и площадь основания.
Нужно сложить площадь боковой поверхности и удвоенную площадь основания.
Нужно сложить площади оснований.

Ответы: 1. — 4 2. — 1 3. — 2 4. — 4 5. — 3

Источник

Пересечение прямой с призмой

Создаем ассоциативный чертеж по 3d модели

Как найти проекции точек на пирамиде и призме?

Как найти проекции точек на призме?

Как найти проекции точек на пирамиде?

Понравился материал? Подпишись на обновления!

Точки и линии на поверхности призмы

Точки и линии на поверхности тора

←Метод координат

На этой странице вы узнаете

Определение призмы

Строение призмы

Виды призм

Определение параллелепипеда

Прямой параллелепипед

Формулы для призмы

Фактчек

Проверь себя

Не пропустите также: