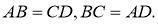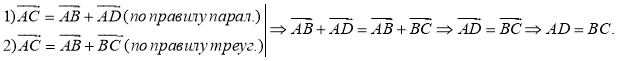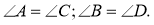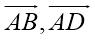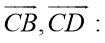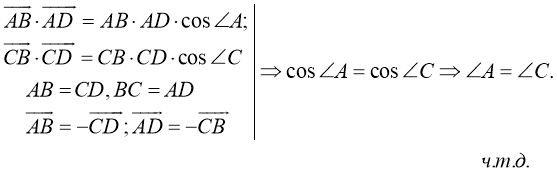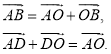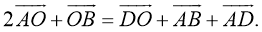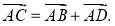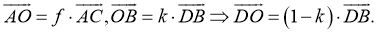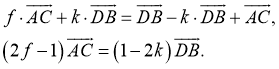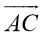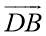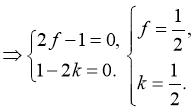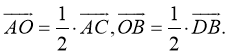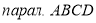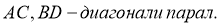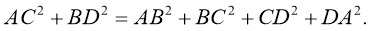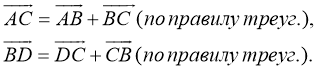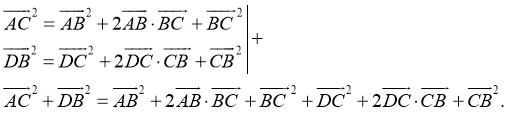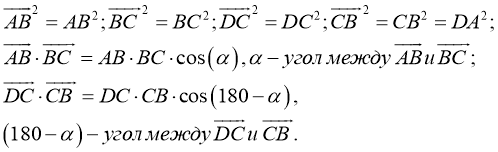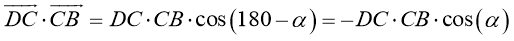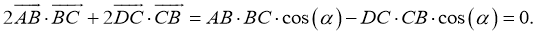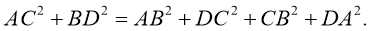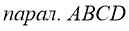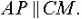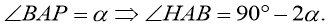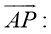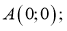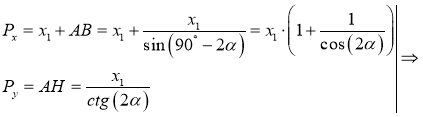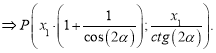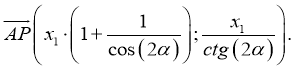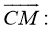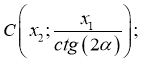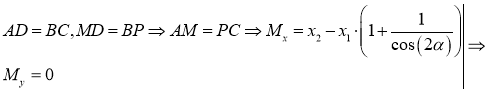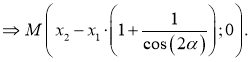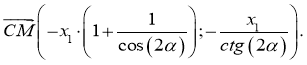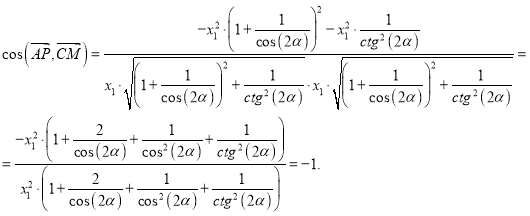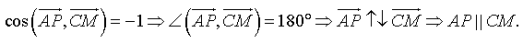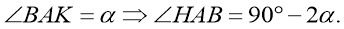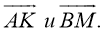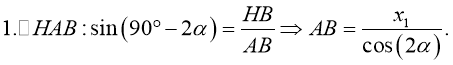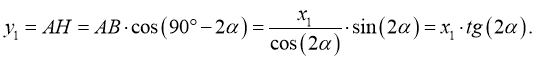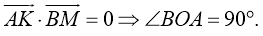Онлайн калькулятор. Площадь параллелограмма построенного на векторах.
Этот онлайн калькулятор позволит вам очень просто найти площадь параллелограмма построенного на векторах.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление площади параллелограмма построенного на векторах и закрепить пройденый материал.
Калькулятор для вычисления площади параллелограмма построенного на векторах
Выберите каким образом задается параллелограмм:
Введите значения векторов: Введите координаты трех любых вершин параллелограмма:
Инструкция использования калькулятора для вычисления площади параллелограмма построенного на векторах
Ввод данных в калькулятор для вычисления площади параллелограмма построенного на векторах
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора вычисления площади параллелограмма построенного на векторах
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.
Теория. Площадь параллелограмма построенного на векторах.
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
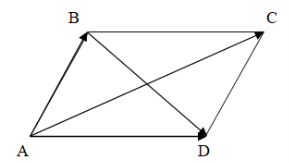
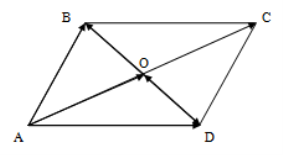
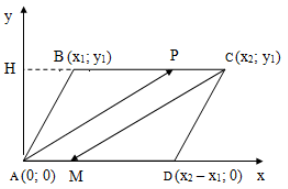
Найти четвертую вершину параллелограмма
Как найти координаты 4-й вершины параллелограмма, зная координаты трёх других его вершин?
В декартовых координатах эту задачу можно решить, используя свойство диагоналей параллелограмма.
Из трёх известных вершин две являются концами одной диагонали. Находим координаты середины этой диагонали. Точка пересечения диагоналей является серединой каждой из них. Для второй диагонали находим второй конец по известным одному концу и середине.
Дано: ABCD — параллелограмм,
1) Найдём координаты точки O — середины диагонали AC.
2) По свойству диагоналей параллелограмма, точка O также является серединой BD:
Дано: ABCD — параллелограмм,
1) Ищем координаты точки O — середины отрезка BD:
2) Точка O также является серединой AC:
2 Comments
А как вы получили -14 в первом примере.
Можно применить основное свойство пропорции: 12+xD=2∙(-1), xD=-2-12=-14.
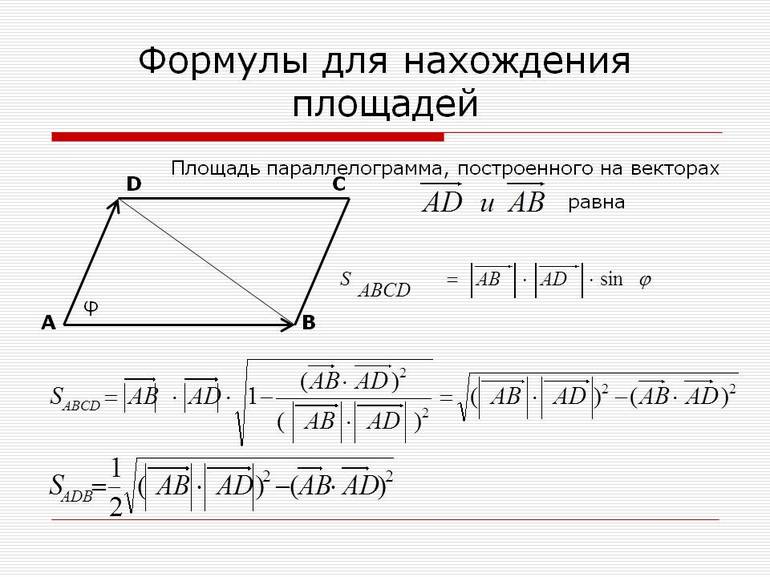
Площадь параллелограмма, построенного на векторах — формула и примеры решения задач
Четырехугольник и вектор на плоскости
Каждый школьник понимает, что параллелограмм является специальным видом плоских четырехугольников. Эта фигура состоит из двух пар параллельных пересекающихся отрезков. Она обладает следующими важными свойствами:
- ее противоположные стороны и углы равны друг другу;
- сумма всех четырех углов составляет 360 градусов;
- если просуммировать лишь два смежных (прилежащих к одной стороне) угла, то получится значение 180 градусов;
- любая диагональ делит фигуру на две равные части (треугольники);
- пересечение диагоналей происходит в точке, которая является геометрическим и массовым центром параллелограмма;
- любая секущая, которая проходит через геометрический центр, делит фигуру на две равные по площади части.
Специальные типы
Исходя из определения параллелограмма, как четырехугольника с параллельными и равными по длине противоположными сторонами, можно привести несколько видов фигуры, которые обладают высокой симметрией по отношению к ряду элементарных операций. Это следующие геометрические типы:
- Квадрат. Все четыре стороны его равны по длине между собой, а углы составляют 90 градусов. Он является фигурой с достаточно высокой симметрией, и его площадь вычисляется просто как квадрат длины любой его стороны.
- Прямоугольник. Еще один вид параллелограмма, все углы которого являются прямыми. Его симметрия несколько ниже, чем у квадрата, поскольку длины сторон равны лишь попарно. Площадь фигуры можно вычислить, перемножив длины смежных сторон.
- Ромб. Специальный геометрический тип параллелограмма, который характеризуется тем, что длины всех его сторон являются одинаковыми. Углы фигуры попарно равны и отличаются от 90 градусов (два тупых и два острых).
Направленные отрезки и операция умножения
Площадь параллелограмма через векторы рассчитать легко, если знать понятие направленного отрезка и уметь работать с соответствующими математическими операциями. Поскольку любая точка на плоскости может быть представлена в виде набора двух координат в декартовой прямоугольной системе, то для P и Q можно записать:
P (x1, y1); Q (x2, y2).
Где числа x1, y1, x2 и y2 являются соответствующими координатами для точек P и Q по осям абсцисс и ординат. Чтобы получить вектор PQ-, который будет направлен из P в точку Q, необходимо из координат Q попарно вычесть значения для P:
PQ- = Q — P = (x2-x1, y2-y1).
Координаты направленного отрезка на плоскости определяются так же, как и для точки, набором из двух чисел. Чтобы построить такой вектор в системе координат, необходимо его начало расположить в точке (0, 0), а конец со стрелкой будет располагаться в точке (x2-x1, y2-y1). Из этой геометрической интерпретации следует, что существует бесконечное множество направленных отрезков, которые эквивалентны между собой. Получаются они друг из друга с помощью параллельного переноса по всей плоскости координат.
Как и числа, направленные отрезки также можно складывать между собой, вычитать и умножать. Рассматривая вопрос построение параллелограмма на векторах и нахождения его площади, необходимо изучить свойства векторного произведения. Оно представляет собой вектор, перпендикулярный плоскости, в которой лежат исходные направленные отрезки. Пусть a- и b- необходимо умножить векторно. Результатом произведения будет следующий вектор c-:
c- = [a-*b-] = |a-|*|b-|*sin (alfa).
Здесь alfa — угол между a- и b-, а |a-| и |b-| — длины соответствующих направленных отрезков.
Направление c- принято определять с помощью правила правой руки. Оно гласит: если четыре пальца ладони направить от конца первого умножаемого вектора к концу второго, то оттопыренный большой палец укажет направление результирующего векторного умножения.
Координаты вектора c- можно вычислить также, если воспользоваться понятием определителя матрицы. Пусть a- имеет координаты (a1, a2), а b- = (b1, b2), тогда формула для определения c- запишется в следующем виде:
c- = (0, 0, (a1*b2-b1*a2)).
Вектор c- имеет первые две нулевые координаты, поскольку он перпендикулярен плоскости, в которой находятся a- и b-.
Формула площади из геометрии
Чтобы получить формулу площади параллелограмма на векторах, необходимо вспомнить, как рассчитывается эта величина для треугольника. Если известна одна сторона (основание a) и высота, которая на нее опущена (h), то получается простое выражение:
Где S3 — площадь треугольника. Поскольку две таких плоских фигуры, которые соединены одной из своих сторон, образуют четырехугольник-паралелограм, то для него рассмотренную величину можно вычислить по формуле:
Пусть вторая сторона параллелограмма равна b, тогда с высотой h она связана через определение тригонометрической функции синус:
sin (alfa) = h/b => h = b*sin (alfa).
Если подставить это равенство в выражение для S4, то нахождение площади фигуры сведется к расчету произведения двух его смежных сторон и синуса угла между ними:
Поскольку угол alfa изменяется от 0 до 180 градусов, то функция синус всегда имеет положительное значение. Этой формулой часто пользуются на практике. Распространение инженерных калькуляторов позволяет быстро и с высокой точностью вычислять синусы любых углов.
Построение параллелограмма
Определить площадь четырехугольника с попарно параллельными сторонами можно не только через длины его сторон. Если внимательно посмотреть на формулу для S4, то можно заметить, что она идентична по виду векторному произведению направленных отрезков.
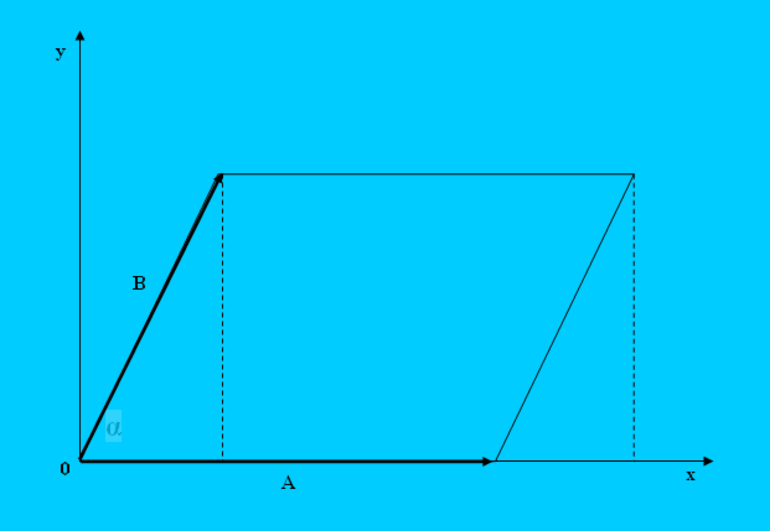
Пусть имеется два вектора a- и b-. Угол между ними равен alfa. Если их начала совместить в одной точке на плоскости, затем, от конца a- продолжить вектор b-, а из b- начертить a-, то получится параллелограмм, побудованый на a- и b-. Очевидно, что модуль векторного произведения этих направленных отрезков будет равен площади полученной фигуры:
S4 = a*b*sin (alfa) = |[a-*b-]|.
Применяя координатное выражение этого произведения, можно записать следующую формулу для площади:
Где a- = (a1,a2) и b-=(b1,b2). Знак модуля необходим потому, что по правилу правой руки могут получаться отрицательные векторы. Площадь же является всегда величиной положительной.
Преимущество последней записанной формулы для S4 по сравнению с выражением, где необходимо знать длины и углы, заключается в том, что ее использование не требует никаких предварительных вычислений. Достаточно лишь знать координаты конца и начала образующих параллелограмм векторов.
Задача с тремя точками
Чтобы научиться пользоваться записанной простой формулой, следует решить простую задачу. Имеется три точки, координаты которых следующие:
На вершинах этих точек следует построить параллелограмм, а затем, рассчитать его площадь S4.
Задачу проще всего решать через использование векторов. Выберем произвольную точку из трех заданных. Пусть это будет A. Из нее выходит два вектора: AB- и AC-. Их координаты определяются таким образом:
AB- = (2−1, 0-(-1)) = (1, 1); AC- = (-4−1, 3- (-1)) = (-5, 4).
Чтобы определить площадь параллелограмма на этих векторах, следует применить формулу для их векторного произведения. Порядок умножения направленных отрезков не имеет значения. Получается следующий результат:
S4 = [AB-*AC-] = 1*4 — (-5)*1 = 9.
Результат получен в единицах квадратных соответствующей двумерной системы координат.
Если была выбрана в качестве исходной не точка A, а B или C, то получился бы тот же результат, что можно доказать, проделав аналогичные вычисления.
Диагонали фигуры
Некоторые задачи по геометрии параллелограммов в качестве начального условия предлагают знание одной или двух его диагоналей. По этим данным необходимо вычислить характеристики всей фигуры, включая ее площадь. Решать такие задачи также удобно с использованием понятия векторов.
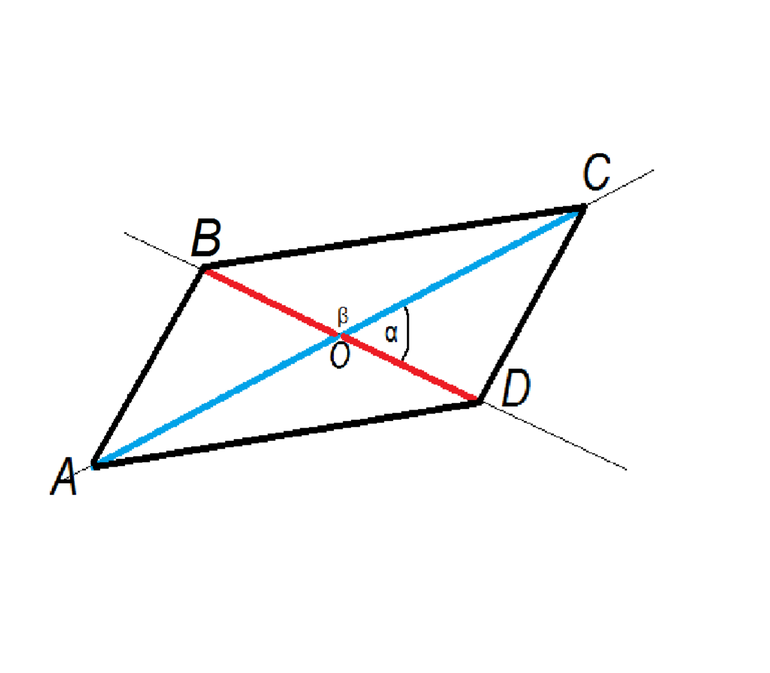
Если дана диагональ, выраженная вектором f- и основание, представленное направленным отрезком a-, то формула для площади параллелограмма имеет вид:
Где beta — угол между a- и f-. Видно, что это выражение не отличается от предыдущих для S4. Доказать его справедливость несложно, если рассмотреть построенные на указанных векторах треугольники и использовать признаки их подобия.
Другой случай, когда даны обе диагонали параллелограмма f- и e-. Воспользовавшись геометрическими построениями на плоскать, можно показать справедливость следующего выражения:
Здесь teta — это угол пересечения e- и f-. Таким образом, чтобы вычислить площадь параллелограмма, диагоналями которого служат вектора, следует вычислить половину модуля их векторного произведения.
Пример решения
Все разнообразие задач на определение площади параллелограмма сводится к знанию единственной формулы векторного произведения. Пусть известны две диагонали фигуры. Они имеют координаты:
Чтобы определить величину S4, достаточно без промежуточных вычислений воспользоваться формулой векторного произведения заданных направленных отрезков:
В связи с развитием интернета, всегда можно использовать калькулятор-онлайн для расчета величины S4. Соответствующий электронный ресурс можно знайти, воспользовавшись любой поисковой системой в браузере.
Трехмерное пространство
В пространственной системе координат каждый вектор задается тремя числами, поэтому их векторное произведение c- также будет представлять набор трех цифр. Построенный в пространстве параллелограмм на двух векторах будет иметь площадь, равную длине направленного отрезка c-. Для расчета его модуля следует использовать известное выражение: сумма квадратов трех координат под корнем.
Таким образом, площадь параллелограмма проще всего вычислять, используя операцию умножения векторов. Этот метод является универсальным не только для задач на плоскости, но и для решения проблем в трехмерной системе координат.
http://nauka.club/matematika/geometriya/ploshchad-parallelogramma-postroennogo-na-vektorakh.html
Как найти координаты 4-й вершины параллелограмма, зная координаты трёх других его вершин?
В декартовых координатах эту задачу можно решить, используя свойство диагоналей параллелограмма.
Из трёх известных вершин две являются концами одной диагонали. Находим координаты середины этой диагонали. Точка пересечения диагоналей является серединой каждой из них. Для второй диагонали находим второй конец по известным одному концу и середине.
Примеры.
1)

A(-3;11), B(12;-4), C(1;-7)
Найти: D.
Решение:

По формуле координат середины отрезка
То есть O(-1;2).
2) По свойству диагоналей параллелограмма, точка O также является серединой BD:
Ответ: D (-14; 8).
2)
Дано: ABCD — параллелограмм,
B(7;4), C(-5;10), D(-1;-2)
Найти: A.
Решение:
1) Ищем координаты точки O — середины отрезка BD:
Итак, O (3;1).
2) Точка O также является серединой AC:
Ответ: A (11;-8).
Четырехугольник и вектор на плоскости
Каждый школьник понимает, что параллелограмм является специальным видом плоских четырехугольников. Эта фигура состоит из двух пар параллельных пересекающихся отрезков. Она обладает следующими важными свойствами:
- ее противоположные стороны и углы равны друг другу;
- сумма всех четырех углов составляет 360 градусов;
- если просуммировать лишь два смежных (прилежащих к одной стороне) угла, то получится значение 180 градусов;
- любая диагональ делит фигуру на две равные части (треугольники);
- пересечение диагоналей происходит в точке, которая является геометрическим и массовым центром параллелограмма;
- любая секущая, которая проходит через геометрический центр, делит фигуру на две равные по площади части.
Специальные типы
Исходя из определения параллелограмма, как четырехугольника с параллельными и равными по длине противоположными сторонами, можно привести несколько видов фигуры, которые обладают высокой симметрией по отношению к ряду элементарных операций. Это следующие геометрические типы:
- Квадрат. Все четыре стороны его равны по длине между собой, а углы составляют 90 градусов. Он является фигурой с достаточно высокой симметрией, и его площадь вычисляется просто как квадрат длины любой его стороны.
- Прямоугольник. Еще один вид параллелограмма, все углы которого являются прямыми. Его симметрия несколько ниже, чем у квадрата, поскольку длины сторон равны лишь попарно. Площадь фигуры можно вычислить, перемножив длины смежных сторон.
- Ромб. Специальный геометрический тип параллелограмма, который характеризуется тем, что длины всех его сторон являются одинаковыми. Углы фигуры попарно равны и отличаются от 90 градусов (два тупых и два острых).
Направленные отрезки и операция умножения
Площадь параллелограмма через векторы рассчитать легко, если знать понятие направленного отрезка и уметь работать с соответствующими математическими операциями. Поскольку любая точка на плоскости может быть представлена в виде набора двух координат в декартовой прямоугольной системе, то для P и Q можно записать:
P (x1, y1); Q (x2, y2).
Где числа x1, y1, x2 и y2 являются соответствующими координатами для точек P и Q по осям абсцисс и ординат. Чтобы получить вектор PQ-, который будет направлен из P в точку Q, необходимо из координат Q попарно вычесть значения для P:
PQ- = Q — P = (x2-x1, y2-y1).
Координаты направленного отрезка на плоскости определяются так же, как и для точки, набором из двух чисел. Чтобы построить такой вектор в системе координат, необходимо его начало расположить в точке (0, 0), а конец со стрелкой будет располагаться в точке (x2-x1, y2-y1). Из этой геометрической интерпретации следует, что существует бесконечное множество направленных отрезков, которые эквивалентны между собой. Получаются они друг из друга с помощью параллельного переноса по всей плоскости координат.
Как и числа, направленные отрезки также можно складывать между собой, вычитать и умножать. Рассматривая вопрос построение параллелограмма на векторах и нахождения его площади, необходимо изучить свойства векторного произведения. Оно представляет собой вектор, перпендикулярный плоскости, в которой лежат исходные направленные отрезки. Пусть a- и b- необходимо умножить векторно. Результатом произведения будет следующий вектор c-:
c- = [a-*b-] = |a-|*|b-|*sin (alfa).
Здесь alfa — угол между a- и b-, а |a-| и |b-| — длины соответствующих направленных отрезков.
Направление c- принято определять с помощью правила правой руки. Оно гласит: если четыре пальца ладони направить от конца первого умножаемого вектора к концу второго, то оттопыренный большой палец укажет направление результирующего векторного умножения.
Координаты вектора c- можно вычислить также, если воспользоваться понятием определителя матрицы. Пусть a- имеет координаты (a1, a2), а b- = (b1, b2), тогда формула для определения c- запишется в следующем виде:
c- = (0, 0, (a1*b2-b1*a2)).
Вектор c- имеет первые две нулевые координаты, поскольку он перпендикулярен плоскости, в которой находятся a- и b-.
Формула площади из геометрии
Чтобы получить формулу площади параллелограмма на векторах, необходимо вспомнить, как рассчитывается эта величина для треугольника. Если известна одна сторона (основание a) и высота, которая на нее опущена (h), то получается простое выражение:
S3 = ½*h*a.
Где S3 — площадь треугольника. Поскольку две таких плоских фигуры, которые соединены одной из своих сторон, образуют четырехугольник-паралелограм, то для него рассмотренную величину можно вычислить по формуле:
S4 = 2*S3 = h*a.
Пусть вторая сторона параллелограмма равна b, тогда с высотой h она связана через определение тригонометрической функции синус:
sin (alfa) = h/b => h = b*sin (alfa).
Если подставить это равенство в выражение для S4, то нахождение площади фигуры сведется к расчету произведения двух его смежных сторон и синуса угла между ними:
S4 = a*b*sin (alfa).
Поскольку угол alfa изменяется от 0 до 180 градусов, то функция синус всегда имеет положительное значение. Этой формулой часто пользуются на практике. Распространение инженерных калькуляторов позволяет быстро и с высокой точностью вычислять синусы любых углов.
Построение параллелограмма
Определить площадь четырехугольника с попарно параллельными сторонами можно не только через длины его сторон. Если внимательно посмотреть на формулу для S4, то можно заметить, что она идентична по виду векторному произведению направленных отрезков.
Пусть имеется два вектора a- и b-. Угол между ними равен alfa. Если их начала совместить в одной точке на плоскости, затем, от конца a- продолжить вектор b-, а из b- начертить a-, то получится параллелограмм, побудованый на a- и b-. Очевидно, что модуль векторного произведения этих направленных отрезков будет равен площади полученной фигуры:
S4 = a*b*sin (alfa) = |[a-*b-]|.
Применяя координатное выражение этого произведения, можно записать следующую формулу для площади:
S4 = |(a1*b2-b1*a2)|.
Где a- = (a1,a2) и b-=(b1,b2). Знак модуля необходим потому, что по правилу правой руки могут получаться отрицательные векторы. Площадь же является всегда величиной положительной.
Преимущество последней записанной формулы для S4 по сравнению с выражением, где необходимо знать длины и углы, заключается в том, что ее использование не требует никаких предварительных вычислений. Достаточно лишь знать координаты конца и начала образующих параллелограмм векторов.
Задача с тремя точками
Чтобы научиться пользоваться записанной простой формулой, следует решить простую задачу. Имеется три точки, координаты которых следующие:
- A (1,-1);
- B (2, 0);
- C (-4, 3).
На вершинах этих точек следует построить параллелограмм, а затем, рассчитать его площадь S4.
Задачу проще всего решать через использование векторов. Выберем произвольную точку из трех заданных. Пусть это будет A. Из нее выходит два вектора: AB- и AC-. Их координаты определяются таким образом:
AB- = (2−1, 0-(-1)) = (1, 1); AC- = (-4−1, 3- (-1)) = (-5, 4).
Чтобы определить площадь параллелограмма на этих векторах, следует применить формулу для их векторного произведения. Порядок умножения направленных отрезков не имеет значения. Получается следующий результат:
S4 = [AB-*AC-] = 1*4 — (-5)*1 = 9.
Результат получен в единицах квадратных соответствующей двумерной системы координат.
Если была выбрана в качестве исходной не точка A, а B или C, то получился бы тот же результат, что можно доказать, проделав аналогичные вычисления.
Диагонали фигуры
Некоторые задачи по геометрии параллелограммов в качестве начального условия предлагают знание одной или двух его диагоналей. По этим данным необходимо вычислить характеристики всей фигуры, включая ее площадь. Решать такие задачи также удобно с использованием понятия векторов.
Если дана диагональ, выраженная вектором f- и основание, представленное направленным отрезком a-, то формула для площади параллелограмма имеет вид:
S4 = [a-*f-] = |a-|*|f-|*sin (beta).
Где beta — угол между a- и f-. Видно, что это выражение не отличается от предыдущих для S4. Доказать его справедливость несложно, если рассмотреть построенные на указанных векторах треугольники и использовать признаки их подобия.
Другой случай, когда даны обе диагонали параллелограмма f- и e-. Воспользовавшись геометрическими построениями на плоскать, можно показать справедливость следующего выражения:
S4 = ½*|[e-*f-]| = ½*|e-|*|f-|*sin (teta).
Здесь teta — это угол пересечения e- и f-. Таким образом, чтобы вычислить площадь параллелограмма, диагоналями которого служат вектора, следует вычислить половину модуля их векторного произведения.
Пример решения
Все разнообразие задач на определение площади параллелограмма сводится к знанию единственной формулы векторного произведения. Пусть известны две диагонали фигуры. Они имеют координаты:
e- = (2, -1); f- = (1, -4).
Чтобы определить величину S4, достаточно без промежуточных вычислений воспользоваться формулой векторного произведения заданных направленных отрезков:
S4 = ½*|[e-*f-]| = ½*|-8+1| = 3,5.
В связи с развитием интернета, всегда можно использовать калькулятор-онлайн для расчета величины S4. Соответствующий электронный ресурс можно знайти, воспользовавшись любой поисковой системой в браузере.
Трехмерное пространство
В пространственной системе координат каждый вектор задается тремя числами, поэтому их векторное произведение c- также будет представлять набор трех цифр. Построенный в пространстве параллелограмм на двух векторах будет иметь площадь, равную длине направленного отрезка c-. Для расчета его модуля следует использовать известное выражение: сумма квадратов трех координат под корнем.
Таким образом, площадь параллелограмма проще всего вычислять, используя операцию умножения векторов. Этот метод является универсальным не только для задач на плоскости, но и для решения проблем в трехмерной системе координат.
Библиографическое описание:
Карымов, И. А. Доказательство основных свойств параллелограмма при помощи векторно-координатного метода / И. А. Карымов. — Текст : непосредственный // Молодой ученый. — 2021. — № 13 (355). — С. 1-8. — URL: https://moluch.ru/archive/355/79495/ (дата обращения: 25.05.2023).
Векторно-координатный метод решения задач является одним из самых мощных способов, использование которого позволяет решать многие физические, технические и математические задачи. Привлекательность данного метода обусловлена его алгоритмичностью — возможностью построения систем последовательных операций, описывающих порядок действий для решения той или иной задачи. В данной статье доказываются основные свойства параллелограмма векторно-координатным методом.
Ключевые слова:
векторно-координатный метод, геометрическая задача, свойства параллелограмма.
Решение геометрических задач, как правило, требует широкого пространственного мышления, наглядного представления сложных конфигураций, грамотной корреляции богатого математического знания. Еще В. Г. Болтянский отмечал: «Трудность решения геометрических задач заключается не только и не столько в том, что надо выполнить несколько операций; основная трудность состоит в
отыскании необходимой последовательности действий
, выполнения которых ведет к решению задачи» [2, с. 28].
Данное обстоятельство, сопровождающееся нехваткой времени, необходимого для решения той или иной задачи, вызывают трудности, провоцирующие нас к поиску наиболее оптимального метода решения геометрических задач и его использовании на технологическом уровне.
Векторно-координатный метод используется в различных областях науки и техники, общественной жизни. Данный метод лежит в основе механики, геодезии, экономики, астрономии, географии, медицине. Особая его роль отводится в математике, в частности, при решении геометрических задач. Так данный метод позволяет сопоставить геометрическим объектам (фигурам, отрезкам, векторам), соответствующие им алгебраические соотношения, в результате чего появляются возможности более рационально решать многие задачи, строить доказательства [4].
В данной статье приводятся доказательства основных свойств параллелограмма при помощи векторно-координатного метода.
Основная часть
Для обеспечения овладением первичными навыками использования векторно-координатного метода на практическом уровне рассмотрим основные свойства параллелограмма, установим их истинность при помощи данного метода. Анализ учебников геометрии (Атанасян Л. С. [1], Погорелов А. В. [3], Смирнова, И.М. [5], Шарыгин И.Ф [6]) позволил синтезировать основные свойства параллелограмма.
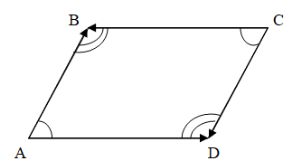
Свойство 1.
Противоположные стороны параллелограмма равны.
Дано
:
.
.
Доказать
:
Доказательство:
Свойство 2.
Противоположные углы параллелограмма равны.
Дано
:
.
.
Доказать
:
Доказательство:
Воспользуемся скалярным произведением векторов
и
Свойство 3.
Диагонали параллелограмма пересекаются и точкой пересечения делят друг друга пополам.
Дано:
.
Доказать
:
Доказательство:
- По правилу треугольника получаем:
- Просуммируем первое и второе равенство:
- По правилу параллелограмма получаем:
-
Пусть
- Подставим полученные результаты в пункт 2:
-
и
— не коллинеарные
-
Таким образом,
Свойство 4.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
Дано:
.
Доказать
:
Доказательство:
-
- Возведем левые и правые части равенств и соответственно их просуммируем:
- Воспользуемся скалярным произведением:
Преобразуем последнее равенство, получим:
.
- Принимая во внимание свойство 1, получим:
-
Таким образом,
Свойство 5.
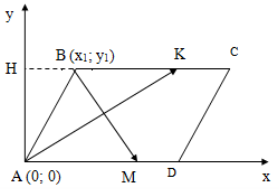
Биссектрисы противоположных углов параллелограмма всегда параллельны.
Дано:
.
Доказать:
Доказательство: Пусть
Определим координаты векторов
Таким образом,
2.
-
Определим косинус угла между векторами
ч. т. д.
Свойство 6.
Биссектрисы односторонних углов параллелограмма взаимно перпендикулярны.
Дано:
Доказать:
Доказательство
: Пусть
Определим координаты векторов
-
Определим координаты векторов
-
Определим скалярное произведение векторов
-
ч. т. д.
Заключение
Векторно-координатный метод соединяет в себе метод координат и векторный метод и позволяет при помощи необходимых формул найти удобный подход к решению сложных геометрических задач.
Особо важно подчеркнуть прикладной характер изучения векторно-координатного метода как отправной точки подготовки к ЕГЭ по профильной математике, что придает ему значимость и определяет перспективы настоящего исследования.
Литература:
- Атанасян Л. C. Геометрия, 7–9: учеб. для общеобразоват. учреждений / JI. C. Атанасян и др.. — 12-е изд. — М.: Просвещение, 2002. — 384 с.
- Болтянский В. Г., Савин А. П. Беседы по математике. Кн. 1. Дискретные объекты. — М.: ФИМА, МЦНМО, 2002. — 368 с.
- Погорелов А. В. Геометрия. 10–11 классы: учебник для общеобразовательных учреждений / А. В. Погорелов. — 9-е изд. — М.: Просвещение, 2009.- 175 с.
- Потоскуев Е. В. Векторы и координаты как аппарат решения геометрических задач. 10–11 класс: Элективные курс / Е. В. Потоскуев. — М.: Издательство «Дрофа», 2008. — 176 с.
- Смирнова И. М. Геометрия. 7–9 классы: учеб. для общеобразоват. учреждений / И. М. Смирнова, В. А. Смирнов. 3-е изд., стер. — М.: Мнемозина, 2008. — 376 с.
- Шарыгин И. Ф. Геометрия. 7–9 кл.: учеб. для общеобразоват. учеб. заведений / И. Ф. Шарыгин. 5-е изд. стереотип. — М.: Дрофа, 2001. — 368 с.
Основные термины (генерируются автоматически): векторно-координатный метод, основное свойство параллелограмма, доказательство, задача, координата векторов, противоположный угол параллелограмма, решение, свойство, скалярное произведение векторов.
Ключевые слова
геометрическая задача,
векторно-координатный метод,
свойства параллелограмма
векторно-координатный метод, геометрическая задача, свойства параллелограмма
Похожие статьи
Развитие когнитивных способностей у учеников 10–11-х классов…
класса «Векторно—координатный метод решения задач стереометрии» все это учитывалось. Элективный курс расширяет базовый курс по математике, дает более глубокие знания, связанные с понятием вектор в пространстве, способствует более полному усвоению…
История в загадках. Петр I. Царь-реформатор | Статья в журнале…
Для реализации творческо-исследовательского проекта мне необходимо было решить следующие задачи : Ознакомиться с материалами, посвященными Петру I и его реформам; Составить перечень указов, с которыми стоит познакомить современных младших школьников
Обобщение одной из основных задач аналитической геометрии
Библиографическое описание: Гульманов, Н. К. Обобщение одной из основных задач аналитической
Как известно, если даны координаты концов отрезка, то можно найти координаты точки, лежащей на
Построим на координатной плоскости прямоугольник (рис. 2).
Геометрия Лобачевского | Статья в журнале «Юный ученый»
Это отличительное свойство лишь евклидовой геометрии, в других геометриях число 1 заменено другими (в геометрии Лобачевского таких
В геометрии Лобачевского сохраняются все теоремы, которые можно доказать без использования аксиомы параллельности.
Применение различных способов решения геометрических задач…
Способ 1. Метод координат. Поставим точку — как начало координат, расположим на ось и на ось .
Способ 2. Метод векторов. Сделаем следующие обозначения: (Рис. 2). Мы знаем, что . Из свойства биссектрисы угла треугольника найдем
Координатный метод решения задачи.
Использование среды GeoGebra при решении задач с параметрами
В данной статье рассмотрим решение задания с параметром графическим способом, используя программную среду
Решение: В первом неравенстве дано произведение двух выражений.
Поэтапно-вычислительный метод решения задачи. Данный способ заключается в следующем…
Теорема Стюарта и применение её для решения задач
Произведение квадрата одной стороны треугольника на не прилежащий к ней отрезок второй стороны плюс произведение квадрата третьей стороны на не прилежащий к ней отрезок
Предлагаем самостоятельно доказать теорему Стюарта используя: а) метод координат
Преобразования переменных в системах координат a, b, c и α, β
Рис. 1. Проекции вектора в системах координат a, b, c и α, β.
В трехфазной системе a, b, c пространственный вектор определяется по следующей зависимости
Основные уравнения математической модели АД, записаны в векторной форме в относительных единицах, имеют…
Похожие статьи
Развитие когнитивных способностей у учеников 10–11-х классов…
класса «Векторно—координатный метод решения задач стереометрии» все это учитывалось. Элективный курс расширяет базовый курс по математике, дает более глубокие знания, связанные с понятием вектор в пространстве, способствует более полному усвоению…
История в загадках. Петр I. Царь-реформатор | Статья в журнале…
Для реализации творческо-исследовательского проекта мне необходимо было решить следующие задачи : Ознакомиться с материалами, посвященными Петру I и его реформам; Составить перечень указов, с которыми стоит познакомить современных младших школьников
Обобщение одной из основных задач аналитической геометрии
Библиографическое описание: Гульманов, Н. К. Обобщение одной из основных задач аналитической
Как известно, если даны координаты концов отрезка, то можно найти координаты точки, лежащей на
Построим на координатной плоскости прямоугольник (рис. 2).
Геометрия Лобачевского | Статья в журнале «Юный ученый»
Это отличительное свойство лишь евклидовой геометрии, в других геометриях число 1 заменено другими (в геометрии Лобачевского таких
В геометрии Лобачевского сохраняются все теоремы, которые можно доказать без использования аксиомы параллельности.
Применение различных способов решения геометрических задач…
Способ 1. Метод координат. Поставим точку — как начало координат, расположим на ось и на ось .
Способ 2. Метод векторов. Сделаем следующие обозначения: (Рис. 2). Мы знаем, что . Из свойства биссектрисы угла треугольника найдем
Координатный метод решения задачи.
Использование среды GeoGebra при решении задач с параметрами
В данной статье рассмотрим решение задания с параметром графическим способом, используя программную среду
Решение: В первом неравенстве дано произведение двух выражений.
Поэтапно-вычислительный метод решения задачи. Данный способ заключается в следующем…
Теорема Стюарта и применение её для решения задач
Произведение квадрата одной стороны треугольника на не прилежащий к ней отрезок второй стороны плюс произведение квадрата третьей стороны на не прилежащий к ней отрезок
Предлагаем самостоятельно доказать теорему Стюарта используя: а) метод координат
Преобразования переменных в системах координат a, b, c и α, β
Рис. 1. Проекции вектора в системах координат a, b, c и α, β.
В трехфазной системе a, b, c пространственный вектор определяется по следующей зависимости
Основные уравнения математической модели АД, записаны в векторной форме в относительных единицах, имеют…
Вектор – это направленный прямолинейный отрезок, то есть отрезок, имеющий
определенную длину и определенное направление. Пусть точка А – начало вектора, а точка B – его конец, тогда вектор обозначается символом 


вектору 
обозначен 
Сформулируем ряд базовых определений.
Длиной
или модулем
вектора 
длина отрезка и обозначается 

не имеет. Вектор 
направление которого совпадает с направлением вектора 

Векторы
называются коллинеарными, если они лежат на одной прямой или на
параллельных прямых, записывают
противоположные направления. Нулевой вектор считают коллинеарным любому
вектору.
Векторы
называются равными 
одинаковые длины.
Три вектора в пространстве называются компланарными,
если они лежат в одной плоскости или на параллельных плоскостях. Если среди
трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы
компланарны.
Рассмотрим в
пространстве прямоугольную систему координат 0xyz. Выделим на осях координат 0x, 0y, 0z единичные векторы (орты) и
обозначим их через 
Выберем произвольный вектор
пространства и совместим его начало с началом
координат. Спроектируем вектор
на координатные
оси и обозначим проекции через ax, ay, az
соответственно. Тогда нетрудно показать, что

Эта
формула является основной в векторном исчислении и называется разложением
вектора по ортам координатных осей. Числа ax, ay, az называются координатами вектора 
проекциями на оси координат. Векторное равенство (2.25) часто записывают в
виде

скобках, чтобы визуально легче различать координаты вектора и координаты точки.
С использованием формулы длины отрезка, известной из школьной геометрии, можно
найти выражение для вычисления модуля вектора
:

то
есть модуль вектора равен корню квадратному из суммы квадратов его координат.
Обозначим углы между вектором
и осями
координат через α, β, γ соответственно. Косинусы этих углов называются
для вектора 

свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем
пункте 4.
Пусть в трехмерном пространстве заданы векторы 
координатами. Имеют место следующие
операции над ними: линейные (сложение, вычитание, умножение на число и
проектирование вектора на ось или другой вектор); не линейные – различные
произведения векторов (скалярное, векторное, смешанное).
1. Сложение двух векторов производится покоординатно, то
есть если

Данная
формула имеет место для произвольного конечного числа слагаемых.
Геометрически
два вектора складываются по двум правилам:
а) правило треугольника –
результирующий вектор суммы двух векторов соединяет начало первого из них с
концом второго при условии, что начало второго совпадает с концом первого
вектора; для суммы векторов –
результирующий вектор суммы соединяет начало первого из них с концом последнего
вектора-слагаемого при условии, что начало последующего слагаемого совпадает с
концом предыдущего;
б)
правило
параллелограмма (для двух
векторов) – параллелограмм строится на векторах-слагаемых как на сторонах,
приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой
векторов.
2. Вычитание двух векторов производится
покоординатно, аналогично сложению, то есть если 

Геометрически два
вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов
является диагональ, соединяющая концы векторов, причем результирующий вектор
направлен из конца вычитаемого в конец уменьшаемого вектора.
Важным следствием
вычитания векторов является тот факт, что если известны координаты начала и
конца вектора, то для вычисления координат вектора необходимо из координат его конца
вычесть координаты его начала. Действительно, любой вектор пространства 
представлен в виде разности двух векторов, исходящих из начала координат: 


координатами точек А и В, так как начало координат О(0;0;0). Таким образом, по правилу
вычитания векторов следует произвести вычитание координат точки А из координат точки В.
3. Умножение вектора на число λ покоординатно:
При λ>0
– вектор





4. Пусть в пространстве задана
направленная прямая (ось l), вектор 
координатами конца и начала. Обозначим проекции точек A и B на ось l
соответственно через A’ и B’.
Проекцией 


знаком «+», если вектор 
знаком «–», если 
Если
в качестве оси l взять некоторый другой вектор 


Рассмотрим некоторые
основные свойства проекций:
1) проекция вектора 
вектора 
между вектором и осью, то есть 
2.) проекция вектора на ось
положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и
равна нулю, если этот угол – прямой;
3) проекция суммы нескольких
векторов на одну и ту же ось равна сумме проекций на эту ось.
Сформулируем определения и
теоремы о произведениях векторов, представляющих нелинейные операции над
векторами.
5. Скалярным произведением 


число (скаляр), равное произведению длин этих векторов на косинус угла φ между
ними, то есть

Очевидно, что скалярный квадрат любого ненулевого вектора равен квадрату его длины, так как в этом случае угол 
Теорема 2.2. Необходимым и достаточным условием
перпендикулярности двух векторов является равенство нулю их скалярного
произведения
Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть
Теорема 2.3. Скалярное произведение двух векторов 
заданных своими координатами, равно сумме произведений их одноименных координат, то есть

С помощью скалярного произведения векторов можно
вычислить угол между ними.
Если заданы два ненулевых вектора
своими координатами 

Отсюда
следует условие перпендикулярности ненулевых векторов



Нахождение проекции вектора 
заданное вектором 

С помощью скалярного произведения векторов находят
работу постоянной силы 
прямолинейном участке пути.
Предположим, что под действием постоянной силы 
положения А в положение B. Вектор силы 



равна 
Следовательно, работа постоянной силы
при прямолинейном перемещении точки ее приложения равна скалярному произведению
вектора силы на вектор перемещения.
Пример
2.9. С
помощью скалярного произведения векторов найти угол при вершине A параллелограмма ABCD, построенного на векторах
Решение. Вычислим модули векторов и их скалярное произведение
по теореме (2.3):
Отсюда согласно формуле (2.29) получим косинус
искомого угла
Пример 2.10. Затраты сырьевых и материальных ресурсов, используемых
на производство одной тонны творога, заданы в таблице 2.2 (руб.).
Какова общая цена этих ресурсов, затрачиваемых на изготовление одной
тонны творога?
Таблица 2.2
Решение. Введем в рассмотрение два вектора: вектор затрат
ресурсов на тонну продукции 
соответствующего ресурса 
Тогда 
ресурсов 
векторов 
Таким образом, общая цена затрат на производство одной
тонны творога составляет 279 541,5 рублей
Примечание. Действия с векторами, осуществленные в примере 2.10,
можно выполнить на персональном компьютере. Для нахождения скалярного
произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве
аргументов указываются адреса диапазонов элементов матриц, сумму произведений
которых необходимо найти. В MathCAD
скалярное произведение двух векторов выполняется при помощи соответствующего
оператора панели инструментов Matrix
Пример 2.11. Вычислить работу, произведенную силой 
из положения A(2;4;6) в положение A(4;2;7). Под каким углом к AB направлена сила 
Решение. Находим вектор перемещения, вычитая из координат его конца координаты
начала


Угол φ между 

формуле (2.29), то есть
6. Три некомпланарных вектора 
тройку, если при наблюдении из конца третьего вектора 
поворот от первого вектора 
вектору 
если по часовой стрелке.
Векторным
произведением 


вектор 
– 


– имеет длину, равную 


– векторы 
тройку (рис. 2.15).

условием коллинеарности двух векторов является равенство нулю их векторного
произведения 
Теорема 2.5. Векторное произведение векторов 
третьего порядка вида

Примечание. Определитель (2.25)
раскладывается по свойству 7 определителей
Следствие 1. Необходимым и достаточным условием коллинеарности двух
векторов является пропорциональность их соответствующих координат
Следствие 2. Векторные произведения единичных орт равны
Следствие 3. Векторный квадрат любого вектора равен нулю
Геометрическая
интерпретация векторного произведения состоит в том, что длина результирующего
вектора численно равна площади S
параллелограмма, построенного на векторах–сомножителях как на сторонах,
приведенных к одному началу. Действительно, согласно определению, модуль
векторного произведения векторов равен 
построенного на векторах 


. Следовательно,

Также с помощью векторного произведения можно
определить момент силы относительно точки и линейную скорость вращения.
Пусть в точке A приложена
сила 
некоторая точка пространства (рис. 2.16). Из курса физики известно, что моментом
силы 
точки O называется вектор 
— перпендикулярен плоскости, проходящей через точки O, A, B;
— его модуль численно равен произведению силы на плечо 
— 


Следовательно,
момент силы 
точки O представляет собой векторное произведение


Линейная скорость 
угловой скоростью 
неподвижной оси, определяется формулой Эйлера 
точка оси (рис. 2.17).
Пример 2.12. С помощью
векторного произведения найти площадь треугольника ABC, построенного на векторах

Решение. Найдем векторное произведение заданных векторов по
формуле (2.32).

произведения двух неколлинеарных векторов численно равен площади
параллелограмма, построенного на данных векторах как на сторонах, приведенных к
общему началу, то есть 

. Следовательно, искомая площадь равна 
площади)
7. Рассмотрим произведение трех векторов 

результирующий вектор – скалярно на третий. Такое произведение 
произведением трех векторов
(векторно–скалярным произведением).
Теорема 2.6. Необходимым и достаточным условием компланарности
трех векторов является равенство нулю их смешанного произведения
Теорема 2.7. Если три вектора 
произведение представляет собой определитель третьего порядка, составленный из
координат векторов- сомножителей соответственно, то есть

Нетрудно показать, что объем параллелепипеда,
построенного на векторах 
сторонах, приведенных к общему началу, численно равен модулю смешенного
произведения этих векторов 
Объем треугольной пирамиды, построенной на этих же
векторах, равен

Пример 2.13. Вершинами пирамиды служат точки 
Решение. Найдем
координаты векторов

По формуле (2.36) объем пирамиды, построенной на
векторах 


Рассмотрим очень важный вопрос о
разложении вектора по базису. Приведем
следующие определения.
Система векторов 
линейно зависимой, если существуют такие числа 
место равенство

Отсюда всегда можно один из линейно
зависимых векторов выразить через линейную комбинацию остальных. Действительно,
допустим для определенности, что 
получим выражение вектора 
остальные векторы
Линейно независимыми называют векторы, если равенство
(2.37) выполняется только тогда, когда
все


независимых векторов равняется рангу матрицы, которая составлена из координат
этих векторов (смотри раздел I.5).
Базисом n – мерного
пространства En называют любую совокупность линейно независимых векторов n – мерного пространства.
Произвольный вектор 
– мерного пространства можно представить
в виде линейной комбинации векторов базиса
таким образом:
Числа

вектора 
векторов 
Линейное пространство называется
конечномерным и имеет размерность n, если в этом
пространстве существует система из n линейно независимых векторов (базис) такая,
что каждое ее расширение приводит к линейной зависимости системы.
Например, в трехмерном пространстве
существует базис единичных орт 
линейно независимых векторов, то есть каждый вектор 
пространства, приводит к линейной зависимости векторов (является линейной
комбинацией орт 

по ортам 

пространстве.
Вопросы для самопроверки