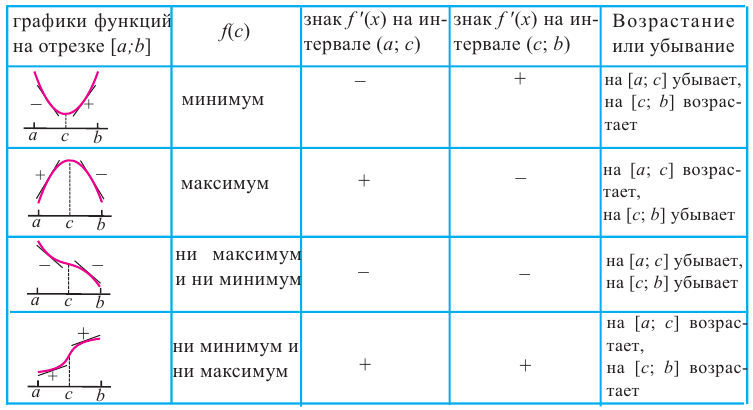
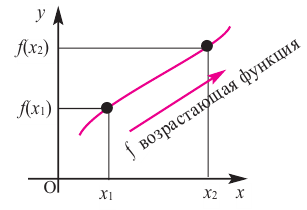
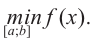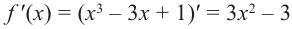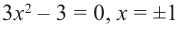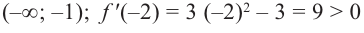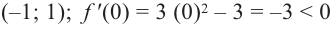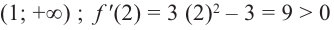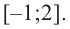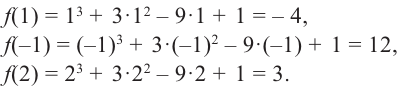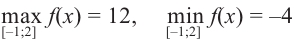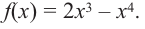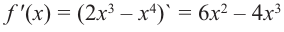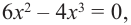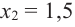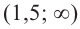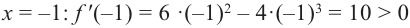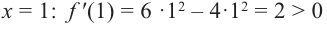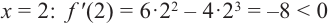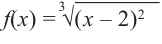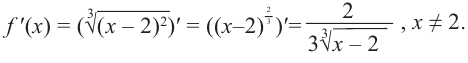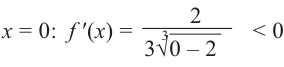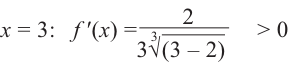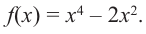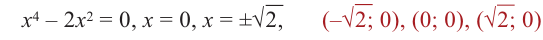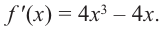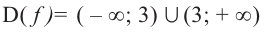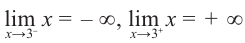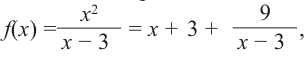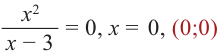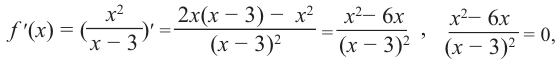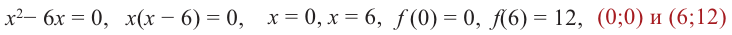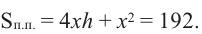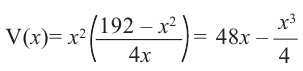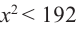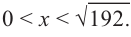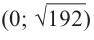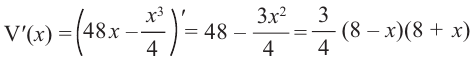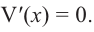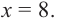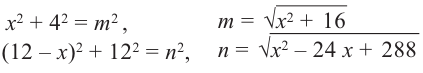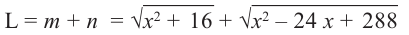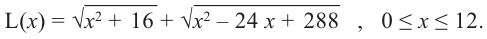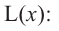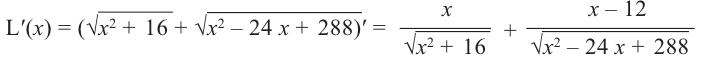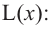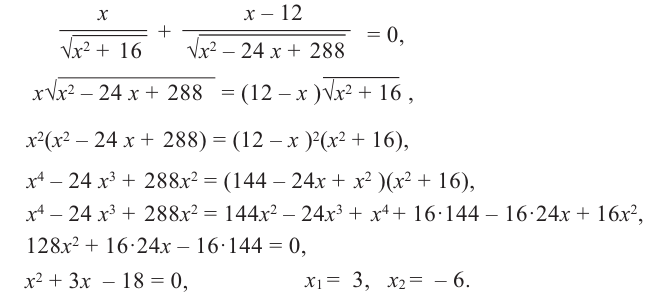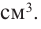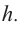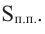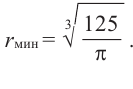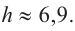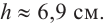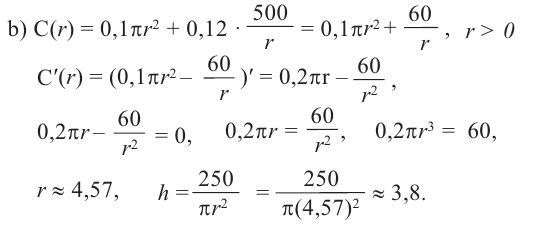Что такое возрастание функции
В начале прочитаем определение возрастания функции.
Запомните!
Функция « y(x) » называется возрастающей на некотором промежутке, если
для любых
« x1 » и « x2 »
принадлежащих данному промежутку, таких, что « x2 > x1 »
выполняется неравенство
« y( x2 ) > y( x1 )».
Определение сложно понять без наглядного примера.
Поэтому сразу перейдём к разбору задачи на возрастание функции.
По-другому можно сказать, что, если каждому бóльшему значению « x »
соответствует бóльшее значение « y », значит,
функция « y(x) » возрастает.
|
x2 > x1 |
Обязательное условие возрастания функции |
Давайте разберем определение возрастания функции на конкретном примере.
Разбор примера
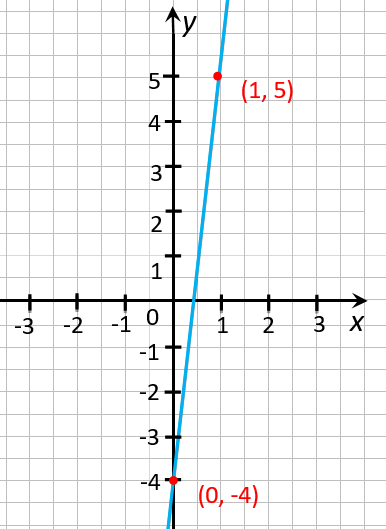
Возрастающей или убывающей является функция « y = 9x − 4 » ?
Для начала определим
область определения функции
« y = 9x − 4 ».
y = 9x − 4
D(y): x ∈ R ,
то есть « x » —
любое действительное число.
Построим график функции
« y = 9x − 4 ».
Так как функция
« y = 9x − 4 »
линейная, ее график — прямая.
Используем правила построения графика линейной функции. Нам достаточно найти две точки, чтобы построить ее график.
Область определения функции
« y = 9x − 4 » — все действительные числа,
поэтому можно подставить любое число вместо « x » и вычислить « y » по
формуле функции
« y = 9x − 4 ». Например, возьмем
« x = 0 ».
x = 0
y(x) = 9x − 4
y(0) = 9 · 0 − 4 = −4
Для второй точки возьмем « x = 1 ».
x = 1
y(x) = 9x − 4
y(1) = 9 · 1 − 4 = 5
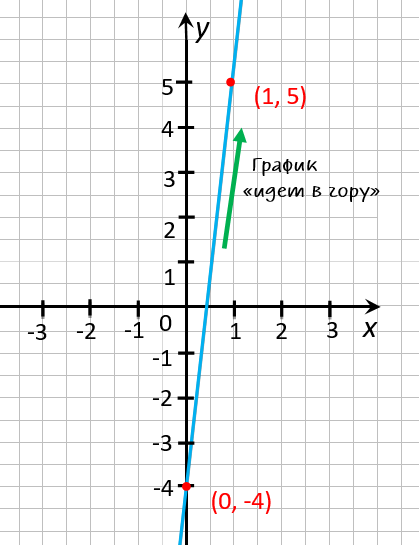
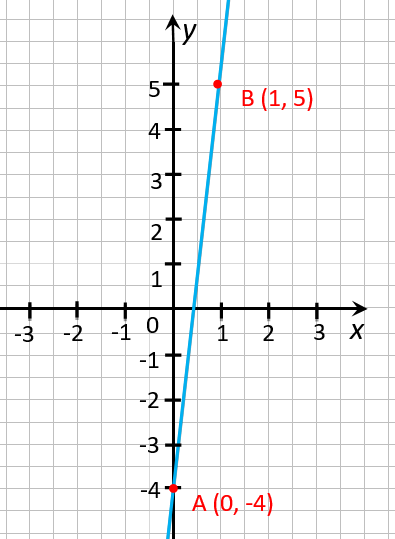
Отметим две полученные
точки «(0; −4)» и «(1; 5)» на
координатной плоскости
и проведем через них прямую.
Докажем, что функция
« y = 9x − 4 » возрастает на всей своей области определения двумя способами: по ее графику и
аналитически
(по ее формуле).
Как определить по графику, что функция возрастает
По определению возрастания функции мы знаем, что
если « x » увеличивается,
то « y » тоже должен увеличиваться.
На рисунке ниже видно, что график функции « y = 9x − 4 »
«идет в гору». Другими словами, при увеличении « x »
↑ растет
значение « y » ↑.
В этом можно убедиться, если взять две любые точки на графике. Например, точки, по
которым мы построили график функции. Назовем эти точки:
« (·)A » и « (·)B ».
У первой точки « (·)A »
координаты:
x1 = 0 ; y1 = − 4
У второй точки « (·)B » координаты:
x2 = 1 ; y2 = 5
На примере точек « (·)A » и « (·)B » видно, что
при увеличении
« x ↑ ( x2 > x1 )»
растет
« y ↑ ( y2 > y1 ) ».
Поэтому график зрительно «идет в гору».
Как по формуле доказать, что функция возрастает
Вернёмся к нашей функции
« y = 9x − 4 ».
По графику мы поняли, что
функция « y = 9x − 4 » возрастает,
так как ее график «идет в гору».
Но как доказать по формуле, что функция
возрастает на всей своей области определения?
Запомните!
Функция возрастает на всей области определения, когда при
« x2 > x1 »
выполняется условие
« y( x2 ) > y( x1 ) ».
Формулировка выше не самая простая для понимания. Давайте разберем ее на практике.
По определению возрастания функции нам нужно доказать, что при
« x2 > x1 » увеличивается значение функции
« y( x2 ) > y( x1 ) ».
Но как нам найти значения функции
« y( x1 )» и
«y( x2 ) »?
Для нахождения « y( x1 )» и
«y( x2 ) »
достаточно подставить « x1 » и
« x2 » в исходную формулу « y = 9x − 4 ».
y( x1 ) = 9x1 − 4
y( x2 ) = 9x2 − 4
Теперь запишем обязательное условие возрастания функции.
|
x2 > x1 |
Обязательное условие возрастания функции |
Подставим в неравенство
« y( x2 ) >
y( x1 ) » полученные формулы
« y( x1 ) = 9x1 − 4» и
« y( x2 ) = 9x2 − 4 » .
y( x2 ) > y( x1 )
9x2 − 4 > 9x1 − 4
Упростим полученное
неравенство.
9x2 − 9x1 > − 4 + 4
9x2 − 9x1 > 0
Вынесем общий множитель
в левой части неравенства.
9(x2 − x1) > 0
Разделим левую и правую часть на «9».
При делении нуля на любое число получается ноль.
x2 − x1 > 0
x2 > x1
Мы доказали, что выполняется исходное условие возрастания функции «x2 > x1».
Отсюда следует, что функция
« y = 9x − 4 » возрастает на всей области определения.
В завершении вместо ответа следует написать фразу:
«Что и требовалось доказать».
Посмотрим другой пример, где требуется доказать, что функция возрастает.
Разбор примера
Доказать, что функция возрастает на всей области определения: y = 13x − 1
По аналогии с предыдущим примером составим неравенства, которые доказывают, что функция возрастает.
|
x2 > x1 |
Обязательное условие возрастания функции |
Вместо « y( x1 )» и
«y( x2 ) » запишем
формулу функции « y = 13x − 1 » и упростим полученное неравенство.
y( x2 ) > y( x1 )
13x2 − 1 > 13x1 − 1
13x2 − 13x1 > 1 − 1
13(x2 − x1) > 0 |: 13
>
x2 − x1 > 0
x2 > x1
Что и требовалось доказать.
Что такое убывание функции
Запомните!
Функция « y(x) » называется убывающей на некотором промежутке, если для любых
« x1 » и « x2 »
принадлежащих данному промежутку, таких,
что « x2 > x1 »
выполняется неравенство « y( x2 ) < y( x1 )».
|
x2 > x1 |
Обязательное условие убывания функции |
Как по графику понять, что функция убывает
Разбор примера
Доказать, что функция убывает на всей области определения: y = 1 − 3x
По определению убывания функции мы знаем, что,
если « x »
↑ растет, то
« y » ↓ должен уменьшаться.
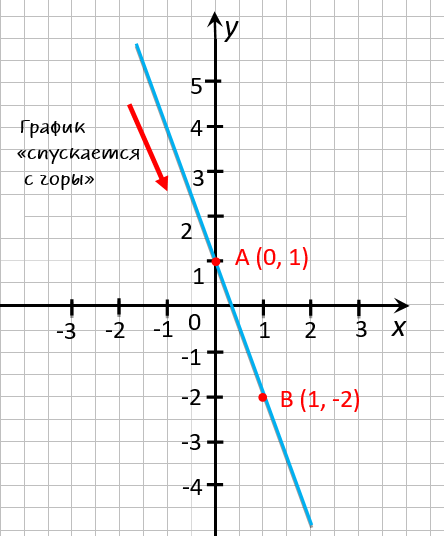
Построим график функции
« y = 1 − 3x ». Ее график — прямая, поэтому нам будет достаточно двух точек.
Область определения функции
« y = 1 − 3x » — все действительные числа,
поэтому можно поставить любое число вместо « x » и вычислить « у » по
формуле функции
« y = 1 − 3x ». Например, возьмем
« x = 0 »
и « x = 1 ».
x = 0
y(x) = 1 − 3x
y(0) = 1 − 3 · 0 = 1
(·) А (0; 1)
x = 1
y(1) = 1 − 3x
y(1) = 1 − 3 · 1 = 1 − 3 = −2
(·) B (1; −2)
Построим график функции
« y = 1 − 3x » по полученным точкам
« (·)A » и « (·)B ».
На графике функции видно, что зрительно график «спускается с горы», то есть функция убывает. Другими словами, при увеличении
« x »
↑ уменьшается
значение
« y » ↓.
Как по формуле доказать, что функция убывает
Вернёмся к нашей функции
« y = 1 − 3x ».
По ее графику мы поняли, что функция убывает, так как график «спускается с горы». Но как доказать по формуле,
что функция « y = 1 − 3x » убывает на всей области определения?
Запомните!
Чтобы доказать, что функция убывает требуется доказать, что при любых
« x2 > x1 » выполняется
« y( x2 ) < y( x1 ) ».
Давайте разберем на примере функции
« y = 1 − 3x ». Докажем, что она убывает
на всей своей области определения.
|
x2 > x1 |
Обязательное условие убывания функции |
Подставим « y( x1 )» и
«y( x2 ) » в
формулу функции « y = 1 − 3x » и упростим полученное неравенство.
y( x2 ) < y( x1 )
1 − 3x2 < 1 − 3x1
3x1 − 3x2 < 1 − 1
3(x1 − x2) < 0 | :3
<
x1 − x2 < 0
−x2 < −x1
Умножим на « −1 » левую и правую часть неравенства. При
умножении неравенства на отрицательное число знак неравенства поменяется на
противоположный.
−x2 < −x1 | · (−1)
x2 > x1
Что и требовалось доказать.
Как по графику функции определить
возрастание и убывание
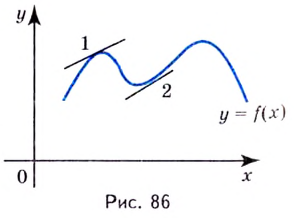
Потренируемся только по графику функции определять промежутки возрастания и убывания функции.
Разбор примера
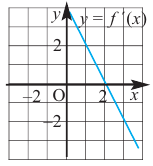
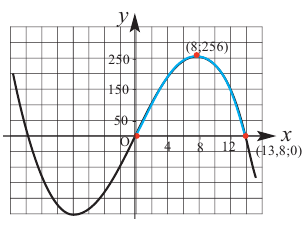
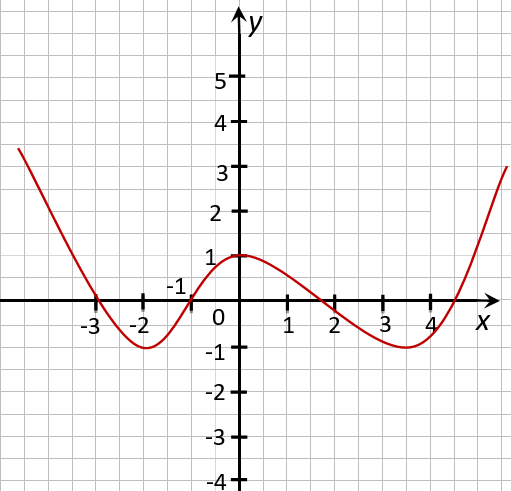
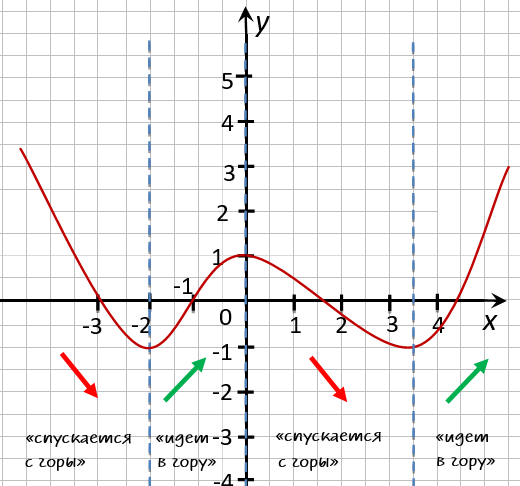
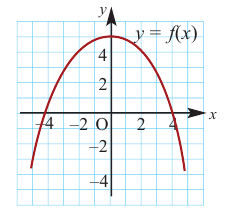
На рисунке ниже изображён график функции, определенной на множестве действительных чисел.
Используя график, найдите промежутки возрастания и промежутки убывания функции.
Отметим с помощью штриховых линий промежутки, где график функции убывает
(«спускается с горы») и где он возрастает («идет в гору»).
Запишем через знаки неравенств,
какие значения принимает « x » на полученных промежутках.
Обратите внимание, что во всех случаях при указании промежутков, мы указываем, что их
концы входят в промежуток, то есть используем знаки нестрогого неравенства.
Остаётся записать полученные промежутки возрастания и убывания функции в ответ.
Ответ:
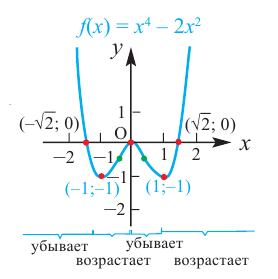
- функция убывает при
x ≤ −2; 0 ≤ x ≤ 3,5 - функция возрастает при
−2 ≤ x ≤ 0 ; x ≥ 3,5
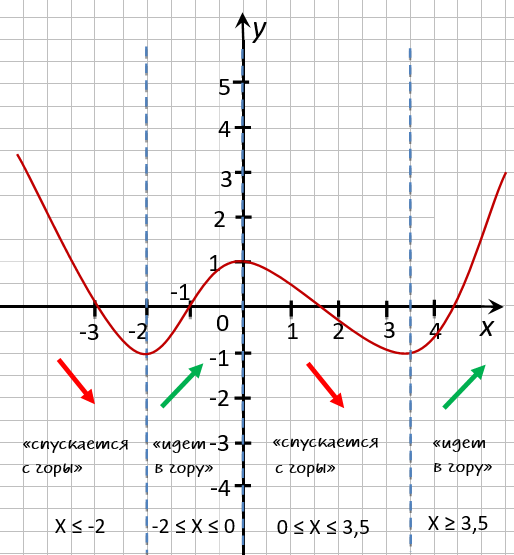
Более грамотно будет записать ответ с помощью специальных
математических символов.
Ответ:
- функция убывает на промежутках
x ∈ (−∞ ; −2] ∪ [0; 3,5] - функция возрастает на промежутках x ∈ [−2 ; 0] ∪ [3,5 ; +∞]
При каких значениях
« m »
функция является убывающей или возрастающей
Ещё один тип заданий, в которых требуется определить,
при каких
« m » ( « а, b » или других буквах) функция убывает или возрастает.
Разбор примера
При каких значениях « m » функция
« y = mx − m − 3 + 2x » является убывающей?
Обратимся снова к определению убывания функции. Вспомним, как записать условия убывания функции с точки зрения формул.
|
x2 > x1 |
Обязательное условие убывания функции |
Запишем эти условия, используя формулу функции « y = mx − m − 3 + 2x », заданную в
задаче. Вместо
« x »
подставим « x1 » и « x2 ».
y( x2 ) < y( x1 )
mx2 − m − 3 + 2x2 < mx1 − m − 3 + 2x1
Упростим полученное неравенство. Перенесем из правой части все члены неравенства в левую часть с противоположными знаками.
mx2 − m − 3 + 2x2 − mx1
+ m
+ 3
− 2x1
< 0
Упростим полученное выражение. Некоторые члены неравенства взаимоуничтожатся.
mx2 − mx1
− m + m − 3 + 3 + 2x2 − 2x1
< 0
mx2 − mx1 + 2x2 − 2x1
< 0
Вынесем общие множители за скобки.
m( x2 − x1) + 2(x2 − x1)
< 0
Теперь
вынесем общий множитель
« ( x2 − x1 ) ».
( x2 − x1) (m + 2)
< 0
Вспомним обязательное условие убывания функции.
|
x2 > x1 |
Обязательное условие убывания функции |
Преобразуем исходное условие убывания функции « x2 > x1 ».
Перенесем все в левую часть.
x2 > x1
x2 − x1 > 0
По условию убывания функции
« x2 − x1 > 0 »,
значит, чтобы
произведение
«( x2 − x1) (m + 2)
» было меньше нуля, требуется, чтобы множитель «(m + 2)» был меньше нуля. Так как по
правилу знаков:
плюс на минус даёт минус.
| + | · | − | < 0 |
| (x2 − x1) | · | (m + 2) | < 0 |
Решим полученное неравенство.
m + 2 < 0
m < −2
Ответ: при «m < −2» функция
« y = mx − m − 3 + 2x »
является убывающей.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
оксана николаевна кузнецова
Эксперт по предмету «Математика»
Задать вопрос автору статьи
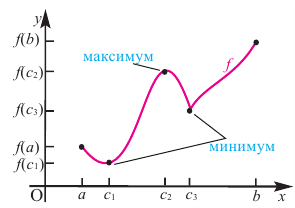
Экстремумы функции
Определение 1
Точки $x_0$ называются точками экстремума функции, если они являются точками максимума и минимума для функции $f(x)$.
Определение 2
Точка $x_0$ называется точкой максимума функции $f(x)$, если существует такая окрестность данной точки, что для всех $x$ из этой окрестность выполняется неравенство $f(x)le f(x_0)$.
Определение 3
Точка $x_0$ называется точкой максимума функции $f(x)$, если существует такая окрестность данной точки, что для всех $x$ из этой окрестность выполняется неравенство $f(x)ge f(x_0)$.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Понятие экстремума функции тесно связано с понятием критической точки функции. Введем её определение.
Определение 4
$x_0$ называется критической точкой функции $f(x)$, если:
1) $x_0$ — внутренняя точка области определения;
2) $f’left(x_0right)=0$ или не существует.
Для понятия экстремума можно сформулировать теоремы о достаточных и необходимых условиях его существования.
Теорема 1
Необходимое условие экстремума
Если функция $y=f(x)$ имеет экстремум в точке $x_0$, то либо $f’left(x_0right)=0$, либо производная в точке $x_0$ не существует.
Теорема 2
Достаточное условие экстремума
Пусть точка $x_0$ является критической для функции $y=f(x)$ и лежит в интервале $(a,b)$. Пусть на каждом интервале $left(a,x_0right) и (x_0,b)$ производная $f'(x)$ существует и сохраняет постоянный знак. Тогда:
1) Если на интервале $(a,x_0)$ производная $f’left(xright)>0$, а на интервале $(x_0,b)$ производная $f’left(xright)
2) Если на интервале $(a,x_0)$ производная $f’left(xright)0$, то точка $x_0$ — точка минимума для данной функции.
3) Если и на интервале $(a,x_0)$, и на интервале $(x_0,b)$ производная $f’left(xright) >0$ или производная $f’left(xright)
Данная теорема проиллюстрирована на рисунке 1.
Рисунок 1. Достаточное условие существования экстремумов
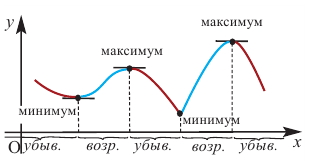
Примеры экстремумов (Рис. 2).
Рисунок 2. Примеры точек экстремумов
«Возрастание и убывание функций, экстремумы» 👇
Правило исследования функции на экстремум
1) Найти область определения функции $f(x)$;
2) Найти производную $f'(x)$;
3) Найти точки, в которых выполняется равенство $f’left(xright)=0$;
4) Найти точки, в которых $f'(x)$ не существует;
5) Отметить на координатной прямой все найденные точки и область определения данной функции;
6) Определить знак производной $f'(x)$ на каждом получившемся промежутке;
7) Сделать выводы о наличии максимумов и минимумов на каждом промежутке, используя теорему 2.
Возрастание и убывание функции
Введем, для начала, определения возрастающей и убывающей функций.
Определение 5
Функция $y=f(x)$, определенная на промежутке $X$, называется возрастающей, если для любых точек $x_1,x_2in X$ при $x_1
Определение 6
Функция $y=f(x)$, определенная на промежутке $X$, называется убывающей, если для любых точек $x_1,x_2in X$ при $x_1f(x_2)$.
Исследование функции на возрастание и убывание
Исследовать функции на возрастание и убывание можно с помощью производной.
Для того чтобы исследовать функцию на промежутки возрастания и убывания, необходимо сделать следующее:
1) Найти область определения функции $f(x)$;
2) Найти производную $f'(x)$;
3) Найти точки, в которых выполняется равенство $f’left(xright)=0$;
4) Найти точки, в которых $f'(x)$ не существует;
5) Отметить на координатной прямой все найденные точки и область определения данной функции;
6) Определить знак производной $f'(x)$ на каждом получившемся промежутке;
7) Сделать вывод: на промежутках, где $f’left(xright)0$ функция возрастает.
Примеры задач на исследования функций на возрастание, убывание и наличие точек экстремумов
Пример 1
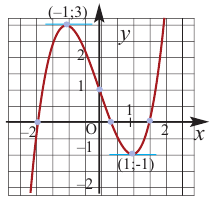
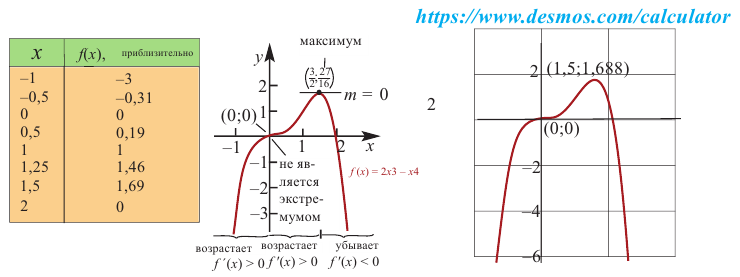
Исследовать функцию на возрастание и убывание, и наличие точек максимумов и минимумов: $f(x)={2x}^3-15x^2+36x+1$
Так как первые 6 пунктов совпадают, проведем для начала их.
1) Область определения — все действительные числа;
2) $f’left(xright)=6x^2-30x+36$;
3) $f’left(xright)=0$;
[6x^2-30x+36=0] [x^2-5x+6=0] [x=3, x=2]
4) $f'(x)$ существует во всех точках области определения;
5) Координатная прямая:
Рисунок 3.
6) Определить знак производной $f'(x)$ на каждом промежутке:
[f’left(xright) >0, при left(-infty ,2right) (3,+infty )] [f’left(xright)7) Изобразим все на одном рисунке:
Рисунок 4.
Получаем:
Функция возрастает, при $left(-infty ,2right) (3,+infty )$, функция убывает, при $left(2,3right)$.
Точка $x=2$ — точка максимума, точка $x=3$ — точка минимума.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Интервалы возрастания и убывания функции
С помощью данного сервиса можно найти интервалы возрастания и убывания функции в онлайн режиме с оформлением решения в Word.
- Решение онлайн
- Видеоинструкция
Исследование функции с помощью производной
Определение: Точка х0 называется точкой локального максимума, если для любого х из окрестности точки х0 выполняется неравенство: f(x0)>f(x).
Определение: Точка х0 называется точкой локального минимума, если для любого х из окрестности точки х0 выполняется неравенство: f(x0)<f(x).
Точки минимума и максимума функции называются точками экстремума данной функции, а значения функции в этих точках – экстремумами функции.
Точками экстремума могут служить только критические точки I рода, т.е. точки, принадлежащие области определения функции, в которых производная f′(x) обращается в нуль или терпит разрыв.
Правило нахождения экстремумов функции y=f(x) с помощью первой производной
- Найти производную функции f′(x).
- Найти критические точки по первой производной, т.е. точки, в которых производная обращается в нуль или терпит разрыв.
- Исследовать знак первой производной в промежутках, на которые найденные критические точки делят область определения функции f(x). Если на промежутке f′(x)<0, то на этом промежутке функция убывает; если на промежутке f′(x)>0, то на этом промежутке функция возрастает.
- Если в окрестности критической точки f′(x) меняет знак с «+» на «-», то эта точка является точкой максимума, если с «-» на «+», то точкой минимума.
- Вычислить значения функции в точках минимума и максимума.
С помощью приведенного алгоритма можно найти не только экстремумы функции, но и промежутки возрастания и убывания функции.
Пример №1: Найти промежутки монотонности и экстремумы функции: f(x)=x3–3x2.
Решение: Найдем первую производную функции f′(x)=3x2–6x.
Найдем критические точки по первой производной, решив уравнение 3x2–6x=0; 3x(x-2)=0 ;x = 0, x = 2
Исследуем поведение первой производной в критических точках и на промежутках между ними.
| x | (-∞, 0) | 0 | (0, 2) | 2 | (2, +∞) |
| f′(x) | + | 0 | — | 0 | + |
| f(x) | возрастает | max | убывает | min | возрастает |
f(0) = 03 – 3*02 = 0
f(2) = 23 – 3*22 = -4
Ответ: Функция возрастает при x∈(-∞ ; 0)∪(2; +∞); функция убывает при x∈(0;2);
точка минимума функции (2;-4); точка максимума функции (0;0).
Правило нахождения экстремумов функции y=f(x) с помощью второй производной
- Найти производную f′(x).
- Найти стационарные точки данной функции, т.е. точки, в которых f′(x)=0.
- Найти вторую производную f″(x).
- Исследовать знак второй производной в каждой из стационарных точек. Если при этом вторая производная окажется отрицательной, то функция в такой точке имеет максимум, а если положительной, то – минимум. Если же вторая производная равна нулю, то экстремум функции надо искать с помощью первой производной.
- Вычислить значения функции в точках экстремума.
Отсюда следует, что дважды дифференцируемая функция f(x) выпукла на отрезке [a, b], если вторая производная f»(x) ≥ 0 при всех х [a, b].
Все вычисления можно проделать в онлайн режиме.
Пример №2. Исследовать на экстремум с помощью второй производной функцию: f(x) = x2 – 2x — 3.
Решение: Находим производную: f′(x) = 2x — 2.
Решая уравнение f′(x) = 0, получим стационарную точку х=1. Найдем теперь вторую производную: f″(x) = 2.
Так как вторая производная в стационарной точке положительна, f″(1) = 2 > 0, то при x = 1 функция имеет минимум: fmin = f(1) = -4.
Ответ: Точка минимума имеет координаты (1; -4).
Исследовать функцию — это значит установить её свойства: указать её область определения и область значений; промежутки возрастания и убывания; промежутки, на которых функция приобретает положительные значения, на которых — отрицательные; выяснить, не является ли данная функция чётной или нечётной и т. д.
Содержание:
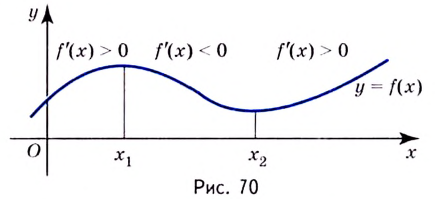
Что такое исследование функции
Одна из важных задач исследования функции — определение промежутков её возрастания и убывания. Как отмечалось, в тех точках, в которых функция возрастает, её производная (угловой коэффициент касательной) положительная, а в точках убывания функции её производная отрицательная {рис. 70).
Правильными будут следующие утверждения.
- Если производная функции в каждой точке некоторого промежутка положительная, то функция на этом промежутке возрастает.
- Если производная в каждой точке промежутка отрицательная, то функция на этом промежутке убывает.
- Если производная в каждой точке промежутка тождественно равна нулю, то на этом промежутке функция постоянная.
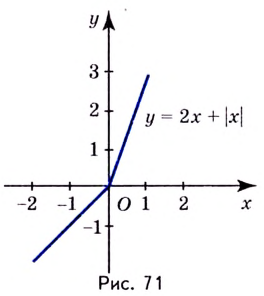
Строгое доказательство этого утверждения достаточно громоздкое, поэтому мы его не приводим. Заметим только, что в нём выражается достаточный признак возрастания или убывания функции, но не необходимый. Поэтому функция может возрастать и на промежутке, в некоторых точках которого она не имеет производной. Например, функция
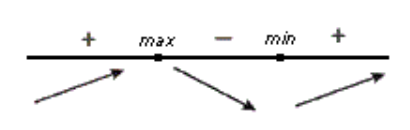
Из сказанного следует, что два соседних промежутка, на одном из которых функция возрастает, а на другом — убывает, могут разделяться только такой точкой, в которой производная функции равна нулю или не существует.
Внутренние точки области определения функции, в которых её производная равна нулю или не существует, называют критическими точками функции.
Следовательно, чтобы определить промежутки возрастания и убывания функции 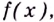
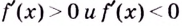
Пример:
Найдите промежутки возрастания и убывания функции
Решение:
Уравнение 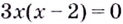
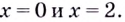
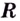
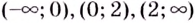
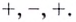
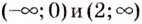
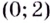
Замечание: Если функция непрерывна в каком-нибудь конце промежутка возрастания или убывания, то эту точку можно присоединить к рассматриваемому промежутку. Поскольку функция 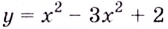
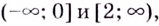
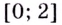
Пример:
Найдите промежутки убывания функции
Решение:
Критические точки: 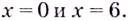
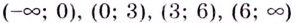
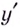
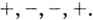
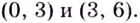
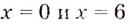
Пример:
Найдите критические точки функции 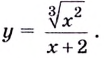
Решение:
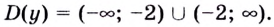
Найдём точки, в которых производная равна нулю или не существует: 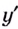
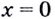
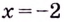

Ответ. 0 и 4.
Пример:
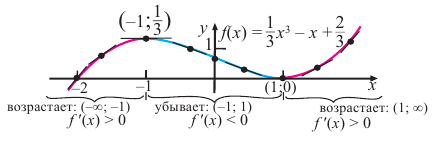
Докажите, что функция 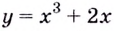
Решение:
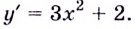
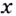
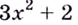
Пример:
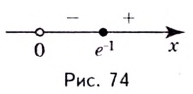
Установите, на каком промежутке функция 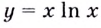
Решение:
Способ 1. 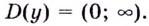
Найдём критические точки функции:
Эта точка разбивает область определения функции на два промежутка (рис. 74). Определим знак производной на каждом из них.
Следовательно, функция 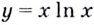
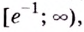
Способ 2. Решим неравенство 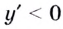
Ответ. Возрастает, если 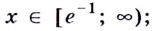
Применение второй производной к исследованию функций и построению их графиков
При помощи первой производной можно исследовать функцию на монотонность и экстремумы и схематично построить график. Оказывается, что поведение некоторых функций не всегда можно охарактеризовать, используя первую производную. Более детальное исследование проводится при помощи второй производной. Вспомним, что такое вторая производная.
Пусть функция 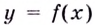
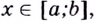
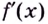
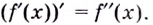
Например, найти производную 2-го порядка функции 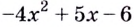
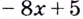
Кривая 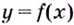
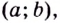
Кривая 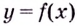
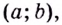
Точкой перегиба называется такая точка кривой, которая отделяет её выпуклую часть от вогнутой.
Интервалы выпуклости и вогнутости находят при помощи такой теоремы.
Теорема. Если вторая производная дважды дифференцируемой функции 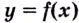
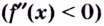
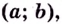
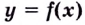
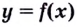
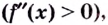
Из теоремы следует, что точками перегиба кривой 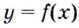
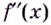
Установим до статочное условие существования точки перегиба.
Теорема. Пусть 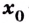
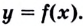
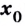
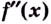
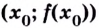
Для нахождения промежутков выпуклости и точек перегиба графика функции целесообразно пользоваться следующей схемой:
- найти область определения функции;
- найти критические точки второго рода;
- определить знак второй производной на образованных интервалах. Если
то кривая выпуклая; если
— кривая вогнутая;
- если производная
меняет знак при переходе через точку
то точка
является точкой перегиба кривой
Пример №1
Найдите интервалы выпуклости, вогнутости и точки перегиба кривой
Решение:
1) Область определения функции:
2) Найдём вторую производную: 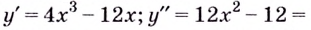
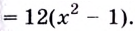
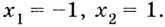
3) Разбиваем область определения на интервалы 
Если 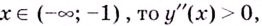
Если 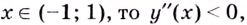
Если 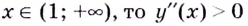
Следовательно, точки 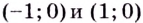
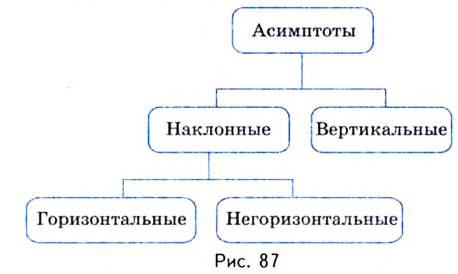
Напомним, что прямая 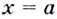
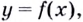
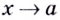
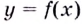
Уравнение наклонной асимптоты:
Если записанные пределы существуют, то существует наклонная асимптота; если хотя бы один из них не существует или равен 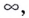
Если 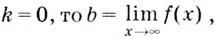
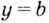
Замечание: Рассмотренные пределы могут быть односторонними, а под символом 
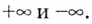
Пример №2
Найдите асимптоты кривых:
Решение:
а) 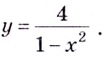
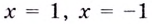
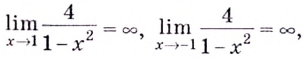
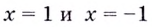
Найдём наклонную асимптоту: 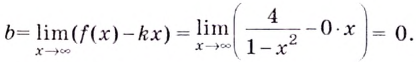
Следовательно, заданная кривая имеет три асимптоты:
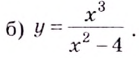
Поскольку функция не определена в точках 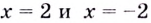
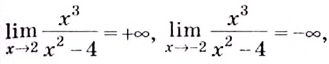
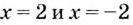
Для наклонной асимптоты
Значит прямая 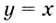
Итак, асимптоты кривой:
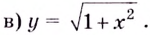
Следовательно, 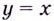
2) если 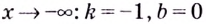

Следовательно, заданная кривая имеет две асимптоты:
Определение точек перегиба, интервалов выпуклости и асимптот существенно помогает в построении графиков различных функций.
Нахождение промежутков возрастания и убывания функции
Интервалы возрастания и убывания функции
возрастающая функция
Если для любых 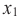
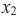
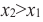
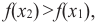
убывающая
Если для любых 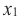
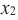
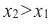
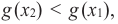
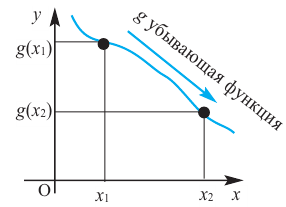
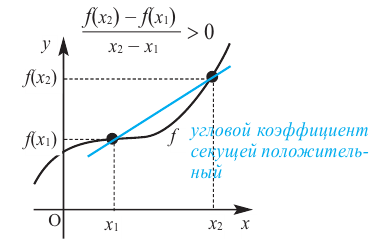
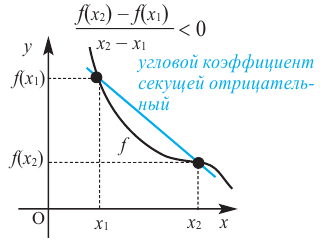
Связь промежутков возрастания и убывания функции с угловым коэффициентом секущей можно выразить следующим образом.
Если на заданном промежутке угловой коэффициент любой секущей положителен, то на этом промежутке функция 
Если на заданном промежутке угловой коэффициент любой секущей отрицателен, то на этом промежутке функция 
Промежутки возрастания и убывания функции
Пусть на определенном промежутке производная функции 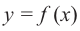
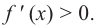
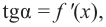
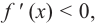
Теорема. Если функция 
Примечание: если функция 
По графику функции 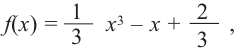
На интервалах 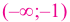
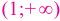
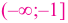
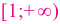
На интервале 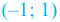
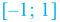
Пример №3
При помощи производной определите промежутки возрастания и убывания функции
Решение: 1. Алгебраический метод.
Найдем производную функции
Функция 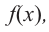
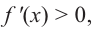
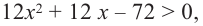
Для решения неравенства сначала надо решить соответствующее уравнение
Значит, при 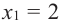
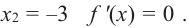
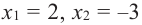
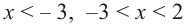
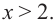
Из таблицы и непрерывности функции 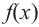
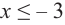
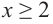
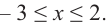
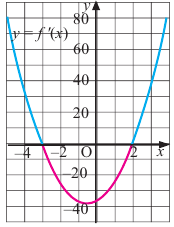
2. Промежутки возрастания и убывания функции можно определить но графику производной. На рисунке изображен график производной
График производной 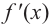
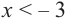
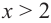
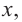
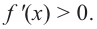
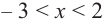
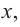
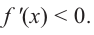
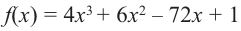
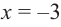
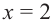
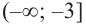
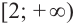
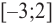
Пример №4
Изобразите схематично график непрерывной функции согласно еле дующим условиям:
a) при 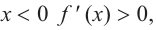
b) при 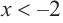
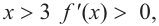
Решение:
а) при 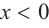
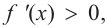
функция возрастает. При 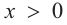
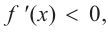
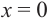
b) При 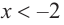
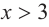
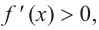
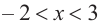
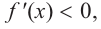
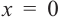
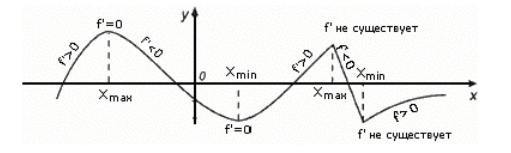
Критические точки и экстремумы функции
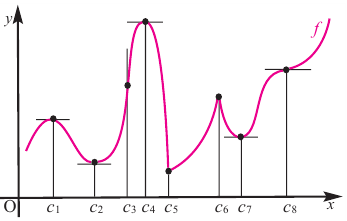
В некоторых точках из области определения производная функции может быть равна нулю или вообще может не существовать. Такие точки из области определения называются критическими точками функции. Покажем критические точки на графике заданной функции.
1. Для значений 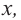
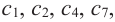
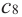
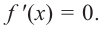
2. В точках 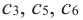
3. Для рассматриваемой нами функции критические точки 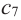
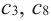
По графику видно, что в точках внутреннего экстремума(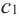
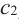
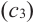
Теорема Ферма (Необходимое условие существовании экстремумов)
Во внутренних точках экстремума производная либо равна нулю, либо не существует.
Примечание. Точка, в которой производная равна нулю, может и не быть точкой экстремума. Например, в точке 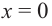
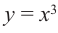
На отрезке непрерывности функция может иметь несколько критических точек, точек максимума и минимума. Существование экстремума в точке зависит от значения функции в данной точке и в точках, близких к данной, т. е. имеет смысл локального (местного) значения. Поэтому иногда используют термин локальный максимум и локальный минимум.
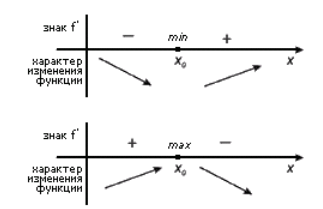
Достаточное условие существования экстремума
Пусть функция 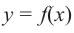
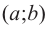
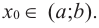
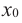
слева от точки
положительна, а справа — отрицательна, то точка
является точкой максимума.
слева от
отрицательна, а справа — положительна, то точка
является точкой минимума
с каждой стороны от точки
имеет одинаковые знаки, то точка
не является точкой экстремума.
Чтобы найти наибольшее (абсолютный максимум) или наименьшее (абсолютный минимум) значение функции, имеющей конечное число критических точек на отрезке, надо найти значение функции во всех критических точках и на концах отрезка, а затем из полученных значений выбрать наибольшее или наименьшее.
Соответствующие наибольшее и наименьшее значения функции 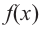
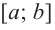
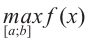
Ниже представлены примеры определения максимума и минимума в соответствии со знаком производной первого порядка.
Пример №5
Для функции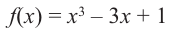
Решение: Для решения задания сначала надо найти критические точки. Для данной функции этими точками являются точки (стационарные), в которых производная равна нулю.
1. Производная функции:
2. Критические точки функции:
3. Точки 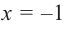
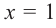
Проверим знак 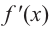
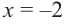
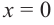
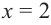

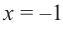
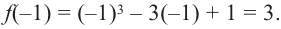
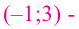
При 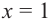
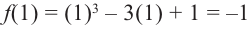
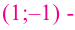
4. Используя полученные для функции 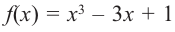
Пример №6
Найдите наибольшее и наименьшее значение функции 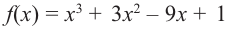
Решение: Сначала найдем критические точки.
Так как 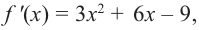
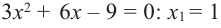
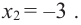
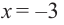
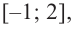
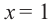
Из этих значений наименьшее — 4, наибольшее 12. Таким образом:
Пример №7
Найдите экстремумы функции
Решение: 1. Производная функции:
2. Критические точки:
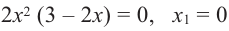
3. Интервалы, на которые критические точки делят область определения функции:
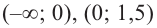
Проверим знак 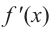
Для промежутка 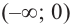
Для промежутка 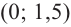
Для промежутка 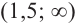
Используя полученную для функции 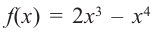
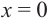
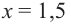
Пример №8
Найдите экстремумы функции
Решение: 1. Производная
2. Критические точки: для этого надо решить уравнение 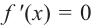
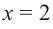
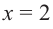
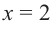
3. Промежутки, на которые критическая точка делит область определения функции: 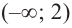
Определим знак 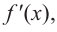
Для 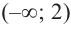
Для 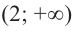
Пример №9
По графику функции производной 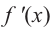
Решение:
Производная 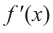
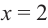
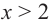
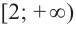
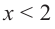
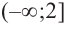
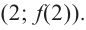
- Заказать решение задач по высшей математике
Построение графиков функции с помощью производной
Функция — многочлен определена и непрерывна на всей числовой оси.
Чтобы построить график функции- многочлен надо выполнить следующие шаги.
- Определите точки пересечения с осями координат.
- Найдите критические точки.
- Найдите промежутки возрастания и убывания функции.
- Найдите максимумы и минимумы.
- Постройте график.
Пример:
Постройте график функции
1) Точки пересечения с осями координат :
2) Критические точки ( точки, в которых производная равна нулю):
значит, точки 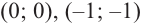
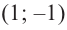
3) Промежутки возрастания и убывания. Экстремумы.
Критические точки 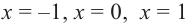
4) Используя полученную информацию, построим график функции.
Чтобы построить график рациональной функции надо выполнить следующие шаги.
- Найдите область определения.
- Найдите асимптоты (если они есть).
- Определите точки пересечения с осями координат.
- Найдите критические точки.
- Найдите промежутки возрастания и убывания и экстремумы.
- Постройте график.
Пример:
Постройте график функции
1) Область определения функции:
2) Асимптоты:
Прямая 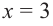
Так как степень многочлена в числителе больше степени многочлена в знаменателе, рациональная функция не имеет горизонтальной асимптоты. Однако, записав следующее:
условии 
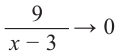
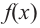
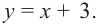
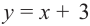
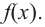
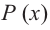
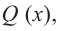
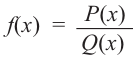
3) Точки пересечения с осями координат:
4) Критические точки:
5) Промежутки возрастания и убывания: в точке 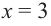
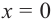
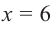
6) Построим график. Отметим на координатной плоскости точки 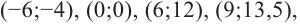
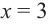
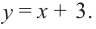
Обратите внимание! В области, близкой к точке 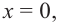
Задачи на экстремумы. Оптимизации
В реальной жизненной ситуации возникает необходимость выбора оптимального варианта и нахождения экстремумов определенной функции. Ежедневно, при решении проблем в различных областях, мы сталкиваемся с терминами наибольшая прибыль, наименьшие затраты, наибольшее напряжение, наибольший объем, наибольшая площадь и т.д. Большое экономическое значение в промышленности, при определении дизайна упаковки, имеет вопрос, как подобрать размеры упаковки с наименьшими затратами. Такого рода задания связаны с нахождением максимального или минимального значения величины. Задачи на нахождение максимального и минимального значения величины называются задачами на оптимизацию. Для решения данных задач применяется производная.
Замечание 1: На интервале 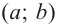
Замечание 2: В рассматриваемом интервале может быть одна стационарная точка: или точка максимума, или точка минимума. В этом случае, в точке максимума функция принимает наибольшее значение, а в точке минимума — наименьшее значение.
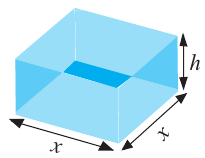
Пример 1. Максимальный объем. Фирма планирует выпуск коробки без крышки, с квадратным основанием и площадью поверхности 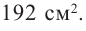
Решение:
Так как основанием коробки является квадрат, то ее объем можно вычислить по формуле 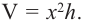
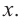
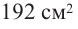
Тогда выразим 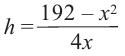
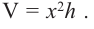
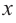
Теперь найдем область определения функции 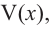
Понятно, что длина не может быть отрицательной, т. е. 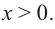
или 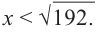
Найдем максимальное значение функции 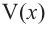
Для этого используем производную первого порядка:
При 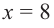
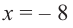
Однако. 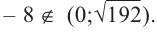
При 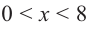
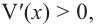
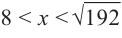
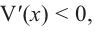
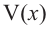
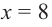
Если длина основания коробки будет 8 см, то высота будет равна
Значит, максимальный объем будет иметь коробка с размерами
Построив при помощи графкалькулятора график функции 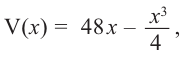
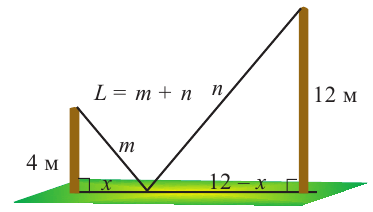
Пример 2. Минимальное потребление. Два столба высотой 4 м и 12 м находятся на расстоянии 12 м друг от друга. Самые высокие точки столбов соединены с металлической проволокой, каждая из которых, в свою очередь крепится на земле в одной точке. Выберите такую точку на земле, чтобы для крепления использовалось наименьшее количество проволоки.
Решение: 1) Изобразим рисунок, соответствующий условию задачи, и обозначим соответствующие данные на рисунке.
2) Аналитически выразим зависимость между переменными.
По теореме Пифагора:
зависимость функции 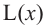
Производная функции
Найдем критические точки функции
Сравнивая значения функции 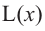
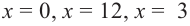
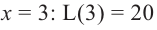
При решении задач на экстремумы обратите внимание на следующее!
1. Внимательно читайте условие. Сделайте соответствующий рисунок.
2. Задайте список соответствующих переменных и констант, которые менялись и оставались неизменными и какие единицы использовались. Если на рисунке есть размеры, обозначьте их.
3. Выберите соответствующий параметр 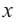
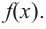
4. Полученные значения объясните экспериментально.
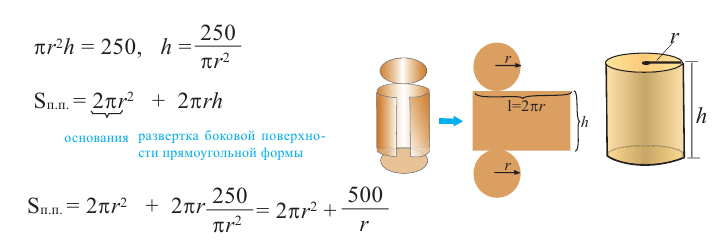
Пример: Минимальное потребление материала. Для мясных консервов планируется использовать банку в форме цилиндра объемом 250
a) Каких размеров должна быть банка, чтобы для ее изготовления использовалось как можно меньше материала?
b) Для круглого основания используется материал, цена 1 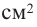
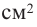
Решение: а) По условию задачи объем равен 250 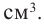
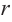
Для функции, выражающей площадь поверхности, область определения представляет собой незамкнутый интервал, и мы должны найти, при каком значении 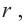
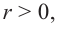
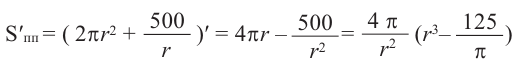
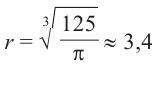
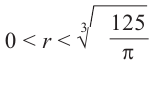
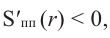
Значит,
Подставим значение 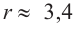
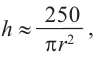
Итак, минимальные затраты на материал будет иметь банка цилиндрической формы с размерами 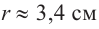
Размеры, при которых затраты на материал будут минимальными
- Приложения производной
- Производные высших порядков
- Дифференциал функции
- Дифференцируемые функции
- Касательная к графику функции и производная
- Предел и непрерывность функции
- Свойства функций, непрерывных в точке и на промежутке
- Предел функции на бесконечности
Определение
возрастающей функции.
Функция y=f(x) возрастает
на интервале X,
если для любых и
выполняется
неравенство .
Другими словами – большему значению
аргумента соответствует большее значение
функции.
Определение
убывающей функции.
Функция y=f(x) убывает
на интервале X,
если для любых и
выполняется
неравенство .
Другими словами – большему значению
аргумента соответствует меньшее значение
функции.
ЗАМЕЧАНИЕ:
если функция определена и непрерывна
в концах интервала возрастания или
убывания (a;b),
то есть при x=a и x=b,
то эти точки включаются в промежуток
возрастания или убывания. Это не
противоречит определениям возрастающей
и убывающей функции на промежутке X.
К
примеру, из свойств основных элементарных
функций мы знаем, что y=sinx определена
и непрерывна для всех действительных
значений аргумента. Поэтому, из возрастания
функции синуса на интервале 
можем утверждать о возрастании на
отрезке .
Точки экстремума, экстремумы функции.
Точку называют точкой
максимума функции y=f(x),
если для всех x из
ее окрестности справедливо неравенство .
Значение функции в точке максимума
называютмаксимумом
функции и
обозначают .
Точку называют точкой
минимума функции y=f(x),
если для всех x из
ее окрестности справедливо неравенство .
Значение функции в точке минимума
называютминимумом
функции и
обозначают .
Под
окрестностью точки понимают
интервал ,
где —
достаточно малое положительное число.
Точки
минимума и максимума называют точками
экстремума,
а значения функции, соответствующие
точкам экстремума, называют экстремумами
функции.
Не
путайте экстремумы функции с наибольшим
и наименьшим значением функции.
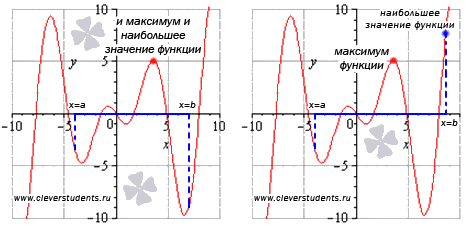
На
первом рисунке наибольшее значение
функции на отрезке [a;b] достигается
в точке максимума и равно максимуму
функции, а на втором рисунке – наибольшее
значение функции достигается в точке x=b,
которая не является точкой максимума.
Достаточные условия возрастания и убывания функции.
На
основании достаточных условий (признаков)
возрастания и убывания функции находятся
промежутки возрастания и убывания
функции.
Вот
формулировки признаков возрастания и
убывания функции на интервале:
-
если
производная функции y=f(x) положительна
для любого x из
интервала X,
то функция возрастает на X; -
если
производная функции y=f(x) отрицательна
для любого x из
интервала X,
то функция убывает на X.
Таким
образом, чтобы определить промежутки
возрастания и убывания функции необходимо:
-
найти
область определения функции; -
найти
производную функции; -
решить
неравенстваи
на
области определения; -
к
полученным промежуткам добавить
граничные точки, в которых функция
определена и непрерывна.
Рассмотрим
пример нахождения промежутков возрастания
и убывания функции для разъяснения
алгоритма.
Пример.
Найти
промежутки возрастания и убывания
функции 
Решение.
Первым
шагом является нахождение
обрасти определения функции. В нашем
примере выражение в знаменателе не
должно обращаться в ноль, следовательно, .
Переходим
к нахождению производной функции:
Для
определения промежутков возрастания
и убывания функции по достаточному
признаку решаем неравенства и
на
области определения. Воспользуемся
обобщением метода интервалов. Единственным
действительным корнем числителя
является x
= 2,
а знаменатель обращается в ноль при x=0.
Эти точки разбивают область определения
на интервалы, в которых производная
функции сохраняет знак. Отметим эти
точки на числовой прямой. Плюсами и
минусами условно обозначим интервалы,
на которых производная положительна
или отрицательна. Стрелочки снизу
схематично показывают возрастание или
убывание функции на соответствующем
интервале.
Таким
образом, 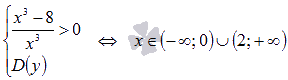

В
точке x=2 функция
определена и непрерывна, поэтому ее
следует добавить и к промежутку
возрастания и к промежутку убывания. В
точке x=0 функция
не определена, поэтому эту точку не
включаем в искомые интервалы.
Приводим
график функции для сопоставления с ним
полученных результатов.
Ответ:
функция
возрастает при ,
убывает на интервале (0;2].
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #




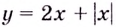
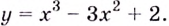
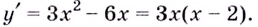
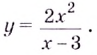
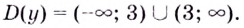
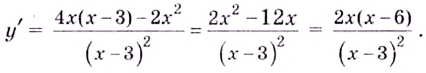
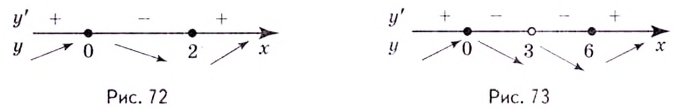
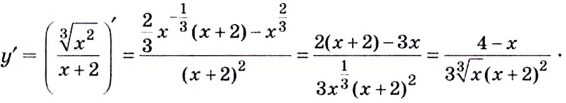
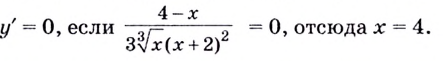
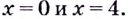
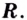
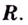
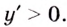
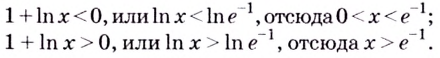
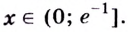
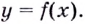
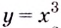
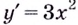
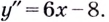
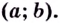
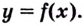
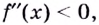 то кривая выпуклая; если
то кривая выпуклая; если 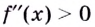 — кривая вогнутая;
— кривая вогнутая;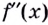 меняет знак при переходе через точку
меняет знак при переходе через точку 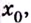 то точка
то точка 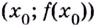 является точкой перегиба кривой
является точкой перегиба кривой 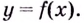
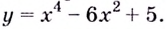
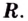
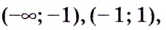
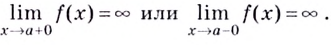
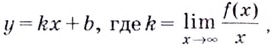
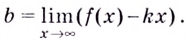
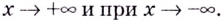
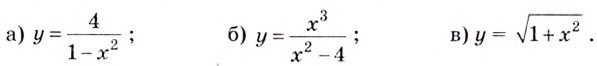
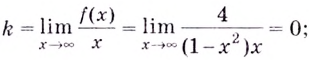
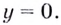
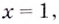
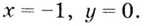
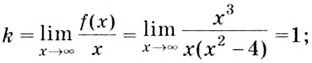
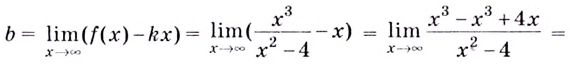
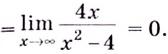
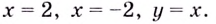
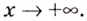
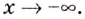
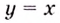
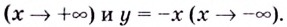
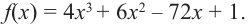
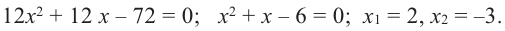

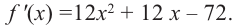
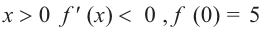
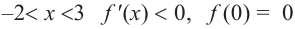
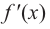 слева от точки
слева от точки 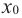 положительна, а справа — отрицательна, то точка
положительна, а справа — отрицательна, то точка 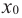 является точкой максимума.
является точкой максимума.