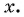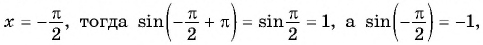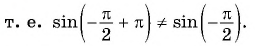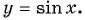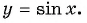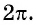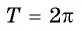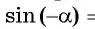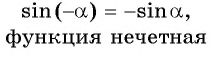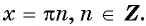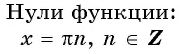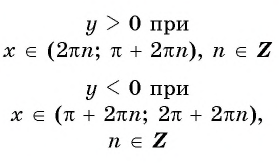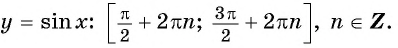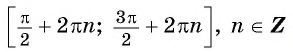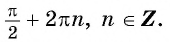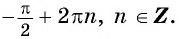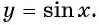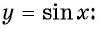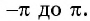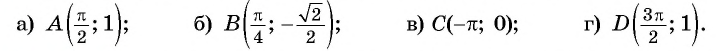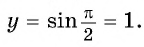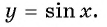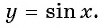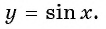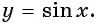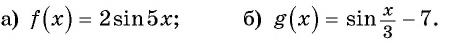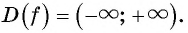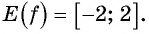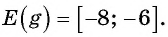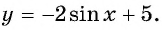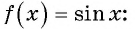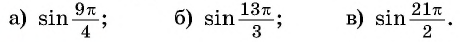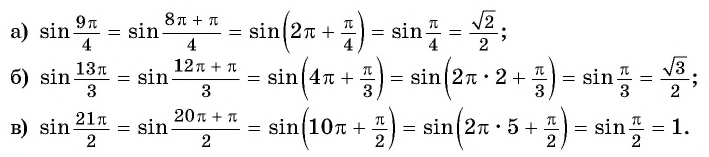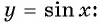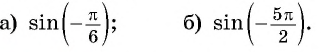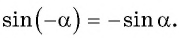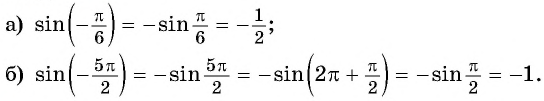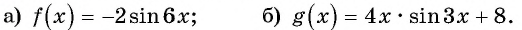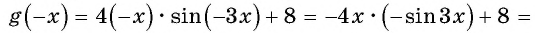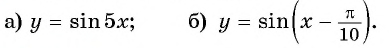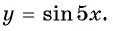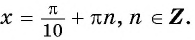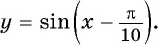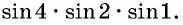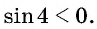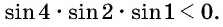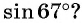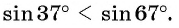Основные понятия
Кривая получается из синусоидальной дуги путём смещения к пи/2 в сторону со знаком минус. Кривая представляет график функции у=sin x. В формуле синусоиды y=a+b cos (cx+d) присутствуют следующие аргументы:
- a: показывает сдвиг графика синусоиды по оси Oy (чем больше значение, тем выше прямая);
- b: описывает растяжения функции по оси Oy (чем выше постоянная, тем сильнее колебания);
- c: определяет растяжение по оси Ох (если постоянная увеличивается, наступает период колебаний);
- d: описывает сдвиг по оси Ох (если d увеличивается, тогда при построении синусоиды учитывается сдвиг в область со знаком минус по оси абсцисс).
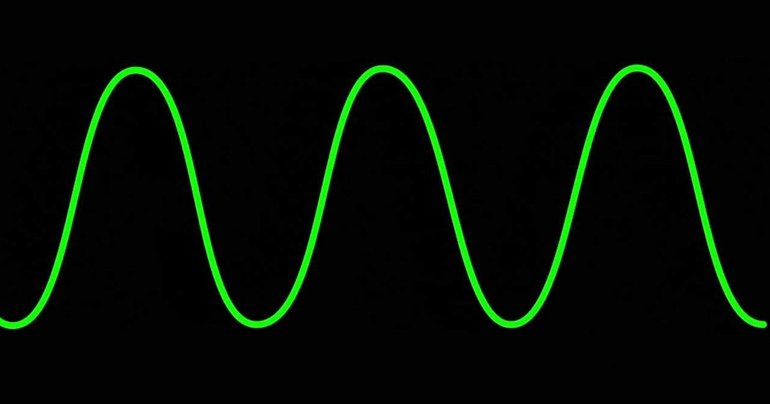
Сжатие, растяжение либо сдвиг кривой приводит к изменению величины. Явления называются гармоническими колебаниями. Примеры синусоиды: экспонент или показательная функция в виде винтовой линии, проведённой на плоскости, скрученный провод, развёрнутый рулон бумаги.
Особенности построения
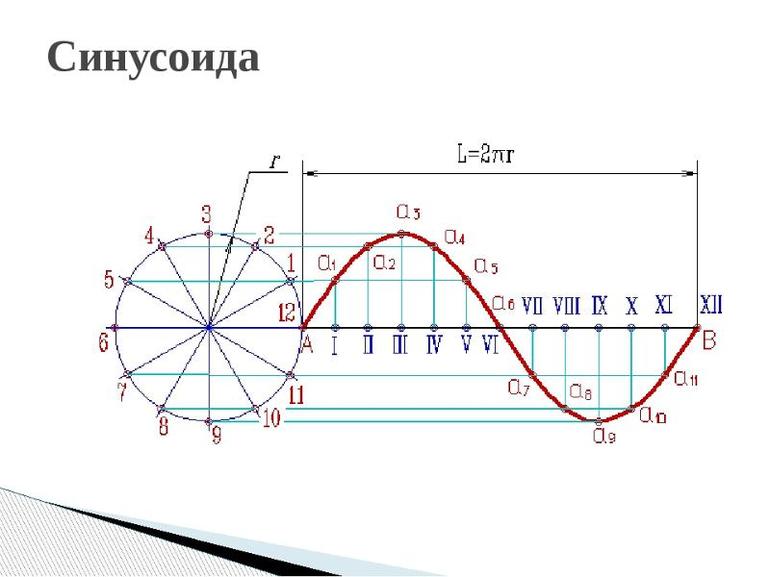
Чтобы выявить свойства синусоиды, необходимо построить её график, провести исследование синуса. В алгебре под функцией представлена плоская кривая, которая выражает закон колебания sin с учётом изменения центрального угла. Сама синусоида строится в схематической последовательности:
- проводится горизонтальная ось, на которой откладывается заданная длина волны;
- отрезок делится на равные части;
- слева чертится окружность с радиусом, равным величине амплитуды;
- окружность делится на 12 одинаковых частей;
- через полученные точки проводятся прямые;
- из точек проводятся перпендикуляры к оси.
График можно построить на онлайн ресурсе либо с помощью специальных программ (Excel). Для расчёта используется калькулятор, основная формула y=sin х. При решении задач учитывается длина волны, которая равна 2 пи. Такое преобразование объясняется тем, что значение функции при любом икс совпадает с её периодичностью x+2π.
Пересечение оси Ох происходит в точках перегиба πK. Максимум достигается при положительном π/2+2πK, а обратное — -π/2+2πK. Свойства кривой проявляются в частном либо комплексном виде:
- размах;
- растяжение/сжатие;
- фазовые колебания;
- круговая частота.
При сдвиге графика влево к значению пи/2 образуется косинусоида. Любое изменение величины характерно для квадрата с гармоническими колебаниями. Примеры подобных явлений: движение маятника, сбои с напряжением в электросети. Другой случай с синусоидальными колебаниями — звук. Он редко бывает чистым, соответствуя y=A sin wt, где:
- А (а) — модуль неизвестной (расстояние от начала координат до точки А);
- w — угловая частота;
- t — время.
Чаще издаются обертоны, для которых характерны низкие амплитуды. Подобные явления изучаются в школе на уроках физики в старших классах.
Свойства и доказательства
К главным свойствам синусоиды относятся область значений (включая нуль) и определений, чётность/нечётность, периодичность, точки пересечения с осью координат, промежуточности постоянства, убывания и возрастания, минимум и максимум. При пересечении графика функции (ГФ) с осью Ох результат равняется нулю. Под значением синуса подразумевается ордината соответствующей точки единичной окружности.
Так как через круг в одной области можно провести только одну прямую, перпендикулярную оси, поэтому для области определения функции подходят все числа. Такое свойство записывается следующим образом: D (sin x) = R.
Значения ординаты единичной окружности (ЕД) расположены на отрезке [—1; 1]. Они принимают значения от -1 до 1. Через любую точку указанного промежутка оси ординат, равного диаметром ЕД, проводится прямая, перпендикулярная оси ординат. Таким способом получается точка с рассматриваемой ординатой.
Из свойства вытекает следующее: функция y= sin x имеет область значений (-1; 1). Утверждение записывается так: E (sin x)=(-1; 1). Максимальное значение функции равняется единице. Подобное возможно, если соответствующей точкой ЕД является точка А. Минимальное число y равно -1 в случае, когда точкой ЕД является В (х=пи/2 +2пиk, где k принадлежит области Z.
Нечётность и постоянство
Функция считается нечётной, если sin (-x)=- sin x. Её график симметричен по отношению к началу координат. Сам синус является периодической величиной, у которой наименьший положительный период. Через отрезок 2пи вид кривой повторяется. Это свойство учитывается при построении графика.
Предварительно чертится кривая на любом отрезке соответствующей длины. При переносе линии влево и вправо соблюдается шаг в kT=2 πk, где k — любая натуральная цифра. Для вычисления точек пересечения линии с осями координат используется равенство х=0. Если значение подставить в функцию, получится следующее: y=sin 0=0. В таком случае график проходит через начало координат.
Так как y равен нулю, поэтому можно рассчитать х, воспользовавшись формулой y= sin x. Координата подходящей точки ЕД равняется нулю. Такое явление будет наблюдаться только в случае, если на ЕД будут выбраны точки D либо C, при x=πk, k принадлежит Z.
Функция имеет положительное значение в первой и во второй четвертях. На этих промежутках sin x больше нуля, а любое значение х находится в пределах 0-π. При решении задач учитывается период при всех x, принадлежащих отрезку (2πk; π+2πk), где k принадлежит Z. Функция считается отрицательной в третьем и четвёртом квадрате. При этом sin меньше нуля, а иск находится в пределах (пи+2пиk; 2пи+2пиk), k принадлежит области Z.
Больше и меньше
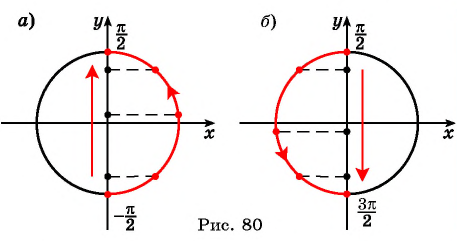
С учётом периодичности y с периодом T=2π исследуется функция на возрастание и убывание на любом отрезке длиной в 2пи. Если T= (-π/2;3π/2), а х принадлежит данному промежутку, тогда при увеличении аргумента изменится в большую сторону и ордината. Следовательно, на указанном отрезке синусоида возрастает.
Если учитывать её периодичность, можно прийти к выводу, что она возрастает на каждом интервале (-π/2+2πk; π/2+2πk), k принадлежит Z. Если х находится на отрезке (-π/2;3π/2), тогда при увеличении аргумента ордината ЕД уменьшается, а функция убывает. С учётом периодичности синусоиды можно сделать вывод, что она бывает на каждом отрезке (π/2+2πk;3π/2+2πk), k находится в области Z.
Основываясь на проведённом исследовании, строится график y=sin x. С учётом периодичности 2π предварительно строится график на любом отрезке соответствующей длины. Чтобы точно построить точки, рекомендуется придерживаться значения синуса (ордината ЕД). На основе нечётности проводится кривая, симметричная началу координат. При этом необходимо придерживаться интервала (-π;0). Так как линия строится на отрезке длиной 2π, поэтому учитывается периодичность величины.
Вид графика повторяется на каждом отрезке с аналогичной длиной. Таким способом получается синусоида. Рассматриваемая тригонометрическая функция получила широкое применение в технике, физике и математике. Большинство процессов, включая колебания струн, напряжения в цепи, описываются с помощью функции, задаваемой формулой y= A sin (wx + f). Подобные явления считаются гармоническими колебаниями.
Кривая получается из синусоиды за счёт разных колебаний и путём параллельного переноса вдоль оси Ох. Чаще изменения результата связаны с функцией времени t. В таком случае используется формула y= A sin (wx + f), где через А обозначается амплитуда колебания, через w — частота, f — начальная фаза, 2пи/f — период колебания.
Свойства функций синуса, косинуса, тангенса и котангенса и их графики
Свойства функций синуса, косинуса, тангенса и котангенса и их графики
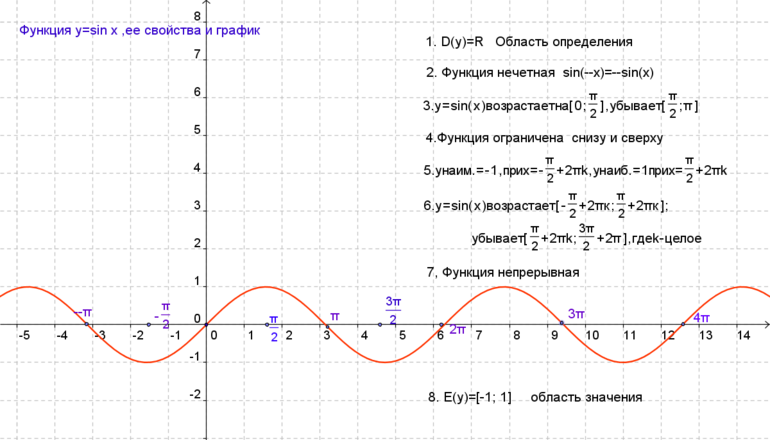
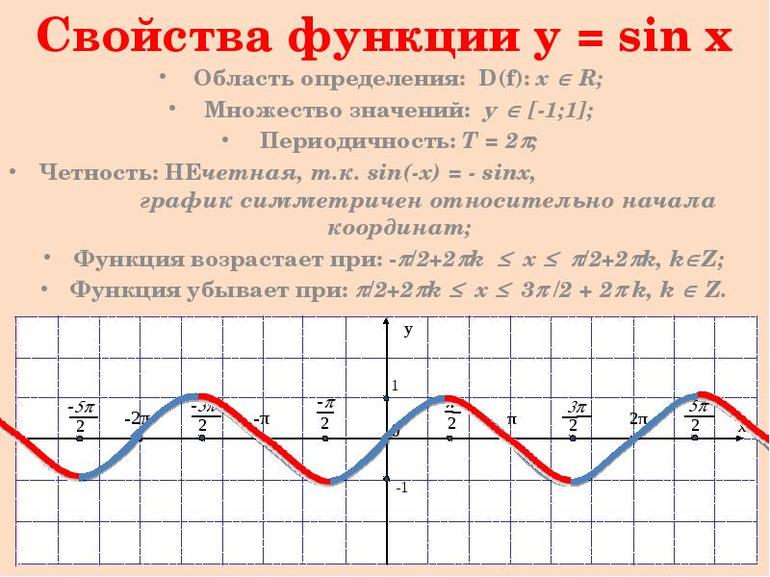
Свойства функции y=sin(x) и ее график.
График функции 
Свойства функции
- Область определения: R (x — любое действительное число) т.е.
- Область значений:
-
Функция нечетная:
(график симметричен относительно начала координат).
- Функция периодическая с периодом
- Точки пересечения с осями координат:
- Промежутки знакопостоянства:
- Промежутки возрастания и убывания:
Объяснение и обоснование
Описывая свойства функций, мы будем чаще всего выделять такие их характеристики: 1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями координат; 6) промежутки знакопостоянства; 7) промежутки возрастания и убывания; 
Замечание. Абсциссы точек пересечения графика функции с осью Ох (то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.
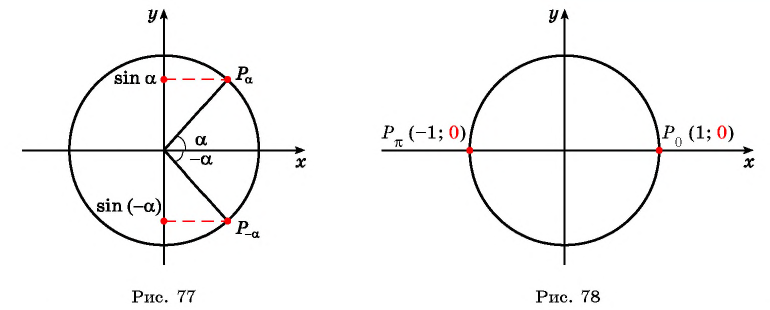
Напомним, что значение синуса — это ордината соответствующей точки единичной окружности (рис. 1).

Поскольку ординату можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности всегда можно провести единственную прямую, перпендикулярную оси ординат), то область определения функции 
Для точек единичной окружности ординаты находятся в промежутке [—1; 1] и принимают все значения от —1 до 1, поскольку через любую точку отрезка [—1; 1] оси ординат (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси ординат, и получить точку окружности, которая имеет рассматриваемую ординату. Таким образом, для функции 
. Это можно записать так:
.Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при
Наименьшее значение функции


Синус — нечетная функция: 
Синус — периодическая функция с наименьшим положительным периодом :

вид графика функции

, а потом полученную линию параллельно перенести вправо и влево вдоль оси Ox на расстояние
, где k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси значение
. Тогда соответствующее значение
, то есть график функции
проходит через начало координат.
На оси значение

, при которых


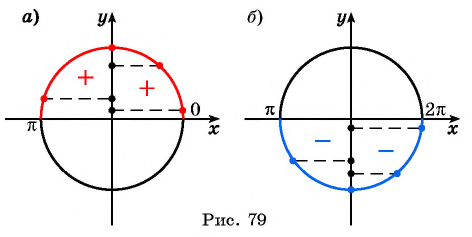
Промежутки знакопостоянства. Значения функции синус положительны (то есть ордината соответствующей точки единичной окружности положительна) в I и II четвертях (рис. 2). Таким образом, 


Значения функции синус отрицательны (то есть ордината соответствующей точки единичной окружности отрицательна) в III и IV четвертях, поэтому 

Промежутки возрастания и убывания. Учитывая периодичность функции 



Если 




Рис.2 Рис.3
Если 




Проведенное исследование позволяет обоснованно построить график функции 







Рис.4
Рис.5
Поскольку мы построили график на промежутке длиной 


на

Рис.6
Замечание. Тригонометрические функции широко применяются в математике, физике и технике. Например, множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п., описываются функцией, которая задается формулой 
График функции 

. Чаще всего гармоническое колебание является функцией времени t. Тогда оно задается формулой

колебания, 


СВОЙСТВА ФУНКЦИИ  И ЕЕ ГРАФИК
И ЕЕ ГРАФИК
График функции (косинусоида).
Свойства функции
- Область определения: R (x — любое действительное число)
.
- Область значений:
-
Функция четная:
(график симметричен относительно оси
).
- Функция периодическая с периодом
:
- Точки пересечения с осями координат
- Промежутки знакопостоянства:
- Промежутки возрастания и убывания:
Объяснение и обоснование
Напомним, что значение косинуса — это абсцисса соответствующей точки единичной окружности (рис.7). Поскольку абсциссу можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности, всегда можно провести единственную прямую, перпендикулярную оси абсцисс), то область определения функции 

Рис.7
Для точек единичной окружности абсциссы находятся в промежутке 

точку окружности, которая имеет рассматриваемую абсциссу. Следовательно, область значений функции 

Как видим, наибольшее значение функции 

Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть при 
Косинус — четная функция: 

Косинус — периодическая функция с наименьшим положительным периодом 



Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси 







Промежутки знакопостоянства. Значения функции косинус положительны (то есть абсцисса соответствующей точки единичной окружности положительна) в I и IV четвертях (рис. 8). Следовательно, 


Значения функции косинус отрицательны (то есть абсцисса соответствующей точки единичной окружности отрицательна) во II и III четвертях, поэтому 
Промежутки возрастания и убывания. Учитывая периодичность функции 


Если 





Если 





Рис.8 Рис.9
Проведенное исследование позволяет построить график функции 
. Но график функции


Рис.10
Эту формулу можно обосновать, например, так. Рассмотрим единичную окружность (рис. 10), отметим на ней точки 
абсциссы и ординаты этих точек. Так как 
прямоугольника 



Укажем также формулы, которые нам понадобятся далее:
Тогда,
Таким образом, 
Учитывая, что 

его параллельным переносом вдоль оси


Рис.11
Рис.12
СВОЙСТВА ФУНКЦИИ  И ЕЕ ГРАФИК
И ЕЕ ГРАФИК
График функции 
Свойства функции 
1. Область определения:
2. Область значений:
3. Функция нечетная:
4. Функция периодическая с периодом
5. Точки пересечения с осями координат:
6. Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.
СВОЙСТВО ФУНКЦИИ  И ЕЕ ГРАФИК
И ЕЕ ГРАФИК
График функции (котангенсоида)
Свойства функции :
1. Область определения:
2. Область значений:
3. Функция нечетная:
4. Функция переодическая с периодом
5. Точки пересечения с осями координат:
6. Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.
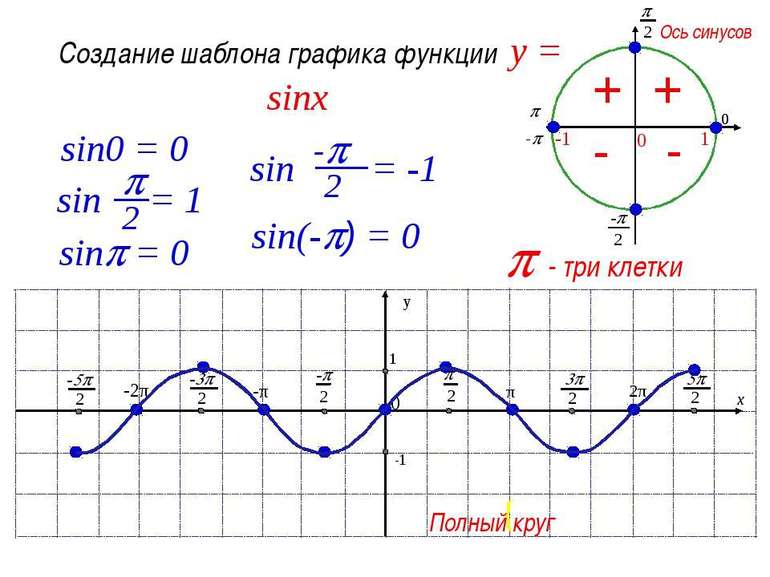
Как построить синусоиду
Синусоида представляет собой график функции y=sin(x). Синус – ограниченная периодическая функция. Перед построением графика необходимо провести аналитическое исследование и расставить точки.

Инструкция
На единичной тригонометрической окружности синус угла определяется отношением ординаты “y” к радиусу R. Поскольку R=1, можно рассматривать просто ординату “y”. Она соответствует двум точкам на этой окружности.
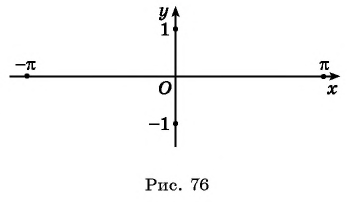
Для будущей синусоиды постройте координатные оси Ox и Oy. На оси ординат отметьте точки 1 и -1. Отрезок для единицы выберите большой, так как за его пределы функция синуса не зайдет. На оси абсцисс выберите масштаб, равный π/2. π/2 примерно равно 1,5, число π примерно равно трем.
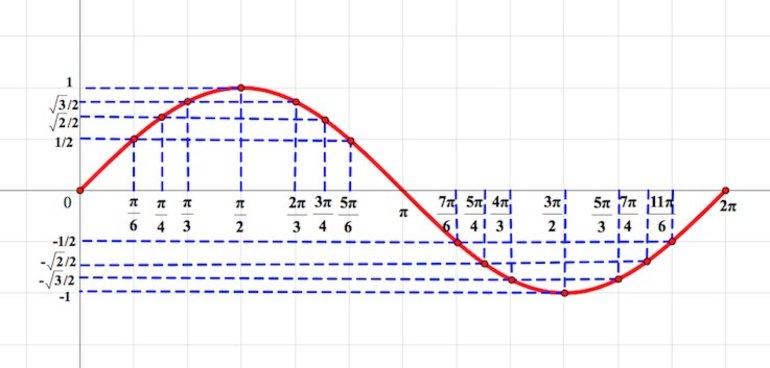
Найдите ключевые точки синусоиды. Посчитайте значение функции для аргумента, равного нулю, п/2, п, 3п/2. Так, sin0=0, sin(п/2)=1, sin(п)=0, sin(3п/2)=-1, sin(2п)=0. Легко видеть, что функция синуса имеет период, равный 2п. То есть через числовой промежуток в 2п значения функции повторяются. Поэтому для исследования свойств синуса достаточно построить график на одном из таких отрезков.
В качестве дополнительных точек можно взять п/6, 2п/3, п/4, 3п/4. Значения синусов в этих точках можно посмотреть в таблице. Чтобы не запутаться, полезно мысленно представлять тригонометрическую окружность. Итак, sin(п/6)=1/2, sin(2п/3)= √3/2≈0,9, sin(п/4)=√2/2≈0,7, sin(3п/4)=√2/2≈0,7.
Осталось лишь плавно соединить полученные точки на графике. Выше оси Ox синусоида будет выпуклая, ниже – вогнутая. Точки, в которых синусоида пересекает ось абсцисс, являются точками перегиба функции. Вторая производная в этих точках равна нулю. Имейте в виду, что в концах отрезка синусоида не заканчивается, она бесконечна.
Нередко встречаются задачи, в которых аргумент находится под знаком модуля: y=sin|x|. В этом случае постройте сначала график для положительных значений x. Для отрицательных значений x отобразите график симметрично относительно оси Oy.
Полезный совет
Из графика синуса легко можно получить график функции косинуса. Для этого сместите синусоиду на п/2 влево. Смещать можно не саму синусоиду, а координатные оси, только уже вправо.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
22
Окт 2013
Категория: Справочные материалыФункции и графики
Графики тригонометрических функций. Синусоида
2013-10-22
2019-09-21
Смешное видео по теме
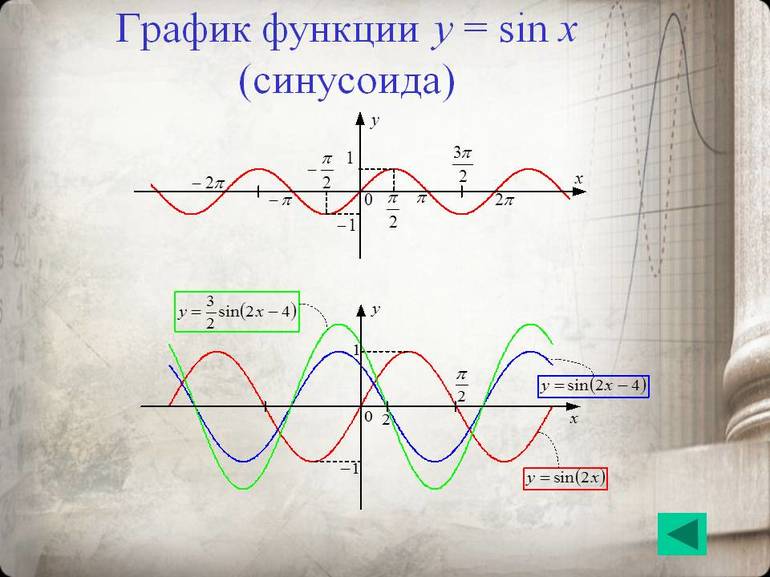
График функции y=sinx
Если вы умеете работать с тригонометрическим кругом, то вам не составит труда построить график функции .
Переносим все основные значения углов, представленные на круге, и соответствующие им значения синуса на координатную плоскость.
По оси абсцисс откладываем угол в радианах, по оси ординат — значения синуса угла.

Переносим все основные значения углов, представленные на круге, и соответствующие им значения синуса на координатную плоскость.
По оси абсцисс откладываем угол в радианах, по оси ординат — значения синуса угла.
Нанесенные на координатную плоскость точки подсказывают нам плавную кривую. Это и есть график функции на
Поскольку на тригонометрическом круге значения синуса повторяются через каждый круг (несколько кругов), то не составит труда построить график функции и на всей числовой прямой.
Указанный выше фрагмент графика синуса будет для нас являться как бы штампом. Тиражируя этот фрагмент, мы и получим вот такой график функции :
График функции называется синусоидой. График симметричен относительно начала координат.
График функции y=cosx
Точно также, как мы строили график при помощи тригонометрического круга, мы могли бы построить и
.
Поступим несколько иначе.
Согласно формулам приведения .
Из чего мы делаем вывод, что график функции будет получен смещением графика функции
на
единиц влево.
То есть график функции – это все таже синусоида, но теперь уже, симметричная относительно оси ординат.
Преобразования синусоиды
Приглашаю посмотреть небольшой видеоролик о том, как меняется поведение синусоиды в зависимости от умножения аргумента или функции на некоторое число или от прибавления к аргументу или функции некоторого числа.
Автор: egeMax |
Нет комментариев
Печать страницы
Содержание:
Рассматривая произвольное действительное число
Таким образом, мы установим соответствие между множеством действительных чисел и множеством значений синусов углов. Каждому действительному числу соответствует единственное значение синуса. Такое соответствие определяет тригонометрическую функцию
Определение функция y=sin x
Определение:
Зависимость, при которой каждому действительному числу 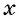
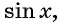
Рассмотрим свойства функции 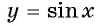
Область определения функции y=sin x
Областью определения функции 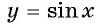
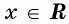
Графически это означает, что для любой абсциссы найдется точка графика функции
Множеством значений функции y=sin x
Множеством значений функции 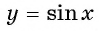
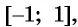
Графически это означает, что график функции 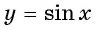
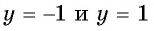
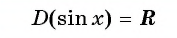
Периодичность функции y=sin x
Периодичность функции 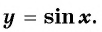
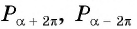
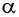
Говорят, что число 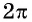
Определение:
Функция 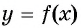
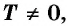
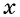
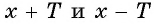
Чтобы определить, является ли функция периодической с периодом 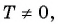
- принадлежат ли области определения функции числа
если
принадлежит области определения функции;
- выполняется ли равенство
Определим, верно ли, что число 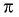
- Числа
принадлежат области определения функции, так как
- Проверим, выполняется ли равенство
для всех
Пусть
Значит, число 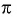
Периодом функции 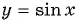
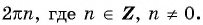
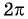
Функция 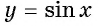
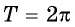
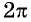
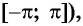
Четность (нечетность) функции y=sin x
Четность (нечетность) функции y=sin x 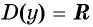
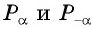
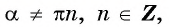
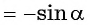
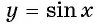
Для построения ее графика достаточно построить его часть для неотрицательных значений аргумента и отобразить эту часть симметрично относительно начала координат.
Нули функции y=sin x
Нули функции. Ординаты точек 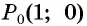
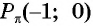
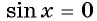
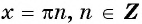
Промежутки знакопостоянства функции y=sin x
На промежутках 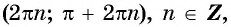
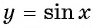
На промежутках 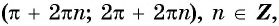
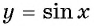
Монотонность функции y=sin x
Монотонность функции. Так как ординаты точек единичной окружности увеличиваются от -1 до 1 при изменении угла от 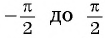
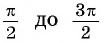
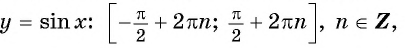
Функции 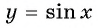
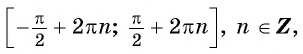
Наибольшее значение функции 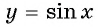
Наименьшее значение функции 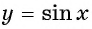
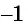
На основании проведенного исследования построим график функции 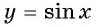
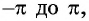
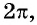
На этом периоде функция
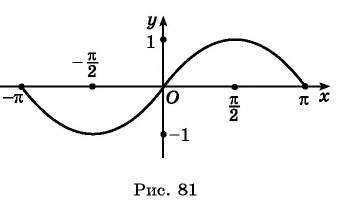
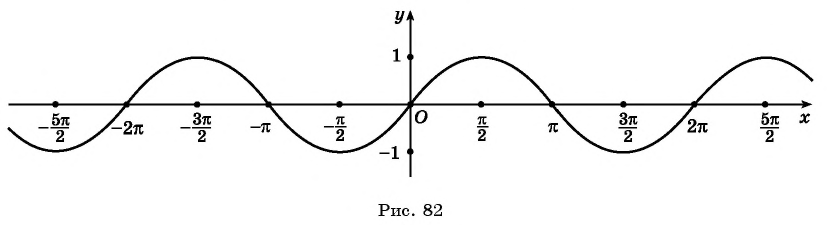
На рисунке 81 изображена часть графика функции 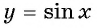
Перенесем эту часть на другие периоды и получим график функции 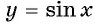
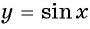
Примеры заданий и их решения
Пример №1
Определите, принадлежит ли графику функции 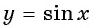
Решение:
а) Подставим в формулу 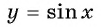
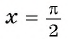
Полученное значение функции равно ординате точки 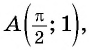
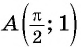
б) При 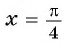
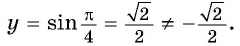
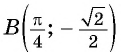
в) При 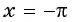
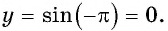
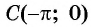
г) При 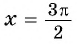
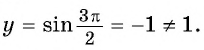
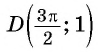
Пример №2
Найдите область определения и множество значений функции:
Решение:
а) Так как область определения функции 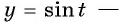
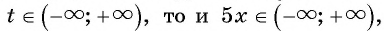
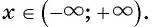
Множеством значений функции 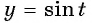
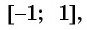
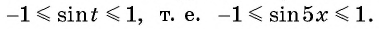
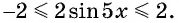
б) 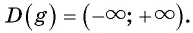
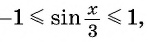
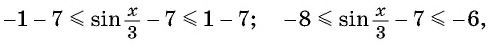
Пример №3
Найдите наибольшее значение функции
Решение:
Так как 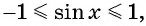
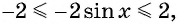
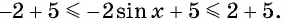
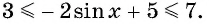
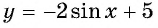
- Заказать решение задач по высшей математике
Пример №4
Найдите значение выражения, используя свойство периодичности функции
Решение:
Так как число 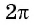
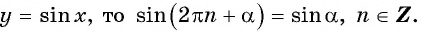
Пример №5
Найдите значение выражения, используя свойство нечетности функции
Решение:
Так как функция 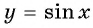
Тогда:
Пример №6
Исследуйте функцию на четность (нечетность):
Решение:
a) 
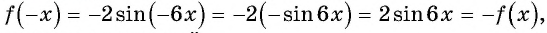
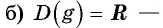
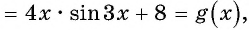
Пример №7
Найдите нули функции:
Решение:
а) Пусть 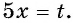
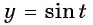
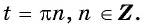
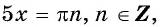
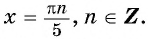
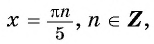
б) Пусть 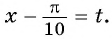
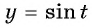
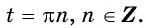
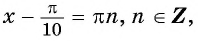
Таким образом, числа 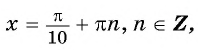
Пример №8
Определите знак произведения
Решение:
Так как 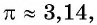
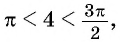
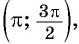
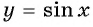
Углы 2 радиана и 1 радиан принадлежат промежутку 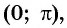
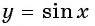
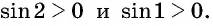
Пример №9
Что больше: 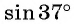
Решение. Так как функция 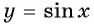
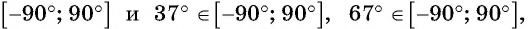
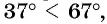
Пример №10
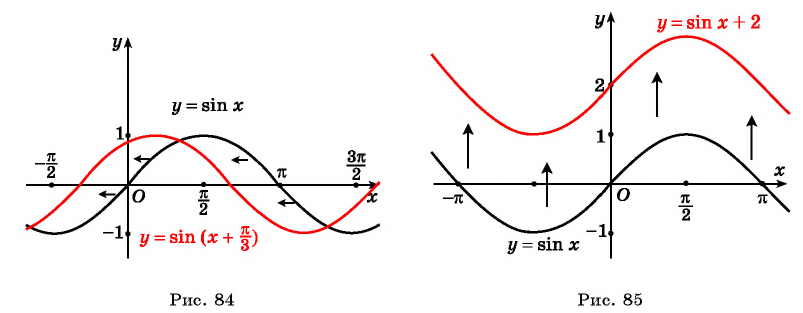
Постройте график функции:
Решение:
а) График функции 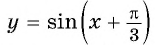
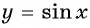
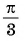
б) График функции 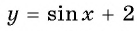
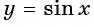
- Функция y=cos x и её свойства и график
- Функции y=tg x и y=ctg x — их свойства, графики
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
- Единичная окружность — в тригонометрии
- Определение синуса и косинуса произвольного угла
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)

![file.[2]](https://ya-znau.ru/information/userfiles/73/file.%5B2%5D.jpg)
![file.[3]](https://ya-znau.ru/information/userfiles/73/file.%5B3%5D.jpg)

![file.[4]](https://ya-znau.ru/information/userfiles/73/file.%5B4%5D.jpg)




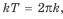









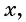
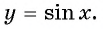
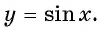
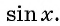
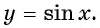
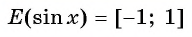
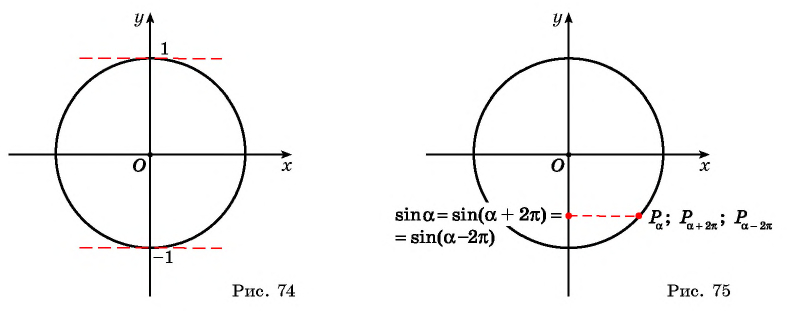
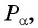
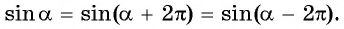
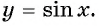
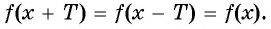
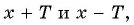 если
если 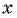 принадлежит области определения функции;
принадлежит области определения функции;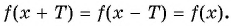
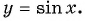
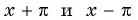 принадлежат области определения функции, так как
принадлежат области определения функции, так как 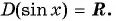
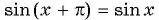 для всех
для всех