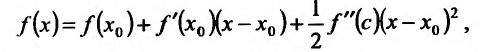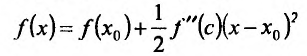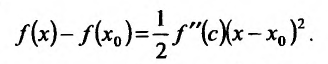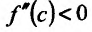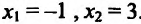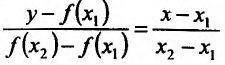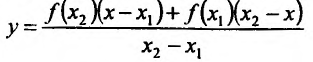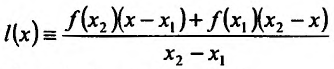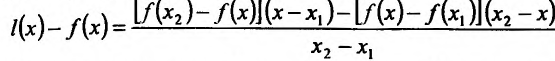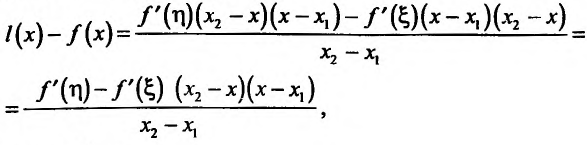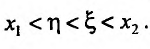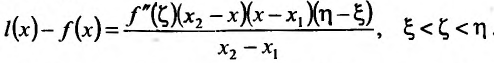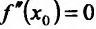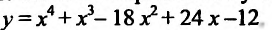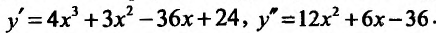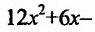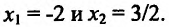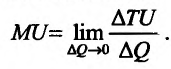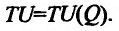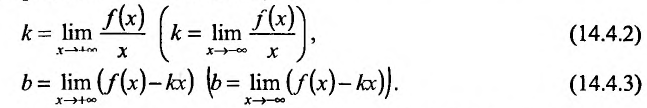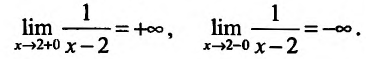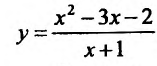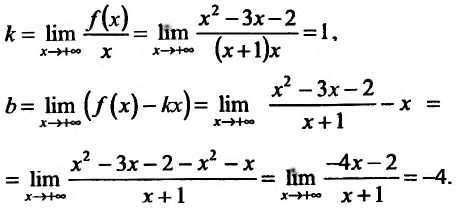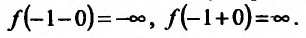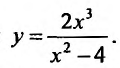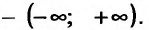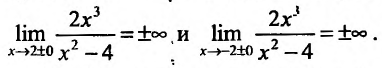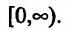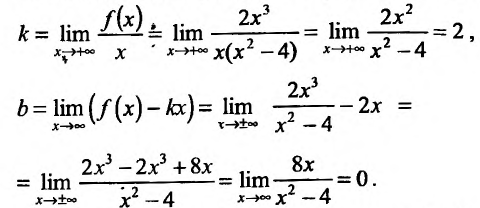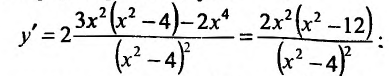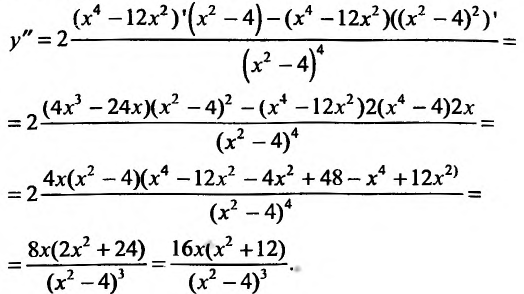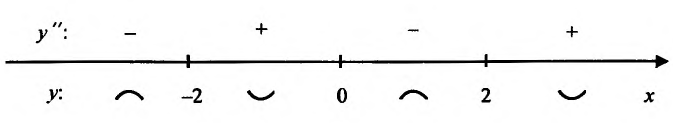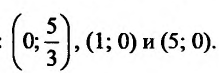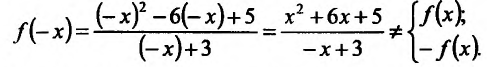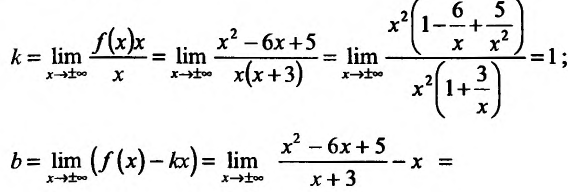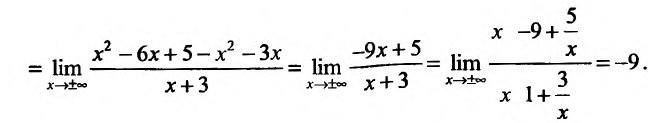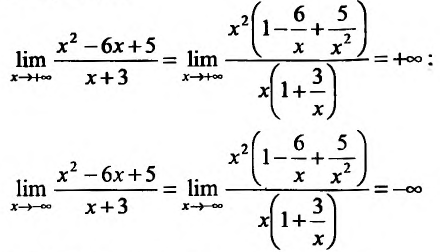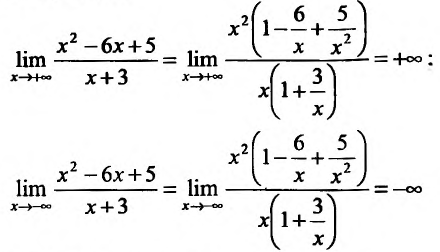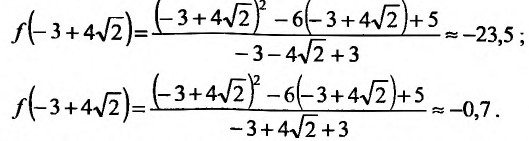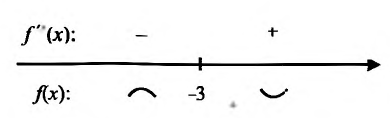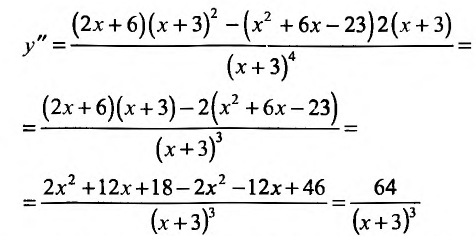1.Если производная функции y
= f(x)
положительна (отрицательна) во всех
точках промежутка, то функцияy
= f(x)
монотонно возрастает (убывает)на этом промежутке.
2.Точкаx0называется точкоймаксимума (минимума)
функцииy = f(x),
если существует интервал, содержащий
точкуx0, такой,
что для всехxиз этого
интервала имеет место неравенствоf(x0)≥ f(x),(f(x0)≤ f(x)).
Точки максимума и точки минимума
называются точкамиэкстремума.
3. Необходимое условие экстремума:
в точке экстремума функции ее производная
либо равна нулю(f
′(x)=0), либо
не существует.
4.Первое достаточное условие
экстремума: если в точке x0функцияy = f(x)
непрерывна, а производная f
′(x)при
переходе через точкуx0меняет знак, то точкаx0– точка экстремума: максимума, если
знак меняется с «+» на «-», и минимума,
если с «–» на «+».
Если при переходе через точку x0производная не меняет знак, то в точкеx0экстремума нет.
5.Второе достаточное условие
экстремума: если в точкеx0
,
а
,
тоx0является точкой
максимума функции. Если
,
а
,
тоx0является точкой
минимума функции.
6.Схема исследования функции
на экстремум:
1) найти производную
;
2) найти критические точки функции, в
которых производная равна нулю или не
существует;
3) исследовать знак производной слева
и справа от каждой критической точки и
сделать вывод о наличии экстремумов
функции;
4) найти экстремальные значения функции.
При исследовании функции на экстремум
с помощью 2-го достаточного условия п.
1), 2), 4) сохраняются, а в п. 3) необходимо
найти вторую производную
и определить ее знак в каждой критической
точке.
7.Чтобы найтинаибольшее и наименьшее
значение(глобальный максимум и
минимум) функции
на отрезке [a,b]
следует выбрать наибольшее (наименьшее)
из значений функции в критических
точках, находящихся в интервале (a,b)
и на концах отрезка (в точкахaиb).
8.Если дифференцируемая на интервале
(a,b) функция
имеетединственнуюточку экстремума,
то в этой точке достигается наибольшее
или наименьшее значение (глобальный
максимум или минимум) функции на интервале
(a,b).
8.35. Найти интервалы монотонности
и экстремумы функции.
Решение. В соответствии со схемой
исследования (п. 6) найдем
.Очевидно, производная существует при
всех значенияхx. Приравниваяy′ к нулю, получаем
уравнение
откудаи
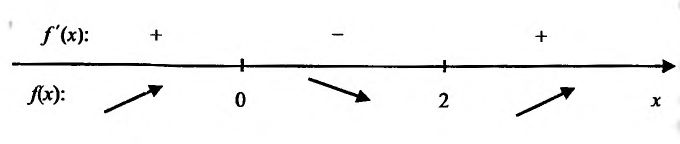
— критические точки. Знаки производной
имеют вид (рис. 8.1):
Рис. 8.1
На интервалах
и
производная
и функция возрастает, на интервале
и функция убывает;
Рис. 8.2
— точка максимума и
— точка минимума и
,
так как при переходе через эти точки
производная меняет свой знак соответственно
с «+» на «-» и с «-» на «+».
Замечание.Установить
существование экстремума в критических
точкахи
,
в которых
можно было и с помощью второй производной
(см.
п. 5). Так как
,
а
,
то— точка максимума, а
— точка минимума.
График данной функции схематично показан
на рисунке 8.2.
8.36. Найти экстремумы и интервалы
монотонности функции.
Решение..
Производная существует во всех точках,
в которых существует и сама функция,
т.е. при x> 0. Точки, в
которых производная обращается в нуль,
задаются равенствамиlnx=0,lnx-1
= 0, откудаx1 =1,x2
= е – критические точки. Знаки
производной указаны на рис. 8.3.
Рис.8.3
Таким образом, функция монотонно
возрастает на промежутках (0;1) и (е;+)
и монотонно убывает на промежутке (1;е).
Точкаx= 1 – точка максимума
и,
точка х = е – точка минимума и.
8.37. Найти экстремумы и интервалы
монотонности функции
Решение..
Производная не существует приcosx=1 т.е. прии равна нулю при
.
Знак производной совпадает со знакомsin(x); таким
образом у’ >0 прииy'<0 при
.
Это, соответственно, интервалы возрастания
и убывания функции.— точки максимума
,
— точки минимума
.
8.38. Найти наибольшее значение
(глобальный максимум) функциина интервале (10;18).
Решение. Найдем.
На интервале (10;18) имеется всего одна
критическая точкаx= 6.
Производная при переходе через эту
точку меняет знак с «+» на «-», т.е.x= 6 – точка максимума. Следовательно,
функция достигает наибольшего значения
приx= 16, т.е..
(Заметим, что наименьшего значения
(глобального минимума) данной функции
на указанном интервале не существует.)
8.40. Забором длиной 24 метра требуется
огородить с трех сторон прямоугольный
палисадник наибольшей площади. Найти
размеры палисадника.
Решение.Пусть длины сторон палисадникаx,y. Тогда
2x+y= 24, т.е.y= 24-2x.
Площадь палисадникаS=xy=x(24-2x)
= 24x-2x2,
где 0<x<12 (ибо 24-2x>0).
Таким образом, задача свелась к отысканию
значенияx, при которомS(x) принимает
наибольшее значение на интервале (0;12).
НайдемS'(x)
= 24-4x= 0 приx= 6. Легко видеть, чтоx= 6
– единственная точка экстремума –
максимума функцииS(x).
Это означает, что на интервале (0;12)S(x)
принимает наибольшее значение приx= 6, т.е. искомые размеры палисадника 6 м
и 24- 2 — 6 = 12 м.
Найти интервалы
монотонности и экстремумы функции:
8.41..8.42.
.8.43.
.
8.44.
.8.45.
8.46.
.
8.47.
.8.48.
.8.49.
.
8.50..8.51.
.8.52.
.
8.53.
.8.54.
.8.55.
.
8.56..8.57.
.8.58.
.
8.59..8.60.
.
Найти наибольшее
и наименьшее значение (глобальный
максимум и минимум) функции
на отрезке [a,b]:
8.61.8.62.
8.63.
8.64.8.65.
8.66.
8.67.8.68.
Найти наибольшее
или наименьшее значение (глобальный
максимум или минимум) функции
на интервале(a,b):
8.69.8.70.
8.71.
8.72.8.73.
8.74.
8.75. Рассматриваются всевозможные
прямоугольные параллелепипеды, основания
которых являются квадратами, а каждая
из боковых сторон имеет периметр, равный
6 см. найти среди них параллелепипед с
наибольшим объемом и найти этот объем.
8.76. Определить размеры открытого
бассейна с квадратным дном, при которых
на облицовку стен и дна пойдет наименьшее
количество материала. Объем бассейнаVфиксирован.
8.77. Требуется огородить два участка:
один в форме правильного треугольника,
другой в форме полукруга. Длина изгороди
фиксирована и равна Р. Определить размеры
участков (сторону треугольника и радиус
полукруга) так, чтобы сумма площадей
этих участков была бы наименьшей.
8.78. В треугольнике с основаниемaи высотойh вписан
прямоугольник, основание которого лежит
на основании треугольника, а две вершины
— на боковых сторонах. Найти наибольшую
площадь вписанного прямоугольника.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Исследование функции на монотонность и экстремумы, выпуклость и точки перегиба
- Производная функции и промежутки монотонности
- Критические точки
- Вторая производная, промежутки выпуклости и точки перегиба
- Примеры
п.1. Производная функции и промежутки монотонности
Рассмотрим кусочно-непрерывную функцию: ( y= begin{cases} x+1, xleq 1\ 2, 1lt xleq 4\ 6-x, xgt 4 end{cases} )
Эта функция интересна тем, что имеет промежуток возрастания при (xleq 1), промежуток постоянства при (1lt xleq 4) и промежуток убывания при (xgt 4).
Посмотрим, как ведет себя производная на каждом из промежутков, используя определение производной (см. §42 данного справочника).
Заметим, что в точках излома x=1 и x=4 функция определена и непрерывна, но её производная не существует.
При (xlt 1): $$ triangle y=(f(x_0+triangle x)-f(x_0)=left((x_0+triangle x)+1right)-(x_0+1)=triangle x $$ Получается, что знаки (triangle y) и (triangle x) всегда совпадают, и их частное (frac{triangle y}{triangle x}=1gt 0) — всегда положительно. Поэтому и производная на промежутке возрастания функции положительна: $$ f'(x_0)=lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{triangle x}{triangle x}=lim_{triangle xrightarrow 0}1=1gt 0 $$ При (1lt xlt 4): $$ triangle y=f(x_0+triangle x)-f(x_0)=2-2=0 $$ Производная на промежутке постоянства равна нулю: $$ f'(x_0)=lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{0}{triangle x}=lim_{triangle xrightarrow 0}0=0 $$ При (xgt 4): $$ triangle y=f(x_0+triangle x)-f(x_0)=left(6-(x_0+triangle x)right)-(6-x_0)=-triangle x $$ Знаки (triangle y) и (triangle x) всегда противоположны, и их частное (frac{triangle y}{triangle x}=-1lt 0) — всегда отрицательны. Поэтому и производная на промежутке убывания функции отрицательна: $$ f'(x_0)=lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{-triangle x}{triangle x}=lim_{triangle xrightarrow 0}(-1)=-1lt 0 $$ Полученные результаты можно обобщить для любой функции, поскольку всегда:
- на промежутках возрастания (frac{triangle y}{triangle x}gt 0) и (f'(x)gt 0,)
- на промежутках постоянства (frac{triangle y}{triangle x}=0) и (f'(x)=0,)
- на промежутках убывания (frac{triangle y}{triangle x}lt 0) и (f'(x)lt 0,)
Верно и обратное утверждение:
Если в каждой точке некоторого промежутка производная функции (y=f(x)):
- положительна, то функция на этом промежутке возрастает;
- равна нулю, то функция на этом промежутке постоянна;
- отрицательна, то функция на этом промежутке убывает.
begin{gather*} f'(x)gt 0Leftrightarrow y=f(x) uparrow\ f'(x)=0Leftrightarrow y=f(x)=const\ f'(x)lt 0Leftrightarrow y=f(x)downarrow end{gather*}
п.2. Критические точки
Внутренние точки области определения функции, в которых производная равна нулю или не существует, называют критическими точками.
Например:
Найдем критические точки функции (y=frac{x^2-10x+16}{x^2})
Точка (x=0notin D) не входит в ОДЗ функции, следовательно, производная в ней не существует и (x=0) – критическая точка.
Найдем точки, в которых производная равна 0.
Преобразуем выражение: (frac{x^2-10x+16}{x^2}=1-frac{10}{x}+frac{16}{x^2}) begin{gather*} y’=left(1-frac{10}{x}+frac{16}{x^2}right)=0+frac{10}{x^2}-frac{16cdot 2}{x^3}=frac{10x-32}{x^3}=frac{10(x-3,2)}{x^3}\ y’=0 text{при} x=3,2 end{gather*} Ответ: x=0 и x=3,2
Напомним, что:
Окрестностью точки (x_0) называется любой сколь угодно малый промежуток, для которого (x_0) является внутренней точкой.
Точка (x_0)является точкой минимума функции (y=f(x)), если для всех (x(xne x_0)) из некоторой окрестности точки (x_0) выполняется неравенство (f(x_0)lt f(x)).
Точка (x_0) является точкой максимума функции (y=f(x)), если для всех (x(xne x_0)) из некоторой окрестности точки (x_0) выполняется неравенство (f(x_0 )gt f(x)).
Все точки минимума и максимума функции (y=f(x)) образуют множество точек экстремума данной функции.
Необходимое условие существования экстремума
Точками экстремума функции могут быть только её критические точки.
Т.е. все критические точки объявляются подозрительными на экстремум.
Достаточное условие существования экстремума
Точка (x_0) принадлежит промежутку непрерывности функции (y=f(x)) и при подходе к точке (x_0) слева и справа производные имеют разные знаки.
Т.е., для всех точек, подозрительных на экстремум, которые лежат в промежутках непрерывности функции и для которых производные слева и справа имеют разные знаки, «подозрение подтверждается» — и такие точки признаются экстремумами.
Например:
Исследуем промежутки монотонности и найдем экстремумы функции (y=frac{x^2-10x+16}{x^2}).
Выше мы уже нашли критические точки: (x=0) и (x=3,2).
Производная: (y’=frac{10(x-3,2}{x^3})
Определить знак производной на промежутке просто: нужно взять любое значение x из промежутка и подставить в производную. При этом не нужно точно считать, сколько получается; главное – понять, какой знак у каждой скобки/множителя.
Составим таблицу:
| (x) | ((-infty;0)) | 0 | (0;3,2) | 3,2 | ((3,2;+infty)) |
| (f'(x)) | >0 | не существует | <0 | 0 | >0 |
| (f(x)) | (nearrow) | не существует | (searrow) | min | (nearrow) |
Вывод:
Функция возрастает при (xin(-infty;0)cup(3,2;+infty))
Функция убывает при (xin(0;3,2))
Точка минимума (x=3,2; y_{min}=f(3,2)=-frac{9}{16})
п.3. Вторая производная, промежутки выпуклости и точки перегиба
Пусть функция (y=f(x)) является дифференцируемой на промежутке (xin(a;b)), и её производная (f'(x)) также является дифференцируемой на этом же промежутке.
Тогда существует производная от производной: (left(f'(x)right)’=f»(x)), которую называют второй производной или производной второго порядка от функции (y=f(x)).
Например:
1) Найдем вторую производную для (y=3x^4+2x^3+4x)
(f'(x)=3cdot 4x+2cdot 3x^2+4cdot 1=12x^3+6x^2+4)
(f»(x)=12cdot 3x^2+6cdot 2x+0=36x^2+12x)
2) Найдем вторую производную для (y=frac{x^2-10x+16}{x^2}).
Первую мы уже нашли выше: (f'(x)=frac{10(x-3,2)}{x^3}=frac{10}{x^2}-frac{32}{x^3})
Получаем: (f»(x)=left(frac{10}{32}-frac{32}{x^3}right)’=-frac{10cdot 2}{x^3}+frac{32cdot 3}{x^4}=frac{-20x+96}{x^4}=-frac{20(x-4,8)}{x^4})
Кривая (y=f(x)) называется выпуклой вверх на интервале ((a;b)), если все точки, кроме точки касания (x_0), лежат под касательной, проведенной через любую точку (x_0in(a;b)).
Кривая (y=f(x)) называется выпуклой вниз на интервале ((a;b)), если все точки, кроме точки касания (x_0), лежат над касательной, проведенной через любую точку (x_0in(a;b)).
Точка кривой (y=f(x)), в которой меняется характер выпуклости, называется точкой перегиба.
Например:
 |
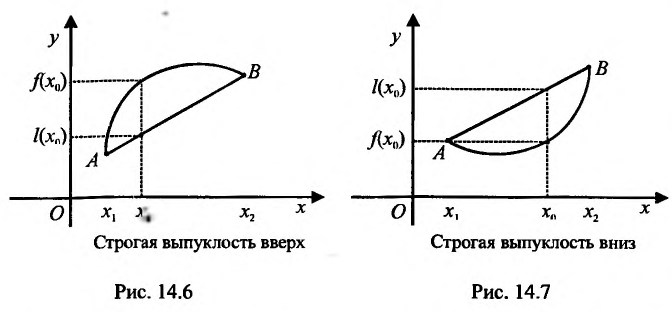
Точка A принадлежит промежутку, выпуклому вверх, т.к. все точки этого промежутка лежат под касательной, проведенной через A.
Точка B принадлежит промежутку, выпуклому вниз, т.к. все точки этого промежутка лежат над касательной, проведенной через B. Точка C — точка перегиба. |
- положительна, то функция на этом промежутке выпуклая вниз;
- равна нулю, то функция на этом промежутке постоянна;
- отрицательна, то функция на этом промежутке выпуклая вверх.
begin{gather*} f»(x)gt 0 forall xin(a;b)Leftrightarrow y=f(x)cup\ f»(x)=0 forall xin(a;b)Leftrightarrow y=f(x)=const\ f»(x)lt 0 forall xin(a;b)Leftrightarrow y=f(x)cap end{gather*}
Внутренние точки области определения функции, в которых вторая производная равна нулю или не существует, называют критическими точками второго порядка.
Необходимое условие существования точки перегиба
Точками перегиба функции могут быть только её критические точки второго порядка.
Т.е. все критические точки второго порядка объявляются подозрительными на перегиб.
Достаточное условие существования точки перегиба
Точка (x_0) принадлежит промежутку непрерывности первой производной (f'(x)) и при подходе к точке (x_0) слева и справа вторые производные имеют разные знаки.
Т.е., для всех точек, подозрительных на перегиб, которые лежат в промежутках непрерывности первой производной и для которых вторые производные слева и справа имеют разные знаки, «подозрение подтверждается» — и такие точки признаются точками перегиба.
Например:
Продолжим исследование функции (y=frac{x^2-10x+16}{x^2}) и найдем промежутки выпуклости и точки перегиба.
Вторая производная: (f»(x)=frac{-20(x-4,8)}{x^4})
Критические точки второго порядка: (x=0) и (x=4,8).
Составим таблицу:
| (x) | ((-infty;0)) | 0 | (0;4,8) | 4,8 | ((4,8;+infty)) |
| (f»(x)) | >0 | не существует | >0 | 0 | <0 |
| (f(x)) | (cup) | не существует | (cup) | перегиб | (cap) |
Вывод:
Функция выпуклая вниз при (xin(-infty;0)cup(0;4,8))
Функция выпуклая вверх при (xin(4,8;+infty))
Точка перегиба (x=4,8; f(4,8)=frac{7}{18})
п.4. Примеры
Пример 1. Найдите промежутки монотонности и точки экстремума функции:
a) ( y=2x^3-6x^2-18x+7 )
ОДЗ: (xinmathbb{R})
Первая производная: begin{gather*} f'(x)=2cdot 3x^2-6cdot 2x-18cdot 1+0=6x^2-12x-18=6(x^2-2x-3)=\ =6(x-3)(x+1)\ f'(x)=0 text{при} left[ begin{array}{l} x=3\ x=-1 end{array} right. end{gather*} Критические точки: (x=-1) и (x=3)
Составляем таблицу:
| (x) | ((-infty;-1)) | -1 | (-1;3) | 3 | ((3;+infty)) |
| (f'(x)) | >0 | 0 | <0 | 0 | >0 |
| (f(x)) | (nearrow) | max | (searrow) | min | (nearrow) |
Вывод:
Функция возрастает при (xin(-infty;-1)cup(3;+infty))
Функция убывает при (xin(-1;3))
Точка максимума (x=-1; y_{max}=f(-1)=-2-6+18+7=17)
Точка минимума (x=3; y_{min}=f(3)=54-54-54+7=-47)
б) ( y=frac{x^2}{x^2-9} )
ОДЗ: (x^2-9=ne 0Rightarrow xnepm 3)
Первая производная: begin{gather*} f'(x)=frac{2x(x^2-9)-x^2cdot 2x}{(x^2-9)^2}=frac{2x(x^2-9-x^2)}{(x^2-9)^2}=-frac{18x}{(x^2-9)^2} end{gather*} Критические точки: (x=left{0;pm 3right})
Составляем таблицу:
| (x) | ((-infty;-3)) | -3 | (-3;0) | 0 | ((0;3)) | 3 | ((3+infty)) |
| (f'(x)) | >0 | не существует | >0 | 0 | <0 | не существует | <0 |
| (f(x)) | (nearrow) | не существует | (nearrow) | max | (searrow) | не существует | (searrow) |
Вывод:
Функция возрастает при (xin(-infty;-3)cup(-3;0))
Функция убывает при (xin(0;3)cup(3;+infty))
Точка максимума (x=0; y_{max}=f(0)=0)
в) ( y=frac3x+frac x3 )
ОДЗ: (xne 0)
Первая производная: begin{gather*} f'(x)=-frac{3}{x^2}+frac13=frac{x^2-9}{3x^2}=frac{(x+3)(x-3)}{3x^2}\ f'(x)=0 text{при} x=pm 3 end{gather*} Критические точки: (x=left{0;pm 3right})
Составляем таблицу:
| (x) | ((-infty;-3)) | -3 | (-3;0) | 0 | ((0;3)) | 3 | ((3+infty)) |
| (f'(x)) | >0 | 0 | <0 | (varnothing) | <0 | 0 | >0 |
| (f(x)) | (nearrow) | max | (searrow) | (varnothing) | (searrow) | min | (nearrow) |
Вывод:
Функция возрастает при (xin(-infty;-3)cup(-3;+infty))
Функция убывает при (xin(-3;0)cup(0;3))
Точка максимума (x=-3; y_{max}=f(-3)=-1-1=-2)
Точка минимума (x=3; y_{min}=f(3)=1+1=2)
г*) ( y=frac{x^2}{8}-ln(x^2-8) )
ОДЗ: (x^2-8gt 0Rightarrow x^2gt 8Rightarrow |x|gt sqrt{8}Rightarrow xlt -2sqrt{2}cup xgt 2sqrt{2})
Критические точки на границе ОДЗ: (x=pm 2sqrt{2})
Первая производная: begin{gather*} f'(x)=frac{2x}{8}-frac{2x}{x^2-8}=2xleft(frac18-frac{1}{x^2-8}right)=frac{2x(x^2-8-8)}{8(x^2-8)}=frac{x(x^2-16)}{4(x^2-8)}=\ =frac{x(x+4)(x-4)}{4(x+2sqrt{2})(x-2sqrt{2})}\ f'(x)=0 text{при} x=left{0;pm 4right} end{gather*} (x=0notin D) – не входит в ОДЗ.
Критические точки: (x=left{pm2sqrt{2};pm 4right})
Составляем таблицу:
| (x) | ((-infty;-4)) | -4 | ((-4;-2sqrt{2})) | (-2sqrt{2}) | ((-2sqrt{2};2sqrt{2})) | (2sqrt{2}) | ((2sqrt{2};4)) | 4 | ((4;+infty)) |
| (f'(x)) | <0 | 0 | >0 | (varnothing) | (varnothing) | (varnothing) | <0 | 0 | >0 |
| (f(x)) | (searrow) | min | (nearrow) | (varnothing) | (varnothing) | (varnothing) | (searrow) | min | (nearrow) |
Вывод:
Функция возрастает при (xin(-4;-2sqrt{2})cup(4;+infty))
Функция убывает при (xin(-infty;-4)cup(2sqrt{2};4))
Точка минимума $$ x=pm 4; y_{min}=f(pm 4)=frac{16}{8}-ln(16-8)=2-ln 8=2-ln 2^3=2-3ln 2 $$
Пример 2. Найдите промежутки выпуклости и точки перегиба функции:
a) ( y=2x^3-6x^2-18x+7 )
Первая производная: begin{gather*} f'(x)=2cdot 3x^2-6cdot 2x-18cdot 1+0=6x^2-12x-18 end{gather*} Вторая производная: begin{gather*} f»(x)=6cdot 2x-12cdot 1-0=12x-12=12(x-1)\ f»(x)=0 text{при} x=1 end{gather*} Критическая точка 2-го порядка: (x=1)
Составляем таблицу:
| (x) | ((-infty;1)) | 1 | ((1;+infty)) |
| (f»(x)) | <0 | 0 | >0 |
| (f(x)) | (cap) | перегиб | (cup) |
Вывод:
Функция выпуклая вверх при (xin(-infty;1))
Функция выпуклая вниз при (xin(1;+infty))
Точка перегиба (x=1; f(1)=2-6-18+7=-15)
б) ( y=frac{x^2}{x^2-9} )
ОДЗ: (x^2-9ne 0Rightarrow xne pm 3)
Первая производная: begin{gather*} f'(x)=frac{2x(x^2-9)-x^2cdot 2x}{(x^2-9)^2}=frac{2x(x^2-9-x^2)}{(x^2-9)^2}=-frac{18x}{(x^2-9)^2} end{gather*} Вторая производная: begin{gather*} f»(x)=-18left(frac{1cdot (x^2-9)^2-xcdot 2(x^2-9)cdot 2x}{(x^2-9)^4}right)=-18left(frac{(x^2-9)-4x^2}{(x^2-9)^3}right)=\ =-28left(frac{-3x^2-9}{(x^2-9)^3}right)=frac{54(x^2+3)}{(x^2-9)^3} end{gather*} ( f»(x)=0 text{при} x=invarnothing) — таких x нет.
Критические точки 2-го порядка: (x=left{pm 3right})
Составляем таблицу:
| (x) | ((-infty;-3)) | -3 | ((-3;3)) | 3 | ((3;+infty)) |
| (f»(x)) | >0 | не существует | <0 | не существует | >0 |
| (f(x)) | (cup) | не существует | (cap) | не существует | (cup) |
Вывод:
Функция выпуклая вверх при (xin(-3;3))
Функция выпуклая вниз при (xin(-infty;-3)cup(3;+infty))
Точек перегиба нет.
в) ( y=frac3x+frac x3 )
ОДЗ: (xne 0)
Первая производная: begin{gather*} f'(x)= -frac{3}{x^2}+frac13=frac{x^2-9}{3x^2} end{gather*} Вторая производная: begin{gather*} f»(x)=frac13left(1-frac{9}{x^2}right)’=frac13left(0+frac{9cdot 2}{x^3}right)=frac{6}{x^3} end{gather*} Вторая производная нулей не имеет.
Критическая точка 2-го порядка: (x=0)
Составляем таблицу:
| (x) | ((-infty;0)) | 0 | ((0;+infty)) |
| (f»(x)) | <0 | (varnothing) | >0 |
| (f(x)) | (cap) | (varnothing) | (cup) |
Вывод:
Функция выпуклая вверх при (xin(-infty;0))
Функция выпуклая вниз при (xin(0;+infty))
Точек перегиба нет.
г*) ( y=frac{x^2}{8}-ln(x^2-8) )
ОДЗ: (x^2-8gt 0Rightarrow x^2gt 8Rightarrow |x|gt sqrt{8}Rightarrow xlt -2sqrt{2}cup xgt 2sqrt{2})
Критические точки на границе ОДЗ: (x=pm 2sqrt{2})
Первая производная: begin{gather*} f'(x)=frac{2x}{8}-frac{2x}{x^2-8}=2xleft(frac18-frac{1}{x^2-8}right)=frac{2x(x^2-8-8)}{8(x^2-8)}=frac{x(x^2-16)}{4(x^2-8)} end{gather*} Вторая производная: begin{gather*} f»(x)=frac14left(frac{x^3-16x}{x^2-8}right)’=frac14cdotfrac{(3x^2-16)(x^2-8)-(x^3-16x)cdot 2x}{(x^2-8)^2}=\ =frac14cdotfrac{3x^4-40x^2+128-2x^4+32x^2}{(x^2-8)^2}=frac14cdotfrac{x^4-8x^2+128}{(x^2-8)^2} end{gather*} Для биквадратного уравнения (x^4-8x^2+128=0) дискриминант (D=64-4cdot 128lt 0)
Значит, (x^4-8x^2+128gt 0) на всей ОДЗ. Нулей у второй производной нет.
Критические точки 2-го порядка: (x=left{pm 2sqrt{2}right})
Составляем таблицу:
| (x) | ((-infty;-2sqrt{2})) | (-2sqrt{2} ) | ((-2sqrt{2};2sqrt{2})) | (2sqrt{2}) | ((2sqrt{2};+infty)) |
| (f»(x)) | >0 | (varnothing) | (varnothing) | (varnothing) | >0 |
| (f(x)) | (cup) | (varnothing) | (varnothing) | (varnothing) | (cup) |
Вывод:
Функция выпуклая вниз при (xin(-infty;-2sqrt{2})cup(2sqrt{2};+infty)) (на всей ОДЗ)
Точек перегиба нет.
Пример 3*. Найдите наименьшее значение функции:
begin{gather*} y=3^x+2cdot 3^{3-x}-xln 27-9 end{gather*} ОДЗ: (xinmathbb{R})
Первая производная: begin{gather*} f'(x)=3^xln 3+2cdot 3^{3-x}cdot (3-x)’cdot ln 3-1cdotln 27-0=\ =3^xln 3-2cdot 3^{3-x}ln 3-ln 3^3=3^xln 3-2cdot 3^3cdot 3^{-x}ln 3-3ln 3=\ =ln 3cdot (3^x-54cdot 3^{-x}-3) end{gather*} Найдём нули первой производной: begin{gather*} ln 3cdot (3^x-54cdot 3^{-x}-3)=0 |:ln 3\ 3^x-54cdot 3^{-x}-3=0 end{gather*} Замена: (t=3^xgt 0) begin{gather*} t-frac{54}{t}-3=0Rightarrow frac{t^2-3t-54}{t}=0Rightarrow begin{cases} t^2-3t-54=0\ tne 0 end{cases} \ (t+6)(t-9)=0Rightarrow left[ begin{array}{l} t=-6lt 0 — text{не подходит}\ t=9 end{array} right. end{gather*} Возвращаемся к исходной переменной: (3^x=9Rightarrow x=2) $$ f'(x)=0 text{при} x=2 $$ Критическая точка (x=2)
Для определения знаков в промежутке ((-infty;2)) можно взять (x=1) и тогда:
$$ f'(1)=ln 3cdot (3^1-54cdot 3^{-1}-3)=ln 3cdot (3-18-3)lt 0 $$ В промежутке ((2;+infty)) можно взять 3 и тогда: $$ f'(3)=ln 3cdot (3^3-54cdot 3^{-3}-3)=ln 3cdot (27-2-3)gt 0 $$ Получаем:
| (x) | ((-infty;2)) | 2 | ((2;+infty)) |
| (f'(x)) | <0 | 0 | >0 |
| (f(x)) | (searrow) | min | (nearrow) |
(x=2) точка минимума.
Значение функции в этой точке: begin{gather*} y_{min}=f(2)=3^2+2cdot 3^{3-2}-2ln 27-9=9+6-2ln 3^3-9=\ =6-6ln 3=6(1-ln 3) end{gather*} Ответ: (y_{min}=6(1-ln 3)) при (x=2)
Пример 4*. Найдите наибольшее значение функции begin{gather*} f(x)=x^4-6bx^2+b^2 end{gather*} на отрезке [-2;1] в зависимости от параметра b.
Первая производная: begin{gather*} f'(x)=4x^3-12bx=4x(x^2-3b)\ f'(x)=0 text{при} x=0 text{и} x=pmsqrt{3b} end{gather*}
Критическая точка (x=0) будет при любом b. При (bgt 0, x=0) будет максимумом, при (bleq 0) – минимумом.
Пара критических точек (x=pmsqrt{3b}) появляется только при условии (bgt 0), и это две точки минимума. Т.к. по условию мы ищем точку максимума (наибольшее значение функции), эти точки нам не интересны.
Поэтому рассмотрим значения на концах отрезка и в нуле в общем случае: begin{gather*} f(-2)=(-2)^4-6bcdot(-2)^2+b^2=b^2-24b+16\ f(0)=b^2\ f(1)=1-6b+b^2 end{gather*} Сравниваем попарно значения функций: begin{gather*} f(1)-f(0)=1-6b+b^2-b^2=1-6b\ f(1)gt f(0) text{при} bltfrac16\ f(1)lt f(0) text{при} bgtfrac16\ \ f(-2)-f(0)=b^2-24b+16-b^2=16-24b=8(2-3b)\ f(-2)gt f(0) text{при} bltfrac23\ f(-2)lt f(0) text{при} bgtfrac23\ \ f(-2)-f(1)=b^2-24b+16-(1-6b+b^2)=-18b+15=3(5-6b)\ f(-2)gt f(1) text{при} bltfrac56\ f(-2)lt f(1) text{при} bgtfrac56\ end{gather*} Получаем таблицу:
| b | Соотношение значений функции |
| (left(-infty;frac16right)) | (f(-2)gt f(1)gt f(0)) |
| (frac16) | (f(-2)gt f(1)=f(0)) |
| (left(frac16;frac23right)) | (f(-2)gt f(0)gt f(1)) |
| (frac23) | (f(-2)=f(0)gt f(1)) |
| (left(frac23;frac56right)) | (f(0)gt f(-2)gt f(1)) |
| (frac56) | (f(0)gt f(-2)=f(1)) |
| (left(frac56;+inftyright)) | (f(0)gt f(1)gt f(2)) |
Получаем, что при (bltfrac23) максимальное значение на отрезке имеет $$ f(-2)=b^2-24b+16 $$ При (bgeq frac23) максимальное значение будет для (f(0)=b^2)
Ответ:
При (bltfrac23, max_{[-2;1]}f(x)=f(-2)=b^2-24b+16)
При (bgeqfrac23, max_{[-2;1]}f(x)=f(0)=b^2)
Алгебра и начала математического анализа, 11 класс
Урок № 16. Экстремумы функции.
Перечень вопросов, рассматриваемых в теме
1) Определение точек максимума и минимума функции
2) Определение точки экстремума функции
3) Условия достаточные для нахождения точек экстремума функции
Глоссарий по теме
Возрастание функции. Функция y=f(x) возрастает на интервале X, если для любых х1 и х2, 

Максимум функции. Значение функции в точке максимума называют максимумом функции
Минимум функции. Значение функции в точке минимума называют минимумом функции
Производная (функции в точке) — основное понятие дифференциального исчисления, которое характеризует скорость изменения функции (в конкретной точке).
Точка максимума функции. Точку х0 называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство 
Точка минимума функции. Точку х0 называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство 
Точки экстремума функции. Точки минимума и максимума называют точками экстремума.
Убывание функции. Функция y = f(x) убывает на интервале X, если для любых х1 и х2, 

Алгоритм исследования функции на монотонность и экстремумы:
1) Найти область определения функции D(f)
2) Найти f’ (x).
3) Найти стационарные (f'(x) = 0) и критические (f'(x) не
существует) точки функции y = f(x).
4) Отметить стационарные и критические точки на числовой
прямой и определить знаки производной на получившихся
промежутках.
5) Сделать выводы о монотонности функции и точках ее
экстремума.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Точки, в которых происходит изменение характера монотонности функции – это ТОЧКИ ЭКСТРЕМУМА.
- Точку х = х0 называют точкой минимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) ≥ f(x0).
- Точку х = х0 называют точкой максимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) ≤ f(x0).
Точки максимума и минимума – точки экстремума.
Функция может иметь неограниченное количество экстремумов.
Критическая точка – это точка, производная в которой равна 0 или не существует.
Важно помнить, что любая точка экстремума является критической точкой, но не всякая критическая является экстремальной.
Алгоритм нахождения максимума/минимума функции на отрезке:
- найти экстремальные точки функции, принадлежащие отрезку,
- найти значение функции в экстремальных точках из пункта 1 и в концах отрезка,
- выбрать из полученных значений максимальное и минимальное.
Примеры и разбор решения заданий тренировочного модуля
№1. Определите промежуток монотонности функции у=х2 -8х +5
Решение: Найдем производную заданной функции: у’=2x-8
2x-8=0
х=4
Определяем знак производной функции и изобразим на рисунке, следовательно, функция возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)
Ответ: возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)
№2. Найдите точку минимума функции у= 2х-ln(х+3)+9
Решение: Найдем производную заданной функции:
Найдем нули производной:
х=-2,5
Определим знаки производной функции и изобразим на рисунке поведение функции:
Ответ: -2,5 точка min
№3. Материальная точка движется прямолинейно по закону x(t) = 10t2 − 48t + 15, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3с.
Решение: Если нас интересует движение автомобиля, то, принимая в качестве функции зависимость пройденного расстояния от времени, с помощью производной мы получим зависимость скорости от времени.
V=х'(t)= 20t – 48. Подставляем вместо t 3c и получаем ответ. V=12 мc
Ответ: V=12 мc
№4. На рисунке изображен график функции. На оси абсцисс отмечены семь точек: x1, x2, x3, x4, x5, x6, x7. Определите количество целых точек, в которых производная функции отрицательна.
Решение: Производная функции отрицательна на тех интервалах, на которых функция убывает. В данном случае это точки х3,х5,х7. Следовательно, таких точек 3
Ответ: 3
Содержание:
Критерий монотонности функции:
Прежде всего, сформулируем определение монотонной функции:
- Функция f называется неубывающей (невозрастающей) на интервале (а,b), если для любых двух точек
- Функция f называется возрастающей (убывающей) на интервале (а,b), если для любых двух точек
из интервала (а, b), удовлетворяющих условию
справедливо неравенство
Неубывающие и невозрастающие функции называют монотонными функциями.
Монотонные функции
Возрастающие и убывающие функции называются строго монотонными функциями.
Например, функция у = х- возрастающая (строго монотонная) на всей числовой оси; функция 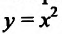
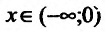
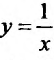
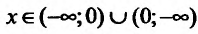
Теорема 14.1.1. (Критерий монотонности) Пусть функция 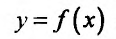
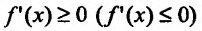
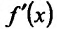
Доказательство: Пусть 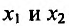
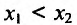
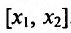
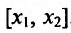
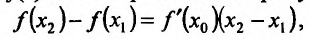
где 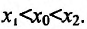
Необходимость. Пусть функция f дифференцируема на интервале (а, b) и не убывает (не возрастает) на этом интервале. Требуется доказать, что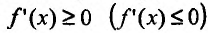
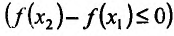
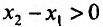
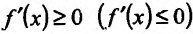
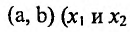
Достаточность. Пусть теперь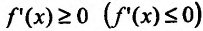
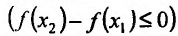
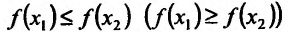
Поскольку 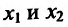
Аналогично теорема доказывается и для возрастающей (убывающей) функции.
Из доказанной теоремы следует, что для определения интервалов монотонности функции нужно:
- Найти область определения функции.
- Вычислить ее производную.
- Приравнять производную к нулю; полученные нули производной разобьют область определения на интервалы, в которых производная сохраняет знак.
- Определить знак производной в каждом интервале при помощи «пробной» точки и сделать вывод.
Пример:
Найти интервалы монотонности функции
Решение:
Область определения заданной функции — вся числовая ось 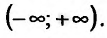
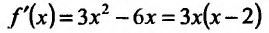
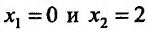
Составим схему изменения знаков производной:
Согласно теореме’ 14.1.1, данная функция возрастает при 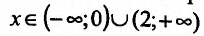
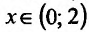
Функция 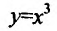
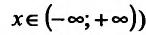
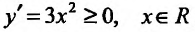
Функция 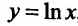
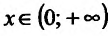
Экстремумы функций
Определение 14.2.1. Пусть функция f определена в некоторой окрестности точки 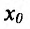
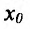
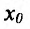
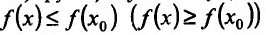
Если выполняются строгие неравенства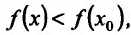
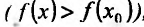
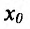
Точки максимума и минимума (строгого максимума и минимума) называются точками экстремума (строгого экстремума).
Теорема 14.2.1 .(необходимое условие экстремума) Если точка 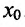
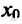
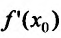
Справедливость этой теоремы следует из теоремы Ферма в силу определения точек экстремума. Действительно, если 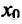
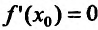
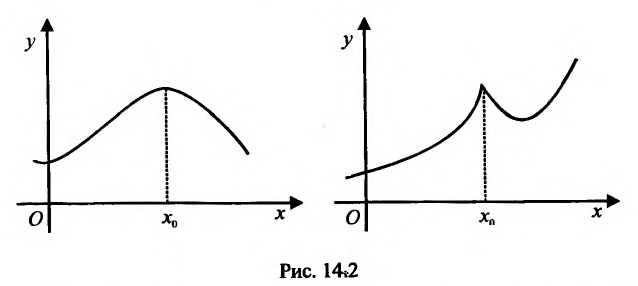
Функция может достигать экстремума также в точке, в которой производная не существует. Например, функция 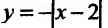
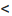
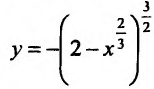
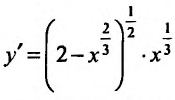
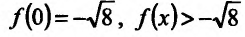
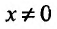
Из приведенных рассуждений следует, что точки экстремума функции нужно искать среди тех точек её области определения, где производная функции равна нулю или не существует.
Если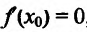
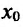
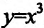
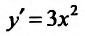
Точки области определения функции, в которых производная равна нулю, называются стационарными, а в которых производная не существует, называются критическими.
Каждая стационарная (критическая) точка — это точка возможного экстремума. Однако сделать заключение о том, что в данной стационарной (критической) точке на самом деле экстремум, можно лишь на основании дополнительного исследования, т.е. на основании достаточных условий экстремума.
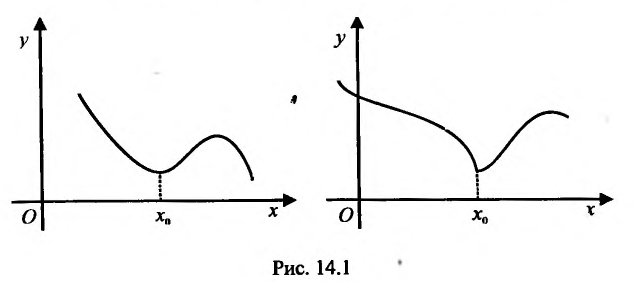
Теорема 14.2.2. (первое достаточное условие экстремума) Пусть функция f определена, дифференцируема в некоторой окрестности точки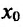
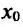
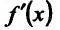
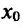
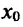
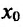
- если
на
и
на
, то точка
— точка максимума функции f(x);
- если
на
и
на
, то точка
— точка минимума функции f(x);
Если же в пределах указанной окрестности точки 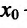
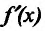
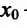
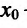
Доказательство. Докажем первое утверждение теоремы.
Предположим, что 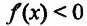
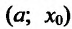
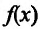
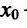
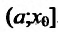
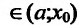
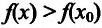
Пусть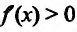
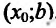
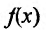
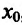
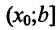
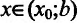
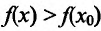
В результате получается, что при любом 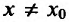
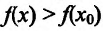
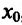
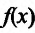
Второе утверждение теоремы доказывается аналогично.
Пример:
Найти точки экстремума функции’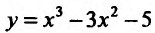
Решение:
Поскольку 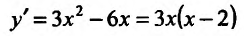
Производная функции 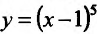
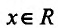
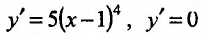
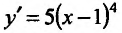
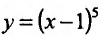
Теорема 14.2.3. (второе достаточное условие экстремума) Если функция f определена в некоторой окрестности точки 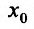
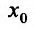

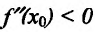
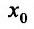
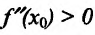
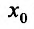
Доказательство: Поскольку функция f дважды дифференцируема в точке 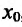
в виде:
где точка с расположена между 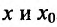
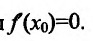
или
Поскольку 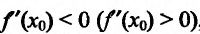
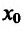
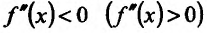
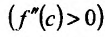
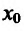
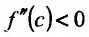
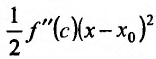
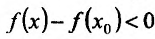
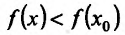
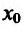
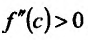
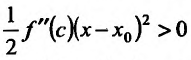
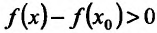
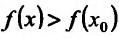
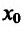
Пример:
Найти точки экстремума функции 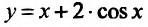
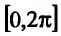
Решение:
Вычислим первую и вторую производные заданной функции: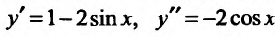
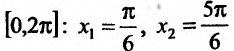
Теперь находим знак второй производной в каждой стационарной точке и определяем ее характер, используя теорему 14.2.3. Поскольку
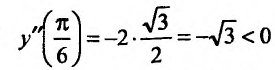
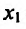
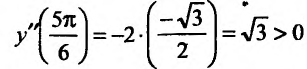
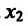
Теорема 14.2.4. (третье достаточное условие экстремума). Пусть функция f определена в некоторой окрестности точки 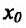
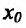
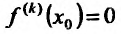
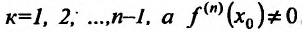
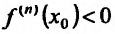
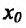
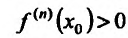
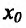
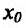
Пример:
Исследовать на экстремум функцию 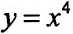
Решение:
Функция определена, непрерывна и дифференцируема на всей числовой оси. Найдем первую производную- 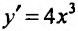
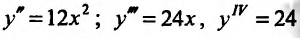
Сформулированные теоремы позволяют решать определенный круг задач. Например, требуется определить наибольшее (найме шее) значение функции f на отрезке [а, b]. Для этого следует на ней все точки, в которых производная функции либо равна нулю, ли’ не существует. Затем из этих точек выбираем те, которые принадлежат отрезку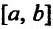
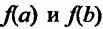
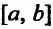
Пример:
Найти наибольшее и наименьшее значениях функции 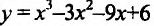
Решение:
Вычислив производную и приравняв ее к ну: 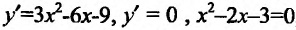
Отрезку [-2;2] принадлежит только одна точка 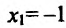
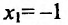
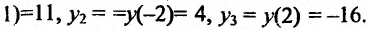
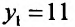
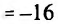
Выпуклость и точки перегиба
Пусть функция f определена на интервале (а; b) и пусть точки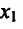
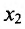
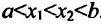
Разрешим это уравнение относительно у:
ИЛИ
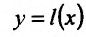
Ясно, что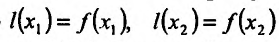
Определение 14.3.1. Функция f называется выпуклой вверх (выпуклой вниз) на интервале 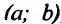
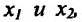
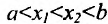
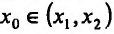
соответственно. А сам интервал называется интервалом выпуклости вверх (выпуклости вниз).
Геометрически это означает, что любая точка хорды АВ (т.е. отрезка прямой у=1(х) с концами в точках А и В) лежит не выше (не ниже) точки графика функции , соответствующей тому же значению аргумента.
Если неравенства (14.3.1) и (14.3.2) строгие, то функция f называется строго выпуклой вверх (рис. 14.6) (строго выпуклой вниз (рис. 14.7)). В этом случае любая точка хорды АВ, исключая ее концы, лежит ниже (выше) соответствующей точки графика функции
Теорема 14.3.1. (достаточное условие строгой выпуклости) Если функция f определена и дважды дифференцируема на интервале (а,b), то 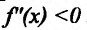
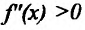
Доказательство. Пусть функция f определена и дважды непрерывно дифференцируема на интервале (а, b). Возьмем некоторые точки 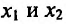
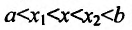
Применяя теорему Лагранжа к каждой разности, т.е. к 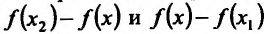
где
Снова применим теорему Лагранжа к разности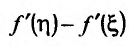
Отсюда видно, что если 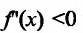
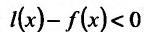
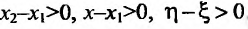
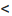

Заметим, что условие знакопостоянства второй производной не является необходимым условием. Так, функция 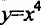
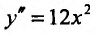
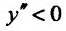
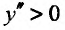
Определение 14.3.2. Пусть фунщия f определена в некоторой окрестности точки 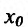
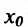
Теорема 14.3.2. (необходимое условие точки перегиба) Если функция f определена и дважды непрерывно дифференцируема на (а,b) и 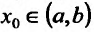
Доказательство. Пусть задана функция f, которая определена и дважды’ непрерывно дифференцируема на (а.b) и пусть точка 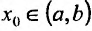
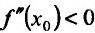
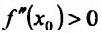

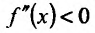
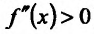
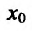
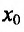
Из теоремы вытекает, что точками перегиба дважды дифференцируемой функции могут быть лишь точки, в которых вторая производная обращается в нуль либо не существует.
Сформулируем и докажем теперь достаточные условия точки перегиба.
Теорема 14.3.3. Если функция f определена и дважды дифференцируема на интервале (а,b), кроме, быть может точки 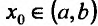
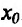
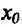
Действительно, в силу теоремы 14.3.1 точка 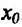
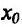
Теорема 14.3.4. Если f трижды непрерывно дифференцируема на (а,b) и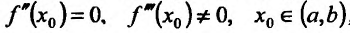
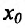
Доказательство (проведем для случая f»(x0) > 0). Так как по предположению 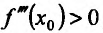
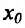
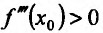
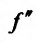
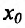
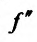
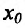
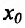
Теорема 14.3.5. Пусть функция f непрерывно дифференцируема n раз на (а,b), причем
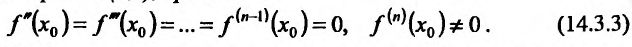
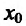
Итак, из изложенного материала вытекает, что выпуклость вверх или вниз графика функции f зависит от знака ее второй производной. Оказывается, что и расположение графика функции относительно касательной также связано со знаком второй производной, т.е. если функция f имеет вторую производную, все значения которой имеют один и тот же знак, то все точки графика функции f лежат над (под) касательной.
Рассмотрим пример, иллюстрирующий исследование графика функции на выпуклость и точки перегиба.
Пример 14.3.1. Найти интервалы выпуклости и точки перегиба графика функции
Решение. Функция определена для всех 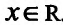
Приравняв вторую производную к нулю 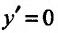
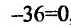
Составляет схему изменения знаков второй производной:
Следовательно, у»>0 на интервалах 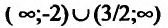
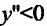
Рассмотрим пример из микроэкономики:
В количественной теории полезности предполагается, что потребитель может дать количественную оценку (в некоторых единицах измерения) полезности любого количества потребляемого им товара.
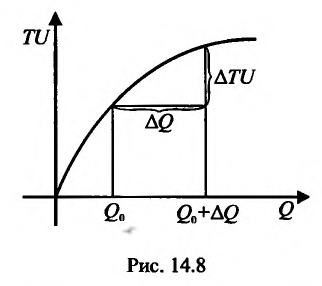
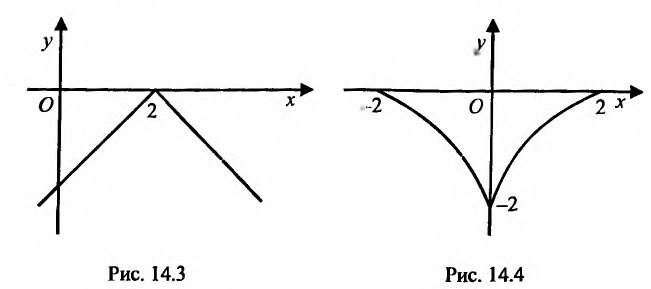
Это означает существование функции полезности TU аргумента Q -количества купленного товара. Введём понятие предельной полезности, как добавочной полезности, прибавляемой каждой последней порцией товара. Построим прямоугольную систему координат и отложим по горизонтальной оси Ох количество потребляемого товара Q, а по вертикальной оси Оу — общую полезность TU (см. рис. 14.3). Рассмотрим график функции TU = TU(Q). Точка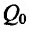
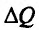
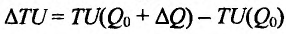
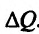
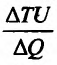
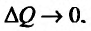
Но предел отношения приращения функции к приращению аргумента, если приращение аргумента стремится к нулю, равен производной функции.
Следовательно, предельная полезность равна производной функции полезности TU=TU(Q). Закон убывающей предельной полезности сводится к уменьшению этой производной с ростом величины Q. Отсюда следует выпуклость графика функции
Асимптоты графика функции
Рассмотрим функцию f определенную на интервале (а;b), . Если 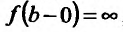
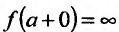
Заметим, что вертикальными асимптотами являются, как правило, нули знаменателей дробно-рациональных функций.
Если функция f определена на и для постоянных 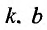
то прямая у = kх + b- называется наклонной асимптотой вправо графика функции f Если соотношение (14.4.1) выполняется и при , то прямая 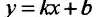
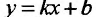
И наоборот, если пределы (14.4.2) и (14.4.3) существуют и конечны, то прямая у = kх + b- наклонная вправо (влево) асимптота графика функции f
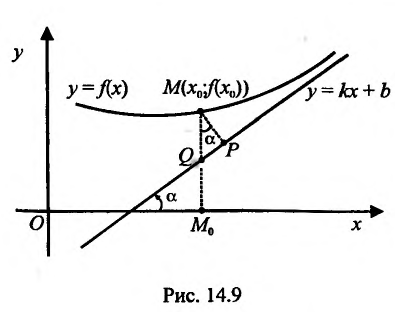
Рассмотрим геометрический смысл асимптоты. Пусть 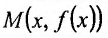
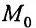
На рис. 14.9 видно, что отрезок 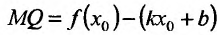
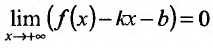
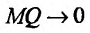
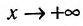
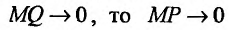
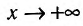
Пример:
График функции 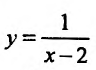
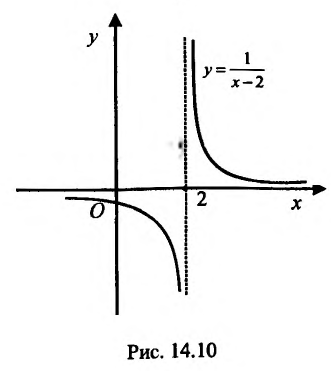
Пример:
Найти асимптоты графика функции
Решение:
Область определения функции D(f): 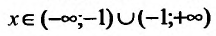
Так как значения пределов останутся такими же и при 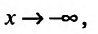
- Заказать решение задач по высшей математике
Общая схема исследования функций и построение их графиков
Под исследованием функций понимается изучение ее изменения в зависимости от изменения аргумента. Исследование функций и построение их графиков можно проводить по следующей схеме:
- Найти область определения и множество значений функции; исследовать на непрерывность, найти точки разрыва и выяснить характер точек разрыва; определить вертикальные асимптоты. Найти точки пересечения с осями координат.
- Исследовать функцию на периодичность; четность, нечетность.
- Исследовать поведение функции на границе области определения; найти асимптоты графика функции.
- Исследовать функцию на монотонность, выяснить характер экстремумов.
- Определить интервалы выпуклости графика функции, точки перегиба.
- Составить таблицу значений функции куда включаются все точки графика функции, найденные на предыдущих этапах исследования и необходимые дополнительные контрольные точки.
- Используя все полученные результаты построить график функции.
Пример:
Построить график функции
Решение:
Проведем полное исследование функции по указанной схеме.
1. Функция определена и непрерывна при всех 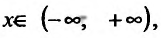
Прямые- х = ±2 являются вертикальными асимптотами, т.к.
График пересекает оси координат в точке O(0; 0).
2. Функция не периодическая. Функция не четная, т.к. выпол-
няется равенство: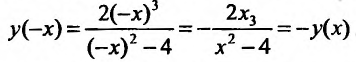
функции симметричный относительно начала координат. Поэтому достаточно провести исследование функции на полуинтервале
3. Найдем наклонную асимптоту. Для этого вычислим пределы:
Подставив значения k и b уравнение 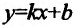
4. Для нахождения промежутков возрастания и убывания найдем первую производную:
приравняем ее к нулю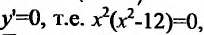
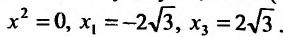

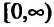
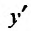
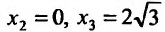
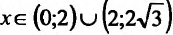
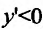
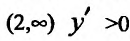
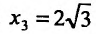
5. Для нахождения промежутков выпуклости и точек перегиба, найдем вторую производную
Вторая производная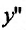
На интервале 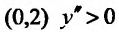
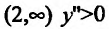
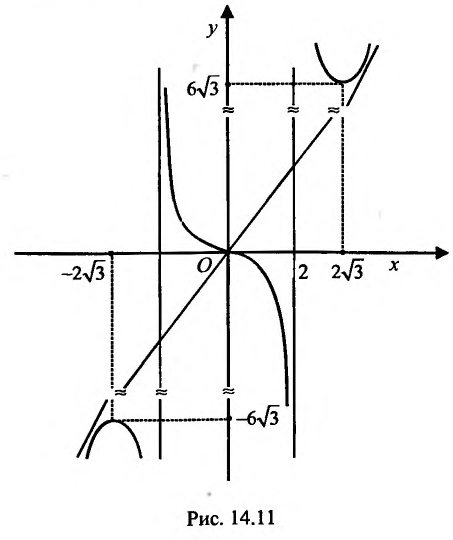
6. Используя результаты исследования и учитывая нечетность функции, строим график (рис. 14.11).
Пример:
Провести полное исследование целевой функции потребления 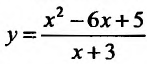
Решение:
Проведём полное и разностороннее изучение свойств функции, применив изложенную выше схему.
1) Функция определена и непрерывна для всех 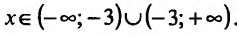
как 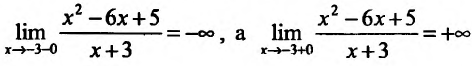
-3 является вертикальной асимптотой. Если х=0, то 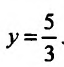
у=О, тс получим уравнение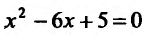
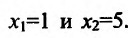
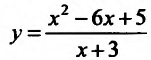
координат в точках:
2) Функция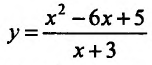
3) Исследуемая функция не является ни чётной, ни нечётной, гак как
4) Исследуем существование наклонных асимптот. Для этого вычислим пределы;
Итак, при 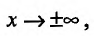
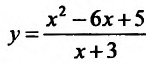
Исследуем повеление функции на границе области определения. Поведение функции в окрестности точки х = -3 исследовано. Поэтому изучим поведение функции при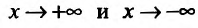
5) Первая производная
обращается в нуль в точках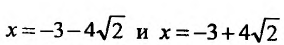
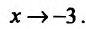
Поскольку 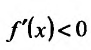
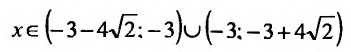
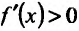
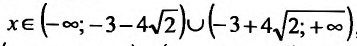
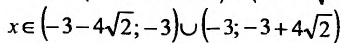
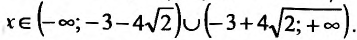
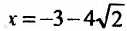
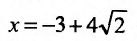
6) Вторая производная не обращается в нуль и стремится к бесконечности при 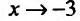
Поскольку 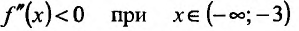
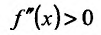
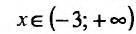
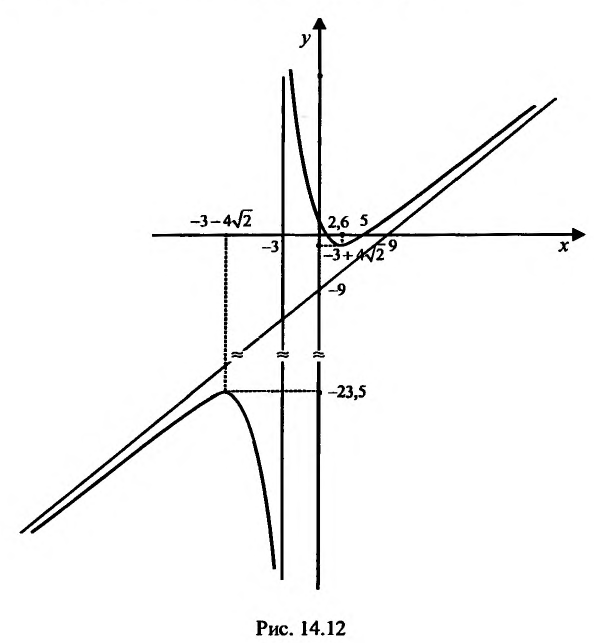
По результатам исследования строим график функции. Вначале строим систему координат; затем вертикальную и горизонтальную асимптоты; наносим точки пересечения с осями координат и точки экстремума функции. Затем строим график (рис. 14.12).
- Предел и непрерывность функции двух переменны
- Дифференцируемость функции нескольких переменных
- Несобственные интегралы
- Дифференциальные уравнения первого порядка
- Плоскость в трехмерном пространстве
- Функция одной переменной
- Производная функции одной переменной
- Приложения производной функции одной переменной


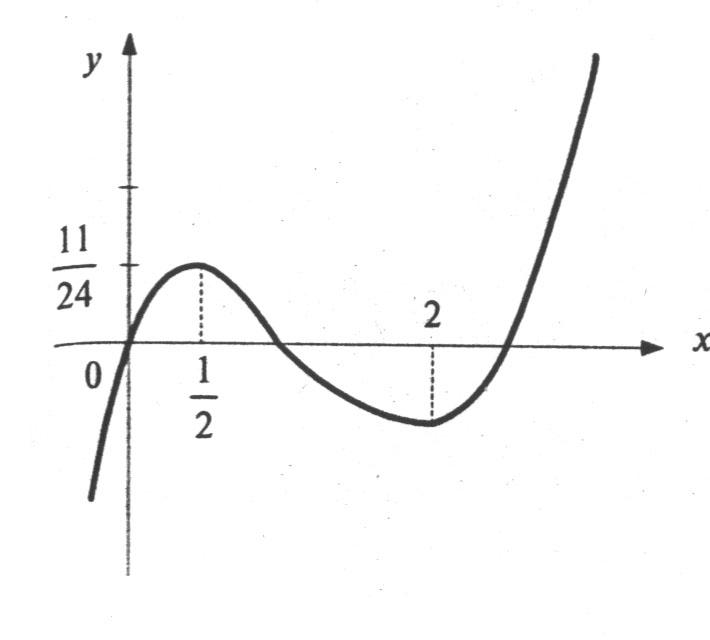






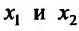
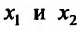 из интервала (а, b), удовлетворяющих условию
из интервала (а, b), удовлетворяющих условию 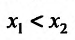 справедливо неравенство
справедливо неравенство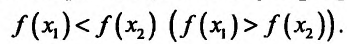 Неубывающие и невозрастающие функции называют монотонными функциями.
Неубывающие и невозрастающие функции называют монотонными функциями.
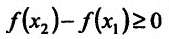
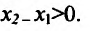
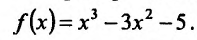
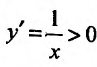
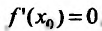
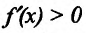 на
на 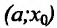 и
и 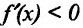 на
на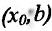 , то точка
, то точка 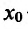 — точка максимума функции f(x);
— точка максимума функции f(x);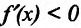 на
на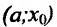 и
и 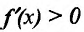 на
на 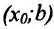 , то точка
, то точка 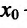 — точка минимума функции f(x);
— точка минимума функции f(x);