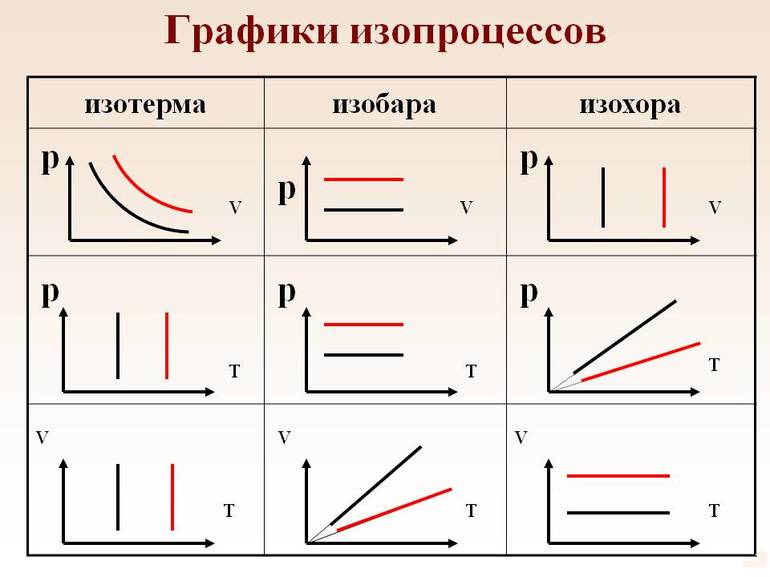
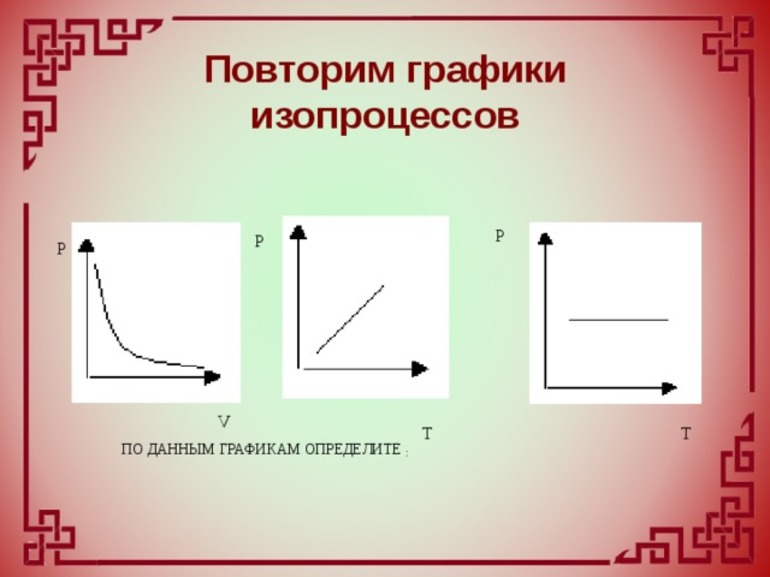
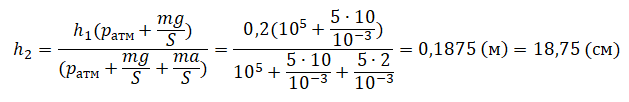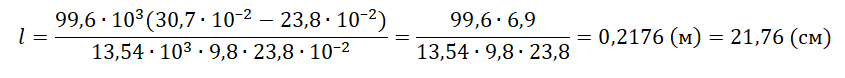Как найти температуру в изопроцессах - Autoru.top

Изопроцессы

Темы кодификатора ЕГЭ: изопроцессы — изотермический, изохорный, изобарный процессы.
Изотермический процесс
Графики изотермического процесса
Изобарный процесс
Графики изобарного процесса
Изохорный процесс
Графики изохорного процесса

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: изопроцессы — изотермический, изохорный, изобарный процессы.

На протяжении этого листка мы будем придерживаться следующего предположения: масса и химический состав газа остаются неизменными. Иными словами, мы считаем, что:

• , то есть нет утечки газа из сосуда или, наоборот, притока газа в сосуд;

• , то есть частицы газа не испытывают каких-либо изменений (скажем, отсутствует диссоциация — распад молекул на атомы).

Эти два условия выполняются в очень многих физически интересных ситуациях (например, в простых моделях тепловых двигателей) и потому вполне заслуживают отдельного рассмотрения.

Если масса газа и его молярная масса фиксированы, то состояние газа определяется тремя макроскопическими параметрами: давлением, объёмом и температурой. Эти параметры связаны друг с другом уравнением состояния (уравнением Менделеева — Клапейрона).

Термодинамический процесс (или просто процесс) — это изменение состояния газа с течением времени. В ходе термодинамического процесса меняются значения макроскопических параметров — давления, объёма и температуры.

Особый интерес представляют изопроцессы — термодинамические процессы, в которых значение одного из макроскопических параметров остаётся неизменным. Поочерёдно фиксируя каждый из трёх параметров, мы получим три вида изопроцессов.

1. Изотермический процесс идёт при постоянной температуре газа: .
2. Изобарный процесс идёт при постоянном давлении газа: .
3. Изохорный процесс идёт при постоянном объёме газа: .

Изопроцессы описываются очень простыми законами Бойля — Мариотта, Гей-Люссака и Шарля. Давайте перейдём к их изучению.

к оглавлению ▴

Изотермический процесс

Пусть идеальный газ совершает изотермический процесс при температуре . В ходе процесса меняются только давление газа и его объём.

Рассмотрим два произвольных состояния газа: в одном из них значения макроскопических параметров равны , а во втором — . Эти значения связаны уравнением Менделеева-Клапейрона:

$p_1V_1=frac{displaystyle m}{displaystyle mu vphantom{1^a}}RT,$

$p_2V_2=frac{displaystyle m}{displaystyle mu vphantom{1^a}}RT.$

Как мы сказали с самого начала,масса и молярная масса предполагаются неизменными.

Поэтому правые части выписанных уравнений равны. Следовательно, равны и левые части:

(1)

Поскольку два состояния газа были выбраны произвольно, мы можем заключить, что в ходе изотермического процесса произведение давления газа на его объём остаётся постоянным:

(2)

Данное утверждение называется законом Бойля — Мариотта.

Записав закон Бойля — Мариотта в виде

$p=frac{displaystyle const}{displaystyle V vphantom{1^a}},$ (3)

можно дать и такую формулировку: в изотермическом процессе давление газа обратно пропорционально его объёму. Если, например, при изотермическом расширении газа его объём увеличивается в три раза, то давление газа при этом в три раза уменьшается.

Как объяснить обратную зависимость давления от объёма с физической точки зрения? При постоянной температуре остаётся неизменной средняя кинетическая энергия молекул газа, то есть, попросту говоря, не меняется сила ударов молекул о стенки сосуда. При увеличении объёма концентрация молекул уменьшается, и соответственно уменьшается число ударов молекул в единицу времени на единицу площади стенки — давление газа падает. Наоборот, при уменьшении объёма концентрация молекул возрастает, их удары сыпятся чаще и давление газа увеличивается.

к оглавлению ▴

Графики изотермического процесса

Вообще, графики термодинамических процессов принято изображать в следующих системах координат:

• -диаграмма: ось абсцисс , ось ординат ;
• -диаграмма: ось абсцисс , ось ординат ;
• -диаграмма: ось абсцисс , ось ординат .

График изотермического процесса называется изотермой.

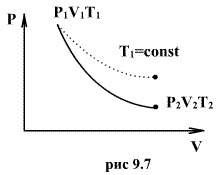
Изотерма на -диаграмме — это график обратно пропорциональной зависимости $p=frac{displaystyle const}{displaystyle V vphantom{1^a}}$ .

Такой график является гиперболой (вспомните алгебру — график функции $y=frac{displaystyle k}{displaystyle x vphantom{1^a}}$ ). Изотерма-гипербола изображена на рис. 1.

Рис. 1. Изотерма на -диаграмме

Каждая изотерма отвечает определённому фиксированному значению температуры. Оказывается, что чем выше температура, тем выше лежит соответствующая изотерма на —диаграмме.

В самом деле, рассмотрим два изотермических процесса, совершаемых одним и тем же газом (рис. 2). Первый процесс идёт при температуре T_1 , второй — при температуре T_2 .

Рис. 2. Чем выше температура, тем выше изотерма

Фиксируем некоторое значение объёма . На первой изотерме ему отвечает давление p_1 , на второй — . Но при фиксированном объёме давление тем больше, чем выше температура (молекулы начинают сильнее бить по стенкам). Значит, .

В оставшихся двух системах координат изотерма выглядит очень просто: это прямая, перпендикулярная оси (рис. 3):

Рис. 3. Изотермы на и -диаграммах

к оглавлению ▴

Изобарный процесс

Напомним ещё раз, что изобарный процесс — это процесс, проходящий при постоянном давлении. В ходе изобарного процесса меняются лишь объём газа и его температура.

Типичный пример изобарного процесса: газ находится под массивным поршнем, который может свободно перемещаться. Если масса поршня и поперечное сечение поршня , то давление газа всё время постоянно и равно

$p=p_0 + frac{displaystyle Mg}{displaystyle S vphantom{1^a}},$

где p_0 — атмосферное давление.

Пусть идеальный газ совершает изобарный процесс при давлении . Снова рассмотрим два произвольных состояния газа; на этот раз значения макроскопических параметров будут равны и .

Выпишем уравнения состояния:

$pV_1=frac{displaystyle m}{displaystyle mu vphantom{1^a}}RT_1,$

$pV_2=frac{displaystyle m}{displaystyle mu vphantom{1^a}}RT_2.$

Поделив их друг на друга, получим:

$frac{displaystyle V_1}{displaystyle V_2 vphantom{1^a}}=frac{displaystyle T_1}{displaystyle T_2 vphantom{1^a}}.$

В принципе, уже и этого могло бы быть достаточно, но мы пойдём немного дальше. Перепишем полученное соотношение так, чтобы в одной части фигурировали только параметры первого состояния, а в другой части — только параметры второго состояния (иными словами, «разнесём индексы» по разным частям):

$frac{displaystyle V_1}{displaystyle T_1 vphantom{1^a}}=frac{displaystyle V_2}{displaystyle T_2 vphantom{1^a}}.$ (4)

А отсюда теперь — ввиду произвольности выбора состояний! — получаем закон Гей-Люссака:

$frac{displaystyle V}{displaystyle T vphantom{1^a}}=const.$ (5)

Иными словами, при постоянном давлении газа его объём прямо пропорционален температуре:

(6)

Почему объём растёт с ростом температуры? При повышении температуры молекулы начинают бить сильнее и приподнимают поршень. При этом концентрация молекул падает, удары становятся реже, так что в итоге давление сохраняет прежнее значение.

к оглавлению ▴

Графики изобарного процесса

График изобарного процесса называется изобарой. На -диаграмме изобара является прямой линией (рис. 4):

Рис. 4. Изобара на -диаграмме

Пунктирный участок графика означает, что в случае реального газа при достаточно низких температурах модель идеального газа (а вместе с ней и закон Гей-Люссака) перестаёт работать. В самом деле, при снижении температуры частицы газа двигаются всё медленнее, и силы межмолекулярного взаимодействия оказывают всё более существенное влияние на их движение (аналогия: медленный мяч легче поймать, чем быстрый). Ну а при совсем уж низких температурах газы и вовсе превращаются в жидкости.

Разберёмся теперь, как меняется положение изобары при изменении давления. Оказывается, что чем больше давление, тем ниже идёт изобара на —диаграмме.
Чтобы убедиться в этом, рассмотрим две изобары с давлениями p_1 и p_2 (рис. 5):

Рис. 5. Чем ниже изобара, тем больше давление

Зафиксируем некоторое значение температуры . Мы видим, что . Но при фиксированной температуре объём тем меньше, чем больше давление (закон Бойля — Мариотта!).

Стало быть, .

В оставшихся двух системах координат изобара является прямой линией, перпендикулярной оси (рис. 6):

Рис. 6. Изобары на и -диаграммах

к оглавлению ▴

Изохорный процесс

Изохорный процесс, напомним, — это процесс, проходящий при постоянном объёме. При изохорном процессе меняются только давление газа и его температура.

Изохорный процесс представить себе очень просто: это процесс, идущий в жёстком сосуде фиксированного объёма (или в цилиндре под поршнем, когда поршень закреплён).

Пусть идеальный газ совершает изохорный процесс в сосуде объёмом . Опять-таки рассмотрим два произвольных состояния газа с параметрами и . Имеем:

$p_1V=frac{displaystyle m}{displaystyle mu vphantom{1^a}}RT_1,$

$p_2V=frac{displaystyle m}{displaystyle mu vphantom{1^a}}RT_2.$

Делим эти уравнения друг на друга:

$frac{displaystyle p_1}{displaystyle p_2 vphantom{1^a}}=frac{displaystyle T_1}{displaystyle T_2 vphantom{1^a}}.$

Как и при выводе закона Гей-Люссака, «разносим» индексы в разные части:

$frac{displaystyle p_1}{displaystyle T_1 vphantom{1^a}}=frac{displaystyle p_2}{displaystyle T_2 vphantom{1^a}}.$ (7)

Ввиду произвольности выбора состояний мы приходим к закону Шарля:

$frac{displaystyle p}{displaystyle T vphantom{1^a}}=const.$ (8)

Иными словами, при постоянном объёме газа его давление прямо пропорционально температуре:

(9)

Увеличение давления газа фиксированного объёма при его нагревании — вещь совершенно очевидная с физической точки зрения. Вы сами легко это объясните.

к оглавлению ▴

Графики изохорного процесса

График изохорного процесса называется изохорой. На -диаграмме изохора является прямой линией (рис. 7):

Рис. 7. Изохора на -диаграмме

Смысл пунктирного участка тот же: неадекватность модели идеального газа при низких температурах.

Далее, чем больше объём, тем ниже идёт изохора на —диаграмме (рис. 8):

Рис. 8. Чем ниже изохора, тем больше объём

Доказательство аналогично предыдущему. Фиксируем температуру и видим, что . Но при фиксированной температуре давление тем меньше, чем больше объём (снова закон Бойля — Мариотта). Стало быть, .

В оставшихся двух системах координат изохора является прямой линией, перпендикулярной оси (рис. 9):

Рис. 9. Изохоры на и -диаграммах

Законы Бойля — Мариотта, Гей-Люссака и Шарля называются также газовыми законами.

Мы вывели газовые законы из уравнения Менделеева — Клапейрона. Но исторически всё было наоборот: газовые законы были установлены экспериментально, и намного раньше. Уравнение состояния появилось впоследствии как их обобщение.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Изопроцессы» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Трактовка понятий

Газ является одним из существующих агрегатных состояний вещества, для которого характерна слабая связь между компонентами и большая подвижность частиц. Последние передвигатся хаотично и свободно. При их столкновения изменяется характер движения.

Реальный газ считается высоко перегретым паром. Его свойства несколько отличаются от идеального компонента. В термодинамики различаются два состояния:

насыщенные пары либо системы с двумя фазами;
перегретые пары либо однофазовые системы.

Газы, как и жидкости, обладают текучестью. Они хорошо сопротивляются деформации. В отличие от воды, газ не имеет фиксированного объёма. Он стремится заполнить весь сосуд. Изопроцессы в газах подчиняются законам, которые определяют зависимость между двумя параметрами вещества при постоянном значении третьего. Так как уравнение справедливо для любой смеси, поэтому формула изотермического процесса (ИЗ) выражается следующим образом: T=const.

Само понятие ИЗ трактуется как новое состояние вещества, которое протекает при неизменной температуре. Процесс соответствует закону Бойля — Мариотта: для газа определённой массы произведение объёма на давление постоянно, если не изменяется температура. Равенство отображается на графике изопроцессов с помощью гиперболы и координат. Отдельно отмечаются изотермы при разных значениях температуры. В последнем случае соблюдается неравенство: Т1< Т2.

Другое понятие, характерное для Р газов — изобарный процесс. Состояние смеси изменяется, но количество давления остаётся постоянным. В сосуде могут происходить следующие явления:

расширение;
сжатие;
охлаждение;
нагревание.

Изобарный процесс подчиняется закону Гей-Люссака: для газовой смеси определённой массы отношение V/t постоянно, если Р не меняется. С математической точки зрения, графическое отображение явления является линейной зависимостью. На рисунке видны изобары для различных давлений газа, при этом соблюдается неравенство р1<р2.

Ещё одним примером состояния газа считается изохорный процесс. Его математический вид: V = const. Под явлением в физике подразумевается изменение состояние смеси, протекающее при постоянном V. Утверждения Шарля: для частиц определённой массы отношение P/t постоянно, если V const. Графически закон изопроцесса действует при разных объёмах.

Изопроцессы и уравнение состояния идеального газа впервые были описаны в работах молекулярного физика Клапейрона Эмиля. Он посвятил свои исследования теплоте, равновесию твёрдых объектов, пластичности. Эмиль первым оценил значение труда Карно. Ему удалось ввести в термодинамику графический способ, диаграммы.

Математические формулы

Состояние газовых масс характеризуется температурой, объёмом и давлением. С помощью уравнения формируется взаимосвязь между показателями. Формула используется в задачах по физике с целью изучения внутреннего теплового процесса. Главные параметры уравнения молекулярно-кинетической теории газовых веществ:

р — давление, измеряется в паскалях, обозначается Па;
m — масса (кг);
n — концентрация молекул на определённом участке.

На уроках физике и на практике применяется несколько выражений для анализа состояния газа. При условии теплового равновесия используется уравнение Клайперона — Менделеева. Его составными показателями являются:

р — давление;
V — объём;
Т — температура;
m — масса;
М — молярная масса, которая измеряется в кг/моль;
R — считается универсальной постоянной, где k — постоянная Больцмана, а Na — постоянная Авогадро.

Значение двух последних показателей указано в специальных таблицах молекулярной физике. Если в задаче описан переход газовых веществ из одного состояния в другое, используется уравнение Клайперона. Для определённой массы газа произведение VP, делённое на абсолютную температуру, есть постоянная величина. Отдельно вычисляются параметры в момент 1 и 2.

Дополнительные выражения, которые используются для расчёта энергии, степени энтропии (неупорядоченность) и упорядоченности, концентрации и других показателей в молекулярно-кинетической теории (МКТ):

Сокращенная формула состояния газа в идеальном виде. Для записи применяется постоянная Больцмана (k), концентрация молекул (n), температура газа (t).
Формула плотности веществ. Её можно получить из главного уравнения.
Закон Дальтона: давление газов из смеси равно сумме парциальных давлений всех газовых компонентов.
Парциальное P. Используется для расписания состояния всех компонентов смеси и определения давления одного вещества, если бы оно занимало сосуд на 100%.

Дополнительные процессы

На практических занятиях по физике проводятся опыты с адиабатным или адиабатическим процессом (изоэнтропийный), связанным с термодинамикой. В явлении нет теплообмена с внешней средой. Чтобы наблюдать за общим случаем всех вышеописанных процессов, используется газ постоянной теплоёмкостью. Явление называется политропическим.

Если давление и температура составных компонентов одинаково, при этом они взяты в равных объёмах, тогда в используемых идеальных газах содержится одно число молекул. На долю одного моля разных веществ приходится N A =6,02·10 ²³молекул. Это считается числом Авогадро.

По закону Дальтона, давление смеси равно сумме парциальных P, входящих в состав. Выражение записывается следующим образом: P cm=P1+P2+…Pn. Последний показатель Pn является давлением газа, который бы занимал весь объёмом сосуда.

Чаще в старших классах физике рассматриваются изохорические процессы, когда переходит идеальный газ из одного состояния в другое, при этом не изменяется его объёмом. Явление впервые рассмотрел француз Жак Шарль. Закон записывается следующим образом: PV=vRT. Так как v= const и V=const, поэтому для любых разных состояний веществ используется равенство: P1/T1=P2/T2=….Pn/Tn. Закон Шарля математически записывается так: P/T=const.

Из выражения следует, что между температурой и давлением наблюдается прямо пропорциональная связь. Если увеличивается P, тогда повышается T, и наоборот. График зависимости данных величин называется изохорой. На промежутке абсолютного нуля для кривых предусмотрена условная зависимость. Прямая доводится до начала координат с помощью пунктирных линий.

Подобная зависимость T от P и V при изобарных и изохорных процессах определяет точность и эффективность измерения температуры газовыми термометрами. Первыми ученые открыли эти явления, которые считаются частными случаями уравнения состояния. Позже физики утвердили закон Клапейрона и Менделеева.

Если следовать хронологии, сначала изучались процессы, которые протекали при постоянной температуре, а затем при одном объеме. Последними рассматривались изобарические процессы. Редким и интересным явлением считается изоэнтропия, когда изменяется термодинамическая система при условии постоянной энтропии. Последнее записывается как S=const.

Примером подобного считается адиабатический обратимый процесс. Чтобы вычислить идеальный газ, используется уравнение: pV^γ = const, где γ — показатель адиабаты (определяется типом газа). Для адиабатического явления характерно отсутствие теплоприёма и теплоотдачи. Физики считают такие процессы быстро протекающими.

Источник

Изопроцессы — термодинамические
процессы,
во время которых количество вещества
и ещё одна из физических величин —
параметров состояния: давление, объёмили температура —
остаются неизменными. Так, неизменному
давлению соответствует изобарный
процесс,
объёму — изохорный,
температуре — изотермический,энтропии — изоэнтропийный (например,
обратимый адиабатический
процесс).
Линии, изображающие данные процессы на
какой-либо термодинамической диаграмме,
называются изобара, изохора, изотерма и адиабата соответственно.
Изопроцессы являются частными
случаями политропного
процесса.

Изобарный процесс

Изобарный
процесс (др.-греч.
ισος, isos — «одинаковый» + βαρος,
baros — «вес») — процесс изменения
состояния термодинамической системы
при постоянном давлении ()

Зависимость объёма
газа от температуры при неизменном
давлении была экспериментально
исследована в 1802 году Жозефом Луи
Гей-Люссаком. Закон
Гей-Люссака:
При постоянном давлении и неизменных
значениях массы газа и его молярной
массы, отношение объёма газа к его
абсолютной температуре остаётся
постоянным: V/T = const.

Изохорный процесс

Основная
статья: Изохорный
процесс

Изохорный процесс (от
греч. хора — занимаемое место) —
процесс изменения состояния
термодинамической системы при постоянном
объёме ().
Для идеальных газов изохорический
процесс описывается законом
Шарля:
для данной массы газа при постоянном
объёме, давление прямо пропорционально
температуре:

Линия, изображающая
изохорный процесс на диаграмме, называется
изохорой.

Ещё стоит указать
что поданная к газу энергия расходуется
на изменение внутренней энергии то есть
Q = 3* ν*R*T/2=3*V*ΔP, где R — универсальная
газовая постоянная, ν количество молей
в газе, T температура в Кельвинах, V объём
газа, ΔP приращение изменения давления.
а линию, изображающая изохорный процесс
на диаграмме, в осях Р(Т), стоит продлить
и пунктиром соединить с началом координат,
так как может возникнуть недопонимание.

Изотермический процесс

Изотермический
процесс (от
греч. «термос» — тёплый, горячий) —
процесс изменения состояния
термодинамической системы при постоянной
температуре ()().
Изотермический процесс описывается законом
Бойля — Мариотта:

При постоянной
температуре и неизменных значениях
массы газа и его молярной массы,
произведение объёма газа на его давление
остаётся постоянным: PV = const.

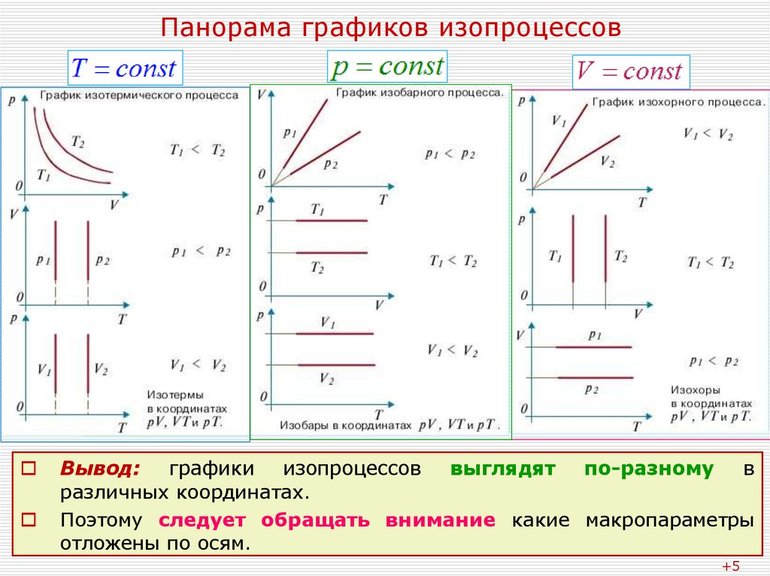
Графики изопроцессов
в различных системах координат

Адиабатический процесс

Адиабатический
процесс — это такое изменение состояний
газа, при котором он не отдает и не
поглощает извне теплоты. Следовательно,
адиабатический процесс характеризуется
отсутствием теплообмена газа с окружающей
средой. Адиабатическими можно считать
быстро протекающие процессы. Так как
передачи теплоты при адиабатическом
процессе не происходит, то и
уравнение I начала термодинамики
принимает вид

(9.20)

или

т.е. внешняя работа
газа может производиться вследствие
изменения его внутренней энергии.
Адиабатное расширение газа (dV>0)
сопровождается положительной внешней
работой, но при этом внутренняя энергия
уменьшается и газ охлаждается (dT<0).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Объединенный газовый закон был открыт экспериментально. Он также является следствием основного уравнения состояния идеального газа. Согласно ему:

Определение

При постоянной массе газа и его неизменной молярной массе отношение произведения давления на объем к его абсолютной температуре остается величиной постоянной:

pVT=const или p1V1T1=p2V2T2

Объединенный газовый закон применительно к изопроцессам

Объединенный газовый закон объединяет три независимых газовых закона: Бойля — Мариотта, Шарля и Гей-Люссака. Газовые законы действуют в частных случаях — изопроцессах.

Определение

Изопроцессы — термодинамические процессы, во время которых количество вещества и один из параметров состояния: давление, объём, температура или энтропия — остаётся неизменным.

Изотермический процесс. Закон Бойля — Мариотта.

Изотермический процесс — термодинамический процесс, происходящий в системе при постоянной температуре и массе:

m = const (m₁ = m₂)

T = const (T₁ = T₂)

Для изотермического процесса действует закон Бойля — Мариотта:

Закон Бойля — Мариотта

Для газа данной массы произведение газа на его объем постоянно, если температура газа не меняется.

pV = const (p₁V₁ = p₂V₂)

Изохорный процесс. Закон Шарля.

Изохорный процесс — термодинамический процесс, происходящий в системе при постоянном объеме и массе:

m = const (m₁ = m₂)

V = const (V₁ = V₂)

Для изохорного процесса действует закон Шарля:

Закон Шарля

Для газа данной массы отношение давления к температуре постоянно, если объем не меняется.

pT=const (p1T1=p2T2)

Изобарный процесс. Закон Гей-Люссака.

Изобарный процесс — термодинамический процесс, происходящий в системе при постоянном давлении и массе:

m = const (m₁ = m₂)

p = const (p₁ = p₂)

Закон Гей-Люссака

Для газа данной массы отношение объема к температуре постоянно, если давление газа не меняется.

VT=const (V1T1=V2T2)

Пример №1. Идеальный газ изобарно нагревают так, что его температура изменяется на ∆T = 240 К, а давление — в 1,6 раза. Масса газа постоянна. Найдите начальную температуру газа по шкале Кельвина.

Так как газ нагревают, то:

T₂ – T₁ = 240 (К)

Отсюда:

T₂ = 240 + T₁ (К)

p₁ = p

p₂ = 1,6p

Запишем закон Шарля применительно к данному случаю:

pT1=1,6p240+ T1

Сделаем некоторые преобразования и вычислим начальную температуру:

pT1=1,6p240+ T1

240+ T1=1,6T1

0,6T1=240

T1=2400,6=400 (К)

Подсказки к задачам на газовые законы

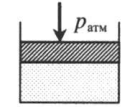	Газ под невесомым поршнем: p = p_атм p — давление газа; p_атм — давление, оказываемое на газ со стороны поршня.
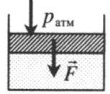	На невесомый поршень действует сила: p=pатм+FS F — сила, действующая на поршень; S — площадь поршня.
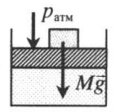	На невесомый поршень поставили груз. В данном случае на поршень дополнительно будет действовать сила тяжести: p=pатм+FтяжS=pатм+MgS F_тяж — сила тяжести, действующая на поршень со стороны груза; M — масса груза; g — ускорение свободного падения.
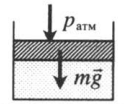	Газ под массивным поршнем. В данном случае на него дополнительно будет действовать сила тяжести поршня: p=pатм+mgS m — масса поршня.
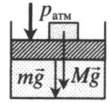	На массивный поршень поставили груз. В данном случае на поршень дополнительно будут действовать силы тяжести со стороны поршня и груза: p=pатм+MgS+mgS
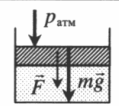	На массивный поршень действует сила. В данном случае газ сдавливается как атмосферным давлением, так и силой тяжести поршня, а также силой, которая на него действует: p=pатм+mgS+FS
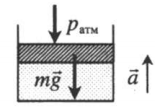	Газ, находящийся в цилиндре под массивным поршнем, находится в лифте, ускорение которого направлено вверх. Когда ускорение движения лифта противоположно направлено ускорению свободного падения, вес тел увеличивается. Поэтому: p=pатм+mgS+maS a — модуль ускорения, с которым движется лифт.
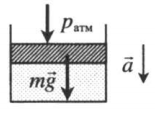	Газ, находящийся в цилиндре под массивным поршнем, находится в лифте, ускорение которого направлено вниз. Когда ускорение движения лифта направлено в сторону вектора ускорения свободного падения, вес тел уменьшается. Поэтому: p=pатм+mgS−maS
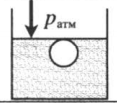	«Пузырек у поверхности воды» — на пузырек действует только атмосферное давоение: p = p_атм
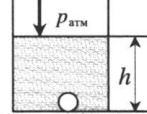	«Пузырек на глубине» — на пузырек действует атмосферное давление и давление столба жидкости: p = p_атм + ρgh ρ — плотность жидкости; h — глубина, на которой находится пузырек.
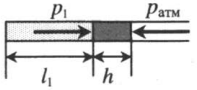	Газ, находящийся в горизонтальной пробирке, отделен от атмосферы столбиком ртути. Объем газа можно вычислить, используя параметры пробирки: V₁ = l₁S V₁ — объем газа; l₁ — длина части пробирки, которую занимает газ; S — площадь поперечного сечения пробирки. Давление газа равно атмосферному давлению: p₁ = p_атм
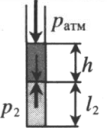	Пробирку поворачивают открытым концом вверх. В этом случае кроме атмосферного давления на газ давит давление со стороны ртути: P₂ = p_атм + ρgh Объем газа можно вычислить, используя параметры пробирки: V₂ = l₂S
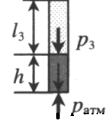	Пробирку поворачивают открытым концом вниз. В этом случае сумма давлений газа и ртути в пробирке равна атмосферному давлению. Отсюда давление газа равно: P₃ = p_атм – ρgh Объем газа можно вычислить, используя параметры пробирки: V₃ = l₃S
Шар или понтон поднимается вверх в воздухе или жидкости	Архимедова сила больше силы тяжести: F_A > F_тяж

Пример №2. Поршень площадью 10 см² массой 5 кг может без трения перемещаться в вертикальном цилиндрическом сосуде, обеспечивая при этом герметичность. Сосуд с поршнем, заполненный газом, покоится на полу неподвижного лифта при атмосферном давлении 100 кПа, при этом расстояние от нижнего края поршня до дна сосуда 20 см. Каким станет это расстояние, когда лифт поедет вверх с ускорением, равным 2 м/с²? Изменение температуры газа не учитывать.

10 см² = 10^–3 м²

20 см = 0,2 м

100 кПа = 10⁵ Па

Составим уравнения для 1 и 2 случая. Когда лифт находится в покое, давление газа равно сумме атмосферного давления и давления, оказываемое массивным поршнем:

p1=pатм+mgS

Когда лифт начал двигаться, появилось дополнительное давление, связанное с увеличением веса поршня при ускоренном движении вверх:

p2=pатм+mgS+maS

Так как изменением температуры можно пренебречь, можно считать, что это процесс изотермический. Следовательно:

p₁V₁ = p₂V₂

Объемы в 1 и 2 случае будут определяться формулами:

V₁ = Sh₁

V₂= Sh₂

h₁ — расстояние от нижнего края поршня до дна сосуда в первом случае. h₂ — та же самая величина, но во втором случае (искомая величина).

Запишем закон Бойля — Мариотта для обоих случаев с учетом объемов:

p1V1=Sh1(pатм+mgS)

p2V2=Sh2(pатм+mgS+maS)

Так как это изотермический процесс, правые части уравнений можно приравнять:

Sh1(pатм+mgS)= Sh2(p
атм+mgS+maS)

Отсюда:

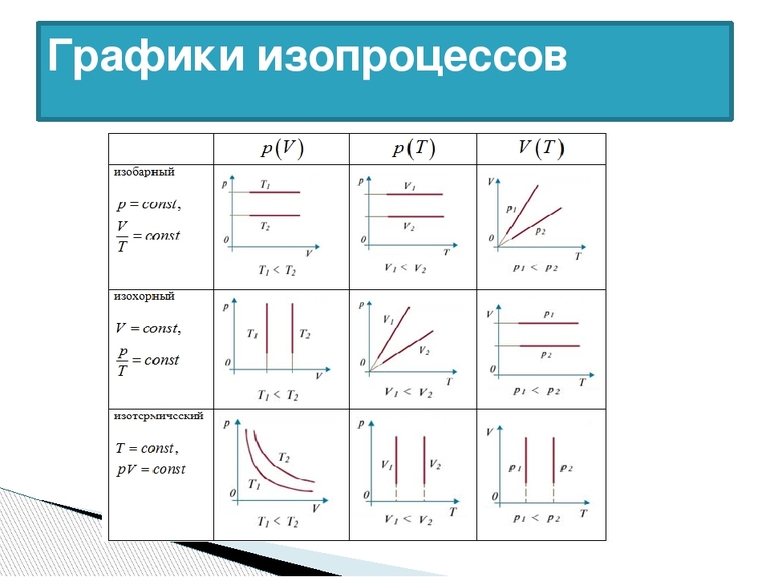
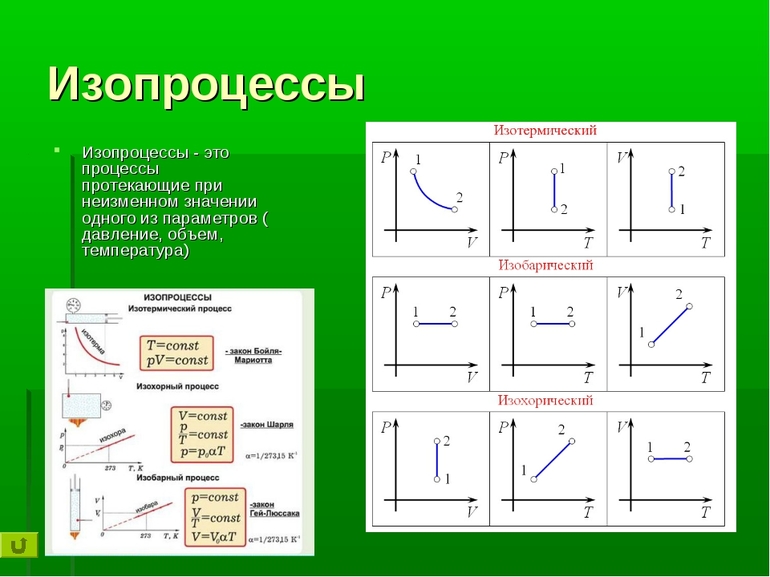
Графики изопроцессов

Изопроцессы можно изобразить графически в координатах (p;V), (V;T) и (p;T). Рассмотрим все виды графиком для каждого из процессов.

Изопроцесс

График в координатах (p;V)

График в координатах (V;T)

График в координатах (p;T)

Изотермический (график — изотерма)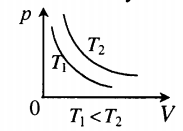

Изотерма в координатах (p;V) — гипербола. Чем ближе изотерма к началу координат и осям, тем меньшей температуре она соответствует.

Характер изменения переменных величин хорошо виден на графике.

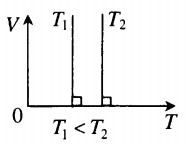
Изотерма в координатах (V;T) — прямая, перпендикулярная оси OT и параллельная оси OV. Чем ближе изотерма к оси OV, тем меньшей температуре она соответствует.

С увеличением объема давление уменьшается.

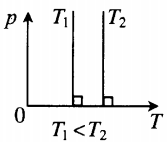
Изотерма в координатах (p;T) — прямая, перпендикулярная оси OT и параллельная оси Op. Чем ближе изотерма к оси Op, тем меньшей температуре она соответствует.

С увеличением давления объем уменьшается.

Изохорный (график — изохора)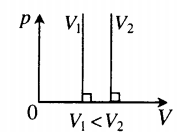

Изохора в координатах (p;V) — прямая, перпендикулярная оси OV и параллельная оси Op. Чем ближе изохора к оси Op, тем меньшему объему она соответствует.

С увеличением давления увеличивается температура.

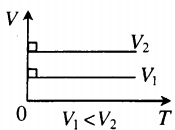
Изохора в координатах (V;T) — прямая, перпендикулярная оси OV и параллельная оси OT. Чем ближе изохора к оси OT, тем меньшему объему она соответствует.

С увеличением температуры увеличивается давление.

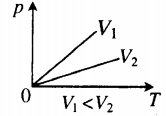
Изохора в координатах (p;T) — прямая, исходящая из начала координат. Чем меньше угол наклона изохоры к оси OT, тем меньшему объему она соответствует.

Характер изменения переменных величин хорошо виден на графике.

Изобарный (график — изобара)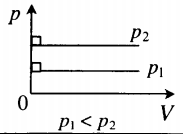

Изобара в координатах (p;V) — прямая, перпендикулярная оси Op и параллельная оси OV. Чем ближе изобара к оси OV, тем меньшему давлению она соответствует.

С увеличением объема температура растет.

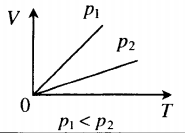
Изобара в координатах (V;T) — прямая, исходящая из начала координат. Чем меньше угол наклона изобары к оси OT, тем меньшему давлению она соответствует.

Характер изменения переменных величин хорошо виден на графике.

Изобара в координатах (p;T) — прямая, перпендикулярная оси Op и параллельная оси OT. Чем ближе изобара к оси OT, тем меньшему давлению она соответствует.

С увеличением температуры объем растет.

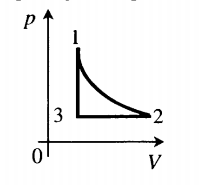
Пример №3. На рисунке представлен график циклического процесса. Вычертить его в координатах (p;T).

Определим характер изменения величин:

Процесс 1–2. Гипербола — это изотерма. Следовательно T₁₂ = const. В координатах (p;T) изотерма будет выглядеть как прямая, перпендикулярная оси OT.
Процесс 2–3. Прямая линия, перпендикулярная оси Op — это изобара. Следовательно p₂₃ = const. В координатах (p;T) изобара будет выглядеть как прямая, перпендикулярная оси Op.
Процесс 3–1. Прямая линия, перпендикулярная оси OV — это изохора. Следовательно V₃₁ = const. В координатах (p;T) изохора будет выглядеть как прямая, выходящая из начала координат.

Теперь, зная, какими будут графики всех величин в координатах (p;T), можно построить сам график. Он примет следующий вид:

Задание EF19012

На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.

Алгоритм решения

1.Указать, в каких координатах построен график.

2.На основании основного уравнения МКТ идеального газа и уравнения Менделеева — Клапейрона выяснить, как меняются указанные физические величины во время процессов 1–2 и 2–3.

Решение

График построен в координатах (V;E_k). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:

T=2−Ek3

Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.

Запишем уравнение Менделеева — Клапейрона:

pV=νRT

Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:

νR=p1V1T1=p2V2T2

Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.

Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.

Ответ:

• Участок 1–2 — изобарный процесс. Температура увеличивается, давление постоянно.

• Участок 2–3 — изотермический процесс. Температура постоянно, давление увеличивается.

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17615

1 моль идеального газа изохорно охлаждают на 200 К, при этом его давление уменьшается в 2 раза. Какова первоначальная абсолютная температура газа?

Ответ:

а) 600 К

б) 400 К

в) 350 К

г) 300 К

Алгоритм решения

1.Записать исходные данные.

2.Определить вид изопроцесса.

3.Выбрать и записать подходящий для данного изопроцесса газовый закон.

4.Выполнить решение в общем виде.

5.Вычислить искомую величину.

Решение

Запишем исходные данные:

• Изменение температуры ∆T = 200 К.

• Первоначальный объем p₁ = 2p.

По условию задачи это изохорный процесс, следовательно он происходит в соответствии с законом Шарля:

p1T1=p2T2

Выразим конечную температуру и получим:

T₂ = T₁ – ∆T

Перепишем закон Шарля применительно к задаче и выразим первоначальную температуру:

2pT1=pT1−ΔT

2(T1−ΔT)=T1

2T1−T1=2ΔT

T1=2ΔT=2·200=400 (К)

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18859

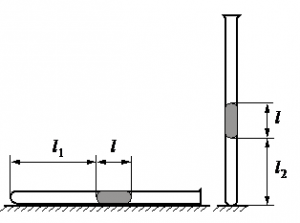
В запаянной с одного конца длинной горизонтальной стеклянной трубке постоянного сечения (см. рисунок) находится столбик воздуха длиной l₁ = 30,7 см, запертый столбиком ртути. Если трубку поставить вертикально отверстием вверх, то длина воздушного столбика под ртутью будет равна l₂ = 23,8 см. Какова длина ртутного столбика? Атмосферное давление 747 мм рт. ст. Температуру воздуха в трубке считать постоянной.

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения физических величин в СИ.

2.Определить вид изопроцесса и записать для него газовый закон.

3.Выполнить решение в общем виде.

4.Вычислить искомую величину.

Решение

Запишем исходные данные:

• Длина столбика воздуха под столбиком ртути в первоначальном состоянии: l₁ = 30,7 см.

• Длина столбика воздуха под столбиком ртути в конечном состоянии: l₂ = 23,8 см.

• Атмосферное давление: p_атм = 747 мм рт. ст.

30,7 см = 30,7∙10^–2 м

23,8 см = 23,8∙10^–2 м

1 мм рт. ст. = 133,322 Па

747 мм рт. ст. = 99,6∙10³ Па

Плотность ртути равна: ρ_рт = 13,54∙10³ кг/м³.

Так как процесс изменения состояния газа происходит при постоянной температуре, процесс можно считать изотермическим. Для него действует газовый закон Бойля — Мариотта:

p₁V₁ = p₂V₂

Первоначальное давление на столбик воздуха равно атмосферному давлению:

p₁ = p_атм

Конечное давление на столбик воздуха равно сумме атмосферного давления и давления, оказываемое силой тяжести столбика ртути:

p2=pатм+mртgS

S —площадь поперечного сечения трубки.

Масса ртути равна произведению плотности на объем столбика металла. Объем в свою очередь равен произведению длины столбика ртути на площадь поперечного сечения трубки. Поэтому:

p2=pатм+ρртVртgS=pатм+ρртlSgS=pатм+ρртlg

Первоначальный объем столбика воздуха равен произведению площади поперечного сечения трубки на высоту этого столбика:

V₁ = Sl₁

Конечный объем столбика воздуха равен произведению площади поперечного сечения трубки на высоту этого столбика:

V₂ = Sl₂

Выразив первоначальные и конечный величины, можем записать закон Бойля — Мариотта применительно к данной задаче:

pатмSl1=(pатм+ρртlg)Sl2

Преобразуем уравнение, выразим искомую величину и произведем вычисления:

pатмl1=pатмl2+ρртlgl2

ρртlgl2=pатмl1−pатмl2

l=pатм(l1−l2)ρртgl2

Ответ: 21,76

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18139

Паук-серебрянка медленно спускается на дно равномерно прогретого озера, неся между волосками брюшка пузырьки воздуха для своего подводного жилища. Какой процесс происходит с воздухом в пузырьках по мере погружения паука?

Ответ:

а) изобарное сжатие

б) изохорное нагревание

в) изотермическое сжатие

г) адиабатное сжатие

Алгоритм решения

Установить, какие величины меняются по мере погружения пузырьков воздуха на глубину.
Выяснить, какие величины сохраняются постоянными.
Установить вид изопроцесса.

Решение

Когда паук спускается в воде на глубину, давление постепенно увеличивается. На пузырьки воздуха будет действовать сумма атмосферного давления и давления столба воды. Под действием этого давления пузырек будет сжиматься. То есть, давление будет уменьшаться. Но само давление воздуха в пузырьке при этом будет равно давлению, оказываемому на него со стороны внешней среды. Следовательно, давление в пузырьке будет увеличиваться. При условии, что количество вещества в пузырьке при этом не меняется, величина температуры также должна оставаться постоянной. Это следует из уравнения состояния идеального газа. Следовательно, воздух в пузырьках претерпевает изотермическое сжатие.

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 11.7k

Источник

Изопроцессы в МКТ — это процессы, протекающие в газах с каким-нибудь неизменным параметром. Для начала мы рассмотрим газ, у которого постоянная масса и химический состав. То есть в газе не меняется количество вещества ν . В этом случае мы можем упростить уравнение Менделеева-Клайперона.

$[frac{p V}{T} = nu R]$

$[frac{p V}{T} = operatorname{const}]$

Я не буду углубляться в названия газовых законов, вы это прочтете в учебниках. Займемся чистой математикой

Итак, у нас есть некий газ постоянной массы. Основные характеристики его состояния определяются $frac{p V}{T} = operatorname{const}$ . То есть, если мы будем на этот газ как-то воздействовать, меняя его характеристики, то

$[frac{p_1 V_1}{T_1} = frac{p_2 V_2}{T_2} = operatorname{const}]$

Получается, что все три его характеристики связаны. Но можно рассмотреть случаи, когда один из этих компонентов не меняется. это и будут изопроцессы. Посмотрим, как будут выглядеть графики изопроцессов в осях p(V), p(T), V(T).

Теперь рассмотрим график конкретного циклического процесса, представленного на рисунке в координатах V-T :

АВ: Изобара

ВC: Изохора

CD: Изобара

DA: Изотерма

Стрелки заменяют слова «увеличивается» и «уменьшается. Отсюда можно смело говорить, что изобара АВ соответствует меньшему давлению, чем изобара CD. Тот же вывод можно сделать, если провести на графике изохору, как показано на рисунке1. При постоянном объеме бОльшей температуре соответствует бОльшее давление.

А теперь можно построить этот же циклический процесс на графиках с другими координатами.

Обратите внимание, что значения в эти графики из риунка1 можно перенести только на оси температуры и объема. Значения для давления произвольные, но… ВС — изохора, следовательно, прямая, ей соответствующая, обязательно должна начинаться в нуле в осях Р-Т! В осях P-V изотерма DA — кривая (гипербола)

Разбор некоторых задач →

Источник

Изопроцессы

Темы кодификатора ЕГЭ: изопроцессы — изотермический, изохорный, изобарный процессы.

Изотермический процесс

Графики изотермического процесса

Изобарный процесс

Графики изобарного процесса

Изохорный процесс

Графики изохорного процесса

Трактовка понятий

Математические формулы

Дополнительные процессы

Изобарный процесс

Изохорный процесс

Изотермический процесс

Адиабатический процесс

Объединенный газовый закон применительно к изопроцессам

Изотермический процесс. Закон Бойля — Мариотта.

Изохорный процесс. Закон Шарля.

Изобарный процесс. Закон Гей-Люссака.

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" loading="lazy" width="629" height="102" src="https://spadilo.ru/wp-content/uploads/2020/08/image14-7.png" />

Графики изопроцессов

Не пропустите также: