Как найти телесный угол

From Wikipedia, the free encyclopedia

Solid angle
Common symbols	Ω
SI unit	steradian
Other units	Square degree
In SI base units	m²/m²
Conserved?	No
Derivations from other quantities	${displaystyle Omega =A/r^{2}}$
Dimension

In geometry, a solid angle (symbol: Ω) is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point.
The point from which the object is viewed is called the apex of the solid angle, and the object is said to subtend its solid angle at that point.

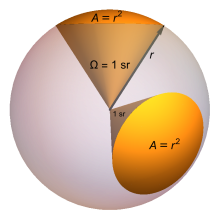
In the International System of Units (SI), a solid angle is expressed in a dimensionless unit called a steradian (symbol: sr). One steradian corresponds to one unit of area on the unit sphere surrounding the apex, so an object that blocks all rays from the apex would cover a number of steradians equal to the total surface area of the unit sphere, 4pi . Solid angles can also be measured in squares of angular measures such as degrees, minutes, and seconds.

A small object nearby may subtend the same solid angle as a larger object farther away. For example, although the Moon is much smaller than the Sun, it is also much closer to Earth. Indeed, as viewed from any point on Earth, both objects have approximately the same solid angle as well as apparent size. This is evident during a solar eclipse.

Definition and properties[edit]

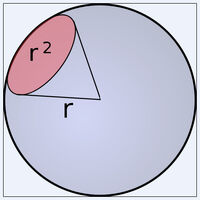
An object’s solid angle in steradians is equal to the area of the segment of a unit sphere, centered at the apex, that the object covers. Giving the area of a segment of a unit sphere in steradians is analogous to giving the length of an arc of a unit circle in radians. Just like a planar angle in radians is the ratio of the length of an arc to its radius, a solid angle in steradians is the ratio of the area covered on a sphere by an object to the area given by the square of the radius of said sphere. The formula is

${displaystyle Omega ={frac {A}{r^{2}}},}$

where is the spherical surface area and is the radius of the considered sphere.

Solid angles are often used in astronomy, physics, and in particular astrophysics. The solid angle of an object that is very far away is roughly proportional to the ratio of area to squared distance. Here «area» means the area of the object when projected along the viewing direction.

Any area on a sphere which is equal in area to the square of its radius, when observed from its center, subtends precisely one steradian.

The solid angle of a sphere measured from any point in its interior is 4π sr, and the solid angle subtended at the center of a cube by one of its faces is one-sixth of that, or 2π/3 sr. Solid angles can also be measured in square degrees (1 sr = (180/π)² square degrees), in square minutes and square seconds, or in fractions of the sphere (1 sr = 1/4π fractional area), also known as spat (1 sp = 4π sr).

In spherical coordinates there is a formula for the differential,

where θ is the colatitude (angle from the North Pole) and φ is the longitude.

The solid angle for an arbitrary oriented surface S subtended at a point P is equal to the solid angle of the projection of the surface S to the unit sphere with center P, which can be calculated as the surface integral:

${displaystyle Omega =iint _{S}{frac {{hat {r}}cdot {hat {n}}}{r^{2}}},dS =iint _{S}sin theta ,dtheta ,dvarphi ,}$

where is the unit vector corresponding to , the position vector of an infinitesimal area of surface dS with respect to point P, and where represents the unit normal vector to dS. Even if the projection on the unit sphere to the surface S is not isomorphic, the multiple folds are correctly considered according to the surface orientation described by the sign of the scalar product .

Thus one can approximate the solid angle subtended by a small facet having flat surface area dS, orientation , and distance r from the viewer as:

${displaystyle dOmega =4pi left({frac {dS}{A}}right),({hat {r}}cdot {hat {n}}),}$

where the surface area of a sphere is A = 4πr².

Practical applications[edit]

Defining luminous intensity and luminance, and the correspondent radiometric quantities radiant intensity and radiance
Calculating spherical excess E of a spherical triangle
The calculation of potentials by using the boundary element method (BEM)
Evaluating the size of ligands in metal complexes, see ligand cone angle
Calculating the electric field and magnetic field strength around charge distributions
Deriving Gauss’s Law
Calculating emissive power and irradiation in heat transfer
Calculating cross sections in Rutherford scattering
Calculating cross sections in Raman scattering
The solid angle of the acceptance cone of the optical fiber

Solid angles for common objects[edit]

Cone, spherical cap, hemisphere[edit]

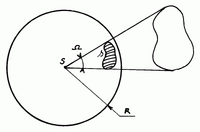
Section of cone (1) and spherical cap (2) inside a sphere. In this figure θ = A/2 and r = 1.

The solid angle of a cone with its apex at the apex of the solid angle, and with apex angle 2θ, is the area of a spherical cap on a unit sphere

${displaystyle Omega =2pi left(1-cos theta right) =4pi sin ^{2}{frac {theta }{2}}.}$

For small θ such that cos θ ≈ 1 − θ²/2 this reduces to πθ², the area of a circle.

The above is found by computing the following double integral using the unit surface element in spherical coordinates:

${displaystyle {begin{aligned}int _{0}^{2pi }int _{0}^{theta }sin theta ',dtheta ',dphi &=int _{0}^{2pi }dphi int _{0}^{theta }sin theta ',dtheta '\&=2pi int _{0}^{theta }sin theta ',dtheta '\&=2pi left[-cos theta 'right]_{0}^{theta }\&=2pi left(1-cos theta right).end{aligned}}}$

This formula can also be derived without the use of calculus. Over 2200 years ago Archimedes proved that the surface area of a spherical cap is always equal to the area of a circle whose radius equals the distance from the rim of the spherical cap to the point where the cap’s axis of symmetry intersects the cap.^[1] In the diagram this radius is given as

${displaystyle 2rsin {frac {theta }{2}}.}$

Hence for a unit sphere the solid angle of the spherical cap is given as

${displaystyle Omega =4pi sin ^{2}{frac {theta }{2}}=2pi left(1-cos theta right).}$

When θ = π/2, the spherical cap becomes a hemisphere having a solid angle 2π.

The solid angle of the complement of the cone is

${displaystyle 4pi -Omega =2pi left(1+cos theta right)=4pi cos ^{2}{frac {theta }{2}}.}$

This is also the solid angle of the part of the celestial sphere that an astronomical observer positioned at latitude θ can see as the Earth rotates. At the equator all of the celestial sphere is visible; at either pole, only one half.

The solid angle subtended by a segment of a spherical cap cut by a plane at angle γ from the cone’s axis and passing through the cone’s apex can be calculated by the formula^[2]

${displaystyle Omega =2left[arccos left({frac {sin gamma }{sin theta }}right)-cos theta arccos left({frac {tan gamma }{tan theta }}right)right].}$

For example, if γ = −θ, then the formula reduces to the spherical cap formula above: the first term becomes π, and the second π cos θ.

Tetrahedron[edit]

Let OABC be the vertices of a tetrahedron with an origin at O subtended by the triangular face ABC where are the vector positions of the vertices A, B and C. Define the vertex angle θ_a to be the angle BOC and define θ_b, θ_c correspondingly. Let ${displaystyle phi _{ab}}$ be the dihedral angle between the planes that contain the tetrahedral faces OAC and OBC and define ${displaystyle phi _{ac}}$ , ${displaystyle phi _{bc}}$ correspondingly. The solid angle Ω subtended by the triangular surface ABC is given by

${displaystyle Omega =left(phi _{ab}+phi _{bc}+phi _{ac}right) -pi .}$

This follows from the theory of spherical excess and it leads to the fact that there is an analogous theorem to the theorem that «The sum of internal angles of a planar triangle is equal to π«, for the sum of the four internal solid angles of a tetrahedron as follows:

${displaystyle sum _{i=1}^{4}Omega _{i}=2sum _{i=1}^{6}phi _{i} -4pi ,}$

where $phi _{i}$ ranges over all six of the dihedral angles between any two planes that contain the tetrahedral faces OAB, OAC, OBC and ABC.^[3]

A useful formula for calculating the solid angle of the tetrahedron at the origin O that is purely a function of the vertex angles θ_a, θ_b, θ_c is given by L’Huilier’s theorem^[4]^[5] as

${displaystyle tan left({frac {1}{4}}Omega right)={sqrt {tan left({frac {theta _{s}}{2}}right)tan left({frac {theta _{s}-theta _{a}}{2}}right)tan left({frac {theta _{s}-theta _{b}}{2}}right)tan left({frac {theta _{s}-theta _{c}}{2}}right)}},}$

where

${displaystyle theta _{s}={frac {theta _{a}+theta _{b}+theta _{c}}{2}}.}$

Another interesting formula involves expressing the vertices as vectors in 3 dimensional space. Let be the vector positions of the vertices A, B and C, and let a, b, and c be the magnitude of each vector (the origin-point distance). The solid angle Ω subtended by the triangular surface ABC is:^[6]^[7]

${displaystyle tan left({frac {1}{2}}Omega right)={frac {left|{vec {a}} {vec {b}} {vec {c}}right|}{abc+left({vec {a}}cdot {vec {b}}right)c+left({vec {a}}cdot {vec {c}}right)b+left({vec {b}}cdot {vec {c}}right)a}},}$

where

denotes the scalar triple product of the three vectors and denotes the scalar product.

Care must be taken here to avoid negative or incorrect solid angles. One source of potential errors is that the scalar triple product can be negative if a, b, c have the wrong winding. Computing the absolute value is a sufficient solution since no other portion of the equation depends on the winding. The other pitfall arises when the scalar triple product is positive but the divisor is negative. In this case returns a negative value that must be increased by π.

Pyramid[edit]

The solid angle of a four-sided right rectangular pyramid with apex angles a and b (dihedral angles measured to the opposite side faces of the pyramid) is

If both the side lengths (α and β) of the base of the pyramid and the distance (d) from the center of the base rectangle to the apex of the pyramid (the center of the sphere) are known, then the above equation can be manipulated to give

${displaystyle Omega =4arctan {frac {alpha beta }{2d{sqrt {4d^{2}+alpha ^{2}+beta ^{2}}}}}.}$

The solid angle of a right n-gonal pyramid, where the pyramid base is a regular n-sided polygon of circumradius r, with a
pyramid height h is

${displaystyle Omega =2pi -2narctan left({frac {tan left({pi over n}right)}{sqrt {1+{r^{2} over h^{2}}}}}right).}$

The solid angle of an arbitrary pyramid with an n-sided base defined by the sequence of unit vectors representing edges {s₁, s₂}, … s_n can be efficiently computed by:^[2]

${displaystyle Omega =2pi -arg prod _{j=1}^{n}left(left(s_{j-1}s_{j}right)left(s_{j}s_{j+1}right)-left(s_{j-1}s_{j+1}right)+ileft[s_{j-1}s_{j}s_{j+1}right]right).}$

where parentheses (* *) is a scalar product and square brackets [* * *] is a scalar triple product, and i is an imaginary unit. Indices are cycled: s₀ = s_n and s₁ = s_{n + 1}. The complex products add the phase associated with each vertex angle of the polygon. However, a multiple of
2pi is lost in the branch cut of and must be kept track of separately. Also, the running product of complex phases must scaled occasionally to avoid underflow in the limit of nearly parallel segments.

Latitude-longitude rectangle[edit]

The solid angle of a latitude-longitude rectangle on a globe is

${displaystyle left(sin phi _{mathrm {N} }-sin phi _{mathrm {S} }right)left(theta _{mathrm {E} }-theta _{mathrm {W} },!right);mathrm {sr} ,}$

where φ_N and φ_S are north and south lines of latitude (measured from the equator in radians with angle increasing northward), and θ_E and θ_W are east and west lines of longitude (where the angle in radians increases eastward).^[8] Mathematically, this represents an arc of angle ϕ_N − ϕ_S swept around a sphere by θ_E − θ_W radians. When longitude spans 2π radians and latitude spans π radians, the solid angle is that of a sphere.

A latitude-longitude rectangle should not be confused with the solid angle of a rectangular pyramid. All four sides of a rectangular pyramid intersect the sphere’s surface in great circle arcs. With a latitude-longitude rectangle, only lines of longitude are great circle arcs; lines of latitude are not.

Celestial objects[edit]

By using the definition of angular diameter, the formula for the solid angle of a celestial object can be defined in terms of the radius of the object, , and the distance from the observer to the object, :

${displaystyle Omega =2pi left(1-{frac {sqrt {d^{2}-R^{2}}}{d}}right):dgeq R.}$

By inputting the appropriate average values for the Sun and the Moon (in relation to Earth), the average solid angle of the Sun is 6.794×10⁻⁵ steradians and the average solid angle of the Moon is 6.418×10⁻⁵ steradians. In terms of the total celestial sphere, the Sun and the Moon subtend average fractional areas of 0.0005406% (5.406 ppm) and 0.0005107% (5.107 ppm), respectively. As these solid angles are about the same size, the Moon can cause both total and annular solar eclipses depending on the distance between the Earth and the Moon during the eclipse.

Solid angles in arbitrary dimensions[edit]

The solid angle subtended by the complete (d − 1)-dimensional spherical surface of the unit sphere in d-dimensional Euclidean space can be defined in any number of dimensions d. One often needs this solid angle factor in calculations with spherical symmetry. It is given by the formula

${displaystyle Omega _{d}={frac {2pi ^{frac {d}{2}}}{Gamma left({frac {d}{2}}right)}},}$

where Γ is the gamma function. When d is an integer, the gamma function can be computed explicitly.^[9] It follows that

${displaystyle Omega _{d}={begin{cases}{frac {1}{left({frac {d}{2}}-1right)!}}2pi ^{frac {d}{2}} &d{text{ even}}\{frac {left({frac {1}{2}}left(d-1right)right)!}{(d-1)!}}2^{d}pi ^{{frac {1}{2}}(d-1)} &d{text{ odd}}.end{cases}}}$

This gives the expected results of 4π steradians for the 3D sphere bounded by a surface of area 4πr² and 2π radians for the 2D circle bounded by a circumference of length 2πr. It also gives the slightly less obvious 2 for the 1D case, in which the origin-centered 1D «sphere» is the interval [−r, r] and this is bounded by two limiting points.

The counterpart to the vector formula in arbitrary dimension was derived by Aomoto^[10]^[11]
and independently by Ribando.^[12] It expresses them as an infinite multivariate Taylor series:

${displaystyle Omega =Omega _{d}{frac {left|det(V)right|}{(4pi )^{d/2}}}sum _{{vec {a}}in mathbb {N} _{0}^{binom {d}{2}}}left[{frac {(-2)^{sum _{i<j}a_{ij}}}{prod _{i<j}a_{ij}!}}prod _{i}Gamma left({frac {1+sum _{mneq i}a_{im}}{2}}right)right]{vec {alpha }}^{vec {a}}.}$

Given d unit vectors ${vec {v}}_{i}$ defining the angle, let V denote the matrix formed by combining them so the ith column is ${vec {v}}_{i}$ , and ${displaystyle alpha _{ij}={vec {v}}_{i}cdot {vec {v}}_{j}=alpha _{ji},alpha _{ii}=1}$ . The variables ${displaystyle alpha _{ij},1leq i<jleq d}$ form a multivariable ${displaystyle {vec {alpha }}=(alpha _{12},dotsc ,alpha _{1d},alpha _{23},dotsc ,alpha _{d-1,d})in mathbb {R} ^{binom {d}{2}}}$ . For a «congruent» integer multiexponent ${displaystyle {vec {a}}=(a_{12},dotsc ,a_{1d},a_{23},dotsc ,a_{d-1,d})in mathbb {N} _{0}^{binom {d}{2}},}$ define ${textstyle {vec {alpha }}^{vec {a}}=prod alpha _{ij}^{a_{ij}}}$ . Note that here $mathbb {N} _{0}$ = non-negative integers, or natural numbers beginning with 0. The notation ${displaystyle alpha _{ji}}$ for means the variable $alpha_{ij}$ , similarly for the exponents $a_{ji}$ .
Hence, the term ${textstyle sum _{mneq l}a_{lm}}$ means the sum over all terms in in which l appears as either the first or second index.
Where this series converges, it converges to the solid angle defined by the vectors.

References[edit]

^ «Archimedes on Spheres and Cylinders». Math Pages. 2015.
^ ^a ^b Mazonka, Oleg (2012). «Solid Angle of Conical Surfaces, Polyhedral Cones, and Intersecting Spherical Caps». arXiv:1205.1396 [math.MG].
^ Hopf, Heinz (1940). «Selected Chapters of Geometry» (PDF). ETH Zurich: 1–2. Archived (PDF) from the original on 2018-09-21.
^ «L’Huilier’s Theorem – from Wolfram MathWorld». Mathworld.wolfram.com. 2015-10-19. Retrieved 2015-10-19.
^ «Spherical Excess – from Wolfram MathWorld». Mathworld.wolfram.com. 2015-10-19. Retrieved 2015-10-19.
^ Eriksson, Folke (1990). «On the measure of solid angles». Math. Mag. 63 (3): 184–187. doi:10.2307/2691141. JSTOR 2691141.
^ Van Oosterom, A; Strackee, J (1983). «The Solid Angle of a Plane Triangle». IEEE Trans. Biomed. Eng. BME-30 (2): 125–126. doi:10.1109/TBME.1983.325207. PMID 6832789. S2CID 22669644.
^ «Area of a Latitude-Longitude Rectangle». The Math Forum @ Drexel. 2003.
^ Jackson, FM (1993). «Polytopes in Euclidean n-space». Bulletin of the Institute of Mathematics and Its Applications. 29 (11/12): 172–174.
^ Aomoto, Kazuhiko (1977). «Analytic structure of Schläfli function». Nagoya Math. J. 68: 1–16. doi:10.1017/s0027763000017839.
^ Beck, M.; Robins, S.; Sam, S. V. (2010). «Positivity theorems for solid-angle polynomials». Contributions to Algebra and Geometry. 51 (2): 493–507. arXiv:0906.4031. Bibcode:2009arXiv0906.4031B.
^ Ribando, Jason M. (2006). «Measuring Solid Angles Beyond Dimension Three». Discrete & Computational Geometry. 36 (3): 479–487. doi:10.1007/s00454-006-1253-4.

External links[edit]

Arthur P. Norton, A Star Atlas, Gall and Inglis, Edinburgh, 1969.
M. G. Kendall, A Course in the Geometry of N Dimensions, No. 8 of Griffin’s Statistical Monographs & Courses, ed. M. G. Kendall, Charles Griffin & Co. Ltd, London, 1961
Weisstein, Eric W. «Solid Angle». MathWorld.

Источник

Телесный угол

Теле́сный у́гол — часть пространства, ограниченная некоторой конической поверхностью, которая является объединением всех лучей, выходящих из данной точки (вершины угла) и пересекающих некоторую поверхность (которая называется поверхностью, стягивающей данный телесный угол). Частными случаями телесного угла являются трёхгранные и многогранные углы. Границей телесного угла является некоторая коническая поверхность.^[1]

Телесный угол измеряется отношением площади той части сферы с центром в вершине угла, которая вырезается этим телесным углом, к квадрату радиуса сферы:

${displaystyle Omega ,=,{S over R^{2}}.}$

Стерадиан

Очевидно, телесные углы измеряются отвлечёнными (безразмерными) числами. Единицей измерения телесного угла в системе СИ является стерадиан, равный телесному углу, вырезающему из сферы единичного радиуса поверхность с площадью в 1 квадратную единицу. Полная сфера образует телесный угол, равный 4π стерадиан (полный телесный угол), для вершины, расположенной внутри сферы, в частности, для центра сферы; таким же является телесный угол, под которым видна любая замкнутая поверхность из точки, полностью охватываемой этой поверхностью, но не принадлежащей ей. Кроме стерадианов, телесный угол может измеряться в квадратных градусах, квадратных минутах и квадратных секундах, а также в долях полного телесного угла.

Телесный угол имеет нулевую физическую размерность.

Двойственный телесный угол к данному телесному углу Ω определяется как угол, состоящий из лучей, образующих с любым лучом угла Ω неострый угол.

Коэффициенты пересчёта единиц телесного угла

	Стерадиан	Кв. градус	Кв. минута	Кв. секунда	Полный угол
1 стерадиан =	1	(180/π)² ≈ ≈ 3282,806 кв. градусов	(180×60/π)² ≈ ≈ 1,1818103×10⁷ кв. минут	(180×60×60/π)² ≈ ≈ 4,254517×10¹⁰ кв. секунд	1/4π ≈ ≈ 0,07957747 полного угла
1 кв. градус =	(π/180)² ≈ ≈ 3,0461742×10⁻⁴ стерадиан	1	60² = = 3600 кв. минут	(60×60)² = = 12 960 000 кв. секунд	π/(2×180)² ≈ ≈ 2,424068×10⁻⁵ полного угла
1 кв. минута =	(π/(180×60))² ≈ ≈ 8,461595×10⁻⁸ стерадиан	1/60² ≈ ≈ 2,7777778×10⁻⁴ кв. градусов	1	60² = = 3600 кв. секунд	π/(2×180×60)² ≈ ≈ 6,73352335×10⁻⁹ полного угла
1 кв. секунда =	(π/(180×60×60))² ≈ ≈ 2,35044305×10⁻¹¹ стерадиан	1/(60×60)² ≈ ≈ 7,71604938×10⁻⁸ кв. градусов	1/60² ≈ ≈ 2,7777778×10⁻⁴ кв. минут	1	π/(2×180×60×60)² ≈ ≈ 1,87042315×10⁻¹² полного угла
Полный угол =	4π ≈ ≈ 12,5663706 стерадиан	(2×180)²/π ≈ ≈ 41252,96125 кв. градусов	(2×180×60)²/π ≈ ≈ 1,48511066×10⁸ кв. минут	(2×180×60×60)²/π ≈ ≈ 5,34638378×10¹¹ кв. секунд	1

Телесный угол обычно обозначается буквой Ω.

Вычисление телесных углов

Для произвольной стягивающей поверхности телесный угол , под которым она видна из начала координат, равен

${displaystyle Omega =iint limits _{S}dOmega =iint limits _{S}sin vartheta dvarphi dvartheta =iint limits _{S}{frac {(mathbf {r} /r)cdot mathbf {n} dS}{r^{2}}},}$

где — сферические координаты элемента поверхности — его радиус-вектор, — единичный вектор, нормальный к

Свойства телесных углов

Полный телесный угол (полная сфера) равен стерадиан.
Сумма всех телесных углов, двойственных к внутренним телесным углам выпуклого многогранника, равна полному углу.

Величины некоторых телесных углов

${displaystyle Omega =2,mathrm {arctg} ,{frac {(mathbf {r} _{1}mathbf {r} _{2}mathbf {r} _{3})}{r_{1}r_{2}r_{3}+(mathbf {r} _{1}cdot mathbf {r} _{2})r_{3}+(mathbf {r} _{2}cdot mathbf {r} _{3})r_{1}+(mathbf {r} _{3}cdot mathbf {r} _{1})r_{2}}},}$

где ${displaystyle (mathbf {r} _{1}mathbf {r} _{2}mathbf {r} _{3})}$ — смешанное произведение данных векторов, ${displaystyle (mathbf {r} _{i}cdot mathbf {r} _{j})}$ — скалярные произведения соответствующих векторов, полужирным шрифтом обозначены векторы, нормальным шрифтом — их длины. Используя эту формулу, можно вычислять телесные углы, стянутые произвольными многоугольниками с известными координатами вершин (для этого достаточно разбить многоугольник на непересекающиеся треугольники).

См. также

Угол
Двугранный угол
Трехгранный угол
Многогранный угол
Стерадиан

Ссылки

↑ http://bse.sci-lib.com/article109615.html

Источник

Рассмотрим
точечный источник светаS,
излучающий во всех направлениях (см.
рис. 30.3). Практически это источник
света, размеры которого малы по сравнению
с расстоянием до места, в котором
изучается действие света. Выделим
элементарный телесный угол
.Телесный
угол – это
часть пространства, ограниченная
прямыми, проведенными из одной точки
(вершины) ко всем токам какой-либо
замкнутой кривой. В нашем случае вершиной
телесного угла является точечный
источник света. Единицей измерения
телесного угла является стерадиан
(ср). Телесный угол в стерадианах
определяется как отношение площади
поверхности, вырезаемой телесным углом
на поверхности сферы, к квадрату радиуса
сферы. Таким образом, телесный угол
является величиной безразмерной. Но
для удобства пользования единице
телесного угла присвоено название –
стерадиан.

Обозначим поток
излучения точечного источника в пределах
телесного угла
через.
Отношение

(30.4)

называется
силой излучения в данном направлении.
Сила
излучения
численно равняется потоку излучения,
приходящемуся на единичный телесный
угол. Единица измерения силы излучения
– Вт/ср. Если точечный источник является
изотропным, т. е. поток излучения
испускается источником равномерно во
всех направлениях, то

,
(29.5)

где
– полный поток излучения, испускаемый
точечным источником во всех направлениях,
т. е. в пределах полного телесного
угла.

30.4. Сила света

Энергетическими
фотометрическими величинами пользуются
преимущественно для измерения
характеристик лазерного излучения. Это
связано с тем, что излучение многих
лазеров лежит в инфракрасном диапазоне
и не воспринимается глазом. Для
характеристики света, даваемого
осветительными приборами (лампы
накаливания, люминесцентные лампы и
пр.), а также солнечного света пользуются
световыми фотометрическими величинами.

Энергетической
фотометрической величине сила излучения
соответствует световая фотометрическая
величина – сила
света.
Основной фотометрической единицей
системы СИ является единица измерения
силы света кандела (кд). Кандела
равняется силе света в заданном
направлении источника, испускающего
монохроматический свет частотой 540 ТГц
(),
сила излучения которого в этом направлении
составляет.

30.5. Световой поток. Связь между энергетическими и световыми величинами

Определения
фотометрических величин светового ряда
и математические соотношения между
ними аналогичны соответствующим
величинам и соотношениям энергетического
ряда. Поэтому световой
поток
,
распространяющийся в пределах телесного
угла,
равняется.
Единица измерения светового потока(люмен).
Для монохроматического света связь
между энергетическими и световыми
величинами
дается формулами:

,
(30.6)

,
(30.7)

где
– константа, называемаямеханическим
эквивалентом света.

Световой
поток, приходящийся на интервал длин
волн от 
до
,

,
(30.8)

где

– функция распределения энергии по
длинам волн (см. рис. 30.1). Тогда полный
световой поток, переносимый всеми
волнами спектра,

.
(30.9)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Мера того, насколько большим объект кажется наблюдателю в данной точке трехмерного пространства

Телесный угол
Общие символы	Ω
Единица СИ	Стерадиан
Другие единицы	Квадратный градус
В Основные единицы СИ	м / м
Расширенный ?	Да
Интенсивный ?	No
Сохранение ?	No
Производные от. других величин	Ω = A / r 2 { displaystyle Omega = A / r ^ {2}} ${ displaystyle Omega = A / r ^ {2}}$
Размер	1 { displaystyle 1}

В геометрии телесный угол (символ: Ω) — это мера величины поля обзора с некоторой конкретной точки, в которой данный объект крышки. То есть это мера того, насколько большим объект кажется наблюдателю, смотрящему с этой точки. Точка, из которой рассматривается объект, называется вершиной телесного угла, и говорят, что объект расширяет свой телесный угол от этой точки.

В Международной системе единиц (СИ) телесный угол выражается в безразмерных единицах, называемых стерадиан (символ: SR). Один стерадиан соответствует одной единице площади на единичной сфере, окружающей вершину, поэтому объект, который блокирует все лучи от вершины, будет покрывать количество стерадианов, равное общей площади поверхности единичной сферы, 4 π { displaystyle 4 pi} 4 pi . Телесные углы также могут быть измерены в квадратах угловых единиц, таких как градусов, минуты и секунды.

Маленький объект поблизости может образовывать тот же телесный угол, что и более крупный объект дальше. Например, хотя Луна намного меньше Солнца, она также намного ближе к Земле. Действительно, если смотреть из любой точки на Земле, оба объекта имеют примерно одинаковый телесный угол и кажущийся размер. Это очевидно во время солнечного затмения.

Содержание

1 Определение и свойства
2 Практическое применение
3 Телесные углы для обычных объектов
- 3.1 Конус, сферическая крышка, полусфера
- 3.2 Тетраэдр
- 3.3 Пирамида
- 3.4 Прямоугольник широты и долготы
- 3.5 Солнце и Луна
4 Телесные углы в произвольных размерах
5 Ссылки
6 Дополнительная литература
7 Внешние ссылки

Определение и свойства

Телесный угол объекта в стерадианах равен площади сегмента единичной сферы с центром в вершине, который покрывает объект. Телесный угол в стерадианах равен площади сегмента единичной сферы точно так же, как плоский угол в радианах равен длине дуги единичной окружности ; следовательно, точно так же, как плоский угол в радианах — это отношение длины дуги окружности к ее радиусу, телесный угол в стерадианах — это следующее отношение:

Ω = A r 2 { displaystyle Omega = { frac {A} {r ^ {2}}}} ${ displaystyle Omega = { frac {A} {r ^ {2}}}}$

где A — площадь сферической поверхности, а r — радиус рассматриваемой сферы.

Телесные углы часто используются в астрономии, физике и, в частности, астрофизике. Телесный угол объекта, который находится очень далеко, примерно пропорционален отношению площади к квадрату расстояния. Здесь «площадь» означает площадь объекта при проецировании в направлении взгляда.

Любая область на сфере, площадь которой равна квадрату ее радиуса, если смотреть из ее центра, составляет ровно один стерадиан.

Телесный угол сферы, измеренный из любой точки внутри ее внутренней части, равен 4 π sr, а телесный угол, образуемый одной из его граней в центре куба, составляет одну шестую этого угла, или 2π / 3 sr. Телесные углы также могут быть измерены в квадратных градусах (1 sr = (180 / π) квадратных градусов), в квадратных минутах и квадратных секундах или в долях сферы (1 sr = 1 / 4π дробная площадь), также известный как spat (1 sp = 4π sr).

В сферических координатах есть формула для дифференциала,

d Ω = sin ⁡ θ d θ d φ { displaystyle d Omega = sin theta , d theta , d varphi}

где θ — широта (угол от северного полюса), а φ — долгота.

Телесный угол для произвольной ориентированной поверхности S, обращенной в точку P, равен телесному углу проекции поверхности S на единичную сферу с центром P, который может быть вычисляется как интеграл поверхности :

Ω = ∬ S r ^ ⋅ n ^ d S r 2 = ∬ S sin ⁡ θ d θ d φ { displaystyle Omega = iint _ {S} { frac { { hat {r}} cdot { hat {n}} , dS} {r ^ {2}}} = iint _ {S} sin theta , d theta , d varphi } $Omega = iint _ {S} { frac {{ hat {r}} cdot { hat {n}} , dS} {r ^ {2}}} = iint _ {S} sin theta , d theta , d varphi$

где r ^ = r → r { displaystyle { hat {r}} = { tfrac { vec {r}} {r}}} ${ displaystyle { hat {r}} = { tfrac { vec {r}} { r}}}$ — это единичный вектор, соответствующий r → { displaystyle { vec {r}}}, вектор положения бесконечно малой площади поверхности dS относительно точка P, и где n ^ { displaystyle { hat {n}}}представляет единицу вектора нормали к dS. Даже если проекция единичной сферы на поверхность S не изоморфна, множественные складки правильно рассматриваются в соответствии с ориентацией поверхности, описываемой знаком скалярного произведения r ^ ⋅ n ^ { displaystyle { hat {r}} cdot { hat {n}}}.

Таким образом, можно аппроксимировать телесный угол, образованный небольшой гранью с плоской поверхностью dS, ориентация n ^ { displaystyle { hat {n}}}и расстояние r от зрителя как:

d Ω = 4 π (d SA) (r ^ ⋅ п ^) { displaystyle d Omega = 4 pi left ({ frac {dS} {A}} right) , ({ hat {r}} cdot { hat {n}})} ${ displaystyle d Omega = 4 pi left ({ frac {dS} {A}} right) , ({ hat {r}} cdot { hat {n}) })}$

, где площадь поверхности сферы равна A = 4πr.

Практическое применение

Определение силы света и яркости и соответствующих радиометрических величин интенсивности излучения и яркости
Расчет сферического избытка E сферического треугольника
Расчет потенциалов с использованием метода граничных элементов (БЭМ)
Оценка размера лиганды в металлических комплексах, см. угол конуса лиганда
Расчет электрического поля и напряженности магнитного поля вокруг зарядовых распределений
Получение Закон Гаусса
Расчет мощности излучения и излучения при теплопередаче
Расчет сечений в резерфордском рассеянии
Расчет сечений в комбинационном рассеянии
Телесный угол приемный конус оптического волокна

Телесные углы для обычных объектов

Конус, сферический колпачок, полусфера

Сечение конуса (1) и сферического колпачка (2) внутри сферы. На этом рисунке θ = A / 2 и r = 1.

Телесный угол конуса с вершиной на вершине телесного угла и с вершиной углом 2θ., это площадь сферической крышки на единичной сфере

Ω = 2 π (1 — cos ⁡ θ) = 4 π sin 2 ⁡ (θ 2) { displaystyle Omega = 2 pi left (1- cos { theta} right) = 4 pi sin ^ {2} left ({ frac { theta} {2}} right) } ${ displaystyle Omega = 2 pi left (1- cos { theta} right) = 4 pi sin ^ {2} left ({ frac { theta} {2}} right) }$

Для малых θ таких, что cos θ ≈ 1 — θ / 2, это сводится к площади круга πθ.

Вышеупомянутое находится путем вычисления следующего двойного интеграла с использованием единичного элемента поверхности в сферических координатах :

∫ 0 2 π ∫ 0 θ sin ⁡ θ ′ d θ ′ d ϕ знак равно 2 π ∫ 0 θ грех ⁡ θ ′ d θ ′ = 2 π [- cos ⁡ θ ′] 0 θ = 2 π (1 — cos ⁡ θ) { displaystyle int _ {0} ^ {2 pi} int _ {0} ^ { theta} sin theta ‘, d theta’ , d phi = 2 pi int _ {0} ^ { theta} sin theta ‘, d theta ‘ = 2 pi left [- cos theta’ right] _ {0} ^ { theta} = 2 pi left (1- cos theta right) } ${displaystyle int _{0}^{2pi }int _{0}^{theta }sin theta ',dtheta ',dphi =2pi int _{0}^{theta }sin theta ',dtheta ' =2pi left[-cos theta 'right]_{0}^{theta } =2pi left(1-cos theta right) }$

Эту формулу можно также получить без использования исчисления. Более 2200 лет назад Архимед доказал, что площадь поверхности сферической шапки всегда равна площади круга, радиус которого равен расстоянию от края сферической шапки до точки, где находится ось симметрии крышки. пересекает шапку. На диаграмме этот радиус представлен как:

2 r sin ⁡ θ 2 { displaystyle 2r sin { frac { theta} {2}}} ${ displaystyle 2r sin { frac { theta} {2}}}$

Следовательно, для единичной сферы телесный угол сферической крышка задается как:

Ω = 4 π sin 2 ⁡ (θ 2) = 2 π (1 — cos ⁡ θ) { displaystyle Omega = 4 pi sin ^ {2} left ({ frac { theta} {2}} right) = 2 pi left (1- cos { theta} right) } ${ displaystyle Omega = 4 pi sin ^ {2} left ({ frac { theta} {2}} right) = 2 pi left (1- соз { тета} право) }$

Когда θ = π / 2, сферическая крышка становится полусферой с телесным углом 2π.

Телесный угол дополнения к конусу равен:

4 π — Ω = 2 π (1 + cos ⁡ θ) = 4 π cos 2 ⁡ (θ 2) { displaystyle 4 pi — Omega = 2 pi left (1+ cos { theta} right) = 4 pi cos ^ {2} left ({ frac { theta} {2}} right)} ${ displaystyle 4 pi - Omega = 2 pi left (1+ cos { theta} right) = 4 pi cos ^ {2} left ( { гидроразрыва { theta} {2}} right)}$

Это также телесный угол той части небесной сферы, которую астрономический наблюдатель, находящийся на широте θ, может видеть при вращении Земли. На экваторе видна вся небесная сфера; на любом полюсе только одна половина.

Телесный угол, образованный сегментом сферической крышки, разрезанной плоскостью под углом γ от оси конуса и проходящей через вершину конуса, можно рассчитать по формуле:

Ω = 2 [arccos ⁡ (грех ⁡ γ грех ⁡ θ) — соз ⁡ θ arccos ⁡ (загар ⁡ γ загар ⁡ θ)] { displaystyle Omega = 2 left [ arccos left ({ frac { sin gamma} { sin theta}} right) — cos theta arccos left ({ frac { tan gamma} { tan theta}} right) right] } $Omega = 2 left [ arccos left ({ frac { sin gamma} { sin theta}} right) - cos theta arccos left ({ frac { tan гамма} { tan theta}} right) right]$

Например, если γ = -θ, тогда формула сводится к формуле сферической крышки, приведенной выше: первый член становится π, а второй πcosθ.

Тетраэдр

Пусть OABC — это вершины тетраэдра с началом в точке O, к которому присоединяется треугольная грань ABC, где a →, b →, c → { displaystyle { vec {a}} , , { vec {b}} , , { vec {c}}}— векторные позиции вершин A, B и C. Определите угол при вершине θ a как угол BOC и определите θ b, θ c соответственно. Пусть ϕ ab { displaystyle phi _ {ab}} ${ displaystyle phi _ {ab}}$ будет двугранным углом между плоскостями, содержащими тетраэдрические грани OAC и OBC, и определим ϕ ac { displaystyle phi _ {ac}} ${ displaystyle phi _ {ac }}$ , ϕ bc { displaystyle phi _ {bc}} ${ displaystyle phi _ {bc}}$ соответственно. Телесный угол Ω, образуемый треугольной поверхностью ABC, задается формулой

Ω = (ϕ ab + ϕ bc + ϕ ac) — π { displaystyle Omega = left ( phi _ {ab} + phi _ { bc} + phi _ {ac} right) — pi } $Omega = left ( phi _ {ab} + phi _ {bc} + phi _ {ac} right) - pi$

Это следует из теории сферического избытка и приводит к тому, что существует аналогичная теорема теореме что «Сумма внутренних углов плоского треугольника равна π» для суммы четырех внутренних телесных углов тетраэдра следующим образом:

∑ i = 1 4 Ω i = 2 ∑ i = 1 6 ϕ я — 4 π { displaystyle sum _ {i = 1} ^ {4} Omega _ {i} = 2 sum _ {i = 1} ^ {6} phi _ {i} -4 pi } $sum _ {i = 1} ^ {4} Omega _ {i} = 2 sum _ {i = 1} ^ {6} phi _ {i} - 4 pi$

где ϕ i { displaystyle phi _ {i}} $phi _ {i}$ располагается по всем шести двугранным углам между любыми двумя плоскостями, которые содержат тетраэдрические грани OAB, OAC, OBC и ABC.

Полезная формула для вычисления телесного угла Ω, образованного треугольной поверхностью ABC, где a →, b →, c → { displaystyle { vec {a}} , , { vec {b}} , , { vec {c}}}— векторные позиции ve точки A, B и C были даны Остеромом и Стракки (хотя результат был известен ранее Эйлером и Лагранжем):

tan ⁡ (1 2 Ω) = | a → b → c → | abc + (a → ⋅ b →) c + (a → ⋅ c →) b + (b → ⋅ c →) a { displaystyle tan left ({ frac {1} {2}} Omega right) = { frac { left | { vec {a}} { vec {b}} { vec {c}} right |} {abc + left ({ vec {a}} cdot { vec {b}} right) c + left ({ vec {a}} cdot { vec {c}} right) b + left ({ vec {b}} cdot { vec { c}} right) a}}} $tan left ({ frac {1} {2}} Omega right) = { frac { left | { vec {a}} { vec {b }} { vec {c}} right |} {abc + left ({ vec {a}} cdot { vec {b}} right) c + left ({ vec {a}} cdot { vec {c}} right) b + left ({ vec {b}} cdot { vec {c}} right) a}}$

где

| a → b → c → | знак равно a → ⋅ (b → × c →) { displaystyle left | { vec {a}} { vec {b}} { vec {c}} right | = { vec {a} } cdot ({ vec {b}} times { vec {c}})}

обозначает тройное скалярное произведение трех векторов;

a → { displaystyle { vec {a}}}

— векторное представление точки A, а a — величина этого вектора (расстояние от начала до точки)

a → ⋅ b → { displaystyle { vec {a}} cdot { vec {b}}}

обозначает скалярное произведение.

. При реализации приведенного выше уравнения необходимо соблюдать осторожность функция, позволяющая избежать отрицательных или неправильных телесных углов. Одним из источников потенциальных ошибок является то, что скалярное тройное произведение может быть отрицательным, если a, b, c имеют неправильную обмотку . Вычисления — достаточное решение, поскольку никакая другая часть уравнения не зависит от обмотки. Другая ошибка возникает, когда скалярное тройное произведение положительно, а делитель отрицателен. В этом случае возвращается отрицательное значение, которое необходимо увеличить на π.

Еще одна полезная формула для вычисления телесного угла тетраэдра в начале координат O, который является чисто функцией углов при вершинах θ a, θ b, θ c определяется теоремой Л’Юилье как

tan ⁡ (1 4 Ω) = tan ⁡ (θ s 2) tan ⁡ (θ s — θ a 2) загар ⁡ (θ s — θ б 2) загар ⁡ (θ s — θ с 2) { displaystyle tan left ({ frac {1} {4}} Omega right) = { sqrt { tan left ({ frac { theta _ {s}} {2}} right) tan left ({ frac { theta _ {s} — theta _ {a}} {2}} right) tan left ({ frac { theta _ {s} — theta _ {b}} {2}} right) tan left ({ frac { theta _ {s} — theta _ {c}} {2}} right)}}} $tan left ({ frac {1} {4}} Omega right) = { sqrt { tan left ({ frac { theta _ {s}} {2}} right) tan left ({ frac { theta _ {s} - theta _ {a}} {2}} right) tan left ({ frac { theta _ {s} - theta _ {b}} {2}} right) tan left ({ frac { theta _ {s} - theta _ {c}} {2}} справа)}}$

где

θ s = θ a + θ b + θ c 2 { displaystyle theta _ {s} = { frac { theta _ {a} + theta _ {b} + theta _ {c}} {2}}} $theta _ {s} = { frac { theta _ {a} + theta _ {b} + theta _ {c}} {2}}$

Пирамида

Телесный угол четырехгранной правой прямоугольной пирамиды с вершиной углами a и b (двугранными углами, измеренными к противоположным боковым граням пирамиды) составляет

Ω = 4 arcsin ⁡ (sin ⁡ (a 2) sin ⁡ ( б 2)) { Displaystyle Omega = 4 arcsin left ( sin left ({a over 2} right) sin left ({b over 2} right) right)}

Если обе стороны (α и β) основания пирамиды и расстояние (d) от центра базового прямоугольника до вершины пирамиды (центра сферы), то указанное выше уравнение можно изменить, чтобы получить

Ω Знак равно 4 arctan ⁡ α β 2 d 4 d 2 + α 2 + β 2 { displaystyle Omega = 4 arctan { frac { alpha beta} {2d { sqrt {4d ^ {2} + alpha ^ {2} + beta ^ {2}}}}}} $Omega = 4 arctan { гидроразрыва { альфа бета} {2d { sqrt {4d ^ {2} + alpha ^ {2} + beta ^ {2}}}}$

Телесный угол прямой n-угольной пирамиды, в которой основание пирамиды представляет собой правильный n-сторонний многоугольник с описанным радиусом r, с высотой пирамиды h

Ω знак равно 2 π — 2 n arctan ⁡ (tan ⁡ (π n) 1 + r 2 h 2) { displaystyle Omega = 2 pi -2n arctan left ({ frac { tan left ({ pi over n} right)} { sqrt {1+ {r ^ {2} over h ^ {2}}}} right)} $Омега = 2 pi -2n arctan left ({ frac { tan left ({ pi over n} right)} { sqrt {1+ {r ^ {2} over h ^ {2 }}}}} right)$

Телесный угол произвольной пирамиды с n-сторонняя база, определяемая последовательностью единичных векторов, представляющих ребра {s 1, s 2 },… s n, может быть эффективно вычислена по:

Ω = 2 π — arg ⁡ ∏ j = 1 n ((sj — 1 sj) (sjsj + 1) — (sj — 1 sj + 1) + i [sj — 1 sjsj + 1]) { Displaystyle Omega = 2 pi — arg prod _ {j = 1} ^ {n} left ( left (s_ {j-1} s_ {j} right) left (s_ {j} s_ {j + 1} right) — left (s_ {j-1} s_ {j + 1} right) + i left [s_ {j-1} s_ {j} s_ {j + 1} right ] right)} $Omega = 2 pi - arg prod _ {j = 1 } ^ {n} left ( left (s_ {j-1} s_ {j} right) left (s_ {j} s_ {j + 1} right) - left (s_ {j-1} s_ {j + 1} right) + i left [s_ {j-1} s_ {j} s_ {j + 1} right] right)$

где круглые скобки (* *) — это скалярное произведение, а квадратные скобки [* * *] — это тройное скалярное произведение, а i — мнимая единица. Индексы циклически меняются: s 0 = s n и s 1 = s n + 1.

прямоугольник широты-долготы

Телесный угол прямоугольника широты и долготы на глобусе равен

(sin ⁡ ϕ N — sin ⁡ ϕ S) (θ E — θ W) sr { displaystyle left ( sin phi _ { mathrm {N}} — sin phi _ { mathrm {S}} right) left ( theta _ { mathrm {E}} — theta _ { mathrm {W}} , ! right) ; mathrm {sr}} ${ displaystyle left ( sin phi _ { mathrm {N}} - si n phi _ { mathrm {S}} right) left ( theta _ { mathrm {E}} - theta _ { mathrm {W}} , ! right) ; mathrm { sr}}$

где φ N и φ S — северная и южная линии широты ( измеряется от экватора в радианах с углом, увеличивающимся к северу), а θ E и θ W являются линиями востока и запада долгота (где угол в радианах увеличивается в восточном направлении). Математически это представляет собой дугу угла ϕ N — ϕ S, охватывающую сферу на θ E — θ W радиан. Когда долгота составляет 2π радиан, а широта — π радиан, телесный угол равен углу сферы.

Прямоугольник широты и долготы не следует путать с телесным углом прямоугольной пирамиды. Все четыре стороны прямоугольной пирамиды пересекают поверхность сферы по дугам большого круга. В прямоугольнике широты и долготы только линии долготы являются дугами большого круга; линий широты нет.

Солнце и Луна

Солнце видно с Земли при среднем угловом диаметре 0,5334 градуса или 9,310 × 10 радиан. Луна видна с Земли со средним угловым диаметром 9,22 × 10 радиан. Мы можем подставить их в приведенное выше уравнение для телесного угла, образованного конусом с вершиной углом 2θ:

Ω = 2 π (1 — cos ⁡ θ) { displaystyle Omega = 2 pi left (1- cos { theta} right)}

{ displaystyle Omega = 2 пи влево (1- соз { тета} вправо)}

Результирующее значение для Солнца составляет 6,807 × 10 стерадиан. Результирующее значение для Луны составляет 6,67 × 10 стерадиан. Что касается всей небесной сферы, то Солнце и Луна увеличивают доли площади 0,000542% (5,42 ppm ) и 0,000531% (5,31 ppm) соответственно.. В среднем Солнце больше на небе, чем Луна, хотя оно намного, намного дальше.

Телесные углы в произвольных размерах

Телесный угол, образованный полной (d — 1) -мерной сферической поверхностью единичной сферы в d-мерном евклидовом пространстве, может быть определенным в любом количестве измерений d. Этот коэффициент телесного угла часто требуется при расчетах со сферической симметрией. Он задается формулой

Ω d = 2 π d 2 Γ (d 2) { displaystyle Omega _ {d} = { frac {2 pi ^ { frac {d} {2}}} { Gamma left ({ frac {d} {2}} right)}} } $Omega _ {d} = { frac {2 pi ^ { frac {d} {2}}} { Gamma left ({ frac {d} {2}} right)}}$

где Γ — гамма-функция. Когда d является целым числом, гамма-функцию можно вычислить явно. Отсюда следует, что

Ω d = {1 (d 2 — 1)! 2 π d 2 d даже (1 2 (d — 1))! (d — 1)! 2 d π 1 2 (d — 1) d нечетное { displaystyle Omega _ {d} = { begin {cases} { frac {1} { left ({ frac {d} {2}} — 1 right)!}} 2 pi ^ { frac {d} {2}} d { text {even}} \ { frac { left ({ frac {1} {2}} left (d-1 right) right)!} {(d-1)!}} 2 ^ {d} pi ^ {{ frac {1} {2}} (d-1)} d { text {odd}} end {ases}}} $Omega _ { d} = { begin {cases} { frac {1} { left ({ frac {d} {2}} - 1 right)!}} 2 pi ^ { frac {d} {2} } d { text {even}} \ { frac { left ({ frac {1} {2}} left (d-1 right) right)!} {(d-1)! }} 2 ^ {d} pi ^ {{ frac {1} {2}} (d-1)} d { text {odd}} end {cases}}$

Это дает ожидаемые результаты 4π стерадианов для трехмерной сферы, ограниченной поверхностью площадью 4πr и 2π радиан для двумерной окружности, ограниченной окружностью длиной 2πr. Это также дает немного менее очевидное значение 2 для одномерного случая, в котором одномерная «сфера» с центром в начале координат является интервалом [−r, r] и ограничена двумя предельными точками.

Аналог векторной формулы в произвольной размерности был получен Аомото и независимо Рибандо. Он выражает их как бесконечный многомерный ряд Тейлора:

Ω = Ω d | det ⁡ (V) | (4 π) d / 2 ∑ a → ∈ N (d 2) [(- 2) ∑ i < j a i j ∏ i < j a i j ! ∏ i Γ ( 1 + ∑ m ≠ i a i m 2) ] α → a →. {displaystyle Omega =Omega _{d}{frac {|operatorname {det} (V)|}{(4pi)^{d/2}}}sum _{{vec {a}}in mathbb {N} ^{binom {d}{2}}}left[{frac {(-2)^{sum _{i ${ displaystyle Omega = Omega _ {d} { frac {| operatorname {det} (V) |} {(4 pi) ^ {d / 2}}} sum _ {{ vec {a}} in mathbb {N} ^ { binom {d} {2}}} left [{ frac {(-2) ^ { sum _ {i <j} a_ {ij}}} { prod _ {i <j} a_ {ij}!}} prod _ {i} Gamma left ({ frac {1+ sum _ {m neq i} a_ {im}} {2}} right) right] { vec { alpha}} ^ { vec {a}}.}$

Даны d единичных векторов vi → { displaystyle { vec {v_ {i}}}} ${ displaystyle { vec {v_ {i}}}}$ , определяя угол, пусть V обозначает матрицу, образованную их объединением, поэтому i-й столбец имеет вид vi → { displaystyle { vec {v_ {i}}}} ${ displaystyle { vec {v_ {i}}}}$ , и α ij = vi → ⋅ vj → = α ji, α ii = 1 { displaystyle alpha _ {ij} = { vec {v_ {i}}} cdot { vec {v_ {j}} } = alpha _ {ji}, alpha _ {ii} = 1} ${ displaystyle alpha _ {ij} = { vec {v_ {i}}} cdot { vec { v_ {j}}} = alpha _ {ji}, alpha _ {ii} = 1}$ . Переменные α ij, 1 ≤ i < j ≤ d {displaystyle alpha _{ij},1leq i ${ displaystyle alpha _ {ij}, 1 leq i <j leq d}$ образуют многомерную α → = (α 12,…, α 1 d, α 23,…, α d — 1, d) ∈ R (d 2) { displaystyle { vec { alpha}} = ( alpha _ {12}, dotsc, alpha _ {1d}, alpha _ {23}, dotsc, alpha _ {d- 1, d}) in mathbb {R} ^ { binom {d} {2}}} ${ displaystyle { vec { alpha}} = ( alpha _ {12}, dotsc, alpha _ {1d}, alpha _ {23}, dotsc, alpha _ {d-1, d}) in mathbb {R} ^ { binom {d} {2}}}$ . Для «конгруэнтной» целочисленной мультиэкспоненты a → = (a 12,…, a 1 d, a 23,…, ad — 1, d) ∈ N (d 2) { displaystyle { vec {a}} = (a_ {12}, dotsc, a_ {1d}, a_ {23}, dotsc, a_ {d-1, d}) in mathbb {N} ^ { binom {d} {2}} } ${ displaystyle { vec {a}} = (a_ {12}, dotsc, a_ {1d}, a_ {23}, dotsc, a_ {d-1, d}) in mathbb {N} ^ { binom {d} {2}}}$ мы определяем α → a → = ∏ α ijaij { displaystyle { vec { alpha}} ^ { vec {a}} = prod alpha _ {ij} ^ { а_ {ij}}} ${ displaystyle { vec { альфа}} ^ { vec {a}} = prod alpha _ {ij} ^ {a_ {ij}}}$ . Обозначение α ji { displaystyle alpha _ {ji}} ${ displaystyle alpha _ {ji}}$ для j>i { displaystyle j>i}означает переменную α ij { displaystyle alpha _ {ij}} $alpha_ {ij}$ , аналогично для показателей aji { displaystyle a_ {ji}} $a_ {ji}$ . Следовательно, термин ∑ m ≠ lalm { displaystyle sum _ {m neq l} a_ {lm}} ${ displaystyle sum _ {m neq l} a_ {lm}}$ означает сумму по всем членам в a → { displaystyle { vec {a}}}, где l отображается как первый или второй индекс. Когда этот ряд сходится, он сходится к телесному углу, определяемому векторами.

Ссылки

Дополнительная литература

Jaffey, AH (1954). «Телесный угол, образуемый круглой апертурой в точечных и рассеянных источниках: формулы и некоторые таблицы». Rev. Sci. Instrum. 25 . Pp. 349–354. Bibcode : 1954RScI… 25..349J. doi : 10.1063 / 1.17710 61.
Маскет, А. Виктор (1957). «Контурные интегралы телесного угла, ряды и таблицы». Rev. Sci. Instrum. 28 (3). п. 191. Bibcode : 1957RScI… 28..191M. doi : 10.1063 / 1.1746479.
Найто, Минору (1957). «Метод вычисления телесного угла, образуемого круглой апертурой». J. Phys. Soc. Jpn. 12 (10). С. 1122–1129. Bibcode : 1957JPSJ… 12.1122N. doi : 10.1143 / JPSJ.12.1122.
Пакстон, Ф. (1959). «Расчет телесного угла круглого диска». Rev. Sci. Instrum. 30 (4). п. 254. Bibcode : 1959RScI… 30..254P. doi : 10,1063 / 1,1716590.
Gardner, R.P.; Карнесейл, А. (1969). «Телесный угол, ограниченный в точке круглым диском». Nucl. Instrum. Методы. 73 (2). С. 228–230. Bibcode : 1969NucIM..73..228G. doi : 10.1016 / 0029-554X (69) 90214-6.
Gardner, R.P.; Verghese, К. (1971). «О телесном угле, образованном круговым диском». Nucl. Instrum. Методы. 93 (1). С. 163–167. Bibcode : 1971NucIM..93..163G. doi : 10.1016 / 0029-554X (71) 90155-8.
Асвестас, Джон С. Инглунд, Дэвид С. (1994). «Вычисление телесного угла, представленного плоской фигурой». Опт. Англ. 33 (12). С. 4055–4059. Bibcode : 1994OptEn..33.4055A. doi : 10.1117 / 12.183402.
Трика, Станислав (1997). «Угловое распределение телесного угла в точке, охватываемой круговым диском». Опт. Commun. 137 (4–6). С. 317–333. Bibcode : 1997OptCo.137..317T. doi : 10.1016 / S0030-4018 (96) 00789-4.
Прата, М. Дж. (2004). «Аналитический расчет телесного угла, полученного дисковым детектором с точечным косинусом». Nucl. Instrum. Методы Phys. Res. А. 521 . п. 576. arXiv : math-ph / 0305034. Bibcode : 2004NIMPA.521..576P. doi : 10.1016 / j.nima.2003.10.098.
Тимус, Д. М.; Prata, M. J.; Kalla, S.L.; Abbas, M. I.; Oner, F.; Галиано, Э. (2007). «Некоторые дальнейшие аналитические результаты о телесном угле, образованном в точке круглым диском с использованием эллиптических интегралов». Nucl. Instrum. Методы Phys. Res. А. 580 . С. 149–152. Bibcode : 2007NIMPA.580..149T. doi : 10.1016 / j.nima.2007.05.055.

На Викискладе есть материалы, связанные с Телесным углом.

Внешние ссылки

Теория многоугольника HCR ( телесный угол, образуемый любым многоугольником) из Academia.edu
Arthur P. Norton, A Star Atlas, Gall and Inglis, Edinburgh, 1969.
M. Г. Кендалл, Курс геометрии N измерений, № 8 Статистических монографий и курсов Гриффина, изд. М. Г. Кендалл, Чарльз Гриффин и Ко. Лтд., Лондон, 1961
Вайсштейн, Эрик У. «Solid Angle». MathWorld.

Источник

Definition and properties[edit]

Practical applications[edit]

Solid angles for common objects[edit]

Cone, spherical cap, hemisphere[edit]

Tetrahedron[edit]

Pyramid[edit]

Latitude-longitude rectangle[edit]

Celestial objects[edit]

Solid angles in arbitrary dimensions[edit]

References[edit]

Further reading[edit]

External links[edit]

Вычисление телесных углов

Свойства телесных углов

Величины некоторых телесных углов

См. также

Ссылки

30.4. Сила света

30.5. Световой поток. Связь между энергетическими и световыми величинами

Содержание

Определение и свойства

Практическое применение

Телесные углы для обычных объектов

Конус, сферический колпачок, полусфера

Тетраэдр

Пирамида

прямоугольник широты-долготы

Солнце и Луна

Телесные углы в произвольных размерах

Ссылки

Дополнительная литература

Внешние ссылки

Не пропустите также: