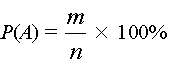Как найти сумму выигрыша - Autoru.top - решение различных проблем

Математик Евгений Пунинский рассказал, что такое теория вероятностей, как она связана с лотереями и можно ли просчитать выигрышную комбинацию.

Портфолио эксперта

Евгений Пунинский

Закончил мехмат МГУ, кафедра Высшей Алгебры.
Больше 10 лет преподавал математику и высшую математику, в частности, теорию вероятностей и статистику в центре London Gates Education Group
Подготовил множество студентов к поступлению в английские и международные вузы
Занимается аналитикой данных и Data Science
Лотереи и теория вероятностей

Что такое теория вероятностей и как она связана с лотереями?

Теория вероятностей — это наука, изучающая случай и пытающаяся этот случай как-то предсказать. Свести кажущиеся хаотичными явления к чему-то предсказуемому. К каким-то математическим формулам, которые скажут нам, что примерно будет вот так. А лотерея — это пример использования теории вероятностей в жизни.

Истоками теория вероятностей уходит в глубокую древность. Люди всегда интересовались случайностью. А аксиоматические основы современной теории вероятностей заложил советский математик Андрей Николаевич Колмогоров . Той теории вероятностей, которую мы сейчас изучаем, например, на мехмате МГУ.

Можно на простом примере рассказать или показать, как работает теория вероятностей?

Проще всего продемонстрировать на монетке. Это базовый пример, с чего начинается любая теория вероятностей. Если мы подбросим монетку, вероятность, что выпадет решка 50 на 50 — то есть 1/2. И так каждый раз, когда я кидаю монетку.

Если мы кинем монетку два раза, вероятность того, что выпадет два раза решка, — 1/4. То есть 1/2 на одной монетке и 1/2 на другой монетке. Мы просто перемножаем эти две вероятности.

Если в поисковике вбить запрос «Как выиграть в лотерею», то выпадет огромное количество ссылок на программы и сайты, где якобы помогают просчитать выигрышную комбинацию. Это вообще возможно?

Нет, таких формул не существует. Это обман. Можно только оценить свой средний ожидаемый выигрыш. Например, ты сыграл миллион раз в одну и ту же лотерею. Один раз ты ничего не выиграл, в другой раз ты выиграл 100 рублей, в третий раз — 500 рублей, а потом опять ничего не выиграл. Все эти доходы мы складываем и делим на общее количество розыгрышей.

По поводу оценки лотереи я могу привести простой, но показательный пример. Например, ты можешь выиграть в лотерею 1000 рублей с вероятностью 1/1000. Или ты можешь выиграть 100 рублей, но с вероятностью 1/50. Какая из них лучше? Какая лотерея прибыльнее для тебя, ну вот в среднем?

Я скажу, что, конечно, прибыльнее та, которая, где я выиграю тысячу рублей.

Потому что тебя привлекает большая сумма. Но ты должен учитывать, что вероятность выигрыша там 1/1000. Если умножить сумму выигрыша на вероятность, мы получим, что в среднем выигрыш на один билет— 1 рубль. То есть, если я куплю много-много билетов, у меня средний выигрышный билет будет 1 рубль. Во второй лотерее, где выигрыш 100 рублей с вероятностью 1/50, в среднем выигрыш на один билет — 2 рубля. Поэтому надо всего учитывать два параметра оценки — сумму выигрыша и вероятность выигрыша.

А как насчёт счастливых чисел? Люди верят, что те или иные числа приносят им в жизни удачу. Поэтому часто отмечают их в своих билетах. Как это можно оценить с точки зрения математики?

Во-первых, скажу, что это нормально. Мне тоже какие-то числа больше нравятся, чем другие. Во-вторых, с точки зрения математики, в этом нет никакой проблемы. Одна лотерея никак не связана с другой, каждый тираж независим, поэтому вероятность выиграть с конкретным числом у вас фиксированная в каждом тираже.

В 2020 году житель штата Ноланд выиграл в лотерею 50 тысяч долларов. На протяжении многих лет он отмечал в лотерейных билетах одни и те же числа. Такой подход, он оправдан?

В этом подходе нет ничего криминального. Как я уже говорил, в каждом новом тираже любое число имеет равновероятный шанс выпасть. И те числа, которые ты отмечал в прошлый раз, никак не влияют на вероятность выигрыша сейчас. Поэтому ты вправе выбирать любые, ничего не изменится. Это миф, что здесь какая-то есть связь. Если есть люди, которые думают, что когда-то у меня не выиграло это число, поэтому его не надо больше отмечать, то скажу, что с математической точки зрения — это абсурд.

В лотереях есть такое понятие, как развернутая ставка. Это когда ты отмечаешь в билете больше чисел, чем нужно. Это повышает твои шансы на выигрыш?

Да, я знаком с этим понятием. Например, в выигрышной комбинации должно быть пять чисел, а ты выбираешь шесть. Это равнозначно тому, что ты шесть раз сыграешь в эту лотерею, у тебя будет шесть попыток, шесть комбинаций. Если ты так играешь несколько раз, то, да, у тебя математическое ожидание твоего выигрыша возрастает.

Вопросы и претензии участников

Одна из частых претензий от участников лотерей, что все выигрышные билеты остаются в Москве и Санкт-Петербурге, а до регионов их просто не довозят. Поэтому выигрывают в столицах чаще и больше.

Это утверждение, конечно, не выдерживает критики. В Москве, в Санкт-Петербурге и в любых крупных городах победителей больше, потому что там живёт больше людей. И, соответственно, там просто покупают больше билетов.

Есть ещё такая претензия: иногда в тираже анонсируют предложение «Выигрывает каждый второй билет». Но участники потом пишут: «Я купил два билета и ни один не выиграл. Обман!». Почему так получается?

«Каждый второй билет выигрышный» означает, что на тираж напечатали, например, миллион билетов, половина из которых выигрышные. Но когда вы будете доставать эти билеты из такого воображаемого общего мешка, то у вас могут быть разные исходы. Когда-то вы достанете два выигрышных, когда-то — два проигрышных или поровну. Но в общей массе, половина билетов здесь выигрышные.

Некоторые участники пишут, что вероятность выигрыша в российских лотереях намного ниже, чем в иностранных. А выигрыши там намного больше. Это действительно так?

Я думаю, что это не так. Вряд ли есть какая-то зависимость между странами. Возьмём для сравнения самую популярную в США лотерею — «Powerball». Во-первых, в США живёт гораздо больше людей, и они чаще участвуют в лотереях. Поэтому билетов покупают больше и, соответственно, призовой фонд у лотереи намного больше. Во-вторых, что касается вероятности. Вероятность выиграть суперприз в «Powerball» 1 к 292 миллионам, а вероятность выиграть, например, в «Спортлото «6 из 45» — 1 к 8 миллионам. То есть разница в 36 раз.

Нужно ещё не забывать о налоге на выигрыш. Поскольку выигрыш в лотерею — это мой доход, соответственно, я с дохода отдаю какой-то процент. В России налог на выигрыш 13% и 15%, на выигрыш от 5 миллионов. А в США налог может составлять 35% или даже 40%.

Да, я тоже слышал, что за рубежом во многих странах очень высокие налоги на любые крупные выигрыши. Не только лотерейные на самом деле, любые. И там до 40% можно отдать государству.

Можешь дать какой-то совет напоследок?

Я советую людям изучать математику и теорию вероятностей. Сейчас довольно много качественной информации. Смотрите тематические YouTube-каналы, например, канал Савватеева. Очень много хороших онлайн-курсов доступно от МГУ, от МФТИ, от Высшей школы экономики. Это очень интересно.

Источник

Lottery mathematics is used to calculate probabilities of winning or losing a lottery game. It is based primarily on combinatorics, particularly the twelvefold way and combinations without replacement.

Choosing 6 from 49[edit]

In a typical 6/49 game, each player chooses six distinct numbers from a range of 1-49. If the six numbers on a ticket match the numbers drawn by the lottery, the ticket holder is a jackpot winner—regardless of the order of the numbers. The probability of this happening is 1 in 13,983,816.

The chance of winning can be demonstrated as follows: The first number drawn has a 1 in 49 chance of matching. When the draw comes to the second number, there are now only 48 balls left in the bag, because the balls are drawn without replacement. So there is now a 1 in 48 chance of predicting this number.

Thus for each of the 49 ways of choosing the first number there are 48 different ways of choosing the second. This means that the probability of correctly predicting 2 numbers drawn from 49 in the correct order is calculated as 1 in 49 × 48. On drawing the third number there are only 47 ways of choosing the number; but of course we could have arrived at this point in any of 49 × 48 ways, so the chances of correctly predicting 3 numbers drawn from 49, again in the correct order, is 1 in 49 × 48 × 47. This continues until the sixth number has been drawn, giving the final calculation, 49 × 48 × 47 × 46 × 45 × 44, which can also be written as or 49 factorial divided by 43 factorial or FACT(49)/FACT(43) or simply PERM(49,6) .

608281864034267560872252163321295376887552831379210240000000000 / 60415263063373835637355132068513997507264512000000000 = 10068347520

This works out to 10,068,347,520, which is much bigger than the ~14 million stated above.

Perm(49,6)=10068347520 and 49 nPr 6 =10068347520.

However; the order of the 6 numbers is not significant for the payout! That is, if a ticket has the numbers 1, 2, 3, 4, 5, and 6, it wins as long as all the numbers 1 through 6 are drawn, no matter what order they come out in. Accordingly, given any combination of 6 numbers, there are 6 × 5 × 4 × 3 × 2 × 1 = 6! or 720 orders in which they can be drawn. Dividing 10,068,347,520 by 720 gives 13,983,816, also written as , or COMBIN(49,6) or 49 nCr 6 or more generally as

, where n is the number of alternatives and k is the number of choices. Further information is available at binomial coefficient and multinomial coefficient.

This function is called the combination function, COMBIN(n,k). For the rest of this article, we will use the notation . «Combination» means the group of numbers selected, irrespective of the order in which they are drawn. A combination of numbers is usually presented in ascending order. An eventual 7th drawn number, the reserve or bonus, is presented at the end.

An alternative method of calculating the odds is to note that the probability of the first ball corresponding to one of the six chosen is 6/49; the probability of the second ball corresponding to one of the remaining five chosen is 5/48; and so on. This yields a final formula of

{n choose k}={49 choose 6}={49 over 6}*{48 over 5}*{47 over 4}*{46 over 3}*{45 over 2}*{44 over 1}

A 7th ball often is drawn as reserve ball, in the past only a second chance to get 5+1 numbers correct with 6 numbers played.

Odds of getting other possibilities in choosing 6 from 49[edit]

One must divide the number of combinations producing the given result by the total number of possible combinations (for example, ). The numerator equates to the number of ways to select the winning numbers multiplied by the number of ways to select the losing numbers.

For a score of n (for example, if 3 choices match three of the 6 balls drawn, then n = 3), describes the odds of selecting n winning numbers from the 6 winning numbers. This means that there are 6 — n losing numbers, which are chosen from the 43 losing numbers in ways. The total number of combinations giving that result is, as stated above, the first number multiplied by the second. The expression is therefore .

This can be written in a general form for all lotteries as:

where is the number of balls in lottery, is the number of balls in a single ticket, and is the number of matching balls for a winning ticket.

The generalisation of this formula is called the hypergeometric distribution.

This gives the following results:

Score	Exact Probability	Approximate Decimal Probability	Approximate 1/Probability
0	435,461/998,844	0.436	2.2938
1	68,757/166,474	0.413	2.4212
2	44,075/332,948	0.132	7.5541
3	8,815/499,422	0.0177	56.66
4	645/665,896	0.000969	1,032.4
5	43/2,330,636	0.0000184	54,200.8
6	1/13,983,816	0.0000000715	13,983,816

When a 7th number is drawn as bonus number then we have 49!/6!/1!/42!.=combin(49,6)*combin(49-6,1)=601304088 different possible drawing results.

Score	Calculation	Exact Probability	Approximate Decimal Probability	Approximate 1/Probability
5 + 0		252/13983816	0.0000180208	55,491.33
5 + 1		6/13983816	0.0000004291	2,330,636

You would expect to score 3 of 6 or better once in around 36.19 drawings. Notice that It takes a 3 if 6 wheel of 163 combinations to be sure of at least one 3/6 score.

1/p changes when several distinct combinations are played together. It mostly is about winning something, not just the jackpot.

Ensuring to win the jackpot[edit]

There is only one known way to ensure winning the jackpot. That is to buy at least one lottery ticket for every possible number combination. For example, one has to buy 13,983,816 different tickets to ensure to win the jackpot in a 6/49 game.

Lottery organizations have laws, rules and safeguards in place to prevent gamblers from executing such an operation. Further, just winning the jackpot by buying every possible combination does not guarantee to break even or make a profit.

If is the probability to win; $c_{t}$ the cost of a ticket; $c_{l}$ the cost for obtaining a ticket (e.g. including the logistics); $c_{f}$ one time costs for the operation (such as setting up and conducting the operation); then the jackpot $m_{j}$ should contain at least

${displaystyle m_{j}geq c_{f}+{frac {c_{t}+c_{l}}{p}}}$

to have a chance to at least break even.

The above theoretical «chance to break-even» point is slightly offset by the sum ${displaystyle sum _{i}{}m_{i}}$ of the minor wins also included in all the lottery tickets:

${displaystyle m_{j}geq c_{f}+{frac {c_{t}+c_{l}}{p}}-sum _{i}{}m_{i}}$

Still, even if the above relation is satisfied, it does not guarantee to break even. The payout depends on the number of winning tickets for all the prizes $n_{x}$ , resulting in the relation

${displaystyle {frac {m_{j}}{n_{j}}}geq c_{f}+{frac {c_{t}+c_{l}}{p}}-sum _{i}{}{frac {m_{i}}{n_{i}}}}$

In probably the only known successful operations^[1] the threshold to execute an operation was set at three times the cost of the tickets alone for unknown reasons

${displaystyle m_{j}geq 3times {frac {c_{t}}{p}}}$

I.e.

${displaystyle {frac {n_{j}p}{c_{t}}}left(c_{f}+{frac {c_{t}+c_{l}}{p}}-sum _{i}{}{frac {m_{i}}{n_{i}}}right)ll 3}$

This does, however, not eliminate all risks to make no profit. The success of the operations still depended on a bit of luck. In addition, in one operation the logistics failed and not all combinations could be obtained. This added the risk of not even winning the jackpot at all.

Powerballs and bonus balls[edit]

Many lotteries have a Powerball (or «bonus ball»). If the powerball is drawn from a pool of numbers different from the main lottery, the odds are multiplied by the number of powerballs. For example, in the 6 from 49 lottery, given 10 powerball numbers, then the odds of getting a score of 3 and the powerball would be 1 in 56.66 × 10, or 566.6 (the probability would be divided by 10, to give an exact value of ${textstyle {frac {8815}{4994220}}}$ ). Another example of such a game is Mega Millions, albeit with different jackpot odds.

Where more than 1 powerball is drawn from a separate pool of balls to the main lottery (for example, in the EuroMillions game), the odds of the different possible powerball matching scores are calculated using the method shown in the «other scores» section above (in other words, the powerballs are like a mini-lottery in their own right), and then multiplied by the odds of achieving the required main-lottery score.

If the powerball is drawn from the same pool of numbers as the main lottery, then, for a given target score, the number of winning combinations includes the powerball. For games based on the Canadian lottery (such as the lottery of the United Kingdom), after the 6 main balls are drawn, an extra ball is drawn from the same pool of balls, and this becomes the powerball (or «bonus ball»). An extra prize is given for matching 5 balls and the bonus ball. As described in the «other scores» section above, the number of ways one can obtain a score of 5 from a single ticket is . Since the number of remaining balls is 43, and the ticket has 1 unmatched number remaining, 1/43 of these 258 combinations will match the next ball drawn (the powerball), leaving 258/43 = 6 ways of achieving it. Therefore, the odds of getting a score of 5 and the powerball are .

Of the 258 combinations that match 5 of the main 6 balls, in 42/43 of them the remaining number will not match the powerball, giving odds of ${textstyle {{258cdot {frac {42}{43}}} over {49 choose 6}}={frac {3}{166,474}}approx 1.802times 10^{-5}}$ for obtaining a score of 5 without matching the powerball.

Using the same principle, the odds of getting a score of 2 and the powerball are for the score of 2 multiplied by the probability of one of the remaining four numbers matching the bonus ball, which is 4/43. Since ${textstyle 1,851,150cdot {frac {4}{43}}=172,!200}$ , the probability of obtaining the score of 2 and the bonus ball is ${textstyle {frac {172,200}{49 choose 6}}={frac {1025}{83237}}=1.231%}$ , approximate decimal odds of 1 in 81.2.

The general formula for matching balls in a choose lottery with one bonus ball from the pool of balls is:

${displaystyle {frac {{frac {K-B}{N-K}}{K choose B}{N-K choose K-B}}{N choose K}}}$

The general formula for matching balls in a choose lottery with zero bonus ball from the pool of balls is:

The general formula for matching balls in a choose lottery with one bonus ball from a separate pool of balls is:

The general formula for matching balls in a choose lottery with no bonus ball from a separate pool of balls is:

Minimum number of tickets for a match[edit]

It is a hard (and often open) problem to calculate the minimum number of tickets one needs to purchase to guarantee that at least one of these tickets matches at least 2 numbers. In the 5-from-90 lotto, the minimum number of tickets that can guarantee a ticket with at least 2 matches is 100.^[2]

Information theoretic results[edit]

As a discrete probability space, the probability of any particular lottery outcome is atomic, meaning it is greater than zero. Therefore, the probability of any event is the sum of probabilities of the outcomes of the event. This makes it easy to calculate quantities of interest from information theory. For example, the information content of any event is easy to calculate, by the formula

In particular, the information content of outcome of discrete random variable is

${displaystyle operatorname {I} _{X}(x):=-log {left[p_{X}{left(xright)}right]}=log {left({frac {1}{p_{X}{left(xright)}}}right)}.}$

For example, winning in the example § Choosing 6 from 49 above is a Bernoulli-distributed random variable with a 1/13,983,816 chance of winning («success») We write with ${textstyle p={tfrac {1}{13,983,816}}}$ and ${textstyle q={tfrac {13,983,815}{13,983,816}}}$ . The information content of winning is

${displaystyle operatorname {I} _{X}({text{win}})=-log _{2}{p_{X}{({text{win}})}}=-log _{2}!{tfrac {1}{13,983,816}}approx 23.73725}$

shannons or bits of information. (See units of information for further explanation of terminology.) The information content of losing is

${displaystyle {begin{aligned}operatorname {I} _{X}({text{lose}})&=-log _{2}{p_{X}{({text{lose}})}}=-log _{2}!{tfrac {13,983,815}{13,983,816}}\&approx 1.0317times 10^{-7}{text{ shannons}}.end{aligned}}}$

The information entropy of a lottery probability distribution is also easy to calculate as the expected value of the information content.

${displaystyle {begin{alignedat}{2}mathrm {H} (X)&=sum _{x}{-p_{X}{left(xright)}log {p_{X}{left(xright)}}} &=sum _{x}{p_{X}{left(xright)}operatorname {I} _{X}(x)}\&{overset {underset {mathrm {def} }{}}{=}} mathbb {E} {left[operatorname {I} _{X}(x)right]}end{alignedat}}}$

Oftentimes the random variable of interest in the lottery is a Bernoulli trial. In this case, the Bernoulli entropy function may be used. Using representing winning the 6-of-49 lottery, the Shannon entropy of 6-of-49 above is

${displaystyle {begin{aligned}mathrm {H} (X)&=-plog(p)-qlog(q)=-{tfrac {1}{13,983,816}}log !{tfrac {1}{13,983,816}}-{tfrac {13,983,815}{13,983,816}}log !{tfrac {13,983,815}{13,983,816}}\&approx 1.80065times 10^{-6}{text{ shannons.}}end{aligned}}}$

References[edit]

^ The man who won the lottery 14 times [1]
^ Z. Füredi, G. J. Székely, and Z. Zubor (1996). «On the lottery problem». Journal of Combinatorial Designs. 4 (1): 5–10. doi:10.1002/(sici)1520-6610(1996)4:1<5::aid-jcd2>3.3.co;2-w.{{cite journal}}: CS1 maint: multiple names: authors list (link) [2]

External links[edit]

Euler’s Analysis of the Genoese Lottery – Convergence (August 2010), Mathematical Association of America
Lottery Mathematics – INFAROM Publishing
13,983,816 and the Lottery – YouTube video with James Clewett, Numberphile, March 2012

Источник

Математика поможет подсчитать вероятность выигрыша и определить, что выгоднее: купить 10 лотерейных билетов на одну игру или по билету на 10 разных.

Денис Пешехонов
По образованию магистр-технарь, в жизни занимается разработкой программ и иногда строит математические модели для игр.

В американском сериале «4исла» (Numb3rs) главный персонаж — математик, помогающий ФБР в раскрытии преступлений. В одной из серий он произносит фразу о том, что вероятность быть убитым по пути за лотерейным билетом выше, чем вероятность выиграть в лотерею. В конце статьи я приведу расчёт, связанный с этим утверждением, а сейчас хочу немного рассказать о математике, стоящей за массовыми азартными играми, и о том, как она может помочь чуть повысить свои шансы.

Правило 1. Оценивайте риски

Для современного просвещённого человека не секрет, что казино и различные игорные заведения рассчитывают все свои игры так, чтобы всегда быть в выигрыше и иметь прибыль. Делается это очень просто: человеку нужно вернуть выигрыш, который соотносится с его ставкой в меньшую сторону по сравнению с его шансами выиграть.
Да, так или иначе, даже самые сложные математические модели в среднем сводятся к одному: если вы ставите 1 рубль, а вам предлагают получить 1 000 рублей, значит, ваш шанс выиграть — меньше, чем 1/1 000.
Исключений нет, если только кто-то специально не хочет подарить вам денег. Держите в голове это простое правило, чтобы всегда трезво смотреть на ситуацию.
Теория игр оценивает любую стратегию аналогично: вероятность получить выигрыш умножается на его размер. Грубо говоря, математика считает, что гарантированно получить 1 000 рублей — это как получить 2 000 рублей с 50-процентным шансом. Этот принцип даёт вам возможность грубо сравнивать различные игры между собой. Что лучше: миллион долларов с шансом 1/100 000 или 50 долларов с шансом 1/4? Интуитивно кажется, что первое предложение интереснее, но математически выгоднее второе.
Если оставаться в рамках одной лишь математики, можно вычислить: выиграть в казино невозможно, ведь любая выбранная стратегия приводит к тому, что произведение вероятности победы на размер выплаты для игрока всегда ниже ставки, которую он уже сделал.
Однако люди играют потому, что выигрыш для них заключается не только в деньгах, но ещё и в эмоциях от процесса — и уж тем более от победы.
А ещё потому, что деньги для нас нелинейны: формально получить 1 рубль прямо сейчас — это как получить миллион рублей с шансом 1/1 000 000, но по факту потеря рубля никак не скажется на нашем состоянии, в жизни не изменится совершенно ничего, а вот получение миллиона — очень серьёзное событие.

Правило 2. Играйте в открытую

К сожалению, проникнуть на внутреннюю кухню лотереи мы не можем. Но полезно понимать хотя бы формальную процедуру того, как именно идёт розыгрыш.
Например, знаменитые игровые автоматы «Однорукий бандит» и другие слот-машины — это на самом деле немного обман: на колесе, которое видит игрок, нарисованы символы различной стоимости, но при этом всё устроено так, чтобы игрок подумал, будто шансы выпадения каждого символа одинаковые. На самом деле (в старых автоматах — механически, а в современных — с помощью программы) за каждым видимым колесом скрывается настоящее, на котором ценные символы встречаются редко, а дешёвые – часто.
Шансы выпадения 777 на слот-машине ниже, чем вероятность получить какие-нибудь три вишни, причём отличие может быть в десятки раз.
«Открытые» лотереи в этом смысле гораздо честнее. В США распространён формат, когда билет либо содержит в себе последовательность чисел, либо она выбирается покупателем самостоятельно. В России, например, предпочитают формат лото: на билете расположены несколько линий чисел, и нужно закрыть или одну из них (обычная победа), или все (джекпот). В теории проводящая лотерею фирма может «специально» печатать и продавать невыигрышные билеты, а потом подтасовывать порядок шаров, но на практике крупные компании этого не делают: организаторы лотереи и так всегда в выигрыше, а скандал в случае вскрытия недобросовестности будет огромен.
Если вы намерены сыграть в азартную игру, полезно будет понять её механику и убедиться в отсутствии влияния заинтересованных лиц на результаты.

Правило 3. Знайте свои шансы

Вероятность джекпота в любой лотерее считается, как правило, одной формулой. А вот расчёт вероятности, например, закрыть в лото хоть одну строчку весьма нетривиален и занял бы целую статью, а может, и не одну. Поэтому на самом деле шанс получить какие-то деньги в лотерее выше за счёт того, что в большинстве лотерей есть дополнительные призы помимо главного. Но я остановлюсь именно на джекпоте для простоты оценки.
Допустим, мы купили лотерейный билет со случайным набором чисел. Во время розыгрыша вытаскивают столько же шаров, и если числа на них совпали с числами в билете (в любом порядке, это важно!), то мы выиграли. Вероятность такого выигрыша рассчитывается так:
Вероятность выигрыша = 1 ÷ Количество комбинаций шаров.
Количество комбинаций без учёта порядка называется в математике числом сочетаний, и если формула для его расчёта вам известна и понятна, то из этой статьи вы, скорее всего, не узнаете ничего нового. Если вы не математик, то проще будет воспользоваться онлайн-сервисом, например вот этим. Подобные сервисы (и формула, лежащая в основе их работы) предлагают задать два числа:
n — общее количество возможных вариантов одного предмета. В нашем случае предмет — это шар, а всего шаров столько, сколько чисел в лотерее, об этом ниже.
k — количество предметов в одной выборке. В нашем случае — сколько шаров лотерея разыгрывает и сколько при этом чисел в билете (предполагается, что эти величины равны).
Итак, если у нас есть лотерея с розыгрышем 5 шаров, а всего в лотерее 50 шаров с числами от 1 до 50, то вероятность выиграть в неё будет равна единице к числу сочетаний при k = 5 и n = 50, то есть:
1 ÷ 2 118 760 = 0,00005 %.
Рассмотрим более сложный случай — популярную американскую лотерею PowerBall, в которой величина джекпота превышала миллиард долларов. По правилам есть базовая выборка из 5 чисел (от 1 до 69), а также одно дополнительное число (от 1 до 26). Нужно получить совпадение всех 6 чисел, чтобы выиграть.
Несложно понять, что шанс получить первый набор равен единице к числу сочетаний при k = 5 и n = 69 (то есть 11 238 513), а шанс «поймать» последний шар — 1 к 26. Чтобы получить всё сразу, эти шансы нужно умножить, потому что события должны произойти одновременно:
(1 ÷ 11 238 513) × (1 ÷ 26) = 1 ÷ 292 201 338 = 0,0000003%.
Иными словами, если 300 миллионов человек купят билеты, то выиграет кто-то один. Это показывает, почему выигрыш джекпота зачастую вообще не состоится: организаторы лотереи просто не печатают так много билетов, чтобы среди них попался выигрышный.

Правило 4. Вовремя начинайте

Лотерейный билет PowerBall, кстати, стоит 2 доллара. Чтобы подсчитать выгоду, которая окупила бы покупку билета, нужно умножить цену билета на 292 201 338.
Подробнее о расчётах. Это отсылка к первому пункту, где говорится о том, что выгода от решения равна его ценности, умноженной на вероятность. Если у нас есть событие с вероятностью 1/X и ценностью N, то выгода будет N/X. Мы тратим 2 доллара и можем подсчитать, какого размера выигрыш окупил бы покупку билета:
2 = N ÷ X.
N = 2 × X, а X тут как раз равен 292 201 338, как показали расчёты из предыдущей части.
Ещё надо учесть налоги (узнать, какой процент от заявленной суммы фактически достанется победителю, обычно это около 70%). То есть джекпот должен составлять как минимум 850 миллионов долларов, и такое в этой лотерее бывает. Как же так, я ведь в начале сказал, что выигрыш при таком умножении всегда не в пользу игрока?
Дело в том, что если розыгрыш джекпота не состоялся, то он переходит на следующий раз, и поэтому какое-то время деньги копятся, а продажи билетов продолжаются.
В идеальной ситуации вам нужно пропускать все игры, не покупая билет, а потом купить именно на ту игру, в которой розыгрыш действительно состоится.
Но узнать это заранее невозможно. Однако можно начать покупать билеты, как только размер джекпота станет больше упомянутой суммы. В такой ситуации математически игра будет выгодной.
Ещё можно понять, что выгоднее: купить много билетов на одну игру или покупать по одному билету на много игр? Давайте подумаем.
В теории вероятностей есть понятие несвязанных событий. Это означает, что исход одного события никак не влияет на исход другого. Например, если вы кидаете два кубика, то выпадения чисел на них не связаны между собой: с точки зрения случайности, один кубик не влияет на поведение второго. А вот если вы тянете из колоды две карты, то эти события связаны, ведь от первой карты зависит то, какие карты останутся в колоде.
Популярное заблуждение по этому поводу так и называется — ошибка игрока. Оно возникает из-за интуитивного представления человека о связанности несвязанных событий.
Например, если монета много раз подряд выпадает орлом, то мы склонны считать, что шансы выпадения решки из-за этого увеличатся, но на самом деле это не так, шансы всегда одинаковые.
Возвращаясь к лотереям: разные игры — это несвязанные события, потому что последовательность шаров выбирается заново. Так что шансы выиграть в любую конкретную лотерею никак не зависят от того, сколько раз раньше вы в неё играли. Это очень сложно принять интуитивно, потому что человек каждый раз, покупая билет, думает: «Ну вот сейчас-то повезёт, сколько можно, я уже кучу времени играю!» Но нет, теория вероятностей — бессердечная штука.
А вот покупка нескольких билетов для одной игры увеличивает ваши шансы пропорционально, потому что билеты внутри одной игры связаны: если выиграет один, значит другой (с другой комбинацией) точно не выиграет. Покупка 10 билетов увеличивает шансы в 10 раз, если все комбинации на билетах разные (по факту почти всегда так и есть). Иными словами, если у вас есть деньги на 10 билетов, лучше купить их на одну игру, чем покупать по билету на 10 игр.
Если вы просто с зарплаты раз в месяц берёте билетик азарта ради, то, скорее всего, значение для вас имеет сам процесс игры. Математически выгоднее скопить эти деньги и в конце года купить сразу 12 билетов, хотя, конечно, проигрыш в такой ситуации будет восприниматься более сокрушительно.

Правило 5. Вовремя останавливайтесь

Ну и напоследок хочу сказать, что даже вероятность 1/100 с точки зрения отдельного человека — это очень мало. Если вы проверяете такую вероятность раз в месяц, то 100 таких проверок сделаете за 8 лет. Представьте себе, во сколько раз ниже вероятность 1/1 000 000 или 1/100 000 000? Поэтому ставьте всегда только ту сумму, которую не боитесь полностью потерять, и ни рублём больше.
В заключение, как обещал, приведу оценку утверждению из начала статьи. Эти данные для США, потому что утверждение было сформулировано именно для этой страны, к тому же мы выше уже посчитали шансы для американской лотереи.
По статистике, за 2016 год в США было совершеноCrime in the US — 2016 около 17 000 убийств, будем считать это средней цифрой. А ещё предположим, что человек является потенциальной целью для убийства, когда он уже взрослый, но не старый — то есть около 50 лет в течение своей жизни. Значит, за эти 50 лет будет совершено около 850 000 убийств. Население США составляетUnited States Population 325,7 миллиона человек, то есть шансы попасть в случайную выборку размером 850 000 такие:
850 000 ÷ 325 700 000 = 1 ÷ 383 = 0,3%.
Но погодите, это просто шанс быть убитым. А именно по пути за лотерейным билетом? Предположим, вы выходите из дома на работу каждый будний день, в один выходной куда-то выбираетесь, а в другой остаётесь дома. В среднем получается 6 дней в неделю, или около 26 дней в месяц. И один раз в месяц вы покупаете лотерейный билет. Поэтому полученные числа нужно ещё и разделить на 26:
(1 ÷ 383) ÷ 26 = 1 ÷ 9 958 = 0,01%.
И даже при такой грубой оценке это существенно вероятнее, чем выигрыш. Если точнее, то в 30 000 раз вероятнее. На самом деле, конечно, числа будут другие: человек подвергается опасности не только на улице, одни люди больше рискуют, чем другие, женщин убивают почти в четыре раза реже, чем мужчин. Но принцип такой.
Хотя жить без веры в хорошие события и с постоянным ожиданием плохих, даже зная математику, — это не самый лучший выбор.

Источник

Математические формулы в лотерее являются частью теории вероятностей и комбинаторной математики.

Что же мы подразумеваем под этим интуитивным понятием вероятности? С точки зрения математики возможны две различные интерпретации этого сугубо абстрактного понятия. В первой из них понятие вероятности ассоциируется с частотой появления данного события в серии опытов, в каждом из которых анализируемое событие может появиться или не появиться. Такое событие математики называют случайным.

Как вычислить вероятность?

Существует так называемый закон больших чисел, справедливость которого доказывается в теории вероятностей. Согласно этому закону, в любой серии опытов при увеличении их числа, частота появления случайного события всегда стабильно стремится к одной и той же величине и это предельное значение можно принять за вероятность Р(А) (probability — на английском языке):

Таким образом, согласно этому утверждению, чтобы найти вероятность события, нужно провести достаточно длинную серию опытов и полученную частоту выразить в процентах.

А нельзя ли определить вероятность выигрыша априори, то есть до начала опытов? Оказывается, что в ряде случаев это возможно. Метод, который используется для априорного определения величин вероятности, основан на втором возможном варианте ее интерпретации и состоит он в следующем:

то — есть вероятность появления события А равна отношению числа m — благоприятных событий для А к полному числу n — возможных элементарных событий, выраженному в процентах.

Рассмотрим теперь задачу, более близкую к нашим интересам. А эти интересы в данном случае связаны с подсчетом вероятностей угадывания цифр в розыгрышах Лото 6/49. По правилам этой игры, требуется угадать шесть отобранных (счастливых) номеров из общего количества имеющихся в наличии сорока девяти. Для наглядности заштрихуем «счастливые номера», как это показано на рисунке.

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49

Какова вероятность того, что перевернутый номер окажется заштрихованным? Очевидно, она и в этом случае равна отношению числа благоприятных для нас исходов (заштрихованных номеров, а их число равно 6) к полному числу всех возможных исходов (то есть полному числу номеров, число которых 49). Таким образом, вероятность угадать одну из шести отобранных номеров равна 6/49, а вероятность не угадать, соответственно — 43/49.

Если сложить теперь вероятности этих двух возможных исходов, то, как и следовало ожидать, сумма всех вероятностей окажется равной 1. Конечно, хоть что-нибудь, но должно же случиться с достоверностью (то есть с вероятностью 100%). Как говорят, уж если не выиграю, то проиграю.

При второй попытки полное число оставшихся номеров, уже становится равным 48 (один номер уже был разыгран в первом туре). Таким образом, для всех возможных вариантов исхода получаем:

Если в первом туре был угадан заштрихованный номер:
Вероятность угадать заштрихованный номер становится равно 5/48, а вероятность выпадения незаштрихованного номера составит 43/48.
Если в первом туре был угадан незаштрихованный номер:
Вероятность угадать заштрихованный номер становится равно 6/48, а вероятность выпадения незаштрихованного номера составит 42/48.

Таким образом, при двух подходах жеребьевки возможны четыре варианта результата (первый подход + второй подход):

1) угадал + не угадал: p = 6/49 x 43/48 = 0,1097

2) не угадал + угадал: p = 43/49 x 6/48 = 0,1097

3) угадал + угадал: p = 6/49 x 5/48 = 0,0128

4) не угадал + не угадал: p = 43/49 x 42/48 = 0,7679

Нетрудно убедиться, что и в этом случае сумма вероятностей равна 1.

Как вычислить количество всех возможных результатов?

Легко заметить, что по мере увеличения количества подходов общее количество возможных вариантов результата увеличивается очень быстро, а именно: общее количество возможных вариантов результата для n подходов розыгрышей равно 2ⁿ (2 в степени n).

Например, при трех подходах у нас уже будет 2³ = 8 возможных вариантов результата:

1) угадал + угадал + угадал: вероятность = 0,0011

2) угадал + угадал + не угадал: вероятность = 0,0117

3) угадал + не угадал + угадал: вероятность = 0,0117

4) не угадал + угадал + угадал: вероятность = 0,0117

5) угадал + не угадал + не угадал: вероятность = 0,0980

6) не угадал + угадал + не угадал: вероятность = 0,0980

7) не угадал + не угадал + угадал: вероятность = 0,0980

не угадал + не угадал + не угадал: вероятность = 0,6698

Как вычислить количество комбинаций?

Зная общее количество возможных вариантов, давайте теперь выясним, сколько из этих вариантов содержат угаданные числа. Количество этих вариантов на самом деле является количеством всех возможных комбинаций угаданных заштрихованных чисел.

Предположим, что мы отметили шесть произвольных чисел и хотим узнать, сколько существует вариантов, в которых будет угадано 4 цифры из 6. Число способов, которыми можно угадать 4 из этих 6 номеров, математики называют числом сочетаний и обозначают его . Эта запись читается так: «число сочетаний из шести по четыре».

Предположим, что угаданы числа 12, 14, 30 и 36. Сколько вариантов существует для такого угадывания? Число 12 может быть угадано в любой из 6 попыток, то-есть может быть названо 1-м, 2-м, 3-м, 4-м, 5-м или 6-м. Следовательно, для угадывания числа 12 существует 6 различных вариантов. Второе число 14 может быть угадано в любой из оставшихся пяти попытках, следовательно, для его угадывания имеется 5 различных вариантов. Продолжая эти рассуждения, легко прийти к выводу, что для угадывания числа 30 существует 4 различных варианта, а числа 36 — 3 варианта. Следовательно, для угадывания четверки чисел из шести «счастливых» существуют всего 6х5х4х3 вариантов.

Но не все эти варианты различны. Предположим, что эти числа были угаданы в первых же четырех попытках. Тогда все эти варианты, соответствующие различной последовательности заполнения «счастливых» номеров в тех же самых попытках (всего 24 варианта), фактически представляют 1 вариант (число перестановок 4 элементов равно 4х3х2х1=24).

Окончательно для искомого числа сочетаний мы получили формулу:

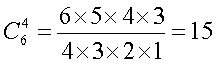
Эта формула для числа сочетаний является справедливой и при любых других количествах отмеченных чисел и количествах «угаданных». В общем случае можно сформулировать следующее правило: для того, чтобы определить количество возможных вариантов с m угаданными числами для отмеченных n чисел, необходимо вычислить число сочетаний:

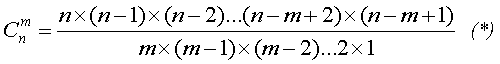
В этой формуле число сомножителей в числителе и знаменателе одинаково и равно m.

Также по этой формуле рассчитывается общее количество возможных комбинаций для игр в лотереи. А для Лото 6 из 49 получаем:

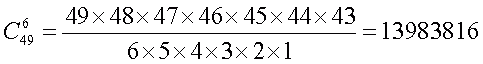
На основе формулы (*) заполняется таблица с количеством выигрышей для каждой категории выигрышей, в зависимости от того, сколько чисел было отмечено и сколько чисел было угадано. См. В качестве примера таблицу для Лото 6/49.

Средний выигрыш одной комбинации

Теперь перейдем к оценке выигрышей, которые рассчитываются на основе среднего выигрыша одного игрового варианта, разыгранного для каждой призовой категории. Средний выигрыш представляет собой вероятность возникновения этого выигрыша, умноженную на общую сумму денег, предложенную для данной призовой категории.

Согласно математическим расчетам, средние значения выигрыша для каждого рубля, потраченного в простой игровой системе и в развернутой игровой системе, одинаковы, независимо от того, сколько чисел было отмечено. Но все же различие между этими двумя игровыми системами существует.

Если мы возьмем статистическую характеристику для большого количества участников игры, то заметим, что при увеличении количества отмеченных чисел в билете в целом, выигрыши становятся крупнее, но вероятность более мелких выигрышей при этом резко уменьшается. Отсюда можно сделать вывод, что если вы стремитесь только к крупному выигрышу, то для вас предпочтительнее будет развернутая система игры, но если не любите сильно рисковать и считаете, что лучше иметь «синицу в руках, чем журавля в небе», то лучше подойдет простая система игры.

Вероятность последовательных неудач

Какова вероятность длинной серии неудач, если ставить в каждом туре на одну и ту же комбинацию? Существует формула, которая называется формулой Бернулли. Она позволяет найти вероятность того, что в результате участия в n турах игры количество туров без единого выигрыша будет равно m:

где q определяет вероятность «несчастного» случая только для одного тура т.е. не были угаданы 6, 5 и 4 номеров и определяется формулой:

где , и вероятности угадывания 4-х, 5-ти и 6-ти чисел соответственно.

Для примера, на основе формулы Бернулли и некоторых исходных статистических данных были получены следующие результаты вероятностей неудач для 4 розыгрышей:

1) Не было ни одного выигрыша: m = 4, P = 0,02 (2%)

2) Был один выигрыш: m = 3, P = 0,13 (13%)

3) Было два выигрыша: m = 2, P = 0,33 (33%)

4) Было три выигрыша: m = 1, P = 0,37 (37%)

5) Все туры были выигрышными: m = 0, P = 0,15 (15%)

2% + 13% + 33% + 37% + 15% = 100%

Как видим, вероятность последовательных проигрышей с одной и той же комбинацией чисел уменьшается с увеличением количества участий, но появление выигрыша не гарантирует того, что он будет большим.

И все-таки, несмотря на то, что непредсказуемость результатов азартной игры является ее основной чертой, нельзя ли избрать какую-то оптимальную стратегию? Единственный совет, который можно дать в этом случае — это рационально выбрать определенную систему игры и последовательно придерживаться её.

Источник

Есть ли у вас шанс выиграть в лотерею

Денис Пешехонов

По образованию магистр-технарь, в жизни занимается разработкой программ и иногда строит математические модели для игр.

Правило 1. Оценивайте риски

Да, так или иначе, даже самые сложные математические модели в среднем сводятся к одному: если вы ставите 1 рубль, а вам предлагают получить 1 000 рублей, значит, ваш шанс выиграть — меньше, чем 1/1 000.

Исключений нет, если только кто-то специально не хочет подарить вам денег. Держите в голове это простое правило, чтобы всегда трезво смотреть на ситуацию.

Теория игр оценивает любую стратегию аналогично: вероятность получить выигрыш умножается на его размер. Грубо говоря, математика считает, что гарантированно получить 1 000 рублей — это как получить 2 000 рублей с 50-процентным шансом. Этот принцип даёт вам возможность грубо сравнивать различные игры между собой. Что лучше: миллион долларов с шансом 1/100 000 или 50 долларов с шансом 1/4? Интуитивно кажется, что первое предложение интереснее, но математически выгоднее второе.

Если оставаться в рамках одной лишь математики, можно вычислить: выиграть в казино невозможно, ведь любая выбранная стратегия приводит к тому, что произведение вероятности победы на размер выплаты для игрока всегда ниже ставки, которую он уже сделал.

Однако люди играют потому, что выигрыш для них заключается не только в деньгах, но ещё и в эмоциях от процесса — и уж тем более от победы.

А ещё потому, что деньги для нас нелинейны: формально получить 1 рубль прямо сейчас — это как получить миллион рублей с шансом 1/1 000 000, но по факту потеря рубля никак не скажется на нашем состоянии, в жизни не изменится совершенно ничего, а вот получение миллиона — очень серьёзное событие.

Правило 2. Играйте в открытую

К сожалению, проникнуть на внутреннюю кухню лотереи мы не можем. Но полезно понимать хотя бы формальную процедуру того, как именно идёт розыгрыш.

Например, знаменитые игровые автоматы «Однорукий бандит» и другие слот-машины — это на самом деле немного обман: на колесе, которое видит игрок, нарисованы символы различной стоимости, но при этом всё устроено так, чтобы игрок подумал, будто шансы выпадения каждого символа одинаковые. На самом деле (в старых автоматах — механически, а в современных — с помощью программы) за каждым видимым колесом скрывается настоящее, на котором ценные символы встречаются редко, а дешёвые – часто.

Шансы выпадения 777 на слот-машине ниже, чем вероятность получить какие-нибудь три вишни, причём отличие может быть в десятки раз.

«Открытые» лотереи в этом смысле гораздо честнее. В США распространён формат, когда билет либо содержит в себе последовательность чисел, либо она выбирается покупателем самостоятельно. В России, например, предпочитают формат лото: на билете расположены несколько линий чисел, и нужно закрыть или одну из них (обычная победа), или все (джекпот). В теории проводящая лотерею фирма может «специально» печатать и продавать невыигрышные билеты, а потом подтасовывать порядок шаров, но на практике крупные компании этого не делают: организаторы лотереи и так всегда в выигрыше, а скандал в случае вскрытия недобросовестности будет огромен.

Если вы намерены сыграть в азартную игру, полезно будет понять её механику и убедиться в отсутствии влияния заинтересованных лиц на результаты.

Правило 3. Знайте свои шансы

Допустим, мы купили лотерейный билет со случайным набором чисел. Во время розыгрыша вытаскивают столько же шаров, и если числа на них совпали с числами в билете (в любом порядке, это важно!), то мы выиграли. Вероятность такого выигрыша рассчитывается так:

Вероятность выигрыша = 1 ÷ Количество комбинаций шаров.

Количество комбинаций без учёта порядка называется в математике числом сочетаний, и если формула для его расчёта вам известна и понятна, то из этой статьи вы, скорее всего, не узнаете ничего нового. Если вы не математик, то проще будет воспользоваться онлайн-сервисом, например вот этим. Подобные сервисы (и формула, лежащая в основе их работы) предлагают задать два числа:

n — общее количество возможных вариантов одного предмета. В нашем случае предмет — это шар, а всего шаров столько, сколько чисел в лотерее, об этом ниже.
k — количество предметов в одной выборке. В нашем случае — сколько шаров лотерея разыгрывает и сколько при этом чисел в билете (предполагается, что эти величины равны).

Итак, если у нас есть лотерея с розыгрышем 5 шаров, а всего в лотерее 50 шаров с числами от 1 до 50, то вероятность выиграть в неё будет равна единице к числу сочетаний при k = 5 и n = 50, то есть:

1 ÷ 2 118 760 = 0,00005%.

Рассмотрим более сложный случай — популярную американскую лотерею PowerBall, в которой величина джекпота превышала миллиард долларов. По правилам есть базовая выборка из 5 чисел (от 1 до 69), а также одно дополнительное число (от 1 до 26). Нужно получить совпадение всех 6 чисел, чтобы выиграть.

Несложно понять, что шанс получить первый набор равен единице к числу сочетаний при k = 5 и n = 69 (то есть 11 238 513), а шанс «поймать» последний шар — 1 к 26. Чтобы получить всё сразу, эти шансы нужно умножить, потому что события должны произойти одновременно:

(1 ÷ 11 238 513) × (1 ÷ 26) = 1 ÷ 292 201 338 = 0,0000003%.

Иными словами, если 300 миллионов человек купят билеты, то выиграет кто-то один. Это показывает, почему выигрыш джекпота зачастую вообще не состоится: организаторы лотереи просто не печатают так много билетов, чтобы среди них попался выигрышный.

Правило 4. Вовремя начинайте

Лотерейный билет PowerBall, кстати, стоит 2 доллара. Чтобы подсчитать выгоду, которая окупила бы покупку билета, нужно умножить цену билета на 292 201 338.

Подробнее о расчётах. Это отсылка к первому пункту, где говорится о том, что выгода от решения равна его ценности, умноженной на вероятность. Если у нас есть событие с вероятностью 1/X и ценностью N, то выгода будет N/X. Мы тратим 2 доллара и можем подсчитать, какого размера выигрыш окупил бы покупку билета:

2 = N ÷ X.
N = 2 × X, а X тут как раз равен 292 201 338, как показали расчёты из предыдущей части

Ещё надо учесть налоги (узнать, какой процент от заявленной суммы фактически достанется победителю, обычно это около 70%). То есть джекпот должен составлять как минимум 850 миллионов долларов, и такое в этой лотерее бывает. Как же так, я ведь в начале сказал, что выигрыш при таком умножении всегда не в пользу игрока?

Дело в том, что если розыгрыш джекпота не состоялся, то он переходит на следующий раз, и поэтому какое-то время деньги копятся, а продажи билетов продолжаются.

В идеальной ситуации вам нужно пропускать все игры, не покупая билет, а потом купить именно на ту игру, в которой розыгрыш действительно состоится.

Но узнать это заранее невозможно. Однако можно начать покупать билеты, как только размер джекпота станет больше упомянутой суммы. В такой ситуации математически игра будет выгодной.

Ещё можно понять, что выгоднее: купить много билетов на одну игру или покупать по одному билету на много игр? Давайте подумаем.

В теории вероятностей есть понятие несвязанных событий. Это означает, что исход одного события никак не влияет на исход другого. Например, если вы кидаете два кубика, то выпадения чисел на них не связаны между собой: с точки зрения случайности, один кубик не влияет на поведение второго. А вот если вы тянете из колоды две карты, то эти события связаны, ведь от первой карты зависит то, какие карты останутся в колоде.

Популярное заблуждение по этому поводу так и называется — ошибка игрока. Оно возникает из-за интуитивного представления человека о связанности несвязанных событий.

Например, если монета много раз подряд выпадает орлом, то мы склонны считать, что шансы выпадения решки из-за этого увеличатся, но на самом деле это не так, шансы всегда одинаковые.

Возвращаясь к лотереям: разные игры — это несвязанные события, потому что последовательность шаров выбирается заново. Так что шансы выиграть в любую конкретную лотерею никак не зависят от того, сколько раз раньше вы в неё играли. Это очень сложно принять интуитивно, потому что человек каждый раз, покупая билет, думает: «Ну вот сейчас-то повезёт, сколько можно, я уже кучу времени играю!» Но нет, теория вероятностей — бессердечная штука.

А вот покупка нескольких билетов для одной игры увеличивает ваши шансы пропорционально, потому что билеты внутри одной игры связаны: если выиграет один, значит, другой (с другой комбинацией) точно не выиграет. Покупка 10 билетов увеличивает шансы в 10 раз, если все комбинации на билетах разные (по факту почти всегда так и есть). Иными словами, если у вас есть деньги на 10 билетов, лучше купить их на одну игру, чем покупать по билету на 10 игр.

После ваших уточнений в комментариях справедливо будет заметить, что вероятность выиграть хотя бы в одной игре в серии из N игр выше, чем вероятность выиграть в любой одной конкретной игре. Впрочем, она всё ещё немного меньше, чем шансы выиграть, купив N билетов на одну игру, но разрыв довольно небольшой.

Если вы просто с зарплаты раз в месяц берёте билетик азарта ради, то, скорее всего, значение для вас имеет сам процесс игры. Математически выгоднее скопить эти деньги и в конце года купить сразу 12 билетов, хотя, конечно, проигрыш в такой ситуации будет восприниматься более сокрушительно.

Правило 5. Вовремя останавливайтесь

В заключение, как обещал, приведу оценку утверждению из начала статьи. Эти данные для США, потому что утверждение было сформулировано именно для этой страны, к тому же мы выше уже посчитали шансы для американской лотереи.

По статистике, за 2016 год в США было совершено около 17 000 убийств, будем считать это средней цифрой. А ещё предположим, что человек является потенциальной целью для убийства, когда он уже взрослый, но не старый — то есть около 50 лет в течение своей жизни. Значит, за эти 50 лет будет совершено около 850 000 убийств. Население США составляет 325,7 миллиона человек, то есть шансы попасть в случайную выборку размером 850 000 такие:

850 000 ÷ 325 700 000 = 1 ÷ 383 = 0,3%.

Но погодите, это просто шанс быть убитым. А именно по пути за лотерейным билетом? Предположим, вы выходите из дома на работу каждый будний день, в один выходной куда-то выбираетесь, а в другой остаётесь дома. В среднем получается 6 дней в неделю, или около 26 дней в месяц. И один раз в месяц вы покупаете лотерейный билет. Поэтому полученные числа нужно ещё и разделить на 26:

(1 ÷ 383) ÷ 26 = 1 ÷ 9 958 = 0,01%.

И даже при такой грубой оценке это существенно вероятнее, чем выигрыш. Если точнее, то в 30 000 раз вероятнее. На самом деле, конечно, числа будут другие: человек подвергается опасности не только на улице, одни люди больше рискуют, чем другие, женщин убивают почти в четыре раза реже, чем мужчин. Но принцип такой.

Хотя жить без веры в хорошие события и с постоянным ожиданием плохих, даже зная математику, — это не самый лучший выбор.

*Деятельность Meta Platforms Inc. и принадлежащих ей социальных сетей Facebook и Instagram запрещена на территории РФ.

Источник

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49

Портфолио эксперта

Что такое теория вероятностей и как она связана с лотереями?

Вопросы и претензии участников

Choosing 6 from 49[edit]

Odds of getting other possibilities in choosing 6 from 49[edit]

Ensuring to win the jackpot[edit]

Powerballs and bonus balls[edit]

Minimum number of tickets for a match[edit]

Information theoretic results[edit]

References[edit]

External links[edit]

Правило 1. Оценивайте риски

Правило 2. Играйте в открытую

Правило 3. Знайте свои шансы

Правило 4. Вовремя начинайте

Правило 5. Вовремя останавливайтесь

Как вычислить вероятность?

Как вычислить количество всех возможных результатов?

Как вычислить количество комбинаций?

Средний выигрыш одной комбинации

Вероятность последовательных неудач

Есть ли у вас шанс выиграть в лотерею

Правило 1. Оценивайте риски

Правило 2. Играйте в открытую

Правило 3. Знайте свои шансы

Правило 4. Вовремя начинайте

Правило 5. Вовремя останавливайтесь

Не пропустите также:

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49