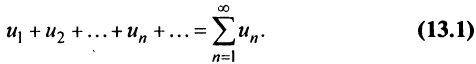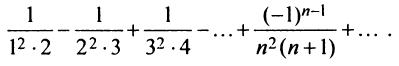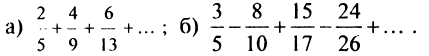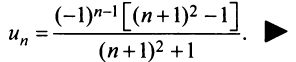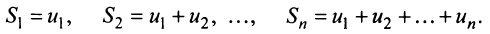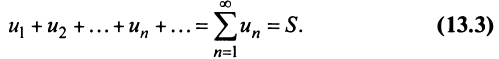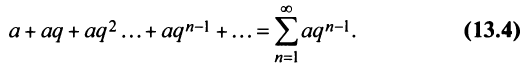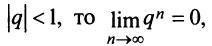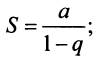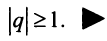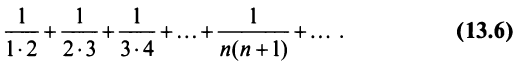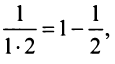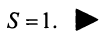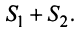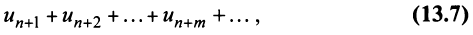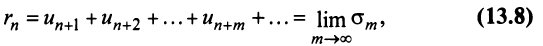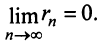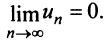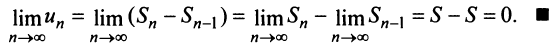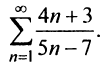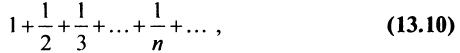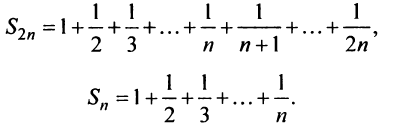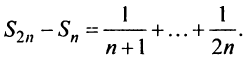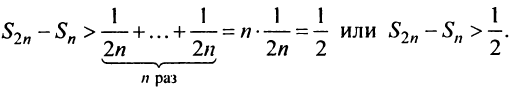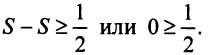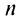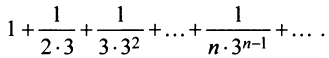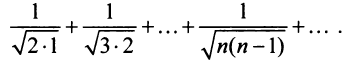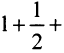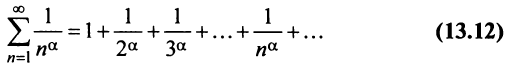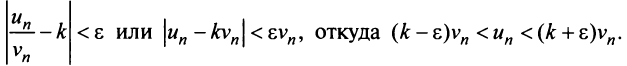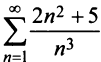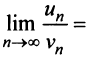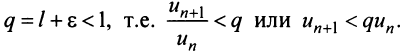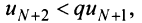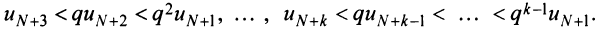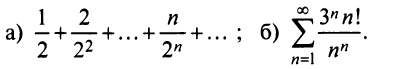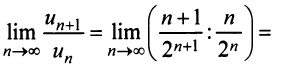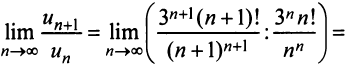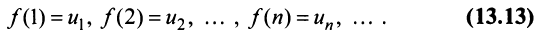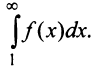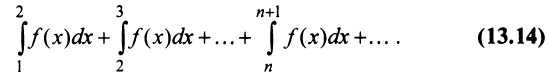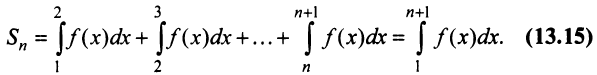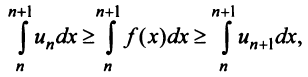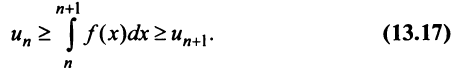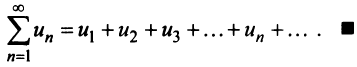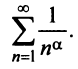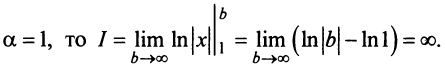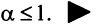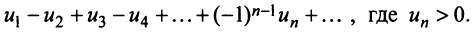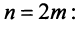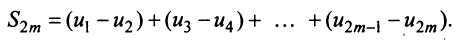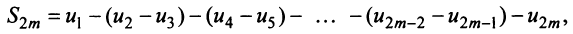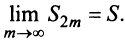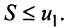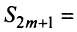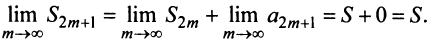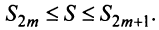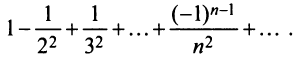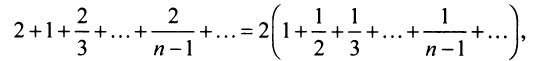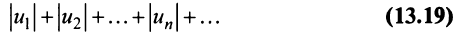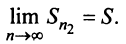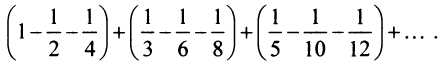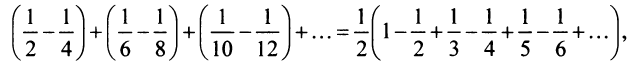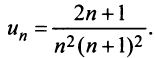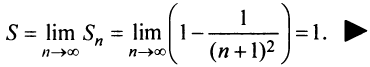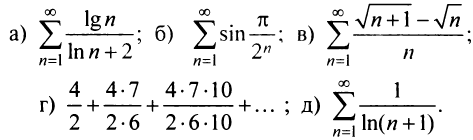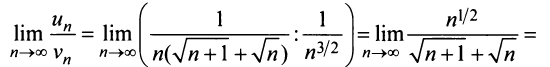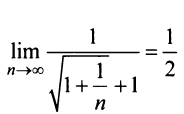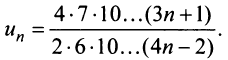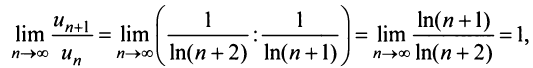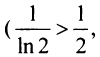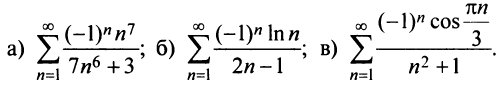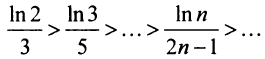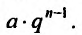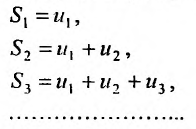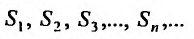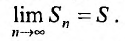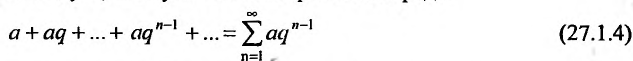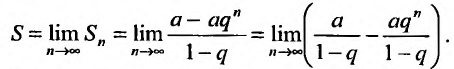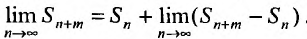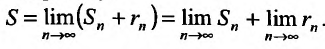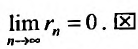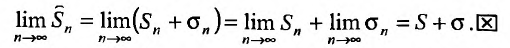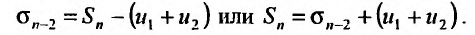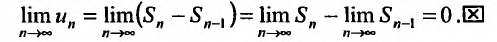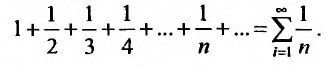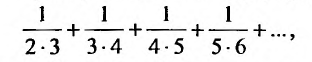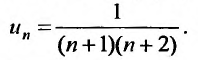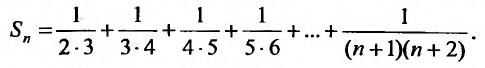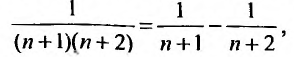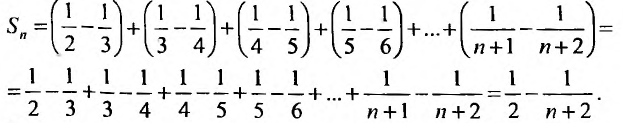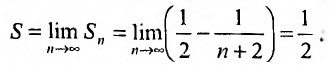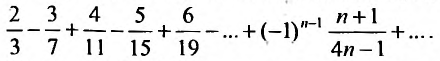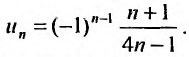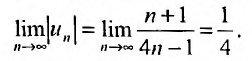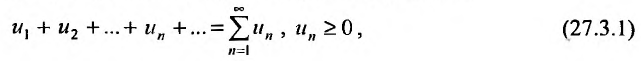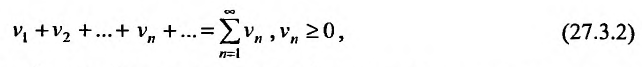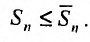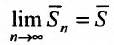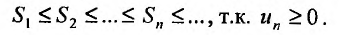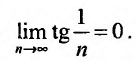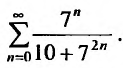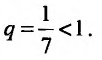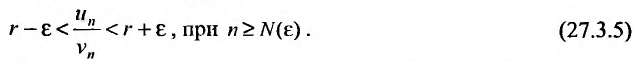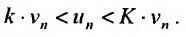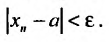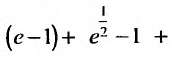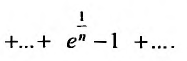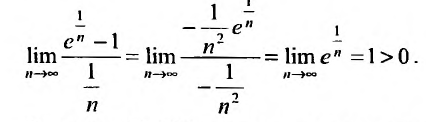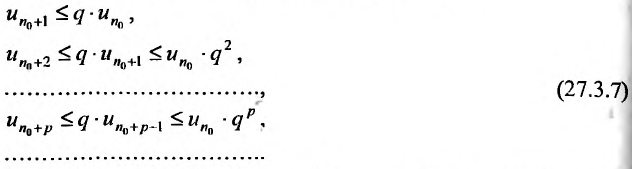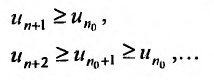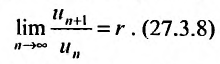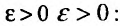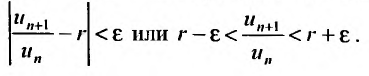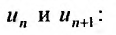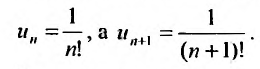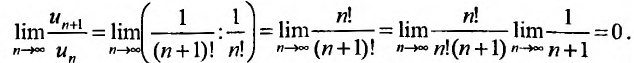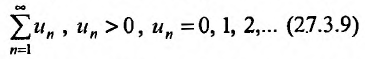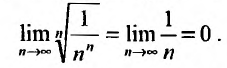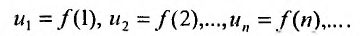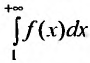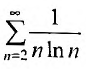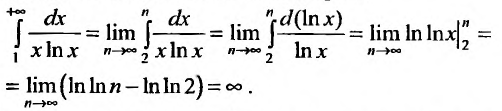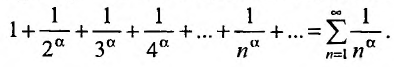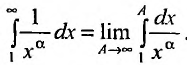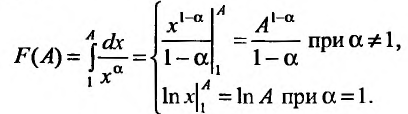Общий член ряда представляе собой рациональную дробь. Выполним разложение дроби на простейшие с помощью метода неопределенных коэффициентов:
$$ frac{1}{(2n+1)(2n+3)} = frac{A}{2n+1} + frac{B}{2n+3} = frac{A(2n+3)+B(2n+1)}{(2n+1)(2n+3)} $$
Приравниваем числитель последней дроби к числителю первой дроби:
$$ A(2n+3)+B(2n+1) = 1 $$
Раскрываем скобки:
$$ 2An + 3A + 2Bn + B = 1 $$
Теперь определяем находим неизвестные коэффициенты:
$$ begin{cases} n^0: &2A+2B=0 \ n^1: &3A+B=1 end{cases}Rightarrow begin{cases} A=frac{1}{2} \ B=-frac{1}{2} end{cases} $$
После разложения общий член ряда записывается следующим образом:
$$ a_n =frac{1}{(2n+1)(2n+3)}=frac{1}{2} frac{1}{2n+1} — frac{1}{2} frac{1}{2n+3} $$
Далее составим частичную сумму ряда: $$ S_n = a_1 + a_2 + a_3 + a_4 + … + a_n $$
$$ a_1 = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}bigg ) $$
$$ a_2 = frac{1}{2} bigg (frac{1}{5}-frac{1}{7}bigg ) $$
$$ a_3 = frac{1}{2} bigg (frac{1}{7}-frac{1}{9}bigg ) $$
$$ …………………………………. $$
$$ a_{n-1}=frac{1}{2} bigg (frac{1}{2n-1}-frac{1}{2n+1} bigg ) $$
$$ a_n = frac{1}{2} bigg (frac{1}{2n+1}-frac{1}{2n+3} bigg ) $$
| Замечание |
|
Достаточно часто читатели нам присылают просьбы найти суммы своих рядов по причине того, что они не понимают, откуда получается $ a_{n-1} $. Обратите внимание, чтобы составить $ a_{n-1} $ необходимо подставить в $ a_n $ вместо буковки $ n $ выражение $ n-1 $. После выполнить раскрытие скобок. |
Итого, получаем:
$$ S_n = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}bigg ) + frac{1}{2} bigg (frac{1}{5}-frac{1}{7}bigg ) + frac{1}{2} bigg (frac{1}{7}-frac{1}{9}bigg ) + … $$
$$ … + frac{1}{2} bigg (frac{1}{2n-1}-frac{1}{2n+1} bigg ) + frac{1}{2} bigg (frac{1}{2n+1}-frac{1}{2n+3} bigg ) = $$
Выносим дробь одну вторую $ frac{1}{2} $ за скобки:
$$ = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}+frac{1}{5}-frac{1}{7}+frac{1}{7}-frac{1}{9} … + $$
$$ + … frac{1}{2n-1} — frac{1}{2n+1} + frac{1}{2n+1} — frac{1}{2n+3} bigg) = $$
Замечаем, что в скобках есть подобные слагаемые, которые взаимно уничтожаются. Остаются только лишь два из них:
$$ S_n = frac{1}{2}bigg (frac{1}{3}-frac{1}{2n+3} bigg ) $$
Теперь осталось вычислить предел частичной суммы $ S_n $. Если он существует и конечен, то он является суммой ряда, а сам ряд сходится:
$$ S=lim_{ntoinfty} S_n = lim_{ntoinfty} frac{1}{2}bigg (frac{1}{3}-frac{1}{2n+3} bigg ) = $$
$$ = frac{1}{2} lim_{ntoinfty} bigg (frac{1}{3}-frac{1}{2n+3} bigg ) = frac{1}{2} cdot frac{1}{3} = frac{1}{6} $$
Содержание:
- Понятие суммы ряда
- Вычисление суммы ряда почленным интегрированием
- Вычисление суммы ряда почленным дифференцированием
Понятие суммы ряда
Постановка задачи. Найти сумму ряда
где 
План решения. Суммой ряда 


где
1. По условию задачи
Если корни знаменателя различаются на целое число, т.е. 



По этой ссылке вы найдёте полный курс лекций по высшей математике:
2. Разлагаем общий член ряда на элементарные дроби:
и выписываем несколько членов ряда так, чтобы было видно, какие слагаемые сокращаются при вычислении частичных сумм ряда.
3. Находим 

сократив соответствующие слагаемые.
4. Вычисляем сумму ряда по формуле (1)
и записываем ответ.
Пример:
Найти сумму ряда
Решение:
1. Корни знаменателя 




2. Разлагаем общий член ряда на элементарные дроби
и выписываем несколько членов ряда:
3. Сокращая все слагаемые, какие возможно, находим 
4. Вычисляем сумму ряда по формуле (1):
Ответ:
Возможно вам будут полезны данные страницы:
Вычисление суммы ряда почленным интегрированием
Постановка задачи. Найти сумму функционального ряда вида
и указать область сходимости ряда к этой сумме.
План решения.
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
Если 

2. Делаем в исходном ряде замену 
с областью сходимости 
3. Известна формула для вычисления суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке
, целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем
Заметим, что так как ряд (1) сходится в граничной точке 
6. Вычисляем интеграл, делаем замену 

Замечание. Если ряд имеет вид
то применяем теорему о почленном интегрировании степенного ряда дважды или разлагаем дробь на элементарные:
и вычисляем сумму каждого ряда почленным интегрированием.
Пример:
Найти сумму ряда
и указать область сходимости ряда к этой сумме.
Решение:
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
В граничных точках при 

Следовательно, данный ряд сходится при всех 
2. Сделаем замену 
3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке 
Заметим, что так как ряд (1) сходится в граничной точке 

6. Заменяя 

Ответ.
Вычисление суммы ряда почленным дифференцированием
Постановка задачи. Найти сумму функционального ряда вида
и указать область сходимости ряда к этой сумме.
План решения.
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
Если 

2. Делаем в исходном ряде замену 
Следовательно, достаточно найти суммы рядов

3. Известна формула для суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (1), получаем
6. Вычисляем производную и делаем замену 

Замечание. Если ряд имеет вид
то вычисляем сумму трех рядов, причем при вычислении суммы ряда
применяем теорему о почленном дифференцировании степенного ряда дважды.
Пример:
Найти сумму ряда
и указать область сходимости ряда к этой сумме.
Решение:
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством 



2. Делаем в исходном ряде замену 
Следовательно, достаточно найти суммы рядов
3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии:
Следовательно, 

4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (2), получаем
Таким образом,
Заменяя 

Ответ.
Лекции:
- Метод Якоби
- Метод интегрирования
- Свойства функций, имеющих конечный предел
- Дифференциал длины дуги кривой. Формула парабол
- Дифференциальное уравнение Бернулли
- Область сходимости ряда
- Метод Ритца
- Разложение в ряд фурье функций
- Построение графиков функции с помощью производной
- Формулы двойного угла
Нахождение суммы числового ряда. Первая часть.
В теме про основные понятия числовых рядов было указано определение суммы ряда. Вот оно:
Если существует конечный предел $S=lim_{ntoinfty}S_n$, то его называют суммой ряда $sumlimits_{n=1}^{infty}u_n$ и сам ряд именуют сходящимся. Если же $lim_{ntoinfty}S_n=infty$ или $lim_{ntoinfty}S_n$ не существует, то ряд называют расходящимся.
Если понятие «частичная сумма» вызывает вопросы, то советую посмотреть раздел про частичную сумму ряда, обратив внимание на пример №4. В этом примере подробно раскрывается суть частичной суммы и остатка.
В данной теме нас будет интересовать вопрос нахождения сумм числовых рядов по определению. Определение суммы ряда опирается на значение $lim_{ntoinfty}S_n$, поэтому для нахождения суммы нам нужно выполнить два шага:
- Составить n-ю частичную сумму $S_n$;
- Найти $lim_{ntoinfty}S_n$ (если он существует).
Если конечный $lim_{ntoinfty}S_n$ существует, то его значение и будет суммой рассматриваемого ряда, а сам ряд будет именоваться сходящимся. Если же $lim_{ntoinfty}S_n=infty$ или $lim_{ntoinfty}S_n$ не существует, то ряд будет расходиться. Есть несколько стандартных приёмов, которые применяются для нахождения суммы числовых рядов. Например, для нахождения суммы ряда, общий член которого имеет вид рациональной дроби $u_n=frac{P(n)}{Q(n)}$, вполне подходит такой алгоритм:
- Разложить дробь $frac{P(n)}{Q(n)}$ на элементарные дроби (процедура разложения описана тут).
- Записать выражение для частичной суммы $S_n$, используя результаты предыдущего пункта.
- Перегруппировать слагаемые в выражении для $S_n$, приведя их к удобному для сокращения виду.
- Используя результат предыдущего пункта, найти $lim_{ntoinfty}S_n$.
Для нахождения суммы ряда нередко удобно использовать и такое свойство:
Пусть общий член ряда $sumlimits_{n=1}^{infty}u_n$ можно представить в виде $u_n=b_{n+1}-b_n$. Если существует конечный предел $lim_{ntoinfty}b_n=b$, то ряд $sumlimits_{n=1}^{infty}u_n$ сходится. При этом частичная сумма ряда равна $S_{n}=b_{n+1}-b_1$, а сумма ряда $S=b-b_1$.
Доказательство этого свойства может быть интересно не всем читателям, поэтому я скрою его под примечание.
Доказательство свойства: показатьскрыть
Во всех изложенных ниже примерах члены рядов будем обозначать буквами $u_1$ (первый член ряда), $u_2$ (второй член ряда) и так далее. Запись $u_n$ будет обозначать общий член ряда.
Пример №1
Найти сумму ряда $sumlimits_{n=1}^{infty}(-1)^{n+1}$.
Решение
Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=(-1)^{n+1}$. Составим n-ю частичную сумму ряда, т.е. просуммируем первые $n$ членов числового ряда:
$$
S_n=u_1+u_2+u_3+u_4+ldots+u_n=\=(-1)^2+(-1)^3+(-1)^4+(-1)^5+ldots+(-1)^{n+1}=1-1+1-1+ldots+(-1)^n.
$$
Вопрос в следующем: чему равна эта сумма? Если в частичных суммах мы станем брать чётное количество слагаемых, они попарно сократятся:
begin{aligned}
& S_2=1-1=0;\
& S_4=1-1+1-1=0;\
& S_6=1-1+1-1+1-1=0;\
& S_8=1-1+1-1+1-1+1-1=0.
end{aligned}
Итак, частичная сумма, содержащая чётное количество слагаемых, равна 0. Т.е. если $n$ – чётное число, то $S_n=0$. Фразу «n – чётное число» можно записать так: $n=2k$, $kin N$. В самом деле, подставляя вместо $k$ значения 1, 2, 3, 4 будем получать $n=2cdot 1=2$, $n=2cdot 2=4$, $n=2cdot 3=6$, $n=2cdot 4=8$ и так далее. Итак, $S_{2k}=0$.
Если мы станем брать нечётное количество слагаемых (1, 3, 5 и т.д.), то сумма станет равна 1:
begin{aligned}
& S_1=1;\
& S_3=1-1+1=1;\
& S_5=1-1+1-1+1=1;\
& S_7=1-1+1-1+1-1+1=1.
end{aligned}
Таким образом, если $n$ – нечётное число, то $S_n=1$. Фразу «n – нечётное число» можно записать так: $n=2k-1$, $kin N$. В самом деле, подставляя вместо $k$ значения 1, 2, 3, 4 будем получать $n=2cdot 1-1=1$, $n=2cdot 2-1=3$, $n=2cdot 3-1=5$, $n=2cdot 4-1=7$ и так далее. Итак, $S_{2k-1}=1$.
Формально равенство $S_{2k-1}=1$ можно доказать с помощью формулы $S_{2k}=S_{2k-1}+u_{2k}$. Так как $S_{2k}=0$, то $S_{2k-1}+u_{2k}=0$, т.е. $S_{2k-1}=-u_{2k}$. Так как $u_{2k}=(-1)^{2k+1}=left((-1)^2right)^kcdot (-1)^1=-1$, то $S_{2k-1}=-(-1)=1$.
Возникает вопрос: как быть с пределом $lim_{ntoinfty}S_n$? Ведь если $n$ – чётное число, т.е. $n=2k$, то:
$$
lim_{ntoinfty}S_n=lim_{ktoinfty}S_{2k}=lim_{ktoinfty}0=0.
$$
С другой стороны, если $n$ – нечётное число, то:
$$
lim_{ntoinfty}S_n=lim_{ktoinfty}S_{2k-1}=lim_{ktoinfty}1=1.
$$
Что мы получили? А получили мы следующее: последовательность частичных сумм ${S_n}$ имеет две подпоследовательности: ${S_{2k-1}}$ и ${S_{2k}}$, пределы которых различны. Следовательно, последовательность ${S_n}$ не имеет предела. Вывод: ряд не имеет суммы, т.е. расходится.
Здесь стоит обратить внимание вот на что: следует различать случаи, когда предел равен бесконечности (см. следующий пример №2), и когда предела попросту не существует. Хотя и в том и в другом случаях ряд будет расходиться.
Ответ: ряд расходится.
Пример №2
Найти сумму ряда $sumlimits_{n=1}^{infty}(3n+1)$.
Решение
Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=3n+1$. Составим n-ю частичную сумму ряда, т.е. просуммируем первые $n$ членов заданного числового ряда:
$$
S_n=u_1+u_2+u_3+u_4+ldots+u_n=4+7+10+13+ldots+3n+1.
$$
Эту сумму можно записать в более коротком виде. Дело в том, что последовательность 4, 7, 10, 13 и т.д. есть арифметическая прогрессия, первый член которой равен 4, а разность равна 3. Сумма первых n членов этой прогрессии такова:
$$
4+7+10+13+ldots+3n+1=frac{4+3n+1}{2}cdot n=frac{3n+5}{2}cdot{n}.
$$
Итак, $S_n=frac{3n+5}{2}cdot n$. Найдем $lim_{ntoinfty}S_n$:
$$
lim_{ntoinfty}S_n=lim_{ntoinfty}left(frac{3n+5}{2}cdot nright)=+infty.
$$
Так как $lim_{ntoinfty}S_n=+infty$, то ряд расходится.
Если немного выйти за рамки данной темы, то стоит отметить, что расходимость этого ряда легко доказывается с помощью необходимого признака сходимости.
Ответ: ряд расходится.
Пример №3
Найти сумму ряда $sumlimits_{n=1}^{infty}frac{2}{(2n+1)(2n+3)}$.
Решение
Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=frac{2}{(2n+1)(2n+3)}$. Составим n-ю частичную сумму ряда, т.е. просуммируем первые $n$ членов заданного числового ряда:
$$
S_n=u_1+u_2+u_3+u_4+ldots+u_n=frac{2}{3cdot 5}+frac{2}{5cdot 7}+frac{2}{7cdot 9}+frac{2}{9cdot 11}+ldots+frac{2}{(2n+1)(2n+3)}.
$$
Почему я пишу именно $frac{2}{3cdot 5}$, а не $frac{2}{15}$, будет ясно из дальнейшего повествования. Однако запись частичной суммы ни на йоту не приблизила нас к цели. Нам ведь нужно найти $lim_{ntoinfty}S_n$, но если мы просто запишем:
$$
lim_{ntoinfty}S_n=lim_{ntoinfty}left(frac{2}{3cdot 5}+frac{2}{5cdot 7}+frac{2}{7cdot 9}+frac{2}{9cdot 11}+ldots+frac{2}{(2n+1)(2n+3)}right),
$$
то эта запись, совершенно верная по форме, ничего нам не даст по сути. Чтобы найти предел, выражение частичной суммы предварительно нужно упростить.
Для этого есть стандартное преобразование, состоящее в разложении дроби $frac{2}{(2n+1)(2n+3)}$, которая представляет общий член ряда, на элементарные дроби. Вопросу разложения рациональных дробей на элементарные посвящена отдельная тема (см., например, пример №3 на этой странице). Раскладывая дробь $frac{2}{(2n+1)(2n+3)}$ на элементарные дроби, будем иметь:
$$
frac{2}{(2n+1)(2n+3)}=frac{A}{2n+1}+frac{B}{2n+3}=frac{Acdot(2n+3)+Bcdot(2n+1)}{(2n+1)(2n+3)}.
$$
Приравниваем числители дробей в левой и правой частях полученного равенства:
$$
2=Acdot(2n+3)+Bcdot(2n+1).
$$
Чтобы найти значения $A$ и $B$ есть два пути. Можно раскрыть скобки и перегруппировать слагаемые, а можно просто подставить вместо $n$ некие подходящие значения. Сугубо для разнообразия в этом примере пойдём первым путём, а следующем – будем подставлять частные значения $n$. Раскрывая скобки и перегруппировывая слагаемые, получим:
$$
2=2An+3A+2Bn+B;\
2=(2A+2B)n+3A+B.
$$
В левой части равенства перед $n$ стоит ноль. Если угодно, левую часть равенства для наглядности можно представить как $0cdot n+ 2$. Так как в левой части равенства перед $n$ стоит ноль, а в правой части равества перед $n$ стоит $2A+2B$, то имеем первое уравнение: $2A+2B=0$. Сразу разделим обе части этого уравнения на 2, получив после этого $A+B=0$.
Так как в левой части равенства свободный член равен 2, а в правой части равенства свободный член равен $3A+B$, то $3A+B=2$. Итак, имеем систему:
$$
left{begin{aligned}
& A+B=0;\
& 3A+B=2.
end{aligned}right.
$$
Можно решать эту систему методом Крамера, методом Гаусса или с помощью обратной матрицы. Однако проще всего банально выразить из первого уравнения $A=-B$ и подставить во второе:
$$
3cdot (-B)+B=2;; -2B=2; ; B=-1.
$$
Так как $B=-1$, то $A=-B=1$. Подставляя найденные значения $A=1$ и $B=-1$ в формулу $frac{2}{(2n+1)(2n+3)}=frac{A}{2n+1}+frac{B}{2n+3}$, будем иметь:
$$
frac{2}{(2n+1)(2n+3)}=frac{1}{2n+1}+frac{-1}{2n+3}=frac{1}{2n+1}-frac{1}{2n+3}.
$$
Итак, $u_n=frac{1}{2n+1}-frac{1}{2n+3}$. Используем полученное разложение для того, чтобы упростить формулу частичной суммы ряда. Покажу сначала решение стандартным путём, принятым в большинстве решебников и методичек.
Первый способ упрощения формулы для частичной суммы.
Мы получили разложение общего члена ряда на две дроби: $u_n=frac{1}{2n+1}-frac{1}{2n+3}$. Чтобы этот результат был более наглядным, я распишу несколько первых членов ряда по этой формуле:
begin{aligned}
& u_1=frac{2}{3cdot 5}=frac{1}{3}-frac{1}{5};\
& u_2=frac{2}{5cdot 7}=frac{1}{5}-frac{1}{7};\
& u_3=frac{2}{7cdot 9}=frac{1}{7}-frac{1}{9};\
& u_4=frac{2}{9cdot 11}=frac{1}{9}-frac{1}{11}.
end{aligned}
Давайте распишем частичную сумму, учитывая полученное разложение каждого элемента:
$$
S_n=u_1+u_2+u_3+u_4+ldots+u_n=frac{1}{3}-frac{1}{5}+frac{1}{5}-frac{1}{7}+frac{1}{7}-frac{1}{9}+frac{1}{9}-frac{1}{11}+ldots+frac{1}{2n+1}-frac{1}{2n+3}.
$$
Как видите, все слагаемые этой суммы сокращаются, – кроме первого и последнего:
Итак, $S_n=frac{1}{3}-frac{1}{2n+3}$. Этот способ упрощения формулы для частичной суммы имеет простую суть: разложить общий член ряда на элементарные дроби, а потом сократить слагаемые.
Однако можно ли считать вышеуказанные рассуждения строгим доказательством? Полагаю, что в общем случае нет, и поясню почему. Дело в том, что мы должны «увидеть» (как любят писать некоторые авторы – «легко увидеть»), что слагаемые сокращаются. А если мы «увидим» не все слагаемые, которые останутся после сокращения? Где гарантии, что мы сократим именно то, что нужно? Нет гарантий. Понятно, что в случае рассматриваемой конкретной задачи всё тривиально и очевидно, но далеко не все частичные суммы рядов имеют такую простую структуру.
Формулу $S_n=frac{1}{3}-frac{1}{2n+3}$ можно принять в качестве гипотезы, которую ещё нужно доказать. Доказательство удобнее всего проводить методом математической индукции. Так как доказательством заинтересуются не все читатели, то я его скрыл под примечание.
Доказательство формулы $S_n=frac{1}{3}-frac{1}{2n+3}$: показатьскрыть
В стандартном курсе высшей математики обычно довольствуются «вычёркиванием» сокращающихся слагаемых, не требуя никаких доказательств. Итак, мы получили выражение для n-й частичной суммы: $S_n=frac{1}{3}-frac{1}{2n+3}$. Найдём значение $lim_{ntoinfty}S_n$:
$$
lim_{ntoinfty}S_n=lim_{ntoinfty}left(frac{1}{3}-frac{1}{2n+3}right)=frac{1}{3}-0=frac{1}{3}.
$$
Вывод: заданный ряд сходится и сумма его $S=frac{1}{3}$.
Второй способ упрощения формулы для частичной суммы.
Этот способ основан на свойстве, записанном в начале страницы. По сути, он схож с предыдущим, – разница лишь в применении уже готовой теоремы, доказанной нами ранее. Вернёмся к записи общего члена ряда:
$$
u_n=frac{1}{2n+1}-frac{1}{2n+3}
=frac{-1}{2n+3}-frac{-1}{2n+1}
$$
Обозначим $b_n=frac{-1}{2n+1}$, тогда $b_{n+1}=frac{-1}{2(n+1)+1}=frac{-1}{2n+3}$. Таким образом, $u_{n}=b_{n+1}-b_{n}$. При этом $lim_{ntoinfty}b_n=0$. Согласно упомянутому свойству, ряд $sumlimits_{n=1}^{infty}u_n$ сходится. При этом его сумма равна $S=0-b_1=frac{1}{3}$. Если есть необходимость, можно записать и частичную сумму ряда:
$$
S_n
=b_{n+1}-b_1
=frac{-1}{2n+3}-left(-frac{1}{3}right)
=frac{1}{3}-frac{1}{2n+3}
$$
Третий способ упрощения формулы для частичной суммы.
Честно говоря, я сам предпочитаю большей частью именно этот способ 
$$
S_n=sumlimits_{k=1}^{n}u_k=sumlimits_{k=1}^{n}frac{2}{(2k+1)(2k+3)}.
$$
Мы получили ранее, что $u_k=frac{1}{2k+1}-frac{1}{2k+3}$, поэтому:
$$
S_n=sumlimits_{k=1}^{n}frac{2}{(2k+1)(2k+3)}=sumlimits_{k=1}^{n}left(frac{1}{2k+1}-frac{1}{2k+3}right).
$$
Сумма $S_n$ содержит конечное количество слагаемых, поэтому мы можем переставлять их так, как нам заблагорассудится. Я хочу сначала сложить все слагаемые вида $frac{1}{2k+1}$, а уж затем переходить к слагаемым вида $frac{1}{2k+3}$. Это означает, что частичную сумму мы представим в таком виде:
$$
S_n
=frac{1}{3}-frac{1}{5}+frac{1}{5}-frac{1}{7}+frac{1}{7}-frac{1}{9}+frac{1}{9}-frac{1}{11}+ldots+frac{1}{2n+1}-frac{1}{2n+3}=\
=frac{1}{3}+frac{1}{5}+frac{1}{7}+frac{1}{9}+ldots+frac{1}{2n+1}-left(frac{1}{5}+frac{1}{7}+frac{1}{9}+ldots+frac{1}{2n+3}right).
$$
Конечно, развёрнутая запись крайне неудобна, поэтому представленное выше равенство оформим более компактно:
$$
S_n=sumlimits_{k=1}^{n}left(frac{1}{2k+1}-frac{1}{2k+3}right)=sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=1}^{n}frac{1}{2k+3}.
$$
Теперь преобразуем выражения $frac{1}{2k+1}$ и $frac{1}{2k+3}$ к одному виду. Приведём, например, дробь $frac{1}{2k+3}$ к виду $frac{1}{2k+1}$. Выражение в знаменателе дроби $frac{1}{2k+3}$ я представлю в таком виде:
$$
frac{1}{2k+3}=frac{1}{2k+2+1}=frac{1}{2(k+1)+1}.
$$
И сумму $sumlimits_{k=1}^{n}frac{1}{2k+3}$ теперь можно записать так:
$$
sumlimits_{k=1}^{n}frac{1}{2k+3}=sumlimits_{k=1}^{n}frac{1}{2(k+1)+1}=sumlimits_{k=2}^{n+1}frac{1}{2k+1}.
$$
Если равенство $sumlimits_{k=1}^{n}frac{1}{2k+3}=sumlimits_{k=2}^{n+1}frac{1}{2k+1}$ не вызывает вопросов, то пойдём далее. Если же вопросы есть, то прошу развернуть примечание.
Как мы получили преобразованную сумму? показатьскрыть
Таким образом, частичную сумму можно представить в следующем виде:
$$
S_n=sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=1}^{n}frac{1}{2k+3}=sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=2}^{n+1}frac{1}{2k+1}.
$$
Заметьте, что суммы $sumlimits_{k=1}^{n}frac{1}{2k+1}$ и $sumlimits_{k=2}^{n+1}frac{1}{2k+1}$ отличаются лишь пределами суммирования. Сделаем эти пределы одинаковыми. Начнём с первой суммы.
Сделаем так, чтобы верхний предел суммирования стал равен $n+1$. Если $k=n+1$, то $frac{1}{2k+1}=frac{1}{2n+3}$. Прибавляя и вычитая из первой суммы $frac{1}{2n+3}$, получим:
$$
sumlimits_{k=1}^{n}frac{1}{2k+1}
=sumlimits_{k=1}^{n}frac{1}{2k+1}+frac{1}{2n+3}-frac{1}{2n+3}
=sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{2n+3}
$$
Для второй суммы $sumlimits_{k=2}^{n+1}frac{1}{2k+1}$ сделаем так, чтобы нижний предел суммирования был равен 1. Если $k=1$, то $frac{1}{2k+1}=frac{1}{3}$. Прибавляя и вычитая $frac{1}{3}$, получим:
$$
sumlimits_{k=2}^{n+1}frac{1}{2k+1}
=sumlimits_{k=2}^{n+1}frac{1}{2k+1}+frac{1}{3}-frac{1}{3}
=sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{3}
$$
С учётом полученных результатов, выражение для $S_n$ примет такой вид:
$$
S_n
=sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{2n+3}-left(sumlimits_{k=1}^{n}frac{1}{2k+1}-frac{1}{3}right)
=frac{1}{3}-frac{1}{2n+3}
$$
Если пропустить все пояснения, то процесс нахождения сокращённой формулы для n-й частичной суммы примет такой вид:
$$
S_n=sumlimits_{k=1}^{n}u_k
=sumlimits_{k=1}^{n}frac{2}{(2k+1)(2k+3)}
=sumlimits_{k=1}^{n}left(frac{1}{2k+1}-frac{1}{2k+3}right)=\
=sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=1}^{n}frac{1}{2k+3}
=sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=2}^{n+1}frac{1}{2k+1}=\
=sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{2n+3}-left(sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{3}right)
=frac{1}{3}-frac{1}{2n+3}
$$
Напомню, что мы приводили дробь $frac{1}{2k+3}$ к виду $frac{1}{2k+1}$. Разумеется, можно поступить и наоборот, т.е. представить дробь $frac{1}{2k+1}$ в виде $frac{1}{2k+3}$. Конечное выражение для частичной суммы не изменится. Процесс нахождения частичной суммы в этом случае я скрою под примечание.
Как найти $S_n$, если приводить к виду иной дроби? показатьскрыть
Итак, $S_n=frac{1}{3}-frac{1}{2n+3}$. Находим предел $lim_{ntoinfty}S_n$:
$$
lim_{ntoinfty}S_n=lim_{ntoinfty}left(frac{1}{3}-frac{1}{2n+3}right)=frac{1}{3}-0=frac{1}{3}.
$$
Заданный ряд сходится и сумма его $S=frac{1}{3}$.
Ответ: $S=frac{1}{3}$.
Продолжение темы нахождения суммы ряда будет рассмотрено во второй и третьей частях.
Сумма ряда.
Пример 1:
Найти сумму ряда
Решение от преподавателя:
Пример 2:
Вычислить сумму ряда с точностью до Δ:
Решение от преподавателя:


Вычисляем члены ряда:
Вычисления прекращаем, получаем сумму ряда с заданной точностью:
Пример 3:
Вычислить при любом натуральном n:
Решение от преподавателя:
Выразим сумму n-ого и (n+2)-го члена суммы:
Таким образом, имеем тождества:
Просуммируем все левыые и правые части:
Таким образом, мы имеем формулу для нахождения суммы ряда для любого n.
Пример 4:
Найдите сумму ряда:
Решение от преподавателя:
Степенной ряд в общем виде записывается следующим образом: ∑anxn
где an — формула числовых коэффициентов. Для данного ряда:
Областью сходимости степенного ряда является интервал (-R;R), где:
R — радиус сходимости. Вычислим его:
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу (-1;1)
Теперь проверим сходимость ряда на концах этого интервала.
Пусть x = 1
Получаем ряд:
Это знакочередующийся числовой ряд который сходится согласно признаку Лейбница.
При x = -1
получаем ряд:
Это знакочередующийся числовой ряд, который сходится согласно признаку Лейбница.
То есть функциональный рядсходится при x∈[−1;1]
Чтобы вычислить сумму ряда, преобразуйте его следующим образом:
Во-первых, докажем, что данный ряд сходится. В самом деле, ряд 


По теореме Лейбница данный ряд сходится к некоторому числу S
Пример 5:
Найти сумму ряда
Решение от преподавателя:
Пример 6:
Доказать, что при любом n > 1, сумма ряда больше 0,5 и меньше 0,75.
Решение от преподавателя:
Проверим для Sn
Таким образом, по методу математической индукции исходрное утверждение доказано.
Пример 7:
Вычислить при любом натуральном n:
Решение от преподавателя:
Выразим сумму n-ого и (n+2)-го члена суммы:
Таким образом, имеем тождества:
Просуммируем все левыые и правые части:
Таким образом, мы имеем формулу для нахождения суммы ряда для любого n.
Пример 8:
Решение от преподавателя:
Пример 9:
Оценить ошибку, получаемую при замене суммы ряда 
Решение от преподавателя:
Пример 10:
Найти сумму ряда:
Решение от преподавателя:
Предположим, что
Приведем правую сторону к общему знаменателю:
Приравниваем получившееся значение к первоночальному, получаем:
Знаменатели дробей равны, следовательно равны и числители:
Получаем систему уравнений:
Зная численные значения А и В, имеем:
Тогда сумма ряда равна:
Получаем верную формулу, следовательно:
Пример 11:
Сколько нужно взять слагаемых ряда 
Решение от преподавателя:
Погрешность суммы ряда не превышает по модулю первого отброшенного члена ряда. Поэтому находим искомое число членов ряда:
Поэтому начиная с k = 10-го члена ряда соответствующие члены ряда можно отбросить. Следовательно, необходимо взять m = 9 членов ряда, чтобы получить его сумму с точностью до 0,01.
Пример 12:
Найти сумму ряда:
Решение от преподавателя:
Используем формулу арифметической прогрессии:
Получим, что
Тогда имеем тождество:
Докажем верность для (n+1) равенства:
Значит, сумма такого ряда:
Пример 13:
Найти сумму ряда:
Решение от преподавателя:
Пример 14:
Найти сумму ряда:
Решение от преподавателя:
Пример 15:
Решение от преподавателя:
Пример 16:
Решение от преподавателя:
Пример 17:
Вычислить сумму ряда с заданной точностью ε.
Решение от преподавателя:
Работа вам нужна срочно. Не волнуйтесь, уложимся!
Заполните, пожалуйста, данные для автора:
- 22423 авторов готовы помочь тебе.
- 2402 онлайн
Содержание:
Числовые ряды:
При решении ряда математических задач, в том числе и в приложениях математики в экономике, приходится рассматривать суммы, составленные из бесконечного множества слагаемых. Из теории действительных чисел известно лишь, что означает сумма любого конечного числа чисел. Задача суммирования бесконечного множества слагаемых решается в теории рядов.
Основные понятия. Сходимость ряда
Определение. Числовым рядом называется бесконечная последовательность чисел
Числа 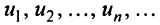
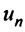
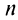
Ряд (13.1) считается заданным, если известен его общий член 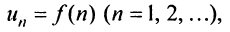
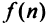
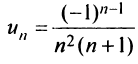
Более сложной является обратная задача: по нескольким первым членам ряда написать общий член. Эта задача имеет бесконечно много решений, но иногда удается найти самое естественное решение.
Пример:
Найти в простейшей форме общий член ряда:
Решение:
Нетрудно убедиться, что для ряда а) общий член 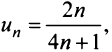
Рассмотрим суммы конечного числа членов ряда:
Сумма п первых членов ряда 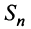
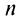
Определение. Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т.е.
Число 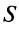
Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся.
Пример:
Исследовать сходимость геометрического ряда, т.е. ряда, составленного из членов геометрической профессии
Решение:
Необходимо установить, при каких значениях знаменателя профессии 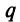
Из школьного курса алгебры известно, что сумма 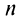
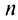
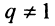
Возможно несколько случаев:
1) если
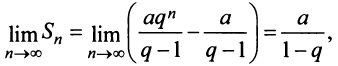
2) если 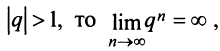
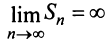
3) если 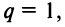
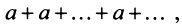
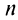
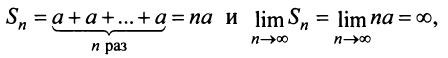
4) если 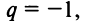
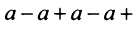
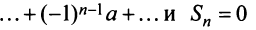
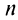
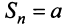
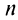
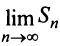
Таким образом, геометрический ряд сходится к сумме 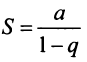
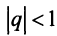
Пример:
Найти сумму ряда
Решение:
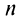
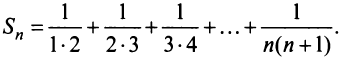
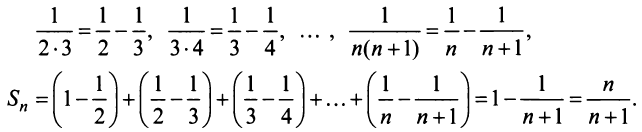
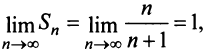
Свойства сходящихся рядов. 1. Если ряд 
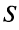
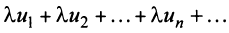
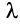
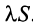
2. Если ряды 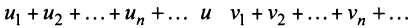
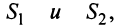
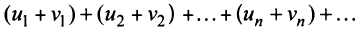
Свойства 1 и 2 непосредственно вытекают из свойств пределов числовых последовательностей.
3. Если ряд сходится, то сходится и ряд, полученный из данного путем отбрасывания (или приписывания) конечного числа членов.
Пусть в сходящемся ряде (13.1) отброшены 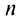
имеющий частичную сумму 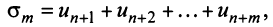
Очевидно, что 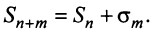
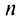
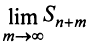
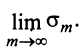
Ряд (13.7), полученный из данного отбрасыванием его первых 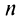
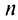
Если сумму 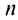
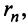
то сумму ряда (13.1) можно представить в виде
В результате мы подошли к свойству 4.
4. Для того чтобы ряд (13.1) сходился, необходимо и достаточно, чтобы при 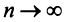
Это свойство вытекает из теоремы о связи бесконечно малых с пределами функций (см. § 6.3).
Установить сходимость (расходимость) ряда путем определения 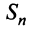
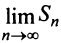
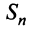
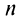
Необходимый признак сходимости. Гармонический ряд
Теорема (необходимый признак сходимости). Если ряд сходится, то предел его общего члена 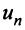

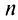
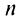
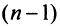
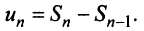
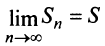
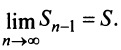
Пример №1
Проверить выполнение необходимого признака для ряда (13.6).
Решение:
Выше было доказано, что ряд (13.6) сходится, и действительно 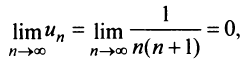
Следствие. Если предел общего члена ряда (13.1) при 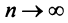
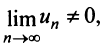
Предположим противное, т.е. ряд (13.1) сходится. Но в этом случае из приведенной выше теоремы следует 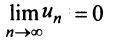
Пример №2
Исследовать сходимость ряда
Решение:
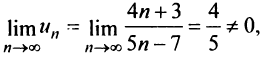
Замечание. Следует подчеркнуть, что рассмотренная теорема выражает лишь необходимый, но недостаточный признак сходимости ряда. Если 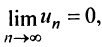
В качестве примера рассмотрим ряд
называемый гармоническим.
Необходимый признак сходимости выполнен: 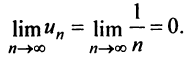

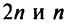
Найдем разность
Заменяя в сумме каждое слагаемое наименьшим, равным 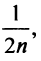
Предположим противное, т.е. что гармонический ряд сходится, тогда 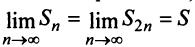
Мы пришли к противоречию, следовательно, наше предположение о сходимости гармонического ряда неверно, т.е. гармонический ряд расходится. ■
В следующих двух параграфах рассмотрим достаточные признаки сходимости.
Ряды с положительными членами
Теорема (признак сравнения). Пусть даны два ряда с положительными членами: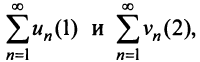
Тогда: а) если сходится ряд 2, то сходится и ряд 1; б) если расходится ряд 1, то расходится и ряд 2.

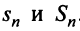
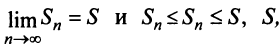
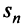
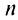
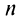
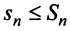
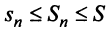
Следовательно, на основании признака существования предела (см. § 6.5) последовательность 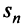
б) Применим метод доказательства от противного. Предположим, что ряд 2 сходится. Тогда согласно первой части теоремы сходится и ряд 1, что противоречит предположению; т.е. ряд 2 расходится. ■
Замечание. Так как сходимость ряда не изменяется при отбрасывании конечного числа членов ряда, то условие (13.11) не обязательно должно выполняться с первых членов рядов и только для членов с одинаковыми номерами 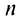
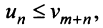
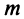
Пример №3
Исследовать сходимость ряда
Решение:
Сравним данный ряд со сходящимся геометрическим рядом 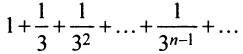
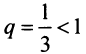
Так как члены данного ряда, начиная со второго, меньше членов сходящегося геометрического ряда 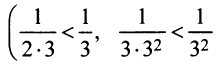
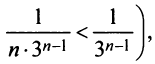
Пример №4
Исследовать сходимость ряда
Решение:
Сравним данный ряд с гармоническим 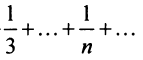
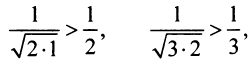
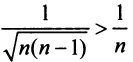
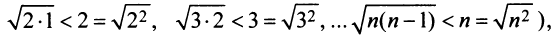
сходится при 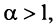
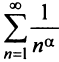
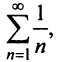
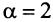
Нестандартность применения признака сравнения заключается в том, что надо не только подобрать соответствующий «эталонный» ряд, но и доказать неравенство (13.11), для чего часто требуется преобразование рядов (например, отбрасывание или приписывание конечного числа членов, умножение на определенные числа и т.п.). В ряде случаев более простым оказывается предельный признак сравнения.
Теорема (предельный признак сравнения)
Теорема (предельный признак сравнения). Если 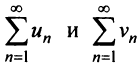
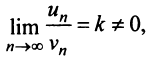

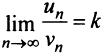
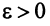
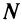
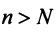
Если ряд 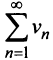
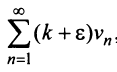
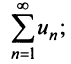
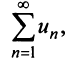
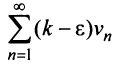
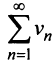
Пример №5
Исследовать сходимость ряда
Решение:
Сравним данный ряд с расходящимся гармоническим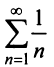
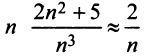
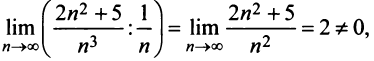
Весьма удобным на практике является признак Даламбера.
Теорема (признак Даламбера)
Теорема (признак Даламбера). Пусть для ряда 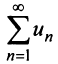
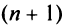
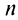
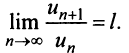
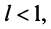
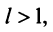
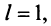
Из определения предела последовательности следует, что для любого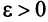
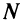
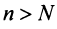
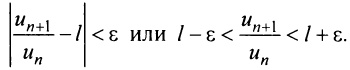
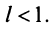
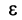
Последнее неравенство будет выполняться для всех 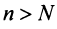
Получили, что члены ряда 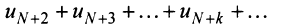
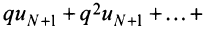
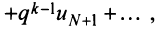
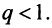
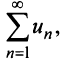
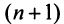
2) Пусть 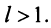
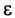
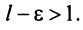
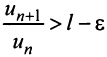
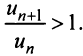
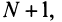
Пример №6
Исследовать сходимость рядов:
Решение:
а) Так как 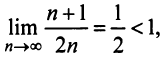
б) Так как
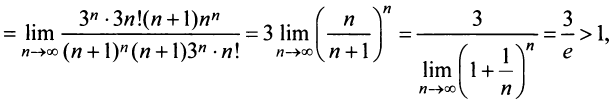
Замечание 1. Если 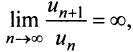
Замечание 2. Если 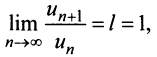
Теорема (интегральный признак сходимости)
Теорема (интегральный признак сходимости). Пусть дан ряд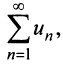

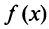
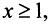
Тогда для сходимости ряда 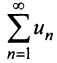
Рассмотрим ряд
Его 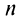
Сходимость ряда (13.14) означает существование предела последовательности его частичных сумм (13.15), т.е. сходимость несобственного интеграла 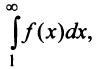
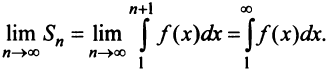
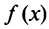
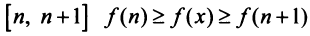
Интегрируя (13.16) на отрезке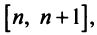
откуда
Если ряд 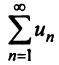
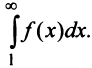
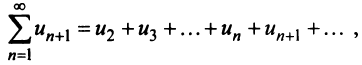
Пример №7
Исследовать сходимость обобщенного гармонического ряда
Решение:
Пусть 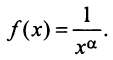
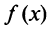
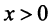
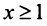
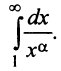
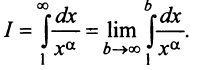
Если 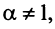
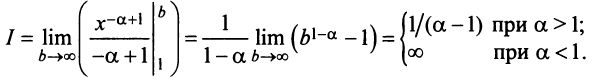
Ряды с членами произвольного знака
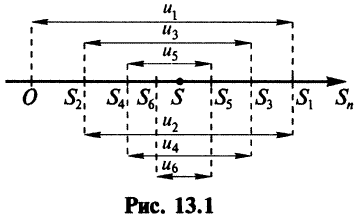
Знакочередующиеся ряды. Под знакочередующимся рядом понимается ряд, в котором члены попеременно то положительны, то отрицательны
Теорема (признак Лейбница). Если члены знакочередующегося ряда убывают по абсолютной величине 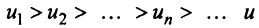
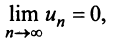
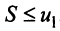
Рассмотрим последовательность частичных сумм четного числа членов при
Эта последовательность возрастающая (так как с ростом 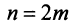
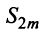
откуда следует, что 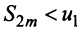
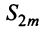
Попутно заметим, что, переходя к пределу в неравенстве 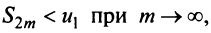
Теперь рассмотрим последовательность частичных сумм нечетного числа членов при 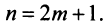
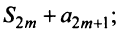
Итак, при любом 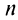
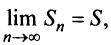
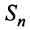
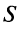
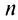
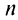
Из рис. 13.1 вытекает еще одна оценка для суммы 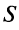
Пример №8
Исследовать сходимость ряда
Решение:
Так как члены знакочередующегося ряда убывают по абсолютной величине 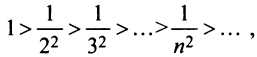
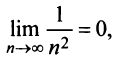
Замечание. В теореме Лейбница существенно не только условие 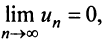
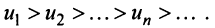
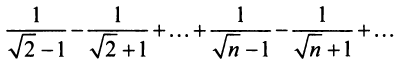
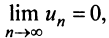
т.е. «удвоенного» гармонического ряда.
Следствие. Погрешность при приближенном вычислении суммы сходящегося знакочередующегося ряда, удовлетворяющего условиям теоремы Лейбница, по абсолютной величине не превышает абсолютной величины первого отброшенного члена.
По формуле (13.9) сумму сходящегося ряда можно представить как сумму 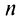
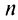
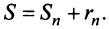
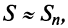
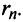
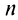
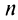
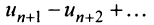
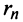
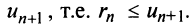
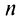
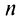
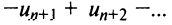
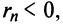
Пример №9
Какое число членов ряда 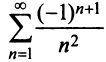
Решение:
По условию 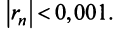
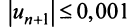
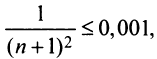
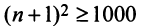
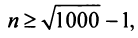
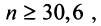
Знакопеременные ряды. Пусть 
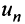
Теорема (достаточный признак сходимости знакопеременного ряда). Если ряд, составленный из абсолютных величин членов данного ряда (13.1)
сходится, то сходится и данный ряд.
Обозначим 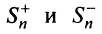
Тогда частичная сумма данного ряда 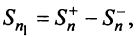
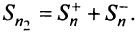
Последовательности 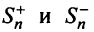
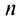
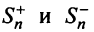
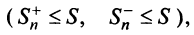
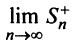
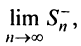
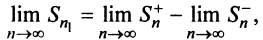
Следует отметить, что обратное утверждение неверно. Ряд (13.19) может расходиться, а ряд (13.1) сходиться. Например, ряд 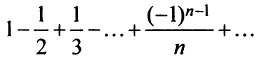
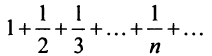
Поэтому введем следующие определения.
Определение 1. Ряд называется абсолютно сходящимся, если сходится как сам ряд, так и ряд, составленный из абсолютных величин его членов.
Определение 2. Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.
Таким образом, рассмотренный выше ряд 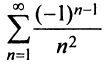
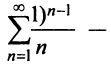
Грубо говоря, различие между абсолютно сходящимися и условно сходящимися рядами заключается в следующем: абсолютно сходящиеся ряды сходятся в основном в силу того, что их члены быстро убывают, а условно сходящиеся — в результате того, что положительные и отрицательные слагаемые уничтожают друг друга.
Свойства абсолютно и условно сходящихся рядов существенно отличаются. Абсолютно сходящиеся ряды по своим свойствам напоминают конечные суммы, их можно складывать, перемножать, переставлять местами члены ряда.
Условно сходящиеся ряды такими свойствами не обладают.
Возьмем, например, ряд 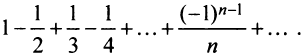
Перепишем ряд в виде:
т.е. от перестановки членов ряда сумма его уменьшилась в 2 раза.
Можно показать (теорема Римана), что от перестановки членов условно сходящегося ряда можно получить ряд, имеющий любую наперед заданную сумму, и даже расходящийся ряд.
Пример №10
Найти сумму ряда 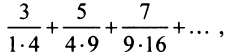
Решение:
Очевидно, что общий член ряда
Представим сумму 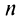
Пример №11
Исследовать сходимость ряда:
Решение:
а) Проверим выполнение необходимого признака сходимости, найдя предел общего члена:
Для вычисления предела отношения двух бесконечно больших функций натурального аргумента правило Лопиталя непосредственно применять нельзя, ибо для таких функций не определено понятие производной. Поэтому применяя теорему о «погружении» дискретного аргумента 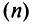
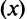
следовательно, ряд расходится.
б) Очевидно, что задан ряд с положительными членами, так как 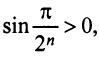
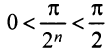
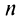
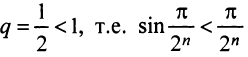
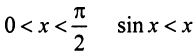
в) Представим общий член ряда в виде
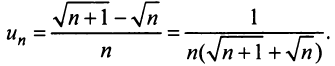
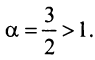
есть конечное число, не равное нулю, то данный ряд, так же как и «эталонный», сходится.
г) Применим признак Даламбера, заметив, что общий член ряда 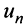
Тогда 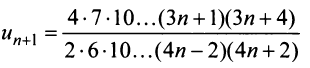
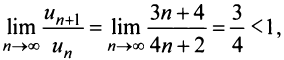
д) Применим признак Даламбера:
т.е. вопрос о сходимости ряда остается открытым. Проверим выполнение необходимого признака (с этого можно было начать исследование): 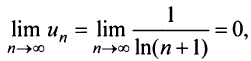
Применим признак сравнения в более простой предельной форме. Сравним данный ряд, например, с гармоническим.
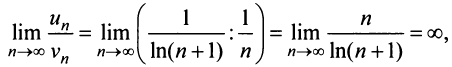
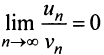
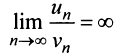
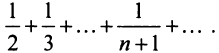
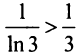
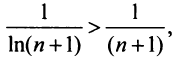
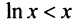
Пример №12
Исследовать сходимость ряда:
Решение:
а) Предел общего члена ряда 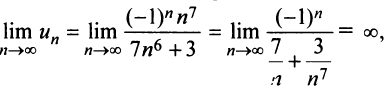
б) Так как члены знакочередующегося ряда, начиная со второго, убывают по абсолютной величине —
и предел общего члена 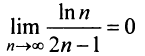
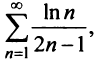
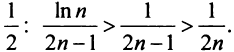
в) Ряд, составленный из абсолютных величин членов данного ряда, сходится, так как его члены меньше членов сходящегося ряда (13.12) при 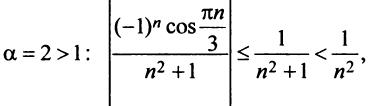
Определение ряда и его сходимость
Пусть
бесконечная последовательность чисел.
Определение 27.1.1. Выражение
называется числовым рядом, а элементы последовательности 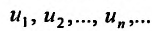
Поскольку выражение (27.1.2) рассматривается как единое целое, то для задания ряда необходимо задать каждый его член 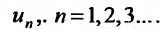
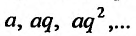
Припишем теперь определенный смысл выражению (27.1.2), т.е. введем определение.
Определение 27.1.2. Сумма n первых членов ряда (27.1.2) 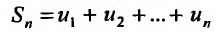
Ясно, что первая, вторая, третья и т.д. частичные суммы ряда
составляют бесконечную последовательность:
Определение 27.1.3. Ряд (27.1.2) называется сходящимся, если последовательность 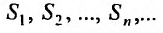
Значение S этого предела называется суммой ряда (27.1.2). Ряд (27.1.2) называется расходящимся, если последовательность его частичных сумм предела не имеет (например, если члены последовательности возрастают по модулю неограниченно).
Содержание теории числовых рядов состоит в установлении сходимости или расходимости тех или иных рядов и в вычислении сумм сходящихся рядов.
В принципе можно доказывать сходимость или расходимость каждого ряда, а также вычислять сумму сходящегося ряда, опираясь непосредственно на определения сходимости и суммы. Для этого в каждом случае составляется аналитическое выражение для n- ой частичной суммы ряда и находится предел этого выражения при возрастании n.
Пример:
Для ряда 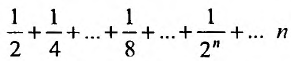
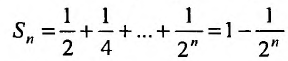
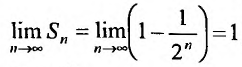
Пример:
Последовательность вида
называется геометрической прогрессией, где а — первый член, а
q — её знаменатель; выражение 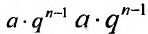
Числовой ряд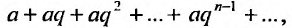
Если в прогрессии (27.1.3) имеется только конечное число членов, то прогрессия называется конечной; в противном случае, если за каждым членом прогрессии следует ещё хотя бы один член, то прогрессия называется бесконечной.
В случае конечной прогрессии 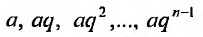
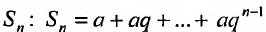
Известно, что при 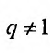
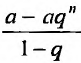
называется предел её частичных сумм 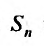
Так как а и q от n не зависят, то последнюю формулу представим в виде:
Если 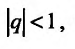
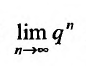
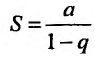
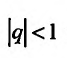
но, сходится и ряд (27.1.4). Если же 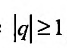
Итак, мы привели примеры, в которых исследование сходимости рядов проводили, применяя определение 27.1.3., т.е. вычисляли частичные суммы и находили предел их последовательностей. Ясно, что в общем случае, составление аналитического выражения для n- ой частичной суммы трудный вопрос. Кроме того, при исследовании рядов нередко значения сумм не представляют интереса, т.к. нужно определить только сходится ряд или нет. Поэтому представляют интерес методы анализа рядов, когда не требуется вычислять суммы рядов. Далее перейдем к изложению таких методов.
Свойства сходящихся рядов
Пусть дан ряд
Определение 27.2.1. Ряд 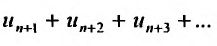
Очевидно, m- я частичная суммаn -го остатка ряда равна разности 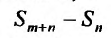
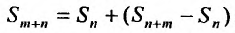
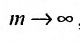
Предел слева есть сумма исходного ряда, а предел справа-сумма 
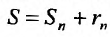
Теорема 27.2.1. Если ряд (27.2.1) сходится, то сумма его n-го остатка с ростом n стремится к нулю.
Доказательство. Выше показано, что 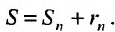
Но для сходящегося ряда 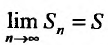
Рассмотрим теперь свойства сходящихся рядов, которые позволяют действовать с ними, как с конечными суммами.
Теорема 27.2.2. Если ряд
имеет сумму S, то ряд
полученный из предыдущего умножением всех членов на одно и тоже число a, имеет сумму aS.
Доказательство. Обозначим последовательность частичных сумм ряда (27.2.2) 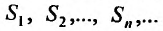
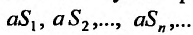
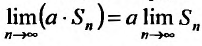
(27.2.2) сходится, то 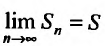
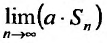
Теорема 27.2.3. Если ряды
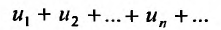
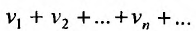
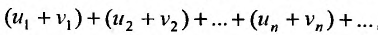
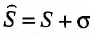
Доказательство. Пусть 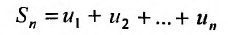
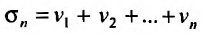
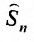
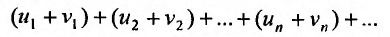
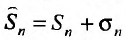
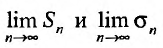
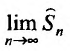
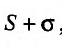
Следствие. Разность двух сходящихся рядов-ряд сходящийся.
Теорема 27.2.4. Свойства сходимости или расходимости ря-,ki не нарушается, если в ряде исключить или приписать к нему любое конечное число членов.
Доказательство. Пусть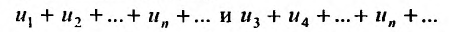
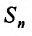
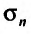
Из этого равенства следует, что, если 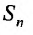
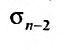
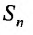
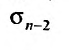
Теорема 27.2.5. (Необходимое условие сходимости ряда). Если ряд 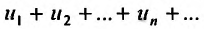
Доказательство. Пусть ряд 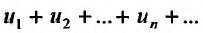
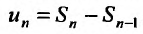
Отметим, что условие (27.2.4) не является достаточным, т.е. общий член может стремиться к нулю, но ряд все же может быть расходящимся. Но если общий член ряда не стремится к нулю, то ряд будет расходящийся.
- Заказать решение задач по высшей математике
Пример №13
Исследуем на сходимость гармонический ряд
Решение:
Вначале находим предел общего члена: 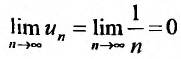
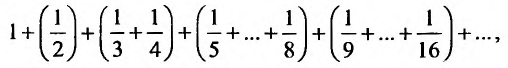
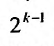
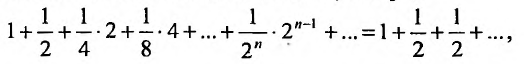
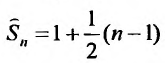
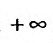
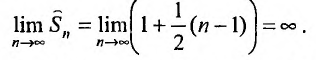
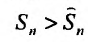
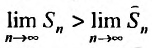
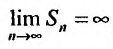
Пример №14
Найти формулу для общего члена ряда
считая, что каждый его последующий член определяется по тому же закону, по которому образованы записанные члены, и найти ею сумму.
Решение:
Каждый член данного ряда представляет собой дробь, числитель которой равен 1, а знаменатель равен произведению двух последовательных натуральных чисел 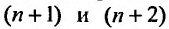
Для вычисления суммы ряда составим n -ую частичную сумму:
Представим выражение для общего члена в виде разности:
тогда
Переходя к пределу, получаем сумму ряда:
Пример №15
Исследовать сходимость ряда
Решение:
Общий член ряда определяется формулой
Вычислим предел модуля общего члена:
Так как предел общего члена не стремится к нулю, то ряд расходится.
Признаки сходимости числовых знакоположительных рядов
Рассмотрим числовые ряды с положительными членами. Существует много приёмов, называемых признаками сходимости, позволяющих установить сходимость или расходимость числовых рядов Так мы познакомились с методом исследования сходимости ряда на основании выяснения имеет ли предел последовательность частичных сумм. Стремление к нулю члена ряда по мерс роста его номера также является признаком сходимости, хотя только необходимым. Ниже мы приведём ряд достаточных признаков сходимости.
Признаки сравнения
Теорема 27.3.1. (I признак сравнения). Пусть
и
два ряда, причём члены первого ряда, начиная с некоторого номера k , не превосходят соответствующих членов второго
Тогда из сходимости ряда (27.3.2) следует сходимость ряда (27.3.1), а из расходимости ряда (27.3.1) следует расходимость ряда (27.3.2).
Доказательство. Так как исключение конечного числа членов ряда не влияет на его сходимость (теорема 27.2.4.), то достаточно доказать теорему для случая когда неравенства (27.3.3) выполняются для k = 1.
Пусть 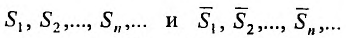
Пусть ряд (27.3.2) сходится. Тогда сходится соответствующая последовательность частичных сумм ряда (27.3.2), т.е.
Поскольку выполняются неравенства (27.3.3), то члены последовательности частичных сумм ряда (27.3.1) удовлетворяют неравенству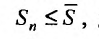
Поэтому, в силу признака Больцано-Всйсрштраса, последовательность частичных сумм ряда (27.3.1) сходится. По определению 27.1.3, сходится и ряд (27.3.1).
Пусть теперь ряд (27.3.1) расходится. Это значит, что его частичные суммы неограниченно возрастают. Но тогда, в силу неравенств (27.3.3), неограниченно возрастают и частичные суммы ряда (27.3.2), что означает, что этот ряд расходится.
Пример №16
Пусть дан ряд
Исследуем его сходимость.
Решение:
Необходимый признак выполняется, т.е.
Для исследования сходимости заданного ряда применим 1 признак
сравнения (теорему 27.3.1). Сравним заданный ряд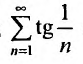
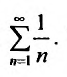
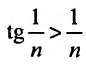
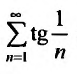
Пример №17
Исследовать сходимость ряда
Решение:
Очевидно, что предел общего члена при возрастании т стремится к нулю.
Сравним данный ряд, общий член которого 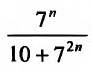
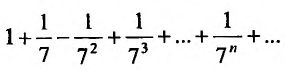
Поскольку 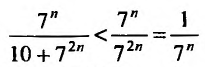
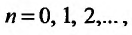
Теорема 27.3.2. (II признак сравнения). Если для рядов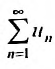
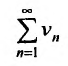
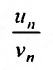
то ряды 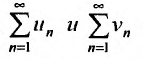
Доказательство. Предельное соотношение (27.3.4), в силу определения 
выполняется неравенство
Обозначив 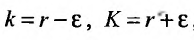
Предположим, что ряд 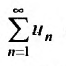
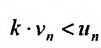
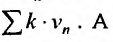
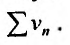
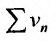
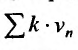
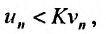
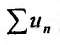
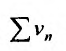
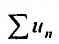
Последовательность 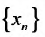
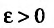
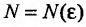
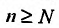
Пример №18
Исследовать сходимость ряда
Решение:
Очевидно, что 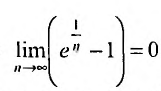
Теорема 27.3.2 выполняется, поэтому из расходимости гармонического ряда 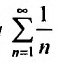
Признаки Д’Аламбсра и Коши
Иногда вместо признаков сравнения оказываются полезными некоторые специальные признаки сходимости ряда. Отметим среди них признаки Д’Аламбсра и Коши, непосредственно получающиеся из признаков сравнения, если в качестве ряда сравнения взять соответствующим образом выбранную геометрическую прогрессию.
Теорема 27.3.3. (признак Д’Аламбера). Если для ряда
с положительными членами существует такой номер 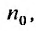
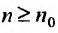
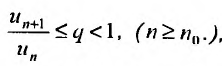
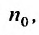
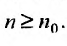
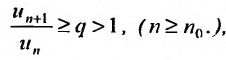
Доказательство. Пусть 0 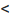
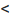
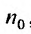
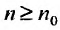
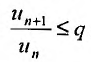
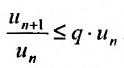
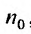
Ряд 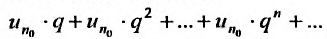
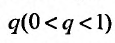
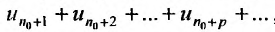
т.к. на сходимость ряда не влияет исключение конечного числа е^ членов.
Если же существует такое 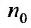
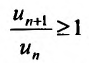
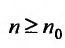
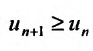
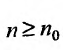
Так как по предположению 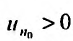
Следствие 1. Пусть существует предел отношения последующего члена ряда (27.3.6) к предыдущему равный r :
Тогда, если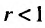
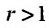
Доказательство. Воспользовавшись определением предела, для фиксированного 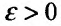
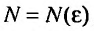
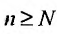
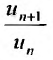
Рассмотрим правую часть двойного неравенства: 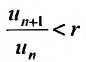
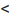
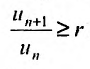
Пример №19
Рассмотрим ряд 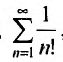
Решение:
Выпишем вначале значения
Затем вычислим предел отношения последующего члена ряда к предыдущему:
Так как этот предел меньше 1, то, в силу следствия 1, данный ряд сходится.
Заметим, что при исследовании сходимости ряда обычно (как правило, но не всегда) применяют следствие 1 из теоремы 27.3.3.
Теорема 27.3.4. (признак Kouiu). Если для ряда
с положительными членами, начиная с некоторого номера 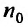
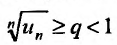
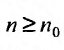
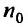
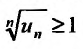
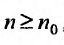
Доказательство. Пусть существует такой номер 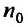
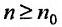
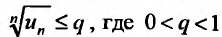
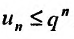
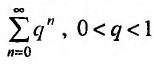
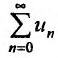
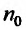
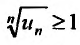
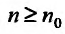
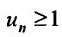
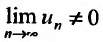
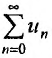
Следствие 2. Пусть существует предел корня n -ой степени из n-го члена ряда (27.3.9):
Тогда, если 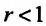
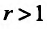
Доказательство. Из определения предела следует, что для фиксированного 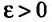
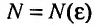
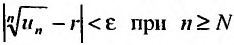
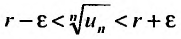
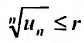
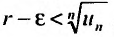
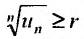
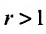
Пример №20
Рассмотрим ряд 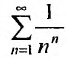
Решение:
Выпишем значение n-го члена ряда 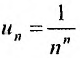
Так как этот предел меньше 1, то, согласно следствию 2, ряд сходится.
Замечание. Если пределы (27.3.8) и (27.3.10) равны 1, то для исследования сходимости ряда (27.3.9) нужно применять другие признаки, с которыми можно ознакомиться в [3].
Интегральный признак сходимости
Рассмотрим признак, достоинство которого состоит в исключительно высокой его чувствительности. Этим признаком проводится исследование сходимости там, где сформулированные признаки Д’Аламбсра и Коши «не работают».
Каждый член числового ряда 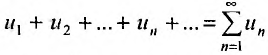
Эта функция определена пока только для целых положительных значений аргумента. Поэтому, доопределив значение функции f для всех нецелых значений аргумента, больших единицы, мы сможем, говорить о функции f(x), принимающей значения для любого 
члены которого положительны и не возрастают 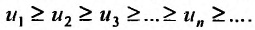
расходится интеграл
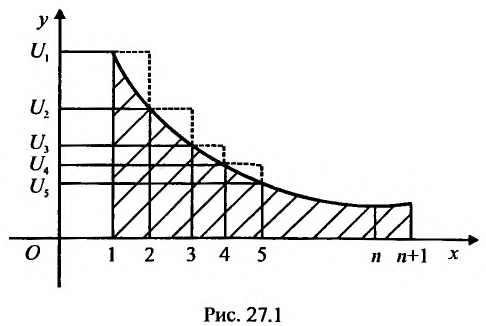
Доказательство. Пусть члены ряда (27.3.11) удовлетворяют условиям теоремы. Изобразим их графически, откладывая по оси Ох независимую переменную, а по оси Оу — соответствующие значения 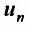
При таком графическом изображении сумма n первых членов ряда 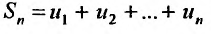
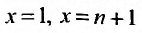
С другой стороны, криволинейная трапеция содержит сумму площадей вписанных прямоугольников, которая равна 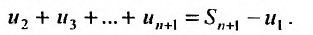
Из (27.3.12) и (27.3.13) следует неравенство:
Предположим, что несобственный интеграл 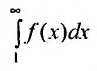
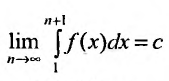
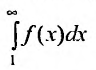
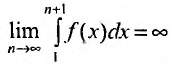
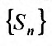
Пример №21
Исследовать сходимость ряда
Решение:
Применим интегральный признак. Рассмотрим функцию 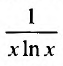
Так как несобственный интеграл расходится, то расходится и ряд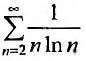
Замечание. Исследовать сходимость данного ряда при помощи следствий 1 и 2 не представляется возможным, так как соответствующие пределы равны 1.
Пример №22
Исследовать сходимость ряда Дирихле
Решение:
Если 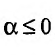
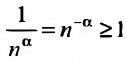
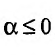
Пусть а > 0, тогда необходимый признак, очевидно, выполняется. Применим интегральный признак Коши. Введем функцию
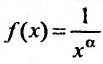
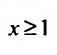
Вычислим определенный интеграл, записанный под знаком предела:
Если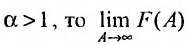
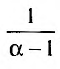
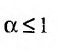
Таким образом, при a>1 несобственный интеграл 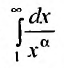
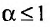
- Знакопеременные ряды
- Степенные ряды
- Элементы матричного анализа
- Уравнение линии
- Несобственные интегралы
- Дифференциальные уравнения первого порядка
- Линейные дифференциальные уравнения второго порядка
- Системы дифференциальных уравнений






















 , целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем
, целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем