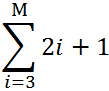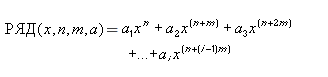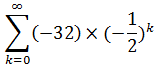Как найти сумму ряда информатика - Autoru.top - решение различных проблем

Как найти сумму числового и функционального ряда

Числовой ряд является некой последовательностью, которая рассматривается совместно с другой последовательностью (ее еще называют последовательностью частичных сумм). Подобные понятия применяются в математическом и комплексном анализе.

Сумму числового ряда можно легко вычислить в Excel с помощью функции РЯД.СУММ. Рассмотрим на примере, как работает данная функция, а после построим график функций. Научимся применять числовой ряд на практике при подсчете роста капитала. Но для начала немного теории.

Сумма числового ряда

Числовой ряд можно рассматривать как систему приближений к числам. Для его обозначения применяют формулу:

Здесь показана начальная последовательность чисел ряда и правило суммирования:

∑ — математический знак суммы;
a_i — общий аргумент;
_i — переменная, правило для изменения каждого последующего аргумента;
∞ — знак бесконечности, «предел», до которого проводится суммирование.

Запись 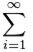обозначает: суммируются натуральные числа от 1 до «плюс бесконечности». Так как _i = 1, то подсчет суммы начинается с единицы. Если бы здесь стояло другое число (например, 2, 3), то суммировать мы начинали бы с него (с 2, 3).

В соответствии с переменной _i ряд можно записать развернуто:

= а₁ + а₂ + а₃ + а₄ + а₅ + … (до «плюс бесконечности).

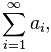
Определение суммы числового ряда дается через «частичные суммы». В математике они обозначаются Sn. Распишем наш числовой ряд в виде частичных сумм:

S₁= а₁

S₂= а₁+ а₂

S₃= а₁+ а₂ + а₃

S₄ = а₁+ а₂ + а₃+ а₄

Сумма числового ряда – это предел частичных сумм S_n. Если предел конечен, говорят о «сходящемся» ряде. Бесконечен – о «расходящемся».

Сначала найдем сумму числового ряда:

М = 10.

Теперь построим в Excel таблицу значений членов ряда:

Общий первый аргумент берем из формулы: i=3.

Все следующие значения _i находим по формуле: =B4+$B$1. Ставим курсор в нижний правый угол ячейки В5 и размножаем формулу.

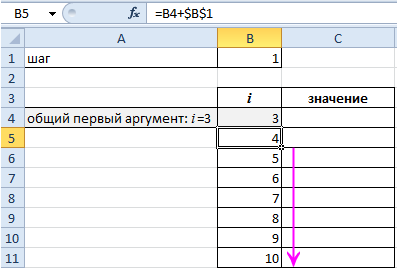
Найдем значения. Делаем активной ячейку С4 и вводим формулу: =СУММ(2*B4+1). Копируем ячейку С4 на заданный диапазон.

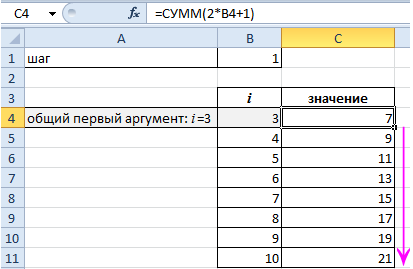
Значение суммы аргументов получаем с помощью функции: =СУММ(C4:C11). Комбинация горячих клавиш ALT+«+» (плюс на клавиатуре).

Функция РЯД.СУММ в Excel

Для нахождения суммы числового ряда в Excel применяется математическая функция РЯД.СУММ. Программой используется следующая формула:

Аргументы функции:

х – значение переменной;
n – степень для первого аргумента;
m – шаг, на который увеличивается степень для каждого последующего члена;
а – коэффициенты при соответствующих степенях х.

Важные условия для работоспособности функции:

все аргументы обязательные (то есть все должны быть заполнены);
все аргументы – ЧИСЛОвые значения;
вектор коэффициентов имеет фиксированную длину (предел в «бесконечность» не подойдет);
количество «коэффициентов» = числу аргументов.

Вычисление суммы ряда в Excel

Та же функция РЯД.СУММ работает со степенными рядами (одним из вариантов функциональных рядов). В отличие от числовых, их аргументы являются функциями.

Функциональные ряды часто используются в финансово-экономической сфере. Можно сказать, это их прикладная область.

Например, положили в банк определенную сумму денег (а) на определенный период (n). Имеем ежегодную выплату х процентов. Для расчета наращенной суммы на конец первого периода используется формула:

S₁ = a (1 + x).

На конец второго и последующих периодов – вид выражений следующий:

S₂ = a (1 + x)²;
S₃ = a (1 + x)² и т.д.

Чтобы найти общую сумму:

S_n = a (1 + x) + a (1 + x)² + a (1 + x)³ + … + a (1 + x)ⁿ

Частичные суммы в Excel можно найти с помощью функции БС().

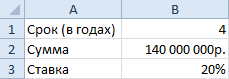
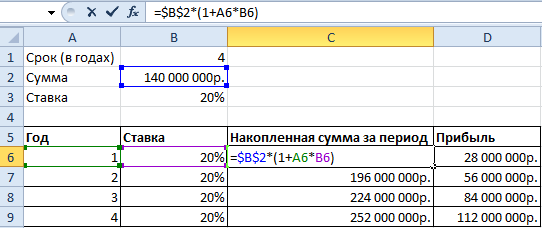
Исходные параметры для учебной задачи:

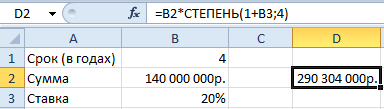
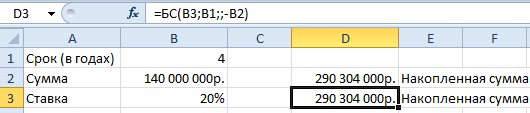
Используя стандартную математическую функцию, найдем накопленную сумму в конце срока сумму. Для этого в ячейке D2 используем формулу: =B2*СТЕПЕНЬ(1+B3;4)

Теперь в ячейке D3 решим эту же задачу с помощью встроенной функции Excel: =БС(B3;B1;;-B2)

Результаты одинаковые, как и должно быть.

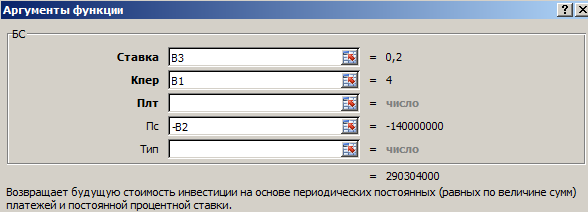
Как заполнить аргументы функции БС():

«Ставка» — процентная ставка, под которую оформлен вклад. Так как в ячейке В3 установлен процентный формат, мы в поле аргумента просто указали ссылку на эту ячейку. Если было бы указано число, то прописывали бы его сотую долю (20/100).
«Кпер» — число периодов для выплат процентов. В нашем примере – 4 года.
«Плт» — периодические выплаты. В нашем случае их нет. Поэтому поле аргумента не заполняем.
«Пс» — «приведенная стоимость», сумма вклада. Так как мы на время расстаемся с этими деньгами, параметр указываем со знаком «-».

Таким образом, функция БС помогла найти нам сумму функционального ряда.

В Excel есть и другие встроенные функции для нахождения разных параметров. Обычно это функции для работы с инвестиционными проектами, ценными бумагами и амортизационными платежами.

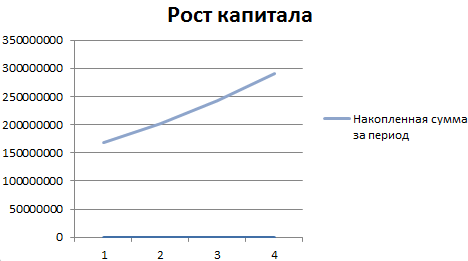
Построение графика функций суммы числового ряда

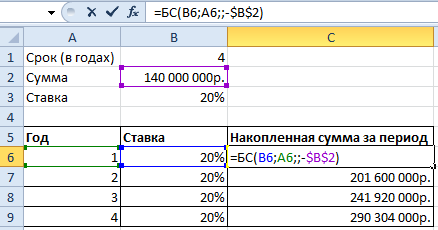
Построим график функций, отражающий рост капитала. Для этого нам нужно построить график функции являющейся суммой построенного ряда. За пример, возьмем те же данные по вкладу:

Дальше нам нужна функция для начисления сложных процентов — БС(). Мы узнаем будущею стоимость инвестиций при условии равных платежей и постоянной процентной ставке. Используя функцию БС(), заполним таблицу:

В первой строке показана накопленная сумма через год. Во второй – через два. И так далее.

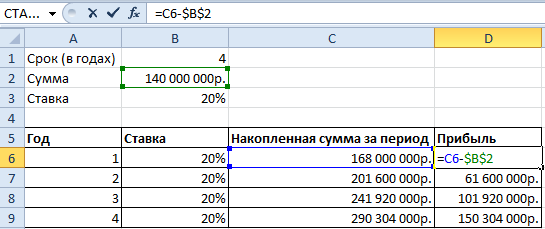
Сделаем еще один столбец, в котором отразим прибыль:

Как мы считали – в строке формул.

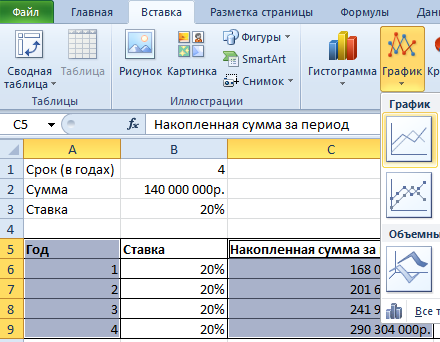
На основании полученных данных построим график функций.

Выделим 2 диапазона: A5:A9 и C5:C9. Переходим на вкладку «Вставка» — инструмент «Диаграммы». Выбираем первый график:

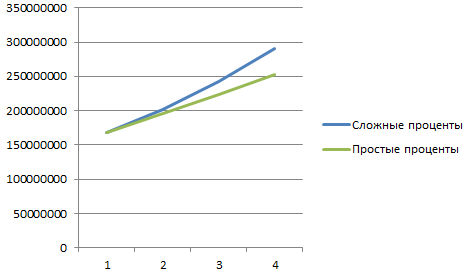
Сделаем задачу еще более «прикладной». В примере мы использовали сложные проценты. Они начисляются на наращенную в предыдущем периоде сумму.

Возьмем для сравнения простые проценты. Формула простых процентов в Excel: =$B$2*(1+A6*B6)

Добавим полученные значения в график «Рост капитала».

Какие именно выводы сделает инвестор – очевидно.

Математическая формула частичной суммы функционального ряда (с простыми процентами): S_n = a (1 + x*n), где а – первоначальная сумма вклада, х – проценты, n – период.

Источник

Вычисление суммы бесконечного ряда (циклы с неизвестным числом повторений)

Для
выполнения данной лабораторной работы
используют оператор цикла do
loop
{while
|until|}.

Оператор
цикла
DO
LOOP [{WHILE |
UNTIL}].
Этот
оператор называется циклом с постусловием,
т. к. проверка условия осуществляется
после каждого выполнения тела цикла,

<операторы>

LOOP
[{WHILE
| UNTIL}
условие]

Цикл выполняется
до тех пор, пока условие не станет
истинным. Например, проверка на то,
чтобы задать длину последовательности,
осуществляется следующим образом:

PRINT
«ВВЕДИТЕ ДЛИНУ ПОСЛЕДОВАТЕЛЬНОСТИ
N = «

INPUT
N%

LOOP
UNTIL N% >0

Цикл
выполняется до тех пор, пока пользователь
не введет положительное число.

При использовании UNTIL
цикл выполняется до тех пор, пока не
выполнится условие, а при использовании
WHILE
цикл выполняется только при выполнении
условия и заканчивается, если условие
нарушается.

Операторы
цикла
DO WHILE/UNTIL LOOP и
WHILE WEND.

Эти
циклы называются циклами с предусловием,
т. к.
проверка
проводится до начала очередной операции:

DО
[{WHILE
UNTIL}условие]

<тело
цикла>

LOOP

или

WHILE
<условие>

<тело
цикла>

WEND

Цикл WHILE
выполняется, пока условие истинно. Как
только условие нарушается, выполнение
цикла завершается. Если используется
UNTIL,
то выполнение происходит до тех пор,
пока условие не станет истинным.

Например, та же проверка вводимой длины
последовательности может быть задана
как

INPUT
N%

WHILE
N%
<=0

PRINT
«ВВЕДИТЕ ДЛИНУ ПОСЛЕДОВАТЕЛЬНОСТИ
N =«

INPUT
N%

WEND

Обратите внимание, что до первого входа
цикл переменной N%
уже должно быть присвоено какое-либо
значение!

Типичным
примером итерационного цикла служат
задачи вычисления с заданной точностью.

Итерационные
циклы широко используются в численных
методах решениях алгоритмических и
трансцендентных уравнений, при вычислении
интегралов, определении суммы бесконечного
ряда и т.д. Во всех этих задачах
вычисления прекращаются при достижении
некоторой точности (результатов).

Рассмотрим пример
вычисления суммы бесконечного ряда
чисел.

Структурный
подход предполагает использование
простейших структур, перечисленных и
списанных выше, для построения блок –
схемы алгоритмов любой сложной задачи.
Рассмотрим это на примере.

В
отчете по работе должно быть:

Математическая
постановка задачи
Блок-схема
алгоритма
Программа
на QBASIC
Результаты
выполнения задачи

Пример.
Вычислить
значение sin
x по формуле

SinX
=

Общая
формула члена ряда
гдеn
– номер члена ряда n

Вычисления
продолжать до тех пор пока
>E,
это условие
и есть условие выхода из цикла, где Е –
точность вычислений.

При достаточно
большом n возведение в степень занимает
значительное машинное время . Поэтому
каждый член ряда следует получать в
соответствии с рекуррентным соотношением

R = Rx

Где n = 3,5,7……..; R
начальное = х. Тогда рекуррентное
соотношение для получения суммы ряда
будет S = S+R (-1), где S начальное= Х. Блок
– схема алгоритма вычисления суммы
ряда представлены на рисунке 27.

Вычисления ведутся
до тех пор , пока величина члена ряда R
не станет меньше , либо равной некоторой
малой величине Е. Значение R с каждым
циклом уменьшается. После выполнения
цикла первый раз имеем

R =

S =

После
выполнения цикла второй раз

R =

S =

И
т.д.

Блок-схема

Программа
на Qbasic
имеет вид:

input
x,e

s=x

r=x

n=3

do
while r>e

r=r*x^2/((n-1)*n)*(-1)

s=s+r

n=n+2

loop

print
s

end

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Improve Article

Save Article

Like Article

Read

Discuss

Improve Article

Save Article

Like Article

A series with the same common difference is known as arithmetic series. The first term of series is a and the common difference is d. The series looks like a, a + d, a + 2d, a + 3d, . . . Task is to find the sum of the series.

Examples:

Input : a = 1
        d = 2
        n = 4
Output : 16
1 + 3 + 5 + 7 = 16

Input : a = 2.5
        d = 1.5
        n = 20
Output : 335

A simple solution to find the sum of arithmetic series.

C++

#include<bits/stdc++.h>

using namespace std;

float sumOfAP(float a, float d, int n)

{

float sum = 0;

for (int i=0;i<n;i++)

{

sum = sum + a;

a = a + d;

}

return sum;

}

int main()

{

int n = 20;

float a = 2.5, d = 1.5;

cout<<sumOfAP(a, d, n);

return 0;

}

Java

class GFG{

static float sumOfAP(float a, float d,

int n)

{

float sum = 0;

for (int i = 0; i < n; i++)

{

sum = sum + a;

a = a + d;

}

return sum;

}

public static void main(String args[])

{

int n = 20;

float a = 2.5f, d = 1.5f;

System.out.println(sumOfAP(a, d, n));

}

Python

def sumOfAP( a, d,n) :

sum = 0

i = 0

while i < n :

sum = sum + a

a = a + d

i = i + 1

return sum

n = 20

a = 2.5

d = 1.5

print (sumOfAP(a, d, n))

C#

using System;

class GFG {

static float sumOfAP(float a, float d,

int n)

{

float sum = 0;

for (int i = 0; i < n; i++)

{

sum = sum + a;

a = a + d;

}

return sum;

}

public static void Main()

{

int n = 20;

float a = 2.5f, d = 1.5f;

Console.Write(sumOfAP(a, d, n));

}

PHP

<?php

function sumOfAP($a, $d, $n)

{

$sum = 0;

for ($i = 0; $i < $n; $i++)

{

$sum = $sum + $a;

$a = $a + $d;

}

return $sum;

}

$n = 20;

$a = 2.5; $d = 1.5;

echo(sumOfAP($a, $d, $n));

?>

Javascript

<script>

function sumOfAP(a, d, n)

{

let sum = 0;

for (let i=0;i<n;i++)

{

sum = sum + a;

a = a + d;

}

return sum;

}

let n = 20;

let a = 2.5, d = 1.5;

document.write(sumOfAP(a, d, n));

</script>

Output:

Time Complexity: O(n)

Space complexity: O(1) because using constant space

Approach 2:

An Efficient solution to find the sum of arithmetic series is to use the below formula as follows:

Sum of arithmetic series 
           = ((n / 2) * (2 * a + (n - 1) * d))
           Where
               a - First term
               d - Common difference
               n - No of terms

Example:

C++

#include<bits/stdc++.h>

using namespace std;

float sumOfAP(float a, float d, float n)

{

float sum = (n / 2) * (2 * a + (n - 1) * d);

return sum;

}

int main()

{

float n = 20;

float a = 2.5, d = 1.5;

cout<<sumOfAP(a, d, n);

return 0;

}

Java

class GFG

{

static float sumOfAP(float a, float d, float n)

{

float sum = (n / 2) * (2 * a + (n - 1) * d);

return sum;

}

public static void main (String[] args)

{

float n = 20;

float a = 2.5f, d = 1.5f;

System.out.print(sumOfAP(a, d, n));

}

Python3

def sumOfAP(a, d, n):

sum = (n / 2) * (2 * a + (n - 1) * d)

return sum

n = 20

a = 2.5

d = 1.5

print(sumOfAP(a, d, n))

C#

using System;

class GFG {

static float sumOfAP(float a,

float d,

float n)

{

float sum = (n / 2) *

(2 * a +

(n - 1) * d);

return sum;

}

static public void Main ()

{

float n = 20;

float a = 2.5f, d = 1.5f;

Console.WriteLine(sumOfAP(a, d, n));

}

PHP

<?php

function sumOfAP($a, $d, $n)

{

$sum = ($n / 2) * (2 * $a +

($n - 1) * $d);

return $sum;

}

$n = 20;

$a = 2.5; $d = 1.5;

echo(sumOfAP($a, $d, $n));

?>

Javascript

function sumOfAP(a, d, n) {

let sum = (n / 2) * (2 * a + (n - 1) * d);

return sum;

}

let n = 20;

let a = 2.5, d = 1.5;

document.write(sumOfAP(a, d, n));

Time Complexity: O(1)

Space complexity: O(1) since using only constant variables

How does this formula work?

We can prove the formula using mathematical induction. We can easily see that the formula holds true for n = 1 and n = 2. Let this be true for n = k-1.

Let the formula be true for n = k-1.
Sum of first k - 1 elements of arithmetic series is
        = (((k-1))/ 2) * (2 * a + (k - 2) * d))
We know k-th term of arithmetic series is
        = a + (k - 1)*d

Sum of first k elements = 
      = Sum of (k-1) numbers + k-th element
      = (((k-1)/2)*(2*a + (k-2)*d)) + (a + (k-1)*d)
      = [((k-1)(2a + (k-2)d) + (2a + 2kd - 2d)]/2
      = ((k / 2) * (2 * a + (k - 1) * d))

This article is contributed by Dharmendra Kumar. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.

Please write comments if you find anything incorrect, or if you want to share more information about the topic discussed above.

Last Updated :
16 Feb, 2023

Like Article

Save Article

Источник

Условие задачи:

Для числового ряда найти

а) сумму членов числового ряда при М=10;

б) точное значение суммы членов числового ряда, вычисленное по формуле Sum2=15е;

в) погрешности вычисления суммы членов числового ряда (абсолютную и относительную) по отношению к точному значению суммы членов числового ряда.

Решение:

Составим блок-схему алгоритма решения задачи (представлена на рисунке слева).

Итак, для решения задачи используем переменные:

М (количество членов вычисляемого числового ряда);

f (вспомогательная переменная, вычисляющая для цикла факториал);

Sum1 (сумма членов числового ряда);

Sum2 (точное значение суммы);

Err1 (абсолютная погрешность);

Err2 (относительная погрешность);

и определимся с типом данных, который они могут содержать. Значения переменных M и k будут короткими целыми (Integer), значение f — длинным целым (Long), а значения переменных Sum1, Sum2, Err1,Err2 — вещественные удвоенной точности [1].

Для ввода значений переменной M, а также вывода результатов используются текстовые поля (объект TextBox). Чтобы сделать поля для вывода неизменяемыми, при определении характеристик поля в строке Enable укажем False [2].

Составим текст программы (приведен с комментариями).

Public Class Form1

Private Sub ButtonOK_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles ButtonOK.Click

‘ описание переменных:

Dim M As Integer ‘ количество членов числового ряда

Dim Sum1 As Double, Sum2 As Double ‘ сумма и точная сумма ряда

Dim Err1 As Double, Err2 As Double ‘ абсолютная и относительная погрешности

Dim k As Integer, f As Long ‘ вспомогат.переменные

‘ для организации цикла и подсчета факториала

‘ количество членов числового ряда вводятся в форме

M = Val(TextM.Text)

‘ вычисления

f = 1

Sum1 = 0

For k = 1 To M

f = f * k

Sum1 = Sum1 + (k + 1) ^ 3 / f

Next k

Sum2 = 15 * 2.718281828495

Err1 = Sum2 — Sum1

Err2 = Err1 / Sum2 * 100

‘ вывод результатов вычислений в поля формы

TextSum1.Text = Format(Sum1, «0.00000»)

TextSum2.Text = Format(Sum2, «0.00000»)

TextErr1.Text = Format(Err1, «0.00000000»)

TextErr2.Text = Format(Err2, «0.00000000»)

End Sub

Private Sub ButtonCancel_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles ButtonCancel.Click

End

End Sub

End Class

На рис.1 представлен вариант реализации формы приложения:

Рисунок 1 — Вычисление суммы ряда

Работа с массивами

Условие задачи:

Дан двумерный массив (матрица) размером NxN.

1. Определить сумму элементов, значения которых кратны заданному числу F.

2. Найти местоположения (номера индексов) минимальных элементов массива.

Решение:

Составим блок-схему алгоритма решения задачи

Программа будет содержать несколько «циклов в цикле» в виду того, что организует работы с массивами.

Текст программы

Public Class Form1

описание переменных уровня модуля: массив

Dim Arr(100, 100) As Integer

Dim N As Integer ‘ количество элементов массива

Private Sub ButtonGenerate_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles ButtonGenerate.Click

описание переменных:

Dim Amin As Integer, Amax As Integer ‘ границы значений элементов массива

Dim i As Integer, j As Integer ‘ вспомогат.переменные

для организации цикла

‘ количество элементов массива и границы значений вводятся в форме

N = Val(TextN.Text)

Amin = Val(TextMin.Text)

Amax = Val(TextMax.Text)

‘ создание массива с помощью генератора случайных чисел

Dim Str1 As String

ListArray.Items.Clear() ‘ количество столбцов в поле вывода массива

For i = 0 To N — 1

Str1 = «»

For j = 0 To N — 1

Arr(i, j) = Amin + Int(Rnd() * (Amax — Amin))

Str1 = Str1 + Space(3) + Str(Arr(i, j))

Next j

ListArray.Items.Add(Str1)

Next i

End Sub

Private Sub ButtonOK_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles ButtonOK.Click

‘ описание переменных:

Dim F As Integer ‘ число (вводимое) для поиска кратных элементов массива

Dim Fsum As Long ‘ сумма (искомая) кратных элементов массива

Dim Amin As Integer ‘ значение минимального элемента

Dim i As Integer, j As Integer ‘ вспомогат.переменные

‘ для организации цикла

‘ число для поиска кратных элементов вводится в форме

F = Val(TextF.Text)

If F = 0 Then Exit Sub

‘ вычисления

Fsum = 0

If N > 0 Then Amin = Arr(0, 0)

For i = 0 To N — 1

For j = 0 To N — 1

If Arr(i, j) / F = Int(Arr(i, j) / F) Then Fsum = Fsum + Arr(i, j)

If Amin > Arr(i, j) Then Amin = Arr(i, j)

Next j

Next i

‘ вывод результатов вычислений в поля формы

LabelSum.Text = Fsum

LabelMin.Text = Amin

‘ очистка полей для повторных нажатий кнопки «Вычислить»

ListMin.Items.Clear()

For i = 0 To N — 1

For j = 0 To N — 1

If Arr(i, j) = Amin Then

ListMin.Items.Add(«элемент (» + Str(i + 1) + «;» + Str(j + 1) + «)»)

End If

Next j

Next i

End Sub

Private Sub ButtonCancel_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles ButtonCancel.Click

End

End Sub

End Class

На рис.2 представлен вариант реализации формы приложения.

Для вывода суммы элементов, кратных заданному числу и минимальных элементов используются поля Label [2].

Рисунок 2 — Работа с массивами

Источник

В этом уроке мы расскажем как вычислить сумму бесконечного сходящегося ряда (последовательности) с определенной точностью. Будет рассмотрена соответствующая программа, написанная на языке программирования Си. В конце статьи можно скачать исходник этой программы для Visual Studio.

Сходящийся ряд — это числовая последовательность элементов множества X, имеющая предел в этом множестве.

Сходящийся ряд

Рассмотрим задачу вычисления суммы сходящегося ряда с определенной точностью на примере. Пусть дан ряд:

Вычисление суммы ряда с определенной точностью ε означает, что сумма ряда вычисляется до тех пор, пока модуль разности между текущим и предыдущим членом последовательности больше ε. В виде формулы это утверждение можно записать так: |a_n — a_n-1| > ε, то есть пока это выражение истинно, вычисления продолжаются.

Сначала напишем на языке Си функцию, которая будет вычислять и возвращать значение k-го члена ряда по переданному в нее значению k.

double f(int k)

{

double res;

res = —32.0;

res *= (double)powf(—0.5, k);

return res;

}

res — это переменная вещественного типа повышенной точности double, в которую будет записан результат вычисления k-го члена ряда. Это же значение и будет возвращаться функцией.

Выражение res *= (double)powf(-0.5, k); эквивалентно выражению res = res * (double)powf(-0.5, k);

Оператор powf — это оператор возведения числа в степень. В нашем случае он вычисляет: -0.5^k.

Функцию f можно записать короче:

double f(int k)

{

return —32.0 * powf(—0.5, k);

}

Теперь перейдем к функции main. Для начала считаем с консоли число e — это и будет заданная точность вычислений ε.

float e;

printf(«e = «);

scanf_s(«%f», &e);

Объявим переменные, в которых будут хранится: значение предыдущего, значение текущего члена ряда, сумма ряда и номер текущего члена ряда (число k) соответственно.

double previous, current;

double sum = 0;

int k = 0;

Отдельно вычислим первый член ряда (потом он станет «предыдущим»), чтобы затем перейти к вычислениям в цикле.

current = f(k);

sum += current;

k++;

Запись выражения sum += current; эквивалентна записи: sum = sum + current;

Теперь перейдем к вычислениям в цикле. Условием выхода из цикла будет ложность выражения: |a_n — a_n-1| > ε.

{

previous = current;

current = f(k);

sum += current;

k++;

} while (abs(current — previous) > e);

Сумма посчитана. Осталось вывести результат вычислений в консоль.

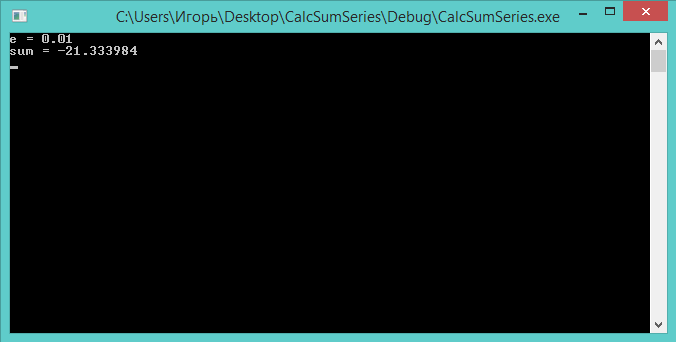
printf(«sum = %fn», sum);

В итоге код программы с необходимыми подключенными библиотеками будет выглядеть следующим образом:

#include <stdio.h>

#include <math.h>

#include <conio.h>

double f(int k)

{

double res;

res = —32.0;

res *= (double)powf(—0.5, k);

return res;

}

int main()

{

float e;

printf(«e = «);

scanf_s(«%f», &e);

double previous, current;

double sum = 0;

int k = 0;

current = f(k);

sum += current;

k++;

{

previous = current;

current = f(k);

sum += current;

k++;

} while (abs(current — previous) > e);

printf(«sum = %fn», sum);

_getch();

return 0;

}

Оператор _getch(); в строке 34 нужен для того, чтобы консоль не закрывалась сразу по завершении исполнения программы.

Демонстрация работы программы для нашего ряда представлена на скриншоте ниже. Точность вычислений составляет: ε = 0.01.

Скачать исходник

Источник

Как найти сумму числового и функционального ряда

Сумма числового ряда

Функция РЯД.СУММ в Excel

Вычисление суммы ряда в Excel

Построение графика функций суммы числового ряда

Вычисление суммы бесконечного ряда (циклы с неизвестным числом повторений)

C++

Java

Python

C#

PHP

Javascript

Approach 2:

C++

Java

Python3

C#

PHP

Javascript

Работа с массивами

Не пропустите также: