Рассмотрим
некоторые приемы нахождения суммы
функционального
ряда и области его сходимости к этой
сумме.
Нахождение
суммы ряда почленным интегрированием.
-
Пусть
дан ряд вида
.
По признаку Коши или
признаку
Даламбера область
сходимости определяется
неравенством
.
Если
,
то ряд
— расходящийся.
Если
,
то ряд
сходится условно (по признаку Лейбница).
Следовательно, область сходимости
находится из неравенства
.
Затем делаем
замену
в исходном ряде; получаем степенной ряд
с областью сходимости
.
Используем формулу для вычисления суммы
членов бесконечно убывающей геометрической
прогрессии со знаменателем
(12)
и
очевидное равенство
(13)
Учитывая,
что степенной ряд можно почленно
интегрировать по любому отрезку
,
целиком принадлежащему интервалу
сходимости, и используя формулу (13),
получаем
Заметим,
что так как ряд (12) сходится в граничной
точке t=-1,
то сумма ряда непрерывна в этой точке
(справа) и
.
Далее вычисляем интеграл (с переменным
верхним пределом), заменяем t
на
и получаем ответ.
-
Если
дан ряд вида
,
то следует либо
применить
теорему о почленном интегрировании
степенного ряда дважды, либо разложить
дробь на элементарные
и
вычислить сумму каждого ряда почленным
интегрированием.
Пример.
Найти сумму ряда
и указать область
его
сходимости к этой сумме.
Решение.
Данный ряд степенной. Находим его
интервал сходимости. По признаку Коши
имеем
.
Из неравенства находим
.
Исследуем поведение ряда в граничных
точках. При
—
расходящийся гармонический ряд. При
— условно сходящийся ряд по признаку
Лейбница. Следовательно, данный ряд
сходится при
.
Для нахождения суммы ряда сделаем замену
.
Получим геометрический ряд
,
сходящийся при
.
Используя равенство (13) и почленное
интегрирование степенного ряда, получаем:

Ответ:
для
.
Замечание.
Степенной ряд (10) сходится абсолютно и
равномерно на всяком отрезке, лежащем
внутри его интервала сходимости; ряд
(10) можно почленно интегрировать и
дифференцировать внутри его интервала
сходимости
,
т.е. если
то для
имеем
и
Задание
17. Найти
сумму ряда и указать область сходимости
к этой сумме.
Задача
1.
Решение.
Имеем
.
Найдем
сумму каждого из этих рядов в их области
сходимости. Сначала рассмотрим ряд
.
Используем
формулу для вычисления суммы членов
бесконечно убывающей геометрической
прогрессии
,
где
,
,
и равенство (13).Учитывая, что степенной
ряд можно почленно интегрировать на
любом отрезке
,
целиком принадлежащем интервалу
сходимости, получаем первую сумму:

Т.к.
ряд
сходится в граничной точке х=-1, то его
сумма непрерывна в этой точке:
.Значит,
при
всех
.
(14)
Аналогично
находим вторую сумму с учетом (14):
Таким
образом, сумма исходного ряда

Ответ:
,
Задача
2.
Решение.
Находим область сходимости функционального
ряда, применяя признак Даламбера
Область
сходимости определяется неравенством
,
или
.
Решая его, получаем
или
.
При
имеем
—
расходящийся ряд (т.к.
~
).
Следовательно, ряд сходится при
.
Сделаем замену
.
Получим ряд
с областью сходимости
.
Используя формулу (12):
равенство (13):
и почленное интегрирование на любом
отрезке, принадлежащем области сходимости,
получаем
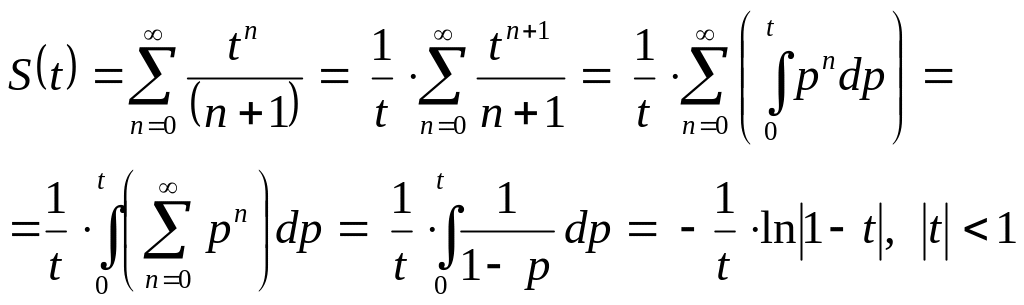
Заменяя
t
на
,
получаем сумму
Ответ:
,
.
Нахождение
суммы ряда почленным дифференцированием.
I.
Пусть дан ряд вида
.
Сначала
определяем область сходимости ряда,
например, по признаку Коши. Получаем
неравенство
.
Если
,
то ряд расходится, т.к. не выполнено
необходимое
условие
сходимости
.
Следовательно, область
сходимости
определяется неравенством
.
Затем делаем замену
и записываем ряд в виде суммы двух рядов
.
Для нахождения сумм этих рядов используем
формулу суммы членов бесконечно убывающей
геометрической прогрессии и очевидное
равенство
.
Учитывая,
что степенной ряд можно почленно
дифференцировать в любой точке интервала
сходимости, и используя равенство
,
получаем
Далее
вычисляем производную, делаем замену
и
записываем ответ.
II.
Если дан ряд вида
,
то вычисляем сумму трех рядов
,
и
,
причем при вычислении суммы ряда
применяем теорему о почленном
дифференцировании степенного ряда
дважды.
Задание
18. Найти
сумму ряда и указать область
сходимости
ряда к этой сумме.
Задача
3.
Решение.
а). Находим
область сходимости данного ряда по
признаку Даламбера
Отсюда
.
В граничных точках
ряд расходится, т.к. не выполнено
необходимое условие сходимости. Итак,
ряд сходится (и притом абсолютно) в
интервале (-1;1).
б).
Делаем в исходном ряде замену
и записываем в виде суммы двух рядов
Для
нахождения S(t)
достаточно найти суммы рядов
и
.
Учитывая,
что степенной ряд можно почленно
дифференцировать
в любой точке интервала сходимости,
получаем
.
И
в)
Заменяя
на
,
получаем
Ответ:
Задача
4.
Решение.
По признаку
Коши интервал сходимости
степенного
ряда определяется неравенством
,
т.е. ряд сходится в интервале (-1;1). Для
нахождения суммы ряда достаточно
представить ряд в виде суммы трех рядов
и найти суммы рядов:
,
где
применили один раз почленное
дифференцирование по x;
.
Т.к.
выше найденная на предыдущем шаге сумма
ряда
,
то еще раз применив почленное
дифференцирование по x
к ряду;
,
получаем
.Таким
образом, сумма исходного ряда равна
.
Ответ:
,
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
01.05.20221.51 Mб0Учебники 60167.doc
- #
01.05.20221.53 Mб0Учебники 60168.doc
- #
- #
- #
- #
- #
01.05.20221.56 Mб0Учебники 60172.doc
- #
- #
- #
Функциональный ряд — ряд, каждым членом которого, в отличие от числового ряда, является не число, а функция 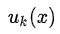
Решение функциональных рядов
Область сходимости
Функциональным рядом называется ряд
членами которого являются функции 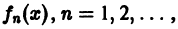
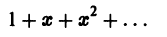
определены на интервале 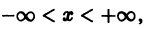
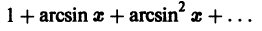
определены на отрезке
Функциональный ряд (1) называется сходящимся в точке 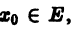
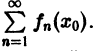
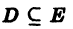
Ряд (1) называется абсолютно сходящимся на множестве D, если на этом множестве сходится ряд
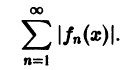
В случае сходимости ряда (1) на множестве D его сумма S будет являться функцией, определенной на D,
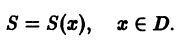
Область сходимости некоторых функциональных рядов можно найти с помощью известных достаточных признаков, установленных для рядов с положительными членами, например, признака Даламбера, признака Коши.
Пример:
Найти область сходимости ряда
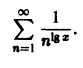
Так как числовой ряд

сходится при р > 1 и расходится при р 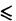
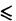
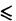
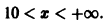
Пример:
Найти область сходимости ряда
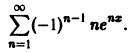
Рассмотрим ряд
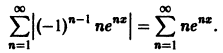
Члены этого ряда положительны при всех значениях х. Применим к нему признак Даламбера. Имеем
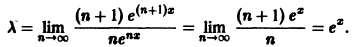
При 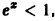
При х > 0 ряд расходится, так как 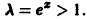
Пример:
Найти область сходимости ряда
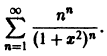
Члены данного ряда определены и непрерывны на множестве 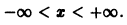
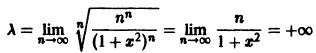
для любого 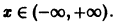
Обозначим через 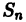
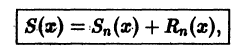
где 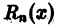
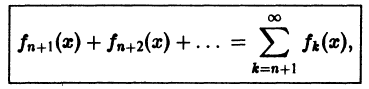
который называется n-м остатком функционального ряда (1). Для всех значений 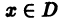
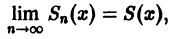
и поэтому.

т. е. остаток 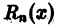
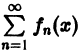
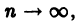
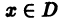
Равномерная сходимость
Среди всех сходящихся функциональных рядов важную роль играют так называемые равномерно сходящиеся ряды.
Пусть дан сходящийся на множестве D функциональный ряд
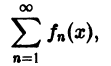
сумма которого равна S(x). Возьмем его n-ю частичную сумму
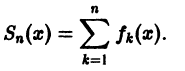
Определение:
Функциональный ряд
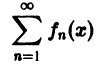
называется равномерно сходящимся на множестве 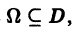
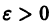
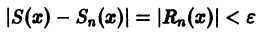
будет выполняться для всех номеров n > N и для всех х из множества 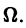
Замечание:
Здесь число N является одним и тем же для всех 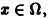
Равномерную сходимость функционального ряда 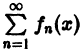
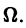
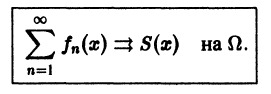
Определение равномерной сходимости ряда 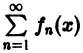
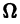
Поясним геометрически смысл равномерной сходимости функционального ряда. Возьмем в качестве множества 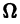
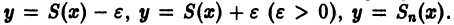
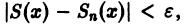
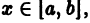
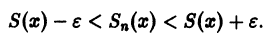
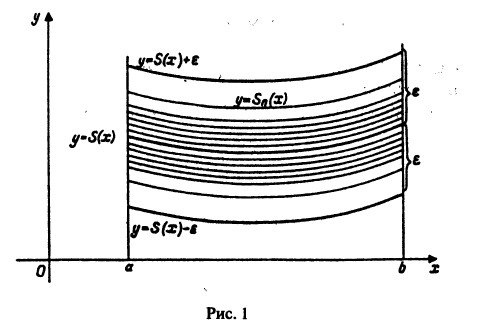
Полученные неравенства показывают, что графики всех функций 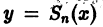
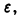
Пример:
Показать, что функциональный ряд
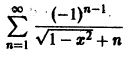
равномерно сходится на отрезке
Данный ряд является знакочередующимся, удовлетворяет условиям признака Лейбница при всяком 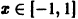
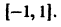
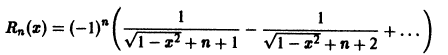
по абсолютной величине не превосходит абсолютной величины своего первого члена:
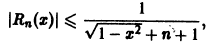
а поскольку 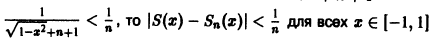
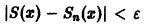
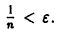
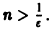
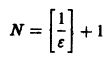
(Здесь через [а] обозначено наибольшее целое число, не превосходящее а), то неравенство |S(x) — 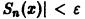
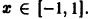
Замечание:
Не всякий сходящийся на множестве D функциональный ряд является равномерно сходящимся на D.
Пример:
Покажем, что ряд
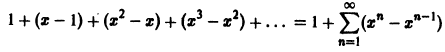
сходится на отрезке 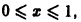
Вычислим n-ю частичную сумму Sn(x) ряда. Имеем
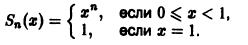
Откуда
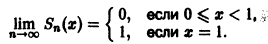
Данный ряд сходится на отрезке [0,1] и его сумма
Абсолютная величина разности 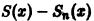
Возьмем число 
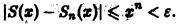
Разрешим неравенство 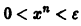
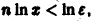
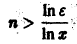
(так как 0 < х < 1, то In х < 0, и при делении на In х знак неравенства меняется на обратный). Неравенство 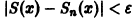
Поэтому такого не зависящего от х числа N(e), чтобы неравенство
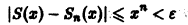
выполнялось для каждого n > N(e) сразу для всех х из отрезка 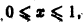
Если же заменить отрезок 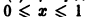
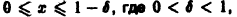
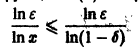
и поэтому
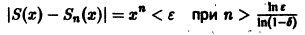
сразу для всех
Признак Вейерштрасса
Достаточный признак равномерной сходимости функционального ряда дается теоремой Вейерштрасса.
Теорема:
Признак Вейерштрасса. Пусть для всех х из множества 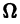
по абсолютной величине не превосходят соответствующих членов сходящегося числового ряда
с положительными членами, т. е.
для всех 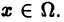
Тек как по условию теоремы члены ряда (1) удовлетворяют условию (3) на всем множестве 
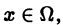
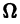
Докажем равномерную сходимость ряда (1). Пусть
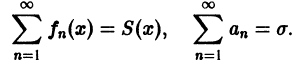
Обозначим через 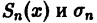
для всех
Возьмем любое (сколь угодно малое) число 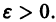
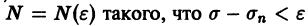
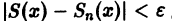
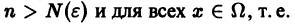
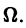
Замечание:
Числовой ряд (2) часто называют мажорирующим, или мажорантным, для функционального ряда (1).
Пример:
Исследовать на равномерную сходимость ряд
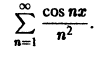
Неравенство
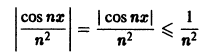
выполняется для всех n = 1, 2, … и для всех 
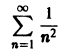
сходится. В силу признака Вейерштрасса рассматриваемый функциональный ряд сходится абсолютно и равномерно на всей оси.
Пример:
Исследовать на равномерную сходимость ряд
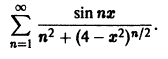
Члены ряда определены и непрерывны на отрезке [-2,2]. Так как
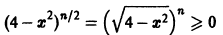
на отрезке [-2,2] для любого натурального n, то
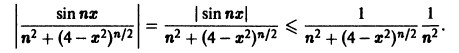
Таким образом, неравенство
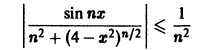
выполняется для n = 1, 2, … и для всех 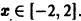
сходится, то по признаку Вейерштрасса исходный функциональный ряд сходится абсолютно и равномерно на отрезке [-2,2].
Замечание:
Функциональный ряд (1) может сходится равномерно на множестве 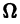
Пример:
Как было показано выше (пример 1 в § 2), ряд
равномерно сходится на отрезке [-1,1 ]. Однако для него мажорантного сходящегося числового ряда (2) не существует. В самом деле, для всех натуральных n и для всех 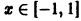
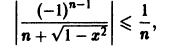
причем равенство достигается при х = — 1 и х = 1. Поэтому члены искомого мажорантного ряда (2) непременно должны удовлетворять условию
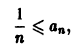
но числовой ряд
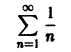
расходится. Значит, будет расходиться и ряд
Свойства равномерно сходящихся функциональных рядов
Равномерно сходящиеся функциональные ряды обладают рядом важных свойств.
Теорема:
Если все члены ряда
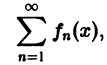
равномерно сходящегося на отрезке [а, b], умножить на одну и ту же функцию g(х), ограниченную на [а, b], то полученный функциональный ряд
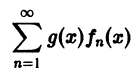
будет равномерно сходиться на [а, b].
Пусть на отрезке [а, b] ряд 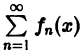
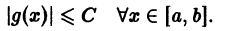
По определению равномерной сходимости ряда для любого числа 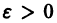
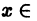
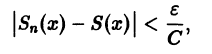
где Sn(x) — частичная сумма рассматриваемого ряда. Поэтому будем иметь
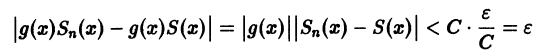
для n > N и для любого 
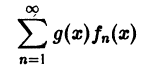
равномерно сходится на [а, b] к функции g(x) S(x).
Теорема:
Пусть все члены fn(x) функционального ряда
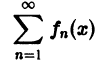
непрерывны и ряд сходится равномерно на отрезке [a, b]. Тогда сумма S(x) ряда непрерывна на этом отрезке.
Возьмем на отрезке [a,b] две произвольные точки 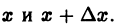
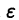
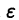
где Sn(х) — частичные суммы ряда 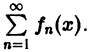
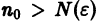
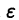
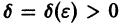
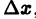
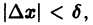
Приращение 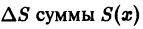
Учитывая неравенства (1) и (2), для приращений 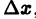
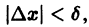
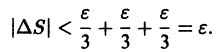
Это означает, что 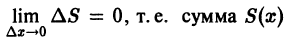
Замечание:
Функциональный ряд
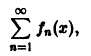
члены которого непрерывны на отрезке [a, b], но который сходится на [а, b] неравномерно, может иметь суммой разрывную функцию.
Пример:
Рассмотрим функциональный ряд
на отрезке [0,1]. Вычислим его n-ю частичную сумму
т.е. сумма ряда
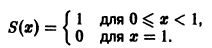
Она разрывна на отрезке [0, 1], хотя члены ряда непрерывны на нем. В силу доказанной теоремы данный ряд не является равномерно сходящимся на отрезке [0,1].
Пример:
Рассмотрим ряд
Как было показано выше, этот ряд сходится при 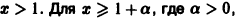
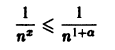
и числовой ряд
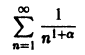
сходится. Следовательно, для любого х > 1 сумма этого ряда непрерывна.
Замечание:
Функция
называется функцией Римана (эта функция играет большую роль в теории чисел).
Теорема:
О почленном интегрировании функционального ряда. Пусть все члены fn(x) ряда
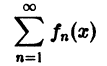
непрерывны, и ряд сходится равномерно на отрезке [а, b] к функции S(х). Тогда справедливо равенство
т. е. данный ряд можно почленно интегрировать в пределах от 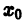
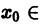
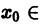
В силу непрерывности функций fn(x) и равномерной сходимости данного ряда на отрезке [а, b] его сумма S(x) непрерывна и, следовательно, интегрируема на [а, b]. Рассмотрим разность
где
Из равномерной сходимости ряда на [a,b] следует, что для любого 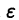
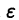
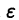
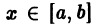
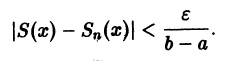
Но тогда
для любого n > N(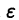
Если ряд 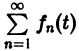
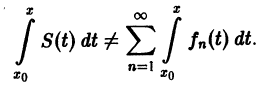
Теорема:
О почленном дифференцировании функционального ряда. Пусть все клены fn(x) сходящегося ряда
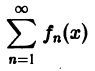
имеют непрерывные производные и ряд
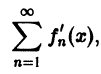
составленный из этих производных, равномерно сходится на отрезке [а, b]. Тогда в любой точке 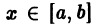
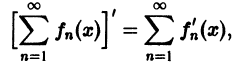
т. е. данный ряд можно почленно дифференцировать.
Положим
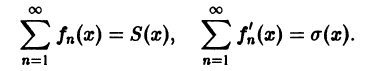
Возьмем две любые точки 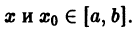
Функция 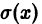
т.е.
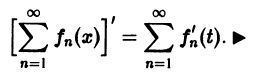
Дополнение к функциональным рядам
Смотрите также:
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Содержание:
- Понятие суммы ряда
- Вычисление суммы ряда почленным интегрированием
- Вычисление суммы ряда почленным дифференцированием
Понятие суммы ряда
Постановка задачи. Найти сумму ряда
где 
План решения. Суммой ряда 


где
1. По условию задачи
Если корни знаменателя различаются на целое число, т.е. 



По этой ссылке вы найдёте полный курс лекций по высшей математике:
2. Разлагаем общий член ряда на элементарные дроби:
и выписываем несколько членов ряда так, чтобы было видно, какие слагаемые сокращаются при вычислении частичных сумм ряда.
3. Находим 

сократив соответствующие слагаемые.
4. Вычисляем сумму ряда по формуле (1)
и записываем ответ.
Пример:
Найти сумму ряда
Решение:
1. Корни знаменателя 




2. Разлагаем общий член ряда на элементарные дроби
и выписываем несколько членов ряда:
3. Сокращая все слагаемые, какие возможно, находим 
4. Вычисляем сумму ряда по формуле (1):
Ответ:
Возможно вам будут полезны данные страницы:
Вычисление суммы ряда почленным интегрированием
Постановка задачи. Найти сумму функционального ряда вида
и указать область сходимости ряда к этой сумме.
План решения.
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
Если 

2. Делаем в исходном ряде замену 
с областью сходимости 
3. Известна формула для вычисления суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке
, целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем
Заметим, что так как ряд (1) сходится в граничной точке 
6. Вычисляем интеграл, делаем замену 

Замечание. Если ряд имеет вид
то применяем теорему о почленном интегрировании степенного ряда дважды или разлагаем дробь на элементарные:
и вычисляем сумму каждого ряда почленным интегрированием.
Пример:
Найти сумму ряда
и указать область сходимости ряда к этой сумме.
Решение:
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
В граничных точках при 

Следовательно, данный ряд сходится при всех 
2. Сделаем замену 
3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке 
Заметим, что так как ряд (1) сходится в граничной точке 

6. Заменяя 

Ответ.
Вычисление суммы ряда почленным дифференцированием
Постановка задачи. Найти сумму функционального ряда вида
и указать область сходимости ряда к этой сумме.
План решения.
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
Если 

2. Делаем в исходном ряде замену 
Следовательно, достаточно найти суммы рядов

3. Известна формула для суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (1), получаем
6. Вычисляем производную и делаем замену 

Замечание. Если ряд имеет вид
то вычисляем сумму трех рядов, причем при вычислении суммы ряда
применяем теорему о почленном дифференцировании степенного ряда дважды.
Пример:
Найти сумму ряда
и указать область сходимости ряда к этой сумме.
Решение:
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством 



2. Делаем в исходном ряде замену 
Следовательно, достаточно найти суммы рядов
3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии:
Следовательно, 

4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (2), получаем
Таким образом,
Заменяя 

Ответ.
Лекции:
- Метод Якоби
- Метод интегрирования
- Свойства функций, имеющих конечный предел
- Дифференциал длины дуги кривой. Формула парабол
- Дифференциальное уравнение Бернулли
- Область сходимости ряда
- Метод Ритца
- Разложение в ряд фурье функций
- Построение графиков функции с помощью производной
- Формулы двойного угла




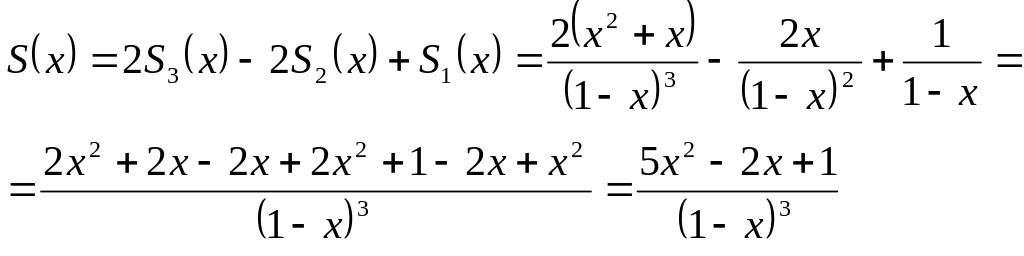

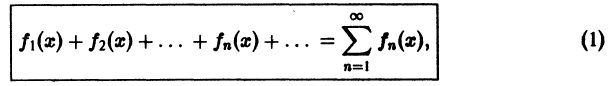
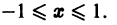
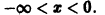
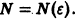
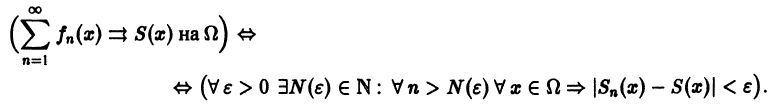
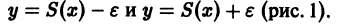

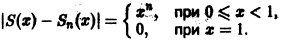
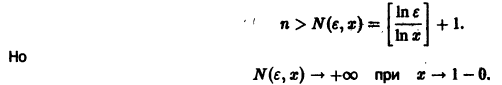
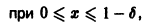
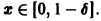


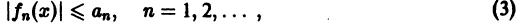
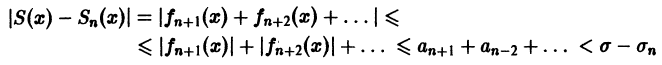
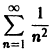
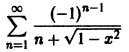
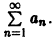
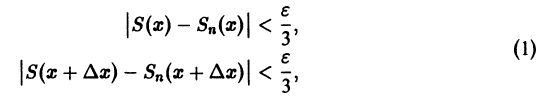
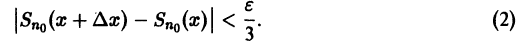
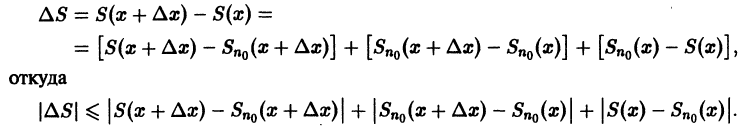
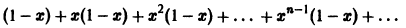
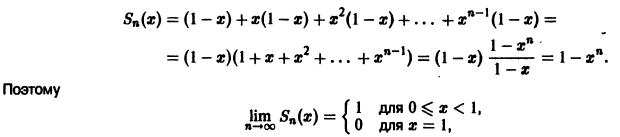
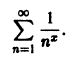
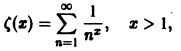
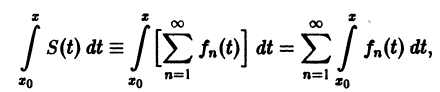
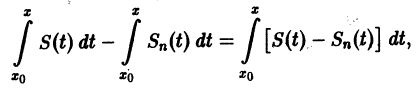
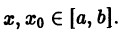
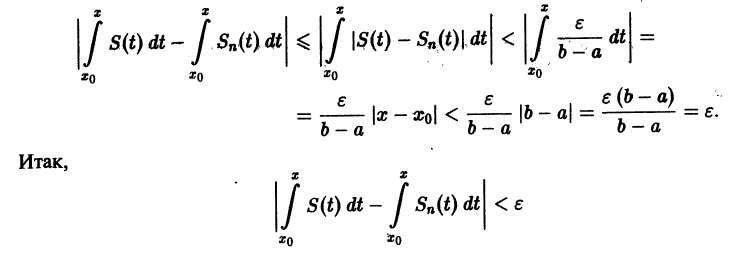
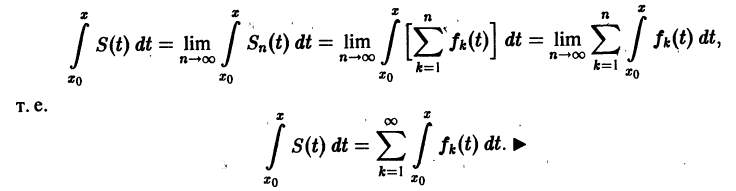
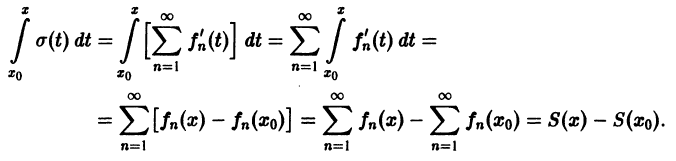
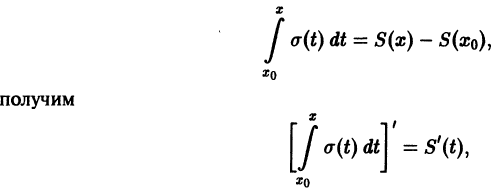
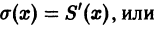




























 , целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем
, целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем
































