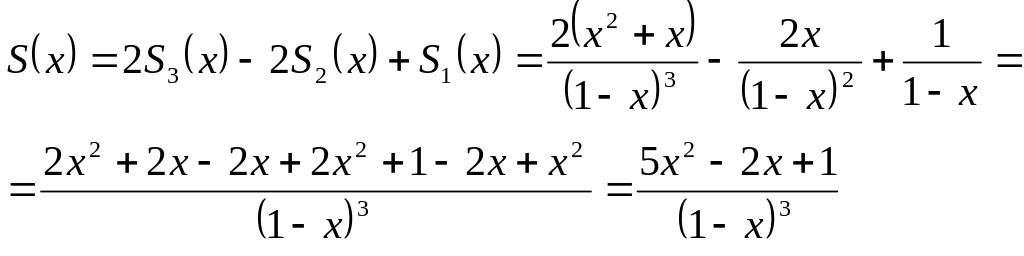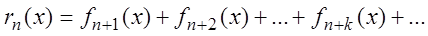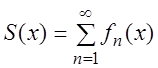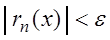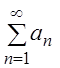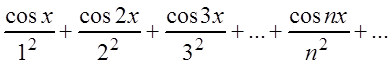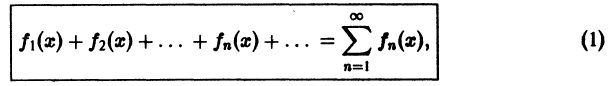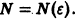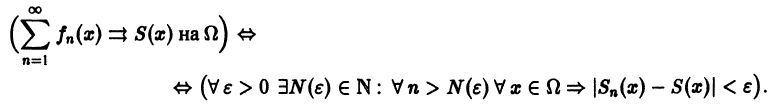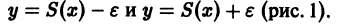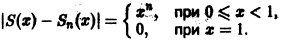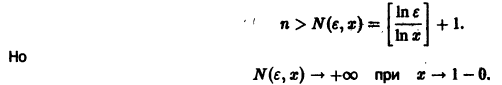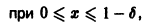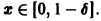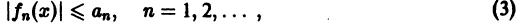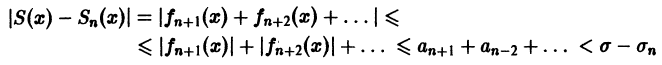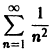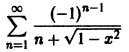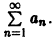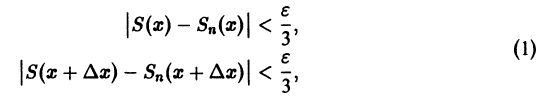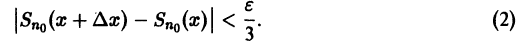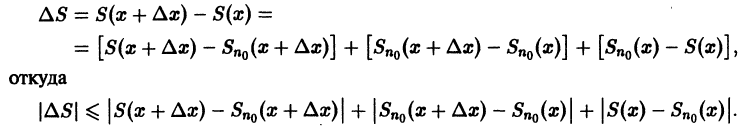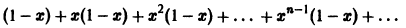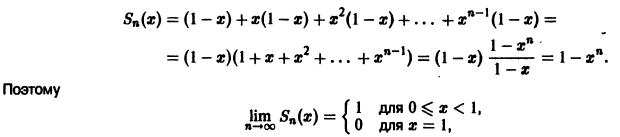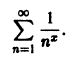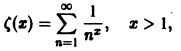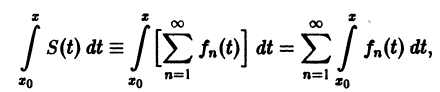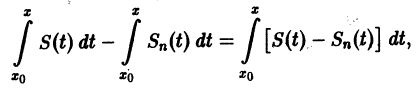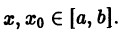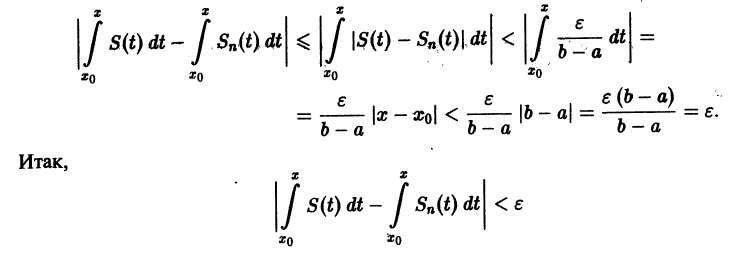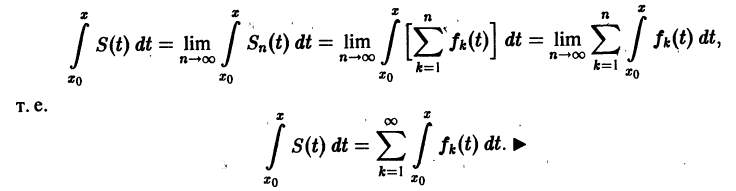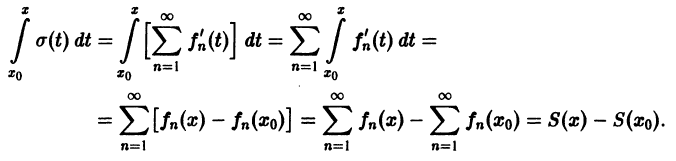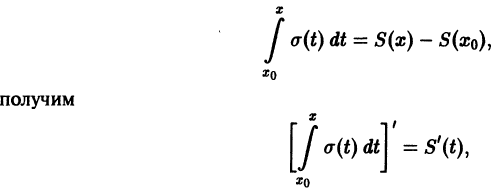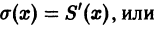Рассмотрим
некоторые приемы нахождения суммы
функционального
ряда и области его сходимости к этой
сумме.
Нахождение
суммы ряда почленным интегрированием.
-
Пусть
дан ряд вида
.
По признаку Коши или
признаку
Даламбера область
сходимости определяется
неравенством
.
Если
,
то ряд
— расходящийся.
Если
,
то ряд
сходится условно (по признаку Лейбница).
Следовательно, область сходимости
находится из неравенства
.
Затем делаем
замену
в исходном ряде; получаем степенной ряд
с областью сходимости
.
Используем формулу для вычисления суммы
членов бесконечно убывающей геометрической
прогрессии со знаменателем
(12)
и
очевидное равенство
(13)
Учитывая,
что степенной ряд можно почленно
интегрировать по любому отрезку
,
целиком принадлежащему интервалу
сходимости, и используя формулу (13),
получаем
Заметим,
что так как ряд (12) сходится в граничной
точке t=-1,
то сумма ряда непрерывна в этой точке
(справа) и
.
Далее вычисляем интеграл (с переменным
верхним пределом), заменяем t
на
и получаем ответ.
-
Если
дан ряд вида
,
то следует либо
применить
теорему о почленном интегрировании
степенного ряда дважды, либо разложить
дробь на элементарные
и
вычислить сумму каждого ряда почленным
интегрированием.
Пример.
Найти сумму ряда
и указать область
его
сходимости к этой сумме.
Решение.
Данный ряд степенной. Находим его
интервал сходимости. По признаку Коши
имеем
.
Из неравенства находим
.
Исследуем поведение ряда в граничных
точках. При
—
расходящийся гармонический ряд. При
— условно сходящийся ряд по признаку
Лейбница. Следовательно, данный ряд
сходится при
.
Для нахождения суммы ряда сделаем замену
.
Получим геометрический ряд
,
сходящийся при
.
Используя равенство (13) и почленное
интегрирование степенного ряда, получаем:

Ответ:
для
.
Замечание.
Степенной ряд (10) сходится абсолютно и
равномерно на всяком отрезке, лежащем
внутри его интервала сходимости; ряд
(10) можно почленно интегрировать и
дифференцировать внутри его интервала
сходимости
,
т.е. если
то для
имеем
и
Задание
17. Найти
сумму ряда и указать область сходимости
к этой сумме.
Задача
1.
Решение.
Имеем
.
Найдем
сумму каждого из этих рядов в их области
сходимости. Сначала рассмотрим ряд
.
Используем
формулу для вычисления суммы членов
бесконечно убывающей геометрической
прогрессии
,
где
,
,
и равенство (13).Учитывая, что степенной
ряд можно почленно интегрировать на
любом отрезке
,
целиком принадлежащем интервалу
сходимости, получаем первую сумму:

Т.к.
ряд
сходится в граничной точке х=-1, то его
сумма непрерывна в этой точке:
.Значит,
при
всех
.
(14)
Аналогично
находим вторую сумму с учетом (14):
Таким
образом, сумма исходного ряда

Ответ:
,
Задача
2.
Решение.
Находим область сходимости функционального
ряда, применяя признак Даламбера
Область
сходимости определяется неравенством
,
или
.
Решая его, получаем
или
.
При
имеем
—
расходящийся ряд (т.к.
~
).
Следовательно, ряд сходится при
.
Сделаем замену
.
Получим ряд
с областью сходимости
.
Используя формулу (12):
равенство (13):
и почленное интегрирование на любом
отрезке, принадлежащем области сходимости,
получаем
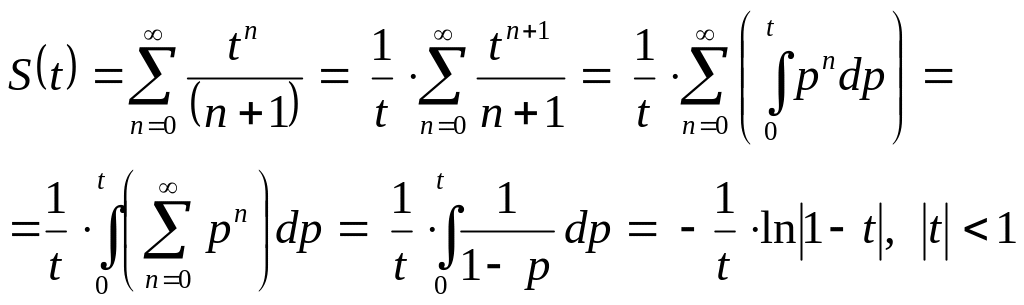
Заменяя
t
на
,
получаем сумму
Ответ:
,
.
Нахождение
суммы ряда почленным дифференцированием.
I.
Пусть дан ряд вида
.
Сначала
определяем область сходимости ряда,
например, по признаку Коши. Получаем
неравенство
.
Если
,
то ряд расходится, т.к. не выполнено
необходимое
условие
сходимости
.
Следовательно, область
сходимости
определяется неравенством
.
Затем делаем замену
и записываем ряд в виде суммы двух рядов
.
Для нахождения сумм этих рядов используем
формулу суммы членов бесконечно убывающей
геометрической прогрессии и очевидное
равенство
.
Учитывая,
что степенной ряд можно почленно
дифференцировать в любой точке интервала
сходимости, и используя равенство
,
получаем
Далее
вычисляем производную, делаем замену
и
записываем ответ.
II.
Если дан ряд вида
,
то вычисляем сумму трех рядов
,
и
,
причем при вычислении суммы ряда
применяем теорему о почленном
дифференцировании степенного ряда
дважды.
Задание
18. Найти
сумму ряда и указать область
сходимости
ряда к этой сумме.
Задача
3.
Решение.
а). Находим
область сходимости данного ряда по
признаку Даламбера
Отсюда
.
В граничных точках
ряд расходится, т.к. не выполнено
необходимое условие сходимости. Итак,
ряд сходится (и притом абсолютно) в
интервале (-1;1).
б).
Делаем в исходном ряде замену
и записываем в виде суммы двух рядов
Для
нахождения S(t)
достаточно найти суммы рядов
и
.
Учитывая,
что степенной ряд можно почленно
дифференцировать
в любой точке интервала сходимости,
получаем
.
И
в)
Заменяя
на
,
получаем
Ответ:
Задача
4.
Решение.
По признаку
Коши интервал сходимости
степенного
ряда определяется неравенством
,
т.е. ряд сходится в интервале (-1;1). Для
нахождения суммы ряда достаточно
представить ряд в виде суммы трех рядов
и найти суммы рядов:
,
где
применили один раз почленное
дифференцирование по x;
.
Т.к.
выше найденная на предыдущем шаге сумма
ряда
,
то еще раз применив почленное
дифференцирование по x
к ряду;
,
получаем
.Таким
образом, сумма исходного ряда равна
.
Ответ:
,
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
01.05.20221.51 Mб0Учебники 60167.doc
- #
01.05.20221.53 Mб0Учебники 60168.doc
- #
- #
- #
- #
- #
01.05.20221.56 Mб0Учебники 60172.doc
- #
- #
- #
Функциональные ряды и их сходимость: равномерная и неравномерная
Понятие функционального ряда и область его сходимости
Функциональным рядом называется формально записанное выражение
где u 1 (x), u 2 (x), u 3 (x), . u n (x), . — последовательность функций от независимой переменной x.
Сокращённая запись функционального ряда с сигмой: .
Примерами функциональных рядов могут служить:
Придавая независимой переменной x некоторое значение x 0 и подставляя его в функциональный ряд (1), получим числовой ряд
Если полученный числовой ряд сходится, то говорят, что функциональный ряд (1) сходится при x = x 0 ; если он расходится, что говорят, что ряд (1) расходится при x = x 0 .
Пример 1. Исследовать сходимость функционального ряда (2) при значениях x = 1 и x = — 1 .
Решение. При x = 1 получим числовой ряд
который сходится по признаку Лейбница. При x = — 1 получим числовой ряд
который расходится как произведение расходящегося гармонического ряда на – 1. Итак, ряд (2) сходится при x = 1 и расходится при x = — 1 .
Если такую проверку на сходимость функционального ряда (1) осуществить относительно всех значений независимой переменной из области определения его членов, то точки этой области разобьются на два множества: при значениях x, взятых в одном из них, ряд (1) сходится, а в другом – расходится.
Множество значений независимой переменной, при которых функциональный ряд сходится, называется его областью сходимости.
Пример 2. Найти область сходимости функционального ряда
Решение. Члены ряда определены на всей числовой прямой и образуют геометрическую прогрессию со знаменателем q = sin x . Поэтому ряд сходится, если
и расходится, если
(значения невозможны). Но при значениях и при остальных значениях x. Следовательно, ряд сходится при всех значениях x, кроме . Областью его сходимости служит вся числовая прямая, за исключением этих точек.
Пример 3. Найти область сходимости функционального ряда
Решение. Члены ряда образуют геометрическую прогрессию со знаменателем q=lnx . Поэтому ряд сходится, если , или , откуда . Это и есть область сходимости данного ряда.
Пример 4. Исследовать сходимость функционального ряда
Решение. Возьмём произвольное значение . При этом значении получим числовой ряд
Найдём предел его общего члена
Следовательно, ряд (*) расходится при произвольно выбранном, т.е. при любом значении x. Область его сходимости – пустое множество.
Равномерная сходимость функционального ряда и её свойства
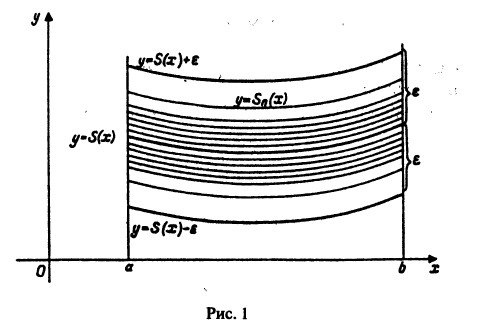
Перейдём к понятию равномерной сходимости функционального ряда. Пусть s(x) — сумма этого ряда, а s n (x) — сумма n первых членов этого ряда. Функциональный ряд u 1 (x) + u 2 (x) + u 3 (x) + . + u n (x) + . называется равномерно сходящимся на отрезке [a, b] , если для любого как угодно малого числа ε > 0 найдётся такой номер N , что при всех n ≥ N будет выполнятся неравенство
Приведённое выше свойство можно геометрически иллюстрировать следующим образом.
Рассмотрим график функции y = s(x) . Построим около этой кривой полосу шириной 2ε n , то есть построим кривые y = s(x) + ε n и y = s(x) − ε n (на рисунке ниже они зелёного цвета).
Тогда при любом ε n график функции s n (x) будет лежать целиком в рассматриваемой полосе. В этой же полосе будут лежать графики всех последующих частичных сумм.
Всякий сходящийся функциональный ряд, который не обладает описанным выше признаком — неравномерно сходящийся.
Рассмотрим ещё одно свойство равномерно сходящихся функциональых рядов:
сумма ряда непрерывных функций, равномерно сходящегося на некотором отрезке [a, b] , есть функция, непрерывная на этом отрезке.
Пример 5. Определить, непрерывна ли сумма функционального ряда
Решение. Найдём сумму n первых членов этого ряда:
Наше исследование показало, что сумма данного ряда — разрывная функция. Её график изображён на рисунке ниже.
Признак Вейерштрасса равномерной сходимости функциональных рядов
К признаку Вейерштрасса подойдём через понятие мажоририуемости функциональных рядов. Функциональный ряд
называется мажорируемым в некоторой области изменения x, если существует такой сходящийся числовой ряд
с положительными членами, что для всех значений x из данной области выполняются соотношения
Иначе говоря, ряд называется мажорируемым, если каждый его член по абсолютной величине (модулю) не больше соответствующего члена некоторого сходящегося числового ряда с положительными членами.
Признак Вейерштрасса равномерной сходимости функциональных рядов. Функциональный ряд, мажорируемый в некоторой области, равномерно сходится во всех точках этой области.
Пример 6. На основании признака Вейерштрасса сделать вывод о том, является ли равномерно сходящимся функциональный ряд
Решение. Известно, что ряд
сходится. Проведём сравнение рядов. Установили, что для всех значений x выполняется соотношение
Поэтому данный функциональный ряд — мажорируемый на всей оси Оx. А значит, что по признаку Вейерштрасса данный ряд — равномерно сходящийся на всей оси Оx.
Глава 5. Представление аналитических функций рядами
Число $S_n=a_1+a_2+dots+a_n$ будем называть частичной суммой этого ряда.
Ряд будем называть сходящимся, если последовательность $$ его частичных сумм сходится, то есть стремится к конечном пределу: $$ lim_ S_n=S. $$ $S$ называют суммой ряда.
Если последовательность $$ стремится к бесконечно удаленной точке или не стремится ни к какому пределу, то ряд будем называть расходящимся.
$R_n=sumlimits_^infty a_k$ называют остатком ряда.
$ S=S_n+R_n $ для сходящегося ряда.
$R_n=S-S_nto0$ при $ntoinfty$ для сходящегося ряда.
Пусть $a_k=x_k+mathbf i y_k$ и $sumlimits_^infty a_k=sumlimits_^infty x_k+mathbf i sumlimits_^infty y_k$.
Сходимость ряда $sumlimits_^infty a_k$ равносильна одновременной сходимости рядов $sumlimits_^infty x_k$ и $sumlimits_^infty y_k$.
Если сходится ряд $ sumlimits_^infty |a_k|$, то сходится и ряд $sumlimits_^infty a_k$ и он называется абсолютно сходящимся.
Необходимый признак сходимости.
Признак Даламбера для абсолютно сходящихся рядов.
Если существует $$lim_ left|frac>right|=p,$$ то при $p<1$ ряд $sumlimits_^infty |a_k|$ сходится, а при $p>1$ расходится.
Признак Коши для абсолютно сходящихся рядов.
Если существует $$lim_sqrt[n]|>=q,$$ то при $q<1$ ряд $sumlimits_^infty |a_k|$ сходится, а при $q>1$ расходится.
Функциональные ряды
Пусть в некоторой области $D$ определена бесконечная последовательность однозначных функций $$. Образуем функциональный ряд begin sumlimits_^infty f_k(z)=f_1(z)+f_2(z)+dots+f_n(z)+dots end
Частичная сумма этого ряда будет функцией $S_n(z)=f_1(z)+f_2(z)+dots+f_n(z)$.
Если в каждой точке $z_0$ области $D$ ряд $sumlimits_^infty f_k(z)$ обращается в сходящийся числовой ряд, то говорят, что ряд сходится в области $D$ и его сумма $$ S(z)=lim_ S_n(z).$$
Если ряд сходится в области $D$, то в каждой точке этой области последовательность остатков стремится к $0$: $$ lim_R_n(z)=lim_(S(z)-S_n(z))=0. $$
Ряд $sumlimits_^infty f_k(z)$, сходящийся в области $D$, называется равномерно сходящимся в этой области, если для любого $varepsilon>0$ можно указать такой номер $N(varepsilon)$, что при $n>N(varepsilon)$ будет выполняться $|R_n(z)|<varepsilon$ одновременно для всех $z$ из области $D$.
Признак Вейрштрасса (достаточный признак равномерной сходимости).
Если в каждой точке $z$ области $D$ модули $|f_k(z)|$ не превосходят (мажорированы) соответствующих элементов какого-нибудь сходящегося числового ряда $sumlimits_^infty a_k$, то функциональный ряд $sumlimits_^infty f_k(z)$ сходится равномерно в $D$.
Свойства суммы функционального ряда
1. Сумма $S(z)$ функционального ряда $sumlimits_^infty f_k(z)$, равномерно сходящегося в $D$, непрерывна в области $D$, если $f_k(z)$ являются непрерывными в $D$ функциями.
2. Равномерно сходящийся в $D$ функциональный ряд $sumlimits_^infty f_k(z)$, составленный из непрерывных функций, можно интегрировать почленно вдоль любой кривой $ell$, принадлежащей области $D$: $$ intlimits_S(z),dz = sumlimits_^infty intlimits_f_k(z),dz. $$
3. Теорема Вейштрасса. Пусть $f_k(z)$ являются аналитическими в области $D$ функциями и ряд сходится равномерно в любой области $bar_1in D$ к функции $S(z)$. Тогда $S(z)$ также аналитична в области $D$ и ее производные можно получить почленными дифференцированием ряда: $$ frac^nS(z)>^n>=sumlimits_^infty frac^n,f_k(z)>^n>. $$
Степенные ряды
Функциональный ряд вида begin sumlimits_^infty c_n(z-z_0)^n=c_0+c_1(z-z_0)+c_2(z-z_0)^2+ ldots+c_n(z-z_0)^n+dots , end где $c_n$ — комплексные постоянные (коэффициенты ряда), называется степенным.
Если степенной ряд $sumlimits_^infty c_n(z-z_0)^n$ сходится в точке $z_1neq z_0$, то он абсолютно сходится внутри круга: $|z-z_0|<|z_1-z_0|$, причем во всяком круге $|z-z_0|leqslantrho<|z_1-z_0|$ ряд сходится равномерно.
Если степенной ряд $sumlimits_^infty c_n(z-z_0)^n$ расходится в некоторой точке $z_2neq z_0$, то он расходится в $|z-z_0|>|z_2-z_0|$.
Областью сходимости степенного ряда называется внутренность круга $|z-z_0|<R$ (на окружности ряд может сходиться, а может и расходиться).
Радиус сходимости $R$ можно определить, пользуясь признаками Даламбера или Коши: $$ R=limlimits_left|frac>right|quad hboxquad R=limlimits_frac1>. $$
Степенной ряд в круге сходимости:
— сходится к аналитической функции;
— можно почленно интегрировать и дифференцировать.
Ряд Тейлора
Один из видов степенного ряда — ряд Тейлора $$ f(z)=sumlimits_^infty c_n(z-z_0)^n,quad c_n=frac1f^(z_0). $$
Кругом сходимости этого ряда является круг $|z-z_0|<R$. Как и всякий степенной ряд, ряд Тейлора внутри круга сходимости определяет некоторую аналитическую функцию.
Функция $f(z)$, аналитическая внутри круга $|z-z_0|<R$, может быть представлена в этом круге сходящимся степенным рядом $$ f(z)=sumlimits_^infty c_n(z-z_0)^n, $$ причем этот ряд определен однозначно.
Разложения в ряд Тейлора для некоторых функций
Примеры построения аналитического продолжения с помощью степенных рядов
Пусть первоначально функция $f_1(z)$ задана своим степенным рядом $$ f_1(z)=sumlimits_^infty z^n. $$ Этот ряд сходится внутри круга $|z|<1$ к аналитической функции $$ f_1(z)=frac1. $$ Всюду вне круга $|z|<1$ ряд расходится: следовательно, $f_1(z)$ не определена вне круга $|z|<1$.
Выберем некоторую точку $z_0$ внутри круга $|z|<1$ и построим разложение $f_1(z)$ в степенной ряд $sumlimits_^infty c_n (z-z_0)^n$ с центром в этой точке. Вычислим коэффициенты $c_$ по формуле $$ c_n=frac(z_0 )>=frac1>. $$ Можно показать, что радиус сходимости данного ряда равен $|1-z_0|$.
Следовательно, функция $$ f_2(z)=sumlimits_^inftyfrac> $$ является аналитическим продолжением функции $f_1(z)$ на область $|z-z_0|<|1-z_0|$.
Заметим, что степенной ряд, определяющий функцию $f_2(z)$, также легко суммируется, причем $f_2(z)=dfrac1$.
Далее, взяв в качестве нового центра разложения точку $z_1$ внутри круга $|z-z_0|<|1-z_0|$, получим ряд $$ sumlimits_^inftyfrac>, $$ сходящийся внутри круга $|z-z_1|< |1-z_1|$ к функции $f_3(z)=dfrac1$, совпадающей с $f_2(z)$ и $f_1(z)$ в общих частях круга $|z-z_1|<|1-z_1|$ и областей определения соответствующих функций.
Тем самым $f_3(z)$ является аналитическим продолжением $f_1(z)$ на новую область.
При любом выборе точки $z_1$ граница соответствующего круга сходимости пройдет через точку $z=1$.
Поступая аналогичным образом, можно построить аналитическое продолжение функции $f_1(z)$ на полную плоскость комплексной переменной, за исключением точки $z=1$. При этом аналитическим продолжением $f_1(z)$, полученным с помощью степенных рядов, является функция $$ F(z)=frac1, $$ определенная и аналитическая всюду, за исключением точки $z=1$.
Ряд Лорана
Рассмотрим ряд, содержащий отрицательные степени $z-z_0$: $$ sumlimits_^infty a_n(z-z_0)^=a_0+a_1(z-z_0)^+a_2(z-z_0)^+ldots+a_n(z-z_0)^+ldots. $$ Областью сходимости этого ряда является внешность круга: $$|z-z_0|>r.$$
Ряд, который содержит как целые неотрицательные степени, так и целые неположительные степени $(z-z_0)$, называется рядом Лорана и имеет вид: $$ sumlimits_^ a_n(z-z_0)^n+sumlimits_^ a_(z-z_0)^=sumlimits_^infty a_n(z-z_0)^n= $$ $$ ldots+ frac>+ldots+frac>+ a_0+a_1(z-z_0)+ldots+a_n(z-z_0)^n+ldots. $$
Областью сходимости ряда Лорана является круговое кольцо $$r<|z-z_0|<R.$$
Часть ряда Лорана с коэффициентами $a_$ называется главной частью ряда Лорана, а с коэффициентами $a_n$ — правильной частью.
Кольцо $r<|z-z_0|<R$ может выродиться
в круг с выколотым центром: $0<|z-z_0|<R_2$
или во внешность круга с выколотой точкой $z=infty$: $R_1<|z-z_0|<infty$,
а также во всю плоскость с двумя выколотыми точками: $0<|z-z_0|<infty$.
Всякая функция $f(z)$ однозначная и аналитическая в круговом кольце $r<|z-z_0|<R$, где $0 leqslant r<R<infty$, может быть единственным образом разложена в ряд Лорана: begin f(z)=sumlimits_^infty c_n(z-z_0)^n= sumlimits_^infty c_n(z-z_0)^n+sumlimits_^infty frac>. end Здесь beginlabel c_n=frac1ointlimits_gammafrac >,dt,quad n=0,pm1,pm2,dots, end а $gamma$ — любая окружность $|t-z_0|=rho$, $r<rho <R$, ориентированная против часовой стрелки.
Функция $$ f(z)=frac1 $$ аналитична на плоскости $z$, за исключением $z=2$ и $z=3$. Проведем через них окружности $|z|=2$, $|z|=3$. Данная функция аналитична в круге $|z|<2$, аналитична в кольце $2<|z|<3$ и аналитична вне круга $|z|>3$ и может быть в этих областях разложена в ряды. Разложим функцию в ряд Лорана в кольце $2<|z|<3$: $$ f(z)=sumlimits_^infty c_kz^k, $$ где $$ c_k=frac1ointlimits_gammafrac >,dvarsigma,quad k=0,pm1,pm2,dots . $$ Здесь $gamma$ — окружность $|varsigma|=rho$, $2<rho<3$, ориентированная против часовой стрелки.
На самом деле для вычисления $c_k$ не обязательно прибегать к таким сложным формулам. Иногда удобнее использовать представление разлагаемой функции в виде суммы функций, каждую из которых можно непосредственно представить в виде разложения по отрицательным или положительным степеням $z-z_0$.
Представим $$ f(z)=frac1=frac1-frac1 $$ и разложим каждое слагаемое по степеням $z$: $$ begin frac1=frac3right)>= -sumlimits_^inftyfrac>, \ frac1=frac1cdotfrac1>=frac1 left(1+frac2+left(frac2right)^2+dotsright)= sumlimits_^inftyfrac>. end $$ Здесь использовалась формула для суммы членов бесконечно убывающей геометрической прогрессии.
Окончательно ряд Лорана этой функции имеет вид $$ f(z)=sumlimits_^inftyfrac>— sumlimits_^inftyfrac>. $$
Разложение около другой точки даст другой вид ряда.
Рассмотрим функцию $$ f(z)=frac1. $$ Она имеет две особые точки $z=1$ и $z=2$ и, значит, в кольце $1<|z|<2$ является аналитической и разлагается в ряд Лорана. Найдем это разложение, представив функцию в виде суммы простейших дробей: $$ frac1=frac1-frac1. $$ Дробь $1/(z-2)$ является аналитической функцией в круге $|z|<2$ и разлагается по положительным степеням аналогично ряду геометрической прогрессии: $$ -frac12cdotfrac12>=-frac12left( 1+frac2+frac+ldots+frac+ldotsright)= -frac12sumlimits_^inftyleft(frac2right)^n. $$ Дробь $-1/(z-1)$ является аналитической вне круга $|z|>1$ и разлагается по степеням $1/z$ также как сумма геометрической прогрессии: $$ frac=!fracright)>= -frac1zleft(1+frac1z+frac1+ldots+frac1+ldots right)=-sumlimits_^inftyfrac1. $$
Окончательно имеем $$ f(z)=-frac12sumlimits_^inftyleft(frac2right)^n -sumlimits_^inftyfrac1=-frac12 -sumlimits_^inftyleft(frac+frac1right). $$ Для этой функции можно получить и другие разложения в других областях. Так, например, в области $|z|<1$ она аналитична и разлагается в ряд Тейлора: $$ frac1=-frac1+frac1=frac1-frac12cdot frac12>= $$ $$ =1+z+z^2+ldots+z^n+ldots-frac12left(1+frac2+frac+ ldots+frac+ldotsright)= $$ $$ =sumlimits_^inftyleft(1-frac1>right)z^n. $$
Разложим ее в кольце $0<|z-1|<1$ (окрестность точки $z_0=1$) по степеням $z-1$: $$ f(z)=-frac1+frac1=-frac1-frac1= $$ $$ =-frac1-sumlimits_^infty(z-1)^n= -sumlimits_^infty(z-1)^n. $$
Таким образом, для одной и той же функции можно получить различные разложения. Это не противоречит единственности разложения, ибо полученные ряды имеют место в различных областях.
Нули аналитических функций
Рассмотрим функцию $f(z)$ не равную тождественно нулю. Точка $z_0$ называется корнем, или нулем, функции $f(z)$, если $f(z_0)=0$.
Пусть $f(z)$ аналитична в точке $z_0$. Точка $z_0$ называется нулем порядка $m$ для аналитической функции $f(z)$, если разложение в степенной ряд функции $f(z)$ имеет вид $$ f(z)=sumlimits_^infty c_k(z-z_0)^k,quad c_ne0, mge 1. $$
Для того, чтобы число $z_0$ являлось нулем порядка $m$ функции $f(z)$, необходимо и достаточно, чтобы функция $f(z)$ делилась на $(z-z_0)^m$: $$ f(z)=(z-z_0)^m,varphi(z), ,, varphi(z_0)neq0. $$
Изолированные особые точки, их классификация с помощью ряда Лорана
Точки, в которых функция $f(z)$ не является аналитической, называются особыми точками данной функции $f(z)$.
Особая точка $z_0$ функции $f(z)$ является изолированной особой точкой, если функция $f(z)$ аналитична в некотором кольце $0<|z-z_0|<R$, т.е. если в достаточно малой окрестности особой точки $z_0$ нет других особых точек.
Другими словами, для точки $z_0$ существует проколотая окрестность, в которой данная функция аналитична, но в самой точке $z_0$ функция $f(z)$ не определена или теряет аналитичность.
В зависимости от поведения функции $f(z)$ вблизи точки $z_0$ различают следующие три типа изолированных особых точек:
Изолированная особая точка $z_0$ функции $f(z)$ называется устранимой (или правильной), если существует конечный предел $$ limlimits_f(z)=Aneqinfty. $$
Изолированная особая точка $z_0$ функции $f(z)$ называется полюсом, если $$ limlimits_ f(z)=infty. $$
Изолированная особая точка $z_0$ функции $f(z)$ называется существенно особой, если $limlimits_f(z)$ не существует.
Для того чтобы изолированная особая точка $z_0$ функции $f(z)$ была устранимой, необходимо и достаточно, чтобы лорановское разложение $f(z)$ в некоторой окрестности $z_0$ не содержало главной части, т.е. представляло бы ряд Тейлора$:$ beginlabel sumlimits_^infty c_n(z-z_0)^n=c_0+c_1(z-z_0)+ldots+ c_n(z-z_0)^n+dots . end
Данная функция $f(z)$ совпадает с суммой ряда $$ sumlimits_^infty c_n(z-z_0)^n=c_0+c_1(z-z_0)+ldots+ c_n(z-z_0)^n+dots, $$ если $zne z_0$. Функция $f(z)$ будет аналитической и в точке $z_0$, если положить $f(z_0)=c_0$, что обычно и делают.
Для того чтобы изолированная особая точка $z_0$ функции $f(z)$ была полюсом, необходимо и достаточно, чтобы главная часть лорановского разложения $f(z)$ в окрестности $z_0$ содержала бы лишь конечное число членов$:$ beginlabel f(z)=frac>+frac>>+ldots +frac>+sumlimits_^infty c_n(z-z_0)^n. end
Если $m>0$, $c_ne0$, то $m$ называется порядком полюса, при $m=1$ полюс, называется простым.
Точка $z_0$ является полюсом функции $f(z)$ порядка $m$, когда эта точка является нулем функции $1/f(z)$ кратности $m$.
Следующие три утверждения эквивалентны:
Для того чтобы изолированная особая точка $z_0 $ функции $f(z)$ была существенно особой, необходимо и достаточно, чтобы главная часть лорановского разложения функции $f(z)$ в окрестности $z_0$ содержала бы бесконечное число членов: beginlabel f(z)=sumlimits_^infty c_n(z-z_0)^n. end
Таблица «Классификация особых точек».
| Тип особой точки | Вид ряда Лорана | Предел функции |
|---|---|---|
| УОТ | $c_0+c_1(z-z_0)+c_2(z-z_0)^2+ldots$ | $c_0$ |
| Полюс порядка $m$ | $dfrac>+ldots +dfrac>+c_0+c_1(z-z_0)+c_2(z-z_0)^2+ldots$ | $infty$ |
| СОТ | $ldots+dfrac>+ldots+dfrac>+c_0+c_1(z-z_0)+c_2(z-z_0)^2+ldots$ | Не существует предела |
Если точка $z_0 $ является существенно особой точкой функции $f(z)$, то для любого числа $A$ (конечного или бесконечного) существует такая последовательность $$ значений аргумента, стремящаяся к пределу $z_0$, для которой последовательность $$ соответствующих значений функции $f(z)$ стремится к $A$.
Функциональные ряды (Понятие функционального ряда. Степенные ряды и их свойства. Ряды Тейлора и Маклорена. Применение степенных рядов. Ряды Фурье)
Определение. Пусть 
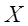
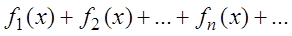
называется функциональным рядом и обозначается сокращённо: 
Пусть число 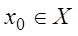
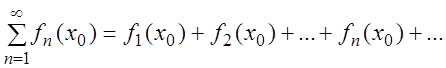
является числовым рядом.
Определение. Если числовой ряд (3.2) сходится, то ряд (3.1) называется сходящимся в точке х0, а число 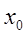
Определение. Множество 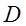
Последнее определение можно сформулировать иначе: областью сходимости функционального ряда называется совокупность значений 
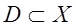
Пример 1. Найти область определения и область сходимости функционального ряда:
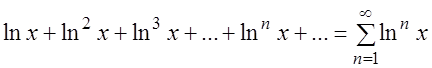
Решение. Так как ряд составлен из функций вида 
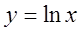

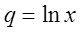
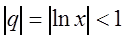

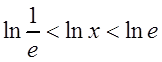
Поэтому областью сходимости является интервал 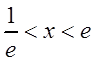
Таким образом, 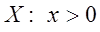
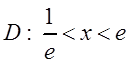
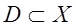
Определение. Как и для числовых рядов, n-й частичной суммой ряда (3.1) называется выражение:
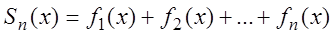
называется n-м остатком ряда.
Для любого 
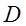

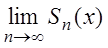
Определение. Функция 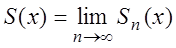
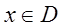

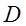
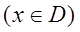
Если 
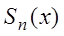
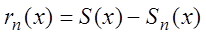
Полезно также другое определение суммы функционального ряда.
Определение. Функция 
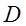
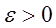
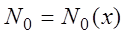

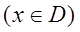
В общем случае 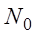

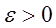
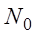
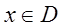
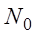

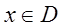
В случае равномерной сходимости функционального ряда его n-я частичная сумма является приближением суммы ряда с одной и той же точностью для всех 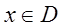
Определение. Функциональный ряд (3.1) называется мажорируемым в некоторой области 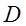
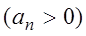
такой, что для всех 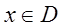

Ряд (3.4) называется мажорантным (мажорирующим) рядом.
Мажорируемый ряд является рядом равномерно сходящимся.
Например, функциональный ряд:
мажорируется рядом 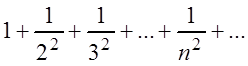
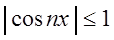
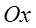

Равномерно сходящиеся ряды обладают некоторыми общими свойствами:
1) если члены равномерно сходящегося ряда непрерывны на некотором отрезке, то его сумма также непрерывна на этом отрезке;
2) если члены ряда (3.1) непрерывны на отрезке 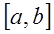

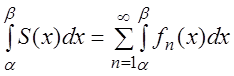
где 
3) если ряд (3.1), составленный из функций, имеющих непрерывные производные на отрезке 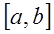

равномерно сходится на том же отрезке, то 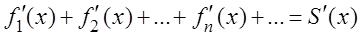
Последние два свойства определяют условия, при которых функциональные ряды можно почленно интегрировать и дифференцировать.
3.2. Степенные ряды
Определение. Степенным рядом называется функциональный ряд вида:
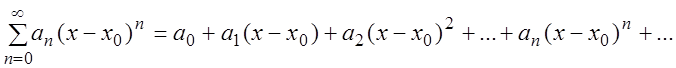
где 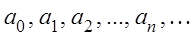

При 
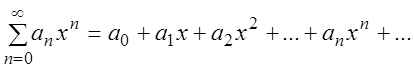
Очевидно, что для (3.5) число 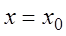
Выясним вопрос об области сходимости степенного ряда.
Теорема 3.1 (теорема Абеля)
1) Если степенной ряд (3.6) сходится при некотором значении 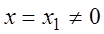

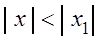
2) Если степенной ряд (3.5) расходится при некотором значении 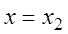


Доказательство
1) Так как по условию числовой ряд 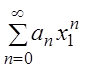
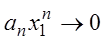

ограничена, т.е. существует число 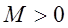

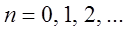
Перепишем ряд (3.6) в виде:

и рассмотрим ряд, составленный из абсолютных величин его членов:
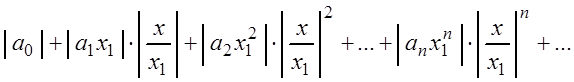
Члены ряда (3.9) в силу неравенства (3.7) меньше соответствующих членов ряда
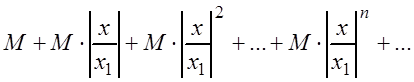
При 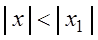
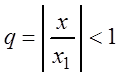

2) Докажем теперь вторую часть теоремы. По условию в точке 




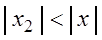
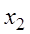

Теорема Абеля утверждает, что если 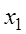

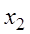
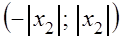
Из этого можно заключить, что существует такое число 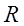
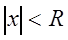
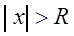
Таким образом, имеет место следующая теорема о строении области сходимости степенного ряда (3.6).
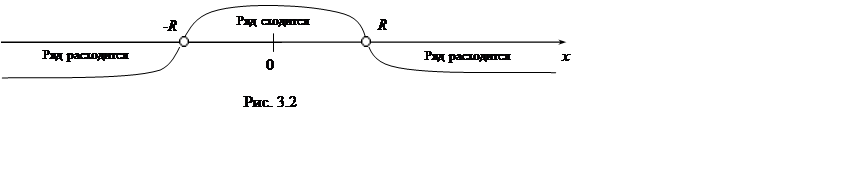
Теорема 3.2. Областью сходимости степенного ряда (3.6) является интервал с центром в начале координат.
Определение. Неотрицательное число 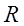
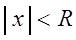
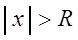
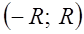
На концах интервала (т.е. при 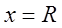
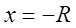
Если ряд (3.6) сходится только в одной точке 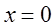
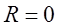

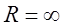
Радиус сходимости степенного ряда обычно находится с использованием признаков Даламбера и Коши. Рассмотрим способ определения радиуса сходимости 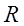
Рассмотрим ряд, составленный из абсолютных величин членов ряда (3.6):
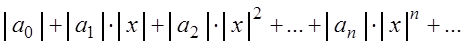
Так как ряд (3.11) с положительными членами, то для определения его сходимости применим признак Даламбера (см. теорему 3.5).
Допустим, что существует предел:
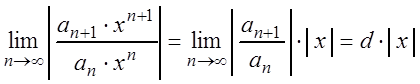
Тогда по признаку Даламбера ряд (3.11) сходится, если 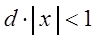
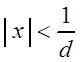
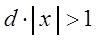
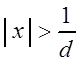
Функциональный ряд — ряд, каждым членом которого, в отличие от числового ряда, является не число, а функция 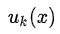
Решение функциональных рядов
Область сходимости
Функциональным рядом называется ряд
членами которого являются функции 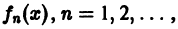
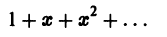
определены на интервале 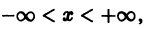
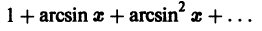
определены на отрезке
Функциональный ряд (1) называется сходящимся в точке 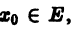
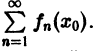
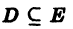
Ряд (1) называется абсолютно сходящимся на множестве D, если на этом множестве сходится ряд
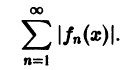
В случае сходимости ряда (1) на множестве D его сумма S будет являться функцией, определенной на D,
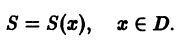
Область сходимости некоторых функциональных рядов можно найти с помощью известных достаточных признаков, установленных для рядов с положительными членами, например, признака Даламбера, признака Коши.
Пример:
Найти область сходимости ряда
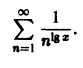
Так как числовой ряд

сходится при р > 1 и расходится при р 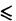
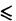
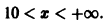
Пример:
Найти область сходимости ряда
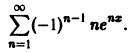
Рассмотрим ряд
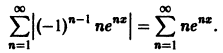
Члены этого ряда положительны при всех значениях х. Применим к нему признак Даламбера. Имеем
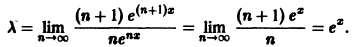
При 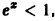
При х > 0 ряд расходится, так как 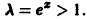
Пример:
Найти область сходимости ряда
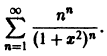
Члены данного ряда определены и непрерывны на множестве 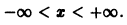
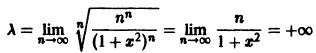
для любого 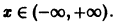
Обозначим через 
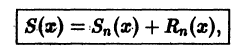
где 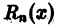
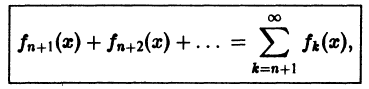
который называется n-м остатком функционального ряда (1). Для всех значений 
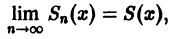
и поэтому.

т. е. остаток 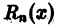
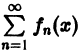
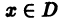
Равномерная сходимость
Среди всех сходящихся функциональных рядов важную роль играют так называемые равномерно сходящиеся ряды.
Пусть дан сходящийся на множестве D функциональный ряд
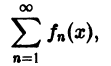
сумма которого равна S(x). Возьмем его n-ю частичную сумму
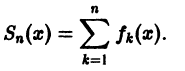
Определение:
Функциональный ряд
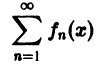
называется равномерно сходящимся на множестве 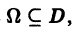
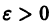
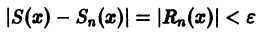
будет выполняться для всех номеров n > N и для всех х из множества 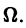
Замечание:
Здесь число N является одним и тем же для всех 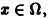
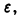
Равномерную сходимость функционального ряда 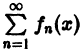
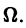
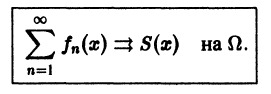
Определение равномерной сходимости ряда 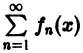
Поясним геометрически смысл равномерной сходимости функционального ряда. Возьмем в качестве множества 
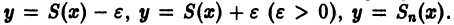
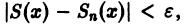
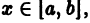
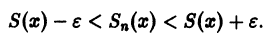
Полученные неравенства показывают, что графики всех функций 
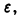
Пример:
Показать, что функциональный ряд
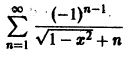
равномерно сходится на отрезке
Данный ряд является знакочередующимся, удовлетворяет условиям признака Лейбница при всяком 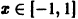
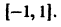
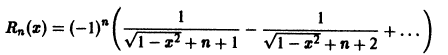
по абсолютной величине не превосходит абсолютной величины своего первого члена:
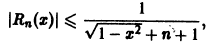
а поскольку 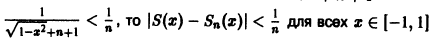
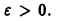
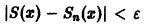
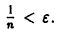
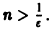
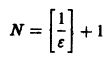
(Здесь через [а] обозначено наибольшее целое число, не превосходящее а), то неравенство |S(x) — 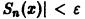
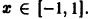
Замечание:
Не всякий сходящийся на множестве D функциональный ряд является равномерно сходящимся на D.
Пример:
Покажем, что ряд
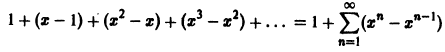
сходится на отрезке 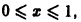
Вычислим n-ю частичную сумму Sn(x) ряда. Имеем
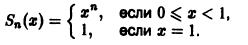
Откуда
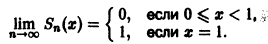
Данный ряд сходится на отрезке [0,1] и его сумма
Абсолютная величина разности 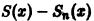
Возьмем число 
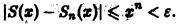
Разрешим неравенство 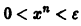
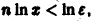
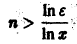
(так как 0 < х < 1, то In х < 0, и при делении на In х знак неравенства меняется на обратный). Неравенство 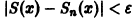
Поэтому такого не зависящего от х числа N(e), чтобы неравенство
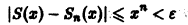
выполнялось для каждого n > N(e) сразу для всех х из отрезка 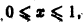
Если же заменить отрезок 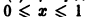
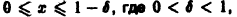
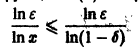
и поэтому
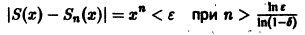
сразу для всех
Признак Вейерштрасса
Достаточный признак равномерной сходимости функционального ряда дается теоремой Вейерштрасса.
Теорема:
Признак Вейерштрасса. Пусть для всех х из множества 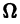
по абсолютной величине не превосходят соответствующих членов сходящегося числового ряда
с положительными членами, т. е.
для всех 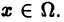
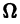
Тек как по условию теоремы члены ряда (1) удовлетворяют условию (3) на всем множестве 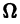
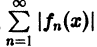
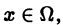
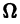
Докажем равномерную сходимость ряда (1). Пусть
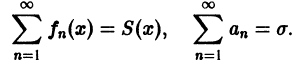
Обозначим через 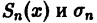
для всех
Возьмем любое (сколь угодно малое) число 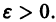
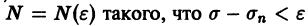
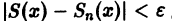
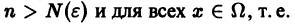
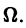
Замечание:
Числовой ряд (2) часто называют мажорирующим, или мажорантным, для функционального ряда (1).
Пример:
Исследовать на равномерную сходимость ряд
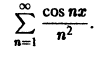
Неравенство
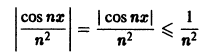
выполняется для всех n = 1, 2, … и для всех 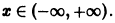
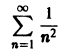
сходится. В силу признака Вейерштрасса рассматриваемый функциональный ряд сходится абсолютно и равномерно на всей оси.
Пример:
Исследовать на равномерную сходимость ряд
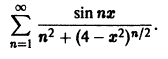
Члены ряда определены и непрерывны на отрезке [-2,2]. Так как
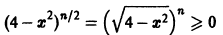
на отрезке [-2,2] для любого натурального n, то
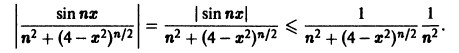
Таким образом, неравенство
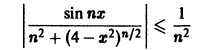
выполняется для n = 1, 2, … и для всех 
сходится, то по признаку Вейерштрасса исходный функциональный ряд сходится абсолютно и равномерно на отрезке [-2,2].
Замечание:
Функциональный ряд (1) может сходится равномерно на множестве 
Пример:
Как было показано выше (пример 1 в § 2), ряд
равномерно сходится на отрезке [-1,1 ]. Однако для него мажорантного сходящегося числового ряда (2) не существует. В самом деле, для всех натуральных n и для всех 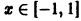
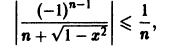
причем равенство достигается при х = — 1 и х = 1. Поэтому члены искомого мажорантного ряда (2) непременно должны удовлетворять условию
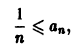
но числовой ряд
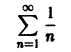
расходится. Значит, будет расходиться и ряд
Свойства равномерно сходящихся функциональных рядов
Равномерно сходящиеся функциональные ряды обладают рядом важных свойств.
Теорема:
Если все члены ряда
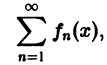
равномерно сходящегося на отрезке [а, b], умножить на одну и ту же функцию g(х), ограниченную на [а, b], то полученный функциональный ряд
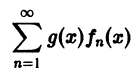
будет равномерно сходиться на [а, b].
Пусть на отрезке [а, b] ряд 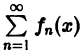
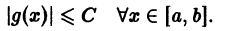
По определению равномерной сходимости ряда для любого числа 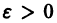
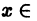
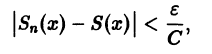
где Sn(x) — частичная сумма рассматриваемого ряда. Поэтому будем иметь
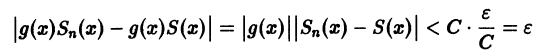
для n > N и для любого 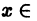
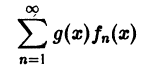
равномерно сходится на [а, b] к функции g(x) S(x).
Теорема:
Пусть все члены fn(x) функционального ряда
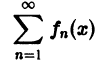
непрерывны и ряд сходится равномерно на отрезке [a, b]. Тогда сумма S(x) ряда непрерывна на этом отрезке.
Возьмем на отрезке [a,b] две произвольные точки 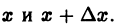
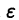
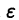
где Sn(х) — частичные суммы ряда 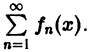
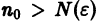
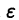
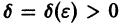
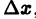
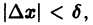
Приращение 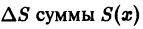
Учитывая неравенства (1) и (2), для приращений 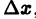
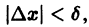
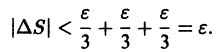
Это означает, что 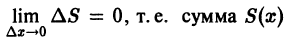
Замечание:
Функциональный ряд
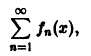
члены которого непрерывны на отрезке [a, b], но который сходится на [а, b] неравномерно, может иметь суммой разрывную функцию.
Пример:
Рассмотрим функциональный ряд
на отрезке [0,1]. Вычислим его n-ю частичную сумму
т.е. сумма ряда
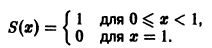
Она разрывна на отрезке [0, 1], хотя члены ряда непрерывны на нем. В силу доказанной теоремы данный ряд не является равномерно сходящимся на отрезке [0,1].
Пример:
Рассмотрим ряд
Как было показано выше, этот ряд сходится при 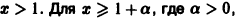
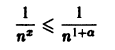
и числовой ряд
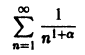
сходится. Следовательно, для любого х > 1 сумма этого ряда непрерывна.
Замечание:
Функция
называется функцией Римана (эта функция играет большую роль в теории чисел).
Теорема:
О почленном интегрировании функционального ряда. Пусть все члены fn(x) ряда
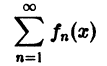
непрерывны, и ряд сходится равномерно на отрезке [а, b] к функции S(х). Тогда справедливо равенство
т. е. данный ряд можно почленно интегрировать в пределах от 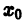
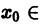
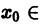
В силу непрерывности функций fn(x) и равномерной сходимости данного ряда на отрезке [а, b] его сумма S(x) непрерывна и, следовательно, интегрируема на [а, b]. Рассмотрим разность
где
Из равномерной сходимости ряда на [a,b] следует, что для любого 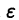
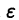
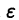
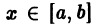
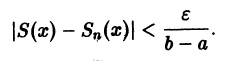
Но тогда
для любого n > N(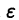
Если ряд 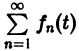
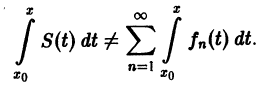
Теорема:
О почленном дифференцировании функционального ряда. Пусть все клены fn(x) сходящегося ряда
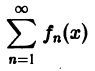
имеют непрерывные производные и ряд
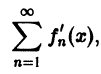
составленный из этих производных, равномерно сходится на отрезке [а, b]. Тогда в любой точке 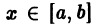
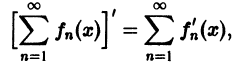
т. е. данный ряд можно почленно дифференцировать.
Положим
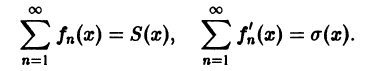
Возьмем две любые точки 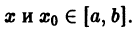
Функция 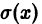
т.е.
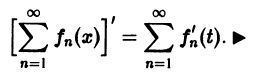
Дополнение к функциональным рядам
Смотрите также:
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат