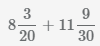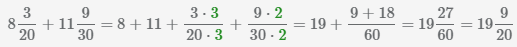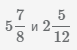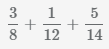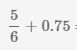Сложение смешанных чисел
- Калькулятор сложения смешанных чисел
Чтобы сложить смешанные числа, надо сложить отдельно их целые и их дробные части и полученные результаты сложить.
Пример.
Условились считать, что любое натуральное число имеет дробную часть, равную нулю, а любая правильная дробь имеет целую часть, равную нулю. Поэтому складывать правильные дроби и натуральные числа со смешанными числами можно по правилу сложения смешанных чисел.
Так как натуральное число имеет дробную часть, равную нулю, то при сложении смешанного числа с натуральным числом, складывается только целая часть c натуральным числом, а дробная часть остаётся без изменений:
Так как правильная дробь имеет целую часть, равную нулю, то при сложении смешанного числа с правильной дробью, складывается только дробная часть с правильной дробью, а целая часть остаётся без изменений:
При сложении дробных частей двух смешанных чисел или дробной части смешанного числа с правильной дробью может получиться неправильная дробь. В этом случае неправильную дробь нужно представить в виде смешанного числа:
Если дробные части смешанных чисел имеют разные знаменатели, то сначала их нужно привести к общему знаменателю:
Также, смешанные числа можно записать в виде неправильных дробей и выполнить сложение, а в конце (если требуется по условию задания) записать результат в виде смешанного числа:
Калькулятор сложения смешанных чисел
Данный калькулятор поможет вам выполнить сложение смешанных чисел. Просто введите слагаемые и нажмите кнопку Вычислить
. Данный калькулятор позволяет также выполнять сложение: натурального числа и дроби, смешанного числа и дроби, натурального и смешанного числа, натуральных чисел.
Чтобы сложить смешанные числа, надо записать их в виде неправильных дробей, а затем сложить как обыкновенные дроби.
Часто удобней вначале сложить целые части, а затем дробные части, избегаю преобразования в неправильную дробь.
Пример Сложить смешанные числа 
Сократим дробь 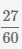
и деления полученного числа на числитель и знаменатель, НОД(27,60)=3,
получим 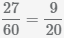
Пример Найти сумму смешанных чисел 
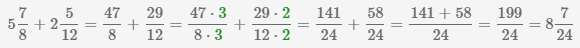
В результате сложения также получим смешанное число.
Сложение нескольких дробей
Пример Сложить 3 дроби 
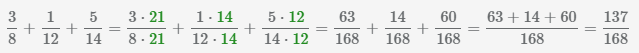
Сложение обыкновенных и десятичных дробей
Пример Найти сумму 
Для сложения десятичных и обыкновенных дробей нужно преобразовать их к одному формату. В данном примере преобразуем десятичную дробь
0.75 в обыкновенную дробь 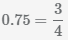

Сложение и вычитание дробей
Навигация по странице:
- Сложение дробей
- Сложение дробей с одинаковыми знаменателями
- Сложение обыкновенных дробей
- Сложение смешаных чисел
- Вычитание дробей
- Вычитание дробей с одинаковыми знаменателями
- Вычитание обыкновенных дробей
- Вычитание смешаных чисел
Сложение дробей
Сложение дробей с одинаковыми знаменателями.
Определение.
Чтобы сложить две дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменений:
| a | + | b | = | a + b |
| c | c | c |
Примеры сложения дробей с одинаковыми знаменателями
Пример 1.
Найти сумму двух дробей с одинаковыми знаменателями:
| 1 | + | 2 | = | 1 + 2 | = | 3 |
| 5 | 5 | 5 | 5 |
Пример 2.
Найти сумму двух дробей с одинаковыми знаменателями:
| 3 | + | 2 | = | 3 + 2 | = | 5 |
| 7 | 7 | 7 | 7 |
Сложение обыкновенных дробей.
Примеры сложения обыкновенных дробей
Пример 3.
Найти сумму двух дробей:
| 1 | + | 1 | = | 1·2 | + | 1 | = | 2 | + | 1 | = | 2 + 1 | = | 3 | = | 3 | = | 1 |
| 3 | 6 | 3·2 | 6 | 6 | 6 | 6 | 6 | 3·2 | 2 |
Пример 4.
Найти сумму двух дробей:
| 29 | + | 44 | = | 29·3 | + | 44·2 | = | 87 | + | 88 | = | 87 + 88 | = |
| 30 | 45 | 30·3 | 45·2 | 90 | 90 | 90 |
| = | 175 | = | 35·5 | = | 35 | = | 18 + 17 | = 1 | 17 |
| 90 | 18·5 | 18 | 18 | 18 |
Сложение смешанных чисел
Примеры сложения смешанных чисел
Пример 5.
Найти сумму двух смешанных чисел:
| 2 | + | 1 | 1 | = | 2·2 | + | 1 | 1·3 | = | 4 | + | 1 | 3 | = | 1 + | 4 + 3 | = |
| 3 | 2 | 3·2 | 2·3 | 6 | 6 | 6 |
| = | 1 + | 7 | = | 1 + | 6 + 1 | = | 1 + 1 | 1 | = 2 | 1 |
| 6 | 6 | 6 | 6 |
Пример 6.
Найти сумму двух смешанных чисел:
| 1 | 5 | + | 2 | 3 | = | 1 | 5·4 | + | 2 | 3·3 | = | 1 | 20 | + | 2 | 9 | = | 3 + | 20 + 9 | = |
| 6 | 8 | 6·4 | 8·3 | 24 | 24 | 24 |
| = | 3 + | 29 | = | 3 + | 24 + 5 | = | 3 + 1 | 5 | = 4 | 5 |
| 24 | 24 | 24 | 24 |
Вычитание дробей
Вычитание дробей с одинаковыми знаменателями.
Определение.
Чтобы найти разницу двух дробей с одинаковыми знаменателями, нужно вычесть из числителя первой дроби числитель второй, а знаменатель оставить без изменений:
| a | — | b | = | a — b |
| c | c | c |
Примеры вычитания дробей с одинаковыми знаменателями
Пример 7.
Найти разность двух дробей с одинаковыми знаменателями:
| 3 | — | 1 | = | 3 — 1 | = | 2 |
| 5 | 5 | 5 | 5 |
Пример 8.
Найти разность двух дробей с одинаковыми знаменателями:
| 8 | — | 5 | = | 8 — 5 | = | 3 |
| 41 | 41 | 41 | 41 |
Вычитание обыкновенных дробей.
Примеры вычитания обыкновенных дробей
Пример 9.
Найти разность двух дробей:
| 5 | — | 1 | = | 5 | — | 1·3 | = | 5 | — | 3 | = | 5 — 3 | = | 2 | = | 2 | = | 1 |
| 6 | 2 | 6 | 2·3 | 6 | 6 | 6 | 6 | 2·3 | 3 |
Пример 10.
Найти разность двух дробей:
| 3 | — | 1 | = | 3·3 | — | 1·5 | = | 9 | — | 5 | = | 9 — 5 | = | 4 | = | 2·2 | = | 2 |
| 10 | 6 | 10·3 | 6·5 | 30 | 30 | 30 | 30 | 15·2 | 15 |
Вычитание смешанных чисел.
Примеры вычитания смешанных чисел
Пример 11.
Найти разность двух смешанных чисел:
| 2 | 1 | — | 1 | 1 | = | 2 | 1·3 | — | 1 | 1·2 | = | (2 — 1) | + | 3 | — | 2 | = |
| 2 | 3 | 2·3 | 3·2 | 6 | 6 |
| = | 1 | + | 3 -2 | = | 1 | + | 1 | = | 1 | 1 |
| 6 | 6 | 6 |
Пример 12.
Найти разность двух смешанных чисел:
| 3 | 1 | — | 1 | 3 | = | 3 | 1·4 | — | 1 | 3·3 | = | 3 | 4 | — | 1 | 9 | = |
| 6 | 8 | 6·4 | 8·3 | 24 | 24 |
| = | 2 | 24 + 4 | — | 1 | 9 | = | 1 + | 28 — 9 | = | 1 + | 19 | = 1 | 19 |
| 24 | 24 | 24 | 24 | 24 |
Пример 13.
Найти разность двух смешанных чисел:
| 1 | 1 | — | 3 | 2 | = | 1 | 1 | — | 3 | 2·2 | = | 1 | 1 | — | 3 | 4 | = | (1-3) | + | 1 — 4 | = |
| 6 | 3 | 6 | 3·2 | 6 | 6 | 6 |
| = -2 | — | 3 | = | -2 | — | 3 | = | -2 | — | 1 | = | -2 | 1 |
| 6 | 2·3 | 2 | 2 |
Для сложения смешанных чисел, надо:
- найти общий знаменатель и привести к нему дробные части;
- сложить целые части смешанных чисел, отдельно сложить дробные части;
- если дробная часть сократима, то её сократить;
- если дробная часть — неправильная дробь, выделить из неё целую часть и добавить к целой части.
Пример 1.
.
Числитель и знаменатель дробной части второго числа умножили на (2). Сложили целые части и отдельно сложили дробные части.
Пример 2.
.
В результате получили дробную часть
1310
— это неправильная дробь, поэтому из неё выделили целую часть
1310=1+310=1310
и полученное число прибавили к целой части:
.
Для вычитания смешанных чисел, надо:
- привести дробные части к общему знаменателю;
- при необходимости «занять» единицу из целой части;
- вычесть отдельно целые части и дробные части;
- если можно, сократить дробную часть.
Пример 3.
.
Числитель и знаменатель дробной части второго числа умножили на ( )(4). Вычли целые части, затем вычли дробные части.
Пример 4.
.
После приведения к общему знаменателю дробная часть первого числа
921
меньше дробной части второго числа
1421
. Поэтому целую часть уменьшили на (1), а эту единицу внесли в дробную часть:
14921−51421=1321+921−51421=133021−51421
.
Калькулятор дробей
- Главная
- /
- Математика
- /
- Арифметика
- /
- Калькулятор дробей
Если вам необходимо произвести математические операции с дробями воспользуйтесь нашим онлайн калькулятором:
Просто заполните необходимые поля и получите ответ и подробное решение.
Данный калькулятор может работать как с положительными, так и с отрицательными дробями.
При этом нужно помнить, что:
− ac = a− c = − ac
Всегда нужно использовать только последний вариант.
Сложение дробей
С одинаковыми знаменателями
При сложении дробей с одинаковыми знаменателями складываются только числители, а знаменатель остаётся прежним.
Формула
ac + bc = a + bc
Пример
Для примера сложим следующие дроби с равными знаменателями:
27 + 47 = 2 + 47 = 67
С разными знаменателями
При сложении дробей с разными знаменателями для начала необходимо привести дроби к общему знаменателю. А затем сложить числители.
Формула (универсальная)
ac + bd = a⋅d + b⋅cc⋅d
Пример №1
Для примера сложим следующие дроби с разными знаменателями:
12+13=1⋅32⋅3+1⋅23⋅2=36+26=3+26=56
Пример №2
Существуют также частные случаи, когда знаменатель одной дроби можно привести к знаменателю второй. Например:
12+14=1⋅22⋅2+14=24+14=2+14=34
Этот же пример можно решить и применяя вышеуказанную универсальную формулу:
12+14=1⋅42⋅4+1⋅24⋅2=48+28=4+28=68=34
Обратите внимание, что мы сократили дробь:
68=3 ⋅ 24 ⋅ 2=34
Сложение смешанных чисел
Смешанные числа — это такие числа, у которых есть как дробная часть, так и целая.
Преобразуя в неправильную дробь
Для начала смешанное число (дробь) нужно преобразовать в неправильную дробь, а потом можно складывать как в предыдущих примерах.
Формула
a bc + d ef = b + a ⋅ cc + e + d ⋅ ff
Пример
Для примера сложим два смешанных числа:
312+123=1+3⋅22+2+1⋅33=72+53=7⋅32⋅3+5⋅23⋅2=216+106=21+106=316=5⋅6+16=5⋅66 + 16=516
Обратите внимание, что из полученной неправильной дроби мы выделили целую часть:
316=5⋅6+16=5⋅66 + 16=516
Складывая целую и дробную части отдельно
Целую и дробную части смешанных чисел можно складывать по отдельности.
Формула
a bc + d ef = (a + d) + (bc + ef)
Пример
Решим предыдущий пример этим способом:
3 12 + 1 23 = (3+1)+(12+23) = 4+1⋅32⋅3+2⋅23⋅2=4+36+46=4+3+46=4+76=4+116 = 516
Вычитание дробей
Вычитание дробей происходит по тем же принципам, что и сложение.
С одинаковыми знаменателями
Формула
ac − bc = a − bc
Пример
Для примера вычтем одну дробь из другой с равными знаменателями:
35−25=3−25=15
С разными знаменателями
Тут также, как и при сложении, дроби нужно подвести под общий знаменатель, а затем вычитать.
Формула
ac − bd = a⋅d − b⋅cc⋅d
Пример
Для примера вычтем одну дробь из другой, с разными знаменателями:
34−13=3⋅34⋅3−1⋅43⋅4=912−412=9−412=512
Вычитание смешанных чисел
Для начала смешанные числа преобразуем в неправильные дроби, потом приводим полученные дроби к общему знаменателю, а затем вычтем одну из другой. Далее выделяем целую часть если она есть.
Формула
a bc − d ef = b + a ⋅ cc − e + d ⋅ ff
Пример
312−123=1+3⋅22−2+1⋅33=72−53=7⋅32⋅3−5⋅23⋅2=216−106=21−106=116=1⋅6+56=1⋅66 + 56=156
Умножение дробей
При умножении дробей неважно одинаковые или разные у них знаменатели. Числитель одной дроби умножается на числитель другой, а знаменатели тоже перемножаются между собой.
Формула
ac ⋅ be = a ⋅ bc ⋅ e
Давайте рассмотрим несколько примеров:
Пример №1
Умножим дроби с одинаковыми знаменателями:
13⋅23=1⋅23⋅3=29
Пример №2
Умножим дроби с разными знаменателями:
13⋅24=1⋅23⋅4=212=1⋅26⋅2=16
Пример №3
Умножим смешанные числа:
112⋅223=1+1⋅22⋅2+2⋅33=32⋅83=3⋅82⋅3=246=4
Деление дробей
При делении одной дроби на другую также неважно одинаковые или разные у них знаменатели. Чтобы разделить одну дробь на другую нужно перемножить числитель первой дроби и знаменатель второй, а знаменатель первой умножить на числитель второй.
Формула
ac : be = a ⋅ ec ⋅ b
Давайте рассмотрим несколько примеров:
Пример №1
Разделим одну дробь на другую с таким же знаменателем:
23:13=23⋅31=2⋅33⋅1=63=2
Пример №2
Делим дроби с разными знаменателями:
12:23=12⋅32=1⋅32⋅2=34
Пример №3
Деление смешанных чисел:
412:223=1+4⋅22:2+2⋅33=92:83=92⋅38=9⋅32⋅8=2716=1⋅16+1116=1⋅1616 + 1116=11116