Решение.
[ begin{align}
& p=Ncdot {{m}_{0}}cdot upsilon (1). \
& I=frac{Delta q}{Delta t},Delta t=frac{Delta q}{I}(2),Delta q=Ncdot e(3),upsilon =frac{l}{Delta t}(4),upsilon =frac{lcdot I}{Ncdot e}(5), \
& p=Ncdot {{m}_{0}}cdot frac{lcdot I}{Ncdot e}={{m}_{0}}cdot frac{lcdot I}{e},(6). \
& p=frac{9,1cdot {{10}^{-31}}cdot 500cdot 20}{1,6cdot {{10}^{-19}}}=56,875cdot {{10}^{-9}}. \
end{align} ]
Где: р – суммарный импульс электронов, I — сила тока в проводнике; Δq — заряд, который проходит через поперечное сечение S проводника за время Δt; N — число электронов, m0 – масса электрона, m0 = 9,1∙10-31 кг, l – длина провода, e = 1,6∙10–19 Кл — модуль заряда электрона.
Ответ: 5,69∙10-8 кг∙м/с.
2018-05-14
Найти суммарный импульс электронов в прямом проводе длины $l = 1000 м$, по которому течет ток $I = 70 А$.
Решение:
Пусть, $n_{0}$ — общее число электронов, тогда общий импульс электронов,
$p = n_{0}m_{e}v_{d}$ (1)
Отсюда $I = rho S_{x}v_{d} = frac{n_{0}e }{V} S_{x}v_{d} = frac{ne}{l} v_{d}$ (2)
Здесь $S_{x} $ — площадь поперечного сечения, $rho $ — плотность заряда электрона, $V $ — объем образца.
Из (1) и (2)
$p = frac{m_{e} }{e} Il = 0,40 мкН cdot с$
| 🎓 Заказ №: 21944 |
| ⟾ Тип работы: Задача |
| 📕 Предмет: Физика |
| ✅ Статус: Выполнен (Проверен преподавателем) |
| 🔥 Цена: 149 руб. |
👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.
➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.
➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.
⚡ Условие + 37% решения:
Определить суммарный импульс электронов в прямом проводе длиной l 500 м , по которому течет ток I 20 А . Масса электрона равна 9,1 10 кг -31 , заряд электрона равен Кл -19 1,610 .
Решение Импульс одного электрона 0 p равен: p0 m Где m – масса электрона; – скорость его движения. Тогда суммарный импульс p электронов будет равен: p Np0 Nm (1) Где N – количество электронов. Сила тока I в проводнике равна: I neS (2) Где n – концентрация электронов в проводнике; e – заряд электрона; S – площадь поперечного сечения проводника. Концентрация электронов равна: V N n
Готовые задачи по физике которые сегодня купили:
- Масса m 10 г кислорода, находящегося при нормальных условиях, сжимается до объема V2 1,4 л .
- Найти среднюю длину свободного пробега молекул гелия при давлении P 101,3 кПа и температуре t C 0 0 , если вязкость гелия 13 мкПа с .
- Сила тока в проводнике меняется со временем по уравнению I=3+6t; I — в амперах и t в секундах.
- Тело вращается вокруг неподвижной оси по закону φ=А+Вt+Сt2 , где А=10 рад; В=20 рад/с; С=2 рад/с2 .
- Определить максимальную полезную мощность аккумулятора с ЭДС=10 В и внутренним сопротивлением 1 Ом.
- Электрическое поле создано двумя бесконечными пластинами, несущими равномерно распределенный по площади заряд с поверхностными плотностями 5 нКл/м2 и –2 нКл/м2 .
- Определите разность давлений p в широком и узком коленах горизонтальной трубы диаметром d1 70 см и d2 50 см , если поток кислорода в узком колене имеет скорость с м 2 24 .
- Кислород массой 160 г нагревают при постоянном давлении от 320 К до 340 К.
- По длинному прямому проводнику течет ток силой 60 А.
- Определите высоту h над поверхностью Земли, на которой ускорение свободного падения уменьшится на k 0,3 от ускорения у поверхности Земли.
Запишем кратка дано:
L = 500 м;
I = 20 A.
Найти:
суммарный импульс электронов в прямом проводе.
Начнем с того, что вспомним формулу для вычисления испульса.
Итак, импульс равен:
p = m * v.
Для вычисления заряда, проходящего по проводнику применим формулу:
q = I * t, где t = L/v.
Подставляем и получаем формулу:
q = IL / v.
Выражаем v:
v = IL / q,
где q = e = 1, 6 * 10 ^ — 19 Кл (величина постоянная).
Подставим v и получим p = mIL/e
Подставляем значения в формулу и находим:
p = (9,1 * 10 ^ — 31 * 20 * 500) / (1,6 * 10 ^ — 19) = 5,7 * 10 ^ — 8 (кг м / с ^2).
Пример 9.1.
Найдите суммарный
импульс электронов в прямом проводе
длиной L ,
по которому течет ток I .
Масса электрона m .
Решение.
Суммарный импульс электронов равен
импульсу одного электрона
умноженному на число электронов в
проводе,
т.е..
Из определения плотности тока найдем,
что,
а.
Для суммарного импульса получим.
Учитывая, что,
окончательно получим.
Пример 9.2.
В цилиндрическом
проводнике с поперечным сечением радиуса
R
вектор плотности тока параллелен оси
проводника, а его модуль зависит о
расстояния r
до этой оси по закону
,
гдеj0 – известная
постоянная. Найдите силу тока в проводнике.
Решение.
Сила тока через элементарную поверхность
радиусаи ширины
,
расположенную в плоскости перпендикулярной
оси проводника, равна.
Суммируя элементарные токи по всей
поверхности поперечного сечения, найдем
.
Пример 9.3.
Металлический
шар радиуса a
окружен концентрической тонкой
металлической оболочкой радиуса b.
Пространство между этими электродами
заполнено однородной слабо проводящей
средой с удельным сопротивлением .
Найдите сопротивление межэлектродного
промежутка. Рассмотрите случай
.
Решение.
Способ 1: Представим, что шар и оболочка
заряжены зарядом
соответственно. Через слабо проводящую
среду, заполняющую пространство между
ними, потечет ток разрядки. В силу
сферической симметрии распределения
зарядов распределение плотности тока
будет обладать такой же симметрией,
т.е..
Поэтому полный ток утечки через
концентрическую сферическую поверхность
радиусаравен
и не зависит от
.
Напряженность электрического поля в
проводящем пространстве будет.
Соответствующее напряжение на проводящих
обкладках равно:
Для величины
,
получим.
Если проводящая среда занимает все
пространство,
то ее сопротивление равно.
Способ 2: Представим ток сквозь любуюзамкнутую поверхность окружающую
металлический шар как поток поля вектора
плотности тока в виде:
,
где
—
заряд металлического шара (—
заряд окружающей сферической оболочки).
Разность потенциалов между заряженными
поверхностями шара и оболочки равна.
Величина сопротивления равная отношению
напряжения к току, как и в первом способе
решения равна.
Способ 3: Разобьем сферически симметричное
пространство проводящей среды на
элементарные сферические слои
концентрические с металлическими
электродами. Сопротивление всей среды
при этом разобьется на последовательно
соединенные элементарные сопротивления,
величина которых равна
.
Полное сопротивление межэлектродного
пространства равно:
.
Пример 9.4.
Два металлических
шара одинакового радиуса a
находятся в однородной слабо проводящей
среде с удельным сопротивлением .
Найдите сопротивление среды между
шарами при условии, что расстояние между
ними значительно больше a.
Р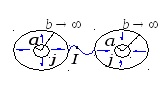
Представим процесс протекания тока
между шарами так, как на рисунке. При
этом сопротивление всей среды равно
последовательно соединенным сопротивлениям,
которые получены в предыдущей задаче
и равны.
Поэтому полное сопротивление среды
.
Соседние файлы в папке Примеры решений
- #
- #
- #
- #
- #
- #


