Как найти сторону куба
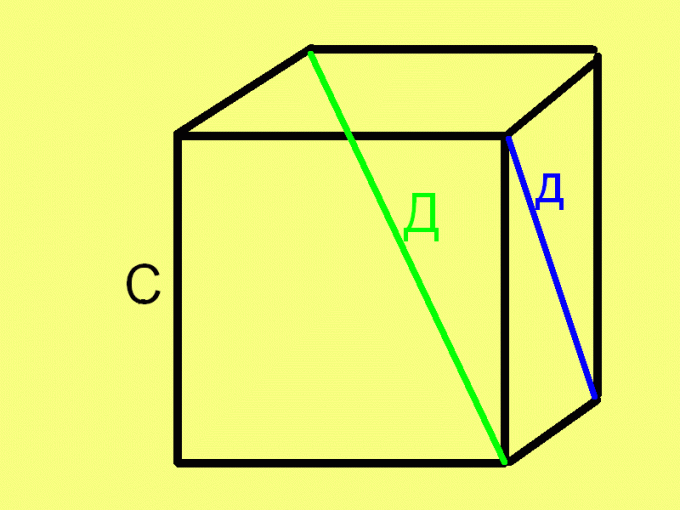
Куб – одна из простейших объемных фигур. Он состоит из шести пересекающихся под прямым углом граней, представляющих из себя равные квадраты. Линии пересечения граней называются его ребрами, а точки пересечения ребер – вершинами. Иногда можно услышать и такой «термин» как «сторона» куба. В зависимости от конкретной ситуации под этим понятием может подразумеваться как грань куба, так и его ребро.В быту и играх (при использовании кубика в качестве игральной кости) стороной куба обычно называют его грань. Если же найти сторону куба пытается ученик, то наверняка требуется определить длину его ребра (куба, а не ученика).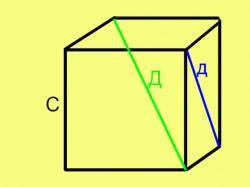
Куб настолько симметричная фигура, что для нахождения его стороны (ребра) достаточно знать хотя бы один из основных параметров куба. К ним относятся его объем, площадь грани, длина диагонали грани и длина диагонали куба (так называемой «большой диагонали»).Чтобы найти сторону куба если известна площадь его грани, извлеките из числового значения площади грани квадратный корень. В виде формулы эту зависимость можно записать в следующем виде:С = √П, где:С – длина стороны (грани) куба,
П — площадь грани куба.Данная формула выводится из того факта, что грань куба представляет собой квадрат со стороной, равной ребру куба, и площадью, равной квадрату ребра.
Нахождение стороны (ребра) куба по заданному объему аналогично. Так как объем куба равен третьей степени (кубу) длины его ребра, то для определения длины ребра куба извлеките из его объема кубический корень. То есть воспользуйтесь формулой:С = ³√Об, где Об – объем куба.
(³√ — функция извлечения кубического корня).
Для нахождения стороны (ребра) куба по диагонали его грани извлеките квадратный корень из квадрата диагонали, разделенного пополам. В виде формулы это правило выглядит следующим образом:С = √(д²/2), где д – длина диагонали грани куба. Справедливость этой формулы вытекает из теоремы Пифагора, так как диагональ и два примыкающих ребра образуют равносторонний прямоугольный треугольник, где диагональ является гипотенузой, а ребра – катетами.
Чтобы найти сторону (ребро) куба по его диагонали (именно диагонали куба, а не грани), извлеките квадратный корень из трети квадрата длины этой диагонали. То есть, воспользуйтесь аналогичной предыдущей формулой:С = √(Д^2/3).Эта формула также выводится на основе теоремы Пифагора, так как диагональ куба, диагональ грани и ребро куба образуют прямоугольный (но, неравносторонний) треугольник.
Как обнаружить сторону куба
Куб – одна из простейших объемных фигур. Он состоит из шести пересекающихся под прямым углом граней, представляющих из себя равные квадраты. Линии пересечения граней куба именуются его ребрами, а точки пересечения ребер – вершинами. Изредка дозволено услышать и такой «термин» как «сторона» куба . В зависимости от определенной обстановки под этим представлением может подразумеваться как грань куба , так и его ребро.В быту и играх (при применении кубика в качестве игральной кости) стороной куба традиционно называют его грань. Если же обнаружить сторону куба пытается ученик, то наверно требуется определить длину его ребра (куба , а не ученика).
Вам понадобится
- калькулятор
Инструкция
1. Куб настоль симметричная фигура, что для нахождения его стороны (ребра) довольно знать правда бы один из основных параметров куба . К ним относятся его объем, площадь грани, длина диагонали грани и длина диагонали куба (так называемой «крупной диагонали»).Дабы обнаружить сторону куба если вестима площадь его грани, извлеките из числового значения площади грани квадратный корень. В виде формулы эту связанность дозволено записать в дальнейшем виде:С = ?П, где:С – длина стороны (грани) куба ,П – площадь грани куба .Данная формула выводится из того факта, что грань куба представляет собой квадрат со стороной, равной ребру куба , и площадью, равной квадрату ребра.
2. Нахождение стороны (ребра) куба по заданному объему подобно. Потому что объем куба равен третьей степени (кубу) длины его ребра, то для определения длины ребра куба извлеките из его объема кубический корень. То есть воспользуйтесь формулой:С = ??Об, где Об – объем куба .(?? – функция извлечения кубического корня).
3. Для нахождения стороны (ребра) куба по диагонали его грани извлеките квадратный корень из квадрата диагонали, поделенного напополам. В виде формулы это правило выглядит дальнейшим образом:С = ?(д?/2), где д – длина диагонали грани куба . Честность этой формулы вытекает из теоремы Пифагора, потому что диагональ и два примыкающих ребра образуют равносторонний прямоугольный треугольник, где диагональ является гипотенузой, а ребра – катетами.
4. Дабы обнаружить сторону (ребро) куба по его диагонали (именно диагонали куба , а не грани), извлеките квадратный корень из трети квадрата длины этой диагонали. То есть, воспользуйтесь аналогичной предыдущей формулой:С = ?(Д^2/3).Эта формула также выводится на основе теоремы Пифагора, потому что диагональ куба , диагональ грани и ребро куба образуют прямоугольный (но, неравносторонний) треугольник.
Полезный совет
Для нахождения квадратных и кубических корней воспользуйтесь инженерным калькулятором. Дабы извлечь корень третьей степени возведите число в степень ?.
Как найти площадь куба зная одну сторону?
Соответственно, площадь стороны куба – одной его грани, будет равна площади полной поверхности разделенной на шесть, а площадь боковой поверхности, состоящей из четырех граней, — двум третям площади полной поверхности куба. S=S_(п. п.)/6 S_(б.
Как можно вычислить куб?
Вычислить объем куба легко — нужно перемножить длину, ширину и высоту. Так как у куба длина равна ширине и равна высоте, то объем куба равен s3, где s — длина одного (любого) ребра куба.
Как найти ребро куба зная его объем?
2. Нахождение грани куба по его объему еще проще. Рассматривая, что объем куба равен кубу (третьей степени) длины ребра куба, получаем что длина ребра куба равняется корню кубическому (третьей степени) из его объема, т.
Как найти объем куба по площади?
Как найти объем куба – способ 2 Найти объем куба можно при помощи формулы площади поверхности куба: S=6a3. Скажем, площадь поверхности куба = 54 см2. Тогда a2 = 54/6 = 9.
Как найти площадь куба 4 класс?
Площадь куба — это сумма площади всех его сторон. Все стороны куба равны, поэтому, чтобы найти площадь куба, надо найти площадь одной из его сторон и умножить на 6.
Какая формула нахождения площади?
S = a × b, где a, b — длина и ширина прямоугольника. S = a × √(d2 — а2), где а — известная сторона, d — диагональ. Диагональ — это отрезок, который соединяет вершины противоположных углов. Она есть во всех фигурах, число вершин которых больше трех.
Как найти объем по длине ширине и высоте?
Как уже упоминалось, формула расчета объема выглядит следующим образом: V = Длина x Ширина x Высота; поэтому для получения объема необходимо просто перемножить все три стороны.
Сколько метров в 1 куб м?
Куби́ческий метр (кубометр) — единица объёма, производная в Международной системе единиц (СИ), а также в системах единиц МКГСС и МТС. Одному кубическому метру равен объём куба с длиной ребра 1 метр.
Как найти ребро куба?
Все грани куба являются квадратами, в которых ребро куба становится стороной квадрата и связано отношениями с его площадью и диагональю. Найти ребро куба, зная диагональ основания, можно разделив ее на корень из двух.
Как найти ребро куба если известна его площадь?
Формулы
| Периметр куба (общая длина ребра) | O = | 12 × a |
|---|---|---|
| Площадь одной стороны | P = | a × a = a² |
| Площадь куба (поверхность) | Q = | 6 × P1 = 6 × a² |
| Объем куба | V = | a × a × a = a³ |
| Диагоналная (стороны/стены) | u2 = | a √2 ≈ a × 1,41 |
•6 сент. 2017 г.
Как найти объем по формуле?
Объем (V) физического тела любой формы можно определить, если знать его массу (m) и среднюю плотность материала (p) — эти две величины надо перемножить: V=m∗p.
Чему равен объем куба?
Объём куба равен произведению трех ребер куба или, так как, ребра куба равны, кубу (третьей степени) его ребра. где H — высота ребра куба.
Как найти площадь и объем?
площадь (S) — это произведение длинны и ширины (S= l*b), а объем – произведение длины, ширины и высоты. Подставьте в формулу вычисления объема вместо l*b площадь. Вы получите выражение V=S*h.
Как найти площадь в физике 7 класс?
Чтобы определить площадь тела, используют формулы: площадь прямоугольника S можно рассчитать, умножив длину прямоугольника на ширину прямоугольника. S = l 1 ⋅ l 2 . Площадь треугольника S = ah 2 , где a — сторона, h — высота, проведённая к данной стороне.
Как найти площадь в 4 классе?
Для вычисления площади прямоугольника нужно умножить его длину на ширину. Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Как найти объем по массе?
Объем (V) физического тела любой формы можно определить, если знать его массу (m) и среднюю плотность материала (p) — эти две величины надо перемножить: V=m∗p.
Как рассчитать метр в кубе?
Кубические метры (м3) — это единица измерения объема, равная объему куба, стороны которого равны одному метру….Для этого просто умножим длину на ширину и на высоту:
- 4 × 3 × 2,5.
- = 12 × 2,5.
- = 30. Объем этой комнаты равен 30 м3.

Калькулятор для прямоугольника: формулы
Прямоугольник – это четырехугольник, у которого все углы прямые, а противоположные стороны попарно равны.
Если все стороны (a,b) прямоугольника равны, это квадрат (все характеристики квадрата можно рассчитать с помощью калькулятора для квадрата).
Свойства прямоугольника: диагонали прямоугольника равны и делятся точкой пересечения пополам.
Диагональ прямоугольника (d) – это отрезок, соединяющий противолежащие вершины прямоугольника. Диагональ делит прямоугольник на два равных прямоугольных треугольника. В прямоугольнике есть две диагонали, которые равны между собой.
Диагональ прямоугольника можно получить из формулы, зная его стороны:
d2 = a2 + b2
Периметр прямоугольника (P) можно получить, зная его стороны:
P = 2a + 2b = 2* (a+b)
Площадь прямоугольника (S) можно вычислить, зная его стороны:
S = a * b
Список всех онлайн-калькуляторов на странице «Калькуляторы«.
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
Cторона квадрата, диаметр вписанной окружности (L)
Диагональ квадрата, диаметр описанной окружности (M)
Радиус вписанной окружности (R1)
Радиус описанной окружности (R2)
Округление:
* — обязательно заполнить
Диагональ, диаметр описанной окружности (M) = 10
Cторона, диаметр вписанной окружности (L) = (sqrt{frac{M^{2}}{2}}) = (sqrt{frac{10^{2}}{2}}) = 7.07
Радиус вписанной окружности (R1) = (frac{L}{2}) = (frac{7.07}{2}) = 3.54
Радиус описанной окружности (R2) = (frac{M}{2}) = (frac{10}{2}) = 5
Периметр (P) = (L*4) = (7.07*4) = 28.28
Площадь (S) = (L^{2}) = (7.07^{2}) = 49.98