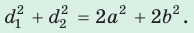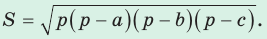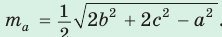Содержание:
Теорема синусов, теорема косинусов:
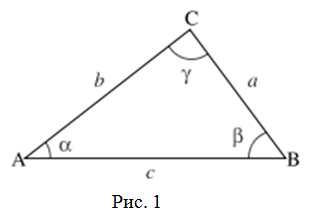
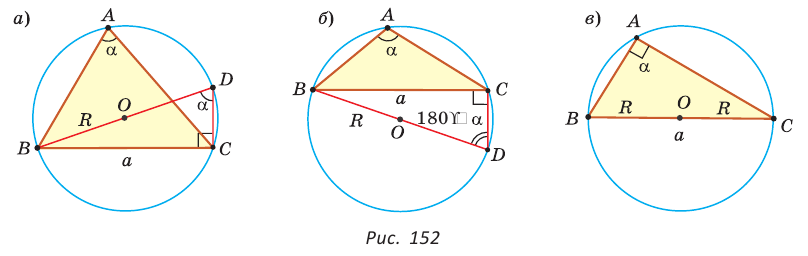
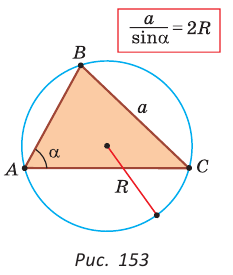
Теорема синусов
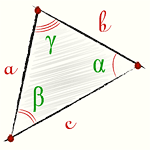
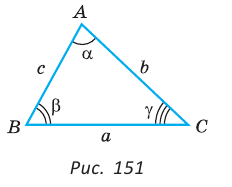
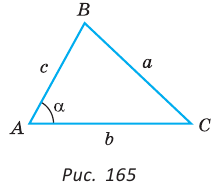
Вы уже знаете, что в треугольнике против большей стороны лежит больший угол, а против большего угла — большая сторона. Пусть
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу окружности, описанной около треугольника, т. е.
Доказательство:
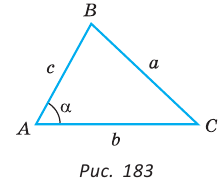
Пусть дан треугольник АВС, ВС = 
1) Угол 
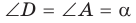
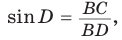
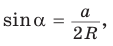
2) Угол 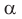
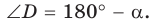
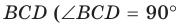
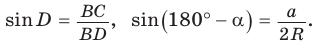
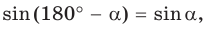
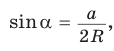
3) Для 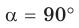
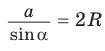
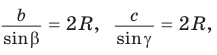
Теорема доказана.
Теорема синусов дает возможность решать широкий круг задач.
Так, пропорция 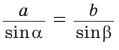
- зная две стороны треугольника и угол, противолежащий одной из них, найти синус угла, противолежащего другой стороне;
- зная два угла треугольника и сторону, противолежащую одному из этих углов, найти сторону, противолежащую другому углу.
С помощью формулы 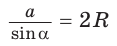
- зная сторону треугольника и противолежащий ей угол, найти радиус окружности, описанной около треугольника;
- зная угол треугольника и радиус описанной окружности, найти сторону треугольника, противолежащую данному углу;
- зная сторону треугольника и радиус его описанной окружности, найти синус угла, противолежащего данной стороне.
Повторение
Пример:
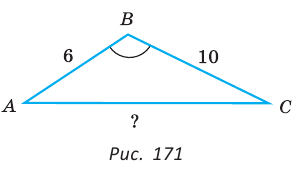
В остроугольном треугольнике известны стороны 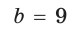
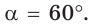
Решение:
По теореме синусов 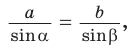
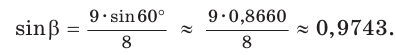
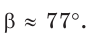
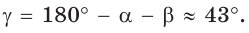
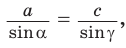
Ответ:
Замечание. Если бы по условию треугольник был тупоугольным с тупым углом 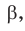
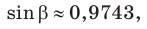
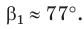
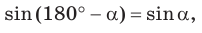
Пример:
Доказать справедливость формулы площади треугольника 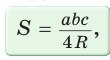
Доказательство:
Воспользуемся известной формулой площади треугольника: 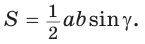
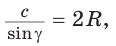
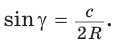
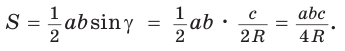
Замечание. Выведенная формула позволяет найти радиус описанной окружности треугольника
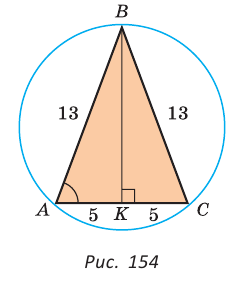
Пример:
Найти радиус R окружности, описанной около равнобедренного треугольника АВС с основанием АС = 10 и боковой стороной ВС =13 (рис. 154).
Решение:
Способ 1. Из формулы 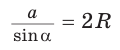
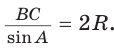
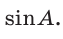
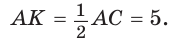
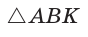
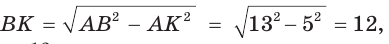
Тогда
Способ 2. Используем формулу 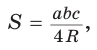
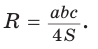
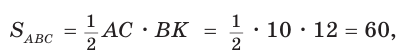
Ответ:
Замечание*. Напомним, что в главе II мы находили радиус R описанной окружности равнобедренного треугольника, проводя серединные перпендикуляры к его сторонам и используя подобие полученных прямоугольных треугольников. Также мы могли использовать формулу 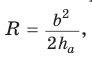
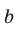
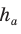
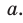
Заменив 
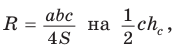
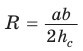

Теорема косинусов
Теорема косинусов позволяет выразить длину любой стороны треугольника через длины двух других его сторон и косинус угла между ними (например, длину стороны 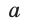
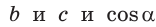
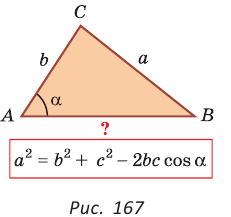
Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними, т. е.
Доказательство:
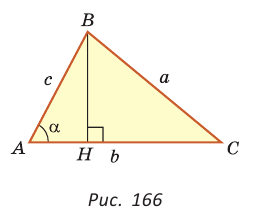
Докажем теорему для случая, когда в треугольнике АВС угол А и угол С острые (рис. 166).
Проведем высоту ВН к стороне АС. Из 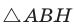
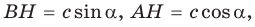
Из 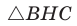
По основному тригонометрическому тождеству
Тогда
Справедливость теоремы для случаев, когда 
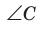
Для сторон 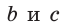
Замечание. Если 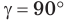
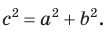
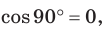
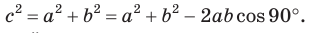
С помощью теоремы косинусов можно решить следующие задачи:
• зная две стороны и угол между ними, найти третью сторону треугольника;
• зная две стороны и угол, противолежащий одной из этих сторон, найти третью сторону (рис. 167) (в этом случае возможны два решения).
Рассмотрим следствия из теоремы косинусов, которые дают возможность решить еще целый ряд задач.
Следствие:
Теорема косинусов позволяет, зная три стороны треугольника, найти его углы (косинусы углов). Из равенства 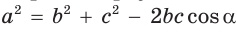
Для углов 
Пример:
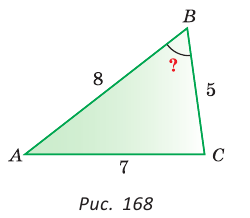
В треугольнике АВС стороны АВ = 8, ВС = 5, АС = 7. Найдем ZB (рис. 168).
По теореме косинусов
Используя записанную выше формулу, можно сразу получить:
Следствие:
С помощью теоремы косинусов можно по трем сторонам определить вид треугольника: остроугольный, прямоугольный или тупоугольный.
Так, из формулы 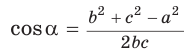
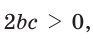
- если
то
и угол
острый;
- если
то
и угол
тупой;
- если
то
и угол
прямой.
При определении вида треугольника достаточно найти знак косинуса угла, лежащего против большей стороны, поскольку только больший угол треугольника может быть прямым или тупым.
Пример:
Выясним, каким является треугольник со сторонами a = 2, 6 = 3 и с = 4. Для этого найдем знак косинуса угла у, лежащего против большей стороны с. Так как 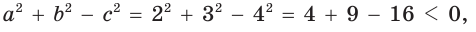
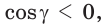
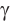
Сформулируем правило определения вида треугольника (относительно углов). Треугольник является:
- остроугольным, если квадрат его большей стороны меньше суммы квадратов двух других его сторон:
- тупоугольным, если квадрат его большей стороны больше суммы квадратов двух других его сторон:
- прямоугольным, если квадрат его большей стороны равен сумме квадратов двух других его сторон:
Следствие:
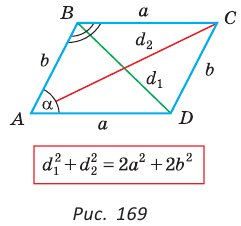
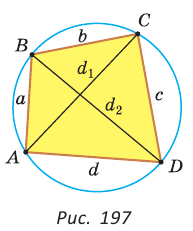
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
Доказательство:
Пусть в параллелограмме ABCD 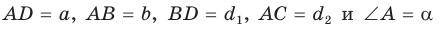
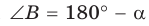
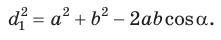
Из 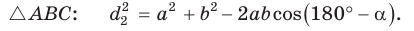
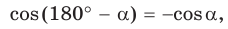
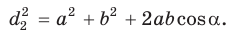
Сложив почленно равенство (1) и равенство (2), получим 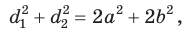
Данная формула дает возможность:
- • зная две соседние стороны и одну из диагоналей параллелограмма, найти другую диагональ;
- • зная две диагонали и одну из сторон параллелограмма, найти соседнюю с ней сторону.
Следствие:
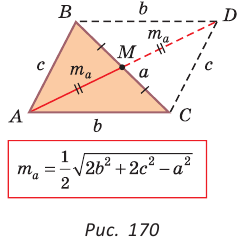
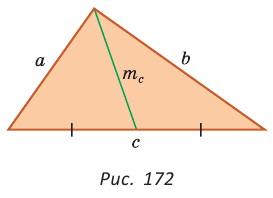
Медиану 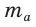
Доказательство:
Рассмотрим 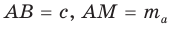
Проведем отрезки BD и DC. Так как у четырехугольника ABDC диагонали AD и ВС точкой пересечения делятся пополам, то он — параллелограмм. По свойству диагоналей параллелограмма 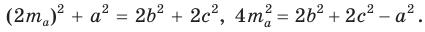
Утверждение доказано.
Аналогично:
Формула медианы позволяет:
- зная три стороны треугольника, найти любую из его медиан;
- зная две стороны и медиану, проведенную к третьей стороне, найти третью сторону;
- зная три медианы, найти любую из сторон треугольника.
Пример:
а) Дан треугольник АВС, а = 5, 5 = 3, 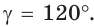
Решение:
а) По теореме косинусов
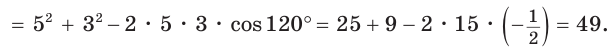
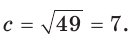
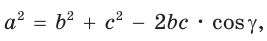
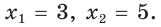
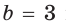
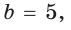
Ответ: а) 7; б) 3 или 5.
Пример:
Две стороны треугольника равны 6 и 10, его площадь —
Найти третью сторону треугольника при условии, что противолежащий ей угол — тупой.
Решение:
Пусть в 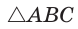
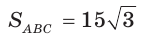
Поскольку 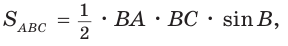
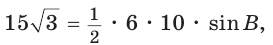
Так как 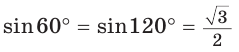

Ответ: 14.
Пример:
Найти площадь треугольника, две стороны которого равны 6 и 8, а медиана, проведенная к третьей стороне, равна 5.
Решение:
Обозначим стороны треугольника 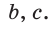
По формуле медианы 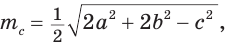
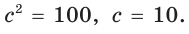
Ответ: 24.
Формула Герона
Мы знаем, как найти площадь треугольника по основанию и высоте, проведенной к этому основанию: 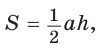
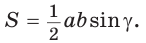
Теорема (формула Герона).
Площадь треугольника со сторонами 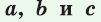
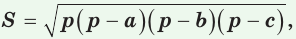
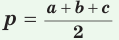
Доказательство:
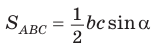
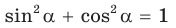
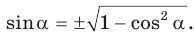
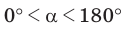
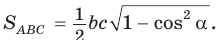
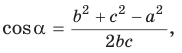
Тогда
Так как
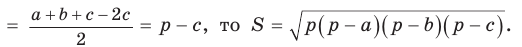
Решение треугольников
Решением треугольника называется нахождение его неизвестных сторон и углов (иногда других элементов) по данным, определяющим треугольник.
Такая задача часто встречается на практике, например в геодезии, астрономии, строительстве, навигации.
Рассмотрим алгоритмы решения трех задач.
Пример №1 (решение треугольника по двум сторонам и углу между ними).
Дано: 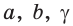
Найти :
Решение:
Рис. 184
1) По теореме косинусов
2) По следствию из теоремы косинусов
3) Угол 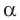
4) Угол
Замечание. Нахождение угла 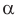
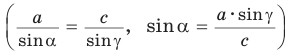
Пример №2 (решение треугольника по стороне и двум прилежащим к ней углам).
Дано: 
Найти:
Решение:
1) Угол
2) По теореме синусов 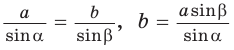
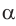
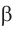
3) Сторону с можно найти с помощью теоремы косинусов или теоремы синусов: 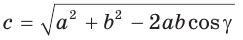
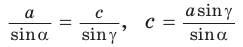
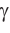
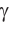
Пример №3 (решение треугольника по трем сторонам).
Дано: 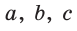
Найти: 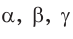
Решение:
1) По следствию из теоремы косинусов
2) Зная 
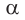
3) Аналогично находим угол
4) Угол
5) Радиус R описанной окружности треугольника можно найти по формуле 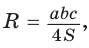
Замечание*. Вторым способом нахождения R будет нахождение косинуса любого угла при помощи теоремы косинусов 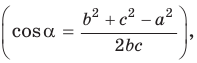
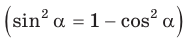
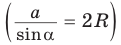
Пример №4
Найти площадь S и радиус R описанной окружности треугольника со сторонами 9, 12 и 15.
Решение:
Способ 1. Воспользуемся формулой Герона. Обозначим а = 9, b = 12, с = 15. Получим:
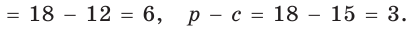
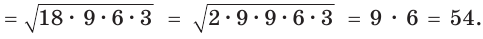
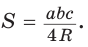
Ответ:
Способ 2. Так как 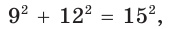
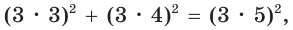
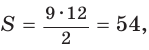
Пример №5
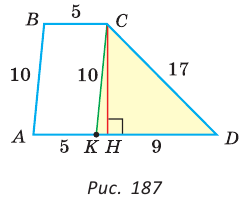
Найти площадь трапеции с основаниями, равными 5 и 14, и боковыми сторонами, равными 10 и 17.
Решение:
Пусть в трапеции ABCD основания AD = 14 и ВС = 5, боковые стороны АВ = 10 и 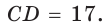
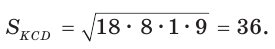
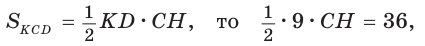
Ответ: 76.
Примеры решения задач с использованием теоремы синусов и теоремы косинусов
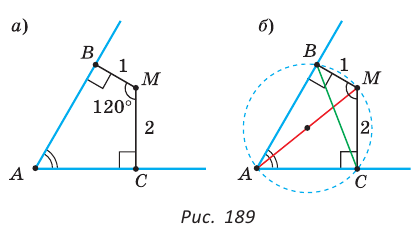
Пример:
Внутри угла А, равного 60°, взята точка М, которая находится на расстоянии 1 от одной стороны угла и на расстоянии 2 от другой стороны. Найти расстояние от точки М до вершины угла А (рис. 189, а).
Решение:
Пусть 
длину отрезка AM. Сумма углов четырехугольника АВМС равна 360°.
Поэтому
Так как в четырехугольнике АВМС 
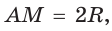
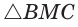
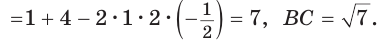
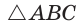
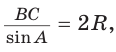
Ответ:
Замечание. Вторым способом решения будет продление отрезка ВМ до пересечения с лучом АС и использование свойств полученных прямоугольных треугольников. Рассмотрите этот способ самостоятельно.
Пример №6
В прямоугольном треугольнике АВС известно: 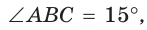
Решение:
Построим 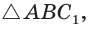
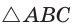
Поскольку 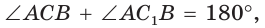
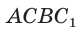
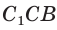
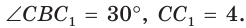
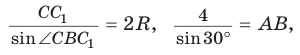
Ответ: 8.
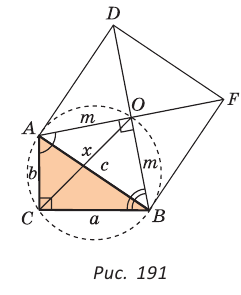
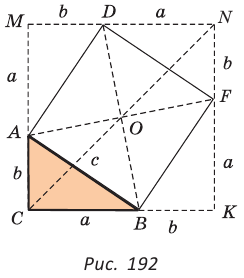
Пример №7
Дан прямоугольный треугольник АВС с катетами ВС = а и АС = 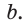
Решение:
Способ 1. Так как 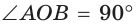
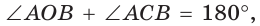
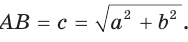
Пусть СО = х. По теореме косинусов из 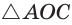
из 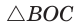
По свойству вписанного четырехугольника 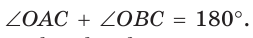
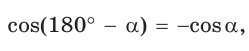
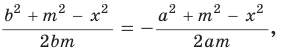
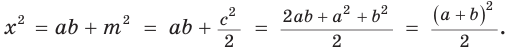
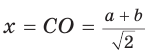
Способ 2. Используем теорему Птолемея, которая гласит: «Произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон». Для нашей задачи получаем (см. рис. 191):
Способ 3. Достроим 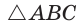
Ответ:
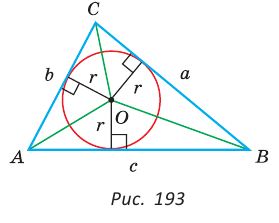
Пример №8
Точка О — центр окружности, вписанной в треугольник АВС, 
Решение:
Пусть 
Тогда
Отсюда 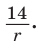
С другой стороны, 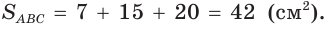
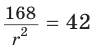
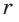
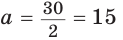
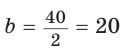
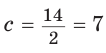
Ответ: 15 см; 20 см; 7 см.
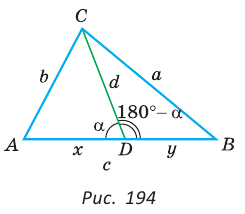
Теорема Стюарта
Следующая теорема позволяет найти длину отрезка, соединяющего вершину треугольника с точкой на противоположной стороне.
Теорема Стюарта. «Если а, b и с — стороны треугольника и отрезок d делит сторону с на отрезки, равные х и у (рис. 194), то справедлива формула
Доказательство:
По теореме косинусов из 
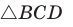
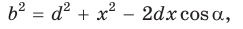
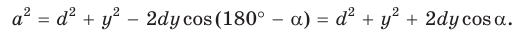
Умножим обе части равенства (1) на у, равенства (2) — на
Сложим почленно полученные равенства:
Из последнего равенства выразим
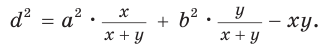
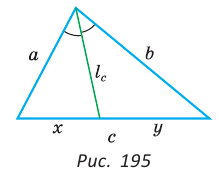
Следствие:
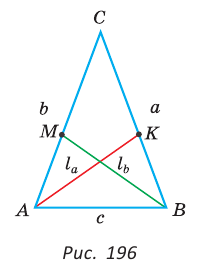
Биссектрису треугольника можно найти по формуле (рис. 195)
Доказательство:
По свойству биссектрисы треугольника 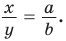
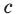
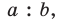
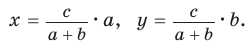
Пример №9
Доказать, что если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера—Лемуса).
Доказательство:
Пусть дан треугольник АВС, 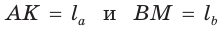
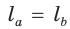
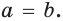
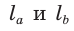
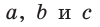
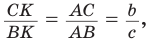
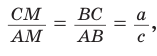
По формуле биссектрисы треугольника
Из условия 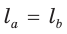
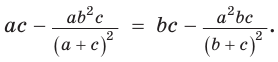
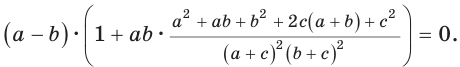
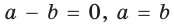
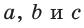
Теорема Птолемея о вписанном четырехугольнике
Произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон, т. е.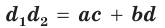
Доказательство:
Из 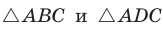
Так как 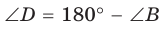
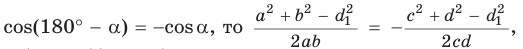
Аналогично из 
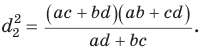
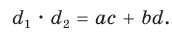
Запомните:
- Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу его описанной окружности:
- Радиус описанной окружности треугольника можно найти, используя формулы:
- Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними:
- Пусть
— стороны треугольника и с — большая сторона. Если
, то треугольник тупоугольный, если
то треугольник остроугольный, если
, то треугольник прямоугольный.
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
- Формула Герона:
- Формула медианы:
- Параллельность прямых и плоскостей
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
- Углы и расстояния в пространстве
- Подобие треугольников
- Решение прямоугольных треугольников
- Параллелограмм
Как найти сторону через синус
Сторону треугольника можно найти не только по периметру и площади, но и по заданной стороне и углам. Для этого используются тригонометрические функции — синус и косинус. Задачи с их использованием встречаются в школьном курсе геометрии, а также в вузовском курсе аналитической геометрии и линейной алгебры.
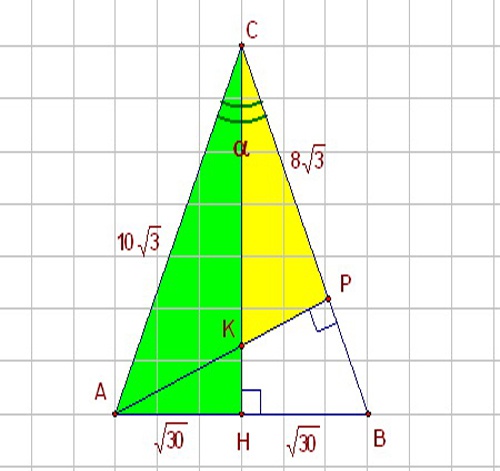
Инструкция
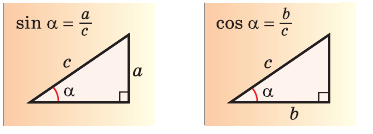
Если известна одна из сторон треугольника и угол между ней и другой его стороной, воспользуйтесь тригонометрическими функциями — синусом и косинусом. Представьте себе прямоугольный треугольник НBC , у которого угол α равен 60 градусам. Треугольник НBC показан на рисунке. Поскольку синус, как известно, представляет собой отношение противолежащего катета к гипотенузе, а косинус — отношение прилежащего катета к гипотенузе, для решения поставленной задачи воспользуйтесь следующим соотношением между этими параметрами:sin α=НB/BCСоответственно, если вы хотите узнать катет прямоугольного треугольника, выразите его через гипотенузу следующим образом:НB=BC*sin α
Если в условии задачи, наоборот, дан катет треугольника, найдите его гипотенузу, руководствуясь следующим соотношением между заданными величинами:BC=НB/sin αПо аналогии найдите стороны треугольника и с использованием косинуса, изменив предыдущее выражение следующим образом:cos α=НC/BC
В элементарной математике существует понятие теоремы синусов. Руководствуясь фактами, которые описывает данная теорема, также можно найти стороны треугольника. Помимо этого, она позволяет найти стороны треугольника, вписанного в окружность, если известен известен радиус последней. Для этого воспользуйтесь соотношением, указанным ниже:a/sin α=b/sin b=c/sin y=2RЭта теорема применима в том случае, когда известны две стороны и угол треугольника, либо дан один из углов треугольника и радиус описанной вокруг него окружности.
Помимо теоремы синусов, существует и аналогичная ей по сути теорема косинусов, которая, как и предыдущая, также применима к треугольникам всех трех разновидностей: прямоугольному, остроугольному и тупоугольному. Руководствуясь фактами, которые доказывают эта теорема, можно находить неизвестные величины, используя следующие соотношения между ними:c^2=a^2+b^2-2ab*cos α
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Теорема синусов
Теорема синусов гласит
Стороны треугольника пропорциональны синусам противолежащих углов
[
frac{a}{sin(α)} = frac{b}{sin(β)} = frac{c}{sin(γ)}
]
Также отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности.
[
frac{a}{sin(α)} = frac{b}{sin(β)} = frac{c}{sin(γ)} = 2R
]
Вычислить, найти сторону треугольника по теореме синусов
Пусть известно: две стороны a, b и угол между ними γ. Нужно найти сторону c и недостающие углы α и β. Используем то, что сумма углов треугольника 180°
[
β = (180° — (α + γ))
]
[
frac{a}{sin(α)} = frac{b}{sin(180° — (α + γ))}
]
По формулам приведения
[
sin(180° — (α + γ)) = sin(α + γ)
]
Подставим в (4)
[
frac{a}{sin(α)} = frac{b}{sin(α + γ)}
]
по формуле синуса суммы углов разделим углы
[
sin(α + γ) = sin(α)cos(γ) + cos(α)sin(γ)
]
Получим
[
frac{b}{a} = frac{sin(α)cos(γ) + cos(α)sin(γ)}{sin(α)}
]
[
frac{b}{a} = cos(γ) + ctg(α)sin(γ)
]
Отсюда найдутся все углы треугольника α и β (см. формула (3)):
[
ctg(α) = frac{Largefrac{b}{a}normalsize — cos(γ)}{sin(γ)}
]
Далее теорема синусов позволит найти оставшуюся сторону c
[
с = bfrac{sin(γ)}{sin(β)} = afrac{sin(γ)}{sin(α)}
]
Вычислить, найти две стороны треугольника по теореме синусов
Пусть известно: одна сторона с, и два прилегающих к ней угла α и β. Нужно найти угол γ и стороны a и b. Используем то, что сумма углов треугольника 180°
[
γ = (180° — (α + β))
]
Теперь когда все углы треугольника известны, а также известна одна сторона, теорема синусов позволит легко найти недостающие стороны:
[
a = c frac{sin(α)}{sin(γ)}
]
[
b = c frac{sin(β)}{sin(γ)}
]
Теорема синусов |
стр. 238 |
|---|
Содержание:
- Формулировка теоремы синусов
- Расширенная теорема синусов
- Примеры решения задач
- Историческая справка
Формулировка теоремы синусов
Теорема
Стороны треугольника пропорциональны синусам противолежащих углов.
$frac{a}{sin alpha}=frac{b}{sin beta}=frac{c}{sin gamma}$
Теорема синусов устанавливает зависимость между сторонами треугольника и противолежащими им углами.
Расширенная теорема синусов
Теорема
Для произвольного треугольника имеет место соотношение:
$frac{a}{sin alpha}=frac{b}{sin beta}=frac{c}{sin gamma}=2 R$
Здесь $R$ — радиус окружности, описанной около рассматриваемого треугольника.
Примеры решения задач
Пример
Задание. Основание треугольника равно 10 см, один из углов при основании равен
$45^{circ}$, а противолежащий основанию угол равен $60^{circ}$. Найдите сторону, противолежащую углу в
$45^{circ}$.
Решение. Пусть искомая сторона — $x$ см. Тогда по теореме синусов имеем:
$$frac{10}{sin 60^{circ}}=frac{x}{sin 45^{circ}} Rightarrow x=frac{10 cdot frac{sqrt{2}}{2}}{frac{sqrt{3}}{2}}=frac{10 sqrt{2}}{sqrt{3}}=frac{10 sqrt{6}}{3} (mathrm{см})$$
Ответ.$frac{10 sqrt{6}}{3}(mathrm{см})$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
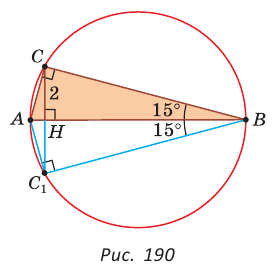
Пример
Задание. В треугольнике $A B C quad angle A=45^{circ}, angle C=15^{circ},$
$B C=4 sqrt{6}$. Найти $A C$ .
Решение. Согласно
теореме о сумме углов треугольника
$$angle A+angle B+angle C=180^{circ} Rightarrow angle B=180^{circ}-45^{circ}-15^{circ}=$$
Сторону $AC$ найдем по теореме синусов:
$$frac{A C}{sin angle B}=frac{B C}{sin angle A} Rightarrow frac{A C}{sin angle 120^{circ}}=frac{4 sqrt{6}}{sin angle 45^{circ}} Rightarrow$$
$$Rightarrow frac{A C}{frac{sqrt{3}}{2}}=frac{4 sqrt{6}}{frac{sqrt{2}}{2}} Rightarrow A C=frac{4 sqrt{18}}{sqrt{2}}=4 cdot sqrt{9}=12$$
Ответ. $A C=12$
Историческая справка
Самое древнее доказательство для теоремы синусов на плоскости описано в книге «Трактат о полном четырёхстороннике» персидского математика,
механика и астронома Насира ад-Дина Ат-Туси (1201 — 1274), которая была написана в 13 веке. Теорема синусов для сферического треугольника
была доказана математиками средневекового Востока ещё в 10 веке. В труде западноарабского математика, астронома и законоведа
Ал-Джайяни (989 — 1050) 11 века «Книга о неизвестных дугах сферы» приводилось общее доказательство теоремы синусов на сфере.
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a, b, c — стороны произвольного треугольника
α, β, γ — противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), (a):
* Внимательно, при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), (a):
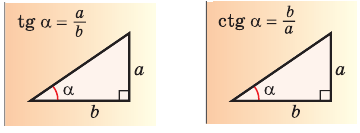
Есть следующие формулы для определения катета или гипотенузы
a, b — катеты
c — гипотенуза
α, β — острые углы
Формулы для катета, (a):
Формулы для катета, (b):
Формулы для гипотенузы, (c):
Формулы сторон по теореме Пифагора, (a,b):
Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)
a — равные стороны
α — углы при основании
β — угол образованный равными сторонами
Формулы длины стороны (основания), (b):
Формулы длины равных сторон , (a):
Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

a — сторона, основание
b, c — стороны
β, γ — углы при основании
p — полупериметр, p=(a+b+c)/2
R — радиус описанной окружности
S — площадь треугольника
Формула длины высоты через стороны, (H):
Формула длины высоты через сторону и угол, (H):
Формула длины высоты через сторону и площадь, (H):
Формула длины высоты через стороны и радиус, (H):
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.
H — высота из прямого угла
a, b — катеты
с — гипотенуза
c1 , c2 — отрезки полученные от деления гипотенузы, высотой
α, β — углы при гипотенузе
Формула длины высоты через стороны, (H):
Формула длины высоты через гипотенузу и острые углы, (H):
Формула длины высоты через катет и угол, (H):
Формула длины высоты через составные отрезки гипотенузы , (H):
L— биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b — стороны треугольника
с — сторона на которую опущена биссектриса
d, e — отрезки полученные делением биссектрисы
γ — угол ABC , разделенный биссектрисой пополам
p — полупериметр, p=(a+b+c)/2
Длина биссектрисы через две стороны и угол, (L):
Длина биссектрисы через полупериметр и стороны, (L):
Длина биссектрисы через три стороны, (L):
Длина биссектрисы через стороны и отрезки d, e, (L):
Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:
L — биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b — катеты прямоугольного треугольника
с — гипотенуза
α — угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):
Формула длины биссектрисы через гипотенузу и угол, ( L):
2. Найти по формулам длину биссектрисы из острого угла на катет:
L — биссектриса, отрезок ME , исходящий из острого угла
a, b — катеты прямоугольного треугольника
с — гипотенуза
α, β — углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):
Формула длины биссектрисы через катет и гипотенузу, (L):
L — высота = биссектриса = медиана
a — одинаковые стороны треугольника
b — основание
α — равные углы при основании
β — угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
Формула высоты, биссектрисы и медианы, через стороны, (L):
Формула для вычисления высоты = биссектрисы = медианы.
В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.
L — высота=биссектриса=медиана
a — сторона треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):
Медиана — отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
M — медиана, отрезок |AO|
c — сторона на которую ложится медиана
a, b — стороны треугольника
γ — угол CAB
Формула длины медианы через три стороны, (M):
Формула длины медианы через две стороны и угол между ними, (M):
Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.
Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).

M — медиана
R — радиус описанной окружности
O — центр описанной окружности
с — гипотенуза
a, b — катеты
α — острый угол CAB
Медиана равна радиусу и половине гипотенузы, (M):
Формула длины через катеты, (M):
Формула длины через катет и острый угол, (M):

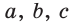
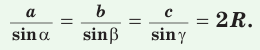
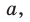
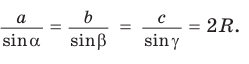
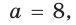
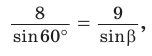
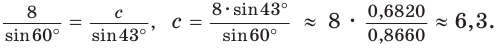
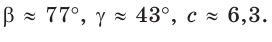


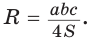
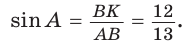
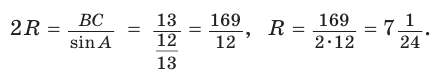
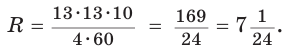
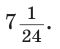
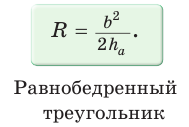
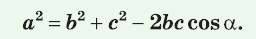
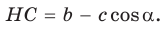
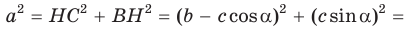
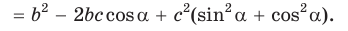
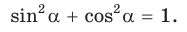
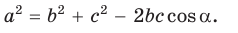
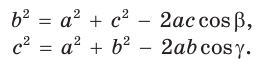
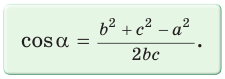
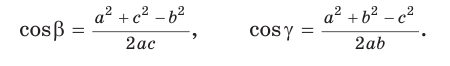

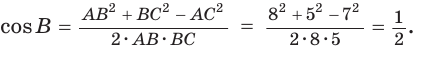
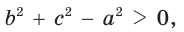 то
то 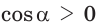 и угол
и угол 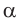 острый;
острый;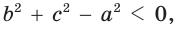 то
то 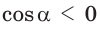 и угол
и угол 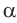 тупой;
тупой; то
то 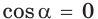 и угол
и угол 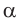 прямой.
прямой.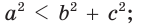
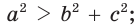
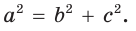
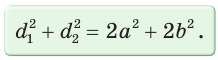
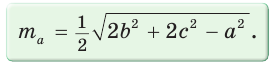
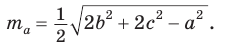
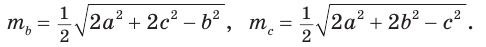
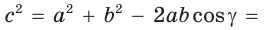
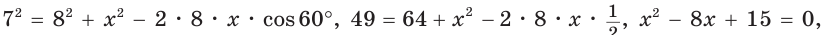
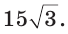
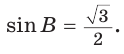
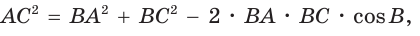
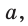
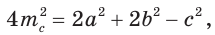
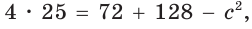
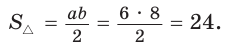
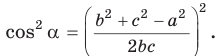
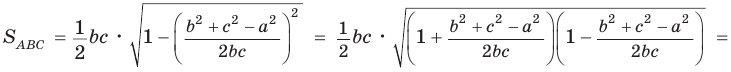
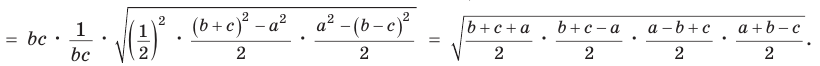
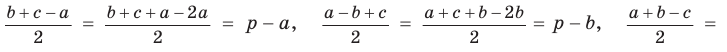
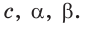
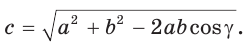
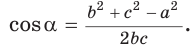
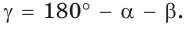
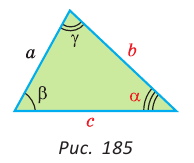
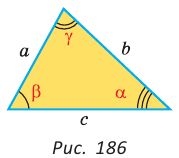
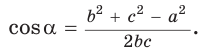
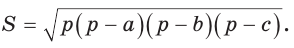
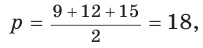
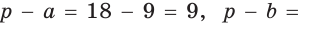
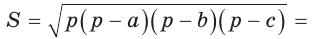
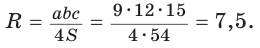
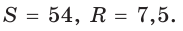
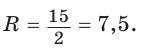
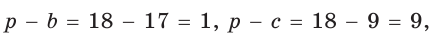
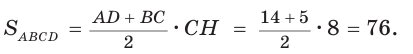
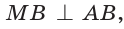
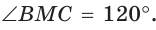
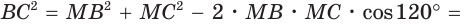
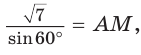
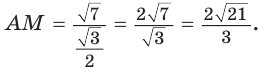
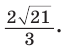
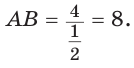
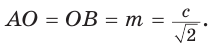
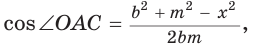
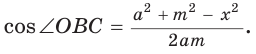
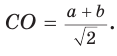
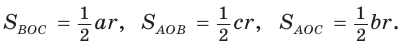
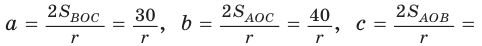
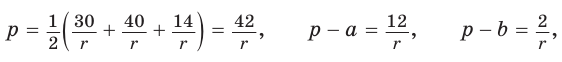
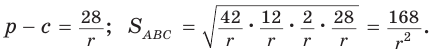
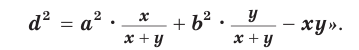
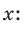
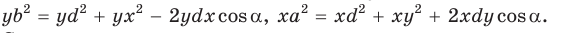
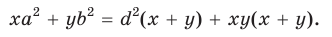
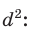
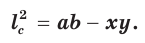
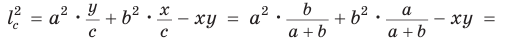
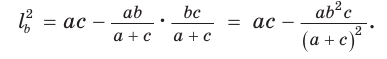
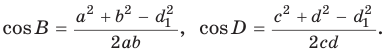
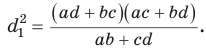
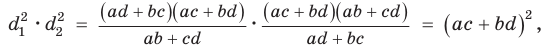
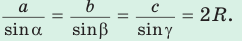
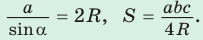
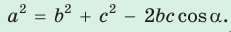
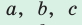 — стороны треугольника и с — большая сторона. Если
— стороны треугольника и с — большая сторона. Если 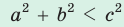 , то треугольник тупоугольный, если
, то треугольник тупоугольный, если 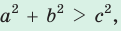 то треугольник остроугольный, если
то треугольник остроугольный, если 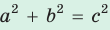 , то треугольник прямоугольный.
, то треугольник прямоугольный.