Как найти сторону куба вписанного в сферу - Autoru.top

Вы отправили работу на проверку эксперту. Укажите номер телефона на него придет СМС

Отправить

Незнайка → ЕГЭ → Математика → Профильная → Вариант 8 → Задание 8

Задание № 21691

Площадь поверхности сферы равна 48π см² . Найдите сторону куба (в см), вписанного в данную сферу.

Показать ответ

Комментарий:
[math]S=picdot D^2=48pi[/math]
D²=48
Диаметр сферы равен диагонали куба, вписанного в сферу. Диагональ куба равна D=3a²
Тогда сторона куба a=4
Ответ: 4

Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.

2 301 984

Уже готовятся к ЕГЭ, ОГЭ и ВПР.
Присоединяйся!

Мы ничего не публикуем от вашего имени

Источник

��:	[	��	]
[	��, ��	]

��: 3
��: 10,11

��

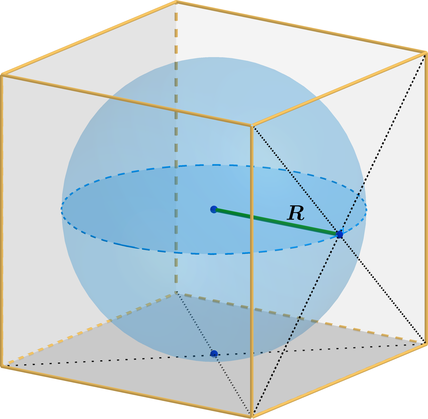
�� , �� R.

��

�� , �� , �� , �� , �� . ��, �� . ��

�� x. �� x


√	3

. �� x


√	3

= 2R

��, �� x =


√	3

��


web-��
��	�� .�.��
URL	http://zadachi.mccme.ru
��
��	8359

Источник

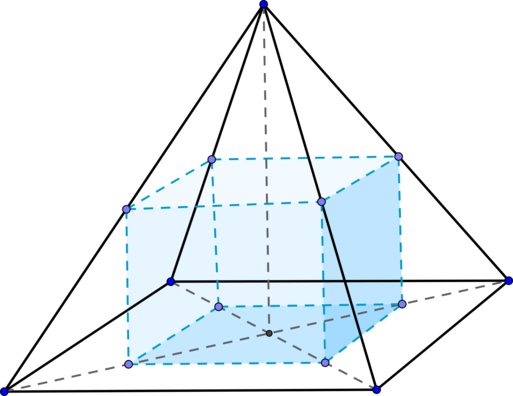
3.4. Вписанные и описанные многогранники

Среди множества выпуклых многогранников выделим два важных семейства: вписанные и описанные многогранники.

Определение 22

Выпуклый многогранник называют вписанным, если все его вершины лежат на сфере. Эта сфера называется описанной для рассматриваемого многогранника.

Определение 23

Выпуклый многогранник называют описанным, если все его грани касаются сферы. Эта сфера называется вписанной для рассматриваемого многогранника.

Очевидно сходство введённых понятий с известными из курса планиметрии понятиями вписанных и описанных многоугольников, описанных и вписанных окружностей.

Не любой многогранник является вписанным или описанным, однако верны следующие две теоремы, аналогичные соответствующим теоремам про треугольник.

Теорема 3.4 (об описанной сфере треугольной пирамиды)

Треугольная пирамида имеет единственную описанную сферу.

Рис. 73

Доказательство. Рассмотрим треугольную пирамиду ABCD (рис. 73). Построим плоскости, перпендикулярные соответственно рёбрам AB, AC и AD и проходящие через их середины. (Геометрическим местом точек пространства, равноудалённых от концов некоторого отрезка, является плоскость, перпендикулярная этому отрезку и проходящая через его середину. Докажите это самостоятельно.) Обозначим через O точку пересечения этих плоскостей. (Такая точка существует, и она единственна. Докажем это. Возьмём первые две плоскости. Они пересекаются, поскольку перпендикулярны непараллельным прямым. Обозначим прямую, по которой пересекаются первые две плоскости, через l. Эта прямая l перпендикулярна плоскости ABC. Плоскость, перпендикулярная AD, не параллельна l и не содержит её, поскольку в противном случае прямая AD перпендикулярна l, т. е. лежит в плоскости ABC.) Точка O равноудалена от точек A и B, A и C, A и D, значит, она равноудалена ото всех вершин пирамиды ABCD, т. е. сфера с центром в O соответствующего радиуса является описанной сферой для пирамиды ABCD.

Итак, мы доказали существование для пирамиды ABCD описанной сферы. Осталось доказать её единственность. Центр любой сферы, проходящей через вершины пирамиды, равноудалён от этих вершин, значит, он принадлежит плоскостям, которые перпендикулярны рёбрам пирамиды и проходят через середины этих рёбер. Следовательно, центр такой сферы совпадает с точкой O.

Теорема доказана. ▼

Отметим, что при этом мы доказали, что все серединные перпендикуляры к рёбрам пирамиды пересекаются в одной точке.

Теорема 3.5 (о вписанной сфере треугольной пирамиды)

У любой треугольной пирамиды существует единственная вписанная сфера.

Рис. 74

Доказательство. Рассмотрим треугольную пирамиду ABCD (рис. 74). Проведём биссекторные плоскости её двугранных углов с рёбрами AB, AC и BC. Эти плоскости имеют единственную общую точку (подумайте почему). Обозначим её через Q. Точка Q равноудалена от всех граней пирамиды. (Она равноудалена от ABC и ABD, ABC и ADC, ABC и CBD.) Значит, сфера соответствующего радиуса с центром в точке Q является вписанной в пирамиду ABCD. Единственность этой сферы доказывается так же, как и в предыдущей теореме. ▼

Как и в предыдущем случае, мы доказали, что все шесть биссекторных плоскостей треугольной пирамиды пересекаются в одной точке.

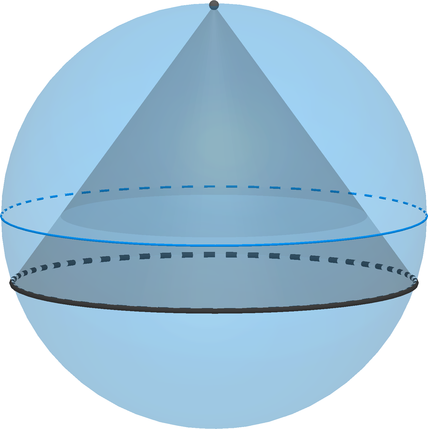
Замечание. Понятия вписанной и описанной сферы могут относиться также к конусу и цилиндру. Любой конус имеет описанную и вписанную сферы. Если провести осевое сечение конуса, то эта плоскость пересечёт описанную и вписанную сферы по большим окружностям этих сфер, причём получившиеся окружности будут соответственно описаны или вписаны в осевое сечение конуса. Цилиндр, как и конус, всегда имеет описанную сферу. Но в отличие от конуса вписать сферу можно не во всякий цилиндр, а лишь в цилиндр с квадратным осевым сечением.

Задачи, задания, вопросы

1(в). Найдите радиусы описанного и вписанного шаров для правильного тетраэдра с ребром a.

2(в). Найдите ребро куба, вписанного в сферу радиуса R.

3(в). Докажите, что если около параллелепипеда можно описать сферу, то этот параллелепипед — прямоугольный.

4(в). Имеется правильная пирамида со стороной основания a и боковым ребром b. Найдите радиус:

а) описанной сферы;

б) вписанного шара;

в) сферы, касающейся всех рёбер пирамиды;

г) сферы, касающейся рёбер основания и продолжений боковых рёбер;

д) радиус сферы, которая касается основания и боковых рёбер.

Каждый пункт решите для пирамиды следующего вида: 1) четырёхугольной; 2) треугольной; 3) шестиугольной.

5(в). Найдите радиус описанного и вписанного шаров для конуса с радиусом основания r и высотой h.

6.Около шара описаны цилиндр и конус, осевым сечением которого является прямоугольный треугольник. Найдите отношение образующих цилиндра и конуса.

7(в). Найдите радиус сферы, описанной около правильной n-угольной призмы с высотой h и стороной основания a.

8(в). В основании правильной треугольной призмы лежит треугольник со стороной 1. Найдите боковое ребро призмы, если известно, что в неё можно вписать шар.

9(т). Известно, что в заданную призму можно вписать шар. Найдите площадь её боковой поверхности, если площадь основания равна S.

10(т). Плоскость проходит на расстоянии a от центра единичной сферы. Найдите ребро куба, одна грань которого лежит в этой плоскости, а вершины противоположной грани находятся на сфере.

11(в). Около призмы можно описать сферу. Докажите, что основание призмы — многоугольник, около которого можно описать окружность. Найдите радиус этой окружности, если высота призмы h, а радиус описанной около неё сферы равен R.

12(в). Основанием пирамиды служит многоугольник, около которого можно описать окружность. Докажите, что существует сфера, описанная около этой пирамиды. Найдите радиус этой сферы, если радиус окружности, описанной около основания пирамиды, равен r, её высота h, а основание высоты совпадает с вершиной основания пирамиды.

13.В треугольной пирамиде ABCD ребро AB равно a, а углы ACB и ADB — прямые. Найдите радиус описанной около этой пирамиды сферы.

14.Найдите ребро куба, одна грань которого принадлежит основанию конуса, а остальные вершины расположены на его боковой поверхности. Радиус основания конуса равен r, его высота h.

15.Через центр сферы радиуса R проведены три попарно перпендикулярные плоскости. Найдите радиус сферы, касающейся всех этих плоскостей и данной сферы.

16.Осевым сечением конуса является правильный треугольник со стороной a. Через ось конуса проведены две перпендикулярные плоскости, которые делят конус на четыре части. Найдите радиус шара, вписанного в одну из этих частей.

17.Внутри единичного куба находятся восемь равных шаров. Каждый шар вписан в один из трёхгранных углов куба и касается трёх шаров, соответствующих соседним вершинам. Найдите радиусы этих шаров.

18(в). Четыре сферы радиуса R попарно касаются друг друга. Найдите радиус сферы, касающейся всех четырёх сфер.

19.Два шара касаются друг друга и граней трёхгранного угла, все плоские углы которого прямые. Найдите отношение радиусов этих шаров.

20(п). Докажите, что если в данный четырёхгранный угол можно вписать шар, то суммы противоположных плоских углов этого четырёхгранного угла равны. Докажите справедливость обратного утверждения: если суммы противоположных плоских углов четырёхгранного угла равны, то в него можно вписать шар.

21(п). Дан трёхгранный угол OABC, в котором ∠BOC = a, ∠COA = b, ∠ AOB = g. Пусть вписанный в него шар касается грани BOC в точке K. Найдите ∠KOB.

22(т). Треугольник ABC вписан в основание конуса, S — вершина конуса. В трёхгранном угле SABC двугранные углы с рёбрами SA, SB и SC равны соответственно x, y и z. Найдите угол между плоскостями SAB и SAO, где SO — высота данного конуса.

23(т). Четырёхгранный угол OABCD (OA, OB, OC, OD — его рёбра) разделён плоскостью OAC на два трёхгранных угла. В каждый из полученных углов вписан шар. Эти шары касаются плоскости OAC в точках K и M. Найдите угол KOM, если ∠BOA = a, ∠DOA = b, ∠BOC = ∠COD.

24(п). Докажите, что радиус шара, проходящего через точки пересечения медиан граней произвольного тетраэдра, в три раза меньше радиуса описанного около рассматриваемого тетраэдра шара. Используя этот факт, докажите, что в произвольном тетраэдре выполняется неравенство R ⩾ 3r, где R и r — соответственно радиусы описанного и вписанного шаров.

25(т). Боковое ребро правильной четырёхугольной пирамиды равно l, а плоский угол при вершине равен a. Найдите радиус описанной около этой пирамиды сферы.

Источник

Помогитееее Срочнооо (((( Найдите длину стороны куба (в см), вписанного в шар с объемом 972 Пи см ^ 3.

На странице вопроса Помогитееее Срочнооо (((( Найдите длину стороны куба (в см), вписанного в шар с объемом 972 Пи см ^ 3? из категории Математика вы найдете
ответ для уровня учащихся 10 — 11 классов. Если полученный ответ не
устраивает и нужно расшить круг поиска, используйте удобную поисковую
систему сайта. Можно также ознакомиться с похожими вопросами и ответами
других пользователей в этой же категории или создать новый вопрос. Возможно,
вам будет полезной информация, оставленная пользователями в комментариях, где
можно обсудить тему с помощью обратной связи.

Источник

8. Геометрия в пространстве (стереометрия)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи на вписанные и описанные поверхности

(blacktriangleright) Если многогранник (M_1) вписан в многогранник (M_2), то все вершины многогранника (M_1) обязаны лежать на поверхности многогранника (M_2).
Пример: куб вписан в правильную четырехугольную пирамиду

(blacktriangleright) Если многогранник вписан в сферу, то все вершины многогранника лежат на поверхности сферы.
Пример:

Например, для того, чтобы конус был вписан в сферу, нужно, чтобы его вершина и граница основания лежали на поверхности сферы.

(blacktriangleright) Если сфера вписана в многогранник, то она касается всех граней многогранника.
Пример:

Задание
1

#2812

Уровень задания: Равен ЕГЭ

(SABCD) – прямоугольная пирамида, вписанная в цилиндр, а (ABCD) – квадрат, (SB)– высота. Площадь боковой поверхности цилиндра равна (36pi), а его объем равен (72pi). Найдите объем пирамиды.

Если разделить объем цилиндра на площадь боковой поверхности, то можно найти радиус окружностей, лежащих в основаниях цилиндра: [frac{V_{text{цил.}}}{S_{text{бок.пов.}}} = frac{pi R^2 H}{2pi
R H} = frac{R}{2} = frac{72pi}{36pi} = 2] (Rightarrow) (R =
4). Зная радиус, можно выразить высоту: (2pi4 H = 36pi) (Rightarrow) (H = 4,5). Так как точка пересечения диагоналей квадрата совпадает с центром описанной вокруг него окружности, то диагональ квадрата равна диаметру окружности. Площадь квадрата можно найти как половину произведения диагоналей, тогда объем пирамиды равен: [V_{SABCD} = frac{1}{3} H frac{1}{2}(2R)(2R) =
frac{1}{3} 4,5 frac{1}{2}8^2 = 48]

Ответ: 48

Задание
2

#3118

Уровень задания: Равен ЕГЭ

Куб описан около сферы радиуса (3). Найдите объем куба.

Так как сфера вписана в куб, то сторона куба равна диаметру сферы. Следовательно, сторона куба равна (2cdot 3=6). Тогда объем куба равен (6^3=216.)

Ответ: 216

Задание
3

#3119

Уровень задания: Равен ЕГЭ

Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен (0,5). Площадь боковой поверхности призмы равна (8). Найдите высоту цилиндра.

Так как четырехугольная призма правильная, то в основании лежит квадрат. Радиус окружности, вписанной в квадрат, равен (0,5). Следовательно, сторона квадрата равна диаметру окружности, то есть (2cdot 0,5=1).
Так как все боковые грани призмы равны, то площадь одной грани равна (8:4=2). Каждая грань представляет собой прямоугольник, следовательно, ее площадь равна произведению бокового ребра призмы на сторону основания (квадрата). Следовательно, боковое ребро призмы равно (2:1=2). Высота цилиндра равна боковому ребру призмы, следовательно, ответ (2).

Ответ: 2

Задание
4

#3120

Уровень задания: Равен ЕГЭ

Куб описан около шара, объем которого равен (3pi). Найдите объем куба.

Так как шар вписан в куб, то сторона куба равна диаметру шара. Так как объем шара равен (3pi) и вычисляется по формуле (frac43pi
R^3), то [R^3=dfrac{3pi}{frac43pi}=dfrac94] Тогда объем куба равен [V=(2R)^3=8R^3=18.]

Ответ: 18

Задание
5

#3121

Уровень задания: Равен ЕГЭ

Шар вписан в куб, площадь поверхности которого равна (dfrac9{pi}). Найдите площадь поверхности шара.

Так как шар вписан в куб, то сторона куба равна диаметру шара. Так как все грани куба – равные квадраты, то площадь одной грани равна (frac9{pi}:6=frac3{2pi}=a^2), где (a) – сторона куба. Следовательно, радиус шара равен половине от (a): (R=frac12a). Значит, (R^2=frac14a^2=frac3{8pi}). Тогда площадь поверхности шара равна [S=4pi R^2=4cdot picdot dfrac3{8pi}=1,5]

Ответ: 1,5

Задание
6

#3122

Уровень задания: Равен ЕГЭ

Правильная четырехугольная призма описана около цилиндра, объем которого равен (7pi). Найдите объем призмы.

Так как четырехугольная призма правильная, то в основании лежит квадрат. Пусть радиус основания цилиндра равен (R), а сторона основания призмы (a). Тогда (a=2R). Пусть (h) – высота цилиндра. Тогда боковое ребро призмы также равно (h). Следовательно, объем цилиндра [V_{text{ц}}=pi R^2cdot h quadRightarrowquad
7pi=pi R^2cdot hquadRightarrowquad R^2cdot h=7] Объем призмы: [V_{text{п}}=a^2h=(2R)^2h=4R^2h=4cdot 7=28.]

Ответ: 28

Задание
7

#2820

Уровень задания: Сложнее ЕГЭ

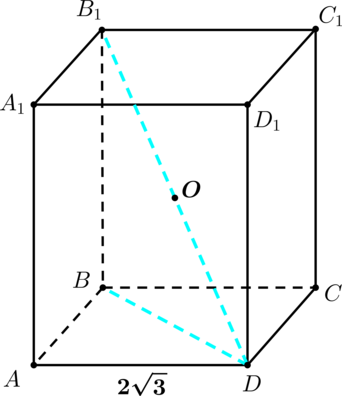
У правильной четырёхугольной призмы (ABCDA_1B_1C_1D_1) сторона основания равна (2sqrt{3}), а площадь одной из боковых граней равна (12). Найдите радиус сферы, описанной около (ABCDA_1B_1C_1D_1).

Так как данная четырёхугольная призма – правильная, то её боковые грани – прямоугольники, следовательно, боковое ребро этой призмы (например, (BB_1)) равно (12 : 2sqrt{3} = 2sqrt{3}).

Пусть точка (O) – середина (B_1D), тогда (O) – центр описанной около (ABCDA_1B_1C_1D_1) сферы. Тогда искомый радиус равен половине (B_1D).

Так как (BD) – диагональ квадрата со стороной (2sqrt{3}), то (BD = 2sqrt{3}cdotsqrt{2} = 2sqrt{6}). По теореме Пифагора (B_1D^2 = BD^2 + B_1B^2), тогда [B_1D^2 = (2sqrt{6})^2 + (2sqrt{3})^2 = 24 + 12 = 36,,] откуда находим: (B_1D = 6), следовательно, искомый радиус равен (6 : 2 = 3).

Ответ: 3