(bullet) Показательное уравнение – уравнение, содержащее переменную (x) в показателе степени.
Выражение (a^n) называется степенью, (a) – основанием степени, (n) – показателем степени.
(bullet) Простейшее показательное уравнение: [a^{f(x)}=a^{g(x)} quad Leftrightarrow quad
f(x)=g(x)] где (a>0, ane 1).
Примеры:
1) Решим уравнение (2^x=4). Так как (4=2^2), то уравнение можно записать в виде (2^x=2^2). Оно равносильно (x=2).
2) Решим уравнение (5^{x+4}=125). Так как (125=5^3), то уравнение можно записать в виде (5^{x+4}=5^3). Оно равносильно (x+4=3), откуда (x=3-4=-1).
(bullet) Основные формулы:
[begin{array}{|ll|}
hline a^0=1 &a^1=a\
a^{nm}=(a^n)^m &a^ncdot a^m=a^{n+m}\
dfrac{a^n}{a^m}=a^{n-m}&a^{-n}=dfrac{1}{a^n}\
a^ncdot b^n=(acdot b)^n &\
a^{frac{k}{r}}=sqrt[r]{a^k} qquad qquad qquad qquad&
dfrac{a^n}{b^n}=left(dfrac{a}{b}right)^n\&\
a,b>0, kin mathbb{Z},& rinmathbb{N}, m,ninmathbb{R}\
hline
end{array}] (bullet) Наиболее часто встречающиеся степени: [begin{array}{|lllll|}
hline
2^2=2 &quad3^2=9 &quad4^2=16 &quad5^2=25 &quad6^2=36\
2^3=8 &quad3^3=27 &quad4^3=64 &quad5^3=125 &quad6^3=216\
2^4=16 &quad3^4=81 &quad4^4=256 &quad5^4=625 &\
2^5=32 &quad3^5=243 &&&\
2^6=64 &quad3^6=729 &&&\
2^7=128 &&&&\
2^8=256 &&&&\
2^9=512 &&&&\
2^{10}=1024 &&&&\
hline end{array}] Примеры:
1) Решить уравнение (2^{5+x}=sqrt[5]{32^2}).
Решение.
Так как (32=2^5), то (32^2=(2^5)^2=2^{10}), следовательно, . Таким образом, (2^{5+x}=2^2), откуда (5+x=2), следовательно, (x=2-5=-3).
2) Решить уравнение (2^{4x-8}=0,5).
Решение.
Так как (0,5=dfrac12), а (dfrac12=2^{-1}), то (2^{4x-8}=2^{-1}), откуда (4x-8=-1), следовательно, (x=dfrac{-1+8}4=dfrac74=1,75).
3) Решить уравнение (left(dfrac1{125}right)^{18-x}=25).
Решение.
Так как (125=5^3), то (dfrac1{125}=dfrac1{5^3}=5^{-3}). Также (25=5^2). Следовательно, (left(5^{-3}right)^{18-x}=5^2) или (5^{-3(18-x)}=5^2), откуда
(-3(18-x)=2quadRightarrowquad
-54+3x=2quadRightarrowquad x=dfrac{2+54}3=dfrac{56}3).
§2. Кто есть кто, или Определение квадратного уравнения . Квадратные уравнения. Часть 1
Квадратным называется уравнение вида ax2 + bx + c = 0, где a, b, c – некоторые заданные действительные числа, причём a ? 0, а x принимается за неизвестное.
Числа a, b, c называют так:
a – старшим или первым коэффициентом,
b – вторым,
c – свободным или третьим1.
«Нумерация» коэффициентов зависит не от их реального месторасположения, а от того, при какой степени неизвестной они находятся. Например, число 2 будет первым коэффициентом в любом из трёх уравнений:
5x +2x2 – 7 = 0,
3 –
x +2x2 = 0,
2x2 +7x +5 = 0.
А вот число 5 в третьем уравнении является свободным коэффициентом, а в первом уравнении – вторым коэффициентом.
То есть первый (старший) коэффициент – это множитель при квадрате неизвестной, второй – при первой степени. Свободный (третий) коэффициент – это слагаемое без неизвестной, то есть «свободный от неизвестной».
Очевидно, что в качестве неизвестного необязательно брать букву x. Более того, привыкнув за школьные годы к этому неизменному обозначению, среднестатистический ученик начинает испытывать затруднения в восприятии (узнавании, интерпретации) квадратных уравнений, встречающихся при решении более сложных математических (физических и других) задач.
Собственно говоря, и коэффициенты квадратного уравнения не всегда могут обозначаться указанными выше буквами. Одним словом, квадратное уравнение имеет вполне определённую структуру, а как обозначаются элементы этой структуры – дело десятое. Человек со сложившимся математическим стилем мышления понимает, что квадратным уравнением будет являться любое равенство, в правой части которого стоит ноль, а в левой – сумма трёх слагаемых, одно из которых является произвольным числом, другое – произведением произвольного числа на первую степень неизвестного и третье – произведением ненулевого числа на вторую степень неизвестного.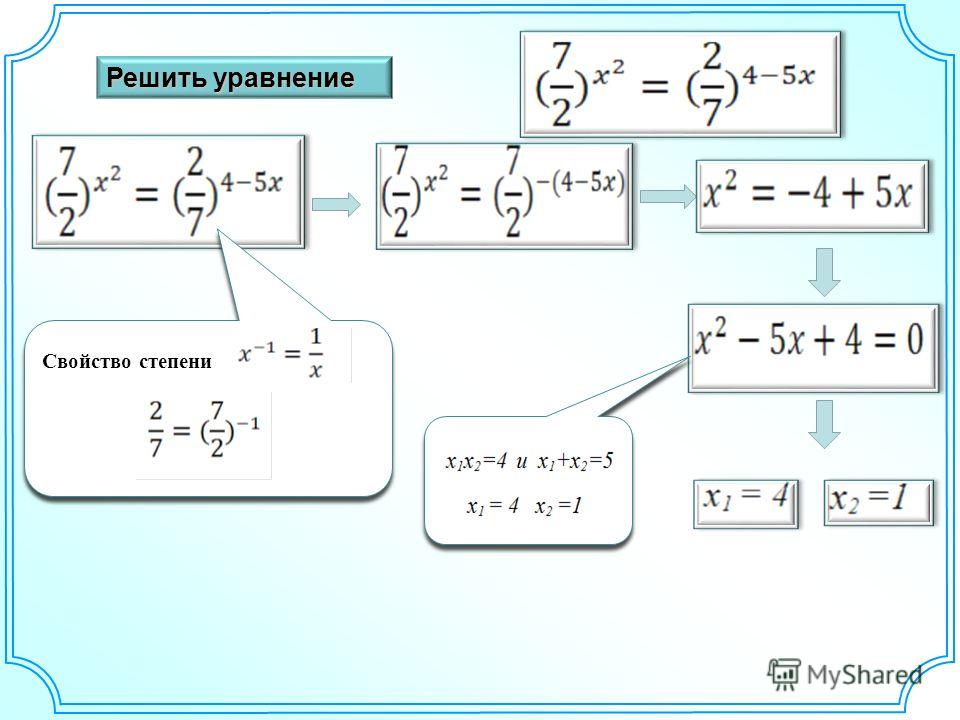
Тогда квадратными будут уравнения:
mx2 + nx + k = 0 (относительно x, m ? 0),
xa2 + ya + z = 0 (относительно a, x ? 0).
Уравнение y2 +
xy + x2 = 0 можно рассматривать как квадратное, но только либо относительно x, либо только относительно y.
Пока же договоримся, что теоретические вопросы будем излагать на привычных обозначениях.
Вернёмся к определению. Давайте выделим внешние, «бросающиеся в глаза», черты квадратного уравнения. Во-первых, наличие знака равенства. Отсутствие его с очевидностью снимает вопрос о правомерности называть объект уравнением.
(Любое ли равенство является уравнением – разговор особый и не в рамках этой книги. )
)
Во-вторых, левая часть нашего равенства представляет собой алгебраическую сумму трёх слагаемых.
Возникает первый вопрос: обязательно трёх?
Другими словами количество слагаемых – это определяющий признак или нет? Давайте посмотрим.
Значения второго и свободного коэффициентов квадратного уравнения в определении никак не ограничиваются (в отличие от первого). Следовательно, они могут быть равными нулю. Тогда под определение квадратного подходят уравнения вида
ax2 + bx = 0 (c = 0, ab ? 0),
ax2 + c = 0 (b = 0, ac ? 0),
ax2 = 0 (b = c = 0, a ? 0).
Но в левых частях этих уравнениях не три слагаемых!
Тем не менее, это – квадратные уравнения, потому что их можно записать так
ax
2 + bx +0 = 0,
ax2 +0 · x + c = 0,
ax2 +0 · x +0 = 0.
Так как количество слагаемых левой части уравнений ax2 + bx = 0, ax2 + c = 0, ax2 = 0 визуально меньше, чем может быть, их называют неполными квадратными уравнениями. Тогда как квадратное уравнение ax2 + bx + c = 0, в котором все коэффициенты отличны от нуля, называют полным.
Таким образом, отсутствие в записи конкретного уравнения свободного члена или слагаемого с первой степенью неизвестного не даёт нам права сомневаться в том, что уравнение всё-таки квадратное. Однако и наличие их не является веской причиной отнести уравнение к квадратным. Об этом чуть ниже.
Следующим возникает вопрос, а почему, собственно a ? 0? (Конечно, искушённый читатель знает почему.) Можно ли, например, уравнение вида ax2 + (a – 1) x + a = 0 (или в общем виде f (a) x2 + g (a) x + h (a) = 0) называть квадратным?
Давайте похулиганим и поставим в качестве первого коэффициента ноль. Тогда уравнение примет вид
bx + c = 0.
Но это же линейное уравнение! Оно имеет свою теорию, свои изюминки.
Пусть будут «мухи отдельно, котлеты отдельно».
Теперь понятно, что требование a ? 0 необходимо для сохранения в квадратном уравнении второй степени – квадрата – неизвестного. Вот этот признак будет определяющим!
В дальнейшем, говоря о квадратном уравнении, мы будем помнить, что старший коэффициент не равен нулю, не оговаривая это каждый раз. Договорились?
Тогда уравнение f (a) x2 + g (a) x + h (a) = 0 правильно называть уравнением с параметром второй степени, которое при определённых условиях может быть квадратным, а может им и не быть (стать линейным).
Однако не будем торопиться. Наличие второй степени неизвестного – необходимый, но не достаточный признак квадратного уравнения.
Рассмотрим следующие уравнения:
ax2 + by + c = 0 и ax2 + bx3 + c = 0.
Выполним сравнительный анализ этих уравнений с квадратным ax2 + bx + c = 0 по трём признакам:
– наличие второй степени неизвестной,
– наибольшая степень неизвестной,
– количество неизвестных.
Зафиксируем для каждого уравнения эти параметры.
Результаты сравнительного анализа организуем в таблицу.
Итак, что мы имеем?
Наличие второй степени неизвестного является общим для всех трёх уравнений. Но по двум другим признакам сравнения, квадратное уравнение отличается: в квадратном уравнении вторая степень неизвестной является наибольшей и неизвестная только одна.
Именно это и важно!
Собственно говоря, квадратным является целое рациональное (или по-другому – алгебраическое) уравнение второй степени с одним неизвестным2.
Процесс ограничения класса алгебраических уравнений можно представить в двух направлениях:
алгебраическое уравнение ? первой степени, второй степени и так далее;
алгебраическое уравнение ? с одной неизвестной, с двумя неизвестными и так далее.
Приведём примеры:
ax + b = 0 – уравнение первой степени с одной неизвестной;
ax + by + c = 0 – уравнение первой степени с двумя неизвестными;
ax2 + bx + c = 0 – уравнение второй степени с одной неизвестной;
ax2 + bxy + cy2 + kx + ly + m = 0 – уравнение второй степени с двумя неизвестными.
Тогда ближайшими родовыми понятиями для квадратного уравнения будут: алгебраическое уравнение второй степени или алгебраическое уравнение с одним неизвестным. Выбирая в качестве родового понятия разные объекты, мы сможем получить различные формулировки определения квадратного уравнения. Попробуйте!
Наконец, рассмотрим правую часть равенства в определении квадратного уравнения. Она представляет собой конкретное число – ноль. А может быть что-нибудь другое?
Если мы хотим видеть квадратное уравнение «в чистом виде», то ничего, кроме нуля, в правой части быть не должно. Но…
Но…
Рассмотрим уравнение ax2 + bx + c = m, где
m число отличное от нуля. Тогда мы, основываясь на равносильности преобразований уравнений3, можем записать
ax2 + bx + c – m = 0
ax2 + bx + (c – m) = 0
ax2 + bx + c1 = 0.
То есть мы, собственно, получили квадратное уравнение.
Ещё пример:
ax2 + bx + c = mx + n
ax2 + bx + c — mx – n = 0
ax2 + bx – mx + c – n = 0
ax2 + (b – m) x + (c – n) = 0
ax2 + b1 x + c1 = 0.
Таким образом, уравнения двух приведённых выше видов
ax2 + bx + c = m и ax2 + bx + c = mx + n есть смысл назвать сводящимися к квадратным. То есть, если в правой части стоит многочлен с одной (той же, что и в левой части!) неизвестной степени не выше первой, то с помощью соответствующих преобразований квадратное уравнение мы получим без проблем.
Если же в правой части будет стоять многочлен с одной неизвестной второй степени, то квадратное уравнение может и не получиться.
Ситуация первая: ax2 + bx + c =ay2 + by + c.
Как бы ни старались, квадратного уравнения мы не получим. Неизвестных две, и это равенство не входит в множество математических объектов «квадратные уравнения». Вывод: неизвестная правой части должна быть такой же, что и в левой!
Ситуация вторая. Преобразуйте самостоятельно, например, два следующих уравнения:
Преобразуйте самостоятельно, например, два следующих уравнения:
ax2 + bx + c = kx2 + mx + n
ax2 + bx + c = ax2 + mx + n.
Получилось ли у вас квадратное уравнение в первом случае? А во втором? Как будет называться уравнение, которое сведётся не к квадратному?
Определите условие, при котором уравнение такого вида всё-таки будет сводиться к квадратному4.
Как ещё один пример рассмотрите уравнение
x2 – 9 = (x – 5) (x +7).
Таким образом, наличие второй степени неизвестной в записи уравнения не всегда будет означать, что оно квадратное.
Очевидно, что если в правой части стоит многочлен с одной переменной степени выше второй, то квадратного уравнения мы ни при каких условиях не получим.
Итак, есть квадратные уравнения, а есть уравнения, сводящиеся к квадратным.
Данный текст является ознакомительным фрагментом.
7.2. Классификация показательных уравнений.
1. Уравнения, решаемые переходом к
одному основанию.
Пример 18. Решить
уравнение
.
Решение:
Воспользуемся тем, что все основания
степеней являются степенями числа 5:
.
2. Уравнения, решаемые переходом к
одному показателю степени.
Эти
уравнения решаются преобразованием
исходного уравнения к виду ,
которое использованием свойства
пропорции приводится к простейшему.
Пример
19. Решить уравнение:
Решение:
.
-
Уравнения,
решаемые вынесением общего множителя
за скобки.
Если
в уравнении каждый показатель степени
отличается от другого на некоторое
число, то уравнения решаются вынесением
за скобки степени с наименьшим показателем.
Пример
20. Решить уравнение
.
Решение:
Вынесем в левой части уравнения степень
с наименьшим показателем за скобки:
.
Пример
21. Решить уравнение
Решение:
Сгруппируем отдельно в левой части
уравнения слагаемые, содержащие степени
с основанием 4, в правой части – с
основанием 3, затем вынесем степени с
наименьшим показателем за скобки:
.
-
Уравнения,
сводящиеся к квадратным (или кубическим)
уравнениям.
К
квадратному уравнению относительно
новой переменной y
сводятся уравнения:
а)
вида
подстановкой,
при этом;
б)
вида
подстановкой,
при этом.
Пример
22. Решить уравнение
.
Решение:
Сделаем замену переменной
и решим квадратное уравнение:
.
Ответ:
0; 1.
-
Однородные
относительно показательных функций
уравнения.
Уравнение
вида
является однородным уравнением второй
степени относительно неизвестныхax
и bx
. Такие уравнения сводятся предварительным
Такие уравнения сводятся предварительным
делением обеих частей на
и
последующей подстановкойк квадратным уравнениям.
Пример
23. Решить уравнение
.
Решение:
Разделим обе части уравнения на
:
.
Положив
,
получим квадратное уравнениес корнями.
Теперь
задача сводится к решению совокупности
уравнений
.
Из первого уравнения находим, что.
Второе уравнение не имеет корней, так
какпри любых значенияx.
Ответ:
-1/2.
-
Рациональные
относительно показательных функций
уравнения.
Пример
24. Решить уравнение
.
Решение:
Разделим числитель и знаменатель дроби
на 3x
и получим вместо двух – одну показательную
функцию:
-
Уравнения
вида
.
Такие
уравнения с множеством допустимых
значений (ОДЗ), определяемым условием
,
логарифмированием обеих частей уравнения
приводятся к равносильному уравнению,
которые в свою очередь равносильны
совокупности двух уравненийили.
Пример
25. Решить уравнение:
.
Решение:
.
Решите уравнения:
1.
; 2.; 3.;
4.
; 5.; 6.;
7.
; 8.;
9.
; 10.; 11.;
12.
; 13.;
14.
; 15.;
16.
; 17.;
18.
; 19.;
20.
; 21.;
22.
; 23.;
24.
; 25..
26. Найдите произведение корней уравнения
.
27. Найдите сумму корней уравнения
.
Найдите значение выражения:
28.
,
гдеx0–
корень уравнения;
29.
,
гдеx0–
целый корень уравнения.
Решите уравнение:
30.
;
31.
; 32. .
.
Ответы: 1. 0; 2. -2/9; 3. 1/36; 4. 0, 0.5; 5. 0; 6. 0;
7. -2; 8. 2; 9. 1, 3; 10. 8; 11. 5; 12. 1; 13. ¼; 14. 2; 15. -2, -1;
16. -2, 1; 17. 0; 18. 1; 19. 0; 20. -1, 0; 21. -2, 2; 22. -2, 2; 23.
4; 24. -1, 2; 25. -2, -1, 3; 26. -0.3; 27. 3; 28. 11; 29. 54; 30. -1,
0, 2, 3; 31.
;
32..
Как решить для показателей степени
Приветствую вас, любители математики! В сегодняшнем посте мы рассмотрим, как решить для показателей. На данный момент мы знакомы с решением для неизвестных переменных в уравнении, но никогда раньше нам не приходилось решать для экспоненты! Понимание того, как это сделать и какие методы использовать, поднимет наши навыки алгебры на совершенно новый уровень. Кроме того, не забудьте посмотреть видео и попрактиковаться в вопросах в этом посте, чтобы увидеть еще больше примеров. Удачных расчетов! 🙂
Что такое экспоненциальное уравнение?
Показательное уравнение — это уравнение, где показатель степени является неизвестной переменной и принимает следующую форму:
Иногда нас попросят решить для неизвестной переменной в показательном уравнении . Есть два основных способа решения этого типа уравнения, и мы рассмотрим каждый из них ниже.
Есть два основных способа решения этого типа уравнения, и мы рассмотрим каждый из них ниже.
(Метод 1) Та же база
(Метод 2) Другая база
Давайте углубимся и рассмотрим три разных примера, применяющих один из двух методов, описанных выше.
Пример #1: Решение экспоненциальных уравнений с одинаковым основанием найти недостающую переменную.
Шаг 1 : Поскольку обе части уравнения имеют одно и то же основание (основание 5), мы можем установить значения экспоненты равными друг другу и использовать базовую алгебру для решения для x.
Пример № 2: Решение экспоненциальных уравнений с одинаковым числом Основание
Мы можем установить показатели степени равными друг другу, когда уравнение может быть записано так, чтобы оно имело одно и то же основание с обеих сторон. Как и в приведенном ниже примере, обе базы могут быть записаны как 5, мы снова можем, , установить показатели степени равными и найти отсутствующую переменную. 2(2x).
2(2x).
Шаг 2: Теперь мы можем установить значения экспоненты равными друг другу и найти x теперь, когда обе стороны имеют совпадающие основания.
Пример #3: Решение экспоненциального уравнения с различными Базой s
Когда экспоненциальное уравнение не имеет одинаковой базы и не может быть записано так, чтобы иметь ту же базу, мы должны использовать журналы найти неизвестную переменную! Итак, убедитесь, что вы знакомы с правилами ведения журнала, перечисленными здесь, чтобы решать вопросы такого типа. В основном мы будем работать с правилом мощности журналов.
S шаг 1: Возьмите журнал обеих сторон и найдите x.
Когда будете готовы, ответьте на практические вопросы ниже, чтобы овладеть новыми навыками экспоненты!
Практические вопросы:
Решите каждое показательное уравнение относительно x.
Решения:
Хотите просмотреть журналы? Проверьте этот пост здесь!
Facebook ~ Twitter ~ TikTok ~ Youtube
Нравится:
Нравится Загрузка. ..
..
Автор Math SuxОпубликовано 6 октября 2021 г. 9{17x + 99} = 42$? Как, черт возьми, мы можем разумно решить это уравнение ?
Мы делаем это, манипулируя логарифмами. Оказывается, мы нашли два действительно полезных типа логарифмов, которыми оснащены большинство стандартных калькуляторов: логарифмы, основанные на числе 10, и хорошо известная константа $e$. Оба они имеют смысл, потому что наша повседневная система счисления использует 10, а $e$ имеет некоторые особые свойства, которые не имеют отношения к этому конкретному обсуждению. Несмотря на это, $log_e$ используется так часто, что его часто называют натуральный логарифм , а основание обычно опускается (поэтому, когда вы видите $log(c)$, это понимается как $log_e(c)$).
Итак, теперь, поскольку мы можем легко работать с логарифмами в любой из этих систем счисления (даже если мы понятия не имеем, что на самом деле представляет собой $e$ или для чего он используется), мы просто должны задаться вопросом, есть ли способ для преобразование логарифма, основанного на произвольном числе, скажем, $a$, в логарифм, основанный на $e$ (или 10).
На этой странице вы узнаете
- Зачем показательная функция смотрится в зеркало?
- Возможна ли дружба в математике?
- Как поменять знак неравенства всего одним действием?
Оценка за тест зависит от набранных баллов, а они зависят от количества и качества ответов. Цена билета в развлекательный центр может меняться от времени суток или дня недели. Погода в городе напрямую связана со временем года, географическим положением, температурой воздуха, влажностью, осадками и многими другими факторами. Функция в математике показывает нам зависимость одной переменной от другой. Об этом подробнее поговорим в статье.
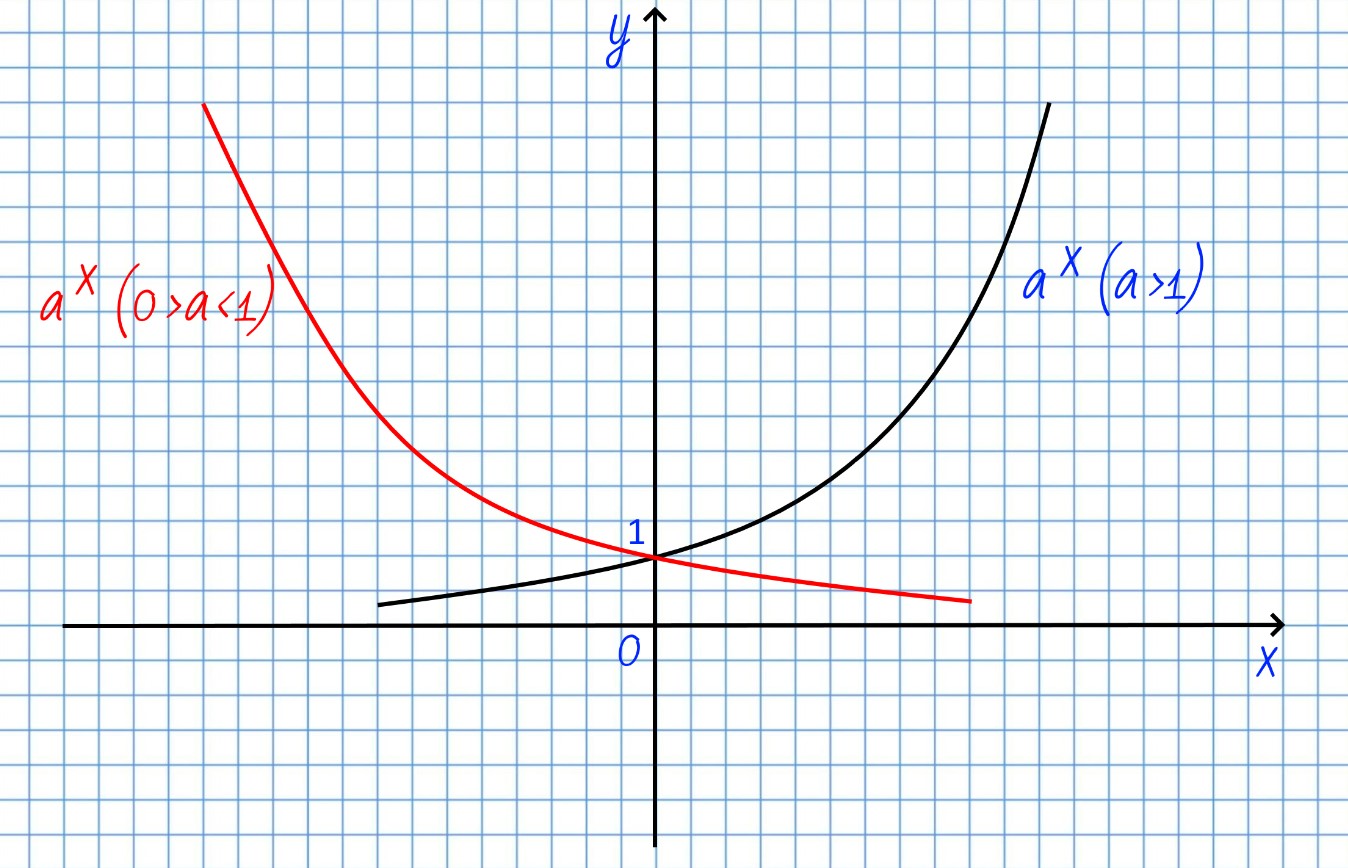
Показательная функция и её основные свойства
Что же нам дает знание о характере этой зависимости?
Показательная функция — это функция, у которой неизвестная находится в показателе.
Она выглядит следующим образом:
y=ax, где
a > 0 и a ≠ 1
Посмотрим на обозначения элементов в показательной функции:

Рассмотрим промежутки, которым может принадлежать a.
При 0 < a < 1 и a > 1 показательные функции отличаются. Графики функций выглядят зеркально друг другу, если основание степени одной из них b, а второй
Например:

Рассмотрим функции с разными основаниями подробней.
Основные свойства функции:
1) Область определения
D(y)=(-∞;+∞)
2) Множество значений функции
Е(y)=(0;+∞)
3) Нет ни наименьшего, ни наибольшего значения.
4) Функция возрастает.
5) Функция непрерывна.

Рассмотрим функции с разными основаниями подробней.
Основные свойства функции:
1) Область определения
D(y)=(-∞;+∞)
2) Множество значений функции
Е(y)=(0;+∞)
3) Нет ни наименьшего, ни наибольшего значения.
4) Функция убывает.
5) Функция непрерывна.

Повторение свойств степеней
Прежде чем переходить к показательным уравнениям, давайте вспомним свойства степеней. Их можно применять для преобразований во время решения.

Методы решения показательных уравнений
Показательное уравнение – это уравнение, где неизвестная находится в показателе степени.
Если неизвестная содержится и в показателе степени, и в основании, уравнение также считается показательным.
Пример показательного уравнения: 54x-2 = 25.
Методы решения показательных уравнений:
- графический метод;
- метод уравнивания показателей;
- метод введения новой переменной;
- метод вынесения общего множителя;
- метод группировки;
- метод умножения/деления на показательную функцию.
- Графический метод
Этот метод заключается в рассмотрении левой и правой частей уравнения, как отдельных функций, и изображении их на плоскости. Данный метод в некоторых случаях может оказаться неточным. Поэтому его лучше использовать для нахождения количества решений, а сами значения находить другим методом.
Решим следующее уравнение:
0,5x+2 = x+5
Разделим его на отдельные функции:

Изобразим их на плоскости и найдем точку пересечения, именно она и будет решением данного уравнения.

Точка пересечения имеет координаты (-1;4). В ответ выпишем х=-1.
- Метод уравнивания показателей
Этот метод заключается в представлении обеих частей уравнения в виде степени с одинаковыми основаниями и приравниванию показателей степеней

Рассмотрим на примере:
2x⋅3x = 36
Воспользуемся свойством степеней для левой части и приведем к такому виду:
6x = 36
Запишем левую часть как степень с основанием 6:
6x = 62
Перейдем к равенству степеней и найдем х:
x = 2
- Метод введения новой переменной
Чтобы решить уравнение данным методом, нужно принять повторяющееся выражение за переменную и решить относительно нее, а после сделать обратную замену. Нельзя забывать про обратную замену, потому что значение введенной переменной не равно значению изначальной переменной.
Можно представить, что повторяющееся выражение и новая переменная – это лучшие друзья . Когда появляются затруднения с решением уравнения, подружка повторяющегося выражения прибегает и заменяет его до того момента, пока у уравнения не будут найдены корни. Затем они снова меняются.

Решим следующее уравнение:
22x-2⋅2x+6 = 5
Соберем все слагаемые слева
22x-2⋅2x+1 = 0
Разложим каждое слагаемое на множители:
2x⋅2x-2⋅2x+1 = 0
Заметим, что 2x можно заменить. Пусть t = 2x, t > 0, тогда уравнение можно записать следующим образом:
t2-2t+1 = 0
Решим его относительно новой переменной:
(t-1)2 = 0
t = 1
Найденное значение подходит под условие t > 0, сделаем обратную замену:
2x = 1
Представим правую часть в виде степени с основанием 2:
2x = 20
Приравняем показатели степеней и найдем х:
x = 0
- Метод вынесения общего множителя
Этот метод заключается в вынесение общего множителя за скобку.
Рассмотрим на примере:
6x-3x = 0
Разложим первое слагаемое на множители:
3x⋅2x-3x = 0
Вынесем общий множитель за скобку:
3x(2x-1) = 0
Так как произведение равно нулю, один из множителей должен равняться нулю. Перейдем к совокупности уравнений:

Так как показательная функция всегда больше 0, то у первого уравнения не будет решений. Из второго уравнения х = 0, значит, единственным решением данного уравнения будет х = 0.
- Метод группировки
Заключается этот метод во взятии слагаемых в скобки с последующим упрощением.
Давай решим такое уравнение:
x⋅5x-5x-3⋅5x+15 = 0
Заметим, что, сгруппировав 1 и 3 слагаемые и 2 и 4 слагаемые и вынося общий множитель за скобки, получаем одинаковые скобки:
(x⋅5x-3⋅5x)-(5x-15) = 0
5x(x-3)-5(x-3) = 0
Вынесем за скобку общий множитель (х — 3):
(5x-5)(x-3) = 0
Перейдем к совокупности уравнений:

Решим уравнения и получим х = 1 и х = 3.
- Метод умножения/деления на показательную функцию
Данный метод заключается в умножении каждого слагаемого уравнения на определенную показательную функцию.
Рассмотрим следующее уравнение:
Для упрощения уравнения умножим каждое слагаемое на 5x и получим:
2x⋅5x-1 = 0
Воспользуемся свойством степеней для первого слагаемого, а второе перенесем вправо:
10x = 1
Представим справа степень с основанием 10:
10x = 100
Приравняем степени и получим ответ:
x = 0
Также можно делить все слагаемые на показательную функцию для упрощения уравнения. Это допустимо, только если эта функция точно не равна нулю, так как на ноль делить нельзя.
Показательные неравенства и методы их решения
Показательное неравенство – это неравенство, у которого переменная находится в показателе степени.
Самый простой вид показательного неравенства:
ax > y , где a и y – числа
Неравенства видов af(x) > y и af(x) > ag(x) называются простейшими показательными неравенствами.
Особые случаи:
- af(x) < y при y ≤ 0 не имеет решений, так как число больше нуля в степени всегда больше 0;
- af(x)>y при y ≤ 0, в таком неравенстве множеством решений является множество действительных чисел, так как:
- число больше нуля в степени всегда положительное,
- положительное число больше отрицательного.
Давайте вспомним, как сравниваются показатели степеней с основаниями от 0 до 1 и основаниями больше 1.

Если основание от 0 до 1, то при переходе к неравенству степеней знак меняется на противоположный, а если основание больше 1, тогда при переходе знак остается прежним.
При делении или умножении каждой части неравенства на отрицательное число знак неравенства меняется на противоположный.
Например:
2x-1 > -3 | : (-1)
-2x+1 < 3
Методы решения показательных неравенств
Для решения показательных неравенств можно использовать те же методы, что и для решения уравнений, но с некоторыми изменениями. Они коснутся графического метода, метода уравнивания показателей и метода умножения/деления на показательную функцию.
- Графический метод
Теперь используя этот метод нужно закрашивать нужную область.
Рассмотрим такое неравенство:
2x ≥ -x+3
Запишем функции:
y = 2x
y = -x+3
Изобразим их на графике:

Так как первая функция больше или равна второй, выделим промежуток на графике, где график первой функции выше графика второй

В ответ получим промежуток [1;+∞).
- Метод уравнивания показателей
Данный метод будет записан по-разному для возрастающей и убывающей показательных функций.
af(x) < ag(x), где a > 1 ⬄ f(x) < g(x)
af(x) < ag(x), где 0 < a < 1 ⬄ f(x) > g(x)
3, 4, 5 методы работают без изменений.
6) Метод умножения/деления на показательную функцию
Используя данный метод для неравенств, нужно учитывать, что при умножении/делении на отрицательное число знак неравенства меняется на противоположный.
Решим одно неравенство:
(frac{1}{3})^{x+1}+frac{1}{3}^x ≥ 12
- Воспользуемся свойством степеней и преобразуем
(frac{1}{3})^{x}⋅frac{1}{3}+ frac{1}{3}^x ≥ 12
- Вынесем общий множитель
(frac{1}{3})^{x}⋅(frac{1}{3}+ 1) ≥ 12
(frac{1}{3})^{x}⋅frac{3}{4} ≥ 12
- Домножим обе части неравенства на
- Представим правую часть неравенства в виде степени с основанием 13
(frac{1}{3})^x ≥ (frac{1}{3})^{-2}
- Перейдем к неравенству степеней, поменяем знак уравнения, так как основание принадлежит промежутку от 0 до 1
x ≤ -2
Ответ: (-∞; -2].
Фактчек
- Вид показательной функции y=ax, где a > 0 и a ≠ 1.
- При 0 < a < 1 показательная функция убывает, а при a > 1 показательная функция возрастает.
- Показательное уравнение или неравенство – это уравнение или неравенство, где неизвестная находится в показателе степени.
- Методы решения показательных уравнений и неравенств:
- графический метод;
- метод уравнивания показателей;
- метод введения новой переменной;
- метод вынесения общего множителя;
- метод группировки;
- метод умножения/деления на показательную функцию.
- Если основание степени в неравенстве от 0 до 1, то при переходе к неравенству степеней знак меняется на противоположный.
- При умножении/делении обеих частей неравенства на отрицательное число, знак неравенства меняется на противоположный.
Термины
Область определения функции – это множество значений, которые может принимать х.
Множество значений функции – это множество значений, которые можно получить подставляя разные х из области определения функции.
Проверь себя
Задание 1.
Решите уравнение 3x3x+2=9
- 2
- -2
- 0
- 1
Задание 2.
Решите уравнение
5^frac{x-5}{x}-5^frac{1}{x} = 0
- 5
- 6
- 0
- 4
Задание 3.
Решите уравнение 4x⋅2=256
- 3,5
- 0
- 1
- 2,8
Задание 4.
Решите неравенство
- -3
- (-3; 3)
- (-∞; -3]
- [-3; +∞)
Задание 5.
Решите неравенство 3x+2-9x ≥ 0
- [2; +∞)
- (-∞; 2)
- (-∞; 2]
- 2
Ответы: 1. — 3; 2. — 2; 3. — 1; 4. — 4; 5. — 3.
На чтение 8 мин. Просмотров 6.5k.
В 10-11 классе в курсе алгебры изучаются показательные уравнения, решение показательных уравнений является обязательным навыком, который проверяется на ЕГЭ. Рассмотрим методы решения показательных уравнений. Показательное уравнение — это уравнение, в котором переменная выступает как показатель степени некоторой другой переменной. Например, уравнение 2^x = 8 является показательным уравнением, потому что переменная x появляется как показатель степени с основанием 2. Экспоненциальные уравнения могут иметь множество различных форм в зависимости от конкретных значений и задействованных переменных.
Как правило, экспоненциальные уравнения могут быть трудны для решения, потому что экспоненциальная функция растет очень быстро, что может затруднить поиск точного значения переменной. Однако есть несколько различных методов, которые можно использовать для решения экспоненциальных уравнений, таких как использование логарифмов или выражение уравнения в виде одного и того же основания с обеих сторон.
Показательными уравнениями называются такие уравнения, в которых неизвестное входит в показатель степени, общий вид их таков:
displaystyle a^{f (x)}=a^{g (x)}. Решением показательного уравнения будет число или выражение, которое называется корнем уравнения. Корней может быть один или несколько. Решить уравнение это значит найти его корни.
Однако некоторые из них (сложные) еще надо к такому виду привести.
Показательные уравнения решаются после степенных преобразований, в которых могут быть использованы показатели степени дробные, нулевые, отрицательные.
Таблица основных свойств показателей степени, которые используются при решении показательных уравнений.
| 1 | displaystyle a^m cdot a^n | displaystyle a^{m+n} |
| 2 | displaystyle frac{a^m}{a^n} | displaystyle a^{m-n} |
| 3 | displaystyle (a cdot b)^n | displaystyle a^n cdot b^n |
| 4 | displaystyle a | displaystyle a^1 |
| 5 | displaystyle (frac{a}{b})^n | displaystyle frac{a^n}{b^n} |
| 6 | displaystyle 1 | displaystyle a^0 |
| 7 | displaystyle sqrt[n]{a^m} | displaystyle a^{frac{m}{n}} |
| 8 | displaystyle a^{-n} | displaystyle frac{1}{a^{n}} |
| 9 | displaystyle (frac{a}{b})^{-n} | displaystyle (frac{b}{a})^{n} |
Рассмотрим примеры решения и методы решения показательных уравнений из ЕГЭ. Они помогут вам понять, как решаются показательные уравнения и какие они могут встретиться на экзамене.
Показательная функция
- Функцию вида y=ax, где а>0, a≠1, х – любое число, называют показательной функцией.
- Область определения показательной функции: D (y)=R — множество всех действительных чисел.
- Область значений показательной функции: E (y)=R+ -множество всех положительных чисел.
- Показательная функция y=ax возрастает при a>1.
- Показательная функция y=ax убывает при 0
График показательной функции:
Решение простейших показательных уравнений вы найдете вот в этих статьях:
Решение простейших показательных уравнений
Показательные уравнения, сводящиеся к квадратным
Повторим решение показательных уравнений на примерах.
Примеры решения показательных уравнений
Метод приведения к одному основанию
Задание 1
Решите уравнение:
3^{2x-1}=27
Решение:
В левой части можно сразу получить степень с основанием 3:
3^{2x-1}=3^3
2x-1=3
2x=3+1
2x=4
x=2
Ответ: 2
Задание 2
Решить 4^{3x-1}=4 cdot 4^{5x+10}
Решение:
В правой части у нас множитель 4, представим его по формуле (4) так: 4=4^1
Нажми, чтобы посмотреть больше шагов в решении
Теперь у нас получается произведение: 4^1 cdot 4^{5x+10} По формуле (1) мы запишем степень с одним основанием вместо произведения степеней: 4^1 cdot 4^{5x+10} = 4^{1+5x+10}
и получаем:
4^{3x-1}=4^{5x+11}
Если основания степеней равны слева и справа от знака «равно», значит, равны и показатели степеней:
3x-1=5x+11
3x-5x=11+1
-2x=12
x=-6
Таким образом, -6 — корень уравнения.
Ответ: x=-6
Метод деления на степень
Задание 3
Допустим нам надо решить вот такое уравнение:
2^{5x-2}=3^{5x-2}
Решение:
Если показатели степени одинаковые, и данные степени равны, хотя их основания разные, это значит, что данные показатели равны нулю.
5x-2=0
5x=2
x=2/5
x=0,4
Однако, данное уравнение легко решается и первым методом, если мы разделим левую и правую части равенства на 3^{5x-2}. Получим:
displaystyle frac{2^{5x-2}}{3^{5x-2}}=1
По формулам (2) и (6) из таблицы, проведем преобразование: displaystyle (frac{2}{3})^{5x-2}=(frac{2}{3})^0
отсюда:
5x-2=0
x=0,4
Ответ: 0,4
Вынесение множителя за скобки
Суть метода заключается в вынесении за скобки степени с наименьшим показателем.
Чтобы решить показательное уравнение, вынеся общий множитель, можно использовать тот факт, что если два числа имеют общий множитель, то на этот множитель можно сократить, разделив оба числа на один и тот же множитель. Это можно использовать для решения экспоненциальных уравнений путем исключения общих множителей, которые появляются как в основании, так и в показателе степени уравнения.
Например, рассмотрим следующее показательное уравнение:
![]()
Чтобы решить это уравнение, мы можем вынести общий множитель ![]() , разделив обе части уравнения на
, разделив обе части уравнения на ![]() :
:
![]()
Это упрощает уравнение до:
![]()
Решением исходного уравнения является ![]() .
.
Это всего лишь один пример того, как решить показательное уравнение, вынеся общий множитель. Решим еще несколько примеров этим методом.
Пример 4
3^{3x+1}-2 cdot 3^{3x}=27
Решение: наименьшим показателем степени является 3x, вынесем за скобки 3^{3x}
3^{3x}(3-2)=27
3^{3x}=27
3^{3x}=3^3
3x=3
x=1
Ответ: x=1
Пример 5
3^{2x-1}+3^{2x-2}-3^{2x-4}=315
Решение: наименьший показатель степени: 2x-4, тогда вынесем за скобки 3^{2x-4}:
3^{2x-4}(3^3+3^2-1)=315
3^{2x-4}(27+9-1)=315
3^{2x-4} cdot 35=315
3^{2x-4}=315:35
3^{2x-4}=9
3^{2x-4}=3^2
2x-4=2
2x=6
x=3
Ответ: x=3
Метод подстановки и сведения к квадратному уравнению
Рассмотрим еще один вид показательных уравнений — это уравнения, которые можно с помощью подстановки привести к квадратному уравнению.
Пример 6
5 cdot 4^{2x}-6 cdot 4^x+1=0
Решение:
5 cdot 4^{2x}-6 cdot 4^x+1=0
Полагая 4^x=t, получим квадратное уравнение:
5 cdot t^{2}-6 cdot t+1=0
Решим его. Здесь a=5, b=-6, c=1.
Дискриминант displaystyle D=b^2-4ac=(-6)^2-4 cdot 5cdot 1=36-20=16
displaystyle sqrt{D}=4.
Используя формулу displaystyle t_{1,2}=frac{-b pm sqrt{D}}{2a}, находим:
displaystyle t_{1}=frac{-6 — 16}{10}=frac{-22}{10}=-2,2
displaystyle t_{1}=frac{-6 + 16}{10}=frac{10}{10}=1
Возвращаемся к первоначальной переменной:
- 4^x=-2,2. Это равенство невозможно, поскольку показательная функция может принимать только положительные значения.
- 4^x=1
x=0
Ответ: x=0
Пример 7
Найдите корни уравнения displaystyle 3^{2x}-4 cdot 3^{x}=45
Решение:
Выполним замену displaystyle 3^x=t:
displaystyle t^2-4t-45=0
Решим с помощью теоремы Виета:
begin{cases} t_1+t_2 = 4, \ t_1 cdot t_2=-45 end{cases}
Подбирая корни, получаем:
displaystyle t_1=-5
displaystyle t_2=9
Переходим к первоначальной переменной:
- displaystyle 3^x=-5. Такое равенство не существует, так как область значений показательной функции — положительные числа.
- displaystyle 3^x=9. Прологарифмируем данное равенство логарифмом по основанию 3.
displaystyle log_{3}{3^x}=log_{3}9
displaystyle x=2
Ответ: 2
Здесь мы использовали логарифмирование, что это такое и как это применяется к решению экспоненциальных уравнений давайте рассмотрим на примерах.
Логарифмирование
Логарифмирование обеих частей показательного уравнения — это математическая операция, которая часто используется для решения показательных уравнений.
Пример 8
Например, рассмотрим следующее показательное уравнение:
![]()
Решение: Чтобы решить это уравнение с помощью логарифмов, мы можем взять логарифм обеих частей уравнения. Это дает нам:
![]()
Поскольку логарифм степени равен показателю степени, мы можем упростить левую часть уравнения до:
![]()
Чтобы найти значение x, мы можем использовать свойство логарифмов, которое гласит, что ![]() эквивалентно
эквивалентно ![]() . В этом случае у нас есть
. В этом случае у нас есть ![]() , поэтому x=3.
, поэтому x=3.
Ответ: x=3.
Пример 9
Решить displaystyle e^{2x}=55
Решение: прологарифмируем левую и правую части равенства логарифмом по основанию e — натуральным логарифмом ln
displaystyle ln e^{2x}=ln 55
displaystyle 2x=ln 55
displaystyle x=frac{1}{2}ln 55
Ответ: displaystyle x=frac{1}{2}ln 55
Пример 10
displaystyle 3^x cdot 5^{2x}=150
Решение: Прологарифмируем левую и правую части уравнения логарифмом по основанию 150:
displaystyle log_{150}(3^x cdot 5^{2x})=log_{150}150
displaystyle log_{150}3^x+log_{150}5^{2x}=1
Нажми, чтобы посмотреть больше шагов в решении
displaystyle xlog_{150}3+2xlog_{150}5=1
displaystyle x (log_{150}3+2log_{150}5)=1
displaystyle x (log_{150}3+log_{150}5^2)=1
displaystyle x (log_{150}3 +log_{150}25)=1
displaystyle x log_{150}75=1
displaystyle x= frac{1}{log_{150}75}=log_{75}{150}
Ответ: displaystyle log_{75}{150}
Далее мы рассмотрим показательное неравенство и систему показательных уравнений и неравенств.
Степень уравнения
Кроме разделения уравнений по количеству неизвестных, уравнения также разделяются по степеням неизвестных: уравнения первой степени, уравнения второй степени и так далее.
Чтобы определить степень уравнения, в нём нужно предварительно сделать следующие преобразования:
- раскрыть скобки,
- освободить уравнение от дробных членов,
- перенести все неизвестные члены в одну из частей уравнения,
- сделать приведение подобных членов.
После выполнения всех этих преобразований, степень уравнения определяется по следующим правилам:
Степенью уравнения с одним неизвестным называется показатель при неизвестном в том члене уравнения, в котором этот показатель наибольший.
10 — x = 2 — уравнение первой степени с одним неизвестным;
x 2 + 7x = 16 — уравнение второй степени с одним неизвестным;
x 3 = 8 — уравнение третьей степени с одним неизвестным.
Степенью уравнения с несколькими неизвестными называется сумма показателей при неизвестных в том члене уравнения, в котором эта сумма наибольшая.
Для примера возьмём уравнение
Для наглядности расставим показатели первой степени (которые обычно не ставят):
3x 2 y 1 + x 1 y 1 + 25 1 = 0.
Теперь посчитаем суммы показателей для тех членов уравнения, в которых присутствуют неизвестные:
3x 2 y 1 — сумма показателей равна 2 + 1 = 3;
x 1 y 1 — сумма показателей равна 1 + 1 = 2.
Сумма показателей у первого члена уравнения больше, чем у второго, значит, при определении степени уравнения будем ориентироваться на сумму показателей первого члена. Это значит, что про данное уравнение можно сказать, что это уравнение третьей степени с двумя неизвестными.
2xy — x = 25 — уравнение второй степени с двумя неизвестным,
xy 2 — 2xy + 8y = 0 — уравнение третьей степени с двумя неизвестными.
Как решать
показательные уравнения?
Решение уравнений – навык, который необходим каждому нацеленному на успешную сдачу ЕГЭ и ОГЭ школьнику. Это поможет решить задания №5, 13 и 15 из профильного уровня математики.
Одна из их разновидностей – степенные уравнения, которые иногда также называют показательными. Основная отличительная особенность – наличие переменной (х) не в основании степени, а в самом показателе. Как это выглядит:
Не бойтесь – это самый общий вид показательных уравнений. Реальные примеры выглядят как-то так:
Внимательно посмотрите на приведенные уравнения. В каждом из них присутствует, так называемая, показательная (степенная) функция. При решении необходимо помнить об основных свойствах степени, а также использовать особые правила, помогающие вычислить значение (х). Познакомиться с понятием степени и ее свойствами можно тут и тут.
И вам понадобится умение решать обыкновенные линейные и квадратные уравнения, те, что вы проходили в 7-8 классе. Вот такие:
И так, любое уравнение, в котором вы увидите показательную (степенную) функцию, называется показательным уравнением. Кроме самой показательной функции в уравнении могут быть любые другие математические конструкции – тригонометрические функции, логарифмы, корни, дроби и т.д. Если вы видите степень, значит перед вам показательное уравнение.
Ура! Теперь знаем, как выглядят показательные уравнения, но толку от этого не очень много. Было бы неплохо научиться их решать. Отличная новость – на наш взгляд показательные уравнения одни из самых простых типов уравнений, по сравнению с логарифмическими, тригонометрическими или иррациональными.
Простейшие показательные уравнения
Давайте начнем с самых простых типов уравнений и разберем сразу несколько примеров:
Что такое решить уравнение? Это значит, что нужно найти такое число, которое при подстановке в исходное уравнение вместо (х) даст верное равенство. В нашем примере нужно найти такое число, в которое нужно возвести двойку, чтобы получить восемь. Ну это просто:
Значит, если (х=3), то мы получим верное равенство, а значит мы решили уравнение.
Решим что-нибудь посложнее.
Такое уравнение выглядит сложнее. Попробуем преобразовать правую часть уравнения:
Мы применили свойство отрицательной степени по формуле:
Теперь наше уравнение будет выглядеть так:
Заметим, что слева и справа у нас стоят показательные функции, и там, и там основания одинаковые и равны (3), только вот степени разные – слева степень ((4х-1)), а справа ((-2)). Логично предположить, что если степени у такой конструкции будут равны, при условии, что основания одинаковые, то мы получим верное равенство. Так и поступим:
Такое мы решать умеем, ведь это обыкновенное линейное уравнение.
Поздравляю, мы нашли корень нашего показательного уравнения.
Попробуем поступить так, как в предыдущем примере – преобразуем левую и правую часть, чтобы слева и справа была показательная функция с одинаковым основанием. Как это сделать? Обращаем внимание, что (125=5*5*5=5^3), а (25=5*5=5^2), подставим:
Воспользуемся одним из свойств степеней ((a^n)^m=a^):
И опять мы получили две показательные функции, у которых одинаковые основания и для того, чтобы равенство выполнялось, необходимо приравнять из степени:
И еще один пример:
Те, кто хорошо знает свойства степеней, знают, что показательная функция не может быть отрицательной. Действительно, попробуйте возводить (2) в различную степень, вы никогда не сможете получить отрицательное число.
Внимание! Показательная функция не может быть отрицательной, поэтому, когда вы встречаете примеры на подобии примера 4, то знайте, что такого быть не может. Здесь корней нет, потому что показательная функция всегда положительна.
Теперь давайте разработаем общий метод решения показательных уравнений. И научимся решать более сложные примеры.
Общий метод решения показательных уравнений
Пусть у нас есть вот такой пример:
Где (a,b) какие-то положительные числа. ((a>0, ; b>0).
Согласно разобранным выше примерам, логично предположить, что для того, чтобы решить данное уравнение, нужно его преобразовать к виду, где слева и справа стоят показательные функции с одинаковым основанием. Так и поступим.
Слева у нас уже стоит (a^x), с этим ничего делать не будем, а вот справа у нас стоит загадочное число (b), которое нужно попытаться представить в виде (b=a^m). Тогда уравнение принимает вид:
Раз основания одинаковые, то мы можем просто приравнять степени:
Вот и весь алгоритм решения. Просто нужно преобразовать исходное уравнение таким образом, чтобы слева и справа стояли показательные функции с одинаковыми основаниями, тогда приравниваем степени и вуаля – сложное показательное уравнение решено. Осталось только разобраться, как так преобразовывать. Опять разберем на примерах:
Замечаем, что (16=2*2*2*2=2^4) это степень двойки:
Основания одинаковые, значит можно приравнять степени:
$$x=4.$$
Пример 6 $$5^<-x>=125 Rightarrow 5^<-x>=5*5*5 Rightarrow 5^<-x>=5^3 Rightarrow –x=3 Rightarrow x=-3.$$
Пример 7 $$9^<4x>=81 Rightarrow (3*3)^<4x>=3*3*3*3 Rightarrow(3^2)^<4x>=3^4 Rightarrow 3^<8x>=3^4 Rightarrow 8x=4 Rightarrow x=frac<1><2>.$$
Здесь мы заметили, что (9=3^2) и (81=3^4) являются степенями (3).
Все здорово, но проблема в том, что такая схема решения показательных уравнений работает не всегда. Что делать, если привести к одинаковому основанию не получается. Например:
(3) и (2) привести к одинаковому основанию затруднительно. Но тем не менее мы должны это сделать. Воспользуемся следующей схемой преобразований: пусть есть некоторое положительное число (b>0), тогда его можно представить в виде степени любого, нужного вам, положительного числа не равного единице (a>0, ; a neq 1):
Эта очень важная формула, рекомендуем ее выучить. Вернемся к нашему примеру и по формуле представим (2) в виде (3) в какой-то степени, где (a=3), а (b=2):
Подставим данное преобразование в наш пример:
Получили равенство двух показательных функций с одинаковым основанием, значит можем приравнять их степени:
Так в ответ и запишем. Никакой ошибки здесь нет, дело в том, что такие логарифмы можно посчитать только на калькуляторе, поэтому на ЕГЭ или в контрольной работе вы просто оставляете ответ в таком виде.
Кто забыл, что такое логарифм, можно посмотреть здесь.
Рассмотрим еще несколько аналогичных примеров.
Те, кто хорошо знает свойства логарифмов, могут поиграться с последней формулой и получить ответ в разном виде:
Все эти варианты ответа верные, их можно смело писать в ответ.
И так, мы с вами научились решать любые показательные уравнения вот такого вида: (a^x=b), где (a>0; ; b>0).
Но это еще далеко не все. Часто вы будете встречать показательные уравнения гораздо более сложного типа. В ЕГЭ по профильной математике это номер 15 из 2й части. Но бояться тут не нужно, все на первый взгляд сложные уравнения при помощи обычно не самых сложных преобразований сводятся к уравнениям типа (a^x=b), где (a>0; ; b>0). Рассмотрим типы сложных уравнений, которые могут попасться:
Решение показательных уравнений при помощи замены
Самое первое, что вы должны всегда делать, это пытаться привести все имеющиеся показательные функции к одинаковому основанию.
Здесь это сделать легко, замечаем, что (9=3^2), тогда (9^x=(3^2)^x=3^<2x>=(3^x)^2). Здесь мы воспользовались свойством степеней: ((a^n)^m=a^). Подставим:
Обратим внимание, что во всем уравнении все (х) «входят» в одинаковую функцию — (3^x). Сделаем замену (t=3^x, ; t>0), так как показательная функция всегда положительна.
Квадратное уравнение, которое решается через дискриминант:
Оба корня больше нуля, значит оба нам подходят. Сделаем обратную замену и уравнение сводится к решению двух простых показательных уравнений:
И второй корень:
И еще один пример на замену:
Воспользуемся нашим правилом, что все нужно приводить к одинаковому основанию – а стоп, тут и так у всех показательных функций основание (3). Давайте еще внимательно посмотрим на наш пример, очень похоже на то, что он тоже делается через замену. Но у нас тут нет одинаковых показательных функций, основания то одинаковые, а вот степени отличаются. Но если быть внимательным, то можно заметить, что в первой степени можно разбить свободный член (3=2+1) и вынести общий множитель (2):
Подставим в исходное уравнение:
Теперь показательные функции одинаковы и можно сделать замену:
Обратная замена, и наше уравнение сводится к простейшему:
И второе значение (t):
Тут у нас две показательные функции с основаниями (7) и (3), и как сделать из них одинаковые основания непонятно. Этот пример решается при помощи деления. Давайте поделим все наша уравнение на (3^x):
Здесь нам придется воспользоваться свойствами степеней:
Разберем каждое слагаемое:
Теперь подставим получившееся преобразования в исходное уравнение:
Теперь видно, что в нашем уравнении есть одинаковая функция, которую можно убрать в замену (t=(frac<7><3>)^x):
Сделаем обратную замену:
И последний пример на замену:
Первым делом нужно сделать так, чтобы все показательные функции были с одинаковым основанием и в идеале с одинаковой степенью. Для этого нам понадобятся формулы для степеней:
Разберем каждое слагаемое нашего уравнения:
Все десятичные дроби всегда разумно представить в виде обыкновенных дробей. И будьте внимательны — отрицательная степень не имеет никакого отношения к знаку показательной функции!
И последнее слагаемое со степенью:
Подставим все наши преобразования в исходное уравнение:
Теперь можно сделать замену (t=2^x) или можно обойтись без замены, просто приведя подобные слагаемые (вынести общий множитель (2^x)):
Особенно стоит подчеркнуть прием, который мы использовали при решении 13-го примера. Всегда старайтесь избавляться от десятичных дробей. Переводите их в обыкновенные дроби.
И другой тип степенных уравнений, где обычно не нужно делать замену, а необходимо отлично знать все свойства степеней, некоторые из них мы уже обсудили выше. Все про свойства степеней можно посмотреть тут
Вот такое уравнение, в котором у нас, во-первых, показательных функции перемножаются, а еще хуже то, что у них у всех разные основания. Катастрофа, а не пример. Но ничего, все не так страшно, как кажется. Внимательно посмотрите на основания: у нас есть в основании (2), (5) и (10). Очевидно, что (10=2*5). Воспользуемся этим и подставим в наше уравнение:
Воспользуемся формулой ((a*b)^n=a^n*b^n):
И перекинем все показательные функции с основанием (2) влево, а с основанием (5) вправо:
Сокращаем и воспользуемся формулами (a^n*a^m=a^) и (frac=a^):
Самая главная идея при решении показательных уравнений – это любыми доступными способами свести все имеющиеся степенные функции к одинаковому основанию. А еще лучше и к одинаковой степени. Вот почему необходимо знать все свойства степеней, без этого решить уравнения будет проблематично.
Как же понять, где какие преобразования использовать? Не бойтесь, это придет с опытом, чем больше примеров решите, тем увереннее будете себя чувствовать на контрольных в школе или на ЕГЭ по профильной математике. Сначала потренируйтесь на простых примерах и постепенно повышайте уровень сложности. Успехов в изучении математики!
Степенные или показательные уравнения.
Для начала вспомним основные формулы степеней и их свойства.
Произведение числа a само на себя происходит n раз, это выражение мы можем записать как a•a•…•a=a n
3. a n • a m = a n + m
5. a n b n = (ab) n
7. a n /a m = a n — m
Степенные или показательные уравнения – это уравнения в которых переменные находятся в степенях (или показателях), а основанием является число.
Примеры показательных уравнений:
В данном примере число 6 является основанием оно всегда стоит внизу, а переменная x степенью или показателем.
Приведем еще примеры показательных уравнений.
2 x *5=10
16 x — 4 x — 6=0
Теперь разберем как решаются показательные уравнения?
Возьмем простое уравнение:
Такой пример можно решить даже в уме. Видно, что x=3. Ведь чтобы левая и правая часть были равны нужно вместо x поставить число 3.
А теперь посмотрим как нужно это решение оформить:
Для того, чтобы решить такое уравнение, мы убрали одинаковые основания (то есть двойки) и записали то что осталось, это степени. Получили искомый ответ.
Теперь подведем итоги нашего решения.
Алгоритм решения показательного уравнения:
1. Нужно проверить одинаковые ли основания у уравнения справа и слева. Если основания не одинаковые ищем варианты для решения данного примера.
2. После того как основания станут одинаковыми, приравниваем степени и решаем полученное новое уравнение.
Теперь прорешаем несколько примеров:
Начнем с простого.
Основания в левой и правой части равны числу 2, значит мы можем основание отбросить и приравнять их степени.
x+2=4 Получилось простейшее уравнение.
x=4 — 2
x=2
Ответ: x=2
В следующем примере видно, что основания разные это 3 и 9.
Для начала переносим девятку в правую сторону, получаем:
Теперь нужно сделать одинаковые основания. Мы знаем что 9=3 2 . Воспользуемся формулой степеней (a n ) m = a nm .
Получим 9 х+8 =(3 2 ) х+8 =3 2х+16
3 3х = 3 2х+16 теперь видно что в левой и правой стороне основания одинаковые и равные тройке, значит мы их можем отбросить и приравнять степени.
3x=2x+16 получили простейшее уравнение
3x — 2x=16
x=16
Ответ: x=16.
Смотрим следующий пример:
2 2х+4 — 10•4 х = 2 4
В первую очередь смотрим на основания, основания разные два и четыре. А нам нужно, чтобы были — одинаковые. Преобразовываем четверку по формуле (a n ) m = a nm .
4 х = (2 2 ) х = 2 2х
И еще используем одну формулу a n • a m = a n + m :
2 2х+4 = 2 2х •2 4
Добавляем в уравнение:
2 2х •2 4 — 10•2 2х = 24
Мы привели пример к одинаковым основаниям. Но нам мешают другие числа 10 и 24. Что с ними делать? Если приглядеться видно, что в левой части у нас повторяется 2 2х ,вот и ответ — 2 2х мы можем вынести за скобки:
2 2х (2 4 — 10) = 24
Посчитаем выражение в скобках:
2 4 — 10 = 16 — 10 = 6
Все уравнение делим на 6:
Представим 4=2 2 :
2 2х = 2 2 основания одинаковые, отбрасываем их и приравниваем степени.
2х = 2 получилось простейшее уравнение. Делим его на 2 получаем
х = 1
Ответ: х = 1.
9 х – 12*3 х +27= 0
Преобразуем:
9 х = (3 2 ) х = 3 2х
Получаем уравнение:
3 2х — 12•3 х +27 = 0
Основания у нас одинаковы равны трем.В данном примере видно, что у первой тройки степень в два раза (2x) больше, чем у второй (просто x). В таком случаем можно решить методом замены. Число с наименьшей степенью заменяем:
Тогда 3 2х = (3 х ) 2 = t 2
Заменяем в уравнении все степени с иксами на t:
t 2 — 12t+27 = 0
Получаем квадратное уравнение. Решаем через дискриминант, получаем:
D=144-108=36
t1 = 9
t2 = 3
Возвращаемся к переменной x.
3 х = 9
3 х = 3 2
х1 = 2
Один корень нашли. Ищем второй, из t2:
t2 = 3 = 3 х
3 х = 3 1
х2 = 1
Ответ: х1 = 2; х2 = 1.
На сайте Вы можете в разделе ПОМОГИТЕ РЕШИТЬ задавать интересующие вопросы мы Вам обязательно ответим.
http://sigma-center.ru/exponential_equations
http://tutomath.ru/uroki/stepennye-pokazatelnye-uravneniya.html