Как вычислить большую степень?
Онлайн калькулятор разложения Шенкса (задача дискретного логарифмирования) выдал подобные результаты.
2^(1⋅24) ≡ 265(mod541)
2^(2⋅24) ≡ 436(mod541)
.
Заранее могу сказать, что посчитал он правильно, однако сам способ вычисления я совершенно не понял.
Какие подходы задействованы для вычисления:
а) большой степени
б) откуда взялось деление с остатком?
в) не понял суть знака «тождественно равно» (вики прочитал, но разницы от обычного знака равенства не уяснил)
- Вопрос задан более трёх лет назад
- 5101 просмотр
- Вконтакте
Большую степень не вычисляют в лоб, тем более, что при выполнении действий в модульной арифметике её не нужно хранить целиком, достаточно хранить остаток от деления на известное постоянное число. Знак «тождественное равенство» используется как знак равенства в модульной арифметике, если модуль указан отдельно, поскольку сами числа, естественно, не равны.
Дискретное логарифмирование — формально, задача на пространстве решений, на котором можно применять модульную арифметику над многочленами или числами, с некоторым простым числом в качестве размера множества, частного для деления по модулю и вообще.
Саму степень по модулю можно вычислить довольно простым образом: Вначале раскладываем показатель на двоичные составляющие: 2*24 = 48 = 32+16 = 2^5+2^4. Потом пользуемся двумя тождествами: Первое x^(a+b)=x^a*x^b — произведение степеней одного числа равно степени числа в сумме показателей (забыл точное название). Второе (x*y) mod n = (x mod n)*(y mod n) — неважно, когда брать остаток, в начале или в конце. В итоге возведение числа 2 в большую степень по модулю N выполняется так: в результат заносится 1, в аргумент 2, потом в цикле по разрядам показателя если текущий двоичный разряд показателя 1, результат множится на аргумент и берется остаток по модулю N, который кладется в результат, а аргумент потом умножается на себя и остаток аргумента по модулю N кладется в аргумент.
Итого: аргумент принимает последовательно значения 2, 4, 16, 256, 65536 mod 541 = 75, 75*75 mod 541 = 215, а результат — 1, 1, 1, 1, 75, 75*215 mod 541 = 436.
Как посчитать число в большой степени
Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.
Понятие возведения в степень
Начнем с формулирования базовых определений.
Возведение в степень – это вычисление значения степени некоторого числа.
То есть слова «вычисление значение степени» и «возведение в степень» означают одно и то же. Так, если в задаче стоит «Возведите число 0 , 5 в пятую степень», это следует понимать как «вычислите значение степени ( 0 , 5 ) 5 .
Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.
Как возвести число в натуральную степень
Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n -ного числа множителей, каждый из которых равен a . Это можно записать так:
Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.
Условие: возведите – 2 в степень 4 .
Решение
Используя определение выше, запишем: ( − 2 ) 4 = ( − 2 ) · ( − 2 ) · ( − 2 ) · ( − 2 ) . Далее нам нужно просто выполнить указанные действия и получить 16 .
Возьмем пример посложнее.
Вычислите значение 3 2 7 2
Решение
Данную запись можно переписать в виде 3 2 7 · 3 2 7 . Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.
Выполним эти действия и получим ответ: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49
Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.
Выполните возведение в квадрат числа π .
Решение
Для начала округлим его до сотых. Тогда π 2 ≈ ( 3 , 14 ) 2 = 9 , 8596 . Если же π ≈ 3 . 14159 , то мы получим более точный результат: π 2 ≈ ( 3 , 14159 ) 2 = 9 , 8695877281 .
Отметим, что необходимость высчитывать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени ( ln 6 ) 3 или преобразовать, если это возможно: 5 7 = 125 5 .
Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:
Это понятно из записи 
От основания степени это не зависит.
Так, ( − 9 ) 1 = − 9 , а 7 3 , возведенное в первую степень, останется равно 7 3 .
Как возвести число в целую степень
Для удобства разберем отдельно три случая: если показатель степени – целое положительное число, если это ноль и если это целое отрицательное число.
В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.
Теперь посмотрим, как правильно возводить в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1 . Ранее мы уже поясняли, что 0 -я степень a может быть определена для любого действительного числа, не равного 0 , и a 0 = 1 .
5 0 = 1 , ( – 2 , 56 ) 0 = 1 2 3 0 = 1
0 0 – не определен.
У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1 a z , где а – любое число, а z – целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач.
Возведите 2 в степень – 3 .
Решение
Используя определение выше, запишем: 2 – 3 = 1 2 3
Подсчитаем знаменатель этой дроби и получим 8 : 2 3 = 2 · 2 · 2 = 8 .
Тогда ответ таков: 2 – 3 = 1 2 3 = 1 8
Возведите 1 , 43 в степень – 2 .
Решение
Переформулируем: 1 , 43 – 2 = 1 ( 1 , 43 ) 2
Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:
В итоге у нас вышло ( 1 , 43 ) – 2 = 1 ( 1 , 43 ) 2 = 1 2 , 0449 . Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).
Ответ: ( 1 , 43 ) – 2 = 10000 20449
Отдельный случай – возведение числа в минус первую степень. Значение такой степени равно числу, обратному исходному значению основания: a – 1 = 1 a 1 = 1 a .
Пример: 3 − 1 = 1 / 3
9 13 – 1 = 13 9 6 4 – 1 = 1 6 4 .
Как возвести число в дробную степень
Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: a m n = a m n при любом положительном a , целом m и натуральном n .
Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n -ной степени.
У нас есть равенство a m n = a m n , которое, учитывая свойства корней, обычно применяется для решения задач в виде a m n = a n m . Это значит, что если мы возводим число a в дробную степень m / n , то сначала мы извлекаем корень n -ной степени из а , потом возводим результат в степень с целым показателем m .
Проиллюстрируем на примере.
Вычислите 8 – 2 3 .
Решение
Способ 1. Согласно основному определению, мы можем представить это в виде: 8 – 2 3 = 8 – 2 3
Теперь подсчитаем степень под корнем и извлечем корень третьей степени из результата: 8 – 2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4
Способ 2. Преобразуем основное равенство: 8 – 2 3 = 8 – 2 3 = 8 3 – 2
После этого извлечем корень 8 3 – 2 = 2 3 3 – 2 = 2 – 2 и результат возведем в квадрат: 2 – 2 = 1 2 2 = 1 4
Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.
Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.
Возведите 44 , 89 в степень 2 , 5 .
Решение
Преобразуем значение показателя в обыкновенную дробь – 44 , 89 2 , 5 = 49 , 89 5 2 .
А теперь выполняем по порядку все действия, указанные выше: 44 , 89 5 2 = 44 , 89 5 = 44 , 89 5 = 4489 100 5 = 4489 100 5 = 67 2 10 2 5 = 67 10 5 = = 1350125107 100000 = 13 501 , 25107
Ответ: 13 501 , 25107 .
Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями – довольно сложная работа. Для нее обычно требуется вычислительная техника.
Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0 m n можно придать такой смысл: если m n > 0 , то 0 m n = 0 m n = 0 ; если m n 0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0 7 12 = 0 , 0 3 2 5 = 0 , 0 0 , 024 = 0 , а в целую отрицательную – значения не имеет: 0 – 4 3 .
Как возвести число в иррациональную степень
Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
Если нам нужно вычислить значение степени a с иррациональным показателем a , то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:
Вычислите приближенное значение 21 , 174367 .
Решение
Ограничимся десятичным приближением a n = 1 , 17 . Проведем вычисления с использованием этого числа: 2 1 , 17 ≈ 2 , 250116 . Если же взять, к примеру, приближение a n = 1 , 1743 , то ответ будет чуть точнее: 2 1 , 174367 . . . ≈ 2 1 , 1743 ≈ 2 , 256833 .
Онлайн калькулятор разложения Шенкса (задача дискретного логарифмирования) выдал подобные результаты.
2^(1⋅24) ≡ 265(mod541)
2^(2⋅24) ≡ 436(mod541)
.
Заранее могу сказать, что посчитал он правильно, однако сам способ вычисления я совершенно не понял.
Какие подходы задействованы для вычисления:
а) большой степени
б) откуда взялось деление с остатком?
в) не понял суть знака «тождественно равно» (вики прочитал, но разницы от обычного знака равенства не уяснил)
- Вопрос задан более года назад
- 602 просмотра
Большую степень не вычисляют в лоб, тем более, что при выполнении действий в модульной арифметике её не нужно хранить целиком, достаточно хранить остаток от деления на известное постоянное число. Знак «тождественное равенство» используется как знак равенства в модульной арифметике, если модуль указан отдельно, поскольку сами числа, естественно, не равны.
Дискретное логарифмирование – формально, задача на пространстве решений, на котором можно применять модульную арифметику над многочленами или числами, с некоторым простым числом в качестве размера множества, частного для деления по модулю и вообще.
Саму степень по модулю можно вычислить довольно простым образом: Вначале раскладываем показатель на двоичные составляющие: 2*24 = 48 = 32+16 = 2^5+2^4. Потом пользуемся двумя тождествами: Первое x^(a+b)=x^a*x^b – произведение степеней одного числа равно степени числа в сумме показателей (забыл точное название). Второе (x*y) mod n = (x mod n)*(y mod n) – неважно, когда брать остаток, в начале или в конце. В итоге возведение числа 2 в большую степень по модулю N выполняется так: в результат заносится 1, в аргумент 2, потом в цикле по разрядам показателя если текущий двоичный разряд показателя 1, результат множится на аргумент и берется остаток по модулю N, который кладется в результат, а аргумент потом умножается на себя и остаток аргумента по модулю N кладется в аргумент.
Итого: аргумент принимает последовательно значения 2, 4, 16, 256, 65536 mod 541 = 75, 75*75 mod 541 = 215, а результат – 1, 1, 1, 1, 75, 75*215 mod 541 = 436.
Предлагаем попробовать наш калькулятор степеней, который поможет возвести в степень онлайн любое число.
Использовать калькулятор очень просто — введите число, которое вы хотите возвести в степень, а затем число — степень и нажмите на кнопку «Посчитать».
Примечательно то, что наш онлайн калькулятор степеней может возвести в степень как положительную, так и отрицательную. А для извлечения корней на сайте есть другой калькулятор.
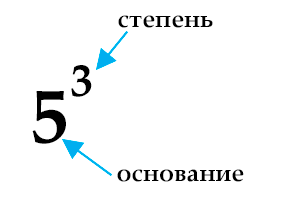
Как возвести число в степень.
Давайте рассмотрим процесс возведения в степень на примере. Пусть нам необходимо возвести число 5 в 3-ю степень. На языке математики 5 — это основание, а 3 — показатель (или просто степень). И записать это можно кратко в таком виде:
Возведение в степень
А чтобы найти значение, нам будет необходимо число 5 умножить на себя 3 раза, т. е.
5 3 = 5 x 5 x 5 = 125
Соответственно, если мы хотим найти значение числа 7 в 5 степени, мы должны число 7 умножить на себя 5 раз, т. е. 7 x 7 x 7 x 7 x 7. Другое дело когда требуется возвести число в отрицательную степень.
Как возводить в отрицательную степень.
При возведении в отрицательную степень необходимо использовать простое правило:
как возводить в отрицательную степень
Все очень просто — при возведении в отрицательную степень мы должны поделить единицу на основание в степени без знака минус — т. е. в положительной степени. Таким образом, чтобы найти значение
2 -3
Возвести в степень (по модулю) + большие числа


alt=»✔» />Заполняем необходимые данные целыми числами, отвечая на вопросы формы.
alt=»✔» />Жмем кнопку вычислить и получаем результат.
alt=»ℹ» />Галочка «по модулю» позволяет указать модуль, по которому необходимо возводить в степень.
alt=»ℹ» />Галочка «с решением» позволяет получить этапы вычисления: каким образом число возводилось в степень.




Алгоритм быстрого возведения в степень (по модулю).

где a, x, m — натуральные числа. Далее считаем, что a < m. Запись у = b (mod m) означает, что у ≡ b (mod m) и 0 ≤ у < m, т.е, y — наименьший неотрицательный вычет по модулю m, лежащий в том классе, что и b.

то нужно выполнить (x — 1) умножение в кольце Zm, Если n — количество разрядов в двоичной записи х, то число умножений не меньше, чем 2 n-1.

Определим целые аj по реккурентным формулам

1. Вычисляем aj (0 ≤ j ≤ n — 1) по формулам (2),














Большую степень не вычисляют в лоб, тем более, что при выполнении действий в модульной арифметике её не нужно хранить целиком, достаточно хранить остаток от деления на известное постоянное число. Знак «тождественное равенство» используется как знак равенства в модульной арифметике, если модуль указан отдельно, поскольку сами числа, естественно, не равны.
Дискретное логарифмирование — формально, задача на пространстве решений, на котором можно применять модульную арифметику над многочленами или числами, с некоторым простым числом в качестве размера множества, частного для деления по модулю и вообще.
Саму степень по модулю можно вычислить довольно простым образом: Вначале раскладываем показатель на двоичные составляющие: 2*24 = 48 = 32+16 = 2^5+2^4. Потом пользуемся двумя тождествами: Первое x^(a+b)=x^a*x^b — произведение степеней одного числа равно степени числа в сумме показателей (забыл точное название). Второе (x*y) mod n = (x mod n)*(y mod n) — неважно, когда брать остаток, в начале или в конце. В итоге возведение числа 2 в большую степень по модулю N выполняется так: в результат заносится 1, в аргумент 2, потом в цикле по разрядам показателя если текущий двоичный разряд показателя 1, результат множится на аргумент и берется остаток по модулю N, который кладется в результат, а аргумент потом умножается на себя и остаток аргумента по модулю N кладется в аргумент.
Итого: аргумент принимает последовательно значения 2, 4, 16, 256, 65536 mod 541 = 75, 75*75 mod 541 = 215, а результат — 1, 1, 1, 1, 75, 75*215 mod 541 = 436.
Как возвести в большую степень
Самое обыкновенное возведение числа в степень нередко вызывает сложности у программ и калькуляторов, если значение степени достаточно велико. Существует несколько приемов, необходимых для того, чтобы заставить калькулятор посчитать правильный результат.

Вам понадобится
- компьютер
- программа-калькулятор
Инструкция
Откройте программу-калькулятор на вашем компьютере. Введите число A, которое нужно возвести в большую степень N. Попробуйте произвести возведение в степень. В большинстве случаев программа-калькулятор успешно справится с заданием и выдаст результат на экран. Однако, прямой метод не всегда срабатывает. Программы-калькуляторы часто написаны не самым лучшим образом и могут не справляться с рядом простых с виду задач. Именно к таким задачам относится возведение в большую степень. Например, для значения N = 10000000000 калькулятор Windows отказывается считать результат, а калькулятор Ubuntu просто зависает.
Разложите показатель степени N на несколько множителей, каждый из которых не превышает по значению 100000. С таким показателем большинство калькуляторов успешно справится. Если один из множителей окажется дробным числом, ничего страшного. Например, показатель степени 333333333 можно разложить на множители 100000 и 3333,33333.
Согласно формуле A^(N1*N2) = (A^N1)^N2 последовательно возведите основание А в степени, равные полученным на предыдущем шаге множителям. Например, сначала возведите число А в степень 100000, а затем получившийся результат возведите в степень 3333,33333. После этих расчетов вы получите необходимый вам результат.
Видео по теме
Обратите внимание
Если один из множителей получился дробным, а основание степени является отрицательным числом, программа-калькулятор не позволит вам произвести возведение отрицательного числа в дробную степень. В этом случае возводите модуль основания в нужную вам степень, а потом, если потребуется, измените знак результата. Результат должен быть отрицательным, если степень является нечетным числом.
Полезный совет
Если значение А близко к единице, а N очень велико, воспользуйтесь формулой (1 + 1/A)^N -> e. Например, 1,000005^200000 приблизительно равняется числу е.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Возвести в степень
❓Инструкция










📖 Теория
Алгоритм быстрого возведения в степень (по модулю).

где a, x, m — натуральные числа. Далее считаем, что a < m. Запись у = b (mod m) означает, что у ≡ b (mod m) и 0 ≤ у < m, т.е, y — наименьший неотрицательный вычет по модулю m, лежащий в том классе, что и b.

то нужно выполнить (x — 1) умножение в кольце Zm, Если n — количество разрядов в двоичной записи х, то число умножений не меньше, чем 2n-1.

Определим целые аj по реккурентным формулам

1. Вычисляем aj (0 ≤ j ≤ n — 1) по формулам (2),
2. Вычисляем y = a0x0 a1x1 … an-1xn-1 (mod m).

➕ Примеры












|
rash
Гость |
Требуется возвести целое число, скажем, 17 в степень, например, 300. |
||
|
|
ysv_
Помогающий |
Я считаю, что лучше использовать массив целых чисел. И выполнять умножение аналогично ручному умножению в столбик. Только вот хранить элементы числа в массиве удобнее в обратном порядке. int n[300]; Код не тестирован. Каждый элемент массива представляет собой число от 0 до 2147483647 (то есть цифру в 2147483648 системе счисления). |
||
|
|
Dimka
Деятель
|
ysv, не рационально по памяти, когда не требуется точность представления. Лучше уж реализовать собственный тип вещественных с плавающей запятой, в которой порядок велик и описывается, например, числом типа int. |
||
Программировать — значит понимать (К. Нюгард) |
|
ysv_
Помогающий |
Так это я предложил один из вариантов решения. Все же лучше чем string использовать. |
||
|
|
rash
Гость |
Код протестировал и немного поправил int n[300]; на long int n[300]; Но всё равно, Каждый элемент массива представляет собой число от 0 до 2147483647 и может содержать значение не более, чем 17^7 т.е. 410338673 или не более, чем 32 бита. Как только значение выходит за диапазон long int, элементы массива содержат случайные значения. |
||
|
|
rash
Гость |
Лучше уж реализовать собственный тип вещественных с плавающей запятой Речь идёт о типе class? |
||
|
|
Dimka
Деятель
|
Речь идёт о типе class? Если вы не совсем (или совсем не) знакомы с классами, то лучше поищите себе другие учебные задания. Поскольку классы — это отдельная большая тема для разговора, к представлению больших чисел имеющая косвенное отношение. P.S. Не знаю точно, о каком языке программирования идёт речь. но в C++ для 32-хразрядных машин тип double поддерживает значения порядка до 308 с 15 цифрами мантисы (максимум 1.7E+308). |
||
Программировать — значит понимать (К. Нюгард) |
|
rash
Гость |
C++ для 32-хразрядных машин тип double поддерживает значения порядка до 308 с 15 цифрами мантисы (максимум 1.7E+308). Не могу с вами не согласиться. |
||
|
|
Dimka
Деятель
|
17^300 Для начала, вы видите разницу между 17^300 и 17E+300? но представление результата в scientific format нежелательно. Тогда только через последовательность целых чисел. P.S. А зачем строка со столькими цифрами? Хотите поразить чьё-то воображение? |
||
Программировать — значит понимать (К. Нюгард) |
|
ysv_
Помогающий |
Как только значение выходит за диапазон long int, элементы массива содержат случайные значения. Уверен??? |
||
|
|
rash
Гость |
Как только значение выходит за диапазон long int, элементы массива содержат случайные значения. Сделал пошаговое выполнение программы и вот что получил при i = 16, Первое значение массива, это то, что получилось, когда 17 возводится в 8 степень. |
||
|
|
rash
Гость |
…вы видите разницу между 17^300 и 17E+300? разница заключается в том, что выполнив эти две операции, мы получим совершенно различные значения Тогда только через последовательность целых чисел. Я не представляю себе, как это реализовать Хотите поразить чьё-то воображение? Нет, ничего воображения я поражать этой задачей не хочу. Эта операция часть программы, целью которой является проверка полученных знаний по СС++ |
||
|
|
Dimka
Деятель
|
Эта операция часть программы, целью которой является проверка полученных знаний по СС++ Если вы не знаете про классы, то не знаете C++. Я уже советовал подобрать другую задачу. Я не представляю себе, как это реализовать К C/C++ это не имеет ни малейшего отношения. Это обычное знание математики и структур данных. разница заключается в том, что выполнив эти две операции, мы получим совершенно различные значения Разница заключается в том, что 17E+300 — это не операция, а 17^300 — это не форма представления числа в языке программирования C/C++. |
||
Программировать — значит понимать (К. Нюгард) |
|
RXL
Технический
|
rash, см.: #define SIZE 2 unsigned long x[SIZE] = { 0x6299ADA1, 0x000001D5 }; // 17^10 = 2015993900449 = 0x01D56299ADA1 void add(unsigned long * dst, unsigned long * src) for (i = SIZE * 2 — 1; i >= 0; i—) x += y + cf; if (i & 1) add(x, y); Пример из головы — не проверял. |
||
… мы преодолеваем эту трудность без синтеза распределенных прототипов. (с) Жуков М.С. |
|
x77
Команда клуба меняю стакан шмали на обратный билет с Марса. |
не знаю, как это будет в сях, но на паскале можно просто сделать динамически массив из сета. т.е. массив заранее неизвестной длины, в котором каждая ячейка принимает значения от 0 до 9 (это лдя любителей классики). а в принципе никто не мешает юзать уже готовый pchar — по сути, тот же динамический массив. решение задачи сводится к написанию функции для работы и отображения этого типа. |
||
|
|
Dimka
Деятель
|
но на паскале можно просто сделать динамически массив из сета. т.е. массив заранее неизвестной длины Нет, паскалевский set — это всего лишь множество битов, где каждый бит соответствует одному элементу множества (в порядке перечисления этих элементов). Т.е. set of 0..9 есть 10 битов, каждый из которых определяет, включена ли цифра во множество или нет. Бит же, как известно, имеет лишь 2 значения. |
||
Программировать — значит понимать (К. Нюгард) |
|
RXL
Технический
|
В некотором плане рулят ассемблерные вставки, но это не переносимо. push esi Кажись так. |
||
… мы преодолеваем эту трудность без синтеза распределенных прототипов. (с) Жуков М.С. |
|
rash
Гость |
поясните, пожалуйста, код с переносом бита |
||
|
|
x77
Команда клуба меняю стакан шмали на обратный билет с Марса. |
но на паскале можно просто сделать динамически массив из сета. т.е. массив заранее неизвестной длины Нет, паскалевский set — это всего лишь множество битов, где каждый бит соответствует одному элементу множества (в порядке перечисления этих элементов). Т.е. set of 0..9 есть 10 битов, каждый из которых определяет, включена ли цифра во множество или нет. Бит же, как известно, имеет лишь 2 значения. совершенно верно. т.е. имеется нечто типа TBits = (One, two, fre, four….), из которого и организуется динамический массив TArray = array of Bits. проще, конечно, объявить array of byte, но тогда и делать это всё имеет смысл в 256-ричной системе счисления, иначе для каждого знака каждого большого числа мы будем хранить избыточные данные. |
||
|
|
Dimka
Деятель
|
из которого и организуется динамический массив TArray = array of Bits. Это уже Object Pascal из Delphi. В Borland Pascal 7.0 нет ни динамических массивов, ни типа Bit, не говоря уже о «каноническом» Паскале. |
||
Программировать — значит понимать (К. Нюгард) |
|
x77
Команда клуба меняю стакан шмали на обратный билет с Марса. |
тип Bit — это мой тип, букву пропустил одну. я ж писал — TBits = (..); type вполне себе компилябельная конструкция. динамических массивов как типа данных в классике действительно нет, но они там всю жизнь благополучно реализуются |
||
|
|
tishka17
Участник Не разбрасывайте мусор |
Да ну вас. Развели болтовню. Это ж стандартная школьно-олимпиадная задачка. (я в своё время возводил 3 в 512 степегь). Стандартное решение через массивы, по принципу умножения столбиком. |
||
//1001101010110100010100110011101111000010110111010101110011 |
|
npak
Команда клуба
|
Ответ: (вывод разбит в колонку по 50 символов) Вычислено в стандартном юниксовом калькуляторе bc. Эта задача состоит из трёх частей — представление больших целых чисел, перемножение больших чисел и возведение в степень. Идея использовать массив десятичных цифр для представления больших чисел имеет одно (но зато какое!) преимущество перед шестнадцатиричным представлением — десятичное готово для вывода на печать. Попробуйте преобразовать шестнадцатиричное число размером 300 шестнадцатиричных цифр в десятичное. Это фокус, сравнимый по сложности с возведением в степень 300. Вторая часть задачи — перемножение больших чисел. Для простоты можно воспользоваться школьным алгоритмом «перемножения в столбик» или закодировать какой-нибудь алгоритм быстрого перемножения (например, алгоритм Карацубы). Третья часть — возведение в степень. Перемножение больших чисел — операция не дешёвая, поэтому в общем случае стараются уменьшить число перемножений. Можно заметить, что 17^300 = (17^150)^2, то есть надо возвести 17 в степень 150, а потом результат в квадрат. Экономия в два раза. Дальше больше: 17^150 = (17^75)^2. 17^75 = 17*(17^37)^2, и так далее до 17^2. Вместо 300 перемножений потребуется около 10. Вот вкратце идея алгоритма быстрого возведения в степень. По-моему, для того, чтобы закодировать эти подзадачи на Си/Си++ и получить искомый результат, не требуется быть гигантом программирования. |
||
|



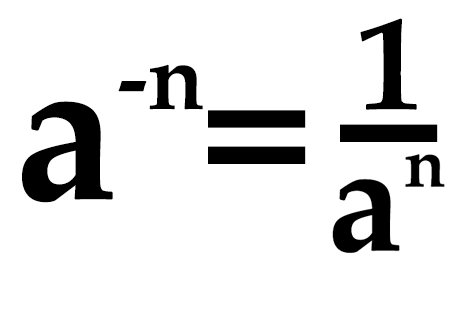













 это несущественно, на самом деле. существенно то, что тут сет в принципе не нужен, каюсь, с этим — прогнал.
это несущественно, на самом деле. существенно то, что тут сет в принципе не нужен, каюсь, с этим — прогнал.