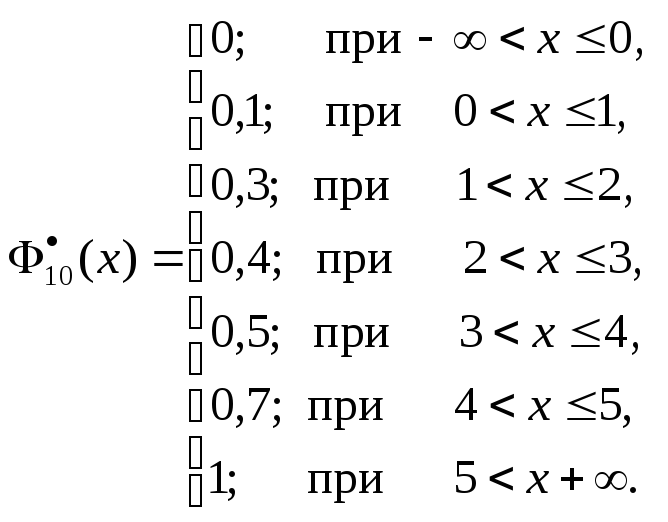Как найти статическое распределение - Autoru.top

эмпирическая
функция распределения

Пусть исследуется произвольная случайная
величина
и
относительно этой случайной величины
производится ряд независимых опытов
(испытаний) при наличии определённого
комплекса условий. Далее, пустьиз
генеральной совокупности извлечена
выборка, причем значениенаблюдалось

раз,
наблюдалосьраз, и так далее
наблюдалосьраз, при этом натуральное числои

выражает объём выборки,
значенияназываютвариантами
с.в..Вся совокупность
значений с.в.представляет
собой первичный статистический материал,
который подлежит дальнейшей обработке,
сначала подлежатьупорядочению.
Операцию по упорядочению значений
случайной величины (признака) по не
убыванию называют «ранжированием»
статистических данных. Полученная таким
способом последовательность значенийслучайной
величины,
где;,называетсявариационным рядом.

Числа
,
показывающие, сколько раз встречаются
варианты (числа)в ряде наблюдений, называютсячастотами.
А числаравное отношениек объёму выборки,
называютсяотносительными частотами,
т.е.

(1)

Перечень вариантов
и соответствующие им частость
или относительных
частот называют
статическим распределением
выборки или статическим рядом.

Статистическое распределение
записывается в виде таблицы, где в первой
строке пишут численные значения
вариантов, а вторая заполняется их
соответствующими частотами.
Из

этой таблицы затем составляют
новую таблицу с указанием частотностей
(относительных

частот)
,
где должен выполняться «контроль»

Пример
2. Задано распределение
частот выборки объема
,

Эта таблица означает, что
принимается
три раза,принимается 10 раз ипринимается 7 раз. В итоге:.

Написать таблицу распределение
относительных частот.

Решение.
Найдем относительные частоты, для чего
разделим частоты на объем выборки:

Теперь, составим таблицу распределения
относительных частот:

Контроль:

Пример 3. В
результате тестирования группы из 10
человек для приёма на работу претенденты
набрали баллы:
Составить

а) вариационный ряд;

б) статический ряд;

в) таблицу частот и относительных
частот.

Решение. а)
Упорядочив статические данные, получим
вариационный ряд:

;

б) Подсчитав частоту
и относительную частотность
вариантов:
получим статическое распределение
выборки (так называемый дискретный
ряд).

	0	1	2	3	4	5
	1	2	1	1	2	3

где
.
Контроль.

Построим таблицу относительную частоту

	0	1	2	3	4	5

где
.
Контроль.

Статистическое распределение выборки
является оценкой неизвестного
распределения.

По теореме Бернулли, относительные
частоты
сходятся прик соответствующим вероятностям,т.е..
Поэтому, при больших значенияхстатическое распределение мало отличается
от истинного распределения.

В случаях, когда количество значений
признака (с.в.)
достаточно велико или когда случайная
величинаявляется непрерывной (т.е. её значение
заполняет некоторый отрезок числовой
прямой),составляют интервальный
статистический ряд.

В первую очередь образуют частичные
промежутки,
которые берут обычно с одинаковыми
длинами, равными.

Интервалы
Частота
Частость

Эта таблица означает, что весь диапазон
изменения величиныразбит на интервалы

(границами
го
интервала являются,и);
числоесть частота попадания вй
интервал,,
гдеколичество
чисел в исходном ряде (выборке),
приходящихся в—
й интервал. На практике число интервалов
выбирается обычно в пределах одного-двух
десятков. Также следует отметить, что
в общем случае длины интервалов не
обязаны быть одинаковыми.

Для определения величины интервала
существуют разные подходы, в качестве
одного из таких способов разбиения,
может быть использована формула
Стерджесса:

где
выражает
разность между наибольшим и наименьшим
значениями признака,

числа интервалов
;.
За начало первого интервала рекомендуется
брать величину,
и если конец последнего промежутка
входит во множестве с.в.,
то оно также включается в число элементов,
входящих в последний промежуток. После
завершения «разбиения» первую строку
таблицы статического распределения
заполняют полученными частичными
промежутками. Во второй строчке
статистического ряда вписывают числа—
количество наблюдений, попавших в каждый
интервал, а затем составляют вторую
таблицу относительных частот по выше
указанному принципу, где мы для удобства
объединили обе таблицы.

Заметим, что в теории вероятностей под
распределением понимают соответствие
между возможными значениями случайной
величины и их вероятностями, а в
математической статистике —
соответствие между наблюдаемыми
вариантами и их частотами, иличастость
(относительные частоты).

Пример 4. Измерили рост (с некоторой
точностью скажем до 1 см.) 30 наудачу
отобранных студентов. Результаты
измерения показали:

Построить интервальный статистический
ряд.

Решение.Сначала упорядочим полученные
данные.

Следует, что
рост
студентов является непрерывной с.в. При
более точном измерении роста значения
с.в.обычно
не повторяется и может отличиться друг
от друга на несколько миллиметров.
Вероятность наличия на Земле двух
человека с одинаковым ростом, например,

метров, равна нулю.

Отсюда следует, что
;
в соответствии с формулой Стерджесса,
при,
находим длину частичного интервала
разбиения:

Если примем за
,
тогдаВсе исходные данные разбиваем наинтервалов (при):

Подсчитав общее число студентов
,
попавших в каждый из полученных
промежутков, получим интервальный
статистический ряд:

Рост	[150-156)	[156-162)	[162-168)	[168-174)	[174-180)	[180-186)
Частота	4	5	6	7	5	3
Частость	0,13	0,17	0,20	0,23	0,17	0,10

Одним из способов статистической
обработки вариационного ряда является
построение

эмпирической функции распределения.

Пусть известно статистическое
распределение частот количественного
признака

число наблюдений, при которых наблюдалось
значение признака,
а
общее
число наблюдений (объем выборки).

Эмпирической (статистической) функцией
распределения называется функция,определяющая для каждого значениячастость события:

(2)
.

В отличие от эмпирической функции
распределения выборки, интегральную
функцию
распределения генеральной совокупности
называюттеоретической функцией
распределения. Различие
между эмпирической и теоретической
функциями состоит в том, что теоретическая
функция

(3)

— определяет вероятность
события,
а эмпирическая функция
определяет
относительную частоту этого же события.

Очевидно, что функция
удовлетворяет
тем же условиям, что и истинная функция(см.Т.3).Другими словами,
числа
и мало отличаются одно от
другого. Уже отсюда следует целесообразность
использования эмпирической функции
распределения выборки для приближенного
представления теоретической (интегральной)
функции

-распределения генеральной
совокупности. Такое заключение
подтверждается и тем, что
обладает всеми
свойствами .
Действительно, из
определения функции вытекают следующие ее
свойства:

1. Значения эмпирической функции
принадлежат отрезку [0,1];

2.
неубывающая функция;

3. Если
наименьшая
варианта, то
при
;
и если

наибольшая варианта, то при
,.

На основании теорем ЗБЧ при увеличении
числа
наблюдений (опытов) относительная
частота событияприближается к истинной вероятности
этого события.

Эмпирическая функция распределения
является
как бы «оценкой» вероятности события,
т.е. оценкой теоретической функции
распределенияс.в..

Таким образом, можно заключить, что
имеет место утверждение,

Пусть
является теоретическая функция
распределения случайной величины,
аеё эмпирической функцией распределения.
Тогда для любогосправедливо предельное соотношение

(4)

Пример 5.В условиях примера 3, и
используя полученные результаты,
построим эмпирическую функцию.

Решение. В нашем случае по условию.
В целях наглядности решения примера
приведём ещё раз полученную таблицу
относительных частот

	0	1	2	3	4	5

где
.
Контроль.

Поэтому
при(наблюдений меньшеотсутствует);при(здесь
по таблице).при(здесь)
и т.д. Таким образом, получаем

График эмпирической функции распределения
имеет вид: (Рис. 72.)

Рисунок 72 из Письменного

Соседние файлы в папке Теория вероятностей от исмоилова

#
#
#
#
#
#
#
#
#
#
06.02.20162.36 Mб71~WRL0002.tmp
#
06.02.20161.87 Mб67~WRL0005.tmp

Источник

Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость

Статистическое распределение выборки

Содержание:

Примеры использования формул и таблиц для решения практических задач
Статистический интервальный ряд распределения

Предположим случай, когда из генеральной совокупности извлекается некоторая выборка, при этом каждому значению соответствует некоторый параметр, означающий количество раз, когда появлялось данное значение. Здесь $x_1$ было зафиксировано $n_1$ раз, $x_2$ было обнаружено $n_2$$x_k$ выявлено $n_k$. При этом

$sum_{i=1}^{k}n_i=n$

Где n — объём рассматриваемой выборки.

Определение 1

Используется следующая терминология: $x_k$ носят наименование вариантов, а последовательность таких вариантов, зафиксированный по возрастанию именуется вариационным рядом. Количество наблюдений каждого из вариантов носят название частот. При этом частное частот и выборки называют относительными частотами.

Определение 2

Статистическое распределение —это название всего набора вариантов и частот, которые с ними соотносятся. Чаще всего задаётся с помощью специальной таблицы, где представлены частоты, а также интервалы им соответствующие.

$x_1$	$x_2$	…	$x_k$
$n_1$	$n_2$	…	$n_k$
$frac{n_1}{n}$	$frac{n_2}{n}$		$frac{n_k}{n}$

Здесь в первой строке представлены варианты, во второй частоты, в третьеq взяты относительные частоты.

Для определения размера интервала используется следующее выражение:

$d=frac{x_{max}- x_{min}}{1+3,332cdot lg n}$

Здесь $x_{max}$, $x_{min}$ наибольшее и наименьшее значения ряда вариантов, а n характеризуем объём выборки.

Примеры использования формул и таблиц для решения практических задач

Пример 1

В ходе проведения измерений в однородных группах, были определены следующие значения выборки: 71, 72, 74, 70, 70, 72, 71, 74, 71, 72, 71, 73, 72, 72, 72, 74, 72, 73, 72, 74. Необходимо использовать данные значения, что определить ряд распределения частот и ряд распределения относительных частот.

Решение.

1) Составим статистический ряд распределения частот:

xi	70	71	72	73	74
ni	2	4	8	2	4

2) Рассчитаем суммарный размер выборки: n=2+4+8+2+4=20. Определим относительные частоты, для этого используем формулы: ni/n=wi: wi=2/20=0.1; w2=4/20=0.2; w3=0.4; w4=4/20=0.1; w5=2/20=0.2. Теперь зафиксируем в таблице распределение относительных частот:

xi	70	71	72	73	74
wi	0.1	0.2	0.4	0.1	0.2

Контрольная сумма должна равняться единице: 0,1+0,2+0,4+0,1+0,2=1.

Полигон частот

Название «полигоном частот» применяют для обозначения ломаной линии, каждый отрезок, которой соединяют точки $(х_1,n_1),(х_2,n_2),…,(х_k,n_k)$. Для построения на графике полигона частот по оси абсцисс отмечают варианты $х_2$, при этом на оси ординат отсчитывают– соответствующие частоты $n_i$. Когда полученные точки $(х_i,n_i)$ соединяются с помощью отрезков, то автоматически получают полигон частот.

Статистический интервальный ряд распределения.

Статистическим дискретным рядом (или эмпирической функцией распределения) обычно пользуются, если число различающихся вариант в полученной выборке не слишком большое. Также применение возможно, когда дискретность имеет важное значение для экспериментатора. В тех случаях, когда важный для задачи признак генеральной совокупности Х распределяется непрерывным образом, либо его дискретность нет возможности учесть, то варианты предпочтительнее всего группировать, чтобы получить интервалы.

Статистическое распределение допустимо задавать в том числе в качестве последовательности интервалов и частот, соответствующих этим интервалам. При это за частоту какого-либо интервала принимается сумма всех частот, вошедших в данный интервал.

Особенно следует отметить ,что $h_i-h_{i-1}=h$ при всех i, т.е. группировка проводится с равным шагом h. Также в вопросе группировки можно ориентироваться на ряд полученных опытным путём рекомендацийу, касающихся таких параметров, как а, k и $h_i$:

1. $Rраз_{мах}=X_{max}-X_{min}$

2. $h=R/k$; k-число групп

3.$ kgeq 1+3.321lgn$ (формула Стерджеса)

4. $a=x_{min}, b=x_{max}$

5.$ h=a+h_i, i=0,1…k$

Определённую в ходе решения задачи группировку удобнее всего скомпоновать и перевести в вид специальной таблицы, которая также может именоваться — «статистический интервальный ряд распределения»:

Интервалы группировки	[h0;h1)	[h1;h2)	…	[hk-2;hk-1)	[hk-1;hk)
Частоты	n1	n2	…	nk-1	nk

Таблицу подобного вида можно сделать, поменяв частоты $n_i$ на относительные частоты:

Интервалы группировки	[h0;h1)	[h1;h2)	…	[hk-2;hk-1)	[hk-1;hk)
Отн. частоты	w1	w2	…	wk-1	wk

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример 2

На склад пришла крупная партия деталей. Из них методом случайного отбора взято 50 экземпляров. Рассматривая изделия по одному, особенно интересующему признаку — размеру, определённому с точностью до 1 см, получим следующий вариационный ряд: 22, 47, 26, 26, 30, 28, 28, 31, 31, 31, 32, 32, 33, 33, 33, 33, 34, 34, 34, 34, 34, 35, 35, 36, 36, 36, 36, 36, 37, 37, 37, 37, 37, 37, 38, 38, 40, 40, 40, 40, 40, 41, 41, 43, 44, 44, 45, 45, 47, 50. Требуется произвести расчёт и определить статистический интервальный ряд распределения.

Решение

Найдём параметры выборки используя сведения из условия задачи.

$k geq1+3,321cdot lg50=1+3.32lg(5cdot10)=1+3.32(lg5+lg10)=6.6$

Получили a=22, k=7, h=(50-22)/7=4, hi=22+4i, i=0,1,…,7.

Интервалы группировки	22-26	26-30	30-34	34-38	38-42	42-46	46-50
Частоты	1	4	10	18	9	5	3
Отн. частоты	0.02	0.08	0.2	0.36	0.18	0.1	0.06

Десятичные логарифмы от 1 до 10

n	1	2	3	4	5	6	7	8	9	10
lnn≈	0	0.3	0.48	0.6	0.7	0.78	0.85	0.9	0.95	1

Не получается написать работу самому?

Доверь это кандидату наук!

Источник

При систематизации данных выборочных обследований используются статистические дискретные и интервальные ряды распределения.

1. Статистическое дискретное распределение. Полигон.
Пусть из генеральной совокупности извлечена выборка, причем х₁ наблюдалось n₁ раз, х₂ – n₂ раз, х_k – n_k раз и ∑n_i=n — объем выборки. Наблюдаемые значения х₁ называют вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом. Число наблюдений варианты называют частотой, а ее отношение к объему выборки — относительной частотой n_i/n=w_i

ОПРЕДЕЛЕНИЕ. Статистическим (эмпирическим) законом распределения выборки, или просто статистическим распределением выборки называют последовательность вариант х_i и соответствующих им частот n_i или относительных частот w_i.

Статистическое распределение выборки удобно представлять в форме таблицы распределения частот, называемой статистическим дискретным рядом распределения:

x₁	x₂	…	x_m
n₁	n₂	…	n_m

(сумма всех частот равна объему выборки ∑n_i=n)
или в виде таблицы распределения относительных частот:

x₁	x₂	…	x_m
w₁	w₂	…	w_m

(сумма всех относительных частот равна единице ∑w_i=1)

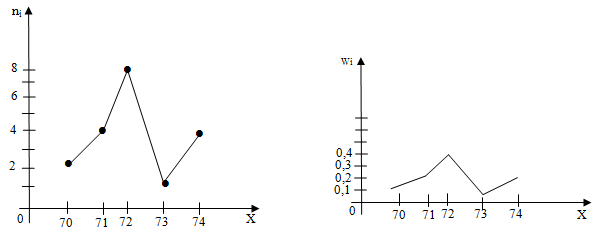
Пример 1. При измерениях в однородных группах обследуемых получены следующие выборки: 71, 72, 74, 70, 70, 72, 71, 74, 71, 72, 71, 73, 72, 72, 72, 74, 72, 73, 72, 74 (частота пульса). Составить по этим результатам статистический ряд распределения частот и относительных частот.

Решение. 1) Статистический ряд распределения частот:

x_i	70	71	72	73	74
n_i	2	4	8	2	4

2) Объем выборки: n=2+4+8+2+4=20. Найдем относительные частоты, для чего разделим частоты на объем выборки n_i/n=w_i: w_i=2/20=0.1; w₂=4/20=0.2; w₃=0.4; w₄=4/20=0.1; w₅=2/20=0.2. Напишем распределение относительных частот:

x_i	70	71	72	73	74
w_i	0.1	0.2	0.4	0.1	0.2

Контроль: 0,1+0,2+0,4+0,1+0,2=1.

Полигоном частот называют ломаную, отрезки, которой соединяют точки (х₁,n₁),(х₂,n₂),…,(х_k,n_k). Для построения полигона частот на оси абсцисс откладывают варианты х₂, а на оси ординат – соответствующие им частоты n_i. Точки (х_i,n_i) соединяют отрезками и получают полигон частот.

Полигоном относительных частот называют ломаную, отрезки, которой соединяют точки (х₁,w₁),(х₂,w₂),…,(х_k,w_k). Для построения полигона относительных частот на оси абсцисс откладывают варианты х_i, а на оси ординат соответствующие им частоты w_i. Точки (х_i,w_i) соединяют отрезками и получают полигон относительных частот.

Пример 2. Постройте полигон частот и относительных частот по данным примера 1.
Решение: Используя дискретный статистический ряд распределения, составленный в примере 1 построим полигон частот и полигон относительных частот:

2. Статистический интервальный ряд распределения. Гистограмма. Статистическим дискретным рядом (или эмпирической функцией распределения) обычно пользуются в том случае, когда отличных друг от друга вариант в выборке не слишком много, или тогда, когда дискретность по тем или иным причинам существенна для исследователя. Если же интересующий нас признак генеральной совокупности Х распределен непрерывно или его дискретность нецелесообразно ( или невозможно) учитывать, то варианты группируются в интервалы.

Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).

Замечание. Часто h_i-h_i-1=h при всех i, т.е. группировку осуществляют с равным шагом h. В этой ситуации можно руководствоваться следующими эмперическими рекомендациями по выборке а, k и h_i:

1. R_размах=X_max-X_min
2. h=R/k; k-число групп
3. k≥1+3.321lgn (формула Стерджеса)
4. a=x_min, b=x_max
5. h=a+ih, i=0,1…k

Полученную группировку удобно представить в форме частотной таблицы, которая носит название статистический интервальный ряд распределения:

Интервалы группировки	[h₀;h₁)	[h₁;h₂)	…	[h_k-2;h_k-1)	[h_k-1;h_k)
Частоты	n₁	n₂	…	n_k-1	n_k

Аналогическую таблицу можно образовать, заменяя частоты ni относительными частотами:

Интервалы группировки	[h₀;h₁)	[h₁;h₂)	…	[h_k-2;h_k-1)	[h_k-1;h_k)
Отн. частоты	w₁	w₂	…	w_k-1	w_k

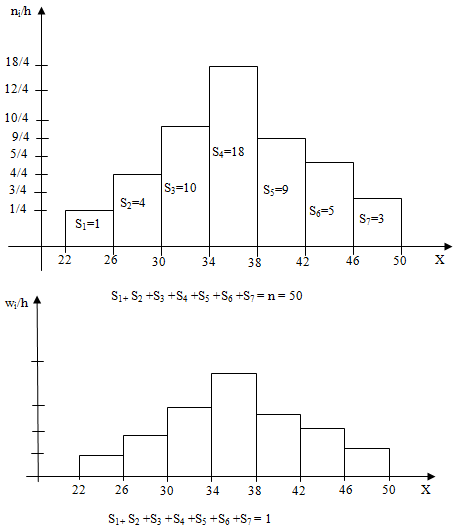
Пример 3. Из очень большой партии деталей извлечена случайная выборка объема 50 интересующий нас признак Х-размеры деталей, измеренные с точностью до 1см, представлен следующим вариоционным рядом: 22, 47, 26, 26, 30, 28, 28, 31, 31, 31, 32, 32, 33, 33, 33, 33, 34, 34, 34, 34, 34, 35, 35, 36, 36, 36, 36, 36, 37, 37, 37, 37, 37, 37, 38, 38, 40, 40, 40, 40, 40, 41, 41, 43, 44, 44, 45, 45, 47, 50. Найти статистический интервальный ряд распределения.

Решение. Определим характеристики группировки с помощью замечания.
k≥1+3.321lg50=1+3.32lg(5•10)=1+3.32(lg5+lg10)=6.6
Имеем, a=22, k=7, h=(50-22)/7=4, h_i=22+4i, i=0,1,…,7.

Интервалы группировки	22-26	26-30	30-34	34-38	38-42	42-46	46-50
Частоты n_i	1	4	10	18	9	5	3
Отн.частоты w_i	0.02	0.08	0.2	0.36	0.18	0.1	0.06

Десятичные логарифмы от 1 до 10

n	1	2	3	4	5	6	7	8	9	10
lnn≈	0	0.3	0.48	0.6	0.7	0.78	0.85	0.9	0.95	1

Наиболее информативной графической формой частот является специальный график, называемы гистограммой частот.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению n_i/h (плотность частоты).

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии n_i/h. Площадь i-го частичного прямоугольника равна h•n_i/h=n_i — сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению w_i/h (плотность относительной частоты).

Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии w_i/h. Площадь i-го частичного прямоугольника равна h•w_i/h=w_i — относительной частоте вариант, попавших в i-й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.

Пример 4. Постройте гистограмму частот и относительных частот по данным примера 3.

Выборочная медиана – это середина вариационного ряда, значение, расположенное на одинаковом расстоянии от левой и правой границы выборки.

Выборочная мода – это наиболее вероятное, т.е. чаще всего встречающееся, значение в выборке.

Добавлять комментарии могут только зарегистрированные пользователи.

Регистрация Вход

Источник

Содержание:

Интервальное статистическое распределение выборки и его числовые характеристики
Двумерное статистическое распределение выборки и его числовые характеристики
Условное статистическое распределение и их числовые характеристики
Корреляционный момент, выборочный коэффициент корреляции
Четное статистическое распределения выборки и его числовые характеристики

Количественные характеристики элементов генеральной совокупности могут быть одномерными и многомерными, дискретными и непрерывными.

Когда реализуется выборка, количественный признак, например приобретает конкретное числовое значение которое называют вариантой.

Возрастающий числовой ряд вариант называют вариационным.

Каждая варианта выборки может быть наблюденной если число частотой варианты .

При этом

где — количество вариант, что отличаются числовым значением; — объем выборки.

Соотношение частоты варианты к объему выборки называют ее относительной частотой и обозначают через то есть

Для каждой выборки выполняется равенство

если исследуется признак генеральной совокупности которая будет непрерывной, то вариант будет много. В этом случае, вариационный ряд — это определенное количество равных или неравных частичных интервалов или групп вариант со своими частотами.

Такие частичные интервалы вариант, которые размещены в возрастающей последовательности, образуют интервальный вариационный ряд.

На практике для удобства, как правило, рассматривают интервальные вариационные ряды, в которых интервалы являются равными между собой.

2. Дискретное статистическое распределение выборки и ее числовые характеристики.

Перечень вариант вариационного ряда и соответственных им частот, или относительных частот, называют дискретным статистическим распределением выборки.

В табличной форме можно представить так:

Дискретное статистическое распределение выборки можно представить эмпирической функцией .

Эмпирическая функция и ее свойства. Функция аргумента что обозначает относительную частоту события то есть

называется эмпирической.

Тут — объем выборки; — количество вариант статистического распределения выборки значения которых меньше фиксированной варианты

— называют еще функцией накопления относительных частот.

Свойства

где является наименьшей вариантой вариационного ряда;

является не спадающей функцией аргумента а именно: при

Полигон частот и относительных частот. Дискретное статистическое распределения выборки можно изобразить графически в виде ломанной линии, отрезки которой образуют координаты точек или

В первом случае ломанную линию называют полигоном частот, а во втором — полигоном относительных частот.

Пример. По заданному дискретному статистическому распределению выборки

нужно:

1. Построить и изобразить ее графически;

2. Начертить полигоны частот и относительных частот.

Решение. Согласно с определением и свойствам имеет такой вид:

Графическое изображение предоставлено на рис. 106.

Полигоны частот и относительных частот изображены на рис. 107, 108.

Числовые характеристики:

1) выборочная средняя величина Величину, которая обозначается формулой

называют выборочной средней величиной дискретного статического распределения выборки.

Тут — варианта вариационного ряда выборки;

— частота этой выборки

— объем выборки

Если все варианты выявляются в выборке только по одному разу, то есть то

2) отклонение вариант. Разницу называют отклонением этих вариант.

При этом

Следует, сумма отклонений всех вариант вариационного ряда выборки всегда равна нулю;

3) мода Модой дискретного статистического распределения выборки называют варианту, что имеет наибольшую частоту появления.

Мод может быть несколько. Когда дискретное статистическое распределение имеет одну моду, то оно называется одномодальным. если имеет две моды — двумодальным и так далее.

4) медиана Модой дискретного статистического распределения выборки называют варианту, которая делит вариационный ряд на две части, равные количеством вариант:

5) дисперсия. Для измерения рассеивания вариант выборки относительно выбирается дисперсия.

Дисперсия выборки — это среднее арифметическое квадратов отклонений вариант относительно , которое вычисляется по формуле

или

6) среднее квадратичное отклонение выборки При вычислении отклонения приводиться к квадрату, а следует, изменяется единица измерения признака потому на основании дисперсии приводится среднее квадратичное отклонение

которое измеряет рассеивание вариант выборки относительно то в тех же единицах, в которых изменяется признак

7) размах Для четкой оценки рассеивания вариант относительно используется величина, которая равна разнице между наибольшей и наименьшей вариантами вариационного ряда. Эта величина называется размахом

коэффициенты вариации Для сравнения оценок вариаций статистических рядов с разными значениями которые не равны нулю, приводится коэффициент вариации, который вычисляется по формуле

Пример. По заданному статистическому распределению выборки

нужно:

1) вычислить

2) найти

Решение. Поскольку то согласно с формулами (354), (357), (358) получим:

Для вычисления обозначается

Тогда

Следует, приведенное статистическое распределение выборки будет двумодальным. поскольку варианта делит вариационный ряд на две части: и которые имеют одинаковое количество вариант

Интервальное статистическое распределение выборки и его числовые характеристики

Перечень долевых интервалов и соответственных им частот, или относительных частот называют интервальным статистическим распределением выборки

В табличной форме это распределение имеет такой вид:

Тут является длиной частичного — нного интервала. Как правило, этот интервал берется одинаковым.

Интервальное статистическое распределение выборки можно преподать графически в виде гистограмм частот или относительных частот, а также, как и для дискретного статистического распределения, эмпирической функцией

Гистограмма частот и относительных частот. Гистограмма частот — фигура, которая складывается из прямоугольников, каждый из которых имеет основу и высоту

Гистограмма относительных частот — фигура, которая складывается из прямоугольников, каждый из которых имеет основу длиной и высоту. что равен

Пример. По заданному интервальному статистическому распределению выборки

нужно построить гистограмму частот и относительных частот

Решение. Гистограммы частот и относительных частот приведены на

Площадь гистограммы частот

Площадь гистограммы относительных частот

Эмпирическая функция . При постройке кумуляты для интервального статистического распределения выборки за основу берется предположение, что признак на каждом частичном интервале имеет равномерную плотность вероятностей. Потому кумулята имеет вид ломанной линии, которая возрастает на каждом частичном интервале и приближается к единице.

Пример. По заданному интервальному статистическому распределению выборки

построить и предоставить ее графически.

Решение

график изображен на рис. 111.

Аналогом эмпирической функции в теории вероятностей будет интегральная функция

Медана. Для обозначения медианы интервального статистического распределения выборки необходимо обозначить медианный частичны интервал. Если, например, на — нном интервале и то обратим внимание, что исследование признака является непрерывной и при этом является не спадающей функцией, на середине интервала обязательно существует такое значение где

Из признаков подобности треугольников и изображенных на рис. 112, получим:

где называют шагом.

Мода. Для определения моды интервального статистического распределения необходимо найти модальный интервал, то есть такой частичный интервал, что имеет наибольшую частоту появления.

Используя линейную интерполяцию, моду вычислим по формуле

где — начало модального интервала;

— длина или шаг частичного интервала;

— частота модального интервала;

— частота домодального интервала;

частота послемодального интервала;

Пример. По заданному интервальному статистическому распределению выборки

построить гистограмму частот и

Обозначим

Решение. Гистограмма частот изображена на рис. 113.

График изображен на рис. 114

Из рис. 113 обозначается модальный интервал, который равен Используя и обратив на внимание, что получим

Следует,

Из графика обозначается медианный интеграл, который равен

Обратим внимание, что и используя (361), получим:

Следует,

для интервального статистического распределения выборки. Для обозначения перейдем от интервального распределение к дискретному, вариантами которого будет середина частичных интервалов и который имеет вид:

Тогда вычисляется по формуле:

Пример. По заданному интервальному статистическому распределению выборки, в котором приведено распределение массы новорожденных

вычислить

Решение. Построим дискретное статистическое распределение к заданным интервальным. Поскольку то получим:

Обращая внимание на и то, что получим:

Следует,

Двумерное статистическое распределение выборки и его числовые характеристики

Перечень вариант и соответственных им частот совместного их появления образуют двумерное статистическое распределение выборки, что реализована из генеральной совокупности, элементам этой выборки присущие количественные признаки и

В табличной форме это распределение имеет такой вид:

Тут — частота совместного появления вариант

Общие числовые характеристики признака

общая средняя величина признака

общая дисперсия признака

общие среднее квадратичное отклонение признака

Общие числовые характеристики признака

общая средняя величина признака :

общая дисперсия признака :

общее среднее квадратичное отклонение признака :

Условное статистическое распределение и их числовые характеристики

Условным статистическим распределением признака при фиксированном значении называют пересечение вариант признака и соответственных им частот, взятых при фиксированном значении .

Тут

Числовые характеристики для такого статистического распределения называют условными. К ним принадлежат: условный средний признак

условная дисперсия признака

условное среднее квадратичное отклонение признака :

измеряют рассеивание вариант признака относительно средней величины

Условным статистическим распределением признака при называют пересечение вариант и соответственных им частот, взятых при фиксированном значении признака

Тут

Условные числовые характеристики для этого распределения: условная средняя величина признака

условная дисперсия признака

условное среднее квадратичное отклонение признака

При известных значениях условных средних общие средние признаки и вычислить по формулам:

Корреляционный момент, выборочный коэффициент корреляции

Во время исследования двумерного статистического распределения выборки предстает потребность использовать наглядность связи между признаками и , какой в статистике называют корреляционным. Для этого вычисляется эмпирический корреляционный момент по формуле

Если то корреляционная связь между признаками и нет. Если же то эта связь существует.

Следует, корреляционный момент дает только ответ на вопросы: существует связь между признаками и или нет.

Для измерения тесноты корреляционной связи вычисляется выборочный коэффициент корреляции по формуле

как и в теории вероятностей

Пример. По заданному двумерному статистическому распределению выборки признаки и

нужно:

1) вычислить

2) построить условно статистические распределения и вычислить условные числовые характеристики.

Решение. 1) Чтобы вычислить обозначим

Поскольку то

Следует,

для обозначения вычисляют

Тогда

Следует, а это свидетельствует о том, что между признаками и существует отрицательная корреляционная связь.

Для измерения тесноты этой связи вычислим выборочный коэффициент корреляции

Следует, то есть теснота корреляционной связи между признаками и является слабой.

Условное статистическое распределение имеет такой вид:

Вычисляют условные числовые характеристики для этого распределения:

Условная средняя величина

Условная дисперсия и среднее квадратичное отклонение

Следует,

Условное статистическое распределение имеет такой вид:

Вычисляются условные числовые характеристики.

Условная средняя величина

Следует,

Условная дисперсия и среднее квадратичное отклонение

Следует,

Четное статистическое распределения выборки и его числовые характеристики

Если частота общего появления признака и для всех вариант, то в этом случае двумерное статистическое распределение приобретает такой вид:

его называют четным статистическим распределением выборки. Тут каждая пара значений признаков и выявляется только один раз.

Объем выборки в этом случае равен количеству пар, то есть

Числовые характеристики признака :

средняя величина

дисперсия

среднее квадратичное отклонение

Числовые характеристики признака :

средняя величина

дисперсия

среднее квадратичное отклонение

эмпирический корреляционный момент

выборочный коэффициент корреляции

Пример. Зависимость количества масла что использует определенная особь за месяц, от ее прибыли в рублях приведена в таблице

Нужно вычислить

Решение. Поскольку объем выборки то получим:

Следует

Поскольку значение близко к единице, то отсюда получается, что зависимость между количеством масла, использованного определенной особой, и ее месячной прибылью почти функциональная.

6. Эмпирические моменты

Начальные эмпирические моменты. Среднее взвешенное значение вариант в степени называют начальным эмпирическим моментом — ого порядка который вычисляется по формуле

При получим начальный момент первого порядка:

При вычислим начальный момент второго порядка:

Следует, дисперсию выборки можно преподать через начальные моменты первого и второго порядков, а именно:

Центральный эмпирический момент — ого порядка. Среднее взвешенное отклонение вариант в степени называют центральным эмпирическом моментом — ого порядка

При получим:

На практике чаще используются центральные эмпирические моменты третьего и четвертого порядков, что вычисляются по формулам:

Преподнося к третьему и четвертому степени отклонения вариант, придадим и через соответственные начальные моменты:

Коэффициент асимметрии Центральный эмпирический момент третьего порядка используется для вычисления коэффициента асимметрии:

Если варианты статистического распределения выборки симметрично распределены относительно то в этом случае поскольку

При варианты статистического распределения преобладают варианты Такую асимметрию называют отрицательной. При статистического распределения преобладают варианты и такую асимметрию называют положительной.

Эксцесс. Центральный эмпиричный момент четвертого порядка используется для вычисления эксцесса:

как правило, используется при исследовании непрерывности признаков генеральных совокупностей, поскольку он оценивает крутизну закона распределения непрерывной случайной величины уравнена с нормальным. Для нормального закона распределения, как известно,

Пример. Оценить в баллах полученные абитуриенты на вступительных испытаниях по математике, приведены в таблице дискретного распределения:

Вычислить

Решение. Используя приведенные выше формулы и учитывая, что вычислим

Откуда

Следует, получим:

поскольку сравнительно малый, то статистическое распределение ближе к симметричному.

Пример. Длина заготовок изготовленных работником за смену, и частоты этих длин приведены в виде статистического распределения:

обозначить

Решение. Вычисляются значения Поскольку то получим:

Следует,

Вычислим центральный эмпирический момент четвертого порядка.

Поскольку то вершина закона распределения случайной величины, заданного плотностью вероятностей, будет плоской, то есть так называемое туповершинное распределение.

Лекции:

Статистические оценки
Статистические гипотезы
Корреляционный и регрессионный анализ
Комбинаторика основные понятия и формулы с примерами
Число перестановок
Непосредственное вычисление вероятностей примеры с решением
Действия над событиями. Теоремы сложения и умножения вероятностей примеры с решением
Примеры решения задач на тему: Случайные величины
Примеры решения задач на тему: основные законы распределения
Примеры решения задач на тему: совместный закон распределения двух случайных величин

Источник

Пусть из генеральной совокупности извлечена выборка объема П, в которой значение X1 некоторого исследуемого признака Х наблюдалось П1 раз, значение X2 — п2 раз, …, значение XK — Nk раз. Значения Xi называются Вариантами, а их последовательность, записанная в возрастающем порядке,— Вариационным рядом. Числа Ni называются Частотами, а их отношения к объему выборки

— Относительными частотами. При этом Ni = П. Модой Мo называется варианта, имеющая наибольшую частоту. Медианой те называется варианта, которая делит вариационный ряд на две части с одинаковым числом вариант в каждой. Если число вариант нечетно, т. е. K = 2L + 1, то Me = Xl+1; если же число вариант четно (k = 2L), То те = (Xl + Xl+1)/2. Размахом варьирования называется разность между максимальной и минимальной вариантами или длина интервала, которому принадлежат все варианты выборки:

Перечень вариант и соответствующих им частот называется Статистическим распределением выборки. Здесь имеется аналогия с законом распределения случайной величины: в теории вероятностей — это соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике — это соответствие между наблюдаемыми вариантами и их частотами (относительными частотами). Нетрудно видеть, что сумма относительных частот равна единице: Wi = 1.

Пример 2. Выборка задана в виде распределения частот:

Найти распределение относительных частот и основные характеристики вариационного ряда.

Решение. Найдем объем выборки: П = 2 + 4 + 5 + 6 + 3 = 20. Относительные частоты соответственно равны W1 = 2/20 = 0,1; W2 = 4/20 = 0,2; W3 = 5/20 = 0,25; W4 = 6/20 = 0,3; W5 = 3/20 = 0,15. Контроль: 0,1 + 0,2 + 0,25 + 0,3 + 0,15 = 1. Искомое распределение относительных частот имеет вид

Мода этого вариационного ряда равна 12. Число вариант в данном случае нечетно: K = 2 ∙ 2 + 1, поэтому медиана Me = X3 = 8. Размах варьирования, согласно формуле (18.48), R = 17 – 4 = 13.

< Предыдущая		Следующая >

Источник

Статистическое распределение выборки

Примеры использования формул и таблиц для решения практических задач

Полигон частот

Статистический интервальный ряд распределения.

Интервальное статистическое распределение выборки и его числовые характеристики

Двумерное статистическое распределение выборки и его числовые характеристики

Условное статистическое распределение и их числовые характеристики

Корреляционный момент, выборочный коэффициент корреляции

Четное статистическое распределения выборки и его числовые характеристики

Не пропустите также: