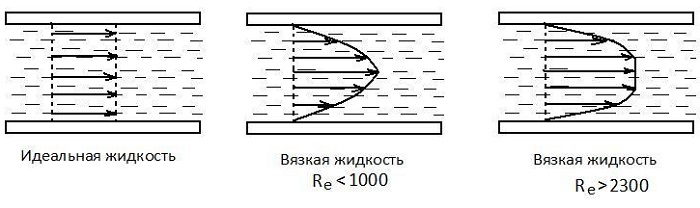
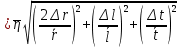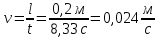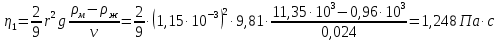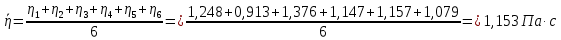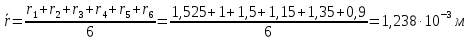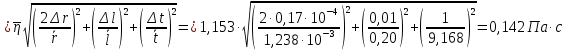Коэффициент вязкости – это величина, используемая для обозначения силы внутреннего трения текучих веществ. Вязкость – разновидность явлений переноса. Жидкости и газы оказывают сопротивление перемещению двух слоев относительно друг друга. Эта особенность характерна для текучих веществ, связана с движением частиц, из которых и состоят вещества.
Вязкость называют внутренним трением. В его основе находится хаотическое движение молекул, передающих импульс между слоями. Такие импульсные обмены выравнивают скорости перемещения слоев.
Коэффициент динамической вязкости
Численное обозначение абсолютной вязкости является индексом сопротивляемости испытуемых веществ взаимному перемещению или скольжению их слоев.
Единицей измерения коэффициента в системе СИ приняты паскаль-секунды:
Физическая основа динамического показателя заключается в его соответствии касательному напряжению, которое происходит между слоями вещества, перемещающимися относительно друг друга, при условии расстояния между ними, равного единице длины, и на скорости, равной единице.
Вязкость жидкости
Вязкость жидкости определяется формулой, в которой динамический коэффициент определяет пропорциональность скорости движения слоев и расстояния между ними:
-
τ – касательное напряжение;
-
µ — показатель пропорциональности, который является динамическим индексом вещества.
Закон вязкости жидкости был установлен Ньютоном в конце 17 века. Абсолютный показатель зависит от типа газа или жидкости, температуры веществ.
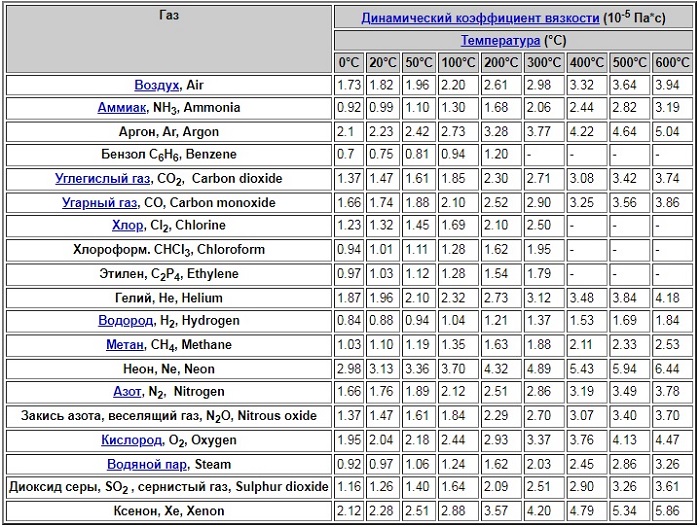
Коэффициент динамической вязкости газа
Для основных газов величины коэффициента при температуре 0 — 600 градусов Цельсия представлены в таблице:
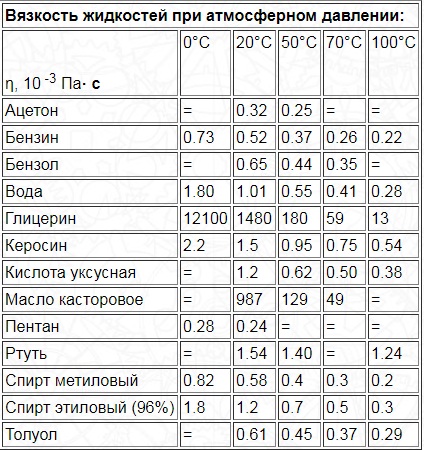
Коэффициент вязкости жидкостей
Для органических жидкостей показания напрямую зависят от температуры. Ниже приведена таблица со значениями абсолютного индекса для веществ при температурах от 0 до 100 градусов Цельсия.
Единица измерения – миллипаскаль-секунды, что соответствует сантипуазам.
Коэффициент динамической вязкости жидкостей уменьшается при условии нагревания вещества. Другими словами, чем выше температура жидкости, тем менее вязкой она становится.
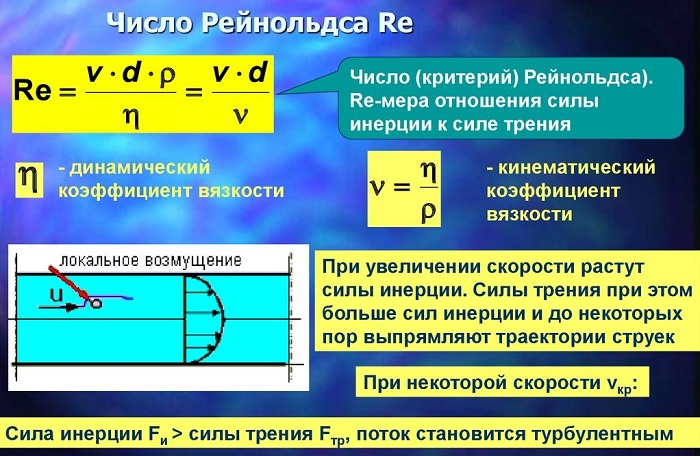
Связь коэффициента вязкости с числами Рейнольдса и силой трения
Английский механик, физик и инженер Оскар Рейнольдс установил (1876 — 1883 гг.), что характер течения зависит от величины, не имеющей размерностью, и называемой числом Re.
Число Рейнольдса используют для отображения соотношения кинематической энергии вещества к энергопотерям на установленной длине в условиях внутреннего трения.
Примеры решения задач
Попробуем решить следующую задачу.
Установить тип движения жидкого вещества по трубам теплообменника, имеющего структуру «труба в трубе». Параметры внутренней трубы – 25*2 мм, внешней – 50*2,5 мм. Массовый расход воды составляет 4000 кг/ч (обозначение G). Плотность жидкости – 1000 кг/м3. Абсолютный индекс составляет 1•10-3 Па*с.
Действие 1.
Следует узнать эквивалентный диаметр сечения межтрубного пространства:
Действие 2.
Определение скорости воды на основе уравнения расхода:
Действие 3.
По формуле Рейнольдса найти число Re:
Подставляя значения, получаем:
Ответ: режим перемещения воды в межтрубном пространстве является турбулентным.
Коэффициент кинематической вязкости
Кинематическая вязкость – это индекс, который отображает отношение абсолютного показателя вещества к его плотности при установленной температуре.
Физическая формула соотношения выглядит и единицы измерения можно увидеть на картинке:
Действие 4. Вычисление кинематического показателя, исходя из формулы:
Подставив в уравнение полученные и имеющиеся расчетные данные, получим кинематический индекс вещества.
Заключение
Физический смысл коэффициента вязкости заключается в том, что он демонстрирует, чему равна величина F внутреннего трения, действующая на 1 ед. площади поверхности соприкасающихся слоев при единичном градиенте скорости.
Размерность данной величины и перевод из одних единиц измерения в другие показаны на картинке:
Федеральное
агентство по образованию
Российской федерации
Государственное
образовательное учреждение высшего
профессионального обучения
Санкт-Петербургский
Государственный Горный Институт им.
Г.В. Плеханова
(технический
университет)
Отчёт
по лабораторной работе № 21
По дисциплине: Физика
Тема:
Определение
коэффициента вязкости жидкости
Выполнил: студент
гр. НГ-04___ _____________ Гладков
П.Д.
(подпись)
(Ф.И.О.)
П роверил:
роверил:
ассистент
____________ Чернобай
В.И.
(должность)
(подпись)
(Ф.И.О.)
Санкт-Петербург
2005
Цель работы:
определить
коэффициент вязкости жидкости методом
Стокса.
Краткое
теоретическое обоснование.
Я
внутреннего трения (вязкости) называется
появление сил трения между слоями
жидкости (или газа) движущимися друг
относительно друга параллельно и с
разными по величине скоростями.
При движении
плоских слоев сила трения между ними
согласно закону Ньютона равна:
где
— коэффициент пропорциональности,
называемый коэффициентом вязкости или
динамической вязкостью; S
— площадь соприкосновения слоев,
—
разница в скорости между соседними
слоями,
—
расстояние между соседними слоями.
Отсюда η численно
равен тангенциальной силе, приходящейся
на единицу площади соприкосновения
слоев, необходимой для поддержания
разности скоростей, равной единице,
между двумя параллельными слоями
вещества, расстояние между которыми
равно единице. В СИ единица вязкости —
паскаль·секунда.
Пусть в заполненном
жидкостью сосуде движется шарик, размеры
которого значительно меньше размеров
сосуда. На шарик действуют три силы:
сила тяжести Р, направленная вниз;
сила внутреннего трения
и выталкивающая сила Fв,
направленные вверх. Шарик сначала падает
ускоренно, но затем очень быстро наступает
равновесие, так как с увеличением
скорости растет и сила трения. Стокс же
показал, что эта сила при малых значениях
скорости пропорциональна скорости
движения шарика v и его
радиусу r:
,
где
— коэффициент вязкости.
Схема
установки.
Основные
расчетные формулы.
-
,
где
—
коэффициент вязкости, r-
радиус шарика,
—
скорость движения шарика;
-
,
где Р- сила
тяжести, действующая на шарик, FА—
сила Архимеда, Fтр—
сила внутреннего трения;
-
,
где м
— плотность материала шарика; V
– объем шарика;
-
,
где—
плотность жидкости;
-
.
Формула
расчета средней квадратичной погрешности.
,
г
—
среднее значение коэффициента вязкости,
—
значение коэффициента вязкости в каждом
отдельном опыте, n—
количество
опытов.
Таблица
измерений и вычислений.
Таблица 1
|
№ опыта |
Т |
ж |
|
d |
r |
t |
l |
v |
|
|
|
Единицы измерений |
К |
кг/м3 |
кг/м3 |
м |
м |
с |
м |
м/с |
Па·с |
Па·с |
|
1 |
298 |
0,97· 103 |
7,8· 103 |
3·10— |
1,5·10-3 |
12,11 |
0,4 |
0,033 |
1,015 |
0,07 |
|
2 |
298 |
0,97· 103 |
7,8· 103 |
3·10-3 |
1,5·10-3 |
11,88 |
0,4 |
0,034 |
0,985 |
0,07 |
|
3 |
298 |
0,97· 103 |
7,8· 103 |
3·10— |
1,5·10-3 |
12,00 |
0,4 |
0,033 |
1,015 |
0,07 |
|
4 |
298 |
0,97· 103 |
7,8· 103 |
3·10— |
1,5·10-3 |
11,91 |
0,4 |
0,034 |
0,985 |
0,07 |
|
5 |
298 |
0,97· 103 |
7,8· 103 |
3·10-3 |
1,5·10-3 |
11,88 |
0,4 |
0,034 |
0,985 |
0,07 |
|
6 |
298 |
0,97· 103 |
11,35·103 |
2,4·10-3 |
1,2·10-3 |
13,72 |
0,4 |
0,029 |
1,124 |
0,07 |
|
7 |
298 |
0,97· 103 |
11,35·103 |
2,2·10-3 |
1,1·10-3 |
16,76 |
0,4 |
0,024 |
1,140 |
0,07 |
|
8 |
298 |
0,97· 103 |
11,35·103 |
2,5·10-3 |
1,25·10-3 |
12,41 |
0,4 |
0,032 |
1,105 |
0,07 |
|
9 |
298 |
0,97· 103 |
11,35·103 |
2,1·10-3 |
1,05·10-3 |
16,93 |
0,4 |
0,024 |
1,039 |
0,07 |
|
10 |
298 |
0,97· 103 |
11,35·103 |
2,6·10-3 |
1,3·10-3 |
12,08 |
0,4 |
0,033 |
1,159 |
0,07 |
Погрешности
прямых измерений.
=0,1К;
=5·10-5м;
=
5·10-5м;
=
5·10-5м;
=0,01с.
Расчет
результатов эксперимента.
-
Рассчитываем
коэффициент вязкости жидкости для
каждого опыта:
;
Расчет для опыта
№1
η1
= (2·2,25·10-6·9,81·(7,8·103-0,97·103))/(9·0,033)
= 1,015 Па·с
η2
= 0,985 Па·с
η3
= 1,015 Па·с
η4
= 0,985 Па·с
η5
= 0,985 Па·с
η6
= 1,124 Па·с
η7
= 1,140 Па·с
η8
= 1,105 Па·с
η9
= 1,039 Па·с
η10
= 1,159 Па·с
2) η =
;
Вычисляем
среднее значение коэффициента вязкости
жидкости:
=
(η1+
η2+
η3+
η4+
η5+
η6+
η7+
η8+
η9+
η10)/10;
=(1,015+0,985+1,015+0,985+0,985+1,124+1,140+1,105+1,039+1,159)/10=1,055
Па·с.
3)
Вычисляем среднюю квадратичную
погрешность:
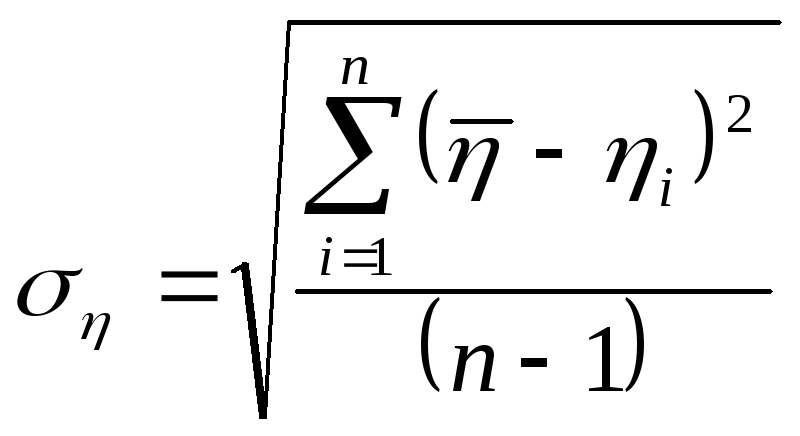
=0,07
Па·с.
Окончательный
ответ.
η =
= 1,0550,07
Па·с.
Вывод.
В данной работе
экспериментально был определен
коэффициент вязкости жидкости. Путем
постановки 10 опытов (для наибольшей
точности) со стальными и свинцовыми
шариками, удалось установить, что
скорость шарика, движущегося в сосуде
с жидкостью, зависит от размеров и
плотности шарика. В результате получили
среднее значение вязкости жидкости
(касторового масла) η=1,0550,07
Па·с. Полученный результат имеет
небольшую погрешность, что позволяет
говорить о точности расчетной формулы
и о незначительных погрешностях при
измерениях и вычислениях.
Соседние файлы в папке №21
- #
02.04.2015207.36 Кб5021.doc
- #
- #
5. измерения, указанные в пунктах 2-5,
повторяем еще для девяти шариков;
6. по расчетной формуле находим
коэффициент вязкости жидкости для каждого шарика и берем hср .
Все измеренные и
вычисленные величины записываем в таблицу.
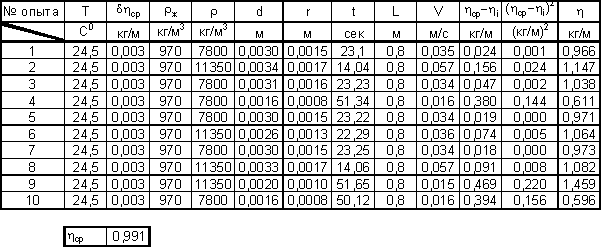
Рассчитываем среднюю квадратическую
погрешность по формуле
где
—
среднее значение коэффициента вязкости жидкости;
n – число измерений.(10 измерений)
Вывод:
Проведя данную лабораторную работу я
получил коэффициент вязкости исследуемой жидкости 0,991 кг/м, что при условии
погрешности в пределах
кг/м
не противоречит справочным данным. Исходя из этого можно сказать что
лабораторная работа была проведена успешно, с выполнением всех необходимых
условий.
Как определить вязкость жидкости методом Стокса?

Формулу определения вязкости Стокс вывел ещё в 1851 году.
Он получил выражение, описывающее действие силы трения (лобового сопротивления) на круглый объект, движущийся в вязкой жидкости с небольшим числом Рейнольдса.
Чтобы понять, как определять вязкость жидкости методом Стокса необходимо узнать теоретическое описание процесса, вывод формулы и сам описание самого метода.
Всё это и конкретные методы описаны далее в статье.
Сама по себе вязкость это свойство жидкости сопротивляться сдвигу слоев. Такой сдвиг выражается в том, что при относительном перемещении слоёв жидкости тот слой, что движется медленнее тормозит слой, который движется быстрее и наоборот.
Вязкость проявляется в наличии между молекулами жидкости сил притяжения, которые пытаются сдерживать движение слоев при перемещении одной части жидкости относительно другой.
По природе все жидкости являются вязкими, потому что между молекулами существуют силы притяжения и отталкивания. Если один слой жидкости вывести из равновесия и сдвигать его относительно другого с некоторой скоростью, то силы взаимного притяжения молекул будут пытаться тормозить это движение.
Движение тела в жидкой среде
Когда твердое тело попадает в жидкость, оно сталкивается с некоторым сопротивлением. Происхождение сил сопротивления жидкости в этом случае может быть объяснено двумя разными механизмами.
Механизм №1 — За твердым телом нет вихрей
Если скорость движения твердого тела маленькая и за ним не образовывается завихрений, то силы сопротивления жидкости характеризуются только вязкостью.
В таком случае слои жидкости, которые прилегают к этому твердому телу, движутся вместе с ним. Но слои жидкости, граничащие с первыми слоями, тоже приходят в движения из-за сил молекулярного притяжения (сцепления).
Таким образом образуются силы, которые затормаживают относительное движение твердого тела в жидкости.
Механизм №2 — При движении тела образуются вихри
Завихрения вокруг твердого тела образуются из-за различия скоростей движения жидкости перед телом и за ним. При этом давление в стационарном потоке жидкости изменяется таким образом, что в области вихрей оно существенном меньше.
Разность давлений в областях перед твердым телом и за ним создает противоположную по направлению движения силу лобового сопротивления жидкости. Эта сила тормозит движение твердого тела.
Сила сопротивления
В случае, когда движение твердого тела в жидкости происходит без образования вихрей, т.е. медленно, сила сопротивления образуется по первому из двух описанных механизмов.
Для тел круглой формы, согласно формуле Стокса, сила сопротивления будет равна:
ТC = 6πμrυ
где
Условие использования формулы
Существует несколько ограничений для применения формулы Стокса.
Формула вязкости

Рассмотрим конкретный случай, когда на шар, движущийся в жидкости действуют три силы:
Для круглого шарика сила тяжести будет:
Сила Архимеда:
Сила сопротивления:
где
В жидкости выталкивающая сила и сила тяжести постоянны. Сила лобового сопротивления пропорциональна скорости движения шарика и на первых этапах она существенно меньше силы тяжести.
При дальнейшем движении шарика наступает момент, когда все три силы уравновешиваются и тогда:
FT = FA + TC
или подставляя формулы
img
таким образом, определение коэффициента вязкости жидкости методом Стокса сводится к формуле

Определение вязкости методом Стокса

Для того чтобы определить вязкость методом Стокса используют высокий сосуд цилиндрической формы.
На сосуд наносят метки А и В. Такие метки располагаются на заведомо известном расстоянии l друг от друга.
Затем в сосуд наливают исследуемую жидкость выше верхней метки А на 4 – 5 сантиметров. Это необходимо для того, чтобы во время прохождения шариком первой метки его скорость можно было считать установившейся.
Далее шарик бросают в сосуд и секундомером определяют время за которое он проход расстояние от метки А до метки В.
Учитывая, что скорость это отношения длины пути ко времени, т.е.:
υ = l / t
и заменяя радиус шарика его диаметром d и определяет коэффициент вязкости жидкости методом стокса

Указанная выше формула применимо в тех случаях, когда шар падает в безграничной среде. Если он падает вдоль оси трубки диаметром R0 (как в этом случае) необходимо ввести поправки на радиус сосуда.

При падении шара радиусом r в трубе радиусом R0 и высотой h формула будет выглядеть

Исходя из всего вышесказанного получаем, что определение вязкости жидкости методом
Стокса требует значения таких параметров, как:
Видео про методы определения вязкости
Вязкость – это важная характеристика жидкой среды. Её необходимо учитывать при перекачке жидкостей и газов по трубопроводам, смазке машин и механизмов, разливке расплавленных металлов.
Для определения вязкости используют специальные приборы вискозиметры и специальные методы определения. Каждый из методов определения вязкости характеризуется своим набором условий применения.
Но независимо от метода общими остаются:
Вместе со статьей «Как определить вязкость жидкости методом Стокса?» смотрят:

Ламинарный режим движения жидкости

Гидростатический парадокс и сила давления на стенку

Скорость звука, критическая скорость и число Маха
Подборка по базе: Прокопьев Отчёт В5.docx, Пример отчета по неразрушающему контролю.docx, фин отчет нов.docx, Риза 22ЭЛК1 Отчет без стр (1).docx, 1-26422. Отчет.docx, 189412. Отчет.docx, 188860. Отчет.docx, 1-27223. Отчет.docx, 191084. Отчет.docx, 1-27449. Отчет.docx
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»
Кафедра общей и технической физики
Отчет
по лабораторной работе №13
«Определение коэффициента вязкости жидкости»
Выполнил: студент _____________ (подпись)
Проверил: _____________
(подпись)
Дата выполнения работы:
Санкт-Петербург
2022
- Цель работы
- Определить коэффициент вязкости жидкости методом Стокса.
- Краткое теоретическое содержание
- Процесс, изучаемый в работе
- В работе производится измерение вязкости жидкости по измерению скорости установившегося равномерного движения маленьких твердых шариков при их падении в исследуемой жидкости.
- Основные определения явлений, процессов, величин
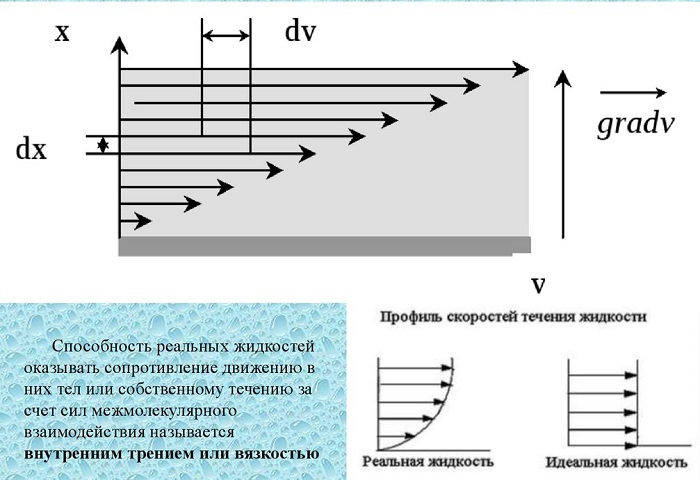
Вязкость (внутреннее трение) — есть свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одного слоя вещества относительно другого.
Градиент скорости — отношение /у, характеризующее быстроту изменения скорости, где и у — разница в скорости и расстояние между соседними слоями соответственно.
Равномерное прямолинейное движение – это движение, при котором за любые равные промежутки времени тело совершает равные перемещения.
Скорость – это физическая векторная величина, равная отношению пути ко времени.
Ускорение – это физическая величина, численно равная изменению скорости в единицу времени.
- Основные законы и соотношения, лежащие в основе вывода расчетных формул
- При движении плоских слоев сила трения между ними согласно закону Ньютона, Н:

где 
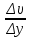
- Выталкивающая сила по закону Архимеда для шарика, Н

Где 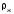


- Закон Стокса, Н

Где — коэффициент вязкости; r- радиус шарика; 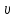
- Второй закон Ньютона, Н

Где 
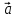
- Схема экспериментальной установки
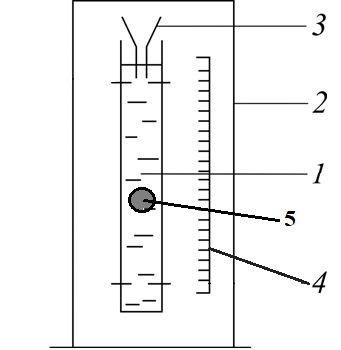
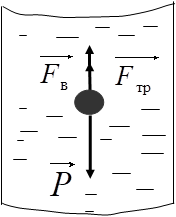
1 – Жидкость 
2 – Установка 
3 – Воронка 
4 – Линейка
5 – Шарик
- Основные расчетные формулы
- Сила внутреннего трения между слоями жидкости (закон Стокса), Н :
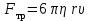
где 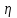
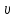
,
где Р- сила тяжести; действующая на шарик; FА— сила Архимеда; Fтр— сила внутреннего трения;
- Сила тяжести, Н
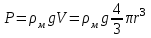
где м — плотность материала шарика; V – объем шарика;
- Выталкивающая сила, Н

где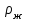


- Коэффициент вязкости жидкости,

Где 

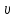

- Скорость,
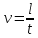
Где 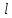
- Радиус, м

Где d – диаметр шарика.
Формулы для расчёта погрешности косвенных измерений
где 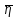
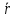

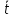
- Таблицы
«Технические данные прибора» Таблица 1
| №
п.п. |
Название прибора | Пределы измерений | Число делений | Цена деления | Класс точности | Абсолютная приборная погрешность |
| 1 | Гигрометр Психрометрический | 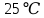 |
125 |  |
– |  |
| 2 | Микроскоп | 21,25 мм | 125 | 0,17 мм | – | 1 дел(0,17мм) |
| 3 | Цилиндрический сосуд | 1000 мм | 1000 | 1 мм | – | 1 см |
| 4 | Секундомер | 99,99 с | — | 0,01 с | — | 1 с |
«Результаты измерений» Таблица 2
| Физ. величина |
Т |
ж | | d | r | t | l | | |  |
| Ед. измер.
Номер опыта |
 |
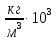 |
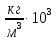 |
мм | мм | С | м | 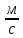 |
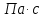 |
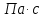 |
| 1 | 23,6 | 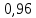 |
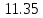 |
2,3 | 1,15 | 8,33 | 0,2 | 0,024 | 1,248 | 0,119 |
| 2 | 23,6 | 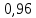 |
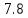 |
3,05 | 1,525 | 5,24 | 0,2 | 0,038 | 0,913 | 0,119 |
| 3 | 23,6 | 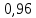 |
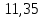 |
2,7 | 1,35 | 6,60 | 0,2 | 0,030 | 1,376 | 0,119 |
| 4 | 23,6 | 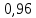 |
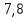 |
2 | 1 | 16,04 | 0,2 | 0,013 | 1,147 | 0,119 |
| 5 | 23,6 | 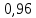 |
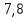 |
3 | 1,5 | 6,83 | 0,2 | 0,029 | 1,157 | 0,119 |
| 6 | 23,6 | 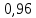 |
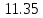 |
1,8 | 0,9 | 11,97 | 0,2 | 0,017 | 1,079 | 0,119 |
- Исходные данные:

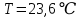
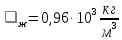

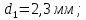
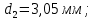




Погрешности прямых измерений:



- Вычисления
Пример вычислений для таблицы 2, опыта 1:
Радиус, м:
Скорость, 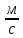
Коэффициент вязкости, 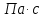
Вычисляем погрешность косвенных измерений 
Среднее значение коэффициента вязкости
Среднее значение радиуса шарика
Среднее значение времени
Погрешность косвенных измерений
- Результаты
Вывод: В данной работе экспериментально был определен коэффициент вязкости жидкости. Получили: 
Путем постановки 6 опытов со стальными и свинцовыми шариками, удалось установить, что скорость шарика, движущегося в сосуде с жидкостью, зависит от размеров и плотности шарика. Полученные результаты имеют небольшую погрешность, что позволяет говорить о точности расчетной формулы и о незначительных погрешностях при измерениях и вычислениях. Коэффициент вязкости при 
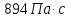
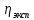

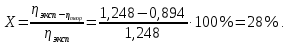

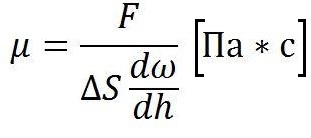
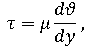

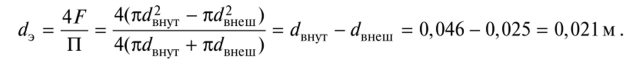
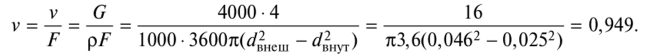
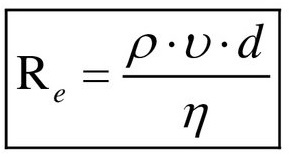
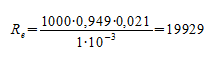
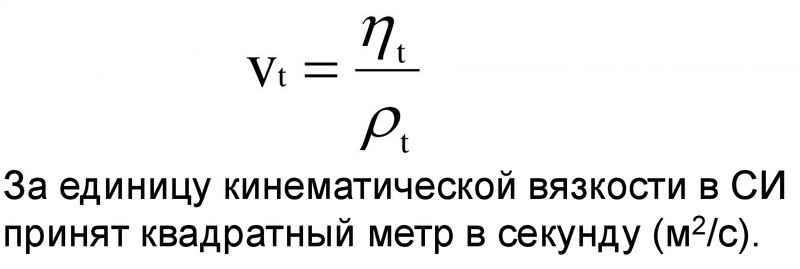
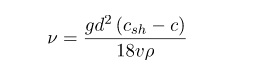




 роверил:
роверил:
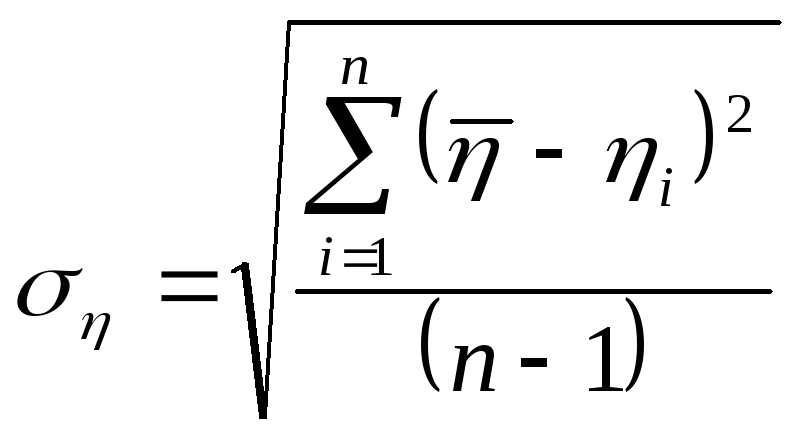
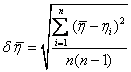






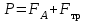 ,
,