Average or mean value of array
Syntax
Description
example
M = mean( returns the mean of theA)
elements of A along the first array dimension whose size is
greater than 1.
-
If
Ais a vector, thenmean(A)returns
the mean of the elements. -
If
Ais a matrix, thenmean(A)returns
a row vector containing the mean of each column. -
If
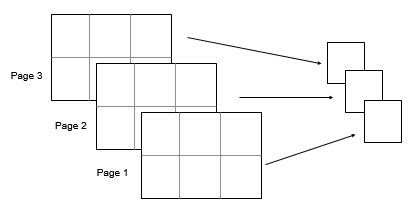
Ais a multidimensional array, then
mean(A)operates along the first array dimension
whose size is greater than 1, treating the elements as vectors. The size of
Min this dimension becomes1,
while the sizes of all other dimensions remain the same as in
A. -
If
Ais a table
or timetable, thenmean(A)returns a one-row table
containing the mean of each variable. (since R2023a)
example
M = mean(A,"all")
returns the mean over all elements of A.
example
M = mean( returns theA,dim)
mean along dimension dim. For example, if A is
a matrix, then mean(A,2) returns a column vector containing the
mean of each row.
example
M = mean(A,vecdim)
returns the mean based on the dimensions specified in the vector
vecdim. For example, if A is a matrix,
then mean(A,[1 2]) returns the mean of all elements in
A because every element of a matrix is contained in the array
slice defined by dimensions 1 and 2.
example
M = mean(___, returns the meanouttype)
with a specified data type for any of the previous syntaxes.
outtype can be "default",
"double", or "native".
example
M = mean(___, specifiesmissingflag)
whether to include or omit missing values in A. For example,
mean(A,"omitmissing") ignores all missing values when
computing the mean. By default, mean includes missing
values.
Examples
collapse all
Mean of Matrix Columns
Create a matrix and compute the mean of each column.
A = [0 1 1; 2 3 2; 1 3 2; 4 2 2]
A = 4×3
0 1 1
2 3 2
1 3 2
4 2 2
M = 1×3
1.7500 2.2500 1.7500
Mean of Matrix Rows
Create a matrix and compute the mean of each row.
A = [0 1 1; 2 3 2; 3 0 1; 1 2 3]
A = 4×3
0 1 1
2 3 2
3 0 1
1 2 3
M = 4×1
0.6667
2.3333
1.3333
2.0000
Mean of 3-D Array
Create a 4-by-2-by-3 array of integers between 1 and 10 and compute the mean values along the second dimension.
rng('default')
A = randi(10,[4,2,3]);
M = mean(A,2)
M =
M(:,:,1) =
8.0000
5.5000
2.5000
8.0000
M(:,:,2) =
10.0000
7.5000
5.5000
6.0000
M(:,:,3) =
6.0000
5.5000
8.5000
10.0000
Mean of Array Page
Create a 3-D array and compute the mean over each page of data (rows and columns).
A(:,:,1) = [2 4; -2 1]; A(:,:,2) = [9 13; -5 7]; A(:,:,3) = [4 4; 8 -3]; M1 = mean(A,[1 2])
M1 =
M1(:,:,1) =
1.2500
M1(:,:,2) =
6
M1(:,:,3) =
3.2500
To compute the mean over all dimensions of an array, you can either specify each dimension in the vector dimension argument, or use the "all" option.
Mean of Single-Precision Array
Create a single-precision vector of ones and compute its single-precision mean.
A = single(ones(10,1));
M = mean(A,"native")
The result is also in single precision.
Mean Excluding Missing Values
Create a matrix containing NaN values.
A = [1.77 -0.005 NaN -2.95; NaN 0.34 NaN 0.19]
A = 2×4
1.7700 -0.0050 NaN -2.9500
NaN 0.3400 NaN 0.1900
Compute the mean values of the matrix, excluding missing values. For matrix columns that contain any NaN value, mean computes with the non-NaN elements. For matrix columns that contain all NaN values, the mean is NaN.
M = 1×4
1.7700 0.1675 NaN -1.3800
Input Arguments
collapse all
A — Input array
vector | matrix | multidimensional array | table | timetable
Input array, specified as a vector, matrix, multidimensional array, table, or timetable.
-
If
Ais a scalar, then
mean(A)returns
A. -
If
Ais an empty 0-by-0 matrix, then
mean(A)returns
NaN.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | char | datetime | duration | table | timetable
dim — Dimension to operate along
positive integer scalar
Dimension
to operate along, specified as a positive integer scalar. If you do not specify the dimension,
then the default is the first array dimension of size greater than 1.
Dimension dim indicates the dimension whose
length reduces to 1. The size(M,dim) is 1,
while the sizes of all other dimensions remain the same.
Consider an m-by-n input matrix,
A:
-
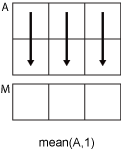
mean(A,1)computes the mean of the elements
in each column ofAand returns a
1-by-nrow
vector. -
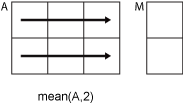
mean(A,2)computes the mean of the elements
in each row ofAand returns an
m-by-1column
vector.
mean returns A when dim is
greater than ndims(A) or when size(A,dim) is 1.
vecdim — Vector of dimensions
vector of positive integers
Vector of dimensions, specified as a vector of positive integers. Each
element represents a dimension of the input array. The lengths of the output
in the specified operating dimensions are 1, while the others remain the
same.
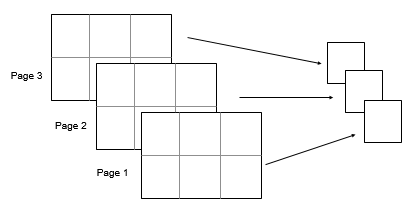
Consider a 2-by-3-by-3 input array, A. Then
mean(A,[1 2]) returns a 1-by-1-by-3 array whose
elements are the means over each page of A.
outtype — Output data type
"default" (default) | "double" | "native"
Output data type, specified as one of the values in this table. These options also specify the
data type in which the operation is performed.
outtype |
Output data type |
|---|---|
"default" |
double, unless the input data type is single,duration,datetime, table, ortimetable, in which case, the outputis "native" |
"double" |
double, unless the data input type is duration,datetime, table,or timetable, in which case,"double" is not supported |
"native" |
Same data type as the input, unless:
|
missingflag — Missing value condition
"includemissing" (default) | "includenan" | "includenat" | "omitmissing" | "omitnan" | "omitnat"
Missing value condition, specified as one of the values in this
table.
| Value | Input Data Type | Description |
|---|---|---|
"includemissing" |
All supported data types |
Include missing values in |
"includenan" |
double, single,duration |
|
"includenat" |
datetime |
|
"omitmissing" |
All supported data types | Ignore missing values inA, and compute the mean over fewerpoints. If all elements in the operating dimension are missing, then the corresponding element in M is missing. |
"omitnan" |
double, single,duration |
|
"omitnat" |
datetime |
More About
collapse all
Mean
For a finite-length vector A made up of
N scalar observations, the mean is defined as
Extended Capabilities
Tall Arrays
Calculate with arrays that have more rows than fit in memory.
This function fully supports tall arrays. For
more information, see Tall Arrays.
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
-
If you specify
dim, then it must
be a constant. -
The
outtypeandmissingflag
options must be constant character vectors or strings. -
Integer types do not support the
"native"output
data type option. -
See Variable-Sizing Restrictions for Code Generation of Toolbox Functions (MATLAB Coder).
GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.
Usage notes and limitations:
-
If you specify
dim, then it must be a constant. -
The
outtypeandmissingflagoptions
must be constant character vectors or strings. -
Integer types do not support the
"native"output data
type option.
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
This function fully supports thread-based environments. For
more information, see Run MATLAB Functions in Thread-Based Environment.
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
The mean function
partially supports GPU arrays. Some syntaxes of the function run on a GPU when you specify the
input data as a gpuArray (Parallel Computing Toolbox). Usage notes and limitations:
-
The
"native"option is not supported.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.
Usage notes and limitations:
-
The
"native"option is not supported.
For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006a
expand all
R2023a: Perform calculations directly on tables and timetables
The mean function can calculate on all variables within a table or
timetable without indexing to access those variables. All variables must have data types
that support the calculation. For more information, see Direct Calculations on Tables and Timetables.
R2023a: Specify missing value condition
Include or omit all missing values in the input array when computing the mean by
using the "includemissing" or "omitmissing"
options. Previously, "includenan", "omitnan",
"includenat", and "omitnat" specified a
missing value condition that was specific to the data type of the input
array.
R2023a: Improved performance with small group size
The mean function shows improved performance when computing
over a real vector when the operating dimension is not specified. The function
determines the default operating dimension more quickly in R2023a than in
R2022b.
For example, this code computes the mean along the default vector dimension. The
code is about 2.2x faster than in the previous release.
function timingMean A = rand(10,1); for i = 1:8e5 mean(A); end end
The approximate execution times are:
R2022b: 0.91 s
R2023a: 0.41 s
The code was timed on a Windows® 10, Intel®
Xeon® CPU E5-1650 v4 @ 3.60 GHz test system using the
timeit function.
R2018b: Operate on multiple dimensions
Operate on multiple dimensions of the input array at a time. Specify a vector of
operating dimensions, or specify the "all" option to operate on
all array dimensions.
mean
Синтаксис
Описание
пример
M = mean( возвращает среднее значение элементов A)A вдоль первого измерения массива, размер которого не равняется 1.
-
Если
Aвектор, затемmean(A)возвращает среднее значение элементов. -
Если
Aматрица, затемmean(A)возвращает вектор-строку, содержащий среднее значение каждого столбца. -
Если
Aмногомерный массив, затемmean(A)действует вдоль первого измерения массива, размер которого не равняется 1, обрабатывая элементы как векторы. Эта размерность становится1в то время как размеры всех других размерностей остаются то же самое.
пример
M = mean( вычисляет среднее значение по всем элементам A,'all')A. Этот синтаксис допустим для MATLAB® версии R2018b и позже.
пример
M = mean( возвращает среднее значение по измерению A,dim)dim. Например, если A матрица, затем mean(A,2) вектор-столбец, содержащий среднее значение каждой строки.
пример
M = mean( вычисляет среднее значение на основе размерностей, заданных в векторном A,vecdim)vecdim. Например, если A матрица, затем mean(A,[1 2]) среднее значение всех элементов в A, поскольку каждый элемент матрицы содержится в срезе массивов, заданном размерностями 1 и 2.
пример
M = mean(___, возвращает среднее значение с заданным типом данных, с помощью любого из входных параметров в предыдущих синтаксисах. outtype)outtype может быть 'default''double', или 'native'.
пример
M = mean(___, задает, включать ли или не использовать nanflag)NaN значения от вычисления для любого из предыдущих синтаксисов. mean(A,'includenan') включает весь NaN значения в вычислении, в то время как mean(A,'omitnan') игнорирует их.
Примеры
свернуть все
Среднее значение столбцов матрицы
Создайте матрицу и вычислите среднее значение каждого столбца.
A = [0 1 1; 2 3 2; 1 3 2; 4 2 2]
A = 4×3
0 1 1
2 3 2
1 3 2
4 2 2
M = 1×3
1.7500 2.2500 1.7500
Среднее значение матричных строк
Создайте матрицу и вычислите среднее значение каждой строки.
A = [0 1 1; 2 3 2; 3 0 1; 1 2 3]
A = 4×3
0 1 1
2 3 2
3 0 1
1 2 3
M = 4×1
0.6667
2.3333
1.3333
2.0000
Среднее значение трехмерного массива
Создайте 4 2 3 массивами целых чисел между 1 и 10 и вычислите средние значения вдоль второго измерения.
rng('default')
A = randi(10,[4,2,3]);
M = mean(A,2)
M =
M(:,:,1) =
8.0000
5.5000
2.5000
8.0000
M(:,:,2) =
10.0000
7.5000
5.5000
6.0000
M(:,:,3) =
6.0000
5.5000
8.5000
10.0000
Среднее значение страницы массивов
Создайте трехмерный массив и вычислите среднее значение по каждой странице данных (строки и столбцы).
A(:,:,1) = [2 4; -2 1]; A(:,:,2) = [9 13; -5 7]; A(:,:,3) = [4 4; 8 -3]; M1 = mean(A,[1 2])
M1 =
M1(:,:,1) =
1.2500
M1(:,:,2) =
6
M1(:,:,3) =
3.2500
Начиная в R2018b, вычислять среднее значение по всем размерностям массива, можно или задать каждую размерность в векторном аргументе размерности или использовать 'all' опция.
Среднее значение массива с одинарной точностью
Создайте вектор с одинарной точностью из единиц и вычислите его среднее значение с одинарной точностью.
A = single(ones(10,1));
M = mean(A,'native')
Результат находится также в одинарной точности.
Значение, исключая NaN
Создайте вектор и вычислите его среднее значение, исключая NaN значения.
A = [1 0 0 1 NaN 1 NaN 0];
M = mean(A,'omitnan')
Если вы не задаете 'omitnan', затем mean(A) возвращает NaN.
Входные параметры
свернуть все
A — Входной массив
вектор | матрица | многомерный массив
Входной массив, заданный как векторный, матричный или многомерный массив.
-
Если
Aскаляр, затемmean(A)возвращаетA. -
Если
Aпустая матрица 0 на 0, затемmean(A)возвращаетNaN.
Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | char | datetime | duration
dim — Размерность, которая задает направление расчета
положительный целочисленный скаляр
Величина для работы, заданная как положительный целый скаляр. Если значение не задано, то по умолчанию это первый размер массива, не равный 1.
Размерность dim указывает на размерность, длина которой уменьшает до 1. size(M,dim) 1, в то время как размеры всех других размерностей остаются то же самое.
Рассмотрите двумерный входной массив, A.
-
Если
dim = 1, затемmean(A,1)возвращает вектор-строку, содержащий среднее значение элементов в каждом столбце. -
Если
dim = 2, затемmean(A,2)возвращает вектор-столбец, содержащий среднее значение элементов в каждой строке.
mean возвращает A когда dim больше ndims(A) или когда size(A,dim) 1.
Типы данных: double | single | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
vecdim — Вектор из размерностей
вектор из положительных целых чисел
Вектор из размерностей в виде вектора из положительных целых чисел. Каждый элемент представляет размерность входного массива. Продолжительности выхода в заданных операционных размерностях равняются 1, в то время как другие остаются то же самое.
Рассмотрите 2 3х3 входным массивом, A. Затем mean(A,[1 2]) возвращает 1 1 3 массивами, элементами которых являются средние значения по каждой странице A.
Типы данных: double | single | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
outtype — Тип выходных данных
'default' (значение по умолчанию) | 'double' | 'native'
Выходные данные вводят в виде 'default''double', или 'native'. Эти опции также задают тип данных, в котором выполняется операция.
outtype |
Тип выходных данных |
|---|---|
'default' |
double, если типом входных данных не является singleдлительность, или datetime, в этом случае выходом является 'native' |
'double' |
double, если типом данных не является duration или datetime, в этом случае, 'double' не поддерживается |
'native' |
совпадающий тип данных как вход, если
|
Типы данных: char
nanflag NaN условие
'includenan' (значение по умолчанию) | 'omitnan'
NaN условие в виде одного из этих значений:
-
'includenan'— ВключайтеNaNзначения при вычислении среднего значения, приведении кNaN. -
'omitnan'— Проигнорируйте весьNaNзначения во входе.
Для datetime массивы, можно также использовать 'omitnat' или 'includenat' не использовать и включать NaT значения, соответственно.
Типы данных: char
Больше о
свернуть все
Среднее значение
Для вектора случайной переменной A составил из скалярных наблюдений N, среднее значение задано как
Расширенные возможности
«Высокие» массивы
Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.
Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.
Указания и ограничения по применению:
-
Если вы задаете
dim, затем это должна быть константа. -
outtypeиnanflagопции должны быть постоянными векторами символов. -
Целочисленные типы не поддерживают
'native'выходные данные вводят опцию. -
«Смотрите информацию о генерации кода функций Toolbox (MATLAB Coder) в разделе «»Ограничения переменных размеров»».».
Генерация кода графического процессора
Сгенерируйте код CUDA® для NVIDIA® графические процессоры с помощью GPU Coder™.
Указания и ограничения по применению:
-
Если вы задаете
dim, затем это должна быть константа. -
outtypeиnanflagопции должны быть постоянными векторами символов. -
Целочисленные типы не поддерживают
'native'выходные данные вводят опцию.
Основанная на потоке среда
Запустите код в фоновом режиме с помощью MATLAB® backgroundPool или ускорьте код с Parallel Computing Toolbox™ ThreadPool.
Эта функция полностью поддерживает основанные на потоке среды. Для получения дополнительной информации смотрите функции MATLAB Запуска в Основанной на потоке Среде.
Массивы графического процессора
Ускорьте код путем работы графического процессора (GPU) с помощью Parallel Computing Toolbox™.
Указания и ограничения по применению:
-
'native'опция не поддерживается.
Для получения дополнительной информации смотрите функции MATLAB Запуска на графическом процессоре (Parallel Computing Toolbox).
Распределенные массивы
Большие массивы раздела через объединенную память о вашем кластере с помощью Parallel Computing Toolbox™.
Указания и ограничения по применению:
-
'native'опция не поддерживается.
Для получения дополнительной информации смотрите функции MATLAB Запуска с Распределенными Массивами (Parallel Computing Toolbox).
Представлено до R2006a
- В этой теме 0 ответов, 1 участник, последнее обновление 3 года, 3 месяца назад сделано Васильев Владимир Сергеевич.
-
Сообщения
-
-
Написать программу, которая для целочисленной матрицы 10х10 определяет среднее арифметическое ее элементов и количество положительных элементов в каждой строке.
Материалы по теме: Массивы в С++
Программа должна:
- осуществлять ввод с клавиатуры значений элементов целочисленной матрицы;
- определять среднее арифметическое элементов целочисленной матрицы;
- определять количество положительных элементов в каждой строке целочисленной матрицы;
- выводить результаты вычислений.
Определение среднего арифметического прямоугольной матрицы воспользуемся формулой:
$$S = frac{sumlimits_{i=0}^{nrow} sumlimits_{j=0}^{ncol} A_{i,j}}{nrowcdot ncol} $$
где
a[i][j]—элемент i-й строки (i= 1, 2,..., nrow), j-го столбца (j=1, 2,..., ncol).Блок-схема алгоритма:
Исходный код программы:
#include <iostream> #include <iomanip> // для использования манипулятора using namespace std; void main() { // инициализация переменных const int nrow = 10, ncol = 20; int a[nrow][ncol]; int i, j; setlocale(LC_ALL, "rus"); // возможность вывода информации на экран на русском языке // ввод элементов массива с клавиатуры cout << "Введите элементы массива:" << endl; for (i = 0; i < nrow; i++) for (j = 0; j < ncol; j++) cin >> a[i][j]; // вывод элементов массива на экран // ширина поля для вывода устанавливается в четыре символа //с помощью манипулятора setw() for (i = 0; i < nrow; i++) { for (j = 0; j < ncol; j++) cout << setw(4) << a[i][j] << " "; cout << endl; } // инициализация переменных int n_posl_el; float s = 0; // обработка элементов матрицы для определения ее характеристик for (i = 0; i < nrow; i++) { n_posl_el = 0; for (j = 0; j < ncol; j++) { s += a[i][j]; // сумма всех элементов матрицы if (a[i][j] > 0) n_posl_el++; // подсчет положительных элементов строки } cout << "Строка:" << i << "количество: " << n_posl_el << endl; } s /= nrow * ncol; // расчет среднего арифметического cout << "Среднее арифметическое" << s << endl; system("pause"); // осуществляет задержку экрана }
-
-
Автор
Сообщения
- Для ответа в этой теме необходимо авторизоваться.
Antisovenok, во-первых, ваша программа с ошибкой. В строках 32-34 вы сбиваете переменную цикла j из цикла в строке 29.
Фрагмент (строки 28-37) может выглядеть так:
| C++ | ||
|
При этом отпадает необходимость в переменной num.
Но на самом деле, всё ещё проще:
| C++ | ||
|
Все элементы главной диагонали имеют равные индексы. Чем грех не воспользоваться.
Во-вторых, вас не учили освобождать память, занятую динамическими массивами?
В конце программы надо написать:
| C++ | ||
|
Сообщение от Antisovenok
нужно переделать его с использованием указателей
Я вам подобную манипуляцию с одной программой уже сделал (Указатель в С++ (Я чайник, так что не кусайтесь, пожалуйста)).
Давайте вы как-то поднапряжётесь и сделаете это сами?
В качестве «информации к размышлению» можете принять следующее:
1. В вашем случае, a, типа double** — это указатель на массив указателей на массив double. Т.е. по адресу, хранящемуся в a располагается массив адресов, по которым располагаются массивы строк матрицы. Т.е. a — это массив массивов. (Для иллюстрации посмотрите строки 11-13 вашего кода. А ещё лучше посмотрите под отладчиком как работает этот кусок и где и как будет изменяться содержимое памяти в строках 11-20.)
2. Если double** pa = a, то *p — это адрес начала первой (нулевой) строки матрицы. Соответственно, после p++, *p будет содержать начала второй строки матрицы. И т.д. Т.е. операторы -- и ++ будут перемещать указатель pa по строкам матрицы вверх или вниз.
3. Если double* pra = *pa, то pra — это адрес начала строки матрицы, а *pra — это первый (нулевой) элемент строки матрицы. Соответственно, операторы -- и ++ будут перемещать указатель pra по строке влево или вправо.
4. Ну и наконец классика адресной арифметики: выражение *(*(a + i) + j) эквивалентно выражению a[i][j]. Советую разобраться почему.
Заказываю контрольные, курсовые, дипломные и любые другие студенческие работы здесь.
Найти среднее арифметическое положительных элементов матрицы, лежащих выше главной диагонали.
Разработать блок-схему алгоритма и программу в среде матлаб для нахождения среднего арифметического.
Найти среднее арифметическое нечетных элементов матрицы, лежащих ниже побочной диагонали
Нужно найти среднее арифметическое нечетных элементов матрицы, лежащих ниже побочной диагонали .
Найти среднее арифметическое элементов матрицы и заменить им элементы последнего столбца и строки.
Найти среднее арифметическое значений элементов матрицы и заме¬нить этим значением элементы.
Найти среднее геометрическое отрицательных элементов матрицы 9х9 лежащих на главной диагонали.
Найти среднее геометрическое отрицательных элементов матрицы 9х9 лежащих на главной диагонали. .
Функции MatLab для первичной обработки статистических данных
В MatLab для первичной обработки данных удобно использовать массивы и функции их обработки:
— mах(А) — возвращает наибольший элемент массива, если А одномерный массив (вектор). Если А матрица, то функция mах(А) возвращает вектор-строку, содержащую максимальные элементы каждого столбца.
>> a=[2 5 7;3 9 6;8 5 4]
— mах(А,В) — возвращает массив того же размера, что А и В, каждый элемент которого есть максимальный из соответствующих элементов этих массивов.
>> a=[2 5 7;3 9 6;8 5 4]
b=[3 5 9;1 7 3;6 8 2]
-max(A,[ ],dim) — возвращает наибольшие элементы по столбцам или по строкам матрицы в зависимости от значения скаляра dim (dim=l по столбцам и dim=2 по строкам соответственно). Например, mах(А,[ ],1) возвращает максимальные элементы каждого столбца матрицы А.
-[C,I] =max(A) — кроме максимальных значений возвращает вектор индексов I этих элементов.
>> a=[2 5 7;3 9 6;8 5 4]
-min(A) — возвращает минимальный элемент, если А — вектор; или возвращает вектор-строку, содержащую минимальные элементы каждого столбца, если А — матрица.
-min(A,B) — возвращает массив того же размера, что А и В, каждый элемент которого есть минимальный из соответствующих элементов этих массивов.
-min(A,[ ],dim) — возвращает наименьший элемент по столбцам или по строкам матрицы в зависимости от значения скаляра dim (dim=l по столбцам и dim=2 по строкам соответственно).
-[C,I] = min(A) — кроме минимальных значений возвращает вектор индексов этих элементов.
-mean (А) — возвращает арифметическое среднее значение элементов массива, если А — вектор; или возвращает вектор-строку, содержащую средние значения элементов каждого столбца, если А — матрица.
-mean(A,dim) — возвращает среднее значение элементов по столбцам или по строкам матрицы в зависимости от значения скаляра dim (dim=l по столбцам и dim=2 по строкам соответственно).
>>A=[5 9 2; 8 4 7; 12 4 1]
8.3333 5.6667 3.33338
-median (A) — возвращает медиану, если А — вектор; или вектор-строку медиан для каждого столбца, если А — матрица.
— median(A,dim) — возвращает значения медиан для столбцов или строк матрицы в зависимости от значения скаляра dim.
>> a=[5 9 2; 8 4 7; 12 4 1]
-std(X) — возвращает стандартное отклонение элементов массива, если X — вектор. Если X — матрица, то std(X) возвращает вектор-строку, содержащую стандартное отклонение элементов каждого столбца (обратите внимание, что оно отличается от среднеквадратического отклонения).
-std(X.flag) — возвращает то же значение, что и std(X), если flag=0; если flag=l, функция std(X.l) возвращает среднеквадратическое отклонение (квадратный корень из несмещенной дисперсии).
-std(X.flag.dim) — возвращает стандартное или среднеквадратическое отклонения по рядам (dim=2) или по столбцам(dim=1) матрицы X в зависимости от значения переменной dim.
>> a=[5 9 2; 8 4 7; 12 4 1]
3.5119 2.8868 3.2146
— sort (А) — в случае одномерного массива А сортирует и возвращает элементы по возрастанию их значений; в случае двумерного массива происходит сортировка и возврат элементов каждого столбца. Допустимы вещественные, комплексные и строковые элементы. Если А принимает комплексные значения, то элементы сначала сортируются по абсолютному значению, а затем, если абсолютные значения равны, по аргументу. Если А включает NaN-элементы, sort помещает их в конец.
-[В, INDEX] = sort(A) — наряду с отсортированным массивом возвращает массив индексов INDEX. Он имеет размер size(A), с помощью этого массива можно восстановить структуру исходного массива.
-sort(A,dim) — для матриц сортирует элементы по столбцам (dim=l) или по рядам в зависимости от значения переменной dim.
-sortrows(A) — выполняет сортировку рядов массива А по возрастанию и возвращает отсортированный массив, который может быть или матрицей, или вектором-столбцом.
-sortrows(A,column) — возвращает матрицу, отсортированную по столбцам, точно указанным в векторе column. Например, sortrows(A,[2 3]) сортирует строки матрицы А сначала по второму столбцу, и затем, если его элементы равны, по третьему.
-[В, index] = sortrows (А) — также возвращает вектор индексов index. Если А — вектор-столбец, то B=A(index). Если А — матрица размера m*n, то B=A(index.:).
-cplxpair(A.[],dim) — сортирует матрицу А по строкам или по столбцам в зависимости от значения параметра dim.
Выполнение работы
Вне зависимости от варианта необходимо рассчитать и дать словесную оценку мерам центральной тенденции и мерам разброса.
1. Дан массив целых чисел X=(x1,x2. xn). Сформировать массив Y=(y1,y2. ym), поместив в него в порядке убывания все различные (неповторяющиеся) числа, входящие в массив X. Определить, насколько отличаются средние арифметические значения элементов массивов X и Y.
2. Массив Х=(x1,x2. xn) содержит большое количество нулевых элементов. Определить положение и размер наиболее длинной серии таких элементов и удалить ее из состава массива.
3. Заданы два массива X=(x1,x2. xn) и Y = (y1,y2. ym), в состав которых входят натуральные числа, причем в каждом из этих массивов нет повторяющихся элементов. Сформировать массив Z, включив в него все элементы, которые одновременно содержатся в массиве X и массиве Y.
4. Задан целочисленный массив X=(x1,x2. xn), в котором могут быть одинаковые числа. Найти максимальный и минимальный элементы среди неповторяющихся чисел и обменять их местами. Учесть частный случай, когда в массиве нет неповторяющихся чисел.
5. Из массива целых положительных чисел X=(x1,x2. xn) удалить все четные по значению элементы, кроме последнего, после чего оставшиеся числа расположить в порядке возрастания. Учесть частные случаи (в массиве нет четных элементов, имеется только один четный элемент, все элементы — четные). Буферный массив не использовать.
6. Задан целочисленный массив X = (x1,x2. xn). Если в этом массиве имеются пары одинаковых, но противоположных по знаку элементов, то обменять их местами при условии, что в массиве больше нет равных им элементов. Например, в массиве (1 8 14 12 -8 -7 6 8 -14 -7 12 4) нужно обменять местами элементы 14 и -14.
7. В массиве X=(x1,x2. xn) переставить местами первый и второй отрицательные элементы, третий и четвертый отрицательные элементы и т.д. Если количество отрицательных элементов в массиве меньше двух, преобразование массива не производить. Определить, как изменилось положение минимального и максимального элементов массива Х при его преобразовании.
8. Найти максимальное и минимальное из чисел, встречающихся в целочисленном массиве X=(x1,x2. xn) более одного раза, и обменять их местами. Просмотр массива X выполнять только один раз.
9. Определить наибольший общий делитель всех чисел, содержащихся в заданной последовательности целых положительных чисел.
10. Элементы массива X = (x1,x2. xn) — это последовательность цифр целого числа, записанного в системе счисления с основанием q, 1 j) нечетных элементов преобразовать в четные элементы по формулам: x[i]:=x[i]+1, x[j]:=x[j]-1. Пары элементов i,j выбирать в порядке их следования в массиве X. Определить, как при этом изменились максимальный и минимальный элементы массива X.
14. В заданном массиве целых чисел X=(x1,x2. xn) найти самый длинный подмассив, который является арифметической прогрессией.
15. По заданному целочисленному массиву X=(x1,x2. xn) сформировать массив Y=(y1. ym) такой, что y[i] — это количество элементов из X, не превосходящих x[i] на конечном отрезке X от элемента i+1 до элемента n.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Учись учиться, не учась! 11083 — 
или читать все.
Урок 5 — Работа с массивами в Матлаб(Matlab)
Все данные MatLab представляет в виде массивов. Очень важно правильно понять, как использовать массивы. Без этого невозможна эффективная работа в MatLab, в частности построение графиков, решение задач линейной алгебры, обработки данных, статистики и многих других. В данном подразделе описаны вычисления с векторами.
Массив — упорядоченная, пронумерованная совокупность однородных данных. У массива должно быть имя. Массивы различаются по числу размерностей или измерений: одномерные, двумерные, многомерные. Доступ к элементам осуществляется при помощи индекса. В MatLab нумерация элементов массивов начинается с единицы. Это значит, что индексы должны быть больше или равны единице.
Важно понять, что вектор, вектор-строка или матрица являются математическими объектами, а одномерные, двумерные или многомерные массивы — способы хранения этих объектов в компьютере. Всюду дальше будут использоваться слова вектор и матрица, если больший интерес представляет сам объект, чем способ его хранения. Вектор может быть записан в столбик (вектор-столбец) и в строку (вектор-строка). Вектор-столбцы и вектор-строки часто будут называться просто векторами, различие будет сделано в тех случаях, если важен способ хранения вектора в MatLab. Векторы и матрицы обозначаются курсивом, а соответствующие им массивы прямым моноширинным шрифтом, например: «вектор а содержится в массиве а», «запишите матрицу R в массив r».
Ввод сложение и вычитание векторов
Работу с массивами начнем с простого примера — вычисления суммы векторов: 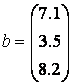
.
Для хранения векторов используйте массивы а и b. Введите массив а в командной строке, используя квадратные скобки и разделяя элементы вектора точкой с запятой:
» a = [1.3; 5.4; 6.9]
a =
1.3000
5.4000
6.9000
Так как введенное выражение не завершено точкой с запятой, то пакет MatLab автоматически вывел значение переменной а. Введите теперь второй вектор, подавив вывод на экран
Для нахождения суммы векторов используется знак +. Вычислите сумму, запишите результат в массив с и выведите его элементы в командное окно:
» с = а + b
с =
8.4000
8.9000
15.1000
Узнайте размерность и размер массива а при помощи встроенных функций ndims и size:
Итак, вектор а хранится в двумерном массиве а размерностью три на один (вектор-столбец из трех строк и одного столбца). Аналогичные операции можно проделать и для массивов b и c. Поскольку числа в пакете MatLab представляются в виде двумерного массива один на один, то при сложении векторов используется тот же знак плюс, что и для сложения чисел.
Ввод вектор-строки осуществляется в квадратных скобках, однако элементы следует разделять пробелами или запятыми. Операции сложения, вычитания и вычисление элементарных функций от вектор-строк производятся так же, как и с вектор-столбцами, в результате получается вектор-строка того же размера, что и исходные. Например:
» s1 = [3 4 9 2]
s1 =
3 4 9 2
» s2 = [5 3 3 2]
s1 =
5 3 3 2
» s3 = s1 + s2
s3 =
8 7 12 4
Замечание 1
Если размеры векторов, к которым применяется сложение или вычитание, не совпадают, то выдается сообщение об ошибке.
Естественно, для нахождения разности векторов следует применять знак минус, с умножением дело обстоит несколько сложнее.
Введите две вектор-строки:
» v1 = [2 -3 4 1];
» v2 = [7 5 -6 9];
Операция .* (не вставляйте пробел между точкой и звездочкой!) приводит к поэлементному умножению векторов одинаковой длины. В результате получается вектор с элементами, равными произведению соответствующих элементов исходных векторов:
» u = v1.*v2
u =
14 -15 -24 9
При помощи .^ осуществляется поэлементное возведение в степень:
» р = v1.^2
p =
4 9 16 1
Показателем степени может быть вектор той же длины, что и возводимый в степень. При этом каждый элемент первого вектора возводится в степень, равную соответствующему элементу второго вектора:
» p = vl.^v2
Р =
128.0000 -243.0000 0.0002 1.0000
Деление соответствующих элементов векторов одинаковой длины выполняется с использованием операции ./
» d = v1./v2
d =
0.2857 -0.6000 -0.6667 0.1111
Обратное поэлементное деление (деление элементов второго вектора на соответствующие элементы первого) осуществляется при помощи операции .
» dinv = vl.v2
dinv =
3.5000 -1.6667 -1.5000 9.0000
Итак, точка в MatLab используется не только для ввода десятичных дробей, но и для указания того, что деление или умножение массивов одинакового размера должно быть выполнено поэлементно.
К поэлементным относятся и операции с вектором и числом. Сложение вектора и числа не приводит к сообщению об ошибке. MatLab прибавляет число к каждому элементу вектора. То же самое справедливо и для вычитания:
» v = [4 6 8 10];
» s = v + 1.2
s =
5.2000 6.2000 9.2000 11.2000
» r = 1.2 — v
r =
-2.8000 -4.8000 -6.8000 -8.8000
» r1 = v — 1.2
r1 = 2.8000 4.8000 6.8000 8.8000
Умножать вектор на число можно как справа, так и слева:
» v = [4 6 8 10];
» p = v*2
р =.
8 12 16 20
» pi = 2*v
pi =
8 12 16 20
Делить при помощи знака / можно вектор на число:
» р = v/2
p =
2 3 4 5
Попытка деления числа на вектор приводит к сообщению об ошибке:
» р = 2/v
. Error using ==> /
Matrix dimensions must agree.
Если требуется разделить число на каждый элемент вектора и записать результат в новый вектор, то следует использовать операцию ./
» w = [4 2 6];
» d = 12./w
d =
3 6 2
Все вышеописанные операции применимы как к вектор-строкам, так и к вектор-столбцам.
Особенность MatLab представлять все данные в виде массивов является очень удобной. Пусть, например, требуется вычислить значение функции sin сразу для всех элементов вектора с (который хранится в массиве с) и записать результат в вектор d. Для получения вектора d достаточно использовать один оператор присваивания:
» d = sin(с)
d =
0.8546
0.5010
0.5712
Итак, встроенные в MatLab элементарные функции приспосабливаются к виду аргументов; если аргумент является массивом, то результат функции будет массивом того же размера, но с элементами, равными значению функции от соответствующих элементов исходного массива. Убедитесь в этом еще на одном примере. Если необходимо найти квадратный корень из элементов вектора dсо знаком минус, то достаточно записать:
» sqrt(-d)
ans =
0 + 0.9244i
0 + 0.7078i
0 + 0.7558i
Оператор присваивания не использовался, поэтому пакет MatLab записал ответ в стандартную переменную ans.
Для определения длины вектор-столбцов или вектор-строк служит встроенная функция length:
Из нескольких вектор-столбцов можно составить один, используя квадратные скобки и разделяя исходные вектор-столбцы точкой с запятой:
Для сцепления вектор-строк также применяются квадратные скобки, но сцепляемые вектор-строки отделяются пробелами или запятыми:
» v1 = [1 2];
» v2 = [3 4 5];
» v = [v1 v2]
v =
1 2 3 4 5
Работа с элементами векторов
Доступ к элементам вектор-столбца или вектор-строки осуществляется при помощи индекса, заключаемого в круглые скобки после имени массива, в котором хранится вектор. Если среди переменных рабочей среды есть массив v, определенный вектор-строкой
» v = [1.3 3.6 7.4 8.2 0.9];
то для вывода, например его четвертого элемента, используется индексация:
Появление элемента массива в левой части оператора присваивания приводит к изменению в массиве
» v(2) = 555
v =
1.3000 555.0000 7.4000 8.2000 0.9000
Из элементов массива можно формировать новые массивы, например
» u = [v(3); v(2); v(1)]
u =
7.4000
555.0000
1.3000
Для помещения определенных элементов вектора в другой вектор в заданном порядке служит индексация при помощи вектора. Запись в массив w четвертого, второго и пятого элементов v производится следующим образом:
» ind = [4 2 5];
» w = v(ind)
w =
8.2000 555.0000 0.9000
MatLab предоставляет удобный способ обращения к блокам последовательно расположенных элементов вектор-столбца или вектор-строки. Для этого служит индексация при помощи знака двоеточия. Предположим, что в массиве w, соответствующем вектор-строке из семи элементов, требуется заменить нулями элементы со второго по шестой. Индексация при помощи двоеточия позволяет просто и наглядно решить поставленную задачу:
» w = [0.1 2.9 3.3 5.1 2.6 7.1 9.8];
» w(2:6) = 0;
» w
w =
0.1000 0 0 0 0 0 9.8000
Присваивание w(2:6) = 0 эквивалентно последовательности команд
w(2) = 0; w(3)=0; w(4)=0; w(5)=0; w(6)=0.
Индексация при помощи двоеточия оказывается удобной при выделении части из большого объема данных в новый массив:
» w — [0.1 2.9 3.3 5.1 2.6 7.1 9.8];
» wl = w(3:5)
wl =
3.3000 5.1000 2.6000
Составьте массив w2, содержащий элементы w кроме четвертого. В этом случае удобно использовать двоеточие и сцепление строк:
» w2 = [w(l:3) w(5:7)]
w2 =
0.1000 2.9000 3.3000 2.6000 7.1000 9.8000
Элементы массива могут входить в выражения. Нахождение, например среднего геометрического из элементов массива u, можно выполнить следующим образом:
Конечно, этот способ не очень удобен для длинных массивов. Для того чтобы найти среднее геометрическое, необходимо набрать в формуле все элементы массива. В MatLab существует достаточно много специальных функций, облегчающих подобные вычисления.
Применение функций обработки данных к векторам
Перемножение элементов вектора-столбца или вектора-строки осуществляется при помощи функции prod:
» z = [3; 2; 1; 4; 6; 5];
» р = prod(z)
p = 720
Функция sum предназначена для суммирования элементов вектора. С ее помощью нетрудно вычислить среднее арифметическое элементов вектора z:
» sum(z)/length(z)
ans =
3.5000
В MatLab имеется и специальная функция mean для вычисления среднего арифметического:
Для определения минимального и максимального из элементов вектора служат встроенные функции min и max:
» m1 = max(z)
m1 =
6
» m2 = min(z)
m2 =
1
Часто необходимо знать не только значение минимального или максимального элемента в массиве, но и его индекс (порядковый номер). В этом случае встроенные функции min и max необходимо использовать с двумя выходными аргументами, например
» [m, k] = min(z)
m =
1
k =
3
В результате переменной m будет присвоено значение минимального элемента массива z, а номер минимального элемента занесен в переменную k.
Для получения информации о различных способах использования функций следует набрать в командной строке help и имя функции. MatLab выведет в командное окно всевозможные способы обращения к функции с дополнительными пояснениями.
В число основных функций для работы с векторами входит функция упорядочения вектора по возрастанию его элементов sort.
» r = [9.4 -2.3 -5.2 7.1 0.8 1.3];
» R = sort(r)
R =
-5.2000 -2.3000 0.8000 1.3000 7.1000 9.4000
Можно упорядочить вектор по убыванию, используя эту же функцию sort:
» R1 = -sort(-r)
R1 =
9.4000 7.1000 1.3000 0.8000 -2.3000 -5.2000
Упорядочение элементов в порядке возрастания их модулей производится с привлечением функции abs:
» R2 = sort(abs(r))
R2 =
0.8000 1.3000 2.3000 5.2000 7.1000 9.4000
Вызов sort с двумя выходными аргументами приводит к образованию массива индексов соответствия элементов упорядоченного и исходного массивов:
» [rs, ind] = sort(r)
rs =
-5.2000 -2.3000 0.8000 1.3000 7.1000 9.4000
ind =
3 2 5 6 4 1
Оценка статьи:
Загрузка…
Adblock
detector