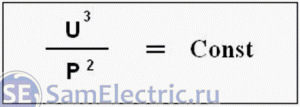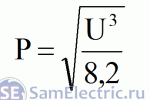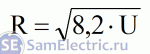Разработка схемы и расчет осложняется еще одним обстоятельством. Ни один производитель не может определить точные параметры для каждого диода, поэтому они определяют среднее напряжение при оптимальном уровне электрического тока для выпускаемой партии. Это означает, что для определения точных значений при проектировании схем и расчете формул лучше всего использовать мультиметр.
Как рассчитать сопротивление лампочки?
Светодиоды пришли на смену традиционным системам освещения – лампам накаливания и энергосберегающим лампам. Чтобы светодиод работал правильно и не перегорал, его нельзя подключать непосредственно к электросети. Идея заключается в том, что он имеет низкое внутреннее сопротивление, поэтому если вы подключите его напрямую, ток будет высоким, и он сгорит. Вы можете ограничить ток с помощью резисторов. Однако необходимо выбрать правильный резистор для светодиода. Для этого производятся специальные расчеты.
Из этой таблицы видно, что сопротивление нити накала лампы накаливания в холодном и горячем состоянии отличается в 12-13 раз. Это означает, что потребляемая мощность в начальный момент времени увеличивается в тот же фактор.
Зависимость сопротивления нити накала лампы накаливания от напряжения
| Напряжение | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
| % напряжения | 8.3 | 16.7 | 25.0 | 33.3 | 41.7 | 50.0 | 58.3 | 66.7 |
| Текущая сторона | 0.55 | 0.7 | 0.84 | 0.97 | 1.08 | 1.19 | 1.29 | 1.38 |
| Сопротивление | 3.6 | 5.7 | 7.1 | 8.2 | 9.3 | 10.1 | 10.9 | 11.6 |
| Мощность | 1.1 | 2.8 | 5.04 | 7.76 | 10.8 | 14.28 | 18.06 | 22.08 |
| Напряжение | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
| % напряжения | 75.0 | 83.3 | 91.7 | 100.0 | 108.3 | 116.7 | 125.0 | 133.3 |
| Текущая страница | 1.47 | 1.55 | 1.63 | 1.7 | 1.77 | 1.84 | 1.92 | 2 |
| Сопротивление | 12.2 | 12.9 | 13.5 | 14.1 | 14.7 | 15.2 | 15.6 | 16.0 |
| Мощность | 26.46 | 31 | 35.86 | 40.8 | 46.02 | 51.52 | 57.6 | 64 |
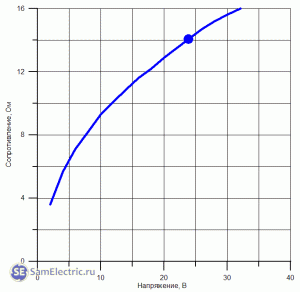
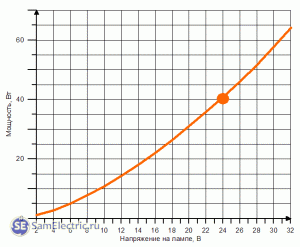
Как видно из таблицы, зависимость сопротивления лампочки от напряжения нелинейна. Это можно проиллюстрировать на графике ниже. Рабочая точка на графике выделяется.
Сопротивление нити накала лампы накаливания в зависимости от напряжения
Кстати, сопротивление тестовой лампочки, измеренное цифровым мультиметром, составляет около 1 Ом. Предел измерения составляет 200 Ом, выходное напряжение вольтметра – 0,5 В. Эти данные также находятся в пределах, полученных ранее.
Зависимость мощности от напряжения:
Зависимость мощности от напряжения
Для ламп 230 В следующая таблица основана на экспериментальных данных:
| Мощность лампочки, W |
25 | 40 | 60 | 75 | 100 |
| R холодной нити накаливания, Ом | 150 | 90-100 | 60-65 | 45-50 | 37-40 |
| R hot нить накала, Ом |
1930 | 1200 | 805 | 650 | 490 |
| R gore./Rhool. | 12 | 12 | 13 | 13 | 12 |
Из этой таблицы видно, что сопротивление холодной и горячей нити накала лампочки отличается в 12-13 раз. Это означает, что потребляемая мощность в начальный момент времени увеличивается в такой же раз.
Следует отметить, что сопротивление в холодном состоянии измерялось мультиметром на пределе 200 Ом при выходном напряжении мультиметра 0,5 В. При измерении сопротивления на пределе 2000 Ом (выходное напряжение 2 В) показания сопротивления увеличиваются более чем в полтора раза, что опять же соответствует идее статьи.
“Горячее” сопротивление измерялось косвенным методом.
Получаем значение 100 Ом для резистора. Найдите рассеиваемую мощность для него (отнимите ток от Imax):
Онлайн-калькулятор сопротивления
Задача усложняется, если необходимо подключить более одного диода.
Чтобы вам было проще самостоятельно выполнять расчеты, мы подготовили онлайн-калькулятор для расчета сопротивления резисторов. Если вы подключаете несколько светодиодов, вам придется выбирать между параллельным и последовательным соединением между ними. И для этих схем нужны дополнительные расчеты для источника питания. Эти данные можно легко найти в Интернете, но мы рекомендуем использовать наш калькулятор.
Вам необходимо знать:
- Напряжение источника питания.
- Вольтамперная характеристика диода.
- Токовая характеристика диода.
- Количество диодов.
Вам также нужно будет выбрать параллельное или последовательное подключение. Мы рекомендуем изучить различия между соединениями в подготовленных ниже разделах.
Это свойство металлов позволяет создавать простые и относительно дешевые лампы накаливания без сложных пускорегулирующих аппаратов, необходимых в светодиодных и люминесцентных светильниках.
Полезная информация для начинающих электриков
Как использовать закон Ома на практике
Почти два столетия назад, в далеком 1827 году, Георг Ом распознал взаимосвязь между фундаментальными характеристиками электричества.
Он изучил и опубликовал данные о влиянии сопротивления участка цепи на величину тока, создаваемого напряжением. Удобно представить это с помощью изображения.
Любая работа всегда создается рабочим электрическим током. Он вращает ротор электродвигателя, заставляет светиться лампочку, сваривает или режет металлы и делает другие вещи.
Поэтому ему должны быть созданы оптимальные условия: значение электрического тока должно поддерживаться на номинальном уровне. Это зависит от:
- значение напряжения, приложенного к цепи;
- сопротивление среды, через которую протекает ток.
Здесь напряжение, как разность потенциалов приложенной энергии, является силой, которая создает электрический ток.
Если нет напряжения, то из-за отсутствия тока в подключенной электрической цепи не может быть совершена полезная работа. Такая ситуация часто возникает, когда кабель питания сломан, перетерт или перегорел.
С другой стороны, сопротивление решает противоположную проблему для напряжения. При очень высоком значении он ограничивает ток так, что он не может совершить никакой работы. Этот режим работы используется для хороших диэлектриков.
Примеры из реальной жизни
Между контактами образуется воздушный зазор. Это отличный изолятор, который препятствует прохождению тока через светильник.
Ток короткого замыкания может пережечь провода, что приведет к пожару в квартире. Поэтому из таких ситуаций есть только один выход: использование защитных устройств, способных как можно быстрее отключить напряжение питания.
В случае бытовой сети эту функцию выполняют автоматические выключатели или предохранители, работу которых я рассмотрю в других статьях.
При использовании резистора важно помнить, что сам по себе он не вечен: имея запас, чтобы выдержать приложенную энергию, он может износиться, выйти из строя и перегореть.
По этой причине в сопротивление вводится понятие диссипативной мощности, которая надежно рассеивается во внешнюю среду. Если тепловая энергия, создаваемая протекающим током, превысит это значение, резистор сгорит.
Что такое участок цепи
Рассмотрим простейшую электрическую цепь, состоящую из батареи, лампочки и нескольких проводов. В нем циркулирует электрический ток.
Показанная схема, или полная цепь, состоит из двух контуров:
- Внутренний источник напряжения.
- Внешняя область: лампочка с подключенными проводами.
Эти процессы, происходящие внутри аккумулятора, интересуют нас в основном как когнитивные процессы. Мы можем сделать их только хуже, если используем их неправильно.
Например, мы не можем контролировать электроэнергию, которая поступает в наш дом из трансформаторной подстанции. Мы просто используем его. Автоматические выключатели, УЗО, реле, разрядники или ограничители перенапряжения и другие современные модули защиты защищают нас от неисправностей и аварийных ситуаций.
Внешняя цепь, подключенная к источнику напряжения, является той частью цепи, в которой, используя закон Ома, мы совершаем полезную для себя работу.
Как использовать треугольник закона Ома
Простой мнемонический принцип представлен тремя частями треугольника. Это облегчает запоминание взаимосвязи между током, сопротивлением и напряжением.
Напряжение всегда находится на самом верху. Ток и сопротивление находятся внизу. Когда мы вычисляем одно значение из двух других, мы выводим его из треугольника и выполняем арифметическую операцию: деление или умножение.
Руководство для начинающих электриков
Треугольник закона Ома легко запомнить, но он не позволяет учитывать потребляемую мощность электроприбора. Этот четвертый параметр, важный для каждого домашнего электрика, всегда должен быть принят во внимание. .
Все бытовые электроприборы показывают потребляемую мощность в ваттах или киловаттах. Его формулу вместе с предыдущими значениями можно прочитать на рисунке ниже.
Этот справочник электрика позволит вам произвести простые расчеты в голове или на бумаге. Формулы из него встроены в алгоритм, по которому работает мой онлайн-калькулятор закона Ома.
Я предлагаю вам провести те же расчеты, используя оба метода, и сравнить результаты. Если вы обнаружили несоответствия, пожалуйста, укажите их в комментариях. Это будет вашей помощью для моего проекта.
Я постарался кратко и просто изложить принципы закона Ома в применении к домашней работе. Я считаю это достаточным и не рассматриваю закон Ома для полной цепи в его обычной форме, комплексные числа или что-то еще.
Однако если вы хотите получить видеоурок по этой теме, воспользуйтесь уроком владельца Физика – Закон Ома.
Возможно, у вас остались вопросы о том, как работает калькулятор? Ответьте на них, и я отвечу. Используйте раздел комментариев.
Наконец, я напоминаю вам, что сейчас самое время поделиться этим материалом со своими друзьями в социальных сетях и подписаться на рассылку. Это позволит вам быть в курсе новых статей.
<t^circ>_1)” />,
<t^circ>_2)” />,
Задача 40: Определение сопротивления нити накала электрической лампы
Для лампы накаливания мощностью сто пятьдесят ватт и напряжением двести двадцать вольт определите сопротивление вольфрамовой нити при температуре двадцать пять градусов Цельсия. Известно, что температура нити лампы составляет две тысячи пятьсот градусов Цельсия. Температурный коэффициент сопротивления вольфрама составляет 5,1×10 -3 град -1 .
Напишем формулы для расчета сопротивления нити накала при комнатной и рабочей температуре


где R1 – Сопротивление нити накала при 25 градусах Цельсия;
R2 – сопротивление нити накала при температуре 2500 градусов Цельсия.


Сопротивление нити накала при рабочей температуре определяется по формуле

Формула для расчета сопротивления нити накала при температуре 25 градусов Цельсия имеет вид

Ответ: сопротивление вольфрамовой нити электрической лампы при температуре двадцать пять градусов Цельсия составляет двадцать шесть целых пять ом.
Из этой таблицы видно, что сопротивление нити накала лампы накаливания в холодном и горячем состоянии отличается в 12-13 раз. Это означает, что потребляемая мощность в начальный момент времени увеличивается в тот же фактор.
Каково сопротивление лампочки?
Однажды я решил проверить закон Ома. Я применил его к лампочке. Я измерил сопротивление лампы Лисма 230В 60Вт и оно составило 59 Ом. Он в несколько раз мощнее, чем заявлено! Я удивился, но потом вспомнил слово, которое все объяснило. бареттер
Дело в том, что сопротивление вольфрамовой нити лампы накаливания сильно зависит от температуры (следствие протекания тока). В моем случае, если бы это был не вольфрам, а обычный резистор, его рассеиваемая мощность при 230 В была бы P = U2/R = 896. Почти 900 ватт!
Кстати, именно поэтому производители датчиков с транзисторным выходом рекомендуют соблюдать осторожность при их подключении.
Как же измерить рабочее сопротивление нити накала? Ты не можешь. Вы можете определить его только косвенно, основываясь на знаменитом законе Ома. (Строго говоря, все омметры используют один и тот же закон – прикладывают напряжение и измеряют ток). Без мультиметра тоже не обойтись.
Используя косвенный метод и лампочку Лисма 24 В мощностью 40 Вт, я составил следующую таблицу:
Зависимость сопротивления нити накала лампы накаливания от напряжения
(Номинальные значения отмечены).
Как видно из таблицы, зависимость сопротивления лампочки от напряжения нелинейная. Это можно проиллюстрировать на графике ниже. Рабочая точка на графике выделяется.
Сопротивление нити накала лампы накаливания в зависимости от напряжения
Кстати, сопротивление тестовой лампочки, измеренное цифровым мультиметром, составляет около 1 Ом. Предел измерения составляет 200 Ом, выходное напряжение вольтметра – 0,5 В. Эти данные также находятся в пределах, полученных ранее.
Зависимость мощности от напряжения:
Зависимость мощности от напряжения
Для ламп на 230 В эта таблица составлена на основе экспериментальных данных:
Сила и сопротивление
Из этой таблицы видно, что сопротивление нити накала холодной и горячей лампочки отличается в 12-13 раз. Это означает, что потребление энергии при включении увеличивается в 12 раз.
Можно говорить о пусковом токе для ламп накаливания.
Стоит отметить, что холодное сопротивление было измерено мультиметром на пределе 200 Ом при выходном напряжении мультиметра 0,5 В. При измерении сопротивления на пределе 2000 Ом (выходное напряжение 2 В) показания сопротивления увеличиваются более чем в полтора раза, что опять же соответствует идее статьи.
“Горячее” сопротивление измерялось косвенным методом.
Сопротивление нити накала лампы накаливания
Дополнение к статье, чтобы сделать ее еще более полной.
Лампы с цоколем T8, сопротивление нити накала зависит от мощности:
Сопротивление измеряется цифровым омметром на пределе 200 Ом.
Формула для мощности и напряжения
Обновление статьи. У меня в блоге есть статья автора Станислава Матросова, который разработал тему сопротивления катушки лампы накаливания с теоретической стороны. Он вывел формулу, согласно которой:
Для каждой лампы существует параметр, который стабилен в широком диапазоне электрических условий. Этот параметр представляет собой отношение куба напряжения к квадрату мощности:
Я решил рассчитать это значение в Excel, используя данные из статьи. Вот что я получил:
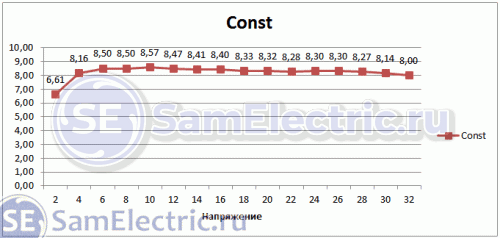
Действительно, константа, которая с некоторой погрешностью по всему диапазону равна 8,2±0,2. Ее размерность – “вольт на куб на ватт в квадрате”.
Расчетная постоянная для лампочки = 8,2
Низкое значение константы в начале диапазона объясняется автором в статье по ссылке.
Теперь, зная значение этой константы (8.2), мы можем написать формулу зависимости мощности от напряжения для лампы накаливания 40 Вт 24 В:
Зависимость мощности лампы накаливания от напряжения
Формула сопротивления
Но давайте вернемся к теме статьи. Проверим вывод Станислава Матросова о том, что сопротивление лампочки пропорционально корню из напряжения. Исходя из предыдущих рассуждений, можно вывести формулу для конкретной лампы накаливания 40 Вт 24 В:
Зависимость сопротивления от напряжения, формула для электрической лампочки
Давайте теперь проверим, как эта формула соотносится с полученными мной экспериментальными данными (см. таблицу в начале статьи). Давайте создадим такую таблицу:
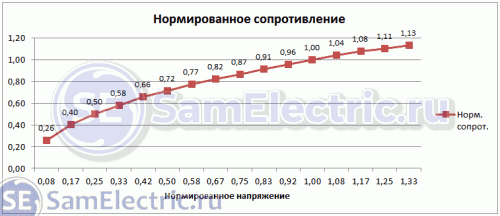
Таблица требует пояснений. Для сохранения размерности я нормализовал экспериментально определенное напряжение (колонка 2) и рассчитанное сопротивление (колонка 4).
Столбец 5 – это корень из нормализованного напряжения, и вы можете видеть, что значения этого столбца идеально совпадают со столбцом 4!
Но давайте вернемся к фактическому сопротивлению и рассчитаем его по приведенной выше формуле (зависимость сопротивление/напряжение). Это столбец 6. Вы можете ясно видеть, что расчет по формуле почти идеально совпадает с расчетом по экспериментальным данным!
Зависимость сопротивления от напряжения. Квадратичная зависимость.
Кто хочет проверить мои расчеты, прилагаю файл: •Файл с расчетами и графиками
/ Файл с расчетами и графиками для статьи о лампочках, xlsx, 19.51 kB, скачан: 430 раз
</t^circ></t^circ>
- 5 причин, почему лампочки часто перегорают в вашей квартире и что делать?.
- Основные параметры выпрямительных диодов; Школа для инженеров-электриков: Электротехника и электроника.
- Правильное переключение светодиодов; STC ORBITA.
- Полупроводниковые диоды.
- Обратный ток. Что такое возвратный ток?.
- Важен ли для вас индикатор уведомлений?.
- Основы электроники. Урок 4: Расчет резистора для светодиода.
Решил
я
как-то
проверить
закон
Ома.
Применительно
к
лампе
накаливания.
Измерил
сопротивление
лампочки
Лисма
230
В
60
Вт,
оно
оказалось
равным
59
Ом.
Я
было
удивился,
но
потом
вспомнил
слово,
которое
всё
объясняло
–
бареттер.
Дело
в
том,
что
сопротивление
вольфрамовой
нити
лампы
накаливания
сильно
зависит
от
температуры
(следствие
протекания
тока).
В
моем
случае,
если
это
бы
был
не
вольфрам,
а
обычный
резистор,
его
рассеиваемая
мощность
при
напряжении
230
Вольт
была
бы
P
=
U2/R
=
896.
Почти
900
Ватт!
Кстати,
именно
поэтому
производители
датчиков
с
транзисторным
выходом
рекомендуют
соблюдать
осторожность
при
подключении
датчиков.
Как
же
измерить
рабочее
сопротивление
нити
лампы
накаливания?
А
никак.
Его
можно
только
определить
косвенным
путем,
из
закона
знаменитого
Ома.
(Строго
говоря,
все
омметры
используют
тот
же
закон
–
прикладывают
напряжение
и
меряют
ток).
И
мультиметром
тут
не
обойдешься.
Используя
косвенный
метод
и
лампочку
Лисма
24
В
с
мощностью
40
Вт,
я
составил
вот
такую
табличку:
Зависимость
сопротивления
нити
лампы
накаливания
от
напряжения
| Напряжение | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
|
% напряжения |
8.3 | 16.7 | 25.0 | 33.3 | 41.7 | 50.0 | 58.3 | 66.7 |
| Ток | 0.55 | 0.7 | 0.84 | 0.97 | 1.08 | 1.19 | 1.29 | 1.38 |
| Сопротивление | 3.6 | 5.7 | 7.1 | 8.2 | 9.3 | 10.1 | 10.9 | 11.6 |
| Мощность | 1.1 | 2.8 | 5.04 | 7.76 | 10.8 | 14.28 | 18.06 | 22.08 |
(продолжение таблицы)
| Напряжение | 18 | 20 | 22 |
24 |
26 | 28 | 30 | 32 |
|
% напряжения |
75.0 | 83.3 | 91.7 |
100.0 |
108.3 | 116.7 | 125.0 | 133.3 |
| Ток | 1.47 | 1.55 | 1.63 |
1.7 |
1.77 | 1.84 | 1.92 | 2 |
| Сопротивление | 12.2 | 12.9 | 13.5 |
14.1 |
14.7 | 15.2 | 15.6 | 16.0 |
| Мощность | 26.46 | 31 | 35.86 |
40.8 |
46.02 | 51.52 | 57.6 | 64 |
(Номинальные параметры выделены)
Как
видно
из
таблицы,
зависимость
сопротивления
лампочки
от
напряжения
нелинейная.
Это
может
проиллюстрировать
график,
приведенный
ниже.
Рабочая
точка
на
графике
выделена.
Сопротивление
нити
лампы
накаливания
в
зависимости
от
напряжения
Кстати,
сопротивление
подопытной
лампочки,
измеренное
с
помощью
цифрового
мультиметра
–
около
1
Ома.
Предел
измерения
–
200
Ом,
при
этом
выходное
напряжение
вольтметра
–
0,5
В.
Эти
данные
также
укладываются
в
полученные
ранее.
Зависимость
мощности
от
напряжения:
Зависимость
мощности
от
напряжения
Для
ламп
на
напряжение
230
В
на
основании
экспериментальных
данных
была
составлена
вот
такая
табличка:
|
Мощность лампочки, Вт |
25 | 40 | 60 | 75 | 100 |
|
R холодной нити,Ом |
150 | 90-100 | 60-65 | 45-50 | 37-40 |
|
R горячей нити, |
1930 | 1200 | 805 | 650 | 490 |
| Rгор./Rхол. | 12 | 12 | 13 | 13 | 12 |
Из
этой
таблицы
видно,
что
сопротивление
нити
лампы
накаливания
в
холодном
и
горячем
состоянии
отличается
в
12-13
раз.
А
это
значит,
что
во
столько
же
раз
увеличивается
потребляемая
мощность
в
первоначальный
момент.
Стоит
отметить,
что
сопротивление
в
холодном
состоянии
измерялось
мультиметром
на
пределе
200
Ом
при
выходном
напряжении
мультиметра
0,5
В.
При
измерении
сопротивления
на
пределе
2000
Ом
(выходное
напряжение
2
В)
показания
сопротивления
увеличиваются
более
чем
в
полтора
раза,
что
опять
же
укладывается
в
идею
статьи.
“Горячее”
сопротивление
измерялось
косвенным
методом.
UPD:
Сопротивление
нити
накаливания
люминесцентных
ламп
Дополнение
к
статье,
чтобы
получился
ещё
более
полный
материал.
Лампы
с
цоколем
Т8,
сопротивление
спирали
в
зависимости
от
мощности
:
10
Вт
–
8,0…8,2
Ом
15
Вт
–
3,3…3,5
Ом
18
Вт
–
2,7…2,8
Ом
36
Вт
–
2,5
Ом.
Сопротивление
измерялось
цифровым
омметром
на
пределе
200
Ом.
Формула
мощности
и
напряжения
Обновление
статьи
от
января
2018.
У
меня
на
блоге
появилась
статья
автора
Станислава
Матросова,
который
развил
тему
сопротивления
спирали
лампочки
с
теоретической
стороны.
Он
вывел
формулу,
согласно
которой:
Для
любой
лампы
накаливания
существует
параметр,
стабильный
в
широком
диапазоне
электрических
режимов. Этим
параметром
является
отношение
куба
напряжения
к
квадрату
мощности:
Я
решил
на
основе
данных,
полученных
в
статье,
посчитать
эту
величину
в
Экселе.
Вот
что
у
меня
получилось:
|
U |
P |
U^3 |
P^2 |
Const |
| 2 | 1,1 | 8 | 1,21 | 6,61157 |
| 4 | 2,8 | 64 | 7,84 | 8,163265 |
| 6 | 5,04 | 216 | 25,4016 | 8,503401 |
| 8 | 7,76 | 512 | 60,2176 | 8,502498 |
| 10 | 10,8 | 1000 | 116,64 | 8,573388 |
| 12 | 14,28 | 1728 | 203,9184 | 8,473978 |
| 14 | 18,06 | 2744 | 326,1636 | 8,412956 |
| 16 | 22,08 | 4096 | 487,5264 | 8,401596 |
| 18 | 26,46 | 5832 | 700,1316 | 8,329863 |
| 20 | 31 | 8000 | 961 | 8,324662 |
| 22 | 35,86 | 10648 | 1285,94 | 8,280327 |
| 24 | 40,8 | 13824 | 1664,64 | 8,304498 |
| 26 | 46,02 | 17576 | 2117,84 | 8,29902 |
| 28 | 51,52 | 21952 | 2654,31 | 8,270321 |
| 30 | 57,6 | 27000 | 3317,76 | 8,138021 |
| 32 | 64 | 32768 | 4096 | 8 |
Действительно,
константа,
которая
с
некоторой
погрешностью
во
всём
диапазоне
равна
8,2±0,2.
Её
размерность
–
“Вольт
в
кубе
на
Ватт
в
квадрате”.
Константа
для
расчета
лампы
накаливания
=
8,2
Низкое
значение
константы
в
начале
диапазона
объяснено
автором
в
приведенной
по
ссылке
статье.
Теперь,
зная
значение
этой
константы
(8,2),
можем
записать
формулу
зависимости
мощности
от
напряжения
лампочки
накаливания
40Вт
24В:
Зависимость
мощности
лампочки
накаливания
от
напряжения
Формула
для
сопротивления
Но
вернёмся
к
теме
статьи.
Проверим
вывод
Станислава
Матросова
о
том,
что
сопротивление
лампочки
пропорционально
корню
из
напряжения.
Из
предыдущих
выводов
можно
вывести
формулу
для
конкретной
лампочки
40Вт
24В:
Зависимость
сопротивления
от
напряжения,
формула
для
лампы
накаливания
Теперь
проверим,
как
эта
формула
соотносится
с
полученными
мною
экспериментальным
данным
(см.
таблицу
в
начале
статьи).
Составим
такую
таблицу:
|
1. Напря- жение, |
2. Норм. напр. |
3. Сопрот., Ом |
4. Норм. сопрот. |
5. Корень из напряж. |
6. Корень из Х из |
| 2 | 0,08 | 3,6 | 0,26 | 0,29 | 4,04 |
| 4 | 0,17 | 5,7 | 0,40 | 0,41 | 5,72 |
| 6 | 0,25 | 7,1 | 0,50 | 0,50 | 7,01 |
| 8 | 0,33 | 8,2 | 0,58 | 0,58 | 8,09 |
| 10 | 0,42 | 9,3 | 0,66 | 0,65 | 9,04 |
| 12 | 0,50 | 10,1 | 0,72 | 0,71 | 9,91 |
| 14 | 0,58 | 10,9 | 0,77 | 0,76 | 10,70 |
| 16 | 0,67 | 11,6 | 0,82 | 0,82 | 11,44 |
| 18 | 0,75 | 12,2 | 0,87 | 0,87 | 12,13 |
| 20 | 0,83 | 12,9 | 0,91 | 0,91 | 12,79 |
| 22 | 0,92 | 13,5 | 0,96 | 0,96 | 13,41 |
| 24 | 1,00 | 14,1 | 1,00 | 1,00 | 14,01 |
| 26 | 1,08 | 14,7 | 1,04 | 1,04 | 14,58 |
| 28 | 1,17 | 15,2 | 1,08 | 1,08 | 15,13 |
| 30 | 1,25 | 15,6 | 1,11 | 1,12 | 15,66 |
| 32 | 1,33 | 16 | 1,13 | 1,15 | 16,18 |
Таблица
требует
пояснений.
Чтобы
была
соблюдена
размерность,
я
нормировал
экспериментально
заданное
напряжение
(столбец
2)
и
рассчитанное
сопротивление
(столбец
4).
Колонка
5
–
это
корень
из
нормированного
напряжения,
и
видно,
что
значения
этой
колонки
отлично
совпадают
с
колонкой
4!
Но
давайте
вернемся
в
реальному
сопротивлению,
и
рассчитаем
его
по
приведенной
выше
формуле
(Зависимость
сопротивления
от
напряжения).
Это
–
6-я
колонка.
Хорошо
видно,
что
расчет
по
формуле
практически
идеально
совпадает
с
расчетом
из
экспериментальных
данных!
Зависимость
сопротивления
от
напряжения.
Квадратичная
зависимость.
Кто
хочет
проверить
мои
расчеты,
прикладываю
файл: •
Файл
с
расчетами
и
графиками
/
Файл
с
расчетами
и
графиками
к
статье
про
лампу
накаливания,
xlsx,
19.51
kB,
скачан:
1064
раз./
Всё,
учебник
физики
можно
переписывать!

Кому
интересно
–
задачкапро
последовательное
подключение
двух
лампочек.
Понравилось?
Поставьте
оценку,
и
почитайте
другие
статьи
блога!
Загрузка…
Внимание!
Автор
блога
не
гарантирует,
что
всё
написанное
на
этой
странице
—
истина.
За
ваши
действия
и
за
вашу
безопасность
ответственны
только
вы!
Содержание
- 1 Как рассчитать сопротивление зная мощность и напряжение?
- 2 Как узнать амперы зная мощность?
- 3 Как сопротивление зависит от мощности?
- 4 Как найти сопротивление Ом?
- 5 Как рассчитать ток по мощности?
- 6 Как найти сопротивление из формулы мощности?
- 7 Сколько идет ампер на 1 квт?
- 8 Сколько ватт в 1 ампере 12 вольт?
- 9 Чему равен 1 ампер?
- 10 Как сила тока зависит от мощности?
- 11 Как рассчитать мощность?
- 12 Какая буква обозначает мощность?
- 13 Как найти сопротивление при параллельном соединении?
- 14 Как найти общее сопротивление в электрической цепи?
Как рассчитать сопротивление зная мощность и напряжение?
Узнать мощность, если известны напряжение и сопротивление. W = 220 в * 220 в / 500 ом = 96.8 вт.
Как узнать амперы зная мощность?
Таким образом, чтобы получить амперы, нужно ватты разделить на вольты питания — мощность разделить на напряжение I = P/U (вольт в бытовой сети 220-230). Бывает часто, что на сетевом электроприборе мощность указана в киловаттах (кВт), тогда может потребоваться перевести киловатты в амперы.
Как сопротивление зависит от мощности?
Получится, что мощность равна квадрату электрического тока, помноженному на сопротивление. … В этом случае подставив вместо значения тока I = U/R, получим значение мощности, равное квадрату напряжения, поделенному на сопротивление.
Как найти сопротивление Ом?
Если известны значения общей силы тока и напряжения в цепи, общее сопротивление вычисляется по закону Ома: R = V/I. Например, напряжение в параллельной цепи равно 9 В, а общая сила тока равна 3 А. Общее сопротивление: RO = 9 В / 3 А = 3 Ом.
Как рассчитать ток по мощности?
Формула расчета мощности электрического тока
Согласно закону Ома, сила тока(I) пропорциональна напряжению(U) и обратно пропорциональна сопротивлению(R), а мощность(P) рассчитывается как произведение напряжения и силы тока. Исходя из этого, ток в участке сети рассчитывается: I = P/U.
Как найти сопротивление из формулы мощности?
U = (P*R)
…
Электрическое сопротивление:
- R = U / I.
- R = U 2/ P.
- R = P / I.
Сколько идет ампер на 1 квт?
Сколько ампер в киловатте и сколько киловатт в ампере
Поскольку в одном киловатте 1000 ватт, то для сетевого напряжения в 220 вольт можно принять, что в одном киловатте 4,54 ампера, потому что I = P/U = 1000/220 = 4,54 ампер.
Сколько ватт в 1 ампере 12 вольт?
А значит, если имеем дело с автомобильной сетью на 12 вольт, то 1 ампер — это 12 Ватт, а в бытовой электросети 220 V такая сила тока будет в электроприборе мощностью 220 Вт (0,22 кВт). В промышленном оборудовании, питающемся от 380 Вольт, целых 657 Ватт.
Чему равен 1 ампер?
Ампе́р (обозначение: А) — единица измерения силы электрического тока в системе СИ, а также единица магнитодвижущей силы и разности магнитных потенциалов (устаревшее наименование — ампер-виток). 1 Ампер это сила тока, при которой через проводник проходит заряд 1 Кл за 1 сек.
Как сила тока зависит от мощности?
Количество электричества, проходящего через поперечное сечение цепи в течение одной секунды, есть не что иное, как сила тока в цепи. Следовательно, мощность электрического тока будет прямо пропорциональна разности потенциалов (напряжению) и силе тока в цепи.
Как рассчитать мощность?
Определите мощность источника питания.
Напряжение – это величина, характеризующая электрическое поле, создаваемое током. Мощность равна произведению силы тока на напряжение, то есть 1 Вт = 1 А х 1 В. Формула: Р = I х V. Например, если сила тока равна 3 А, а напряжение равно 110 В, то мощность равна: 3 х 110 = 330 Вт.
Какая буква обозначает мощность?
Обычно в формулах механики обозначается символом N. В электротехнике обычно обозначается символом P — от лат. potestas (сила, мощь, действенность); Иногда используется символ W (от англ.
Как найти сопротивление при параллельном соединении?
Общее сопротивление цепи при параллельном соединении проводников определяется по формуле: 1 R = 1 R 1 + 1 R 2 . Обратное значение общего сопротивления равно сумме обратных значений сопротивлений отдельных проводников. Для проверки формулы можно использовать омметр.
Как найти общее сопротивление в электрической цепи?
Формула для вычисления общего сопротивления последовательной цепи: Req = R1 + R2 + …. Rn где n — общее количество резисторов в цепи, соединенных последовательно. Таким образом, сопротивления всех резисторов просто суммируются. Например, найдем сопротивление цепи, показанной на рисунке.
Формула зависимости напряжения и мощности лампочки
Это основная формула статьи, вывод которой будет приведён ниже. Формула выглядит так:
Для любой лампы накаливания существует параметр, стабильный в широком диапазоне электрических режимов. Этим параметром является отношение куба напряжения к квадрату мощности.
Методика использования формулы проста.
Берем лампочку, читаем на колбе или на цоколе параметры, на которые она расчитана – напряжение и мощность, рассчитываем константу, потом вставляем в формулу любое произвольное напряжение и вычисляем мощность, которая выделится на лампочке.
Зная мощность, несложно вычислить ток.
Зная ток, несложно вычислить сопротивление нити накаливания.
Вот и рассмотрим вопросы, связанные с правильной эксплуатацией формулы, а так же с теми ограничениями, котрые неизбежны ввиду того что «абсолютных» формул просто не бывает.
Однако, сначала немножко «теории»…
Формула мощности и напряжения
Обновление статьи от января 2021. У меня на блоге появилась статья автора Станислава Матросова, который развил тему сопротивления спирали лампочки с теоретической стороны. Он вывел формулу, согласно которой:
Для любой лампы накаливания существует параметр, стабильный в широком диапазоне электрических режимов. Этим параметром является отношение куба напряжения к квадрату мощности:
Я решил на основе данных, полученных в статье, посчитать эту величину в Экселе. Вот что у меня получилось:
| U | P | U^3 | P^2 | Const |
| 2 | 1,1 | 8 | 1,21 | 6,61157 |
| 4 | 2,8 | 64 | 7,84 | 8,163265 |
| 6 | 5,04 | 216 | 25,4016 | 8,503401 |
| 8 | 7,76 | 512 | 60,2176 | 8,502498 |
| 10 | 10,8 | 1000 | 116,64 | 8,573388 |
| 12 | 14,28 | 1728 | 203,9184 | 8,473978 |
| 14 | 18,06 | 2744 | 326,1636 | 8,412956 |
| 16 | 22,08 | 4096 | 487,5264 | 8,401596 |
| 18 | 26,46 | 5832 | 700,1316 | 8,329863 |
| 20 | 31 | 8000 | 961 | 8,324662 |
| 22 | 35,86 | 10648 | 1285,94 | 8,280327 |
| 24 | 40,8 | 13824 | 1664,64 | 8,304498 |
| 26 | 46,02 | 17576 | 2117,84 | 8,29902 |
| 28 | 51,52 | 21952 | 2654,31 | 8,270321 |
| 30 | 57,6 | 27000 | 3317,76 | 8,138021 |
| 32 | 64 | 32768 | 4096 | 8 |
Действительно, константа, которая с некоторой погрешностью во всём диапазоне равна 8,2±0,2. Её размерность – “Вольт в кубе на Ватт в квадрате”.
Константа для расчета лампы накаливания = 8,2
Низкое значение константы в начале диапазона объяснено автором в приведенной по ссылке статье.
Теперь, зная значение этой константы (8,2), можем записать формулу зависимости мощности от напряжения лампочки накаливания 40Вт 24В:
Зависимость мощности лампочки накаливания от напряжения
Базовые «теоретические» предпосылки
Формула была получена в предположении того, что в металле (из которого состоит нить накаливания) ток и сопротивление имеют единую физическую сущность.
В упрощенном виде это можно рассуждать примерно так.
Сообразно современным воззрениям, ток представляет собой упорядоченное движение носителей заряда. Для металла это будут электроны.
Было сделано предположение, что электрическое сопротивление металла определяется ХАОТИЧЕСКИМ движением тех же самых электронов.
С возрастанием температуры нити, хаотическое движение электронов возрастает, что, в конечном итоге, и приводит к возрастанию электрического сопротивления.
Еще раз. Ток и сопротивление в нити накаливания – суть одно и тоже. С той лишь разницей, что ток – это упорядоченное движение под действием электрического поля, а сопротивление – это хаотическое движение электронов.
Сопротивление нити накала лампы
Экспериментальная проверка наиболее распространенных бытовых ламп накаливания мощностью 25, 40, 60, 75, 100 Вт показывает, что их сопротивление в холодном состоянии составляет 155,5; 103,5; 61,5; 51,5; 40 Ом, а в рабочем — 1936; 1210; 815; 650; 490 Ом, соответственно. Тогда отношение «горячего» сопротивления к «холодному» равняется 12,45; 11,7; 13,25; 12,62; 12,4, а в среднем оно составляет 12,5.
В результате лампа накаливания при включении работает в экстремальных условиях при токах, которые превышают номинальный, что приводит к ускоренному износу нити накала и преждевременному выходу лампы из строя, особенно при превышениях напряжения в питающей сети. Последнее обстоятельство при длительных превышениях напряжения относительно номинального приводит к резкому сокращению срока службы лампы.
Процесс старения и срок службы лампы.
Срок службы лампы накаливания колеблется в широких пределах, потому что зависит:
Немножко «алгебраической схоластики»
Теперь, когда с “теорией” покончено (улыбнулся), приведу алгебраические выкладки для вывода «главной» формулы.
Каноническая запись закона Ома выглядит:
I * R = U
Самые общие соображения подвигают к мысли, что эти коэффициенты должны быть взаимно обратными величинами, а значит:
В этом случае, попарно перемножая правые и левые части (в системе уравнений), мы возвращаемся к исходной записи закона Ома:
I * R = U
Окончательный вывод формулы
Рассмотрим подробнее систему уравнений:
Возведем в квадрат первое уравнение и попарно перемножим их.
В левой части мы видим выражение для мощности, а так же памятуя о том, что произведение коэффициентов равно единице, окончательно перепишем:
Отсюда получим выражение для токового коэффициента:
И для резистивного коэффициента (они взаимообратны):
Осталось подставить эти значения коэффициентов в “РАСЩЕПЛЕННУЮ” формулу Закона Ома, и мы получим окончательные выражения для тока и сопротивления.
Домножая последнее соотношение на Ux, получим:
Чтобы не забивать себе голову этими квадратами, кубами и корнями, достаточно запомнить простую зависимость, которая вытекает из последнего соотношения . Возводя последнее соотношение в квадрат, мы получаем ясную и понятную формулу:
Для любой лампочки с вольфрамовой нитью накала отношение куба напряжения к квадрату мощности является величиной ПОСТОЯННОЙ.
Полученные соотношения показали прекрасное соответствие практическим результатам (измерениям) в широком диапазоне изменения параметров напряжения и для весьма различных типов ламп накаливания, начиная от комнатных, автомобильных и заканчивая лампочками для карманных фонариков…
Какое сопротивление у лампочки?
Решил я как-то проверить закон Ома. Применительно к лампе накаливания. Измерил сопротивление лампочки Лисма 230 В 60 Вт, оно оказалось равным 59 Ом. Это в несколько раз больше заявленной мощности! Я было удивился, но потом вспомнил слово, которое всё объясняло – бареттер
.
Дело в том, что сопротивление вольфрамовой нити лампы накаливания сильно зависит от температуры (следствие протекания тока). В моем случае, если это бы был не вольфрам, а обычный резистор, его рассеиваемая мощность при напряжении 230 Вольт была бы P = U2/R = 896. Почти 900 Ватт!
Кстати, именно поэтому производители датчиков с транзисторным выходом рекомендуют соблюдать осторожность при подключении датчиков.
Как же измерить рабочее сопротивление нити лампы накаливания? А никак. Его можно только определить косвенным путем, из закона знаменитого Ома. (Строго говоря, все омметры используют тот же закон – прикладывают напряжение и меряют ток). И мультиметром тут не обойдешься.
Используя косвенный метод и лампочку Лисма 24 В с мощностью 40 Вт, я составил вот такую табличку:
Зависимость сопротивления нити лампы накаливания от напряжения
Сопротивление лампочки
(Номинальные параметры выделены)
Как видно из таблицы, зависимость сопротивления лампочки от напряжения нелинейная. Это может проиллюстрировать график, приведенный ниже. Рабочая точка на графике выделена.
Сопротивление нити лампы накаливания в зависимости от напряжения
Кстати, сопротивление подопытной лампочки, измеренное с помощью цифрового мультиметра – около 1 Ома. Предел измерения – 200 Ом, при этом выходное напряжение вольтметра – 0,5 В. Эти данные также укладываются в полученные ранее.
Зависимость мощности от напряжения:
Зависимость мощности от напряжения
Для ламп на напряжение 230 В на основании экспериментальных данных была составлена вот такая табличка:
Мощность и сопротивление
Из этой таблицы видно, что сопротивление нити лампы накаливания в холодном и горячем состоянии отличается в 12-13 раз. А это значит, что во столько же раз увеличивается потребляемая мощность в первоначальный момент.
Можно говорить о пусковом токе для ламп накаливания.
Стоит отметить, что сопротивление в холодном состоянии измерялось мультиметром на пределе 200 Ом при выходном напряжении мультиметра 0,5 В. При измерении сопротивления на пределе 2000 Ом (выходное напряжение 2 В) показания сопротивления увеличиваются более чем в полтора раза, что опять же укладывается в идею статьи.
“Горячее” сопротивление измерялось косвенным методом.
Сопротивление нити накаливания люминесцентных ламп
Дополнение к статье, чтобы получился ещё более полный материал.
Лампы с цоколем Т8, сопротивление спирали в зависимости от мощности :
10 Вт – 8,0…8,2 Ом
15 Вт – 3,3…3,5 Ом
18 Вт – 2,7…2,8 Ом
36 Вт – 2,5 Ом.
Сопротивление измерялось цифровым омметром на пределе 200 Ом.
Формула мощности и напряжения
Обновление статьи. У меня на блоге появилась статья автора Станислава Матросова, который развил тему сопротивления спирали лампочки с теоретической стороны. Он вывел формулу, согласно которой:
Для любой лампы накаливания существует параметр, стабильный в широком диапазоне электрических режимов. Этим параметром является отношение куба напряжения к квадрату мощности:
Я решил на основе данных, полученных в статье, посчитать эту величину в Экселе. Вот что у меня получилось:
Зависимость
Действительно, константа, которая с некоторой погрешностью во всём диапазоне равна 8,2±0,2. Её размерность – “Вольт в кубе на Ватт в квадрате”.
Константа для расчета лампы накаливания = 8,2
Низкое значение константы в начале диапазона объяснено автором в приведенной по ссылке статье.
Теперь, зная значение этой константы (8,2), можем записать формулу зависимости мощности от напряжения лампочки накаливания 40Вт 24В:
Зависимость мощности лампочки накаливания от напряжения
Формула для сопротивления
Но вернёмся к теме статьи. Проверим вывод Станислава Матросова о том, что сопротивление лампочки пропорционально корню из напряжения. Из предыдущих выводов можно вывести формулу для конкретной лампочки 40Вт 24В:
Зависимость сопротивления от напряжения, формула для лампы накаливания
Теперь проверим, как эта формула соотносится с полученными мною экспериментальным данным (см. таблицу в начале статьи). Составим такую таблицу:
Таблица требует пояснений. Чтобы была соблюдена размерность, я нормировал экспериментально заданное напряжение (столбец 2) и рассчитанное сопротивление (столбец 4).
Колонка 5 – это корень из нормированного напряжения, и видно, что значения этой колонки отлично совпадают с колонкой 4!
Но давайте вернемся в реальному сопротивлению, и рассчитаем его по приведенной выше формуле (Зависимость сопротивления от напряжения). Это – 6-я колонка. Хорошо видно, что расчет по формуле практически идеально совпадает с расчетом из экспериментальных данных!
Зависимость сопротивления от напряжения. Квадратичная зависимость.
Кто хочет проверить мои расчеты, прикладываю файл: •Файл с расчетами и графиками
/ Файл с расчетами и графиками к статье про лампу накаливания, xlsx, 19.51 kB, скачан: 430 раз./
Всё, учебник физики можно переписывать!
«Радио Всем», №10 октябрь 1926 год.
Как выбирать лампу для приемника
А. Пистолькорс
(Окончание)
Внутреннее сопротивление лампы.
Некоторые ошибочно полагают, что внутреннее сопротивление лампы можно определить, разделив анодное
напряжение на анодный ток по закону Ома 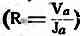
Этот расчет неправилен потому, что он не учитывает влияния сетки. На самом деле внутреннее сопротивление лампы мы можем
определить, если знаем, какое увеличение или уменьшение анодного тока создает то или другое изменение анодного
напряжения. Пусть анодное напряжение, которое раньше было 60, стало 80 вольт (мы добавили 20 вольт); если при этом ток
в цепи анода увеличился, скажем, с 1,5 до 2 миллиампер, то внутреннее сопротивление лампы мы найдем, разделив 80 — 60 =
20 вольт на 2 — 1,5 = 0,5 мА; это будет (20 * 1000) / 0,5 = 40000 ом. Мы конечно полагали, что и в первом и во втором
случае потенциал на сетке лампы был один и тот же. Если мы будем потенциал сетки менять и для каждого потенциала
определять внутреннее сопротивление лампы, то заметим, что оно меняется и весьма значительно.
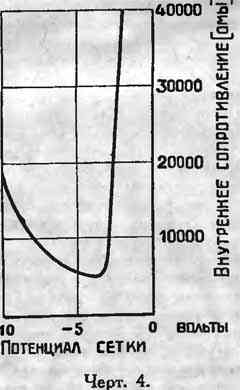
Следовательно, внутреннее сопротивление лампы зависит от сеточного потенциала. Для примера на черт.
4 приведена кривая внутреннего сопротивления для лампы Микро ДС. Знать подобные кривые конструктору очень важно во
многих случаях практики.
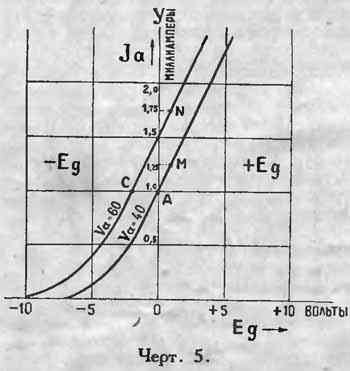
Мы можем построить кривую внутреннего сопротивления для любой лампы, если мы имеем ее характеристики.
Пусть, напр., характеристики эти изображаются кривыми черт. 5. Мы видим, что, при потенциале сетки = +1 вольт, изменив
анодное напряжение с 40 до 60 вольт (точки М, N) мы изменим анодный ток с 1,25 до 1,75 миллиампера (отсчет по
вертикальной оси OJ). Следовательно, при этом потенциале сетки внутреннее сопротивление будет 40000 ом.
Коэффициент усиления.
Коэффициент усиления μ показывает насколько сильнее сеточное напряжение влияет на анодный ток по
сравнению с анодным напряжением. Например (см. черт. 5), мы увеличили анодное напряжение на 20 вольт, анодный ток
увеличился с 1,0 до 1,5 мА при потенциале сетки = 0. Если мы теперь при новом анодном напряжении уменьшим потенциал
сетки на 2 вольта (см. точку C) мы опять вернем току его прежнее значение 1,0 миллиампер. Значит, 2 вольта на
сетке производят такое же изменение анодного тока, что 20 вольт на аноде. Следовательно, коэффициент усиления μ для
этой лампы будет 20 : 2 = 10. Величина μ тоже меняется для каждой лампы в зависимости от потенциала сетки,
но сравнительно в небольших пределах. В среднем эта величина у нормальных ламп равна 8—10, но есть лампы у которых
μ = 30 и выше (1).
Однако μ само по себе не определяет целиком усиления лампы. Усиление зависит от того, какая
применена схема усилителя и какова нагрузка лампы, т. е. какое сопротивление включено в анодную цепь лампы.
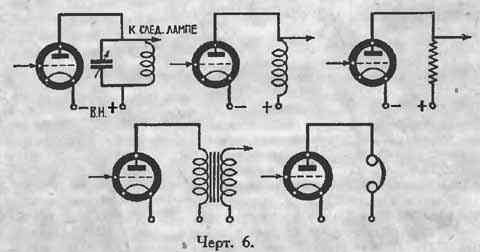
На черт. 6 изображены различные типы нагрузок лампы, при чем между первыми тремя видами и двумя
последними существует большая принципиальная разница. Первые три схемы усиливают главным образом напряжение и поэтому
здесь усиление будет близко к μ и тем ближе, чем больше сопротивление, создаваемое усиливаемому току включением
настроенного контура, дросселя или мегома. Усиленное напряжение подается на сетку следующей лампы, которая, ввиду
большего сопротивления пути сетка—нить, тока почти не берет. В схеме четвертой и пятой требуется усиление мощности;
кроме напряжения там от лампы берется еще усиленный ток. В случае телефона это понятно само собой; в случае
трансформатора расход энергии об’ясняется тем, что вторичная обмотка трансформатора имеет большую собственную емкость,
которая и будет пропускать ток, снижая напряжение на зажимах обмотки. Для получения наибольшего усиления в этом случае,
сопротивление трансформатора или телефона, высчитанное или измеренное для усиливаемого переменного тока, должно быть
равно внутреннему сопротивлению лампы. Кстати заметим, что сопротивление нагрузки влияет также и на самую характеристику
лампы, изменяя ее наклон, но об этом подробнее поговорим в другой раз.
Следует иметь в виду, что высокий коэффициент усиления сопровождается большим внутренним
сопротивлением лампы2), что вообще говоря невыгодно. Включаемое в анодную цепь сопротивление мы
не можем сделать как угодно большим. Напр., для сопротивления трансформаторов существует предел в 25000—30000 ом (нужно
помнить, что здесь все время говорится о сопротивлении переменному току). Большего нельзя добиться, потому, что с
увеличением числа витков увеличивается утечка на токи через емкость обмоток. Следовательно, имея лампу с большим μ,
а потому и с большим Ri мы, применяя трансформаторы, все равно ее использовать не сможем.
Наши лампы.
Подробных данных о всех катодных лампах советского производства еще не имеется. Мы ограничимся общей
характеристикой имеющихся типов, чтобы дать возможность радиолюбителю ориентироваться в дальнейшем. Катодные лампы у нас
вырабатываются Трестом Заводов Слабого Тока и Нижегородской радиолабораторией имени Ленина. Наибольшим распространением
пользуются трестовские лампы типа «Микро» и Р5, принадлежащие обе к, так называемому, универсальному типу и отличающиеся
лишь накалом (Микро — темный, Р5 — яркий накал). Лампы универсального типа имеют μ среднее = 8—12 и также среднее
внутреннее сопротивление порядка 30000 ом. К этому же универсальному типу относятся Нижегородские лампы У (усилительная)
и Д (детекторная) — обе яркие; последняя отличается более резким сгибом характеристики и предназначена для детекторных
схем. Мощные лампы, как Трестовская УТ1 и Нижегородская 10-ти ваттная, обычно имеют небольшое внутреннее
сопротивление, а след. и небольшое μ.
Из других типов можно указать на, сконструированную специально для микродина, «Малютку»
(радиолаборатория им. Ленина), требующую всего 0,045А на накал при 2—3 вольтах, а также небольшое анодное напряжение —
6—12 вольт. В остальном ее данные примерно те же, что и универсального типа.
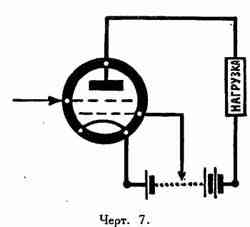
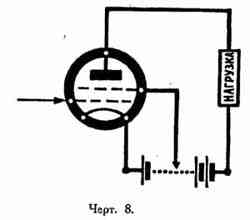
Что же касается двухсеточной лампы Треста — Микро ДС, то в зависимости от способа включения мы можем
получить или (черт. 7) малое внутреннее сопротивление (до 5000 ом) и малое μ (около 5) или (черт. 
μ, порядка 30—40 при большом Ri, доходящем до 200—300 тысяч ом.
Переходим к разбору типовых случаев.
Усилители низкой частоты.
В первых ступенях усиления н. ч. требуется обращать внимание главным образом на большое усиление,
добиваясь наибольшего μ. Внутреннее сопротивление лампы при усилении дросселями или мегомами м. б. довольно
большим, в трансформаторных же схемах не должно превышать 30000 ом.
В последней ступени, где требуется усиление мощности, особенно при громкоговорителях, лампа должна
иметь малое внутреннее сопротивление и хорошую характеристику, сдвинутую в отрицательную сторону. Коэффициентом усиления
здесь нужно жертвовать ради чистоты. Надо обращать особое внимание на правильный выбор анодного напряжения и сеточного
смещения; легче всего это сделать, имея характеристику. Конечно, за недостатком других, здесь придется применять лампы
универсального типа, повышая при этом анодный вольтаж и подбирая смещения. Но очень хорошо может быть здесь использована
также двухсеточная лампа ДС по схеме черт. 7, требующая при этом всего 25 вольт на анод (смещение около 5 вольт). Для
больших же громкоговорящих установок в последней ступени лучше всего применять мощные лампы УТ1 и 10-ваттные.
Усилители высокой частоты.
Здесь приходится бороться не столько с искажением, сколько с нежелательной генерацией собственных
колебаний; как раз лампы с большим коэффициентом усиления особенно содействуют этой генерации, а потому от них нужно
отказаться, употребляя μ средней величины (8—10). Часто для подавления нежелательной генерации приходится давать на
сетку положительный потенциал; это, конечно, вызывает искажения усиливаемого тока, но следует иметь ввиду, что искажение
в высокой частоте подчас мало влияет на чистоту звуковых токов, получающихся после детектирования. Положительный
потенциал на сетке вызывает затухание колебаний потому, что при нем сетка начинает пропускать ток и забирает часть
энергии возникших колебаний, которые гаснут. Наоборот, если мы хотим поддержать колебания, нужно давать на сетку
небольшой отрицательный потенциал. Опасность возникновения колебаний уменьшается с увеличением длины волны и поэтому при
усилении волн длиннее 3000 — 4000 м. можно пользоваться лампами с большим μ. Лампы с большим μ можно применять
и в специальных схемах, устраняющих генерацию, как напр., в нейтродинах, но последние еще не вошли у нас в практику.
Кроме сказанного, лампы для усилителей высокой частоты д. б. обязательно жесткими, т.-е. хорошо
откачаны. Следы газа в лампе отнимают часть энергии на попеременную электризацию частичек (диэлектрический гистерезис);
при звуковой частоте потеря эта незначительна но при высоких частотах, чем короче волна, тем более она становится
заметной. У нас хорошей жесткостью отличается лампа У Нижегородской РЛ.
Все сказанное выше справедливо и для детекторных ламп, для которых, кроме того, желателен возможно
более крутой сгиб характеристики в нижнем конце.
Кроме того, если в цепь ее анода включен трансформатор или телефон, нужно следить, чтобы Ri было не
больше 30000 ом.
В дальнейшем мы предполагаем дать подробные характеристики и описания всех ламп советского
производства, что позволит радиоконструктору совершенно уверенно подходить к вопросу выбора лампы для своего приемника.
1) Существует еще другая величина для определения тех же свойств лампы, т.-наз. проницаемость D. Она равна единице,
деленной на коэффициент усиления. Напр. если μ = 10, D = 1 / 10 или 10% и наоборот, если D = 4%, μ = 1 / 4%
= 100 / 4 = 25.
2) Это неизбежно вытекает из самой конструкции лампы. Чтобы увеличить μ, приходится делать сетку ближе к
волоску и гуще, а это затрудняет доступ электронов к аноду вследствие чего увеличивается внутреннее сопротивление.