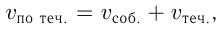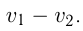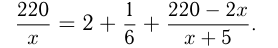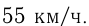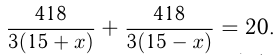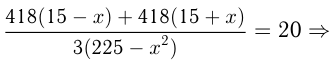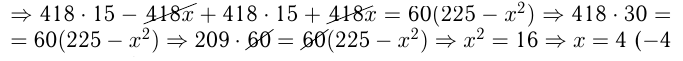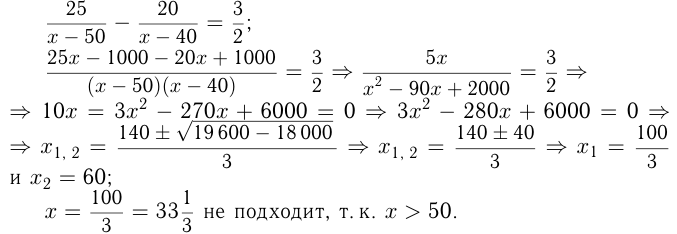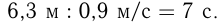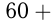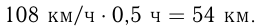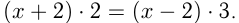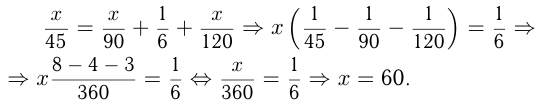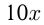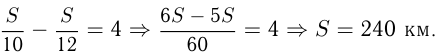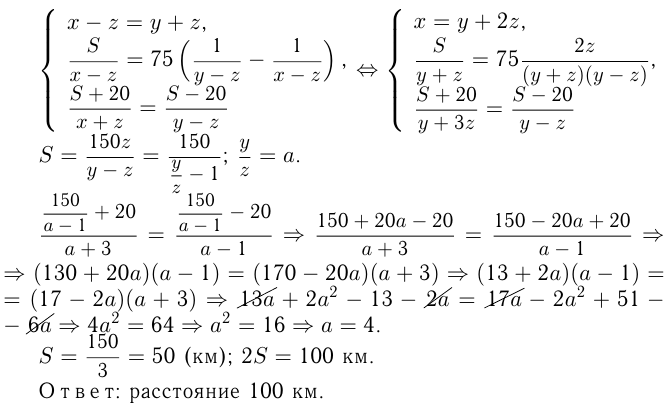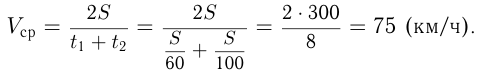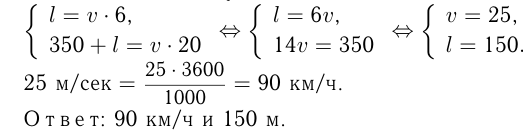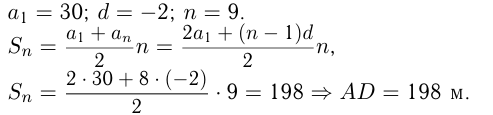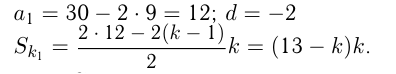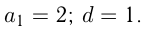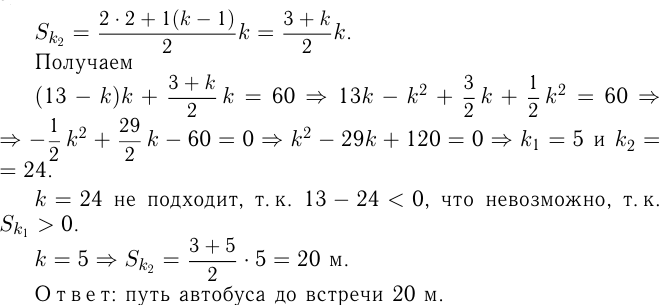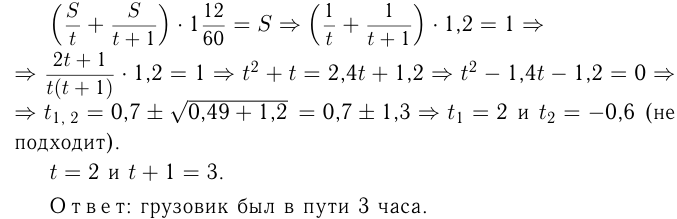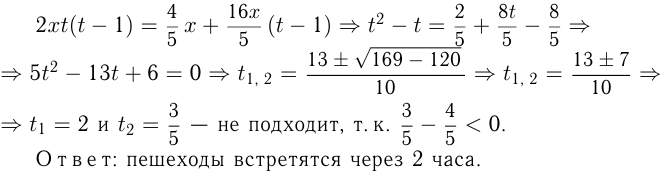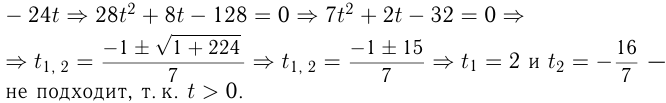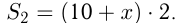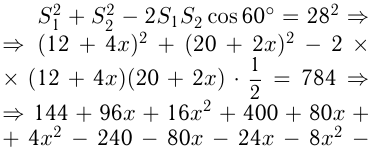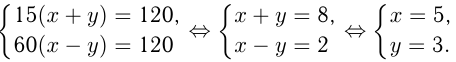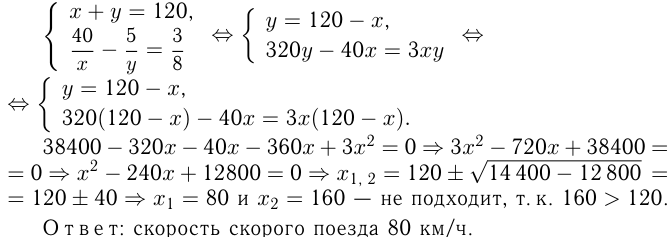Как найти собственную скорость лодки
Решение задач на «движение по воде» многим дается с трудом. В них существует несколько видов скоростей, поэтому решающие начинаю путаться. Чтобы научиться решать задачи такого типа, надо знать определения и формулы. Умение составлять схемы очень облегчает понимание задачи, способствует правильному составлению уравнения. А правильно составленное уравнение — самое главное в решении любого типа задач.

Инструкция
В задачах «на движение по реке» присутствуют скорости: собственная скорость (Vс), скорость по течению (Vпо теч.), скорость против течения (Vпр. теч.), скорость течения (Vтеч.). Необходимо отметить, что собственная скорость водного суда – это скорость в стоячей воде. Чтобы найти скорость по течению, надо к скорости течения прибавить собственную. Для того чтобы найти скорость против течения, надо из собственной скорости вычесть скорость течения.
Первое, что необходимо выучить и знать «на зубок» — формулы. Запишите и запомните:
Vпо теч=Vс+Vтеч.
Vпр. теч.=Vс-Vтеч.
Vпр. теч=Vпо теч. — 2Vтеч.
Vпо теч.=Vпр. теч+2Vтеч.
Vтеч.=(Vпо теч. — Vпр. теч)/2
Vс=(Vпо теч.+Vпр теч.)/2 или Vс=Vпо теч.+Vтеч.
На примере разберем, как находить собственную скорость и решать задачи такого типа.
Пример 1.Скорость лодки по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость лодки и скорость течения реки.
Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. — Vпр. теч)/2, найдем:
Vтеч = (21,8 — 17,2)/2=4,62=2,3 (км/ч)
Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)
Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).
Пример 2. Пароход прошел против течения 24 км и вернулся обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите его собственную скорость в неподвижной воде, если скорость течения равна 3 км/ч.
За Х примем собственную скорость парохода. Составим таблицу, куда занесем все данные.
Против теч. По течению
Расстояние 24 24
Скорость Х-3 Х+3
время 24/ (Х-3) 24/ (Х+3)
Зная, что на обратный путь пароход затратил на 20 минут времени меньше, чем на путь по течению, составим и решим уравнение.
20 мин=1/3 часа.
24/ (Х-3) – 24/ (Х+3) = 1/3
24*3(Х+3) – (24*3(Х-3)) – ((Х-3)(Х+3))=0
72Х+216-72Х+216-Х2+9=0
441-Х2=0
Х2=441
Х=21(км/ч) – собственная скорость парохода.
Ответ: 21 км/ч.
Обратите внимание
Скорость плота считается равной скорости водоема.
Источники:
- решение задач на течение
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как рассчитать по формулам скорость лодки?
Собрали для Вас актуальные формулы, которые могут оказаться полезными каждому
8 июля 2020
4 375
✓ Формула 1
На примере разберем, как находить скорость лодки.
Скорость лодки по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость лодки и скорость течения реки.
Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. — Vпр. теч)/2, найдем:
Vтеч = (21,8 — 17,2)/2=4,62=2,3 (км/ч)
Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)
Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).
✓ Формула 2
Самым простым методом самостоятельного расчета предельной скорости лодки считается использование формулы, учитывающей параметры двигателя.
Для этого используется формула вычисления двигателя V = NK/R, где искомый параметр V – скорость километров в час, R – сопротивление движению (его вы можете взять в технической документации своего катера), K – коэффициент полезной деятельности винта. Определяется он в зависимости от типа лодки. Так, для спортивного катера его значение — 160, для крупных винтов — 140, для средних и малых — 120 и 100 соответственно.
Параметр N – мощность работы двигателя катера. Эту информацию вы можете рассчитать самостоятельно или обратиться за помощью к технической документации. Для того, чтобы вычислить предел скорости катера, возьмите максимально допустимую мощность. Этот метод позволяет рассчитать предел максимальной скорости катера достаточно точно, однако не следует забывать про вероятную погрешность.
Теплоход затратил 5 часов на путь вниз по течению реки от пункта A до пункта B. На обратный путь против течения он затратил 8 часов 20 минут. Найти скорость теплохода, если путь от A до B равен 100 километрам.
Обозначим скорость (собственную) теплохода через параметр «т», а скорость течения реки — р, тогда скорость «по течению» равна (т + р) , а скорость «против» течения, соответственно (т — р).
Умножив соответствующие скорости на время по и «против» течения, получим одно и то же расстояние, равное 100 км. Переведём время 8 час 20 мин в 8 1/3 часа.
Тогда получим два уравнения.
1) (т + р) * 5 (час) = 100 (км);
2) (т — р) * 8 1/3(час) = 100 км. Откуда:
т + р = 100 : 5 = 20;
т — р = 100 : 25/3 = 12. Откуда 2 * т = 32, т = 32 : 2 = 16 (км/час).
Откуда р = 20 — т = 20 — 16 = 4 (км/час).
Ответ: скорость теплохода 16 км/час, течения — 4 км/час.
система выбрала этот ответ лучшим
BRIZ52
[107K]
4 года назад
Решение задачи:
Для начала вспомним формулу определения скорости: V = S/t, где V скорость; S — путь; t — время. 1.Первым действием определяем скорость теплохода по течению:
100 : 5 = 20 (км/ч)
2.Определяем скорость теплохода против течения:
8ч 20 мин = 8 часов + 1/3 (составляет 20 минут) = 8 + 1/3 = 25/3 (часа) — время шел теплоход против течения.
100 : 25/3 = 12 (км/ч)
3.Определяем скорость течения реки:
20 — 12 = 8 (км/ч) — удвоенная скорость течения реки.
8 : 2 = 4 (км/ч) — скорость течения реки.
4.Определяем скорость теплохода:
12 + 4 = 16 (км/ч)
Ответ: 16 км/ч скорость теплохода.
Ведрусс58
[24.5K]
4 года назад
Составляем два уравнения:
(1) (Vт+Vр)км/ч*5ч=100км (Vт+Vр)*300=100, где 5*60мин=300мин
(2) (Vт-Vр)км/ч*8ч20м=100км (Vт-Vр)*500=100, где 8ч20мин=8*60+20=500мин
Из (1) получаем: 300Vт+300Vр=100 300Vр=100-300Vт Vр=100/300-300Vт/300=1/3-Vт
Из (2) получаем: 500Vт-500Vр=100 500Vт=100+500Vр Vт=100/500+500*Vр/500=1/5+Vр
Подставляем полученное из (1) значение Vр=1/3-Vт в уравнение , полученное из (2):
Vт=1/5+Vр= 1/5+1/3-Vт 2Vт=1/5+1/3=(3+5)/15=8/15 Vт=8/15*2=4/15 км/мин Переведём минуты в часы:
Vт=4/15 км/мин* 60мин= 16км/час, получили скорость теплохода в км/час
Можем вычислить и Vр=4км/час
9ХантеР1
[13.8K]
4 года назад
Школу закончила давно, но если мне не изменяет память, то :
скорость по течению V1=100/5=20км/ч
20мин=0,3 часа
Скорость против течения V2=100/8,3=12 км/ч
Vтеч= (V1-V2)/2=(20-12)/2=4 км/ч
Vc=V2+Vтеч=12+4=16 км/ч
Собственная скорость теплохода 16 км/ч
Есть собственная скорость теплохода в стоячей воде, видимо ее и нужно определить. Скорость теплохода относительно берега складывается из собственной скорости и скорости течения реки при движении вниз по течению. Соответственно, при ходе против течения скорости вычитаются. Пусть Х — собственная скорость теплохода. У — скорость течения реки. Составляем 2 уравнения (Х+У)*5=100 и (Х-У)*8,333=100. Два неизвестных и два уравнения, решаемо.
Найдём среднюю скорость теплохода, т.к. о другой какой-то скорости в условии не говорится.
(100 км + 100 км) / (5 ч + 8.3 ч) = 15.04 км/ч
Ответ: средняя скорость 15.04 км/ч
Знаете ответ?
При решении задач на движение следует иметь в виду, что движение тел, о которых идет речь в задаче, если нет специальных оговорок, считается равномерным. Обычно вводятся следующие неизвестные: 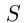
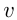
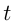
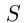
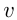
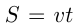
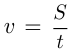
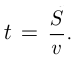
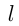
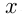
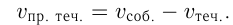
При решении задач на движение часто встречаются следующие две возможности:
1) движение навстречу друг другу; если два тела движутся навстречу друг другу со скоростями 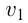
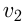
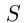
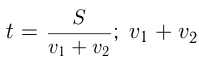
2) движение в одном направлении, когда скорость одного тела превышает скорость другого, и первое тело догоняет второе. Если первоначальное расстояние между ними равно 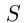
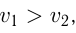
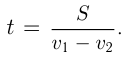
Задача №7
Поезд должен был пройти 220 км за определенное время. Через 2 часа после начала движения он был задержан на 10 мин и, чтобы прийти вовремя в пункт назначения, увеличил скорость на 5 км/ч. Найти первоначальную скорость поезда.
Решение:
Обозначим первоначальную скорость поезда 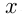
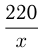
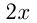
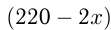
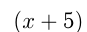
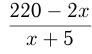
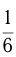
Решим уравнение:
Ответ: первоначальная скорость поезда
Задача №8
Моторная лодка, скорость которой в стоячей воде равна 15 км/ч, прошла 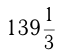
Решение:
Обозначим скорость течения реки 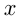
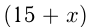
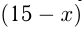
Решим уравнение:
не подходит)
Ответ: скорость течения 4 км/ч.
Задача №9
Две автомашины выехали одновременно из одного пункта в одном и том же направлении. Одна машина движется со скоростью 50 км/ч, другая — 40 км/ч. Спустя полчаса из того же пункта в том же направлении выехала третья машина, которая обогнала 1-ю машину на 1 ч 30 мин позже, чем 2-ю. Найти скорость третьей машины.
Решение:
Пусть скорость 3-й машины 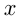
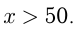
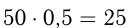
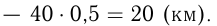
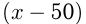
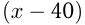
Ответ: скорость третьей машины 60 км/ч.
Задача №45
Стрекоза и муха двигаются по прямой. Стрекоза догоняет муху, их скорости равны 1,2 м/с и 0,3 м/с. Через сколько секунд расстояние между насекомыми сократится с 6,5 м до 20 см?
Решение:
Скорость сближения стрекозы и мухи равна разности их скоростей:
Расстояние, которое нужно преодолеть с этой скоростью, равно 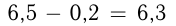
О т в е т: 7 с.
Задача №46
Из двух сел одновременно навстречу друг другу выехали автобус и грузовик. Через 0,5 ч они встретились. Какое расстояние между селами, если скорость автобуса 60, а грузовика 48 км/ч?
Решение:
Скорость сближения автобуса и грузовика: 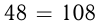
Задача №47
Катер прошел расстояние между пристанями по течению реки за 2 часа, а обратно против течения за 3 часа. Найти собственную скорость катера, если скорость течения реки 2 км/ч.
Решение:
Пусть собственная скорость катера 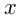
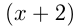
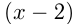
Ответ: собственная скорость катера 10 км/ч.
Задача №48
Пассажирский поезд проходит за 3 часа на 10 км больше, чем товарный за 4 часа. Скорость товарного поезда на 20 км/ч меньше скорости пассажирского. Найти скорость пассажирского поезда.
Решение. Пусть искомая скорость 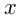
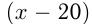
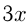

Ответ: скорость пассажирского поезда 70 км/ч.
Задача №49
Велосипедист и пешеход отправились из пунктов 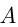
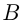
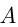
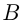
Решение. Пусть скорость пешехода 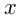
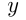
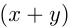
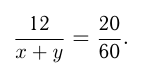
Время пешехода в пути 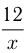
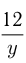
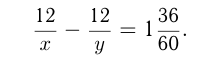
Решаем систему уравнений:
Пара чисел 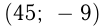
Ответ: скорость пешехода 6 км/ч.
Задача №50
Из пункта 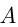
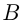
Решение. Пусть скорость товарного поезда 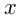
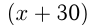
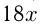
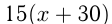
Ответ: скорость товарного поезда 50 км/ч.
Задача №51
Путь от 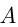
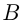
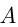
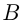


Решение. Пусть 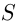


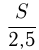
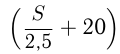
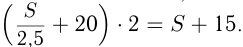
Ответ: расстояние 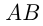
Задача №52
Половину пути мотоциклист ехал с намеченной скоростью 45 км/ч, затем задержался на 10 мин и поэтому, чтобы наверстать время, увеличил скорость на 15 км/ч. Каков весь путь мотоциклиста?
Решение. Примем весь путь за 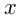
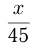
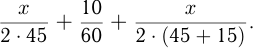
Ответ: путь мотоциклиста 60 км.
Задача №53
Расстояние между двумя пунктами поезд должен пройти за 10 часов. Пройдя первые 9 ч с намеченной скоростью, он снизил скорость на 7 км/ч и прибыл в конечный пункт с опозданием на 6 мин. Найти первоначальную скорость поезда.
Решение. Пусть первоначальная скорость поезда 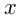
км. Поезд прошел снача-
ла 9х, затем (х — 7) км. Таким образом,
10х = 9® + (х — 7) • 1,1 =► х = 1,1.x — 7,7 => 0,1х = 7,7 => => х = 77.
Ответ: скорость поезда была 77 км/ч.
Задача №54
Велосипедист едет из одного города в другой со скоростью 10 км/ч. Если бы он ехал со скоростью 12 км/ч, то приехал бы в конечный пункт на 4 ч раньше. Какое расстояние преодолеет велосипедист?
Решение. Пусть расстояние между городами 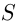
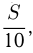
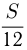
Уравнение
Ответ: 240 км.
Задача №55
Из города 







Решение. Пусть расстояние 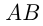
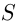
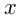
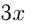
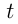
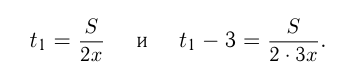
Ответ: расстояние 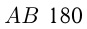
Задача №56
Города 














Решение.
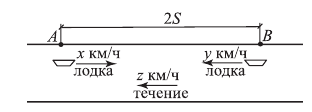
Обозначим: 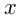

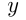

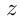
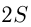


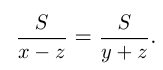
Из 2-го условия следует:
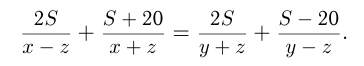
И из 3-го условия следует:
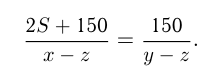
Задача №57
Автомобиль с грузом ехал из одного города в другой со скоростью 60 км/ч, а возвращался обратно порожняком со скоростью 100 км/ч. Найти среднюю скорость автомобиля.
Решение. Пусть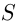
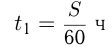
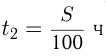
Ответ: средняя скорость автомобиля 75 км/ч.
Задача №58
Поезд прошел мимо наблюдателя за 6 сек, а по мосту длиной 350 метров проходил в течение 20 сек. Найти скорость и длину поезда.
Решение. Пусть 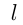
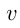
Тогда имеем систему:
Задача №59
В гору ехал автомобиль. В 1-ю секунду после достижения пункта 



Решение.

Автомобиль за 9 сек проехал расстояние 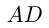
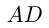
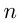
Расстояние 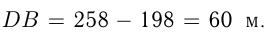
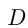

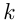
Путь автобуса также можно посчитать как сумму 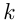
Задача №60
Из пункта 








Решение. Пусть легковой автомобиль был в пути 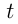
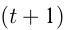


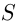
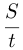
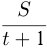
Задача №61
На полпути между городами 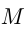
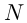
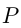
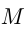
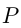
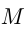
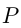
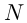
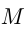

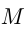
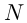
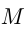

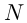

Решение.
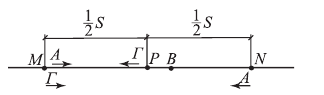
Пусть 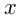
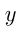
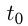
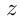
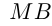
Задача №62
Из пункта 






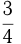



Пусть 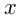
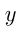
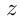
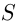
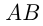
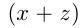

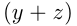

Требуется определить
Решаем 2-е уравнение:
Задача №63
Из двух пунктов одновременно навстречу друг другу вышли два пешехода. Определить, через сколько времени они встретятся, зная следующее: если бы один из пешеходов шел вдвое быстрее, то встреча произошла бы на полчаса раньше, а если бы вдвое быстрее шел другой — то на 48 мин раньше.
Решение.

Введенные обозначения и условия задачи позволяют написать систему трех уравнений с 4-мя неизвестными, где 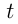
Задача №64
Из пунктов 

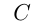
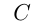
Решение. Пусть 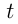
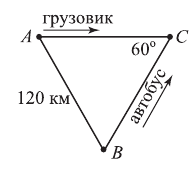
Расстояние 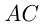
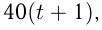

По теореме косинусов
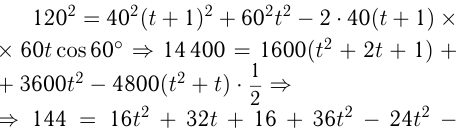
Ответ: автобус ехал 2 часа.
Задача №65
Пункты 

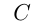
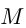
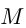


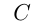
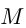
Решение.
Задача №66
Из 2-х пунктов, расстояние между которыми 2400 км, навстречу друг другу выезжают одновременно пассажирский и скорый поезда. Каждый из них едет с постоянной скоростью, и в некоторый момент они встречаются. Если бы оба поезда шли со скоростью скорого, то их встреча произошла бы на 3 часа раньше, если бы оба поезда шли со скоростью пассажирского, то их встреча произошла бы на 5 часов позже фактического момента встречи. Найти скорости поездов.
Решение. Пусть 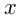
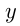
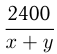
Задача №67
В реку впадает приток. Пароход отходит от пристани 







Решение.
Пусть 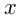
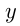

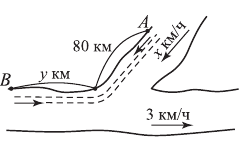
Задача №68
Две реки с прямолинейными руслами и одинаковой скоростью течения впадают в одном и том же месте в озеро, образуя между собой угол 60°. От двух причалов, расположенных на разных реках и отстоящих друг от друга на расстоянии 28 км, одновременно вышли байдарка и лодка, скорости которых в стоячей воде соответственно равны 10 и 3 км/ч. Байдарка достигла озера через 2, а лодка — через 4 часа. Найти скорость течения реки.
Решение.
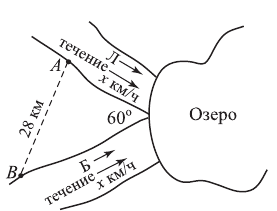
Путь лодки от 
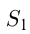
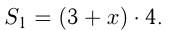

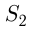
По теореме косинусов
и 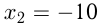
Ответ: скорость течения реки 4 км/ч.
Задача №69
Две точки движутся по окружности длиной 120 м с постоянными скоростями. Если они движутся в разных направлениях, то встречаются через каждые 15 сек. При движении в одном направлении одна точка догоняет другую через каждые 60 сек. Найти скорости точек.
Решение.
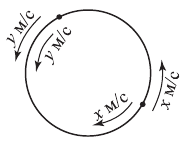
Пусть одна точка движется со скоростью 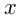
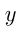
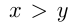
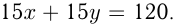
Ответ: скорости точек 5 и 3 м/с.
Задача №70
Из пункта 



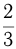


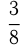
Решение.
Обозначим через 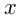
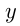
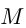
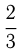
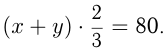
Задача №71
Пароход, отчалив от пристани 



Решение.
Пусть собственная скорость парохода 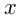
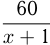
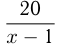
Задача №72
Два тела движутся по окружности равномерно в одну сторону, причем 1-е тело проходит окружность на 2 сек быстрее 2-го и догоняет 2-е тело каждые 12 сек. За какое время каждое тело проходит окружность?
Решение. Пусть 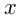
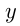
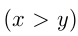
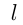
Этот материал взят со страницы решения задач по математике:
Решение задач по математике
Возможно вам будут полезны эти страницы: