Статистические оценки параметров генеральной совокупности
Определение статистической оценки. Точечные статистические оценки: смещенные и несмещенные, эффективные и состоятельные. Интервальные статистические оценки. Точность и надежность оценки; определение доверительного интервала; построение доверительных интервалов для средней при известном и неизвестном среднеквадратическом отклонении.
Определение статистической оценки
Пусть требуется изучить количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак. Возникает задача оценки параметров, которыми определяется это распределение. Например, если известно, что изучаемый признак распределен в генеральной совокупности по нормальному закону, то необходимо оценить математическое ожидание и среднеквадратическое отклонение, так как эти два параметра полностью определяют нормальное распределение. Если имеются основания считать, что признак имеет распределение Пуассона, то необходимо оценить параметр , которым это распределение определяется. Обычно имеются лишь данные выборки, полученные в результате
наблюдений:
. Через эти данные и выражают оцениваемый параметр. Рассматривая
как значения независимых случайных величин
можно сказать, что найти статистическую оценку неизвестного параметра теоретического распределения означает найти функцию от наблюдаемых случайных величин, которая и дает приближенное значение оцениваемого параметра.
Точечные статистические оценки
Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин. Статистическая оценка неизвестного параметра генеральной совокупности одним числом называется точечной. Рассмотрим следующие точечные оценки: смещенные и несмещенные, эффективные и состоятельные.
Для того чтобы статистические оценки давали хорошие приближения оцениваемых параметров, они должны удовлетворять определенным требованиям. Укажем эти требования. Пусть есть статистическая оценка неизвестного параметра
теоретического распределения. Допустим, что по выборке объема
найдена оценка
. Повторим опыт, т. е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным найдем оценку
и т. д. Получим числа
, которые будут различаться. Таким образом, оценку
можно рассматривать как случайную величину, а числа
— как возможные ее значения.
Если оценка дает приближенное значение
с избытком, то найденное по данным выборок число
будет больше истинного значения
. Следовательно, и математическое ожидание (среднее значение) случайной величины
будет превышать
, то есть
. Если
дает приближенное значение
с недостатком, то
.
Использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, приводит к систематическим ошибкам. Поэтому нужно потребовать, чтобы математическое ожидание оценки было равно оцениваемому параметру. Соблюдение требования
устраняет систематические ошибки.
Несмещенной называют статистическую оценку , математическое ожидание которой равно оцениваемому параметру
, то есть
.
Смещенной называют статистическую оценку , математическое ожидание которой не равно оцениваемому параметру.
Однако ошибочно считать, что несмещенная оценка всегда дает хорошее приближение оцениваемого параметра. Действительно, возможные значения могут быть сильно рассеяны вокруг своего среднего значения, т. е. дисперсия величины
может быть значительной. В этом случае найденная по данным одной выборки оценка, например
, может оказаться удаленной от своего среднего значения
, а значит, и от самого оцениваемого параметра
. Приняв
в качестве приближенного значения
, мы допустили бы ошибку. Если потребовать, чтобы дисперсия величины
была малой, то возможность допустить ошибку будет исключена. Поэтому к статистической оценке предъявляются требования эффективности.
Эффективной называют статистическую оценку, которая (при заданном объеме выборки ) имеет наименьшую возможную дисперсию. При рассмотрении выборок большого объема к статистическим оценкам предъявляется требование состоятельности.
Состоятельной называют статистическую оценку, которая при стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при
стремится к нулю, то такая оценка оказывается также состоятельной.
Рассмотрим вопрос о том, какие выборочные характеристики лучше всего в смысле несмещённости, эффективности и состоятельности оценивают генеральную среднюю и дисперсию.
Пусть изучается дискретная генеральная совокупность относительно количественного признака. Генеральной средней называется среднее арифметическое значений признака генеральной совокупности. Она вычисляется по формуле
или
где — значения признака генеральной совокупности объема
;
— соответствующие частоты, причем
Пусть из генеральной совокупности в результате независимых наблюдений над количественным признаком извлечена выборка объема со значениями признака
. Выборочной средней называется среднее арифметическое значений признака выборочной совокупности и вычисляется по формуле
или
где — значения, признака в выборочной совокупности объема
;
— соответствующие частоты, причем
Если генеральная средняя неизвестна и требуется оценить ее по данным выборки, то в качестве оценки генеральной средней принимают выборочную среднюю, которая является несмещенной и состоятельной оценкой. Отсюда следует, что если по нескольким выборкам достаточно большого объема из одной и той же генеральной совокупности будут найдены выборочные средние, то они будут приближенно равны между собой. В этом состоит свойство устойчивости выборочных средних.
Если дисперсии двух совокупностей одинаковы, то близость выборочных средних к генеральным не зависит от отношения объема выборки к объему генеральной совокупности. Она зависит- от объема выборки: чем больше объем выборки, тем меньше выборочная средняя отличается от генеральной.
Для того чтобы охарактеризовать рассеяние значений количественного признака генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику — генеральную дисперсию. Генеральной дисперсией
называется среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения
, которое вычисляется по формуле
или
Для того чтобы охарактеризовать рассеяние наблюденных значений количественного признака выборки вокруг своего среднего значения хв, вводят сводную характеристику — выборочную дисперсию. Выборочной дисперсией называется среднее арифметическое квадратов отклонений наблюденных значений признака от их среднего значения
, которое вычисляется по формуле
или
Кроме дисперсии для характеристики рассеяния значений признака генеральной (выборочной) совокупности вокруг своего среднего значения используют сводную характеристику — среднее квадратическое отклонение. Генеральным средним квадратическим отклонением называют квадратный корень из генеральной дисперсии: . Выборочным средним квадратическим отклонением называют квадратный корень из выборочной дисперсии:
.
Пусть из генеральной совокупности в результате независимых наблюдений над количественным признаком
извлечена выборка объема
. Требуется по данным выборки оценить неизвестную генеральную дисперсию
. Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то эта оценка приведет к систематическим ошибкам, давая заниженное значение генеральной дисперсии. Объясняется это тем, что выборочная дисперсия является смещенной оценкой
. Другими словами, математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно
.
Легко исправить выборочную дисперсию так, чтобы ее математическое ожидание было равно генеральной дисперсии. Для этого нужно умножить на дробь
. В результате получим исправленную дисперсию
, которая будет несмещенной оценкой генеральной дисперсии:
Интервальные оценки
Наряду с точечным оцениванием, статистическая теория оценивания параметров занимается вопросами интервального оценивания. Задачу интервального оценивания можно сформулировать так: по данным выборки построить числовой интервал, относительно которого с заранее выбранной вероятностью можно сказать, что внутри него находится оцениваемый параметр. Интервальное оценивание особенно необходимо при малом количестве наблюдений, когда точечная оценка малонадежна.
Доверительным интервалом для параметра
называется такой интервал, относительно которого с заранее выбранной вероятностью
, близкой к единице, можно утверждать, что он содержит неизвестное значение параметра
, то есть
. Чем меньше для выбранной вероятности число
, тем точнее оценка неизвестного параметра
. И, наоборот, если это число велико, то оценка, проведенная с помощью данного интервала, малопригодна для практики. Так как концы доверительного интервала зависят от элементов выборки, то значения
и
могут изменяться от выборки к выборке. Вероятность
принято называть доверительной (надежностью). Обычно надежность оценки задается наперед, причем в качестве
берут число, близкое к единице. Выбор доверительной вероятности не является математической задачей, а определяется конкретной решаемой проблемой. Наиболее часто задают надежность, равную 0,95; 0,99; 0,999.
Доверительный интервал для генеральной средней при известном значении среднего квадратического отклонения и при условии, что случайная величина (количественный признак ) распределена нормально, задается выражением
где — наперед заданное число, близкое к единице, а значения функции
приведены в таблице прил. 2.
Смысл этого соотношения заключается в следующем: с надежностью можно утверждать, что доверительный интервал
покрывает неизвестный параметр
, точность оценки
. Число
определяется из равенства
, или
. По прил. 2 находят аргумент
, которому соответствует значение функции Лапласа, равное
.
Пример 1. Случайная величина имеет нормальное распределение с известным средним квадратическим отклонением
. Найти доверительные интервалы для оценки неизвестной генеральной средней по выборочным средним, если объем выборок
и надежность оценки
.
Решение. Найдем . Из соотношения
получим, что
. По прил. 2 находим
. Найдем точность оценки
. Доверительные интервалы будут таковы:
. Например, если
, то доверительный интервал имеет следующие доверительные границы:
. Таким образом, значения неизвестного параметра
, согласующиеся с данными выборки, удовлетворяют неравенству
.
Доверительный интервал для генеральной средней нормального распределения признака при неизвестном значении среднего квадратического отклонения задается выражением
Отсюда следует, что с надежностью можно утверждать, что доверительный интервал
покрывает неизвестный параметр
.
Существуют таблицы (прил. 4), пользуясь которыми, по заданным и
находят вероятность
и, наоборот, по заданным
и
находят
.
Пример 2. Количественный признак генеральной совокупности распределен нормально. По выборке объема
найдены выборочная средняя
и исправленное среднеквадратическое отклонение
. Оценить неизвестную генеральную среднюю с помощью доверительного интервала с надежностью
.
Решение. Найдем . Пользуясь прил. 4 по
и
находим
. Найдем доверительные границы:
Итак, с надежностью неизвестный параметр
заключен в доверительном интервале
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Дисциплина «Статистическая обработка информации»
-
Разделы статистической обработки информации: теория оценок, теория проверки статистических гипотез
Статистика
является разделом математики, посвященным
анализу экспериментальных данных,
полученных в ходе наблюдения за некоторым
объектом. В зависимости от решаемых в
ходе анализа задач можно провести
условное разделение математической
статистики на два направления:
описательная (дескриптивная) статистика
и теория статистических выводов
(индуктивная статистика).
Описательная
(дескриптивная) статистика (англ.
descriptive statistics) решает задачи систематизации
экспериментальных данных, их наглядного
представления в виде графиков и
эмпирических зависимостей, а также
количественного анализа отдельных
статистических показателей (напр.
среднего значения, разброса, тренда и
пр.). Типичным примером применения
описательной статистики является
представление результатов соц. опроса
в виде круговых диаграмм или графики
колебания цен на нефть.
Теория
статистических выводов
(англ.
inferential statistics) решает задачи применения
выборочной информации (полученной,
например, в ходе эксперимента) для
выявления количественных и качественных
характеристик наблюдаемого объекта.
Примером может служить экспериментальная
оценка среднего времени выполнения
запроса к базе данных или попытка дать
ответ на вопрос, прием данных с какого
из доступных серверов наиболее надежен.
Приведенное
деление является в известной степени
условным, и зачастую статистическая
обработка информации начинается с
применения чисто описательных методов,
а в дальнейшем завершается применением
теории статистических выводов.
Теорию
статистических выводов, в свою очередь,
можно разделить на теорию оценивания
и
теорию проверки гипотез. Теория
оценивания призвана количественно
охарактеризовать интересующий
исследователя параметр объекта: либо
предположить его конкретное значение
(точечное оценивание), либо предположить
наиболее вероятный диапазон его значений
(интервальное оценивание). Теория
проверки гипотез позволяет на основе
экспериментальных данных
дать
ответ на заранее заданный вопрос
касательно свойств объекта (осуществить
выбор одной из альтернативных гипотез).
-
Смещенность оценки; примеры смещенных и несмещенных оценок
Так
как оценка является функцией от
нескольких случайных величин (элементов
выборки), то очевидно, что и сама оценка
является случайной величиной. Таким
образом, оценка может принимать значение
как превышающее истинное, так и, наоборот,
заниженное. Естественным желанием
является то, чтобы в
среднем
оценка совпадала с истинным значением,
т.е.:
.
Такая
оценка называется несмещенной.
Можно ввести величину
,
характеризующую величину смещения,
вносимого при использовании алгоритма
по выборке объема N:
Здесь
и далее
обозначает оценку параметра
при помощи алгоритма
по выборке объема N.
Если
,
то оценка является смещенной.
Возможны также случаи, когда для
конечного N
оценка – смещенная, но:
.
Данная
оценка называется асимптотически
несмещенной.
Т.е. при достаточно большом объеме
выборки N,
величиной смещения можно пренебречь.
Таким
образом, можно сказать, что смещение
оценки –
это разность между математическим
ожиданием оценки и истинным значением
оцениваемого параметра, несмещенная
оценка –
это оценка, имеющая нулевое смещение
при любом объеме выборки, а смещенная
оценка –
это оценка, имеющая не нулевое смещение.
Пример
несмещенной оценки:
При
анализе трафика, передаваемого с сервера
на компьютеры клиентов, производится
оценка среднего размера пакета
передаваемого по сети. Для этого из
общего потока выбирается N
пакетов,
размеры которых фиксируются и усредняются.
В данном примере случайная величина
характеризует размер пакета, искомый
параметр
— среднее значение
(т.е.
),
элементы выборки
— размеры зарегистрированных пакетов,
алгоритм оценивания
.
Проверим, является ли данная оценка
смещенной:

Таким
образом, данная оценка является
несмещенной.
Пример
смещенной оценки:
Пусть
известно, что время отклика базы данных
на запрос пользователя является
равномерно распределенной случайной
величиной в диапазоне
.
Задачей исследователя является выяснение
величины
— т.е. худшего случая, при котором задержка
максимальна. Применяется следующая
оценка:
,
т.е. максимальная задержка, зарегистрированная
в ход проведения эксперимента, состоящего
из N
запросов. Для упрощения выкладок при
проверке смещенности данной оценки
введем следующее обозначение для
максимального элемента выборки
(т.е.
и
).
Найдем интегральную функцию распределения
величины
:
Для
того чтобы максимальный элемент выборки
не превосходил x,
необходимо и достаточно, чтобы каждый
элемент выборки не превосходил x.
Обратное также верно. Тогда, учитывая
независимость случайных величин
получим:

Учитывая,
что функция
описывает равномерное распределение
в диапазоне
,
получим:
.
Воспользовавшись
формулой
получим
выражение для плотности вероятности
:
.
Тогда:

Таким
образом, данная оценка является
смещенной, причем:
Очевидно,
что
и рассмотренная оценка является
асимптотически несмещенной.
Соседние файлы в предмете Государственный экзамен
- #
- #
Содержание:
Точечные оценки:
Пусть случайная величина имеет неизвестную характеристику а. Такой характеристикой может быть, например, закон распределения, математическое ожидание, дисперсия, параметр закона распределения, вероятность определенного значения случайной величины и т.д. Пронаблюдаем случайную величину n раз и получим выборку из ее возможных значений
Существует два подхода к решению этой задачи. Можно по результатам наблюдений вычислить приближенное значение характеристики, а можно указать целый интервал ее значений, согласующихся с опытными данными. В первом случае говорят о точечной оценке, во втором – об интервальной.
Определение. Функция результатов наблюдений
Для одной и той же характеристики можно предложить разные точечные оценки. Необходимо иметь критерии сравнения оценок, для суждения об их качестве. Оценка 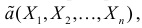
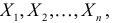
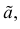
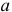
Определение. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемой величине: 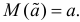
Определение. Оценка называется состоятельной, если при увеличении числа наблюдений она сходится по вероятности к оцениваемой величине, т.е. для любого сколь угодно малого
Если известно, что оценка 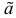
Последнее условие удобно для проверки. В качестве меры разброса значений оценки 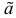
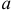
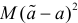
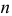
Следует отметить, что несмещенность и состоятельность являются желательными свойствами оценок, но не всегда разумно требовать наличия этих свойств у оценки. Например, может оказаться предпочтительней оценка хотя и обладающая небольшим смещением, но имеющая значительно меньший разброс значений, нежели несмещенная оценка. Более того, есть характеристики, для которых нет одновременно несмещенных и состоятельных оценок.
Оценки для математического ожидания и дисперсии
Пусть случайная величина имеет неизвестные математическое ожидание и дисперсию, причем 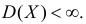
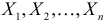
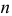
Несмещенность такой оценки следует из равенств
В силу независимости наблюдений
При условии 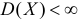
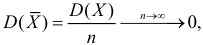
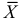
Доказано, что для математического ожидания нормально распределенной случайной величины оценка 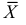
Оценка математического ожидания посредством среднего арифметического наблюдаемых значений наводит на мысль предложить в качестве оценки для дисперсии величину
Преобразуем величину 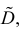
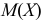
В силу (3.1.2) имеем 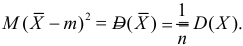
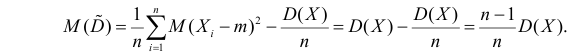
Последняя запись означает, что оценка 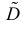
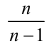
Величина
является несмещенной и состоятельной оценкой дисперсии.
Пример:
Оценить математическое ожидание и дисперсию случайной величины Х по результатам ее независимых наблюдений: 7, 3, 4, 8, 4, 6, 3.
Решение. По формулам (3.1.1) и (3.1.3) имеем
Ответ.
Пример:
Данные 25 независимых наблюдений случайной величины представлены в сгруппированном виде:
Требуется оценить математическое ожидание и дисперсию этой случайной величины.
Решение. Представителем каждого интервала можно считать его середину. С учетом этого формулы (3.1.1) и (3.1.3) дают следующие оценки:
Ответ.
Метод наибольшего правдоподобия для оценки параметров распределений
В теории вероятностей и ее приложениях часто приходится иметь дело с законами распределения, которые определяются некоторыми параметрами. В качестве примера можно назвать нормальный закон распределения 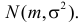
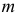
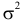
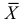
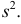
Пусть случайная величина Х имеет функцию распределения 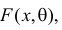
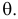
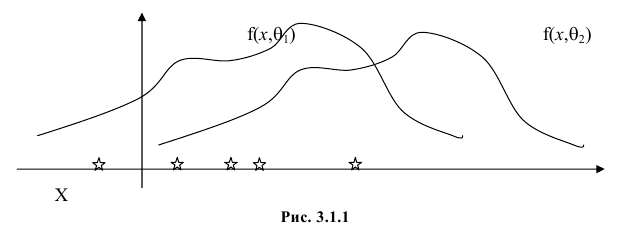
Продемонстрируем идею метода наибольшего правдоподобия на упрощенном примере. Пусть по результатам наблюдений, отмеченных на рис. 3.1.1 звездочками, нужно отдать предпочтение одной из двух функций плотности вероятности 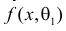
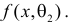
Из рисунка видно, что при значении параметра 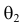
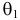
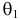
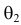
Этот принцип приводит к следующему способу действий. Пусть закон распределения случайной величины Х зависит от неизвестного значения параметра 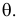
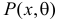
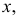
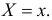
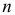
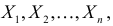
называют функцией правдоподобия. Величина 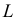
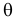
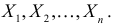
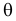


Сформулированный принцип предлагает в качестве оценки значения параметра выбрать такое 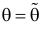

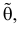
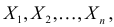
Во многих случаях, когда 
которое следует из необходимого условия экстремума. Поскольку 
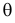

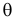
Это уравнение называют уравнением правдоподобия. Им пользоваться удобнее, чем уравнением (3.1.5), так как функция 


Если параметров несколько (многомерный параметр), то следует взять частные производные от функции правдоподобия по всем параметрам, приравнять частные производные нулю и решить полученную систему уравнений.
Оценку, получаемую в результате поиска максимума функции правдоподобия, называют еще оценкой максимального правдоподобия.
Известно, что оценки максимального правдоподобия состоятельны. Кроме того, если для q существует эффективная оценка, то уравнение правдоподобия имеет единственное решение, совпадающее с этой оценкой. Оценка максимального правдоподобия может оказаться смещенной.
Метод моментов
Начальным моментом 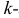
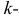
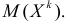
Центральным моментом 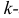
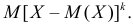
Для оценки параметров распределения по методу моментов находят на основе опытных данных оценки моментов в количестве, равном числу оцениваемых параметров. Эти оценки приравнивают к соответствующим теоретическим моментам, величины которых выражены через параметры. Из полученной системы уравнений можно определить искомые оценки.
Например, если Х имеет плотность распределения 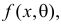
Если воспользоваться величиной 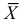
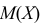
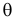
Пример:
Найти оценку параметра показательного закона распределения по методу моментов.
Решение. Плотность вероятности показательного закона распределения имеет вид 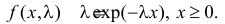
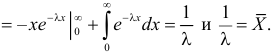
Ответ.
Пример:
Пусть имеется простейший поток событий неизвестной интенсивности 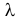
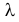
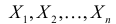

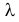
Решение. В простейшем потоке интервалы времени между последовательными моментами наступления событий потока имеют показательный закон распределения 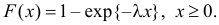
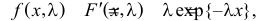
Тогда 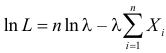
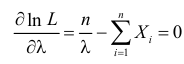
При таком значении 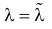
Ответ.
Определение. Пусть 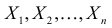
В этой записи 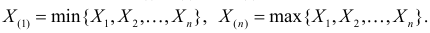
Величины 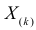
Пример:
Случайная величина Х имеет равномерное распределение на отрезке 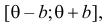


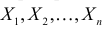


Решение. Функция плотности вероятности величины Х имеет вид
В этом случае функция правдоподобия 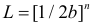




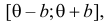
где 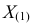
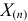

откуда 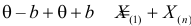
Оценкой наибольшего правдоподобия для параметра 
Ответ.
Пример:
Случайная величина X имеет функцию распределения
где 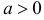
Пусть 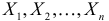

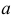
Решение. Для построения функции правдоподобия найдем сначала функцию плотности вероятности
Тогда функция правдоподобия:
Логарифмическая функция правдоподобия:
Уравнение правдоподобия
не имеет решений. Критических точек нет. Наибольшее и наименьшее значения 

По виду функции 



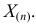
Так как 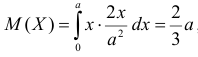
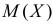
Ответ.
Пример:
Случайная величина Х имеет нормальный закон распределения 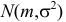
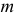
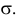
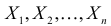
Решение. В соответствии с (3.1.4) функция правдоподобия имеет вид
а логарифмическая функция правдоподобия:
Необходимые условия экстремума дают систему двух уравнений:
Решения этой системы имеют вид:
Отметим, что обе оценки являются состоятельными, причем оценка для 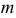
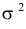
Ответ.
Пример:
По данным эксперимента построен статистический ряд:
Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения случайной величины X.
Решение. 1) Число экспериментальных данных вычисляется по формуле:
Значит, объем выборки n = 50.
2) Вычислим среднее арифметическое значение эксперимента:
Значит, найдена оценка математического ожидания 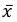
3) Вычислим исправленную выборочную дисперсию:
Значит, найдена оценка дисперсии: 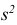
5) Вычислим оценку среднего квадратического отклонения:
Ответ:
Пример:
По данным эксперимента построен статистический ряд:
Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения случайной величины X.
Решение. По формуле
перейдем к условным вариантам:
Для них произведем расчет точечных оценок параметров:
Следовательно, вычисляем искомые точечные оценки:
Ответ:
Пример:
По данным эксперимента построен интервальный статистический ряд:
Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения.
Решение. 1) От интервального ряда перейдем к статистическому ряду, заменив интервалы их серединами
2) Объем выборки вычислим по формуле:
3) Вычислим среднее арифметическое значений эксперимента:
3) Вычислим исправленную выборочную дисперсию:
Можно было воспользоваться следующей формулой:
5) Вычислим оценку среднего квадратического отклонения:
Ответ:
Пример:
Найти доверительный интервал с надежностью 0,95 для оценки математического ожидания M(X) нормально распределенной случайной величины X, если известно среднее квадратическое отклонение σ = 2, оценка математического ожидания 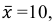
Решение. Доверительный интервал для истинного математического ожидания с доверительной вероятностью 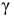
где m = M(X) – истинное математическое ожидание; 𝑥̅ − оценка M(X) по выборке; n – объем выборки; 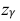
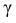
Из табл. П 2.2 приложения 2 находим: 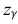
Ответ: (9,216 ; 10,784).
Пример:
По данным эксперимента построен статистический ряд:
Найти доверительный интервал для математического ожидания M (X) с надежностью 0,95.
Решение. Воспользуемся формулой для доверительного интервала математического ожидания при неизвестной дисперсии:
где n – объем выборки; 𝑥̅ оценка M(X); s – оценка среднего квадратического отклонения; 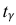
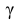
По числам 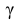
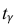
Теперь вычисляем оценки для M(X) и D(X):
Следовательно, s ≈ 1,685. Поэтому искомый доверительный интервал математического ожидания задается формулой:
Ответ: (– 0,76; 0,76).
Пример:
По данным десяти независимых измерений найдена оценка квадратического отклонения 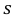
Решение. Задача сводится к нахождению доверительного интервала для истинного квадратического отклонения, так как точность прибора характеризуется средним квадратическим отклонением случайных ошибок измерений.
Доверительный интервал для среднего квадратического отклонения находим по формуле:
где 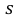
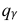
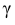
Находим:
Тогда можно записать:
Ответ: (0; 1,04).
- Доверительный интервал для вероятности события
- Проверка гипотезы о равенстве вероятностей
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Системы случайных величин
- Вероятность и риск
- Определения вероятности событий
- Предельные теоремы теории вероятностей
Содержание:
- Точечные статистические оценки параметров генеральной совокупности
- Методы определения точечных статистических оценок
- Законы распределения вероятностей для
- Интервальные статистические оценки для параметров генеральной совокупности
- Построение доверчивого интервала для при известном значении с заданной надежностью
- Построение доверительного интервала для при неизвестном значении из заданной надежности
- Построение доверительных интервалов с заданной надежностью для
- Построение доверительного интервала для генеральной совокупности с заданной надежностью
- Построение доверительного интервала для с помощью неравенства Чебишова с заданной надежностью
Информация, которую получили на основе обработки выборки про признак генеральной совокупности, всегда содержит определенные погрешности, поскольку выборка содержит только незначительную часть от нее 
Потому, следует организовать выборку так, чтобы эта информация была более полной (выборка может быть репрезентабельной) и обеспечивала с наибольшей степенью доверия о параметрах генеральной совокупности ил закон распределение ее признака.
Параметры генеральной совокупности 

Тут через 



Точечные статистические оценки параметров генеральной совокупности
Статистическая оценка 


то 

точечная статистическая оценка 
Разница
называется смещением статистической оценки
Оценочный параметр может иметь несколько точечных несмещенных статистических оценок, что можно изобразить так (рис. 116):
Например, пусть 




Из графиков плотности видим, что оценка 



Но на «хвостах» распределений имеет другую картину: большие отклонения от 





Точечная статистическая оценка называется эффективной, когда при заданном объеме выборки она имеет минимальную дисперсию. Следует, оценка 
Точечная статистическая оценка называется основой, если в случае неограниченного увеличения объема выборки 

Методы определения точечных статистических оценок
Существует три метода определения точечных статистических оценок для параметров генеральной совокупности.
Метод аналогий. Этот метод основывается на том, что для параметров генеральной совокупности выбирают такие же параметры выборки, то есть для оценки 
Метод наименьших квадратов. Согласно с этим методом статистические оценки обозначаются с условием минимизации суммы квадратов отклонений вариант выборки от статистической оценки 
Итак, используя метод наименьших квадратов, можно, например, обозначить статистическую оценку для 

Отсюда, для 

Метод максимальной правдоподобности. Этот метод занимает центральное место в теории статистической оценки параметров 
Пусть признак генеральной совокупности 



В этом варианте рассматриваются как независимые случайные величины, которые имеют один и тот же закон распределения, что ее признак генеральной совокупности 
Суть этого метода состоит в том, что фиксируя значение вариант 


Например, когда признак генеральной совокупности 
При этом статистические оценки 

На практике удобно от функции 
согласно с необходимым условием экстремума для этой функции получим:
Из первого уравнения системы 
из уравнение системы 
Следует, для 

Свойства 

И на самом деле,


Следует,
Проверим на несмещенность статистической оценки
Таким образом, получим
Следует, 


Когда 

Тогда
Следует, 

Отсюда точечной несмещенной статистической оценкой для 

Величину
называют исправленным средним квадратичным отклонением.
Исправленное среднее квадратичное отклонение, следует подчеркнуть, будет смещенной точечной статистической оценкой для 
где 

Пример. 200 однотипных деталей были отданы на шлифование. Результаты измерения приведены как дискретное статистическое распределение, подан в табличной форме:
Найти точечные смещенные статистические оценки для 
Решение. Поскольку точечной несмещенной оценки для 

Для обозначение точечной несмещенной статистической оценки для 
тогда точечная несмещенная статистическая оценка для 
Пример. Граничная нагрузка на стальной болт 
Обозначить точечные несмещенные статистические оценки для
Решение. Для обозначения точечных несмещенных статистических распределений к дискретному, который приобретает такой вид:
Вычислим
Следует, точечная несмещенная статистическая оценка для 
Для обозначения 
Отсюда точечная несмещенная статистическая оценка для 
Законы распределения вероятностей для 
Как уже обозначалось, числовые характеристики выборки являются случайными величинами, что имеют определенные законы распределения вероятностей. Так, 
следует, случайная величина 
Чтобы обозначить закон распределения для 


Пусть признак генеральной совокупности 





Рассмотрим случай, когда варианты выборки имеют частоты 

Перейдем от случайных величин 


Поскольку случайные величины 


Следует, случайные величины 
Построим матрицу 

Транспортируем матрицу 
Если перемножить матрицы 

где 
Следует, случайные величины 

Из курса алгебры известно, что во время ортогональных преобразований вектора сохраняется его длина, то есть
Тогда из формулы для 
Поскольку 
Следует, получим
Когда поделим левую и правую часть 

Поскольку 



То случайная величина
получим распределение 

Отсюда получается, что случайная величина 


Таким образом, приведена: случайная величина 

случайная величина
случайная величина
Интервальные статистические оценки для параметров генеральной совокупности
Точечные статистические оценки 


Статистическая оценка, что обозначается двумя числами, концами интервалов, называется интервальной.
Разница между статистической оценкой 

где 
Поскольку 


Вероятность, с которой берется неравенство 
называется надежностью
Равенство 
Интервал 


Построение доверчивого интервала для  при известном значении
при известном значении  с заданной надежностью
с заданной надежностью 
Пусть признак 








Случайная величина 
Потому 
Отсюда равенство 

или
Согласно с формулой нормированного нормального закона
для 
Из равенства 

Аргумент 

Следует, доверительный интервал равен:
что можно изобразить условно на рисунке 118.
Величина 
Пример. Измеряя 40 случайно отобранных после изготовления деталей, нашли выборку средней, что равна 15 см. Из надежности 
Решение. Для построенного доверчивого интервала необходимо найти:
Из условия задачи имеем: 



Найдем числовые значения концов доверчивого интервала:
Таким образом, получим:
Следует, с надежностью 

Пример. Имеем такие данные про размеры основных фондов (в млн руб.) на 30-ти случайно выбранных предприятий:
построить интервальное статистическое распределение с длиной шага 
С надежностью 


Решение. Интервальное статистическое распределение будет таким:
Для обозначение 
Тогда

Для построения доверительного интервала с заданной надежностью 
Вычислим концы интервала:


Следует, доверительный интервал для 
Пример. Какое значение может получит надежность оценки 


Решение. Обозначим погрешность выборки
Далее получим:
как видим, надежность мала.
Пример. Обозначить объем выборки 


Решение. По условию задачи 




Построение доверительного интервала для  при неизвестном значении
при неизвестном значении  из заданной надежности
из заданной надежности 
Для малых выборок, с какими сталкиваемся, исследуя разные признаки в техники или сельском хозяйстве, для оценки 

что имеет распределение Стьюдента с 
Тогда 
поскольку 
Вычислив по данному статистическому распределению 


Тут 


Пример. Случайно выбранная партия из двадцати примеров была испытана относительно срока безотказной работы каждого из них 
С надежностью 

Решение. Для построения доверительного интеграла необходимо найти среднее выборочное и исправленное среднее квадратичное отклонение.
Вычислим
следует, получили 
Обозначим
следует,
Исправленное среднее квадратичное отклонение равно:

По таблице значений 


Вычислим концы доверительного интервала:


Следует, с надежностью 

При больших объемах выборки, а именно: 

Пример. В таблице приведены отклонения диаметров валиков, изготовленных на станке, от номинального размера:
с надежностью 
Решение. Для постройки доверительного интервала необходимо найти
Для этого от интегрального статистического распределения, приведенного в условии задачи, необходимо перейти к дискретному, а именно:
Вычислим

Следует,
Обозначим
Вычислим исправленное среднее квадратичное отклонение
Учитывая на большой 
Вычислим концы интервалов:
Итак, доверчивый интервал для среднего значения отклонений будет таким:
Отсюда с надежностью 
Построение доверительных интервалов с заданной надежностью  для
для 
В случае, если признак 


что имеет распределение 

Поскольку случайные действия

являются равновероятными, то есть их вероятности равны 
Подставляя в 

Следует, доверительный интервал для 
Тогда доверительный интервал для 

Значения 
где
Пример. Проверена партия однотипных телевизоров 

С надежностью 
Решение. Для построении доверительных интервалов необходимо найти значения
Вычислим значения

Вычислим
Следует
Исправленная дисперсия и исправленное среднее квадратичное отклонение равны:
Поскольку 


По таблице (дополнение 4) находим:
вычислим концы доверительного интервала для
Следует, доверительный интеграл для 
Доверительный интервал для 
Доверительный интервал для 

Поскольку
то равенство 
или
Обозначив 
чтобы найти 
что имеет распределение
Учитывая то, что события

при 
Если умножить все члены двойного неравенства 

Отсюда получим:
Из уравнения 


Доверительный интервал будет таким:
Пример. С надежностью 

Обозначим концы интервала:
Следует, доверительный интервал для 

Построение доверительного интервала для  генеральной совокупности с заданной надежностью
генеральной совокупности с заданной надежностью 
Как величина, полученная по результатам выборки, 
Исправленное среднее квадратичное отклонение для
Для построения доверительного интервала для 
что имеет нормированный нормальный закон распределения 
Воспользовавшись 
Следует. доверительный интервал для 
где 
по таблице значений функции Лапласа.
Пример. Случайно выбранных студентов из потока университета были подвергнуты тестированию по математике и химии. Результаты этих тестирования преподнесено статистическим распределением, где 

Необходимо:
1) с надежностью 

2) с надежностью 
Решение. Вычислим основные числовые характеристики признак 



1. Построим доверительный интервал с надежностью 

нам известные значения 

где 
Обозначим концы интервала:
Следует, доверительный интервал для 
2. Построим доверительный интервал с надежностью 
Поскольку 
На известное значение 
Вычислим концы доверительного интервала:
Таким образом, доверительный интервал для 
Доверительный интеграл с надежностью 

Нам известно значение 

Обозначим концы доверительного интервала:
Следует, доверительный интервал для 
Доверительный интервал для 

Нам известны значения 

Обозначим концы доверительного интервала:
таким образом, доверительный интервал для 
Построение доверительного интервала для  с помощью неравенства Чебишова с заданной надежностью
с помощью неравенства Чебишова с заданной надежностью
В случае, если отсутствует информация про закон распределения признака генеральной совокупности 





Из 
Доверительный интервал дается таким неравенством:
Когда 

Пример. Полученные данные с 100 наугад выбранных предприятий относительно возрастания выработки на одного работника 
Воспользовавшись неравенством Чебишова, построить доверительный интервал для 

Решение. Для построения доверительного интервала с помощью неравенства Чебишова необходимо вычислить 

Тогда получим:
Воспользовавшись 
таким образом, доверительный интервал для 
или
Пример. Заданы размеры основных фондов 
Воспользовавшись неравенством Чебишова с надежностью 
Решение. Для постройки доверительного интервала для 

Следует, 

Обозначить концы доверительного интервала:


Итак, доверительный интервал для 
Лекции:
- Статистические гипотезы
- Корреляционный и регрессионный анализ
- Комбинаторика основные понятия и формулы с примерами
- Число перестановок
- Количество сочетаний
- Действия над событиями. Теоремы сложения и умножения вероятностей примеры с решением
- Примеры решения задач на тему: Случайные величины
- Примеры решения задач на тему: основные законы распределения
- Примеры решения задач на тему: совместный закон распределения двух случайных величин
- Статистические распределения выборок и их числовые характеристики
Отметим, что при соблюдении прочих предпосылок МНК автокорреляция остатков не влияет на свойства состоятельности и несмещенности оценок параметров уравнения регрессии обычным МНК, за исключением моделей авторегрессии. Применение МНК к моделям авторегрессии ведет к получению смещенных, несостоятельных и неэффективных оценок. [c.280]
Полученная модель есть модель двухфакторной линейной регрессии (точнее — авторегрессии). Определив ее параметры, мы найдем X и оценки параметров а п Ьо исходной модели. Далее с помощью соотношений (7.17) несложно определить параметры b, b2,… модели (7.16). Отметим, что применение обычного МНК к оценке параметров модели (7.22) приведет к получению смещенных оценок ее параметров ввиду наличия в этой модели в качестве фактора лаговой результативной переменной yt [c.307]
Однако, как было показано выше, оценка параметра с,, равная 0,440, является смещенной. Для получения несмещенных оценок параметров этого уравнения воспользуемся методом инструментальных переменных. Определим параметры уравнения регрессии (7.43) обычным МНК [c.327]
Если Ek> О, то кривая островершинная, при Ek <0 — плосковершинная (пологая). Метод моментов, как правило, приводит к состоятельным оценкам. Однако при малых выборках оценки могут оказаться значительно смещенными и малоэффективными. Метод моментов достаточно эффективен для оценки параметров нормально распределенных случайных величин. [c.48]
Бухгалтерские коэффициенты бета. Третий подход основывается на оценке параметров рыночного риска на основе бухгалтерских показателей прибыли, а не на рыночных ценах. Таким образом, изменения прибыли в филиале или фирме на квартальной или годовой основе могут быть отнесены к изменениям прибыли для рынка в те же периоды, которые используются для получения оценки бухгалтерского коэффициента бета, используемого в модели САРМ. Хотя данный подход обладает определенной привлекательностью, в нем таятся три потенциальных подводных камня. Во-первых, бухгалтерская прибыль, как правило, сглаживается по отношению к базовой ценности компании, поскольку бухгалтеры разносят расходы и доходы на множество периодов. Это приводит к коэффициентам бета, характеризуемым как смещенные в сторону занижения , особенно в отношении рискованных фирм, или смещенные в сторону завышения , если дело касается более безопасных фирм. Другими словами, коэффициенты бета, по всей вероятности, будут близки к 1 для всех фирм, использующих бухгалтерские данные. [c.267]
Покажем, что коэффициент gi является смещенной оценкой параметра pi. Действительно, gi вычисляется по формуле (4.14) [c.193]
Непосредственное использование МНК для оценки параметров каждого из уравнений регрессии, входящих в систему одновременных уравнений, в большинстве случаев приводит к неудовлетворительному результату. Чаще всего оценки получаются смещенными и несостоятельными, а статистические выводы по ним некорректными. Причины этого, а также возможные процедуры нахождения оценок параметров для систем одновременных уравнений анализируются в данной главе. [c.308]
Покажите, что смещение оценки параметра j во второй регрессии меньше, чем в первой. [c.137]
Дана выборка размера п из нормального распределения N(fj,, a2). Запишите логарифмическую функцию правдоподобия и найдите ML-оценки параметров ц и а2. Найдите смещения этих оценок. [c.260]
Часто индивидуальные факторы коррелированы с другими объясняющими переменными. Так, например, общий уровень культуры семьи и уровень ее дохода естественно считать связанными. В рамках моделей регрессии это означает, что индивидуальный фактор является существенной переменной в модели и ее исключение приводит к смещенным оценкам остальных параметров (см. п. 4.4). Иными словами, модели с панельными данными позволяют получать более точные оценки параметров. [c.359]
Следовательно, факт нулевого или ненулевого спроса на табак обусловлен ненаблюдаемым параметром е, описывающим потребительские предпочтения. Оценка зависимостей с подобными переключениями, которые обусловлены ненаблюдаемыми параметрами, обычно делается при помощи двухшаговых процедур, поскольку можно показать, что МНК — оценка в данном случае приведет к смещенным оценкам параметров функции спроса. Одной из наиболее известных подобных процедур является процедура [c.158]
Оценки, определяемые вектором (4.8), обладают в соответствии с теоремой Гаусса—Маркова минимальными дисперсиями в классе всех линейных несмещенных оценок, но при наличии мультиколлинеарности эти дисперсии могут оказаться слишком большими, и обращение к соответствующим смещенным оценкам может повысить точность оценивания параметров регрессии. На рис. 5.1 показан случай, когда смещенная оценка Ру, [c.110]
При подходе, использующем рыночную модель, в первую очередь необходимо оценить ожидаемую доходность на рыночный индекс. Затем для каждой ценной бумаги нужно оценить коэффициент вертикального смещения и коэффициент бета . В общей сложности надо произвести оценку (1 + 2ЛО параметров (1 для г,, 2Л/для коэффициента вертикального смещения и бета -коэффициентов для каждой из N рискованных ценных бумаг). Полученные значения могут быть использованы для проведения оценок ожидаемой доходности каждой ценной бумаги с помощью уравнения (8.3), которое в данном случае имеет следующий вид [c.226]
Вследствие этого оценка параметров для линеаризуемых функций МНК оказываются несколько смещенной. [c.75]
Основное различие моделей (7.37) и (7.44) состоит в том, что модель (7.37) включает ожидаемые значения факторной переменной, которые нельзя получить эмпирическим путем. Поэтому статистические методы для оценки параметров модели (7.37) неприемлемы. Модель (7.44) включает только фактические значения переменных, поэтому ее параметры можно определять на основе имеющейся статистической информации с помощью стандартных статистических методов. Однако, как и в случае с моделью Кдфка, применение ОМНК для оценки параметров уравнения (7.44) привело бы к получению их смещенных оценок ввиду наличия в правой части модели лагового значения результативного признака у, (. [c.321]
Вторая проблема состоит в том, что поскольку в модели авторегрессии в явном виде постулируется зависимость между текущими значениями результата. у, и текущими значениями остатков н очевидно, что между временными рядами у, и , , также существует взаимозависимость. Тем самым нарушается еще одна предпосылка МНК, а именно предпосылка об отсутствии связи между факторным признаком и остатками в уравнении регрессии. Поэтому применение обычного МНК для оценки параметров уравнения авторегрессии приводит к получению смещенной оценки параметра при переменной yt x. [c.325]
Уравнение (7.46) представляет собой модель с распределенным лагом, для которой не нарушаются предпосылки обычного МНК, приводящие к несостоятельности и смещенности оценок параметров. Определив параметры моделей (7.51) и (7.56), можно рассчитать параметры исходной модели (7.2) а, 40 и с,. Модель [c.326]
Следовательно, оценка bi является смещенной (скорее всего, завышенной при условии, что 0 < pi < 1) оценкой параметра pi. Причем эту смещенность нельзя преодолеть даже при бесконечном увеличении выборки. [c.314]
При анализе временных рядов часто приходится учитывать статистическую зависимость наблюдений в разные моменты времени. Иными словами, для многих временных рядов предположение о некоррелированности ошибок не выполняется. В этом разделе мы рассмотрим наиболее простую модель, в которой ошибки образуют так называемый авторегрессионный процесс первого порядка (точное определение будет дано ниже). Как было показано ранее (глава 5), применение обычного метода наименьших квадратов к этой системе дает несмещенные и состоятельные оценки параметров, однако можно показать (см., например, Johnston and DiNar-do, 1997), что получаемая при этом оценка дисперсии оказывается смещенной вниз, что может отрицательно сказаться при проверке гипотез о значимости коэффициентов. Образно говоря, МНК рисует более оптимистичную картину регрессии, чем есть на самом деле. [c.184]
В п. 4.4 мы рассмотрели проблемы исключения существенных и включения несущественных переменных для линейных регрессионных моделей. Можно поставить аналогичный вопрос какое влияние оказывает пропуск существенных переменных в уравнении (12.4) на оценивание модели бинарного выбора (12.3) Исчерпывающий ответ на него выходит за рамки нашей книги. Отметим лишь, что в данном случае, даже если исключенные существенные переменные ортогональны включенным, оценки параметров будут, в отличие от линейной схемы, смещенными и несостоятельными (подробнее см. (Greene, 1997) и (Johnston and DiNardo, 1997)). [c.329]
Из равенства (12.41) следует, что применение обычного метода наименьших квадратов к наблюдениям yt приведет, в общем случае, к смещенным оценкам параметров /3. Если же а и = 0, т. е. когда механизм выбора и степень участия независимы, смещение отсутствует. Величину (p(z t i]I (z tl B (12.41) обозначают A(zj7) и называют лямбда Хекмана (He kman lambda). [c.344]
Таким образом, нашей задачей является нахождение безусловных моментов pretest-оценки, принимая во внимание то, что процедуры выбора модели и оценки параметров интегрированы в одну процедуру. Мы не утверждаем, что следует избегать предварительного тестирования, хотя хорошо известно, что preiesf-оценки обладают плохими статистическими свойствами, одно из которых — равномерная неэффективность2. На практике избежать предварительного тестирования почти невозможно. Наша точка зрения состоит в том, что следует вычислять корректно смещение и дисперсию (или среднеквадратичное отклонение) оценки, полностью принимая во внимание то, что оценивание и отбор модели интегрированы в одну процедуру. [c.399]
Относительно просто решается такая задача для функций, преобразуемых к линейному виду. Например, степенную функцию можно прологарифмировать, получив линейную зависимость У от X в логарифмах, и применить для оценки параметров уже упоминавшийся метод наименьших квадратов. Однако надо иметь в виду, что при этом оценивается не сама нелинейная функция, но ее линейное преобразование, а это может вызвать смещение оценок параметров. [c.136]
Если матрица ковариации ошибок по наблюдениям отлична от О IN (нарушена 3-я гипотеза основной модели), то МНК-оценки параметров регрессии остаются несмещенными, но перестают быть эффективными в классе линейных. Смещенными оказываются МНК-оценки их ковариции, в частности оценки их стандартных ошибок (как правило, они преуменьшаются). [c.27]
Рассмотрим оценку Ъг параметра 32, полученную простой регрес сией у на xz на основе таблицы, построенной в результате классифи кации данных по переменной Xz, и оценку Ь3 параметра р3, получен ную в результате простой регрессии у на ха на основе таблицы, соот ветствующей классификации по Xs. Обе оценки окажутся смещенными поскольку в каждом случае допущена ошибка спецификации из-з исключения из регрессии существенной переменной. Поэтому [c.234]
Он приблизительно совпадет с оценкой параметра J3, полученной методом наименьших квадратов, если уравнение Yt = РУ< 1 + vt будет подгоняться с учетом свободного члена. Снова ограничиваясь порядком п-1, получим, что смещение для этой оценки равно2 [c.305]
Таким образом, входящие в уравнение возмущающее воздействие Y объясняющая переменная оказываются коррелированными, а значит, как и в случае ошибок в переменных (см. гл. 9), непосредственное применение к (12.1) метода наименьших квадратов приведет к смещенныь оценкам параметров ос и р. Это смещение возникает в случае конечные выборок, однако оценки, найденные обычным методом наименьшие квадратов, будут к тому же и несостоятельными, т. е. смещение сохранится и для бесконечно «больших выборок. [c.343]
В более общем случае, когда модель состоит из одновременных уравнений, не удовлетворяющих специальным предположениям о рекур-сивности, существует простой метод оценивания — косвенный метод наименьших квадратов, но он применим лишь к точно идентифицируемым уравнениям. Состоит этот метод в использовании обыкновенного метода наименьших квадратов для оценивания параметров каждого из уравнений структурной формы в отдельности и в последующем выводе оценок структурных параметров с помощью преобразования ВП = —Г, где вместо матрицы П берется матрица оценок параметров приведенной формы П. Элементы матрицы П будут наилучшими линейными несмещенными оценками, однако это свойство не сохраняется при преобразованиях, и полученные оценки структурных параметров, по-видимому, окажутся смещенными. Тем не менее и оценки П, и оценки косвенного метода наименьших квадратов будут состоятельными. Для [c.375]
Другой метод устранения или уменьшения мультиколлинеар-ности заключается в переходе от несмещенных оценок, определенных по методу наименьших квадратов, к смещенным оценкам, обладающим, однако, меньшим рассеянием относительно оцениваемого параметра, т. е. меньшим математическим ожиданием квадрата отклонения оценки fy от параметра ру или М (bj— p/)2. [c.110]




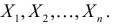
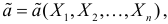
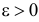
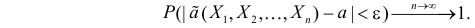
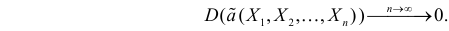
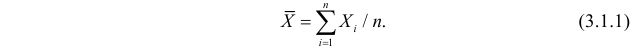
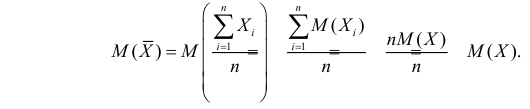
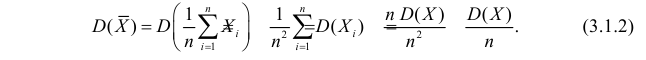

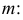
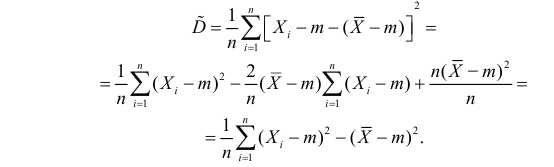
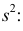
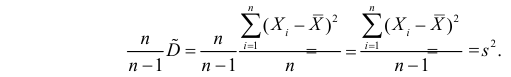
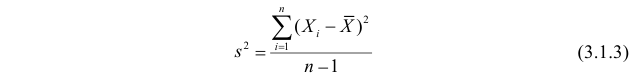
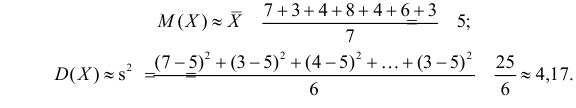
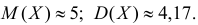

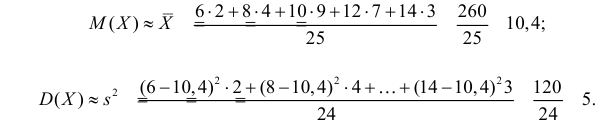
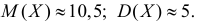
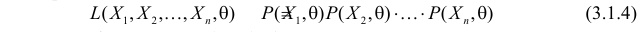
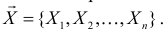
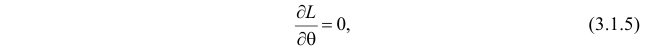
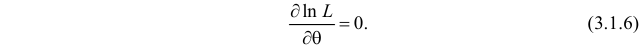
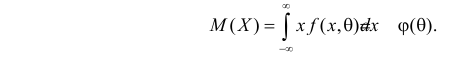
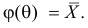
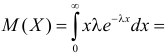
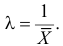
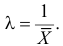
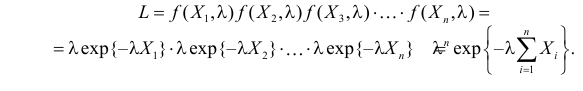
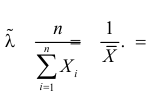
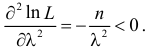
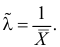

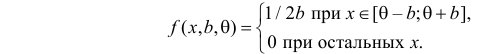
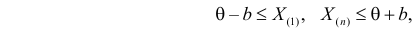
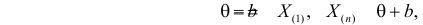
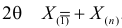

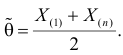
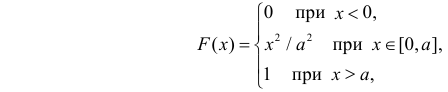
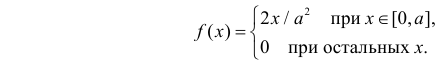
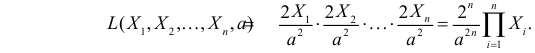
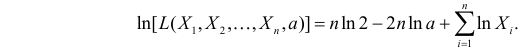

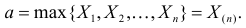
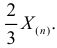
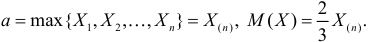
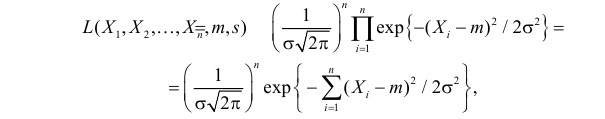
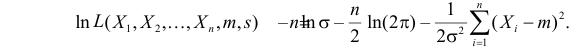
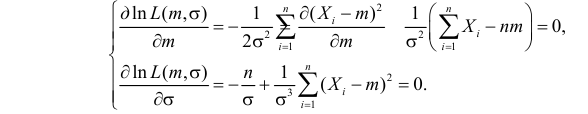
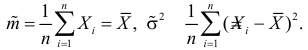
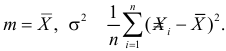

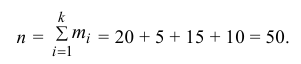
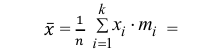
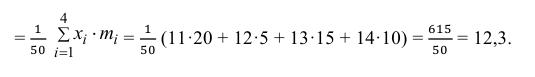
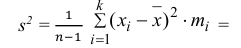
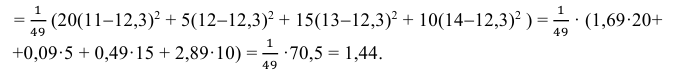
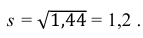
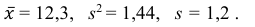

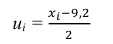

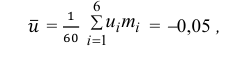
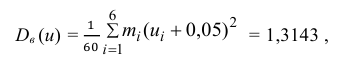
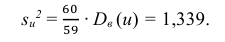
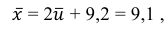
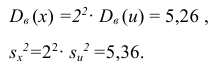
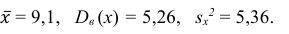

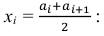

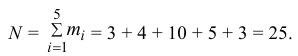
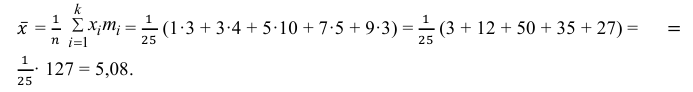
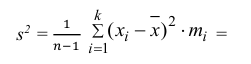
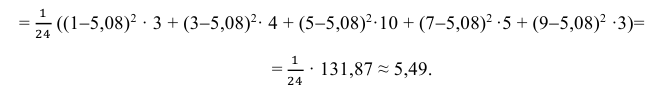
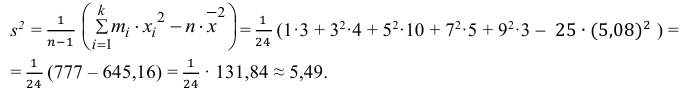
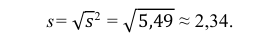
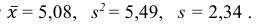
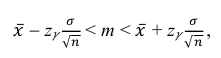
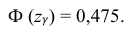
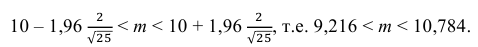

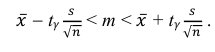
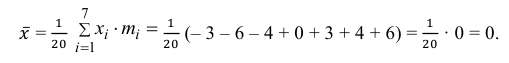
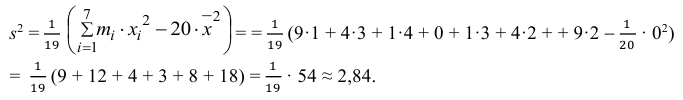
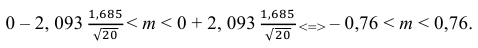
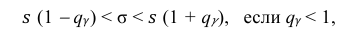
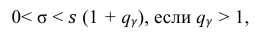
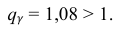
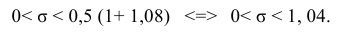










































































 при известном значении
при известном значении  с заданной надежностью
с заданной надежностью 




























 при неизвестном значении
при неизвестном значении  из заданной надежности
из заданной надежности 




























 для
для 











































 генеральной совокупности с заданной надежностью
генеральной совокупности с заданной надежностью 






























 с помощью неравенства Чебишова с заданной надежностью
с помощью неравенства Чебишова с заданной надежностью 

















