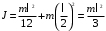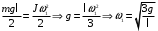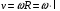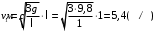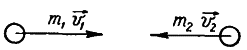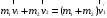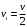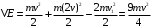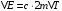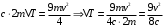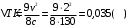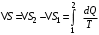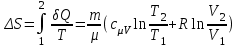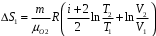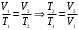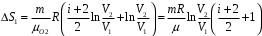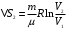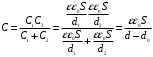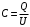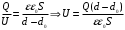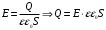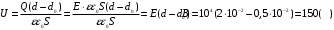Стержень длиной l движется в горизонтальной плоскости. В некоторый момент времени скорости концов стержня равны 



я рассуждал так(как оказалось, неверно):
нарисовав окружность, диаметр которой является стержень, спроецировал векторы 





на скринах решение из задачника. я не понимаю, зачем вводят три новые системы отсчета. 
условие и первая часть решения
вторая часть решения
извиняюсь, что не обрезал изображение, нету возможности.
p.s. сразу извиняюсь за скрины — там и картинки, и решение.
Условие задачи:
В магнитном поле с индукцией 0,01 Тл вращается стержень длиной 0,2 м с постоянной угловой скоростью 100 рад/с. Определить ЭДС индукции, возникающую в стержне, если ось вращения проходит через конец стержня параллельно линиям индукции магнитного поля.
Задача №8.4.50 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(B=0,01) Тл, (l=0,2) м, (omega=100) рад/с, (rm E_i-?)
Решение задачи:
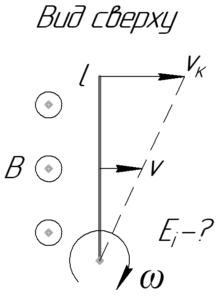
[{{rm E}_i} = Bupsilon l;;;;(1)]
В этой формуле (B) – индукция магнитного поля, (upsilon) – скорость центра масс стержня (т.е. скорость середины проводника), (l) – длина стержня.
На рисунке показано распределение скоростей точек стержня, например, (upsilon_к) – это скорость конца стержня. Очевидно, что точка стержня, находящаяся на оси вращения, имеет нулевую скорость. В этой задаче важно понять, что в формуле (1) используется именно скорость середины стержня (upsilon).
Скорость центра масс стержня (upsilon) легко найти по формуле:
[upsilon = frac{{omega l}}{2};;;;(2)]
Подставим выражение (2) в формулу (1):
[{{rm E}_i} = frac{{Bomega {l^2}}}{2}]
Подставим данные задачи в эту формулу и посчитаем численный ответ:
[{{rm E}_i} = frac{{0,01 cdot 100 cdot {{0,2}^2}}}{2} = 0,02;В]
Ответ: 0,02 В.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
8.4.49 Поток магнитной индукции в проводящем контуре, содержащем 100 витков
8.4.51 Найти максимальный магнитный поток через прямоугольную рамку, вращающуюся
8.4.52 При равномерном изменении силы тока через катушку из 500 витков в ней возникает
(Все задачи по кинематике и ответы к ним находятся также в zip-архиве (332 кб), который можно скачать и открыть на своем компьютере. Попробуйте решить все задачи самостоятельно и только потом сравнивать свои ответы с нашими. Желаем успехов!)
5.21. Из двух точек, расположенных на одной высоте и на расстоянии L друг от друга, одновременно бросают два тела: одно вертикально вверх со скоростью v1; другое горизонтально со скоростью v2 в направлении первого тела. Найти наименьшее расстоянии между телами.
| Ответ к задаче 5.21: dmin = | Lv1 | . |
| √(v12 + 22) |

5.23. Из одной и той же точки одновременно бросают два камня с одинаковыми начальными скоростями vo = 10 м/с: один — вертикально вверх, другой — под углом α = 30° к горизонту. Определить расстояние между камнями через t = 2 с после броска. [20 м]
5.24. По грязной дороге едут друг за другом две машины со скоростью v. При каком минимальном расстоянии между машинами грязь, срывающаяся с колес передней машины, не будет попадать на заднюю? Считать, что в момент отрыва скорость комков грязи равна скорости соответствующей точки колеса. Радиус колеса считать малым по сравнению с дальностью полета грязи. [ Lmin = v2/8 ]
5.25. Магнитофонная лента сматывается с бобины с постоянной скоростью v. Найти зависимость радиуса ленты на бобине от времени, если начальный радиус Ro, а толщина ленты d. d << Ro.
| Ответ к задаче 5.25: R(t) = √(Ro2 − | vtd | ). |
| π |
5.26. Два тела одновременно брошены из одной точки с одинаковыми скоростями vo под углами α и π/2 − α к горизонту. Как зависит от времени расстояние между телами? [ d(t) = vot√(2(1 − sin 2α)) ]

| Ответ к задаче 5.27: vA = | v2t | ; vC = | v | . |
| √(L2 − v2t2) | √2 |
Траекторией точки C является окружность с радиусом L/2 с центром в точке O.


5.30. Велосипедист, не вращая педалями, движется по горизонтальной окружности. При этом переднее колесо велосипеда движется по окружности радиусом R. Найти радиус окружности, по которой движется заднее колесо, если расстояние между осями колес равно L (R > L). [ r = √(R2 − L2). Указание: скорость второго тела направлена вдоль нити и по касательной к окружности]
5.31. Горизонтальная платформа движется со скоростью v. По платформе, с одинаковыми относительно платформы скоростями u, движутся два тела. Скорость одного из них по направлению совпадает с вектором v, а второго — перпендикулярна вектору v. Определить угол между скоростями тел в неподвижной системе отсчета.
| Ответ к задаче 5.31: cos α = | v | . |
| √(u2 + v2) |



| Ответ к задаче 5.34: v1 = | v + u | . |
| 2cos(α/2) |
Указание: сумма проекций среднего блока на левую и правую нити 2v1cos(α/2) равна скорости убывания длины нити между крайними блоками.



5.38. Горизонтальный стержень длиной L вращается вокруг вертикальной оси O с угловой скоростью w (рисунок слева). На движущийся конец стержня насажено колесо радиусом r. Угол между осью колеса и стержнем равен α, а само колесо катится по горизонтальному столу. Найти угловую скорость вращения колеса.


[ xA(t) = vt − Rsin (vt/R);
yA(t) = R(1 − cos (vt/R)). Указание: движение точки A можно представить как сумму поступательного движения с постоянной скоростью v и вращательного вокруг центра колеса с угловой скоростью v/R. ]

Содержание:
- Плоское движение тела
- Определение скоростей точек тела
- Уравнения плоского движения
- Скорости точек фигуры. Мгновенный центр скоростей
- Определение положения мгновенного центра скоростей
- Порядок решения задач на тему: Определение скоростей точек тела
- Примеры решения задач на тему: Определение скоростей точек тела
- Решение задачи графоаналитическим способом
- Решение задачи с помощью мгновенного центра скоростей
- Определение ускорений точек тела
- Ускорения точек плоской фигуры
- Порядок решения задач на тему: Определение ускорений точек тела
- Примеры решения задач на тему: Определение ускорений точек тела
- План скоростей
- Порядок решения задач на тему: План скоростей
- Примеры решения задач на тему: План скоростей
- План ускорений
- Примеры решения задач на тему: План ускорений
Плоское движение тела — это такое движение, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Плоское движение тела
Плоскопараллельное движение (плоское движение) — вид движения абсолютно твёрдого тела, при котором траектории всех точек тела располагаются в плоскостях, параллельных заданной плоскости. Примером плоскопараллельного движения по отношению к вертикальной плоскости, относительно которой тело движется в параллельном направлении, является качение колеса по горизонтальной дороге
Определение скоростей точек тела
Скорости точек тела пропорциональны их расстояниям до мгновенного центра скоростей, и это отношение определяет угловую скорость тела в данный момент времени: Частные случаи определения положения мгновенного центра скоростей. Если плоскопараллельное движение осуществляется путем качения без скольжения одного цилиндрического тела по поверхности другого, то точка касания Р имеет в данный момент времени скорость равную нулю, и, следовательно является мгновенным центром скоростей .
Уравнения плоского движения
Плоским называется такое движение тела, при котором траектории всех его точек лежат в плоскостях, параллельных данной неподвижной плоскости.
При таком движении все точки твердого тела, лежащих на перпендикуляре к этой плоскости, имеют одинаковые траектории, скорости и ускорения.
Плоское движение фигуры можно рассматривать как сложное (то есть, абсолютное) движение, которое включает поступательное движение вместе с произвольно выбранной точкой 
На рис.4.1 с телом 





Уравнения (4.1) называются уравнениями плоского движения твердого тела.
При этом, поступательная часть плоского движения описывается двумя уравнениями:
а относительная вращательная вокруг полюса — третьим уравнением:
Координаты любой точки 



Скорости точек фигуры. Мгновенный центр скоростей
Поскольку плоское движение тела состоит из поступательного вместе с полюсом и вращательного вокруг него, то скорость любой точки тела 





Вектор относительной скорости 



Модуль и направление абсолютной скорости 


Относительная скорость 


где 
Найти скорость любой точки тела можно также на основе теоремы, которая гласит:
Проекции скоростей двух точек фигуры на прямую, что соединяет эти точки, равны между собой.
Согласно этой теореме (рис.4.3) :
или
Если известна скорость 

При плоском движении тела в каждый момент времени существует точка тела, скорость которой равна нулю. Эта точка называется мгновенным центром скоростей и, как правило, обозначается буквой 
Если мгновенный центр скоростей известен, то легко можно найти мгновенное распределение скоростей всех точек тела (рис.4.4).
Выберем за полюс поступательного движения мгновенный центр скоростей 


где 









Поскольку скорость выбранного полюса 

По модулю скорости вращения точек 


Разделив 

Таким образом, мгновенное распределение скоростей точек тела при его плоском движении, такое же, какое было бы при его вращательном движении вокруг мгновенного центра скоростей.
Определение положения мгновенного центра скоростей
Существует несколько способов нахождения положения мгновенного центра скоростей.
Случай 1. Известна скорость 


Мгновенный центр скоростей 


Для нахождения направления перпендикуляра надо повернуть вектор 


Случай 2. Известны направления скоростей 



Мгновенный центр скоростей должен лежать как на перпендикуляре к вектору 


Случай 3. Скорости двух точек 

Говорят, что в этом случае мгновенный центр скоростей лежит на бесконечности. Угловая скорость вращения равна нулю, а скорости всех точек тела геометрически равны, то есть в данный момент времени тело выполняет поступательное движение.
Случай 4. Скорости двух точек 




Мгновенный центр скоростей находится на продолжении отрезка 
Решив это уравнение относительно 
Таким образом, для определения положения мгновенного центра скоростей надо знать не только направления скоростей, но и их величину.
Случай 5. Скорости двух точек 


Мгновенный центр скоростей лежит на отрезке 

Решив уравнение относительно 
Таким образом, для нахождения положения мгновенного центра скоростей надо знать величины и направления скоростей обеих точек.
Случай 6. Тело катится без проскальзывания по неподвижной поверхности (рис.4.10).
В этом случае мгновенный центр скоростей находится в точке 

Тогда и скорость точки 
Порядок решения задач на тему: Определение скоростей точек тела
а) решение графоаналитическим методом:
- выбрать за полюс ту точку тела, скорость которой известна по величине и направлению или легко определяется из условий задачи;
- найти точку тела, направление скорости которой известно;
- пользуясь формулами плоского движения найти скорость этой точки;
- определить угловую скорость тела в данный момент времени;
- по известной угловой скорости и скорости полюса, пользуясь формулами плоского движения найти скорости других точек тела.
б) решение с помощью мгновенного центра скоростей:
- определить положение мгновенного центра скоростей одним из известных способов;
- определить значение мгновенного радиуса той точки тела, скорость которой известна, и найти угловую скорость тела;
- найти скорости других точек тела.
Примеры решения задач на тему: Определение скоростей точек тела
Задача №1
Стержень 






Определить величину скорости точки 

Решение задачи графоаналитическим способом
1. Выберем за полюс точку 
2. Используя формулу распределения скоростей при плоском движении, запишем векторное уравнение для определения скорости точки 
где 




Данное векторное уравнение можно решить построением векторного треугольника скоростей (рис.4.12). Для этого из произвольной точки плоскости 
При построении правой части уравнения (1) из точки 









Теперь из точки 



Точка 


В результате построения получили замкнутый треугольник скоростей, стороны которого в выбранном масштабе определяют искомую скорость точки 

В этом треугольнике известны все углы и одна сторона 

3. Определим угловую скорость вращения стержня 

4. Найдем скорость точки 



где 




Скорость 

Отложив от точки 







Поскольку стороны 




Решение задачи с помощью мгновенного центра скоростей
1. Определим положение мгновенного центра скоростей. Для этого с точек 




2. Определим мгновенные радиусы. Поскольку треугольник 
3. Вычислим угловую скорость вращения фигуры вокруг мгновенного центра скоростей:
4. Найдем скорости точек 

где 




Если надо было бы определить только величину скорости 
Тогда:
Ответ:
Задача №2
Колесо радиусом 


Определить: скорости точек 


Решение.
1. В качестве полюса выберем точку 
2.Используя формулу распределения скоростей точек тела при плоском движении определяем скорости других точек колеса.
Для точки 
где 


По модулю 
Скорость 



Из точки 


Тогда:
Векторное уравнение для определения скорости точки 
где 


Эта скорость параллельна скорости 
Из точки 


Поскольку векторы коллинеарны, то:
Таким образом, скорость точки 


Составляем векторное уравнение для определения скорости точки 
где 


По модулю 
Скорость 


Из точки 






Поскольку векторы 


Ответ:
Задача №3
Колесо радиусом 
Определить: скорости точек 


Решение. Решим задачу с помощью мгновенного центра скоростей.
1. Определим положение мгновенного центра скоростей. Поскольку колесо катится по неподвижной поверхности, то мгновенный центр скоростей находится в точке 
2. Мгновенный радиус для точки 


Направлена угловая скорость по ходу часовой стрелки.
3. Определим величину и направление скоростей точек 


Соединим точки 








По модулю скорости будут равны:
где
Ответ:
Задачи, которые рекомендуются для самостоятельной работы: 16.2; 16.4; 16.11; 16.12 [2]
Определение ускорений точек тела
Теорема: ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки во вращательном движении фигуры вокруг полюса.
Ускорения точек плоской фигуры
Формула распределения ускорений при плоском движении тела имеет вид:
где 






Ускорение любой точки 

Графическое определение ускорения точки 
Вычисление величины ускорения точки 


Учитывая, что 


где
Вектор 




Тогда уравнение (4.10) примет вид:
Если точка 


Порядок решения задач на тему: Определение ускорений точек тела
1. Выбрать точку, которая будет полюсом при записи уравнения плоского движения (как правило выбирают точку, ускорение которой известно).
2. Записать векторное уравнение распределения ускорений.
3. Спроектировать уравнение распределения ускорений на две взаимно перпендикулярные оси, одна из которых совпадает с нормальным ускорением, а вторая – с тангенциальным.
4. Определить мгновенное угловое ускорение плоской фигуры.
5. Найти искомые ускорения точек с помощью уравнения распределения ускорений.
Примеры решения задач на тему: Определение ускорений точек тела
Задача №1
Прямоугольная (рис.4.18, а) пластина 




Ускорение точки 



Определить мгновенную угловую скорость и мгновенное угловое ускорение пластины, и ускорение точки 
Решение.
1. Выберем за полюс точку 
2. Составим векторное уравнение для ускорения точки 
где 









Поскольку направление углового ускорения неизвестное, то направлением 
3. Спроектируем составленное уравнение (1) на оси 

В проекции на ось 
В проекции на ось 
4. Из уравнения (2) получим величину нормального ускорения:
Найдем мгновенную угловую скорость фигуры:
5. Из уравнения (3) получим величину тангенциального ускорения:
Угловое ускорение фигуры:
Поскольку величина 
6. Определим ускорение точки 
Для вычисления ускорения точки 


Направление векторов 

Спроектируем записанное уравнение на оси 

где
Полное ускорение точки 
Ответ: 
Задача №2
Равносторонний треугольник 



Определить ускорение вершины 
Решение. Если известны ускорения двух точек плоской фигуры, например 

1. Рассматривая первую точку 


2. Из уравнения проекций определить величину нормального ускорения 

3. Спроектировать векторное уравнение распределения ускорений при плоском движении на прямую, которая перпендикулярна 


4. Если нужно, то, используя формулу распределения ускорений при плоском движении, определить ускорение любой другой точки плоской фигуры.
Решим задачу, придерживаясь приведенной последовательности.
1. Выберем за полюс точку 

где 









Спроектируем записанное равенство (1) на прямую 
2. Откуда:
Поскольку 
3. Спроектируем векторное уравнение на прямую, которая перпендикулярна 
Откуда:
Учитывая то, что 
Поскольку величина тангенциального ускорения 
4. Определим ускорение точки 

где 










Учитывая, что 
От точки 
Выберем систему координат 


Спроектируем равенство (2) на оси выбранной системы координат:
Подставляя числовые данные, получим:
Таким образом, ускорение вершины 
Поскольку проекция ускорения 






Ответ:
Задача № 3
В шарнирном механизме (рис.4.21) в данный момент времени угловая скорость и угловое ускорение кривошипа 




Найти ускорение точки 


Решение. Скорость точки 

Направлена скорость 


Точка 


Поскольку скорости точек 

Ускорение точки 
где
Направления ускорений 

Выберем точку 


или
где 









Свяжем с точкой 


С другой стороны, при движении точки 


где 






По величине нормальное 

Спроектируем уравнение (4) на оси выбранной системы координат:
Подставим в (3) все рассчитанные величины:
Поскольку
то
Положительное значение величины 

Угловое ускорение тела 
Угловое ускорение 

Для определения тангенциального ускорения 

Откуда
Поскольку величина 

Полное ускорение точки 
Ответ:
Задачи, которые рекомендуются для самостоятельной работы: 18.12; 18.14; 18.22 [2].
План скоростей
План скоростей и план ускорений – физическое изображение векторных уравнений, связывающих скорости и ускорения точек механизма. Изображение механизма, выполненное с помощью условных обозначений (см. выше) называется структурной схемой механизма.
Определение скоростей различных точек движущейся плоской фигуры легко может быть выполнено графически с помощью построения плана скоростей.
План скоростей – это графическое изображение из единого центра (полюса) векторов абсолютных скоростей точек фигуры в фиксированный момент ее движения.
План скоростей может быть построен, если:
- известная скорость одной точки плоской фигуры и направление скорости другой точки;
- известная скорость одной точки плоской фигуры и мгновенная угловая скорость фигуры
Пусть известные скорости 













Установим свойства и правила построения плана скоростей.
По уравнению распределения скоростей при плоском движении фигуры, если за полюс принять точку 

где 





С другой стороны для векторов треугольника 
Учитывая, что векторы 





Таким образом, отрезок 

где 
Аналогично:
Отсюда мгновенная скорость вращения плоской фигуры:
Вектор 






Из рассматриваемого вытекает:
Порядок решения задач на тему: План скоростей
1. Изображают на чертеже в выбранном масштабе плоскую фигуру и вектор скорости той точки, скорость которой известна.
2. Определяют направление скорости второй точки плоской фигуры.
3. Записывают векторное уравнение распределения скоростей при плоском движении, принимая за полюс точку, скорость которой известна, а за искомую ту точку, направление скорости которой известно.
4. Решают записанное векторное уравнение графически путем построения в выбранном масштабе плана скоростей.
5. Определяют мгновенную угловую скорость вращения плоской фигуры.
6. Определяют скорость других точек плоской фигуры.
Примеры решения задач на тему: План скоростей
Задача №1
Найти угловую скорость 

Решение.
1. Согласно исходным данным в произвольном масштабе строим схему механизма (рис.4.25, а).
2. Учитывая, что кривошип 1 вращается вокруг неподвижной точки 


Направлена скорость 


3. Следующей точкой шатуна, скорость которого можно определить, является точка 
Для определения скорости точки 

где 





4. Решим уравнение (1) графически (рис.4.25, б). Для этого с произвольной точки 







Вектор который будет на плане скоростей изображать абсолютную скорость точки 




Определим направление отрезка 







Полученный векторный треугольник 








Перенесем из плана скоростей в точку 


Поскольку скорость 








Аналогично, 



Таким образом, и угол при вершине 



5. Определяем мгновенную угловую скорость шатуна 2. Поскольку 
где 

Направление угловой скорости 


Ответ:
Задача №2
Найти угловые скорости шатуна 2 и коромысла 3 и абсолютные скорости точек 



Угловая скорость кривошипа 1 — 
Решение.
1. В соответствии с исходными данными в произвольном масштабе строим схему механизма (рис.4.27, а).
2. Так как точка 


Вектор скорости 

2. Шатун 2 механизма движется плоскопараллельно. Скорость точки 






3. Для определения скорости точки 
где 









4. Решаем записанное уравнение графически. Для этого из произвольной точки 



Через конец вектора 




Скорость точки 




Полученный на рис. 4.27, б векторный треугольник 










Перенесем направления скоростей 


Поскольку 






Таким образом
Угол при вершине 






Тогда угол при вершине 
Для определения сторон 
Из уравнения (1) получим:
Таким образом:
5. Определим мгновенные угловые скорости шатуна 2 и коромысла 3. Поскольку 
Направление угловой скорости 


Угловая скорость коромысла 3 равна:
где
Направление 

6. Определить величины скоростей 

Поскольку вектор 

Скорости 



Тогда:
7. Для определения скорости точки 
Поскольку фигура 

В левой части пропорции (2) отношение отрезков на схеме механизма, а в правой — на плане скоростей.
Из уравнения (2) получим расстояние от точки 

Поскольку на схеме механизма отрезок 









Вектор скорости 



Ответ: 


Задача №3
В состав рычажного механизма (рис.4.29) входят два кривошипа 1 и 4, и два шатуна 2 и 3. Кривошип 1 вращается с угловой скоростью 

Найти угловые скорости шатунов 2 и 3 и абсолютные скорости точек 



Решение. Особенность этой задачи заключается в том, что определить сразу направление скорости точки 





1. В соответствии с исходными данными в произвольном масштабе строим схему механизма (рис.4.30, а).
2. Так как точка 


Вектор скорости 

Шатун 2 механизма движется плоскопараллельно. Скорость точки 

Для определения скорости точки 
где 








В уравнении (1) три неизвестных: величина и направление скорости точки 

для плоскости позволяет определить только две неизвестных, то решить уравнение (1) невозможно.
3. Рассмотрим определение скорости точки 

Скорость точки 
Вектор скорости 

Учитывая, что шатун 3 механизма движется плоскопараллельно, то для определения скорости точки 
где 






В записанной системе векторных уравнений (1,2) четыре неизвестных: величина и направление скорости точки 


4. Решаем записанную систему векторных уравнений (1) и (2) графически. Для этого из произвольной точки 
Согласно уравнению (1) из произвольной точки 





Тогда масштабный коэффициент плана скоростей будет равен:
Через конец вектора 




Теперь построим из того же самого полюса 




Через конец вектора 




Точка пересечения 





Полученный на рис. 4.30,б четырехугольник 






Перенесем направления скоростей 

5. Определим мгновенные угловые скорости шатунов.
Поскольку 
Направление угловой скорости 


Аналогично, угловая скорость шатуна 3 равна:
Направление 

Для определения скорости точки 



Вектор скорости 



Ответ: 
План ускорений
План ускорений – построенный в определенном масштабе векторный график, характеризующие ускорения всех точек и звеньев механизма. Произвольная точка ра, из которой производится построение плана ускорений, называется полюсом плана ускорений.
Рассмотрим графический способ определения ускорений точек плоской фигуры (тела) с помощью плана ускорений.
Планом ускорений плоской фигуры является геометрическое место концов векторов ускорений любых точек фигуры, что отложены из одной произвольной точки, которую называют полюсом плана ускорений.
Построение плана ускорений основано на представлении ускорения 

где 











Поскольку для определения величины 

Для того, чтобы уравнение (4.18) можно было решить, должно быть известно ускорение 

Кроме того, должно быть известно:
Рассмотрим определение ускорений точек 





Для ускорения точки 

Решим уравнение (4.18) графически. Для этого (рис.4.31, б) из произвольной точки 





Величину ускорения 
а направлен этот вектор вдоль 


К нормальному ускорению добавим, согласно уравнению (4.18), тангенциальное ускорение 





Направление абсолютного ускорения 









Для определения ускорения точки 


Запишем векторные уравнения для ускорения точки 


где 









Первым решаем уравнение (4.19). Поскольку ускорение 






Через конец вектора 



Следующим построим уравнение (4.20). Поскольку ускорение 






Через конец вектора 



Таким образом, конец вектора 




Векторы 







Кроме абсолютных и относительных ускорений точек фигуры 



Для определения же направления углового ускорения 



Треугольник 

Таким образом, для плана ускорений справедливо
правило подобия: фигура, которую образуют концы векторов абсолютных ускорений точек тела на плане ускорений подобная фигуре, которую одноименные точки образуют на теле.
Примеры решения задач на тему: План ускорений
Задача №1
Найти ускорение точки 


Решение. План скоростей для этого механизма был построен в задаче № 1 занятия № 7 (рис.4.25,б) и была определена угловая скорость шатуна 2 
1.Построим схему механизма (рис. 4.32, а).
2. Сначала найдем ускорение точки 

Учитывая, что угловая скорость кривошипа постоянная 





По модулю:
Направлено ускорение 



3. Для определения ускорения точки 

где 













Поскольку направление ускорения точки 

4. Решим уравнение (1) графически путем построения плана ускорений.
Из произвольной точки 

















Поскольку ускорение 








4. Из построенного плана ускорений определим абсолютные величины ускорений 







Из векторного четырехугольника 
Спроектируем векторное уравнение (2) на прямую 
Учитывая, что 


Откуда:
Теперь спроектируем уравнение (2) на прямую 
Учитывая, что 

Откуда:
Поскольку 
Из полученного результата следует, что в данный момент времени шатун механизма вращается равномерно 
Ответ:
Если построение плана ускорений выполнять с соблюдением масштаба, то ускорения характерных точек можно определить непосредственно измерением соответствующих отрезков на плане ускорений.
Задача №2
Найти абсолютное ускорение точек 




Решение. План скоростей механизма для положения, что рассматривается, был построен в задаче № 2 занятие № 7 (рис.4.27, б) и определены мгновенные угловые скорости шатуна 2 и коромысла 3:
Решим задачу путем построения в масштабе плана ускорений.
1. Сначала в произвольном масштабе строим схему механизма (рис.4.34, а).
2.Определим ускорение точки 
Поскольку кривошип 1 вращается вокруг неподвижной точки 





По модулю 
Направлено ускорение 


3.Запишем векторные уравнения для определения ускорения точки 
Точка 







где 



















4.Решим графически систему векторных уравнений (1,2).
Сначала построим уравнение (1). Для этого из произвольной точки 







От конца вектора 






Через конец вектора 




Следующим построим уравнение (2).
Поскольку 


От точки 






Через конец вектора 


Решением системы (1,2) будет точка 




Вектор абсолютного ускорения 



Величины тангенциальных ускорений 

Поскольку 



где 
Для определения направления углового ускорения 




Аналогично, для определения направления 



5.Для определения ускорения точки 



В левой части пропорции (3) отношение отрезков на схеме механизма, а в правой — на плане ускорений.
Из уравнения (3) получим расстояние от точки 

Поскольку на схеме механизма отрезок 









Вектор абсолютного ускорения 



Ответ: 
Задача №3
В состав рычажного механизма (рис.4.35) входят два кривошипа 1 и 4, и два шатуна 2 и 3. Кривошип 1 в настоящий момент времени вращается равномерно с угловой скоростью 

Найти угловые ускорения шатунов 2 и 3 и абсолютные ускорения точек 



Решение. План скоростей механизма для положения, что рассматривается, был построен в задаче №3 занятия №7 (рис.4.30, б) и определены мгновенные угловые скорости шатуна 2 и шатуна 3:
1. В произвольном масштабе построим схему механизма (рис. 4.36, а).
2.Сначала определим абсолютные ускорения точек 

Поскольку кривошип 1 вращается вокруг неподвижной точки 


Направлено ускорение 



Кривошип 4 вращается вокруг неподвижной точки 


Абсолютное ускорение точки 
Нормальная составляющая ускорения точки 



а тангенциальная — перпендикулярно 

3. Запишем векторные уравнения для определения ускорения точки 
Точка 





В уравнении (2):






В уравнении (3):






4. Решим графически систему векторных уравнений (2,3).
Сначала построим уравнение (2). Для этого из произвольной точки 







От конца вектора 






Через конец вектора 




Следующим построим уравнение (3).
Для построения вектора 






Длины векторов 

Абсолютное ускорение 


От точки 






Через конец вектора 


Решением системы (2,3) будет точка 




Вектор абсолютного ускорения 



Величины тангенциальных ускорений 

Поскольку 



Направления угловых ускорений 






5. Для определения ускорения точки 







Ответ: 
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Подборка по базе: ПР Проблема скрытой массы.docx, Проблема скрытой массы.pptx, 4.1 Решение задач.doc, Детский массаж. Поэтапное руководство.pdf, № 363674 Решение.docx, ЗС-12 Особенности феодальной раздробленности на Руси причины, ос, 8. Составная оболочка. Задание. Решение.docx, _Решение задач на прямолинейное равноускоренное движение_ (9 кла, КСП , русский язык, 9 класс _Виды средств массовой информации. Б, 06_ЛР5+ Массивы_и_строки.docx
КР1
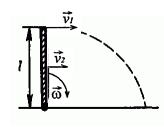
-139. Тонкий однородный стержень длиной l из вертикального положения падает на горизонтальную поверхность. Найти линейные скорости крайней и средней точек стержня в момент времени, когда стержень займет горизонтальное положение.
| Дано:
ℓ=1м |
| v — ? |
Решение:
Рассмотрим движение центра масс стержня. В вертикальном положении он обладает потенциальной энергией, которая при падении переходит в кинетическую энергию вращения.
Кинетическая энергия стержня в момент удара равна потенциальной:
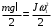
Момент инерции стержня относительно оси, проходящей через его конец, находим по теореме Штейнера:
Подставим в формулу (1) и выразим угловую скорость в момент удара
Линейная скорость стержня связана с угловой соотношением:
Угловая скорость всех частей стержня будет одинакова ω=ω1=ω2
Тогда скорость конца стержня в момент удара
Скорость середины стержня
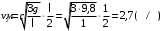
Ответ: v1=5,4 м/с; v2=2,7 м/с;
КР2
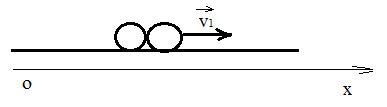
-219. Два свинцовых шара с одинаковой массой движутся навстречу друг другу со скоростями v и 2v. Насколько увеличится температура шаров в результате их неупругого удара при v = 2,0 м/с?
| Дано:
m1=m2 =m v и 2v v = 2,0 м/с |
| ∆T — ? |
Решение:
После неупругого удара шары будут двигаться как одно целое. При этом общую скорость шаров после удара можно определить из закона сохранения импльса:
Или в проекции на ось ох и с учетом условия задачи (см рис):
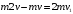
Изменение механической энергии шаров после удара:
Эта же величина может быть выражена через удельную теплоемкость с и изменение температуры:
Тогда изменение температуры
Удельную теплоемкость свинца находим в таблице с=130 Дж/кг·К
Ответ: ∆Т=0,035 К.
239. Кислород массой m = 1,0 кг, находящийся при давлении Р1 = 0,50 МПа и температуре Т1 = 400 К, изобарно расширяясь, увеличил объем в n = 2 раза, а затем сжимается изотермически до давления Р2 = 4,0 МПа. Найти суммарное приращение энтропии.
| Дано:
О2 µ=32·10-3 кг/моль m = 1,0 кг Р1 = 0,50 МПа=5·105 Па Т1 = 400 К 1)P=const V2=nV1;n=2 2)T=const Р2 = 4,0 МПа=4·106 Па |
| ∆S- ? |
Решение:
Приращение энтропии по определению равно
1)Газ совершает переход из состояния 1 в состояние 2 при постоянном давлении, поэтому изменение энтропии в переменных Т, V
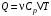
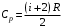
Из уравнения Гей Люссака
Тогда
Изменение энтропии, учитывая, что процесс изотермический,
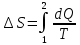
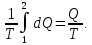
Согласно первому началу термодинамики, количество теплоты, полученное газом, Q = A + ∆U. Для изотермического процесса ∆U = 0, поэтому Q = A. Работа газа в изотермическом процессе
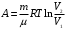
Подставив (2) в (1) найдем искомое изменение энтропии:
Общее изменение энтропии в обоих процессах
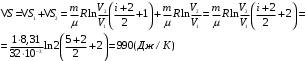
Ответ: ∆S=990 Дж/К.
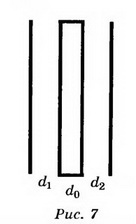
259. Однородное электрическое поле напряженностью Е = 10 кВ/м образовано двумя заряженными параллельными пластинами (плоский воздушный конденсатор), расстояние между которыми d = 2,0 см. Между пластинами параллельно им помещается металлический лист толщиной d0 = 0,50 см. Найти напряжение между пластинами после внесения металлического листа.
| Дано:
Е = 10 кВ/м=104 В/м d = 2,0 см=2·10-2 м d0 = 0,50 см=0,5·10-2 м |
| U — ? |
Решение:
Если между пластинами пометить металлический лист, то получается система из двух последовательно соединённых конденсаторов с расстоянием между пластинами d1 и d2. Ёмкости этих конденсаторов:
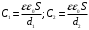
Эти конденсаторы соединены последовательно, поэтому их общая ёмкость
Электроемкость по определению равна
Тогда
Заряд конденсатора найдем из формулы напряженности электрического поля между пластинами конденсатора:
Тогда напряжение будет равно
Ответ: U=150 В.