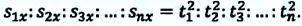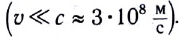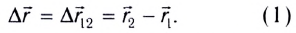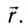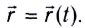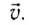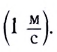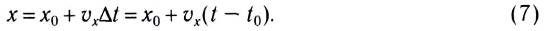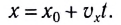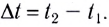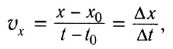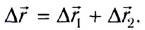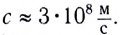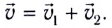Содержание:
Равномерное прямолинейное движение:
Вы изучали равномерное прямолинейное движение, познакомились с понятием «скорость». Скалярной или векторной величиной является скорость? Каковы закономерности равномерного прямолинейного движения?
Вы знаете, что движение, при котором за любые равные промежутки времени тело проходит одинаковые пути, называется равномерным. В каком случае одинаковыми будут не только пути, но и перемещения?
Проделаем опыт. Проследим за падением металлического шарика в вертикальной трубке, заполненной вязкой жидкостью (например, густым сахарным сиропом) (рис. 43). Будем отмечать положение шарика через равные промежутки времени. Опыт показывает, что за равные промежутки времени, например за
Сделаем вывод. При равномерном прямолинейном движении тело за любые равные промежутки времени совершает одинаковые перемещения и проходит одинаковые пути.
В 7-м классе вы находили скорость равномерного движения тела как отношение пути к промежутку времени, за который путь пройден: 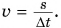
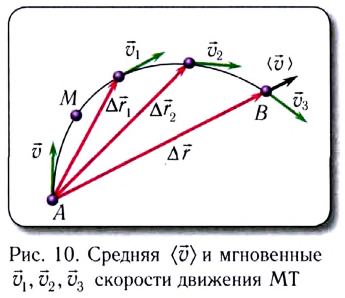
Скорость равномерного прямолинейного движения — это величина, равная отношению перемещения к промежутку времени, за который оно совершено:
Из равенства (1) следует, что скорость 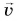
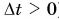
Отношение 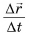
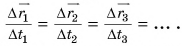
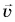
Из формулы (1) легко найти перемещение:
и путь 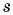
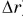
А как определить положение равномерно и прямолинейно движущегося тела в любой момент времени 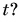
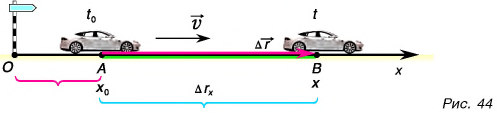
Автомобиль рассматриваем как материальную точку. Из формулы (2) находим проекцию перемещения автомобиля на ось Ох:
Согласно рисунку 44 за время 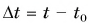
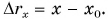
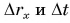
Приняв 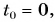
Координата равномерно и прямолинейно движущегося тела линейно зависит от времени.
Зависимость координаты движущегося тела от времени называется кинематическим законом движения. Формула (5) выражает кинематический закон равномерного прямолинейного движения.
Для измерения скорости используются специальные приборы. В автомобилях имеется спидометр (рис. 45), на самолетах — указатель скорости. Эхолокаторы измеряют скорость тел, движущихся под водой, а радиолокаторы (радары) — в воздухе и по земле. Сотрудники службы дорожного движения с помощью портативного радара с видеокамерой (рис. 46) регистрируют скорость транспортных средств.
Для любознательных:
Скорости движения могут сильно отличаться. За одну секунду черепаха может преодолеть несколько сантиметров, человек — до 10 м, гепард — до 30 м, гоночный автомобиль — около 100 м.
Около 8 км за секунду пролетает по орбите спутник Земли (рис. 47). Но даже скорости космических кораблей «черепашьи» по сравнению со скоростью микрочастиц в ускорителях. В современном ускорителе (рис. 48) электрон за одну секунду пролетает почти 300 000 км!
Главные выводы:
- При равномерном прямолинейном движении за любые равные промежутки времени тело совершает одинаковые перемещения.
- Скорость равномерного прямолинейного движения постоянна: с течением времени не изменяется ни ее модуль, ни ее направление.
- При равномерном прямолинейном движении тела модуль перемещения равен пути, пройденному за тот же промежуток времени.
- Координата равномерно и прямолинейно движущегося тела линейно зависит от времени.
Пример решения задачи:
Кинематический закон прямолинейного движения лодки но озеру вдоль оси Ох задан уравнением 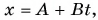
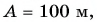
Определите: 1) проекцию скорости лодки 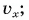
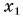
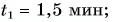
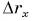
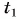
Решение
Сделаем рисунок к задаче.
По условию задачи координата лодки линейно зависит от времени. Значит, лодка движется равномерно. Сравнив 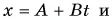
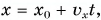
Найдем
Из рисунка 49: проекция перемещения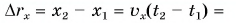
Ответ:
Графическое представление равномерного прямолинейного движения
Зависимости между различными величинами можно наглядно изобразить с помощью графиков. Использование графиков облегчает решение научных, практических задач и даже бытовых проблем.
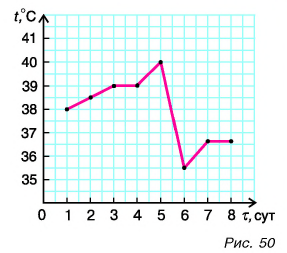
Например, по графику зависимости температуры пациента от времени (рис. 50) видно, что на 5-е сутки температура достигла своего максимума, затем резко упала, а еще через сутки стала приближаться к норме. График дал наглядное представление о течении болезни.
В физике роль графиков чрезвычайно велика. Умение строить и читать графики помогает быстрее и глубже понять физические явления.
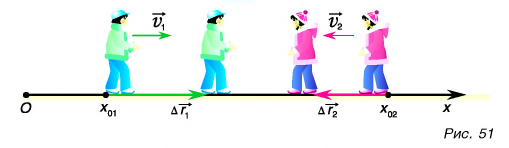
Рассмотрим простой пример из кинематики. Леша и Таня идут навстречу друг другу (рис. 51). Они движутся равномерно и прямолинейно. Модуль скорости Леши 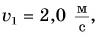
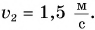
Выберем координатную ось Ох и зададим начальные положения участников движения (см. рис. 51). Пусть при 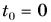
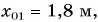
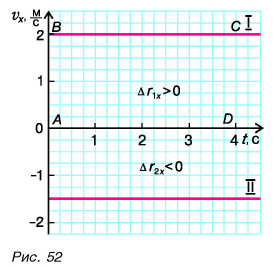
Построим графики зависимости проекции скорости 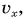
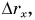
График проекции скорости
Согласно условию и рисунку 52 для проекций скорости движения Тани и Леши на ось Ох получим: 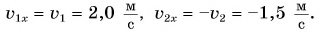
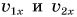
Графики показывают: проекция скорости при равномерном прямолинейном движении с течением времени не изменяется.
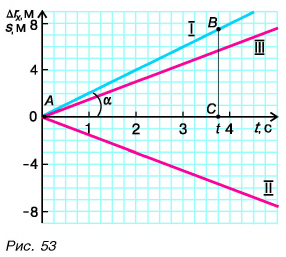
График проекции перемещения
Проекция перемещения 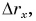
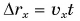
Зависимость проекции перемещения от времени для Леши 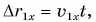
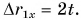
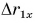
Для Тани 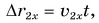
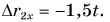
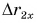
Из графиков и формул следует, что при равномерном прямолинейном движении проекция перемещения прямо пропорциональна времени.
График пути
Путь — величина положительная при любом движении тела. При равномерном прямолинейном движении путь равен модулю перемещения: 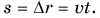
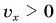
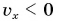
Графики пути показывают: при равномерном прямолинейном движении пройденный путь прямо пропорционален времени.
График координаты
Его называют также графиком движения.
По формуле 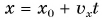
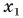
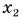
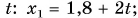
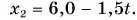
Графики движения показывают: при равномерном прямолинейном движении координата тела линейно зависит от времени.
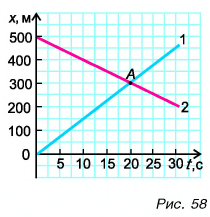
По точке пересечения графиков I и II (точке А) (рис. 54) легко найти момент и координату места встречи Леши и Тани. Определите их самостоятельно.
Что еще можно определить по графикам?
По графику проекции скорости можно найти проекцию перемещения и пройденный путь
Рассмотрим прямоугольник ABCD на рисунке 52. Его высота численно равна 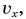
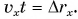
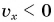
Докажите самостоятельно, что площадь между графиком проекции скорости и осью времени численно равна пройденному пути.
По углу наклона графика проекции перемещения можно оценить скорость движения
Рассмотрим треугольник АВС на рисунке 53. Чем больше угол наклона а графика проекции перемещения, тем больше скорость тела. Объясните это самостоятельно.
Главные выводы:
Для равномерного прямолинейного движения:
- График проекции скорости — прямая, параллельная оси времени.
- Графики проекции перемещения и координаты — прямые, наклон которых к оси времени определяется скоростью движения.
- Площадь фигуры между графиком проекции скорости и осью времени определяет проекцию перемещения.
Пример №1
Мотоциклист едет из города по прямолинейному участку шоссе с постоянной скоростью 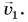
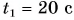
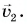
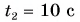
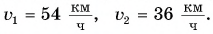
Решение
Изобразим координатную ось Ох, вдоль которой идет движение (рис. 55). Начало системы координат О свяжем с перекрестком.
В начальный момент времени мотоциклист находился на перекрестке, а велосипедист в точке В. Значит, кинематический закон движения мотоциклиста имеет вид:
Найдем координату 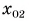
Тогда
Кинематический закон движения велосипедиста имеет вид:
Расстояние между мотоциклистом и велосипедистом через время 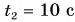
Пример №2
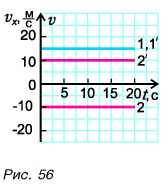
Построим графики проекций и модулей скорости. Для мотоциклиста графики проекции скорости 1 и модуля скорости 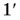
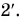
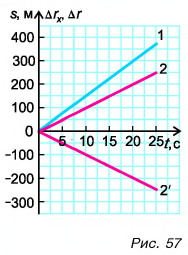
Графиками пути s, проекции 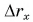
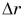
Для мотоциклиста:
Графики пути, модуля и проекции перемещения мотоциклиста совпадают (прямая 1).
Для велосипедиста:
Прямая 2 является графиком пути и модуля перемещения велосипедиста. Прямая 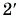
Графики координат представлены на рисунке 58. Они выражают зависимости 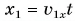
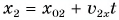
Ответ:
Прямолинейное равномерное движение и скорость
Из курса Физики VII класса вам известно, что равномерное прямолинейное движение является самым простым видом механического движения.
Прямолинейное равномерное движение — это движение по прямой линии, при котором материальная точка за равные промежутки времени совершает одинаковые перемещения.
При прямолинейном равномерном движении модуль и направление скорости с течением времени не изменяются:
Скорость при прямолинейном равномерном движении является постоянной физической величиной, равной отношению перемещения материальной точки ко времени, за которое это перемещение было совершено:
Так как отношение 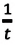
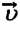
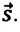
Если скорость 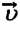
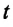
При прямолинейном равномерном движении пройденный телом путь равен модулю перемещения:
Так как уравнение в векторном виде можно заменить алгебраическими уравнениями в проекциях векторов, то для вычисления перемещения используют не формулу, выраженную через векторы, а формулу, содержащую в себе проекции векторов на координатные оси. При прямолинейном движении положение материальной точки определяется одной координатой X, определяются проекции векторов скорости и перемещения материальной точки на эту ось и уравнение решается в этих проекциях. Поэтому выражение (1.2) можно записать в проекциях перемещения и скорости на ось ОХ:
Можно получить формулу для вычисления координаты точки 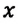
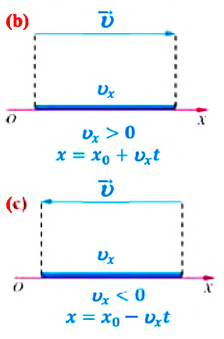
Выражение (1.5) является уравнением прямолинейного равномерного движения тела. Если материальная точка движется по направлению выбранной координатной оси ОХ, то проекция скорости считается положительной (b), если же движется против направления координатной оси, то проекция скорости считается отрицательной (с).
Из формулы (1.5) определяется выражение для проекции скорости:
Из формулы (1.6) становится ясным физический смысл скорости: проекция скорости на ось равна изменению проекции соответствующей координаты за единицу времени.
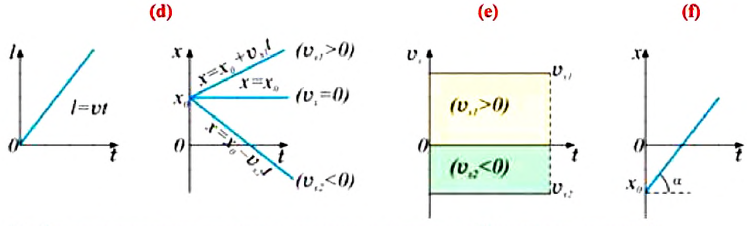
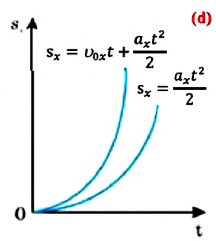
Пройденный путь и координата материальной точки при прямолинейном равномерном движении являются линейной функцией от времени (d). Скорость же является постоянной величиной, поэтому график скорость — время будет представлять собой линию, параллельную оси времени — скорость такого движения не зависит от времени (е):
График координата-время при равномерном движении образует определенный угол с осью времени. Тангенс этого угла равен проекции (модулю) скорости по оси ох (f):
Пример №3
Два велосипедиста одновременно начали движение навстречу друг другу вдоль прямой линии из пунктов А и В, расстояние между которыми 90 км. Скорость первого велосипедиста 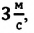
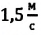
Определите: а) координату и время 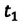
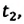
Дано:
Решение:
a) При решении задачи соблюдается следующая последовательность действий:
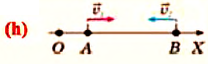
I действие. Выбирается система координат ОХ с началом координат в точке А и рисуется схема (h).
II действие. Уравнение движения записывается в общем виде:
III действие. На основании условия задачи уравнения движения велосипедистов записываются в общем виде:
IV действие. Координаты велосипедистов при встрече равны: 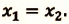
V действие. Для определения координат 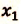
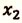
Так как 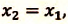
b) Так как по условию задачи велосипедисты движутся прямолинейно и без изменения направления движения, то пройденный путь равен проекции (модулю) перемещения:
c) Время 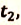
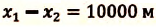
Скорость при равнопеременном прямолинейном движении
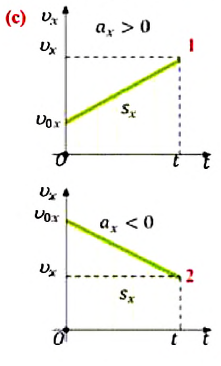
Из формулы (1.14) видно, что если известны ускорение 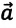
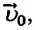
или ее проекцию на ось
Если начальная скорость равна нулю 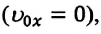
Из этих выражений видно, что скорость при равнопеременном движении является линейной функцией от времени. График зависимости скорости от времени — прямая линия, проходящая через начало координат (или через 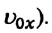
Перемещение при равнопеременном прямолинейном движении
Формулу для определения перемещения при равнопеременном движении можно вывести на основе графика скорость-время. Проекция перемещения равна площади фигуры между графиком 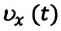
На приведенных графиках — это заштрихованная фигура трапеции (см: с):
или в векторной форме:
Если в последнюю формулу вместо 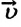
обобщенную формулу перемещения для равнопеременного движения:
Таким образом, формула проекции перемещения (например, на ось 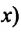
а формула координаты:
(1.23) является формулой перемещения при равнопеременном движении в векторной форме, а (1.24) и (1.25) обобщенными формулами координаты и проекции перемещения, соответственно. Если материальная точка начинает движение из состояния покоя 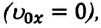
Как видно из формулы, проекция перемещения при прямолинейном равнопеременном движении пропорциональна квадрату времени 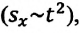
В некоторых случаях возникает необходимость определить перемещение материальной точки, не зная время 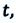
Это выражение подставляется в формулу (1.21):
После простых преобразований получаем:
Для проекции конечной скорости получаем: 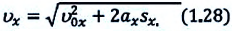
Равноускоренное и равнозамедленное движения
Равнопеременное движение по характеру может быть или равноускоренным, или же равнозамедленным.
При равноускоренном движении векторы 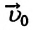
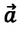
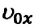
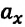
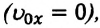
При равнозамедленном движении векторы 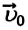
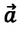
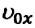
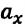
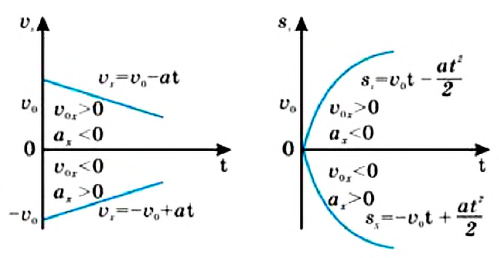
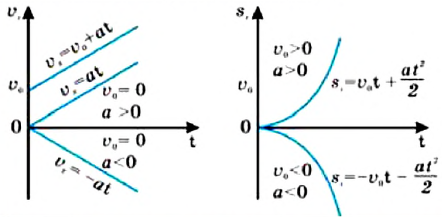
В таблице 1.3 даны формулы и соответствующие графики равноускоренного и равнозамедленного прямолинейного движения.
Таблица 1.3.
| Прямолинейное равноускоренное движение | |
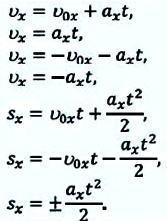 |
 |
|
Примечание: так как Это соотношение иногда называется «правило путей». |
|
| Прямолинейное равнозамедленное движение | |
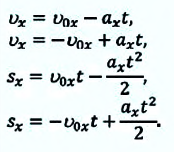 |
|
Кинематика прямолинейного движения
Физические величины бывают скалярные и векторные. Скалярные физические величины характеризуются только численным значением, тогда как векторные определяются и числом (модулем), и направлением. Скалярными физическими величинами являются время, температура, масса, векторными — скорость, ускорение, сила.
Мир вокруг нас непрерывно изменяется, или движется, т. е. можно сказать, что движение (изменение) есть способ существования материи.
Простейшая форма движения материи — механическое движение — заключается в изменении взаимного расположения тел или их частей в пространстве с течением времени. Наука, изучающая механическое движение, называется механикой (от греческого слова 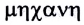
Даже самое простое движение тела оказывается достаточно сложным для изучения и исследования. Соответственно, для того чтобы в сложном явлении «увидеть» главное, в физике строится его адекватная упрощенная модель.
В механике широко используется простейшая модель реального тела, называемая материальной точкой (МТ). Под материальной точкой понимают тело, размерами и формой которого можно пренебречь при описании данного движения. Хотя МТ представляет собой абстрактное понятие, упрощающее изучение многих физических явлений, она, подобно реальному телу, «имеет» массу, энергию и т. д.
Кроме материальной точки, в механике используется модель абсолютно твердого тела. Под абсолютно твердым телом понимают модель реального тела, в которой расстояние между его любыми двумя точками остается постоянным. Это означает, что размеры и форма абсолютно твердого тела не изменяются в процессе его движения. В противном случае говорят о модели деформируемого тела.
В классической (ньютоновской) механике рассматривается движение тел со скоростями, намного меньшими скорости света в вакууме
Классическая механика состоит из трех основных разделов: кинематики, динамики и статики. В кинематике (от греческого слова 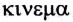
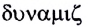
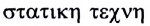
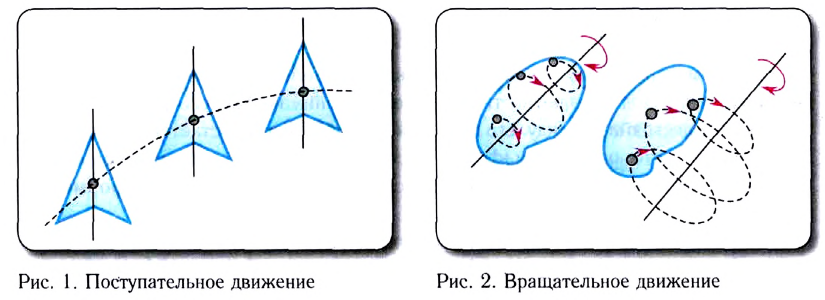
Всякое движение тела можно представить в виде двух основных видов движения — поступательного и вращательного.
Поступательным называется движение тела, при котором прямая, соединяющая в этом теле любые две точки, при перемещении остается параллельной самой себе (рис. 1).
Вращательным называется движение абсолютно твердого тела вокруг неподвижной прямой, называемой осью вращения, при котором все точки тела движутся по окружностям, центры которых лежат на этой оси (рис. 2).
Основными задачами кинематики являются:
описание совершаемого телом движения с помощью математических формул, графиков или таблиц;
определение кинематических характеристик движения (перемещения, скорости, ускорения).
Движение тела можно описать только относительно какого-либо другого тела. Тело, относительно которого рассматривается исследуемое движение, называют телом отсчета (ТО). Для описания движения используются формулы, графики и таблицы, выражающие зависимость координат, скоростей и ускорений от времени.
Основным свойством механического движения является его относительность: характер движения тела зависит от выбора системы отсчета (СО).
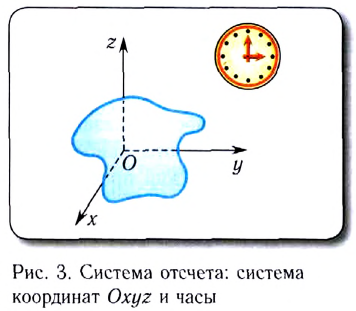
Систему отсчета, выбираемую для описания того или иного движения, образуют: тело отсчета, связанные с ним система координат (СК) и прибор для измерения времени (часы) (рис. 3).
Система координат и часы необходимы для того, чтобы знать, как с течением времени изменяется положение тела относительно выбранного тела отсчета.
Для описания движения материальной точки в пространстве вводятся такие понятия, как траектория, перемещение, путь.
Линию, которую описывает материальная точка в процессе движения по отношению к выбранной СО, называют траекторией (от латинского слова trajectorus — относящийся к перемещению). Если траектория является прямой линией, то движение называется прямолинейным, в противном случае — криволинейным.
Длина участка траектории, пройденного МТ в процессе движения, называется путем (s).
Термин «скаляр», происходящий от латинского слова scalarus — ступенчатый, введен У. Гамильтоном в 1843 г.
Термин «вектор» произошел от латинского слова vector — несущий и введен У. Гамильтоном в 1845 г.
Перемещением называют вектор 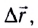
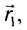
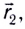
Для количественного описания механического движения тел (МТ) вводятся физические величины, характеризующие пространство и время: длина l, время t.
Длина l определяется как расстояние между двумя точками в пространстве. Основной единицей длины в Международной системе единиц (СИ) является метр (1м).
Время t между двумя событиями в данной точке пространства определяется как разность показаний прибора для измерения времени, например часов. В основе работы прибора для измерения времени лежит строго периодический физический процесс. В СИ за основную единицу времени принята секунда (1с).
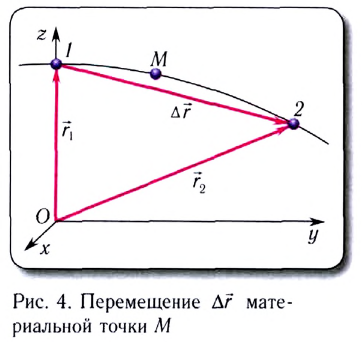
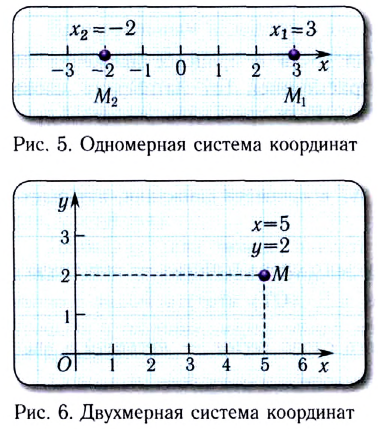
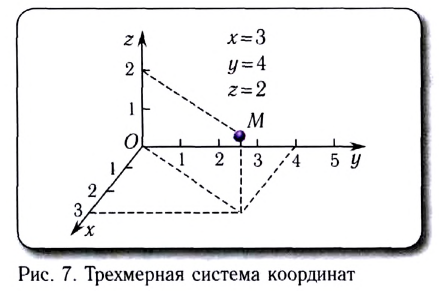
В зависимости от вида движения могут выбираться следующие системы координат: одномерная (на прямой линии) (рис. 5), двухмерная (на плоскости) (рис. 6), трехмерная (в пространстве) (рис. 7).
Произвольное движение материальной точки может быть задано одним из трех способов: векторным, координатным, траекторным (естественным).
При векторном способе описания положение движущейся МТ по отношению к выбранной системе отсчета определяется ее радиус-вектором
Радиус-вектор 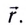
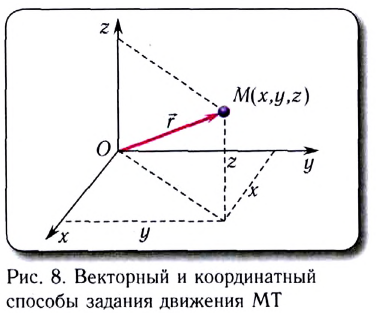
При координатном способе описания положение точки относительно СО определяется координатами х, у, z, а закон движения — уравнениями х = х(t), у = y(t), z = z(t) (см. рис. 8). Исключив из этих уравнений время /, можно найти уравнение траектории движения точки.
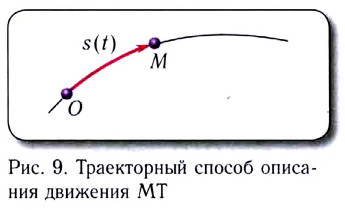
Траекторный (естественный) способ описания движения применяется, когда известна траектория движения материальной точки по отношению к выбранной СО (рис. 9).
Текущее положение материальной точки в данном случае определяется расстоянием s, измеренным вдоль траектории от выбранного на ней начала отсчета (точка О на рисунке 9). Кинематический закон движения МТ при этом задается уравнением s = s(t).
Если положить в основу классификации движений характер изменения скорости, то получим равномерные и неравномерные движения, а если вид траектории, то — прямолинейные и криволинейные.
Для того чтобы описать быстроту изменения положения тела (МТ) и направление движения относительно данной СО, используют векторную физическую величину, называемую скоростью
Чтобы охарактеризовать неравномерное движение тела (МТ), вводят понятие средней скорости 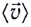
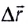
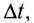
Средней путевой скоростью 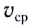
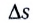
Средняя путевая скорость 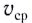
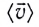
Однако средняя скорость 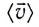
Для того чтобы отразить характер движения в данной точке траектории или в данный момент времени, вводится понятие мгновенной скорости 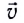
Вектор мгновенной скорости 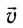
В СИ основной единицей скорости является метр в секунду
Простейший вид движения — равномерное. Равномерным называется движение МТ, при котором она за любые равные промежутки времени совершает одинаковые перемещения.
При прямолинейном движении в одном направлении модуль перемещения 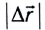
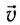
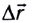
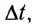
При равномерном движении скорость постоянна 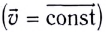
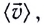
Зависимость перемещения от времени имеет вид 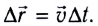
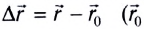
момент времени 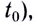
При проецировании радиус-вектора, например, на ось Ох получаем кинематическое уравнение для координаты при равномерном движении:
Здесь 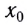
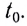
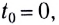
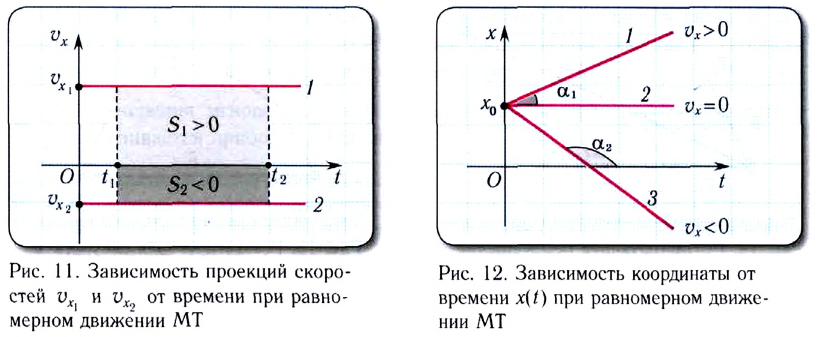
Для наглядности описания механического движения удобно представлять зависимости между различными кинематическими величинами графически.
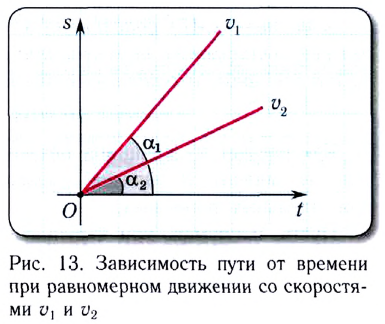
Скорость МТ при равномерном движении постоянна, поэтому график зависимости проекции скорости 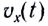
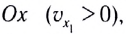
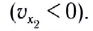
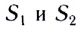
График зависимости координаты материальной точки, движущейся равномерно прямолинейно, от времени x(t) — линейная функция (рис. 12).
На рисунке отрезок / прямой соответствует равномерному движению в положительном направлении оси Ох; отрезок 2 прямой — покою материальной точки; отрезок 3 прямой — равномерному движению в отрицательном направлении оси Ох.
Проекция скорости движения численно равна угловому коэффициенту этой прямой линии:
т. е. тангенсу угла наклона (tga) этой прямой к оси времени.
График зависимости пути (модуля перемещения|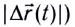
Угловой коэффициент (tga) этой прямой численно равен модулю скорости движения v. Поэтому на рисунке большей скорости у, соответствует больший угловой коэффициент (tg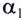
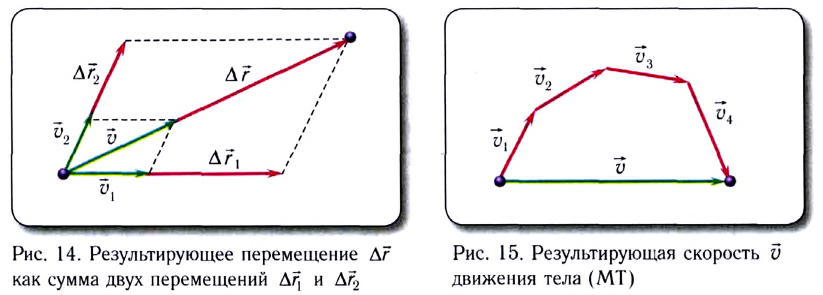
Для тел (МТ), участвующих в нескольких движениях одновременно, справедлив принцип независимости движений:
если тело (МТ) участвует в нескольких движениях одновременно, то его результирующее перемещение равно векторной сумме перемещений за то же время в отдельных движениях:
Как следует из принципа независимости движений, конечное перемещение тела не зависит от порядка (последовательности) суммирования перемещений при отдельных движениях.
Пусть, например, при переправе через реку, скорость течения которой 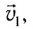
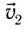
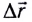
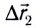
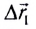
- Заказать решение задач по физике
На основе принципа независимости движений формулируется классический закон сложения скоростей:
результирующая скорость 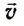
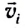
Этот закон справедлив только при условии, что скорость каждого отдельного движения мала по сравнению со скоростью света
Так, для рассмотренного примера (см. рис. 14) результирующая скорость лодки
Равномерное движение по прямой линии в повседневной жизни встречается сравнительно редко. Например, различные транспортные средства (автомобиль, автобус, троллейбус и т. д.) равномерно и прямолинейно движутся лишь на небольших участках своего пути, в то время как на остальных участках их скорость изменяется как по величине, так и по направлению.
Для измерения мгновенной скорости движения на транспортных средствах устанавливается прибор — спидометр.
- Прямолинейное неравномерное движение
- Прямолинейное равноускоренное движение
- Сложение скоростей
- Ускорение в физике
- Пружинные и математические маятники
- Скалярные и векторные величины и действия над ними
- Проекция вектора на ось
- Путь и перемещение
Средняя скорость, теория и онлайн калькуляторы
Средняя скорость
Перемещение материальной точки
Пусть материальная точка совершает движение по оси X все время в одном направлении. Тогда перемещением этой материальной точки за отрезок времени $Delta t=t_2-t_1$ будет отрезок $Delta x=x_2-x_1$. Если материальная точка все время своего движения перемещалась в одном направлении, то пройденный путь ($Delta s$) равен по модулю величине перемещения:
[Delta s=left|Delta xright|left(1right).]
Если точка движется сначала в одном направлении, затем останавливается и движется в противоположном направлении, (например, так движется тело брошенное вертикально вверх) то путь равен сумме модулей перемещений в обоих направлениях:
[Delta s=left|Delta x_1right|+left|Delta x_2right|+dots left(2right).]
Определение средней скорости
Определение
Средней скоростью ($leftlangle vrightrangle $) материальной точки за промежуток времени $Delta t$ называют физическую величину, которая равна отношению перемещения, которое совершило тело к этому промежутку времени:
[leftlangle vrightrangle =frac{Delta x}{Delta t}left(3right).]
Направление средней скорости такое же, как у перемещения.
Единицей скорости является скорость такого движения, при котором перемещение точки в единицу времени равно единице длины:
[left[vright]=frac{left[xright]}{left[tright]}.]
Единица измерения скорости (в том числе и средней скорости) в Международной системе единиц (СИ) является метр в секунду:
[left[vright]=frac{м}{с}.]
Средняя скорость при переменном движении
При неравномерном движении величина средней скорости сильно зависит от выбора промежутка времени движения тела.
Рассмотрим движение тела, которое свободно падает вниз. Закон движения при этом:
[x=4,9t^2left(4right).]
Для моментов времени $t_1=0,1 $c координата тела (подставим время $t_1$ в формулу (4)) равна: $x_1=0,049 $м; для $t_2=0,2 $c$ x_2=0,196$ м, тогда $leftlangle vrightrangle $в промежутке времени от $t_1=0,1$ с до $t_2=0,2 $c будет:
[leftlangle vrightrangle =frac{0,196-0,049}{0,2-0,1}=1,47 left(frac{м}{с}right).]
Если взять для того же свободно падающего тела промежуток времени от $t_1=0,7$ с до $t_2=0,8 $c, то средняя скорость получится равной $leftlangle vrightrangle =7,4frac{м}{с}$.
Средняя скорость равномерного движения
Только при равномерном движении средняя скорость является постоянной величиной и не зависит от выбора промежутка времени, в который движется тело. При равномерном движении материальной точки по оси X кинематические уравнения для перемещения запишем как:
[x=x_0+vt left(5right).]
Тогда:
[x_1left(t_1right)=x_0+vt_1;; x_2left(t_2right)=x_0+vt_2left(6right).]
Найдем среднюю скорость движения, используя определение (3) и выражения (6):
[leftlangle vrightrangle =frac{x_0+vt_2-x_0-vt_1}{t_2-t_1}=vfrac{t_2-t_1}{t_2-t_1}=v.]
Для оценки численной величины средней скорости на практике используют следующее определение $leftlangle vrightrangle $: средняя скорость равна отношению пройдённого пути (s) ко времени (t), которое было затрачено на движение:
[leftlangle vrightrangle =frac{s}{t}left(7right).]
Определяемая таким образом средняя скорость является скалярной величиной.
Примеры задач с решением
Пример 1
Задание. Пешеход, потратил первую половину времени своего движения, двигаясь со скоростью $v_1=5frac{км}{ч}$, вторую половину времени он шел со скоростью $v_3=3frac{км}{ч}$. Какова средняя скорость движения человека?
Решение. Сделаем рисунок.
Для решения задачи используем формулу, определяющую среднюю скорость:
[leftlangle vrightrangle =frac{s}{t} left(1.1right),]
где путь складывается из двух участков движения:
[s=s_1+s_2left(1.2right).]
Причем по условию задачи:
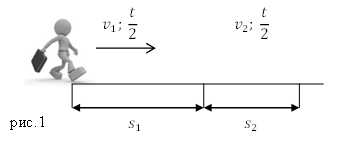
[s_1=v_1t_1=v_1frac{t}{2}left(1.3right) и ]
[s_2=v_2t_2=v_2frac{t}{2}left(1.4right).]
Подставим в определение средней скорости (1.1) правые части выражений (1.2) — (1.4), и учтем, что $t=t_1+t_2$ имеем:
[leftlangle vrightrangle =frac{v_1frac{t}{2}+v_2frac{t}{2}}{t}=frac{v_1+v_2}{2}.]
Вычислим среднюю скорость пешехода:
[leftlangle vrightrangle =frac{5+3}{2}=4 (frac{м}{с}).]
Ответ. $leftlangle vrightrangle =4frac{м}{с}$
Пример 2
Задание. Какова средняя скорость, которую имела материальная точка за промежуток времени $tau $, если уравнение ее скорости имеет вид:
[vleft(tright)=A+Bt+Ct^2 left(0le tle tau right)left(2.1right).]
Решение. В качестве основы для решения задачи используем формулу ($t=tau $):
[leftlangle vrightrangle =frac{s}{t} left(2.1right).]
Найдем путь материальной точки, учитывая уравнение скорости из данных задачи:
[s=intlimits^{tau }_0{vdt=intlimits^{tau }_0{(A+Bt+Ct^2)dt=}}Atau +Bfrac{{tau }^2}{2}+Cfrac{{tau }^3}{3}left(2.2right).]
Подставим правую часть выражения (2.2) в (2.1), имеем:
[leftlangle vrightrangle =frac{Atau +Bfrac{{tau }^2}{2}+Cfrac{{tau }^3}{3}}{tau }=A+frac{Btau }{2}+frac{C{tau }^2}{3}.]
Ответ. $leftlangle vrightrangle =A+frac{Btau }{2}+frac{C{tau }^2}{3}$
Читать дальше: статика.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Тема 7.
Взаимосвязь функции и ее производной
7
.
07
Производная и скорость/ускорение материальной точки
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
взаимосвязь функции и ее производной
Решаем задачи
Показать ответ и решение
Скорость материальной точки, прямолинейно движущейся по закону в момент времени
равна
тогда в момент
с:
Показать ответ и решение
Скорость материальной точки, прямолинейно движущейся по закону , в момент времени
равна
.
, тогда в момент
с:
м/с.
Показать ответ и решение
Скорость движущейся по закону точки в момент времени
равна
Найдем производную закона движения:
Тогда в момент времени с скорость в метрах в секунду равна
Показать ответ и решение
Ускорение в момент времени :
Тогда , откуда
.
Показать ответ и решение
Ускорение материальной точки, прямолинейно движущейся по закону , в момент времени
равно
производной от скорости, то есть равно .
, тогда
.
В момент с:
м/с
.
Показать ответ и решение
Ускорение материальной точки, прямолинейно движущейся по закону , в момент времени
равно
производной от скорости, то есть равно .
, тогда
.
В момент с:
м/с
.
Показать ответ и решение
Скорость материальной точки, прямолинейно движущейся по закону , в момент времени
равна
.
, тогда в момент
с:
м/с.
Дифференцируемый путь материальной точки, движущейся по прямой, имеет вид
. Найдите скорость этой точки в момент
.
Показать ответ и решение
Скорость материальной точки, прямолинейно движущейся по закону , в момент времени
равна
.
, тогда в момент
с:
м/с.
Материальная точка движется прямолинейно по закону
где
— расстояние от точки отсчёта в метрах,
— время в секундах, прошедшее с
начала движения. Найдите её скорость (в метрах в секунду) в момент времени
с.
План урока:
Механическое движение. Система отсчёта. Закон относительности движения
Уравнения движения. Радиус-вектор. Проекция вектора
Траектория. Путь. Перемещение
Равномерное прямолинейное движение: скорость и уравнение движения
Механическое движение. Система отсчёта. Закон относительности движения
Механическим движением в физике называется изменение с течением времени положения тела (или его частей) в пространстве относительно других тел.
То есть, чтобы сказать, что тело или система совершает механическое движение, нам необходимо: 1) наблюдать его во времени; 2) сравнивать его положение с положением какого-то другого тела (относительно этого тела).
Например, пассажир в едущем автомобиле неподвижен относительно кресла, на котором он сидит, но он движется относительно людей, стоящих на автобусной остановке и самой остановки. А сама автобусная остановка неподвижна относительно стоящих людей, ждущих автобус (см. рисунок 1). Однако она движется относительно проезжающих мимо машин. В первом случае наблюдаемым объектом был человек в машине, а точкой отсчета кресло и люди на остановке. Во втором случае наблюдаемой была автобусная остановка, а точками отсчета – люди на остановке и проезжающие мимо машины.
Рисунок 1 – Иллюстрация к примеру
Из примеров можно сделать вывод, что важно, какой именно объект находится под наблюдением и относительно какого объекта – тела отсчета – рассматривается его движение. Отсюда можно сформулировать закон относительности движения: характер движения тела зависит от того, относительно какого объекта мы рассматриваем данное движение.
Тело (или точка) отсчета, связанная с ним система координат и часы, вместе образуют систему отсчета. То есть все сказанное выше можно переформулировать в одно предложение: для наблюдения механического движения важно в какой системе отсчета будет происходить наблюдение.
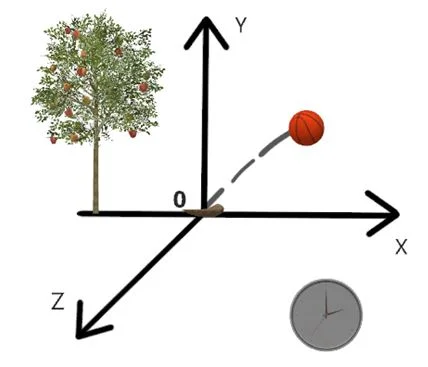
Рисунок 2 – Пример системы отсчета (наблюдаемы объект – летящий мяч, тело отсчета – камень, лежащий в начале координат, система координат и секундомер для отсчета времени)
Однако объекты могут быть очень сложными для наблюдения. Например, автомобиль едет по прямой несколько километров и необходимо описать его движение относительно камня на обочине. Казалось бы, все просто. Но как именно описать движение автомобиля, если корпус его движется по прямой, а колеса совершают вращательные движения.
Для удобства решения подобных задач принято упрощение: если размер и форма тела в данной задаче не играют важной роли для наблюдателя, можно считать это тело за материальную точку.
Материальная точка – это такое тело, размером и формой которого в условиях данной задачи можно пренебречь.
Приведем пример: когда автобус едет из города А в город Б, его можно рассматривать как материальную точку. Когда пассажир идет из одного конца этого автобуса в другой, считать автобус материальной точкой нельзя. В общем случае можно сказать, что тело можно считать материальной точкой, если его размеры значительно меньше расстояния, на которое оно перемещается.
Уравнения движения. Радиус-вектор. Проекция вектора
Для описания движения тела необходимо уметь рассчитывать его положение в каждый момент времени. Как это сделать?
Самый очевидный способ – координатный. Если вернуться к примеру на рисунке 2, можно увидеть, что летящий мяч в каждый момент времени имеет три координаты по осям OX, OY и OZ. Эти координаты являются функциями времени (т.е. они зависят от времени), а значит, их можно записать в виде системы:
Вид этих уравнений будет зависеть от многих вещей: от того, с какой силой бросили мяч в начале, от массы мяча, под каким углом его бросили и так далее. В любом случае, если эти уравнения заданы, можно найти координаты (то есть положение) тела в любой момент времени. Поиск этих уравнений – основная задача кинематики.
Эта система является кинематическими уравнениями движения тела или материальной точки, записанными в координатной форме. Повторим: если вид уравнений движения задан, можно узнать координату движущейся точки в любой момент времени.
В общем случае, координат три, но иногда можно обойтись двумя или даже одной координатой. Например, для описания движения бильярдного шара достаточно двух координат (так как шар не может двигаться вверх и вниз), а для описания движения шарика, катящегося по прямому горизонтальному желобку достаточно одной координаты (шарик не может двигаться вверх-вниз и вправо-влево).
Еще один способ описания движения – векторный.
*Перед дальнейшим прочтением данной статьи желательно вспомнить основную теорию по теме «Векторы» и «Метод координат»
Вектор, проведенный из начала координат к материальной точке, называется радиус-вектором (см. рисунок 3).
Рисунок 3 – Радиус-вектор (серой линией изображены траектория движения материальной точки, r1 и r2* радиус-векторы, проведенные к этой материальной точке в разные моменты времени)
Радиус-вектор проведенный к материальной точке в разные моменты времени будет разным. Значит, его тоже можно представить, как функцию времени:
r = r(t)
Такая функция и будет уравнением движения в векторной форме. Если ее вид задан, можно описать движение тела с той же полнотой, как и при координатной записи.
Еще раз обозначим отличия: при записи уравнения движения в координатной форме в каждый момент времени наблюдающий будет знать три координаты тела; при записи в векторной форме в каждый момент времени известен радиус-вектор (его модуль и направление). Обе записи равносильны.
*На письме векторы обычно обозначаются стрелкой сверху, над величиной. Однако в печатном тексте не всегда удобно нагромождать формулы дополнительными знаками, поэтому в печати векторные величины пишут просто жирным шрифтом. В данной статье далее жирным шрифтом будут написаны только векторные величины.
Покажем, что векторная и координатная записи равносильны. Для этого необходимо вспомнить, как построить проекцию вектора на ось (см. рисунок 4).
Рисунок 4 – Построение проекции вектора на ось
Чтобы построить проекцию вектора на ось, необходимо опустить перпендикуляра из начала и конца вектора на эту ось. Длина получившегося отрезка между проекциями начала и конца вектора, взятая со знаком «+», если вектор а сонаправлен с осью Х, или со знаком «-», если вектор а противонаправлен оси Х, — это и есть искомая проекция.
Если вектор выходит из начала координат, задача облегчается – необходимо опустить перпендикуляр только из конца вектора.
Напоминания из геометрии:
-
два вектора равны, если они параллельны или лежат на одной прямой, сонаправлены, а их модули равны;
-
проекции равных векторов равны.
Рассмотрим пример (см. рисунок 5)
Рисунок 5 – Задача на нахождение проекции векторов
Предлагаем читателю самому подумать, а затем сравнить свои рассуждения с приведенными ниже.
Итак, вектор а: его начала соответствует координате хн=1, а конец хк = 4. Значит ax = хк – хн = 4-1 = 3. Вектор b: его начало лежит в точке хн=2, а конец хк =0. Значит bx = хк – хн = 0-2 = -2.
В двумерном случае, проецировать нужно на две оси, но принцип остается тем же.
Иногда еще нужно находить составляющие компоненты вектора ах и ау. Рассмотрим пример, для простоты возьмем вектор, выходящий из начал координат (см. рисунок 6).
Сумма векторов ах и ау равна а. Модули векторов ах и ау численно равны координатам точек, куда попали перпендикуляры, опущенные из конца вектора а на оси ОХ и ОУ.
Еще следует отметить, что, если известен угол β между вектором а и осью ОХ, воспользовавшись основами тригонометрии, можно найти величины проекций:
ах = а*cos(β);
аy = а*sin(β).
Если бы вектор а совпадал с радиус-вектором какой-нибудь точки, то величины ах и ау совпадали бы с координатами тела по осям ОХ и ОY.
Способ с использованием тригонометрических функций удобен, когда координата конца вектора попадает в нецелое число и опустив перпендикуляр на ось его трудно найти точно. В физических задачах такое часто случается.
Рисунок 6 – Нахождение компонент вектора а
Рассмотрим пример (см. рисунок 7). Модуль вектора r равен 2. Сам вектор направлен под углом в 45 градусов к оси ОХ. Необходимо найти величины проекций (они же координаты) этого вектора на оси ОХ и ОУ.
Рисунок 7 – Задача на нахождение проекций вектора в двумерном пространстве
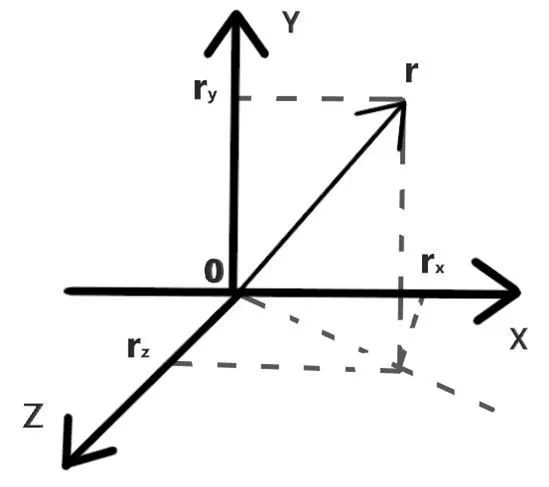
В общем случае радиус-вектор находится в трехмерном пространстве (см. рисунок 8). Построение проекции осуществляется по тому же принципу, что и в рассмотренных выше примерах. Когда строятся проекции на оси ОХ и ОУ, перпендикуляр сначала опускается на плоскость, в которой лежат оси ОХ и ОУ, а затем точка, в которую упал перпендикуляр к плоскости, проецируется на оси ОХ и ОУ.
Точки, в которые попал перпендикуляры к осям – rx, ry, rz – это и есть координаты x, y, z тела в текущий момент времени.
Следует оговориться, что большинство задач 10-го класса будут ограничиваться двумерным пространством.
Рисунок 8 – Построение проекций радиус-вектора
Траектория. Путь. Перемещение
Траектория – это линия, вдоль которой движется тело.
Траектория движения может быть прямолинейной, если тело движется по прямой линии, и криволинейной, если тело движется по кривой.
Путь (S), пройденный телом, равен длине траектории.
Перемещение (r)* – это вектор, проведенный из начала пути в конец.
В случае прямолинейного движения путь и модуль перемещения тела совпадают (см. рисунок 9а). В случае криволинейного – путь и перемещение различаются (см. рисунок 9б), так как длина линии движения тела больше длины вектора, соединяющего начало и конец траектории.
Рисунок 9 – Путь (S) и перемещение (r) при прямолинейном (а) и криволинейном (б) движении
*Иногда перемещение так же, как и путь, называют буквой S — (на письме с вектором над ней, при печати — жирным шрифтом, так как это векторная величина). В данной статье, чтобы не путаться, перемещение называется только буквой r. В целом, обозначения равноправны, поэтому при решении задач можно использовать то, которое удобнее. Однако не стоит забывать отмечать, что именно обозначено под той или иной буквой.
Равномерное прямолинейное движение: скорость и уравнение движения
Путь и перемещение при равномерном прямолинейном движении
Прямолинейное равномерное движение уже рассматривалось в курсе физики ранее, однако приведем основные определения.
Прямолинейное движение – это движение по прямой линии. Равномерное движение – такое, в процессе которого тело за равные временные промежутки проходит один и тот же путь. Если объединить эти два определения получится третье:
- равномерное прямолинейное движение – это такое движение, в ходе которого 1) тело совершает движение по прямой линии; 2) за одинаковые временные промежутки проходит одинаковый путь.
Зная определения пути и перемещения, это определение можно упростить: прямолинейное равномерное движение тела – это такое движение, в процессе которого тело за одинаковые временные промежутки совершает равные перемещения.
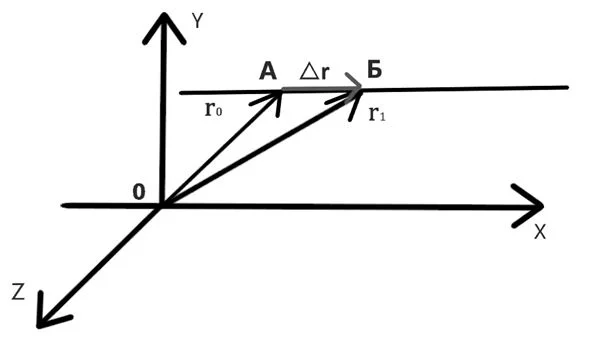
Важной характеристикой является скорость механического движения. Предположим, что при равномерном прямолинейном движении тело за промежуток времени △t перемещается из точки А в точку Б (см. рисунок 8). Радиус-вектор, проведенный в точку A обозначим r0, а радиус-вектор в точку Б обозначим r1. Изменение радиус-вектора назовем △r – нетрудно заметить, что это есть перемещение тела за время △t.
Рисунок 8 – Поиск перемещения тела через радиус-векторы при равномерном прямолинейном движении
Тогда скорость движения (v) будет вычисляться по формуле:
Так как △r – вектор, △t – скаляр, скорость v тоже будет вектором, сонаправленным перемещению.
Если тело начинает двигаться в момент начала отсчета, то △t = t*. Из правила сложения векторов следует, что △r = r1 — r0. Тогда выражение для скорости можно переписать в виде:
Из этого выражения следует:
r1 = r0 + v*t.
Это выражение можно применить к любому произвольно взятому моменту времени, поэтому можно опустить индекс в левой части и переписать:
r = r0 + v*t.
Данное уравнение является уравнением движения при прямолинейном равномерном движении.
*Напоминание: символом △ (дельта) обозначают изменение какой-нибудь величины. Например △t = t – t1, где t – конечный момент времени, t1 – начальный. Если же начальный момент времени совпадает с началом отсчета t1 = 0, то △t = t – 0 = t.
Фактически уравнение равномерного прямолинейного движения означает, что радиус-вектор в произвольный момент времени t можно посчитать, сложив начальный радиус-вектор и приращение v*t.
Найдя проекции радиус-вектора и вектора скорости, можно разложить уравнение движения тела на три составляющие вдоль осей ОX, ОY и ОZ.
rx = r0x + vx*t;
ry = r0y + vy*t;
rz = r0z + vz*t.
В этих выражениях r0x, r0y, r0z и vx, vy, vz – это компоненты изначальных векторов r0 и v вдоль осей ОХ, ОY и ОZ соответственно. И теперь можно перейти к скалярному виду:
rx = r0x + vx*t;
ry = r0y + vy*t;
rz = r0z + vz*t.
Стоит отметить, что при проецировании какие-то компоненты вектора могут стать отрицательными, тогда знаки в выражениях поменяются на противоположные.
В рассмотренном выше примере движение происходит только вдоль оси ОХ (остальные координаты не изменяются). На рисунке 9 приведены проекции начальной (х0) и конечной (х1) точки на ось ОХ.
Рисунок 9 – Перемещение тела в координатном представлении
Уравнение координаты (х) движения будет выглядеть:
x(t) = x0 + v*t.
А это уже похоже на знакомую из прошедшего курса физики формулу для нахождения пути:
S(t) = S0 + v*t.
Если точка начала двигаться из начала отсчета S0 = 0, можно переписать эту формулу в виде:
S(t) = v*t.
Отсюда следуют известные уже формулы для нахождения скорости и времени при равномерном прямолинейном движении:
Приведем последний в этой статье пример: известно, что тело движется вдоль оси ОХ, начиная из точки x0 = 3 см. Скорость тела равна v = 5 м/с и направлена вдоль оси ОХ. Необходимо записать уравнение движения по координате х для этого тела.
Итак, для начала приведем все единицы измерения к СИ:
x0 = 3 см = 0,03 м.
Теперь можно записывать уравнение для координаты х:
x(t) = x0 + v*t = 0,03 + 5*t.
Из этого уравнения можно найти координату тела в любой момент времени. Например, через 2 секунды после начала отсчета тело находилось в точке:
x(2) = 0,03 + 5*2 = 10, 03.
А какой путь прошло тело к этому моменту? В начале оно находилось в точке x(2) = 0,03 м, а через 2 секунды оно стало находиться в точке x(2) = 10, 03. Значит за 2 секунды тело прошло:
S = x(2) – x0 = 10, 03 – 0,03 = 10 м.
А если скорость тела была направлена противоположно оси ОХ, как тогда выглядело бы уравнение движения?
Тогда проекция вектора скорости на ось ОХ была бы отрицательной и в уравнении знак перед скоростью поменялся бы на противоположный:
x(t) = x0 — v*t = 0,03 — 5*t.
Механическое движение.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: механическое движение и его виды, относительность механического движения, скорость, ускорение.
Понятие движения является чрезвычайно общим и охватывает самый широкий круг явлений. В физике изучают различные виды движения. Простейшим из них является механическое движение. Оно изучается в механике.
Механическое движение — это изменение положение тела (или его частей) в пространстве относительно других тел с течением времени.
Если тело A меняет своё положение относительно тела B, то и тело B меняет своё положение относительно тела A. Иначе говоря, если тело A движется относительно тела B, то и тело B движется относительно тела A. Механическое движение является относительным — для описания движения необходимо указать, относительно какого тела оно рассматривается.
Так, например, можно говорить о движении поезда относительно земли, пассажира относительно поезда, мухи относительно пассажира и т. д. Понятия абсолютного движения и абсолютного покоя не имеют смысла: пассажир, покоящийся относительно поезда, будет двигаться с ним относительно столба на дороге, совершать вместе с Землёй суточное вращение и двигаться вокруг Солнца.
Тело, относительно которого рассматривается движение, называется телом отсчёта.
Основной задачей механики является определение положения движущегося тела в любой момент времени. Для решения этой задачи удобно представить движение тела как изменение координат его точек с течением времени. Чтобы измерить координаты, нужна система координат. Чтобы измерять время, нужны часы. Всё это вместе образует систему отсчёта.
Система отсчёта — это тело отсчёта вместе с жёстко связанной с ним («вмороженной»» в него) системой координат и часами.
Система отсчёта показана на рис. 1. Движение точки рассматривается в системе координат
. Начало координат
является телом отсчёта.
 |
| Рисунок 1. |
Вектор называется радиус-вектором точки
. Координаты
точки
являются в то же время координатами её радиус-вектора
.
Решение основной задачи механики для точки состоит в нахождении её координат как функций времени:
.
В ряде случаев можно отвлечься от формы и размеров изучаемого объекта и рассматривать его просто как движущуюся точку.
Материальная точка — это тело, размерами которого можно пренебречь в условиях данной задачи.
Так, поезд можно считать материальной точкой при его движении из Москвы в Саратов, но не при посадке в него пассажиров. Землю можно считать материальной точкой при описании её движения вокруг Солнца, но не её суточного вращения вокруг собственной оси.
К характеристикам механического движения относятся траектория, путь, перемещение, скoрость и ускорение.
Траектория, путь, перемещение.
В дальнейшем, говоря о движущемся (или покоящемся) теле, мы всегда полагаем, что тело можно принять за материальную точку. Случаи, когда идеализацией материальной точки пользоваться нельзя, будут специально оговариваться.
Траектория — это линия, вдоль которой движется тело. На рис. 1 траекторией точки является синяя дуга, которую описывает в пространстве конец радиус-вектора
.
Путь — это длина участка траектории, пройденного телом за данный промежуток времени.
Перемещение — это вектор, соединяющий начальное и конечное положение тела.
Предположим, что тело начало движение в точке и закончило движение в точке
(рис. 2). Тогда путь, пройденный телом, это длина траектории
. Перемещение тела — это вектор
.
 |
| Рисунок 2. |
Скорость и ускорение.
Рассмотрим движение тела в прямоугольной системе координат с базисом (рис. 3).
 |
| Рисунок 3. |
Пусть в момент времени тело находилось в точке
с радиус-вектором
Спустя малый промежуток времени тело оказалось в точке
с
радиус-вектором
Перемещение тела:
(1)
Мгновенная скорость в момент времени
— это предел отношения перемещения
к интервалу времени
, когда величина этого интервала стремится к нулю; иными словами, скорость точки — это производная её радиус-вектора:
(2)
Из (2) и (1) получаем:
Коэффициенты при базисных векторах в пределе дают производные:
(Производная по времени традиционно обозначается точкой над буквой.) Итак,
Мы видим, что проекции вектора скорости на координатные оси являются производными координат точки:
Когда стремится к нулю, точка
приближается к точке
и вектор перемещения
разворачивается в направлении касательной. Оказывается, что в пределе вектор
направлен точно по касательной к траектории в точке
. Это и показано на рис. 3.
Понятие ускорения вводится похожит образом. Пусть в момент времени скорость тела равна
, а спустя малый интервал
скорость стала равна
.
Ускорение — это предел отношения изменения скорости
к интервалу
, когда этот интервал стремится к нулю; иначе говоря, ускорение — это производная скорости:
Ускорение, таким образом, есть «cкорость изменения скорости». Имеем:
Следовательно, проекции ускорения являются производными проекций скорости (и, стало быть, вторыми производными координат):
Закон сложения скоростей.
Пусть имеются две системы отсчёта. Одна из них связана с неподвижным телом отсчёта . Эту систему отсчёта обозначим
и будем называть неподвижной.
Вторая система отсчёта, обозначаемая , связана с телом отсчёта
, которое движется относительно тела
со скоростью
. Эту систему отсчёта называем движущейся. Дополнительно предполагаем, что координатные оси системы
перемещаются параллельно самим себе (нет вращения системы координат), так что вектор
можно считать скоростью движущейся системы относительно неподвижной.
Неподвижная система отсчёта обычно связана с землёй. Если поезд плавно едет по рельсам со скоростью
, это система отсчёта, связанная с вагоном поезда, будет движущейся системой отсчёта
.
Заметим, что скорость любой точки вагона (кроме вращающихся колёс!) равна . Если муха неподвижно сидит в некоторой точке вагона, то относительно земли муха движется со скоростью
. Муха переносится вагоном, и потому скорость
движущейся системы относительно неподвижной называется переносной скоростью.
Предположим теперь, что муха поползла по вагону. Скорость мухи относительно вагона (то есть в движущейся системе ) обозначается
и называется относительной скоростью. Скорость мухи относительно земли (то есть в неподвижной системе
) обозначается
и называется абсолютной скоростью.
Выясним, как связаны друг с другом эти три скорости — абсолютная, относительная и переносная.
На рис. 4 муха обозначена точкой .Далее:
— радиус-вектор точки
в неподвижной системе
;
— радиус-вектор точки
в движущейся системе
;
— радиус-вектор тела отсчёта
в неподвижной системе
.
 |
| Рисунок 4. |
Как видно из рисунка,
Дифференцируя это равенство, получим:
(3)
(производная суммы равна сумме производных не только для случая скалярных функций, но и для векторов тоже).
Производная есть скорость точки
в системе
, то есть абсолютная скорость:
.
Аналогично, производная есть скорость точки
в системе
, то есть относительная скорость:
А что такое ? Это скорость точки
в неподвижной системе, то есть — переносная скорость
движущейся системы относительно неподвижной:
В результате из (3) получаем:
Закон сложения скоростей. Скорость точки относительно неподвижной системы отсчёта равна векторной сумме скорости движущейся системы и скорости точки относительно движущейся системы. Иными словами, абсолютная скорость есть сумма переносной и относительной скоростей.
Таким образом, если муха ползёт по движущемуся вагону, то скорость мухи относительно земли равна векторной сумме скорости вагона и скорости мухи относительно вагона. Интуитивно очевидный результат!
Виды механического движения.
Простейшими видами механического движения материальной точки являются равномерное и прямолинейное движения.
Движение называется равномерным, если модуль вектора скорости остаётся постоянным (направление скорости при этом может меняться).
Движение называется прямолинейным, если направление вектора скорости остаётся постоянным (а величина скорости при этом может меняться). Траекторией прямолинейного движения служит прямая линия, на которой лежит вектор скорости.
Например, автомобиль, который едет с постоянной скоростью по извилистой дороге, совершает равномерное (но не прямолинейное) движение. Автомобиль, разгоняющийся на прямом участке шоссе, совершает прямолинейное (но не равномерное) движение.
А вот если при движении тела остаются постоянными как модуль скорости, так и его направление, то движение называется равномерным прямолинейным.
В терминах вектора скорости можно дать более короткие определения данным типам движения:
Важнейшим частным случаем неравномерного движения является равноускоренное движение, при котором остаются постоянными модуль и направление вектора ускорения:
- равноускоренное движение
Наряду с материальной точкой в механике рассматривается ещё одна идеализация — твёрдое тело.
Твёрдое тело — это система материальных точек, расстояния между которыми не меняются со временем. Модель твёрдого тела применяется в тех случаях, когда мы не можем пренебречь размерами тела, но можем не принимать во внимание изменение размеров и формы тела в процессе движения.
Простейшими видами механического движения твёрдого тела являются поступательное и вращательное движения.
Движение тела называется поступательным, если всякая прямая, соединяющая две какие-либо точки тела, перемещается параллельно своему первоначальному направлению. При поступательном движении траектории всех точек тела идентичны: они получаются друг из друга параллельным сдвигом (рис. 5).
 |
| Рисунок 5. |
Движение тела называется вращательным, если все его точки описывают окружности, лежащие в параллельных плоскостях. При этом центры данных окружностей лежат на одной прямой, которая перпендикулярна всем этим плоскостям и называется осью вращения.
На рис. 6 изображён шар, вращающийся вокруг вертикальной оси. Так обычно рисуют земной шар в соответствующих задачах динамики.
 |
| Рисунок 6. |
Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Механическое движение.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023

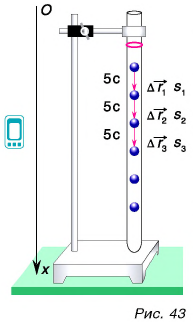
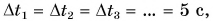




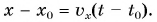




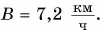
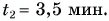


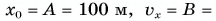
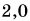
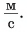
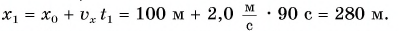
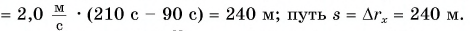
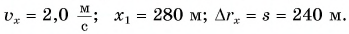
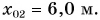
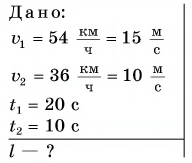

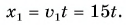
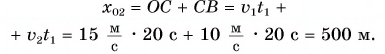
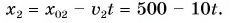
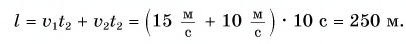
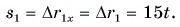
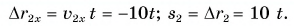
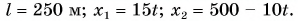
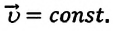
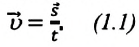
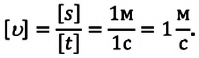

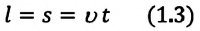
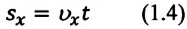
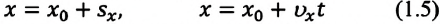
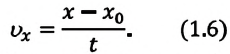
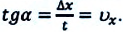
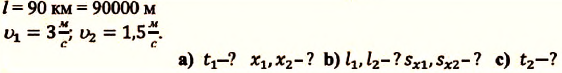
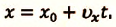
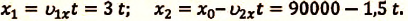
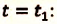
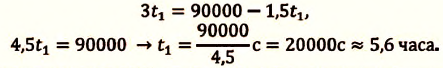
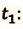
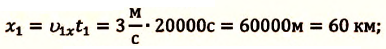
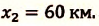
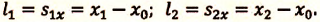
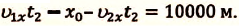
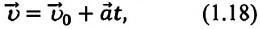
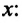
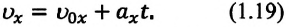

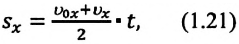
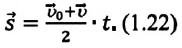
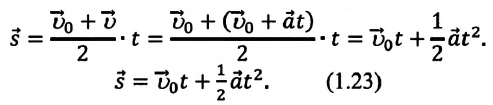
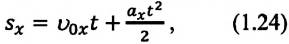
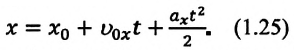
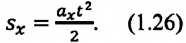
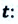
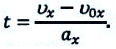
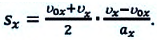

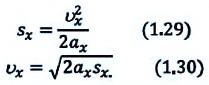
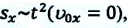 то отношение проекций перемещения равно отношению квадратов соответствующих промежутков времени:
то отношение проекций перемещения равно отношению квадратов соответствующих промежутков времени: