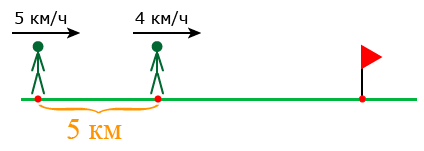
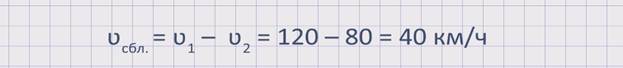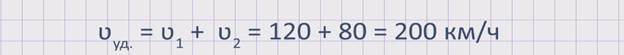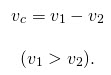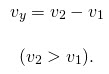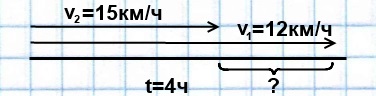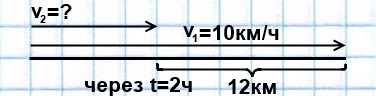Как найти скорость отдаления 4 класс - Autoru.top

Для решения задач на движение стоит прояснить объекты сближаются или удаляются, ответ зависит от вида движения. Когда объекты двигаются навстречу друг другу из разных пунтков, то они сближаются:

(v_1+v_2=20+30=50) км/час скорость сближения

Когда объекты двигаются в противоположных направлениях из одного пункта, то они удаляются:

(v_1+v_2=20+30=50) км/час скорость удаления

Когда объекты двигаются в одном направление одновременно:

Если они выезжают одновременно, то два объекта удаляются друг от друга, так как скорость у них разная, для того чтобы найти скорость их удаления надо из большей скорости вычесть меньшую.

(v_y=v_2-v_1)

Движение в одном направлении

Если они выезжают с интервалом, то два объекта могут удаляться или сближаться в зависимости от их скоростей:

1) если скорость объекта, который впереди больше, то они удаляются. (v_2>v_1)

Движение в одном направлении

2) если скорость объекта, который впереди меньше, то они сближаются . (v_1>v_2)

Движение в одном направлении

Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!

Запишитесь на бесплатное тестирование знаний!

Источник

После долгой прогулки по парку Юра и Яра выехали в противоположных направлениях на автомобилях. Скорость автомобиля Юры — (75) км/ч, а скорость автомобиля, на котором едет Яра — (58) км/ч. Как и с какой скоростью изменится расстояние между ними?

Рассмотрим схему движения Юры и Яры.

Юра и Яра удаляются друг от друга, значит, расстояние между ними увеличивается.

Чтобы найти, с какой скоростью они удаляются друг от друга, рассмотрим правило вычисления скорости удаления.

Получается, что скорость удаления автомобилей Юры и Яры: (75 + 58 = 133) км/ч.

Рассмотрим ещё один пример.

Юра и Яра ехали на автомобилях в одном направлении, но с разной скоростью. Юра ехал первым со скоростью (69) км/ч, а Яра ехала следом со скоростью (46) км/ч. Уменьшится или увеличится расстояние между ними и с какой скоростью?

Рассмотрим схему движения Юры и Яры.

Скорость автомобиля Юры больше, чем автомобиля, на котором едет Яра, значит, расстояние между ними увеличивается. Перед нами движение с отставанием.

Чтобы найти, с какой скоростью удаляются друг от друга Юра и Яра, рассмотрим правило вычисления скорости удаления во время движения с отставанием.

Получается, что скорость удаления автомобилей Юры и Яры: (69) (– 46 = 23) км/ч.

Расстояние, на которое объекты удаляются друг от друга за единицу времени, называется скоростью удаления.

Сделаем вывод:

при движении в противоположных направлениях скорость удаления равна сумме скоростей:

vуд.=v1+v2

При движении с отставанием скорость удаления равна разности скоростей:

vуд.=v1
−v2

Источник

Как найти скорость сближения и скорость удаления? Ответ зависит от вида движения.

I. При движении навстречу друг другу объекты сближаются:

Чтобы найти скорость сближения, надо сложить скорости объектов:

$[{v_c} = {v_1} + {v_2}]$

II. При движении в противоположных направлениях объекты удаляются:

Чтобы найти скорость удаления, надо сложить скорости объектов:

$[{v_y} = {v_1} + {v_2}]$

III. При движении в одном направлении объекты могут как сближаться, так и удаляться.

Если объекты вышли одновременно из одного пункта с разными скоростями, то они удаляются.

Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:

$[{v_y} = {v_1} - {v_2}]$

$[({v_1} > {v_2}).]$

Если объекты выходят одновременно из разных пунктов и движутся в одном направлении, то это — движение вдогонку.

Если скорость идущего впереди объекта меньше скорости объекта, следующего за ним, то они сближаются.

Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:

$[{v_c} = {v_1} - {v_2}]$

$[({v_1} > {v_2}).]$

Если объект, идущий впереди, движется с большей скоростью, чем идущий следом за ним, то они удаляются:

Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:

$[{v_y} = {v_2} - {v_1}]$

$[({v_2} > {v_1}).]$

Если из одного пункта в одном направлении выходит сначала один объект, а спустя некоторое время вслед за ним — другой, то рассуждаем аналогично: если скорость идущего впереди больше, то объекты удаляются, если скорость идущего впереди меньше — сближаются.

Обратите внимание:

При движении навстречу друг другу и движении в противоположных направлениях скорости складываем.

При движении в одном направлении скорости вычитаем.

Источник

§ 1 Скорость сближения и скорость удаления

В этом уроке познакомимся с такими понятиями, как «скорость сближения» и «скорость удаления».

Для ознакомления с понятиями «скорость сближения» и «скорость удаления» рассмотрим 4 реальные ситуации.

Из двух городов навстречу друг другу одновременно выехало два автомобиля. Скорость первого автомобиля ʋ1 = 120 км/ч, а скорость второго автомобиля ʋ2 = 80 км/ч. Сокращается ли расстояние между автомобилями? Если да, то с какой скоростью?

Изобразим движение данных автомобилей на координатном луче.

Из рисунка видно, что два автомобиля, двигаясь навстречу друг другу, приближаются. Значит, расстояние между ними сокращается. Чтобы узнать, с какой скоростью сокращается расстояние между автомобилями или же с какой скоростью сближаются два автомобиля, необходимо к скорости первого автомобиля прибавить скорость второго. А именно, скорость сближения равна сумме скоростей первого и второго автомобилей: ʋсбл. = ʋ1 +ʋ2.

Найдем скорость сближения данных автомобилей:

Значит, расстояние между автомобилями сокращается со скоростью 200 км/ч. Рассмотрим вторую ситуацию.

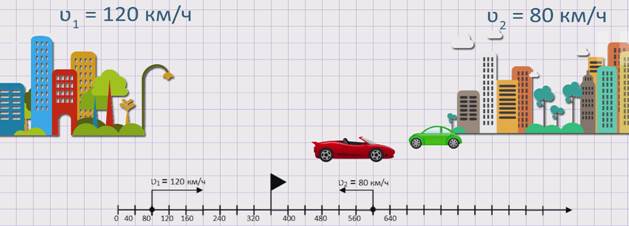
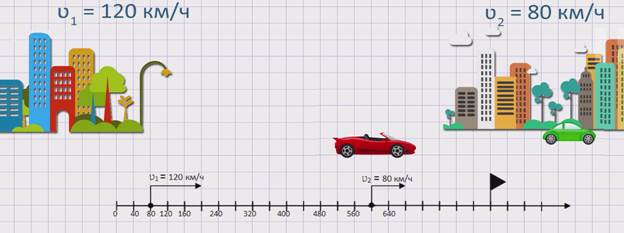
Из двух городов одновременно в одном направлении, вдогонку, выехало два автомобиля. Скорость первого автомобиля ʋ1 = 120 км/ч, а скорость второго автомобиля ʋ2 = 80 км/ч. Сокращается или увеличивается расстояние между автомобилями и на сколько?

Изобразим движение данных автомобилей на координатном луче.

Из рисунка видно, что первый автомобиль движется быстрее второго автомобиля или же движется вдогонку второму автомобилю. Значит, расстояние между автомобилями будет сокращаться. Чтобы узнать, с какой скоростью сокращается расстояние между автомобилями или же с какой скоростью сближаются два автомобиля, необходимо из скорости первого автомобиля вычесть скорость второго автомобиля. А именно, скорость сближения равна разности скоростей двух автомобилей: ʋсбл. = ʋ1 — ʋ2 .

Найдем скорость сближения данных автомобилей: ʋсбл. = ʋ1 — ʋ2 = 120 – 80 = 40 км/ч. Значит, расстояние между автомобилями сокращается со скоростью 40 км/ч.

Рассматривая приведенные выше ситуации, мы познакомились с понятием «скорость сближения». Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.

Рассмотрим следующую третью ситуацию.

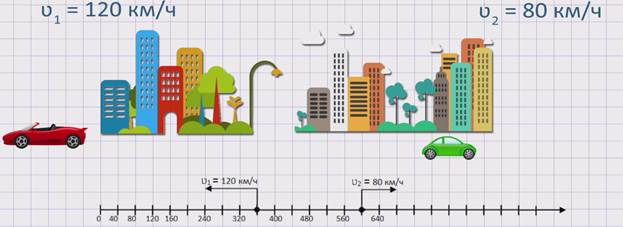
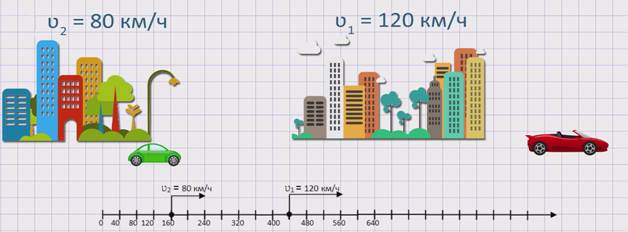
Из двух городов в противоположных направлениях одновременно выехало два автомобиля. Скорость первого автомобиля ʋ1 = 120 км/ч, а скорость второго автомобиля ʋ2 = 80 км/ч. Будет ли увеличиваться расстояние между автомобилями? Если да, то на сколько?

Изобразим движение данных автомобилей на координатном луче.

Из рисунка видно, что два автомобиля, двигаясь в противоположных направлениях, удаляются друг от друга. Значит, расстояние между ними увеличивается. Чтобы узнать, с какой скоростью увеличивается расстояние между автомобилями или же с какой скоростью удаляются два автомобиля друг от друга, необходимо к скорости первого автомобиля прибавить скорость второго автомобиля. А именно, скорость удаления равна сумме скоростей двух автомобилей: ʋуд. = ʋ1 + ʋ2 .

Найдем скорость удаления данных автомобилей: ʋуд. = ʋ1 + ʋ2 = 120 + 80 = 200 км/ч. Значит, расстояние между автомобилями увеличивается со скоростью 200 км/ч.

Рассмотрим последнюю четвертую ситуацию.

Из двух городов водном направление одновременно выехало два автомобиля. Скорость первого автомобиля ʋ1 = 120 км/ч, а скорость второго автомобиля ʋ2 = 80 км/ч. Причем второй автомобиль движется с отставанием. Будет увеличиваться или уменьшаться расстояние между автомобилями и на сколько?

Изобразим движение данных автомобилей на координатном луче.

Из рисунка видно, что второй автомобиль движется медленнее первого автомобиля или же движется с отставанием от первого автомобиля. Значит, расстояние между автомобилями будет увеличиваться. Чтобы узнать, с какой скоростью увеличивается расстояние между автомобилями или же с какой скоростью удаляются два автомобиля друг от друга, необходимо из скорости первого автомобиля вычесть скорость второго автомобиля. А именно, скорость удаления равна разности скоростей двух автомобилей: ʋуд. = ʋ1 — ʋ2 .

Найдем скорость удаления данных автомобилей: ʋуд. = ʋ1 — ʋ2 = 120 – 80 = 40 км/ч. Значит, расстояние между автомобилями увеличивается со скоростью 40 км/ч.

Рассматривая приведенные выше ситуации, мы познакомились с понятием «скорость удаления». Скорость удаления – это расстояние, на которое удаляются объекты за единицу времени.

§ 2 Краткие итоги по теме урока

1.Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.

2.При движении двух объектов навстречу друг другу скорость сближения равна сумме скоростей этих объектов. ʋсбл. = ʋ1 + ʋ2

3.При движении вдогонку скорость сближения равна разности скоростей объектов движения. ʋсбл. = ʋ1 — ʋ2

4.Скорость удаления – это расстояние, на которое удаляются объекты за единицу времени.

5.При движении двух объектов в противоположных направлениях скорость удаления равна сумме скоростей этих объектов. ʋуд. = ʋ1 + ʋ2

6.При движении с отставанием скорость удаления равна разности скоростей объектов движения. ʋуд. = ʋ1 — ʋ2

Источник

Существует несколько типов задач на движение. Примеры решения всех типов задач с пояснениями мы рассмотрим в этой статье.

Задачи на движение в одном направлении

Задачи на движении в одном направлении относятся к одному из трех основных видов задач на движение.
Если два объекта выехали из одного пункта одновременно, то, поскольку они имеют разные скорости, объекты удаляются друг от друга. Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:

Если из одного пункта выехал один объект, а спустя некоторое время в том же направлении вслед за ним выехал другой объект, то они могут как сближаться, так и удаляться друг от друга.
Если скорость объекта, движущегося впереди, меньше движущегося вслед за ним объекта, то второй догоняет первого и они сближаются.
Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:

Если скорость объекта, который идет впереди, больше скорости объекта, который движется следом, то второй не сможет догнать первого и они удаляются друг от друга.
Скорость удаления находим аналогично — из большей скорости вычитаем меньшую:

Задачи на скорость сближения

Задача 1

Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?

Решение:

Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалится от города на:

40 · 4 = 160 (км)

Второй автомобиль движется быстрее первого, значит каждый час расстояние между автомобилями будет сокращаться на разность их скоростей:

60 — 40 = 20 (км/ч) – это скорость сближения автомобилей

Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся:

160 : 20 = 8 (ч)

Решение задачи по действиям можно записать так:

1) 40 · 4 = 160 (км) – расстояние между автомобилями

2) 60 — 40 = 20 (км/ч) – скорость сближения автомобилей

3) 160 : 20 = 8 (ч)

Ответ: Второй автомобиль догонит первый через 8 часов.

Задача 2

Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?

Решение:

Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов:

5 — 4 = 1 (км/ч)

Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого:

5 : 1 = 5 (ч)

Решение задачи по действиям можно записать так:

1) 5 — 4 = 1 (км/ч) – это скорость сближения пешеходов

2) 5 : 1 = 5 (ч)

Ответ: Через 5 часов второй пешеход догонит первого.

Задача 3

Из одного села в одном направлении одновременно выехали два велосипедиста. Скорость одного из них — 15 км/ч, скорость другого — 12 км/ч. Какое расстояние будет через ними через 4 часа?

Решение:

1) 15-12=3 (км/ч) скорость удаления велосипедистов

2) 3∙4=12 (км) такое расстояние будет между велосипедистами через 4 часа.

Ответ: Через 4 часа расстояние между велосипедистами составит 12 км.

Задача 4

Из села на станцию одновременно вышел пешеход и выехал велосипедист. Через 2 часа велосипедист опережал пешехода на 12 км. Найти скорость пешехода, если скорость велосипедиста 10 км/ч.

Решение:

1) 12:2=6 (км/ч) скорость удаления велосипедиста и пешехода

2) 10-6=4 (км/ч) скорость пешехода.

Ответ: Скорость пешехода составляет 4 км/ч.

Задачи на скорость удаления

Задача 1

Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.

Чему равна скорость удаления между автомобилями?
Какое расстояние будет между автомобилями через 3 часа?
Через сколько часов расстояние между ними будет 200 км?

Решение:

Сначала узнаем скорость удаления автомобилей друг от друга, для этого вычтем из большей скорости меньшую:

80 — 40 = 40 (км/ч)

Каждый час автомобили отдаляются друг от друга на 40 км. Теперь можно узнать сколько километров будет между ними через 3 часа, для этого скорость удаления умножим на 3:

40 · 3 = 120 (км)

Чтобы узнать через сколько часов расстояние между автомобилями станет 200 км, надо расстояние разделить на скорость удаления:

200 : 40 = 5 (ч)

Ответ:

Скорость удаления между автомобилями равна 40 км/ч.
Через 3 часа между автомобилями будет 120 км.
Через 5 часов между автомобилями будет расстояние в 200 км.

Движение навстречу друг другу

Если два объекта движутся навстречу друг другу, то они сближаются. Чтобы найти скорость сближения двух объектов, движущихся навстречу друг другу, надо сложить их скорости:

Скорость сближения больше, чем скорость каждого из них.

Задача 1

Из поселка и города навстречу друг другу, одновременно выехали два автобуса. Один автобус до встречи проехал 100 км со скоростью 25 км/час. Сколько километров до встречи проехал второй автобус, если его скорость 50 км/час.

Решение:

1) 100 : 25 = 4 (часа ехал один автобус)

2) 50 * 4 = 200

Решение в виде выражения: 50 * (100 : 25) = 200

Ответ: второй автобус проехал до встречи 200 км.

Расстояние между двумя пристанями 90 км. От каждой из них одновременно навстречу друг другу вышли два теплохода. Сколько часов им понадобится чтобы встретиться, если скорость первого 20 км/час, а второго 25 км/час?

Решение:

1) 25 + 20 = 45 (сумма скоростей теплоходов)

2) 90 : 45 = 2

Решение в виде выражения:90 : (20 + 25) = 2

Ответ: Теплоходы встретятся через 2 часа.

Задача 3

От двух станций, расстояние между которыми 564 км., одновременно навстречу друг другу вышли два поезда. Скорость одного из них 63 км/час. Какова скорость второго, если поезда встретились через 4 часа?

Решение:

1) 63 * 4 = 252 (прошел 1 поезд)

2) 564 — 252 =312 (прошел 2 поезд)

3) 312 : 4 = 78

Решение в виде выражения (63 * 4 — 252) : 4 = 78

Ответ: Скорость второго поезда 78 км/час.

Задача 4

Два велосипедиста выехали навстречу друг другу. Скорость одного из низ 12 км/ч, а другого — 10 км/ч. Через 3 часа они встретились. Какое расстояние было между ними в начале пути?

Решение:

1) 12+10=22 (км/ч) скорость сближения велосипедистов

2) 22∙3=66 (км) было между велосипедистами в начале пути.

Ответ: Расстояние между велосипедистами в начале пути было 66 км.

Задача 5

Два поезда идут навстречу друг другу. Скорость одного из них 50 км/ч, скорость другого — 60 км/ч. Сейчас между ними 440 км. Через сколько часов они встретятся?

Решение:

1) 60+50=110 (км/ч) скорость сближения поездов

2) 440:110=4 (ч) время, через которое поезда встретятся.

Ответ: Поезда встретятся через 4 часа.

Движение в противоположных направлениях

Если два объекта движутся в противоположных направлениях, то они удаляются. Чтобы найти скорость удаления, надо сложить скорости этих объектов:

Скорость удаления больше скорости любого из них.

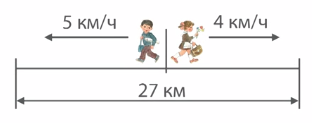
Задача 1

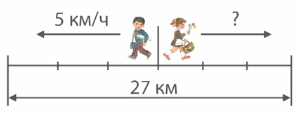
Из поселка вышли одновременно в противоположных направлениях два пешехода. Средняя скорость одного пешехода – 5 км/ч, другого – 4 км/ч. Через сколько часов расстояние между ними будет 27 км ?

Решение:

Чтобы найти время движения пешеходов, нужно знать расстояние и скорость пешеходов. Мы знаем, что за каждый час один пешеход удаляется от поселка на 5 км, а другой пешеход удаляется от поселка на 4 км. Можем найти их скорость удаления.

(км/ч)

Мы знаем скорость удаления и знаем все расстояние – 27 км. Можем найти время, через которое пешеходы удалятся друг от друга на 27 км, для этого нужно расстояние разделить на скорость.

(ч)

Ответ: Через три часа расстояние между переходами будет 27 км.

Задача 2

Из поселка вышли одновременно в противоположных направлениях два пешехода. Через 3 часа расстояние между ними было 27 км. Первый пешеход шел со скоростью 5 км/ч. С какой скоростью шел второй пешеход ?

Решение:

Чтобы узнать скорость второго пешехода, надо знать расстояние, которое он прошел, и его время в пути. Чтобы узнать, какое расстояние прошел второй пешеход, надо знать, какое расстояние прошел первый пешеход и общее расстояние. Общее расстояние мы знаем. Чтобы найти расстояние, которое прошел первый пешеход, надо знать его скорость и его время в пути. Средняя скорость движения первого пешехода – 5 км/ч, его время в пути – 3 часа. Если среднюю скорость умножить на время в пути, получим расстояние, которое прошел пешеход:

(км)

Мы знаем общее расстояние и знаем расстояние, которое прошел первый пешеход. Можем теперь узнать, какое расстояние прошел второй пешеход.

(км)

Теперь мы знаем расстояние, которое прошел второй пешеход, и время, проведенное им в пути. Можем найти его скорость.

(км/ч)

Ответ: Скорость второго пешехода – 4 км/ч.

Задача 3

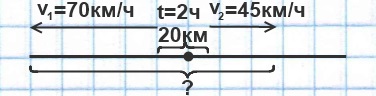
Товарный и пассажирский поезда движутся в противоположных направлениях. Скорость товарного 45 км/ч, скорость пассажирского — 70 км/ч. Сейчас между ними 20 км. Какое расстояние будет между ними через 2 часа ?

Решение:

1) 70+45=115 (км/ч) скорость удаления поездов

2) 115∙2=230 (км) пройдут поезда вместе за 2 часа

3) 230+20=250 (км) такое расстояние между поездами будет через 2 часа.

Ответ: Через 2 часа расстояние между поездами составит 250 км.

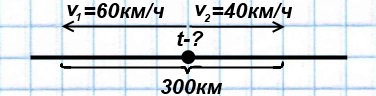
Задача 4

Из одного пункта одновременно в противоположных направлениях выехали два мотоциклиста. Скорость одного из них — 60 км/ч, скорость другого — 40 км/ч. Через какое время расстояние между ними станет равным 300 км?