Будем действовать пошагово. Шаг 1 (связь между скоростями точек A и B при двойном касании) уже сделан выше.
Шаг 2. Запишем все силы, действующие на точки A и B по горизонтали и по вертикали при двойном касании:
точка A: х: –T·cos α + FA = 0, y: T·sin α – mg = maA,
точка B: х: T·cos α + Four = 0, y: –T·sin α – mg + FB = 0.
Здесь FA и FB — силы реакции опоры со стороны стенки и пола, которые строго перпендикулярны поверхности, T — сила напряжения стержня, которую мы считаем положительной, если стержень сжат, и отрицательной — если он растянут (поэтому мы и говорим «сила напряжения», а не «сила натяжения»). Напомним, что стержень абсолютно жесткий, поэтому действующие в нём силы — будь то сила сдавливания или сила растяжения — не меняют его длины, но влияют на баланс сил на его концах. Наконец, Four — это та «наша» сила, которую мы прикладываем к нижней точке, чтобы она двигалась без ускорения, а лишь с постоянной скоростью v. Эта сила неизвестна, и более того, она переменная: в каждый момент времени она подстраивается так, чтобы скомпенсировать другую силу, действующую на точку B по горизонтали.
Заметим, что если сила напряжения может быть как положительной, так и отрицательной, то сила реакции опоры может быть только положительна. Отрицательная сила реакции опоры FA означала бы, что стержень прилип к стенке, а мы тянем стержень на себя и пытаемся его отодрать. Такого в нашей задаче быть не может, поскольку по условию стержень просто прислонен к стене.
Глядя на эти формулы, легко понять, что происходит в момент, когда стержень перестает касаться стенки. До тех пор пока он на нее опирается, сила FA положительна, и значит, сила напряжения T тоже положительна. Эта же сила напряжения толкает точку B вперед, значит наша внешняя сила Four отрицательна, то есть направлена к стенке. Иными словами, для того чтобы конец стержня двигался с постоянной скоростью, мы должны не тянуть его, а подталкивать против движения, сопротивляясь скатывающей силе, передающейся по стержню.
Как только сила напряжения сменится на отрицательную, в точке касания со стенкой перестанет действовать сила реакции опоры: FA = 0. Тогда никакая больше сила не сможет скомпенсировать горизонтальную проекцию силы T, и точка A в результате начнет двигаться в направлении от стенки. Поэтому именно T = 0 (а следовательно, и Four = 0) и есть тот момент, когда произойдет отрыв.
Шаг 3. Теперь необходимо выяснить, при каком угле наклона это произойдет. Это можно сделать разными способами, но здесь я хочу продемонстрировать несколько необычный прием. Мы сейчас покажем, что наша задача с математической точки зрения полностью эквивалентна другой задаче, совсем непохожей на исходную. Эту задачу мы сможем решить без труда и тем самым получим ответ на интересующий нас вопрос.
Давайте обратим внимание на траекторию, которую описывает центр масс стержня при соскальзывании. Если стержень касается своими концами и стенки, и пола, то центр масс движется по дуге с радиусом R = L/2, показанной на рис. 4, слева. Если стержень касается только пола, то центр масс может находиться где угодно справа от дуги. Забраться «под дугу» центр масс не может никак. Поэтому исходная задача — соскальзывание стержня вдоль стенки, а затем отрыв от нее — с точки зрения движения центра масс выглядит так: центр масс без трения скользит по полукруглому холму и в какой-то момент срывается с него (см. рис. 4, справа).
Для того чтобы эта словесная аналогия стала полным математическим эквивалентом, перепишем потенциальную и кинетическую энергию стержня в исходной задаче
через массу центра масс (mcm = 2m), горизонтальную (vx = vB/2) и вертикальную (vy = vA/2) скорости центра масс, а также его высоту:
Обратите внимание на лишнюю двойку в кинетической энергии; она возникла потому, что кроме движения центра масс стержень еще и вращается, и в нашем простом случае кинетическая энергия вращения равна кинетической энергии движения центра масс. Это означает, что задачу нельзя просто так сводить к движению центра масс. Однако если переписать эти энергии вот так
где M = 2mcm = 4m, а = g/2, а скорость
то все формулы становятся привычными. Таким образом, мы приходим к выводу: наша задача математически эквивалентна задаче о скольжении одной-единственной материальной точки с массой M = 4m по полукруглому холму радиуса R = L/2 в ослабленном поле тяжести с ускорением свободного падения a = g/2. Всё это происходит также под действием дополнительной горизонтальной силы (аналог Four), которая обеспечивает постоянство горизонтальной скорости точки (vx = v/2). Из геометрии видно, что тот угол α, при котором точка срывается с холма, как раз равен углу, при котором стержень отрывается от стенки в исходной задаче. Этот угол и требуется найти.
Эту задачу решить уже несложно. Для того чтобы тело массы M двигалось по окружности радиуса R со скоростью u, надо, чтобы центростремительная сила равнялась Mu2/R. Эта сила в нашем случае складывается из проекции силы тяжести Ma·sin α, а также силы реакции опоры и проекции силы Four. В момент отрыва две последние силы исчезают, и это позволяет нам наконец-то записать условие на угол α:
Отсюда получаем:
Поскольку синус не бывает больше единицы, а v и L задаются в условии независимо, мы получаем два разветвления задачи: если скорость велика, отрыв произойдет сразу же, и дальше стержень будет падать свободно. Если же скорость достаточно мала (что и предполагалось в условии), то отрыв произойдет не сразу, а при угле α, задаваемом найденной формулой. Стоит также отметить, что ту же самую формулу можно было найти, рассматривая исходную задачу в системе отсчета точки B (рис. 2, справа) и записав центростремительное ускорение для точки A
Шаг 4. Осталось обсчитать свободное падение стержня с начального угла α. Проще всего это сделать, вновь перейдя в (инерциальную) систему отсчета, где точка B покоится (рис. 2, справа, но только без стенки). В этой системе отсчета сила Four приложена к неподвижной точке, и поэтому она работы не совершает. Значит, в этой системе отсчета можно воспользоваться законом сохранения энергии:
Скорость u1 — это (вертикальная) скорость точки A в этой системе отсчета в момент удара об пол. Возвращаясь обратно в исходную систему отсчета, получаем окончательный ответ:
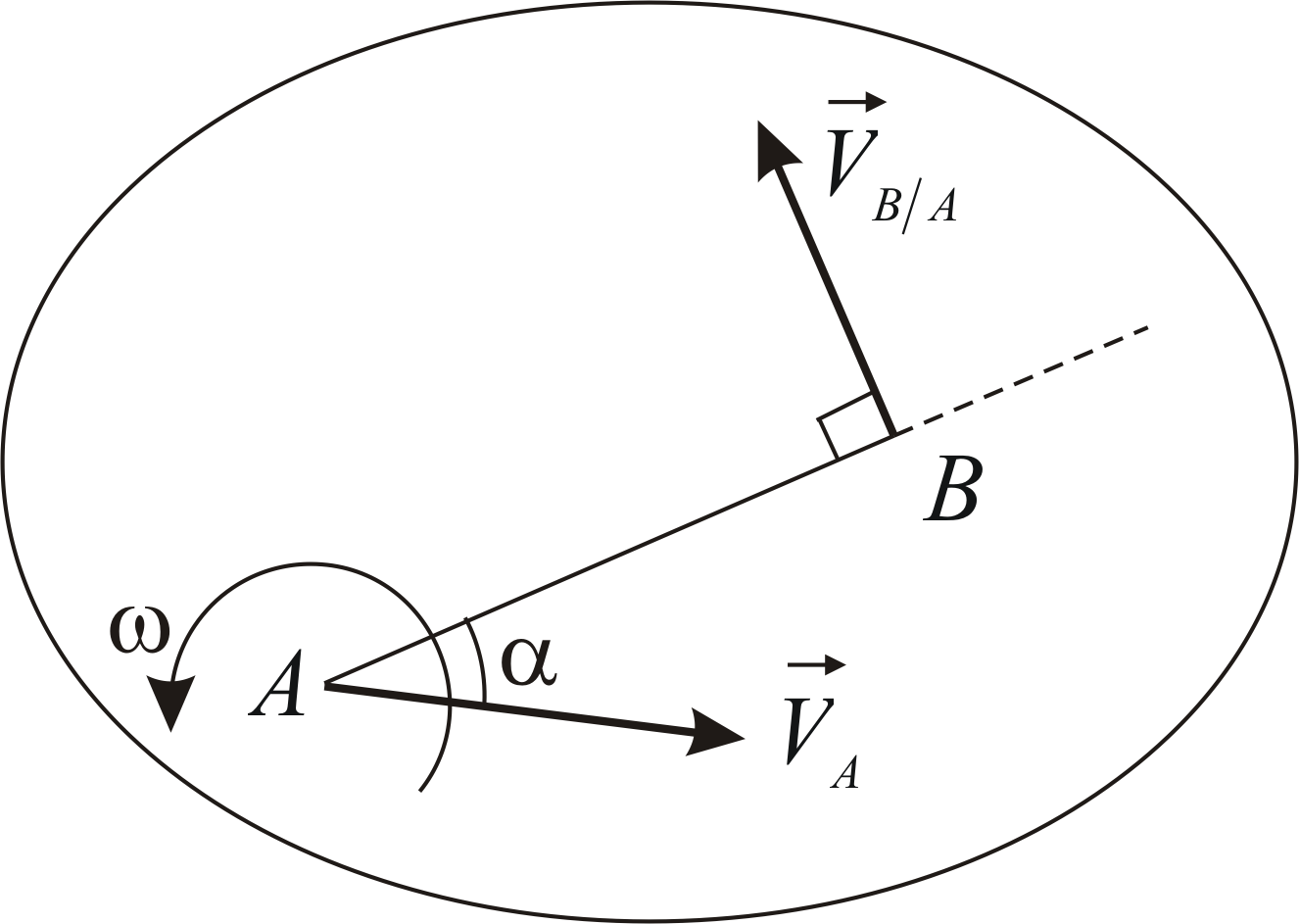
В любой момент времени скорости
любых двух точек плоской фигуры
и
связаны равенством
|
|
|
Рис. 2.3 |
(a)
Вектор
представляет собой скорость, полученную
точкойпри вращении плоской фигуры вокруг оси,
проходящей через полюсперпендикулярно плоской фигуре. Этот
вектор направлен перпендикулярно
отрезку(по касательной к окружности, которую
описывает точкапри вращении тела вокруг оси
),
причем в сторону вращения тела (Рис.
2.3). В соответствии с формулой Эйлера
Пример 2.4
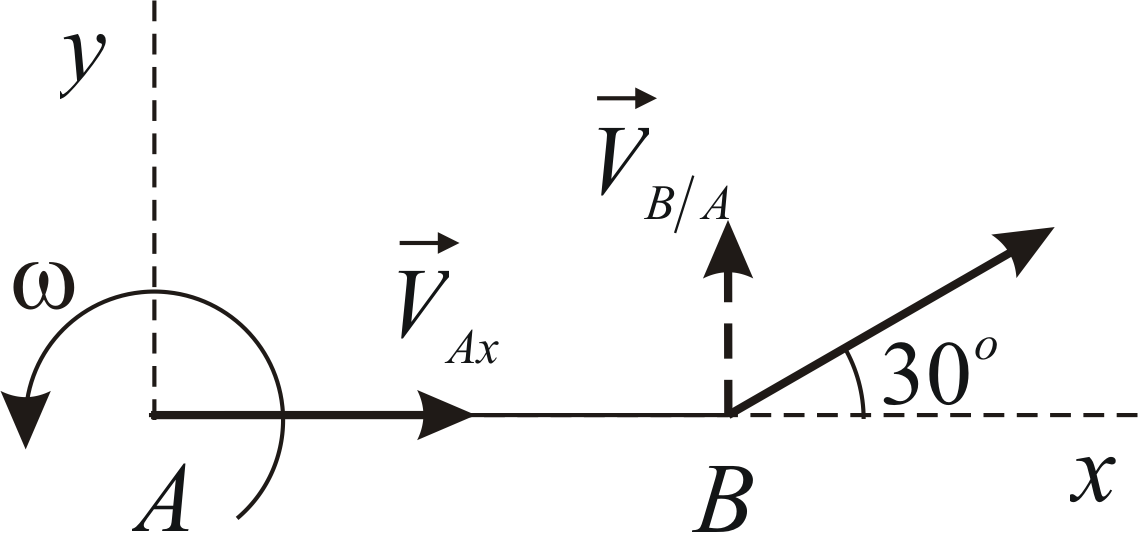
Пластина совершает плоскопараллельное
движение. В данный момент времени угловая
скорость пластины равна
,
проекция на осьскорости точки
пластины равна
.
Скорость точкиобразует с осью
угол
(Рис. 2.4). Определить модули скоростей
точеки
,
если.
|
|
|
Рис. 2.4 |
Запишем уравнение (a)
в проекциях на координатные оси:
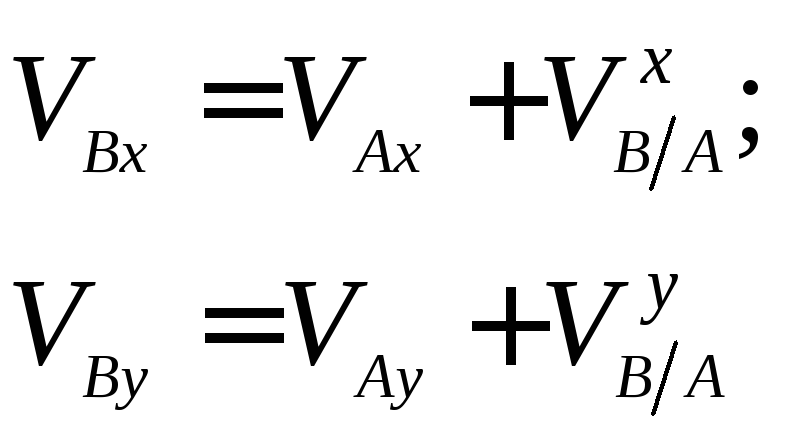
Учитывая данные задачи, получаем:

Отсюда:
Следует заметить, что прямое
использование формулы (a)
целесообразно в довольно небольшом
числе случаев. В некоторых задачах имеет
смысл использовать так называемую
теорему о проекциях. Поскольку векторперпендикулярен отрезку
,
из формулы (a) получаем
утверждение:
проекции скоростей концов отрезка,
соединяющего две точки абсолютно
твердого тела, на направление этого
отрезка равны.
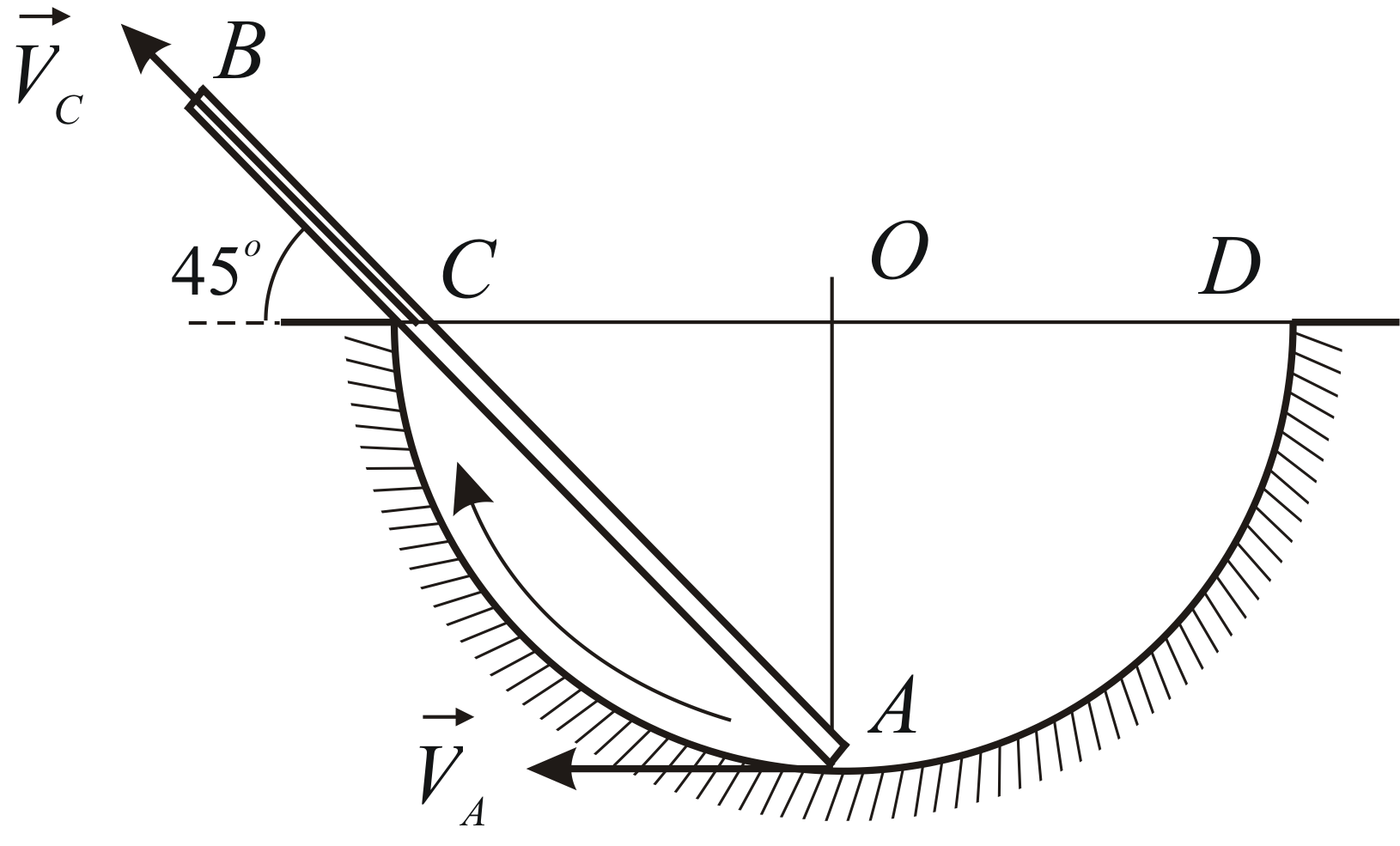
Пример 2.5
Стержень
движется в плоскости рисунка, причём
его конецвсё время находится на полуокружности
,
а сам стержень всё время касается
неподвижного выступа,
расположенного на диаметре(Рис. 2.5). Определить скорость
точки стержня, касающейся выступа, в
тот момент времени, когда радиусперпендикулярен
,
если известно, что скорость точкив этот момент
.
|
|
|
Рис. 2.5 |
Заметим, что направления скоростей
точеки
в данный момент времени известны.
Скорость точкинаправлена по касательной к траектории,
т.е. по касательной к окружности в нижней
точке. Скорость точкинаправлена вдоль стержня, т.к. по условию
задачи стержень не отрывается от выступа.
Таким образом, для заданного положения
стержня известны углы, которые образуют
векторы скоростей точеки
с отрезком
.
В таком случае целесообразно использовать
теорему о проекциях скоростей:
Решение задач с помощью мгновенного
центра скоростей. Основной способ
определения поля скоростей при
плоскопараллельном движении твёрдого
тела основан на использовании мгновенного
центра скоростей.
Как уже говорилось, за полюс можно
принять любую точку плоской фигуры. В
данный момент времени различные точки
тела имеют разные скорости. За полюс
имеет смысл принимать точку, скорость
которой в данный момент времени равна
нулю.
Точка, принадлежащая плоской фигуре
или неизменно с ней связанная, скорость
которой в данный момент времени равна
нулю, называется мгновенным центром
скоростей.
|
|
|
Рис. 2.6 |
Скорость любой точкиплоской фигуры определяется так же, как
если бы тело вращалось вокруг оси,
проходящей через мгновенный центр
скоростей перпендикулярно плоскости
движения плоской фигуры (Рис. 2.6):
Пример 2.6
Кривошипн0-шатунный механизм связан
шарнирно в середине
шатуна со стержнем
,
а последний – со стержнем,
который может вращаться вокруг оси.
Определить угловую скорость стержняв указанном на Рис. 2.7 положении механизма,
если точкии
расположены на одной вертикали; угловая
скоростькривошипа
равна 8 рад/с,
|
|
|
Рис. 2.7 |
Стерженьвращается вокруг неподвижной оси.
Скорость точкиопределяем по формуле Эйлера:
Движение стержня
плоскопараллельное. Мгновенный центр
скоростей находится в точке.
Учитывая, что скорости точек тела
пропорциональны расстояниям до
мгновенного центра скоростей, получаем:
Отсюда:
Движение стержня
плоскопараллельное. Скорость точки
направлена по касательной к окружности
радиуса,
которая является траекторией точки.
При заданном положении механизма
направление скорости точкисовпадает с направлением стержня
.
Для определения скорости точкиимеет смысл использовать теорему о
проекциях скоростей:
Остаётся определить угловую скорость
стержня
.
Поскольку движение этого стержня
вращательное, используем формулу Эйлера:
Пример 2.7
Колесо радиуса
катится без скольжения по неподвижной
поверхности (Рис. 2.8). Скорость центра
колеса.
Определить скорости точеки
|
|
|
Рис. 2.8 |
Мгновенный центр скоростейнаходится в точке касания колеса и
дороги. Зная скорость центра, находим
угловую скорость колеса:
Скорости точек колеса определяем по
формуле Эйлера:
Качение колеса представляет интерес
еще и в том отношении, что позволяет
проиллюстрировать смысл формулы (a).
Пусть колесо, движение которого мы
рассматриваем, – ведущее колесо, т.е.
оно принудительно вращается некоторым
приводом. Рассмотрим возможные
режимы движения.
Может случиться так, что колесо
вращается, но автомобиль не перемещается
– буксует. В этом случае движение колеса
представляет собой вращение вокруг
неподвижной оси
.
Все точки колеса будут описывать
окружности с центром в точке,
радиусы которых равны расстояниям от
этих точек до оси колеса. Скорость любой
точки направлена по касательной к этой
окружности и определяется по формуле
Эйлера.
Другое возможное движение колеса
представляет собой качение с
проскальзыванием. Автомобиль при этом
перемещается, но колеса вращаются
несоразмерно быстро. Скорость оси колеса
отлична от нуля и вступает в свои права
формула (a). Скорость,
например, точки,
которая в первом случае была ее полной
скоростью, становится скоростью,
полученной точкойпри вращении колеса вокруг оси
.
Полная же скорость точкитеперь геометрически складывается из
скорости точкии скорости, полученной точкой
при вращении колеса вокруг оси
Заметим, что в этом случае движение
оси (т.е. автомобиля) и вращение колеса
происходят независимо друг от друга и
каждое из них должно быть задано.
Последний режим движения колеса –
качение без скольжения. Именно этот
случай рассмотрен в примере 2.7. Движение
оси и вращение колеса оказываются
взаимосвязанными. В каждое мгновение
очевидно положение точки, скорость
которой равна нулю. В такой ситуации
при определении скоростей точек колеса
удобнее за полюс брать не точку
,
а мгновенный центр скоростей.
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В
АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 16.3;
16.10; 16.15; 16.16; 16.19; 16.24; 16.28; 16.29; 16.31;
16.32; 16.33; 16.34; 16.35; 16.36; 16.38; 16.39.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА —
теория и практика»: комплект СР-20.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 6
Пример 2.8
Определить скорость и ускорение ползуна
кривошипного механизма, а также угловую
скорость и угловое ускорение шатунав положении, изображенном на Рис. 2.9.
Кривошипвращается замедленно, имея в данный
момент времени угловую скоростьи угловое ускорение
.
Ползун движется по криволинейной
направляющей, имеющей в данном положении
механизма радиус кривизны.
Дано:.
Зная направления скоростей точек
и
,
построим мгновенный центр скоростейстержня
,
после чего определим угловую скорость
стержня
и скорость точки
Попытка определить угловое ускорение
стержня
,
используя определение
закончится неудачей, поскольку зависимость
неизвестна.
Для определения ускорения точки
принимаем за полюс точку
.
Поскольку известны траектории всех
точек во всех их движениях, представим
ускорения точек их составляющими:
Вычислим векторы, входящие в уравнение
.
|
|
|
Рис. 2.9 |
Точка
принадлежит вращающемуся телу
.
Определяем модули составляющих ускорения
этой точки:
направления векторов показаны на
Рис. 2.9.
Точка
движется по криволинейной направляющей.
Касательное и нормальное ускорения
точкиопределяются по формулам:
направления составляющих ускорения
показаны на Рис. 2.9. По приведенной
формуле не удается вычислить касательное
ускорение точки
,
поскольку неизвестны зависимости
расстоянийи
от времени.
Находим составляющие ускорения,
полученного точкой
при вращении шатуна
вокруг оси
.
Заметим, что вращательное ускорение
остается неизвестным по модулю, поскольку
неизвестно угловое ускорение шатуна:
Таким образом, из шести векторов,
входящих в равенство
,
только два неизвестны по модулю. Определим
эти неизвестные из уравнения.
Это уравнение можно решить аналитически
или геометрически. Рассмотрим оба
способа решения.
Имеет смысл выбрать координатные
оси так, чтобы в каждое уравнение в
проекциях входила только одна неизвестная.
Направим ось
вдоль
(перпендикулярно
),
а осьпо направлению
(перпендикулярно
).
Записывая уравнениев проекциях на ось
,
получаем:
Отсюда
Отрицательный знак говорит о том,
что предполагаемое направление вектора
было выбрано ошибочно; в действительности
этот вектор направлен в противоположную
сторону.
Записывая уравнение
в проекциях на ось
,
получаем:
Отсюда
|
|
|
Рис. 2.10 |
Вычислив,
можем определить угловое ускорение
стержня:
Рассмотрим геометрический способ
решения уравнения
.
Построим в масштабе сумму векторов,
стоящих в правой части уравнения.
От некоторой точкиотложим
,
от его конца отложим,
а затем(Рис. 2.10). Остается построить
,
модуль которого неизвестен. Проведем
через конецпунктирную прямую, параллельную
.
Конец суммы векторов, стоящих в правой
части уравнения,
лежит на этой прямой.
Обратимся к левой части уравнения
.
Отложим от точкиизвестный вектор
.
Через его конец проведем пунктирную
прямую, параллельную вектору.
Точка пересечения построенных прямых
определяет положение конца вектора
ускорения точки.
Пример 2.9
Колесо радиуса
катится без скольжения по прямолинейному
пути (Рис. 2.11). Ось колеса движется
ускоренно, имея в данный момент времени
скоростьи ускорение
.
Определить проекции ускорение любой
точкиобода колеса на оси координат.
Принимая за полюс точку
,
получаем:
причем
где
– угловая скорость колеса;
– его угловое ускорение.
|
|
|
Рис. 2.11 |
Зная положение мгновенного
центра скоростей колеса – точка касания
колеса и дороги, определяем угловую
скорость колеса:
В рассматриваемой задаче расстояние
от точки
,
скорость которой известна, до мгновенного
центра скоростейсо временем не изменяется. Это
обстоятельство позволяет найти угловое
ускорение колеса в данный момент времени
по определению углового ускорения:
,
так как
представляет собой проекцию вектора
ускорения точкина направление её вектора скорости,
которая в рассматриваемом случае равна.
Записывая уравнение
в проекциях на координатные оси, получаем
проекции вектора ускорения точки:
Пример 2.10
Колесо радиуса
катится без скольжения по криволинейной
поверхности (Рис.2.12). Ось колеса движется
ускоренно, имея в данный момент времени
скоростьи касательное ускорение
.
Определить проекции ускорения любой
точкиобода колеса на заданные координатные
оси, если радиус кривизны в точкеравен
.
|
|
|
Рис. 2.12 |
Задача решается так же, как в
примере 2.9, но в отличие от предыдущей
задачи, траектория точки– кривая линия. У точки
появляется вторая составляющая ускорения
– нормальная:
В результате получаем:
Пример 2.11
Колесо радиуса
катится без проскальзывания по
прямолинейному пути. Ось колеса движется
равномерно со скоростью(Рис. 2.13). Определить ускорение любой
точкиколеса.
|
|
|
Рис. 2.13 |
Ось колеса движется равномерно
и прямолинейно. Следовательно, точка– мгновенный центр ускорений. Для любой
точкиколеса получаем:
Но угловая скорость колеса
постоянна и, следовательно, угловое
ускорение колеса равно нулю.
Тогда
Таким образом, ускорение любой точки
совпадает с осестремительным ускорением,
полученным этой точкой при вращении
колеса вокруг оси, проходящей через
центр колеса
перпендикулярно плоскости движения.
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В
АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 18.11;
18.13; 18.16; 18.18; 18.22; 18.23; 18.25; 18.26;
18.28; 18.37; 18.38; 18.39; 18.40.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА —
теория и практика»: комплекты СР-21;
СР-22.
ПРАКТИЧЕСКИЕ
ЗАНЯТИЯ № 7-8
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.2015560.03 Кб15PSY — recommendation.pdf
- #
- #
Беляев С.А. Кинематика и связи // Квант. — 1971. — № 2. — С. 44-46.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Кинематика часто рассматривает движение абсолютно твердых тел, то есть тел, расстояния между любыми двумя точками которых остаются постоянными. При этом существуют методы, значительно упрощающие решение кинематических задач. С одним из них мы сейчас познакомимся.
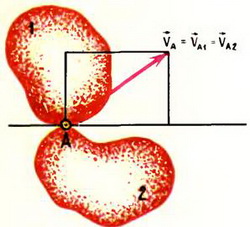
Пусть тела при движении соприкасаются, и скольжение между ними отсутствует. Тогда скорости обоих тел в точке соприкосновения полностью совпадают (рис. 1).
Рис. 1
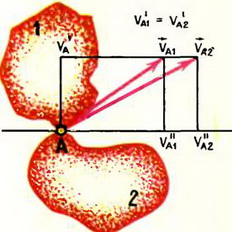
Если же между телами есть проскальзывание, то совпадают лишь проекции скоростей на перпендикуляр к касательной в точке соприкосновения. При этом достаточно, чтобы касательная существовала хотя бы для одной из скользящих поверхностей (рис. 2).
Рис. 2.
Рассмотрим несколько примеров.
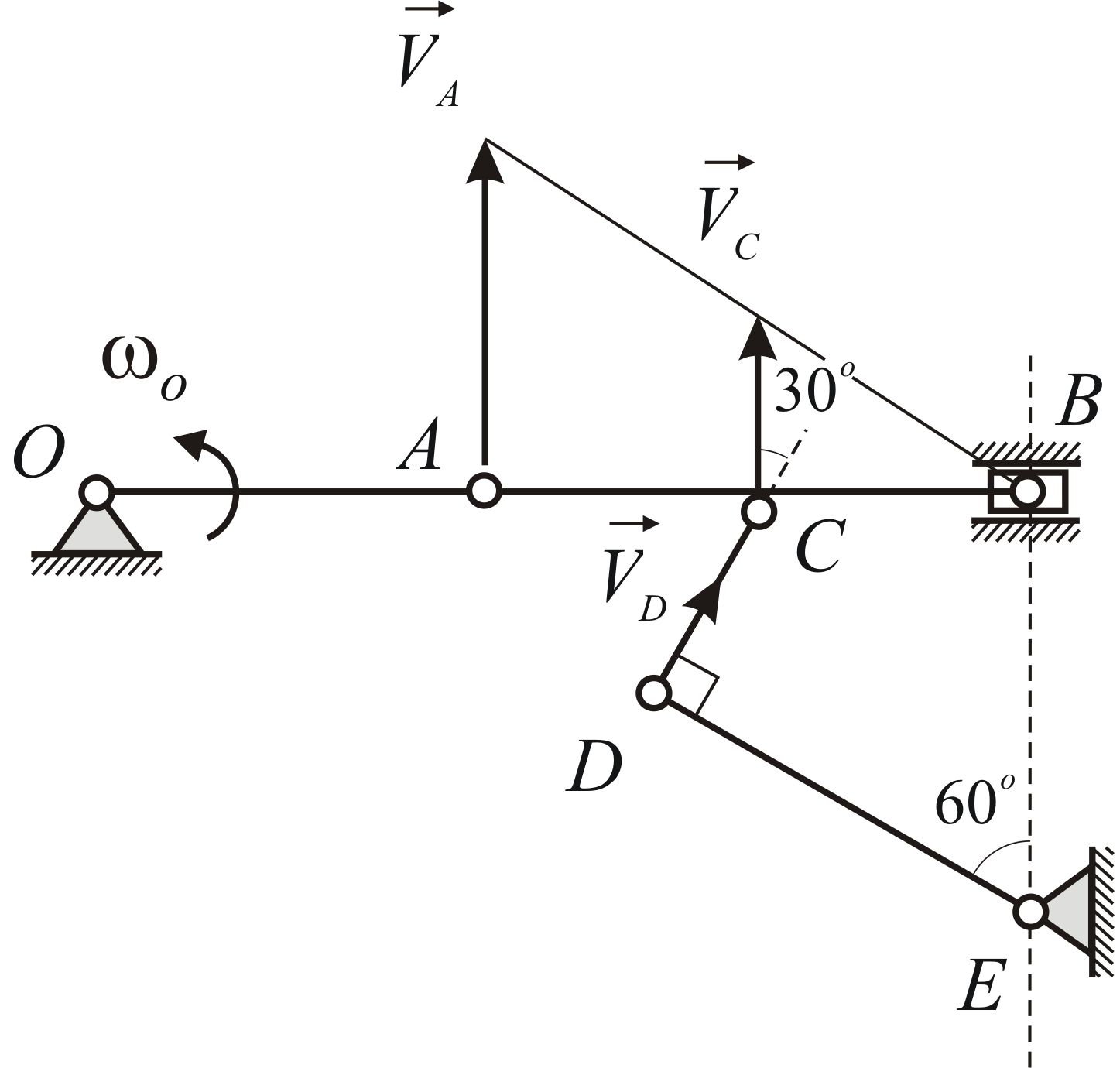
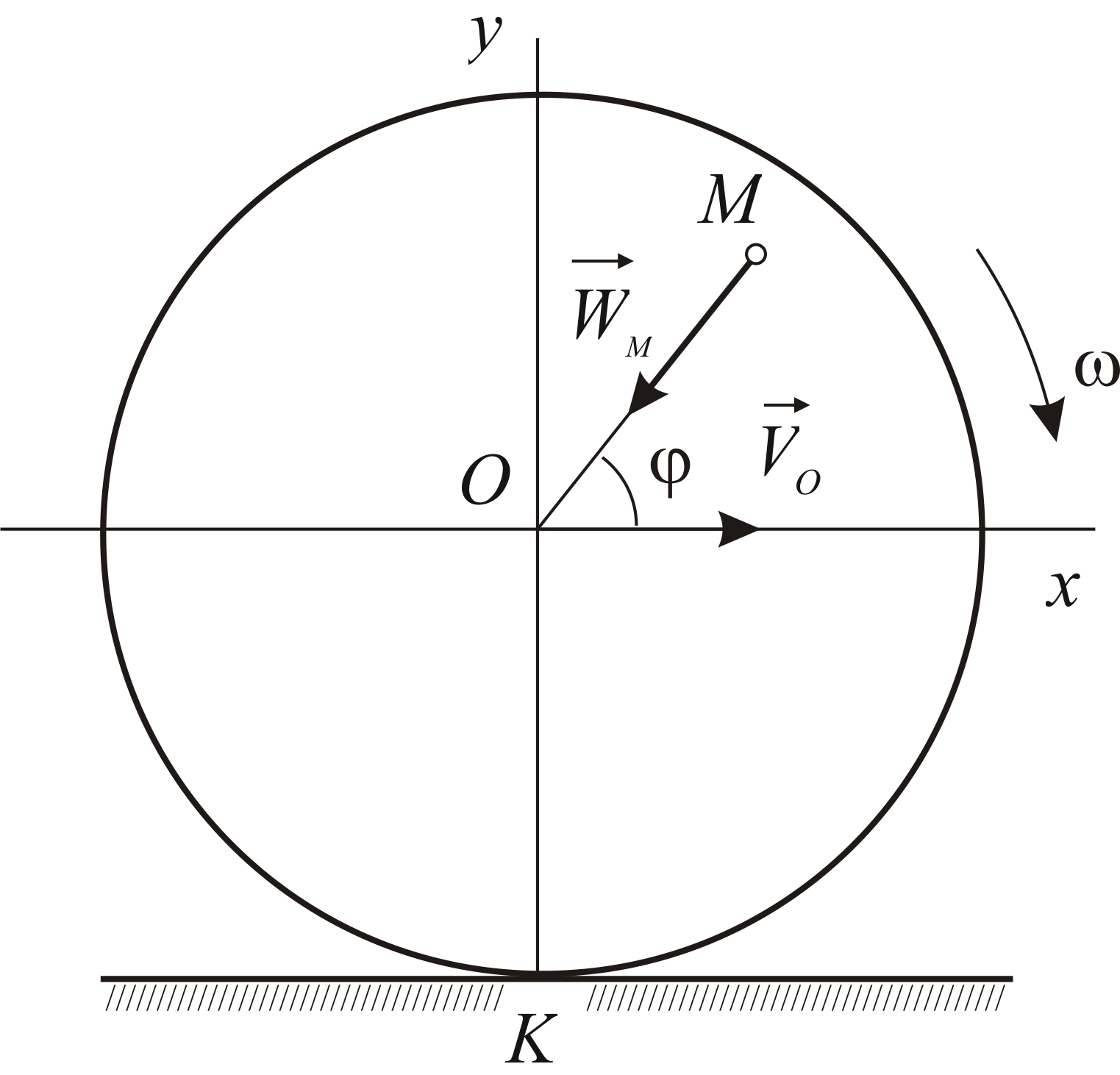
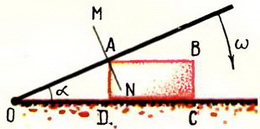
1. Стержень ОА вращается по часовой стрелке с угловой скоростью ω, приводя в движение кирпич ABCD с боковой стороной а (рис. 3). Найти зависимость скорости кирпича υ от угла α.
Решение. Стержень и кирпич соприкасаются в точке А. Следовательно, скорости кирпича и стержня в этой точке в направлении MN 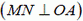
или
Рис. 3.
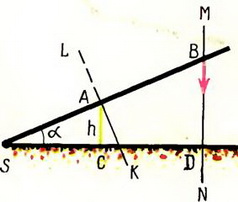
2. Источник света S находится на расстоянии l от экрана MN (рис. 4). В начальный момент времени плоский предмет высоты h начинает равномерно двигаться со скоростью υ от источника к экрану. Найти зависимость скорости движения края тени по экрану от времени.
Рис. 4.
Решение. В данной задаче в роли стержня выступает луч SB. В точке А луч «соприкасается» с предметом, а в точке В с экраном, образуя границу тени. Составим два уравнения, связывающих проекции скоростей в точках А и В: 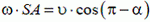
— проекция на MN. Здесь ω — угловая скорость вращения луча. Разделив второе равенство на первое и учитывая, что
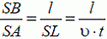
получим
Пусть теперь стержень АВ заданной длины l (рис. 5) движется произвольно. Скорости 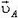
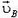
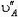
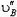
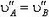
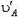
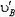
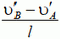
Рис. 5.
Решим две задачи.
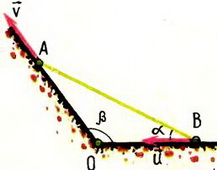
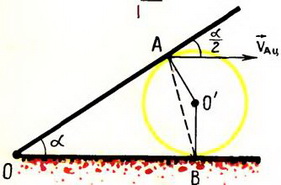
3. Стержень АВ опирается своими концами о стороны тупого угла β (рис. 6). Верхний конец стержня тянут со скоростью υ вдоль стороны АО. Найти зависимость скорости u точки В от угла α.
Рис. 6.
Решение. Так как длина стержня АВ неизменна, проекции скоростей его концов на направление стержня одинаковы:
или
Рассмотрим случай, когда длина стержня изменяется во время движения («стержнем» может служить, например, отрезок, соединяющий две заданные точки, расстояние между которыми меняется). Тогда соотношение, связывающее проекции скоростей концов стержня, принимает вид
где u — скорость изменения длины стержня. (Модуль здесь нужен, так как неизвестно, какая из скоростей больше.)
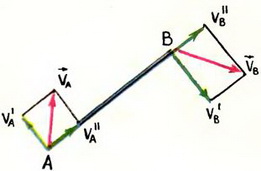
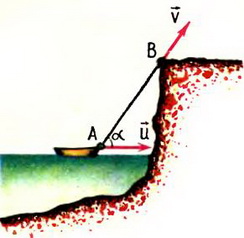
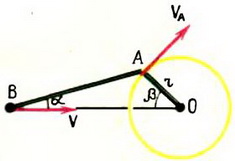
4. Лодку с крутого берега тянут за веревку с постоянной скоростью υ. Найти зависимость скорости лодки u от угла α.
Решение. В данном случае нас интересует часть веревки АВ. Скорость ее сокращения равна υ. Векторы скоростей концов, веревки А и В показаны на рисунке 7.
Рис. 7.
Согласно утверждению, приведенному выше, имеем
или так как 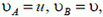
Попробуйте самостоятельно решить подобные задачи.
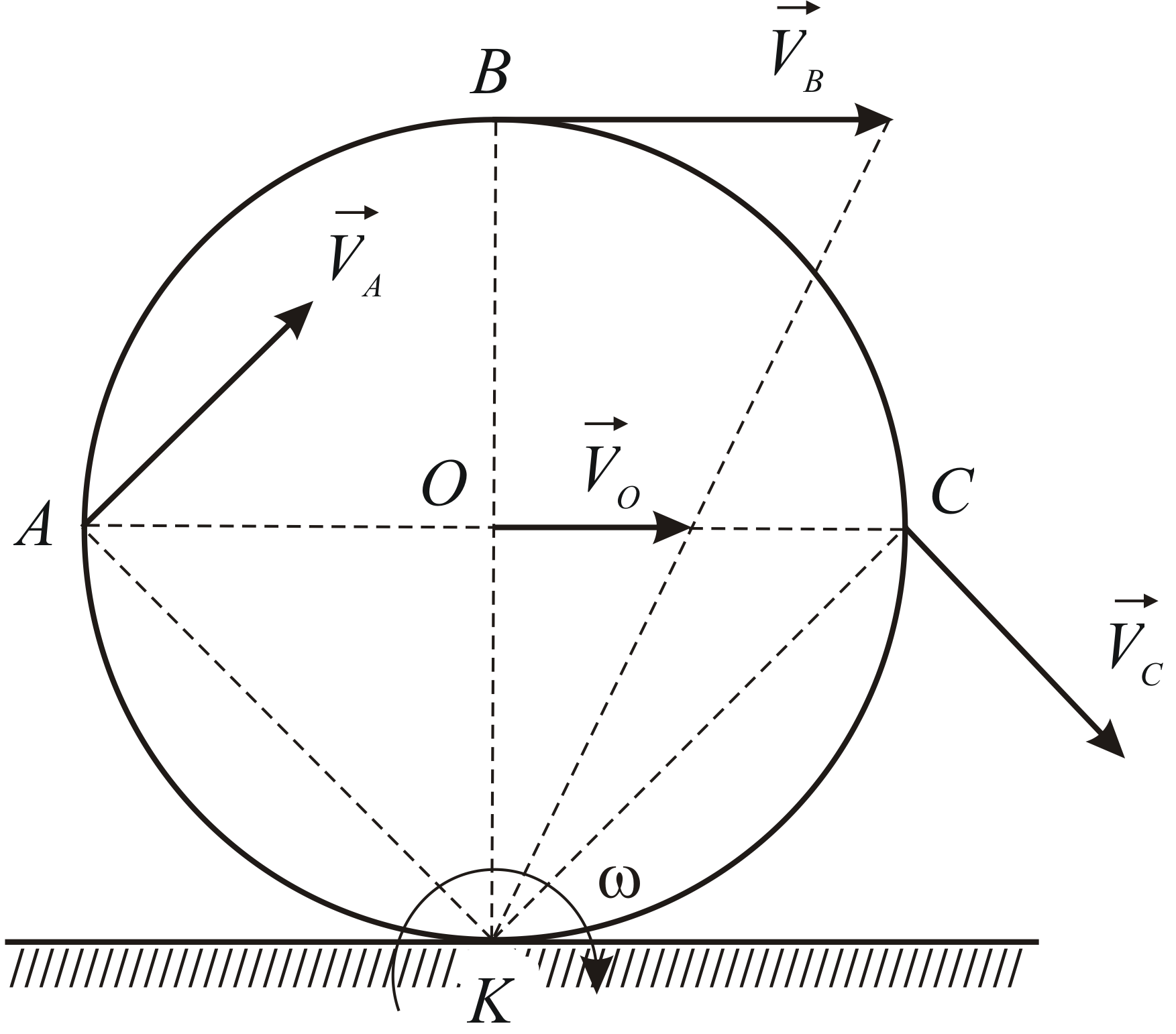
1. Стержень ОА вращается по часовой стрелке с угловой скоростью ω, приводя в движение цилиндр радиуса r (рис. 8). Скольжения между цилиндром и плоскостью нет. Найти зависимость скорости цилиндра υ от угла α.
Рис. 8.
2. Кривошип АО длины r (рис. 9) вращается с угловой скоростью ω, длина шатуна АВ равна l. Найти скорость υ точки В шатуна, если 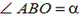
Рис. 9.
3. Шарик, предварительно раскрутив вокруг оси, кладут на горизонтальную поверхность. Коэффициент трения шарика о поверхность отличен от нуля. Под действием силы трения шарик изменяет свое первоначальное вращательное движение и начинает каким-то образом двигаться по поверхности. Описать, как будет происходить это движение.
Ответы
1. (*На рисунке к этой задаче вектор скорости υAц должен быть направлен под углом α/2 к стержню.)
В точке А проекции скоростей цилиндра υAц и стержня υAС на направление АО´ 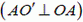
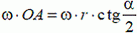
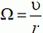
получим
Из условия равенства проекции имеем
или
Откуда
2. Поскольку длина АВ неизменна, проектируя скорости концов шатуна на направление АВ, получим 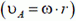
или
Воспользовавшись теоремой синусов
можно найти
Содержание:
Плоское движение тела:
При изучении темы ПЛОСКОЕ ДВИЖЕНИЕ ТЕЛА раздела КИНЕМАТИКА. вы научитесь применять аналитические и графические методы для определения скоростей и ускорений точек тел и механизмов. Хотя эти знания имеют самостоятельную ценность, особенно необходимы они будут для решения задач динамики тела и системы.
Приведены программы расчета кинематики плоского движения в математической системе Maple V. Анимационные возможности этой системы делают решение наглядным, позволяя глубже понять суть задачи.
Методы решения задачи кинематики плоского движения разнообразны. Выбрать оптимальный путь, который может существенно упростить решение, помогут примеры, приведенные в этой главе.
Скорости точек многозвенного механизма
Постановка задачи. Плоский многозвенный механизм с одной степенью свободы находится в движении. Известна угловая скорость какого-либо его звена или скорость одной из точек механизма. Найти скорости точек механизма и угловые скорости его звеньев.
План решения:
Рассмотрим два простых геометрических способа решения задачи, в которых, в отличие от аналитических методов, определяются модули скоростей и угловых скоростей. Не оговаривая отдельно, всякий раз под угловой скоростью
1-й способ. Мгновенные центры скоростей
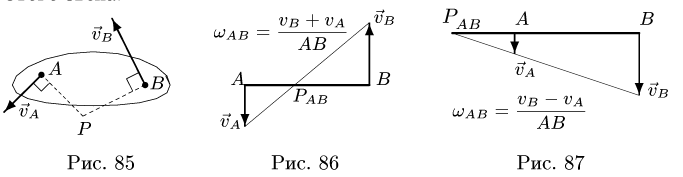
1. Определяем положение мгновенного центра скоростей (МЦС) каждого звена. МЦС лежит на пересечении перпендикуляров, проведенных
к скоростям точек, принадлежащих звену (рис. 85). У тех звеньев, у которых МЦС не существует (скорости двух точек параллельны и не перпендикулярны отрезку, их соединяющему), угловая скорость равна нулю, а скорости всех точек равны. Если векторы скоростей перпендикулярны отрезку их соединяющем}’, то имеют место два частных случая положения МЦС (рис. 86, 87).
Если тело (колесо, диск, цилиндр) катится по поверхности без проскальзывания, то МЦС этого тела находится в точке касания.
2. Для каждого звена определяем расстояния от его точек до МЦС этого звена.
3. Записываем систему уравнений для скоростей N точек звена 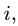
Здесь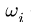
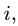
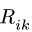
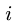
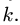
Этот пункт плана выполняем последовательно для всех звеньев механизма. Очередное звено должно иметь общую точку (шарнир) с предыдущим, для которого угловая скорость найдена или известна.
2-й способ. План скоростей
1. Как и в методе МЦС ведем расчет, переходя от одного звена к другому, шарнирно с ним соединенном}’.
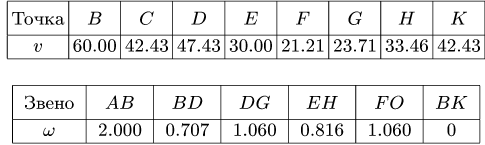
Построение начинаем с вектора, величина и направление которого известны или легко вычисляются. Этот вектор в заданном масштабе откладываем от некоторой произвольной точки О (рис. 91). Его конец определяет первую точку плана скоростей. Точку плана скоростей (конец вектора) отмечаем строчной буквой, соответствующей точке вектора скорости. Пусть первая точка плана скоростей обозначена как b.
2. Рассматриваем очередное звено, на котором имеется точка с уже известной скоростью. Необходимо, чтобы на этом звене была
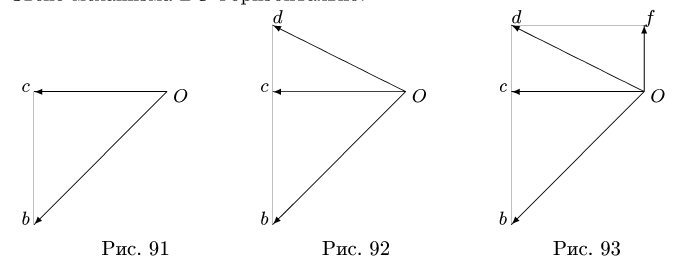
еще одна точка с известным направлением вектора скорости (например, ползун или точка звена, совершающего вращательное движение). Пусть эта точка обозначена как С (рис. 88).
Справедливо правило, согласно которому неизменяемые отрезки механизма, обозначенные прописными буквами, перпендикулярны отрезкам плана скоростей, обозначенными теми же строчными буквами.
Следующая точка плана скоростей лежит на пересечении двух прямых. Одна прямая определяется направлением скорости точки С, вторая перпендикулярна ВС. Длина полученного отрезка Ос является модулем скорости 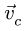
Скорости остальных точек этого звена (если таковые имеются) найдем по правилу подобия неизменяемых фигур механизма и фигур, обозначенных теми же строчными буквами плана скоростей.
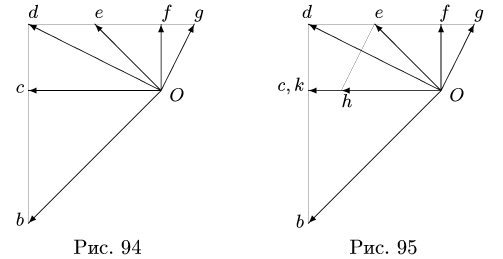
Пункт 2 плана выполняем для всех звеньев механизма (рис. 91-95).
3. После построения плана скоростей определяем угловую скорость каждого звена по простой формуле 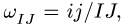
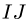
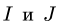
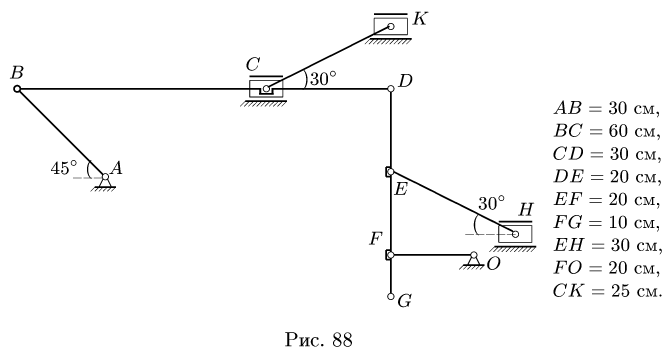
Задача №1
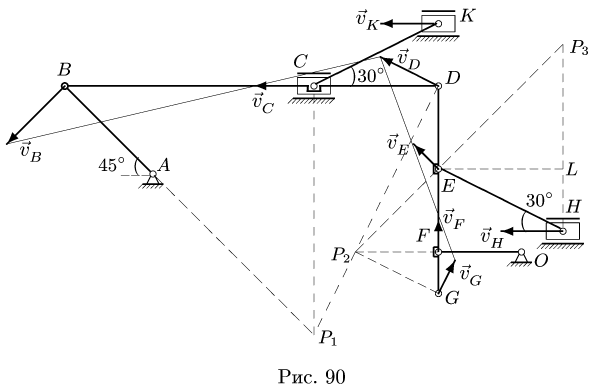
Плоский многозвенный механизм с одной степенью свободы приводится в движение кривошипом АВ, который вращается против часовой стрелки с угловой скоростью 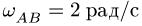
Ползуны С, К, Н движутся горизонтально, 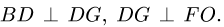
8.1.Скорости точек многозвенного механизма скорости его звеньев АВ, BD, DG, EH, FO, СК.
Решение
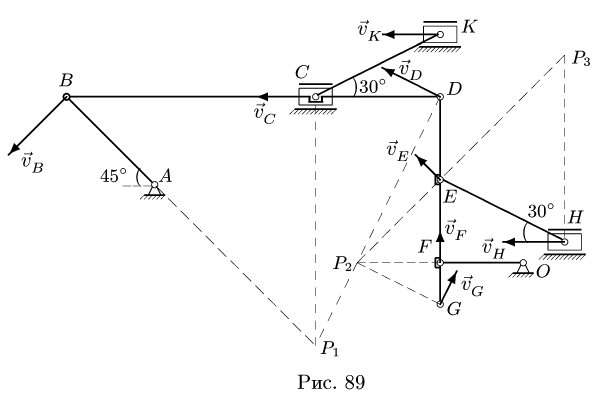
1-й способ. Мгновенные центры скоростей
1. Определяем положение мгновенного центра скоростей каждого звена АВ, BD, DG, СК, EH, FO.
МЦС звеньев АВ и FO искать не требуется. Они совершают вращательное движение вокруг шарниров А и О соответственно. Можно условно считать, что там находятся их МЦС.
Вектор 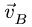
Остается точка С. Ползун С движется строго горизонтально. Вектор скорости 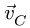
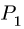
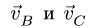
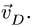
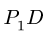
Со стержнем BCD имеют общие точки два стержня: СК и DG. Рассмотрим сначала стержень DG. Направление вектора скорости точки D уже известно. Чтобы определить положение МЦС, надо знать направление вектора еще одной точки на этом звене. Такой точкой является F. Вектор ее скорости перпендикулярен радиусу вращения FO и направлен вертикально. Перпендикуляры к векторам 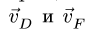
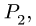
Перпендикулярно радиусам 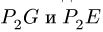
Переходим к звену ЕН, МЦС которого находим на пересечении перпендикуляров к 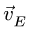
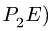
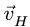
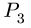
И, наконец, рассматриваем звено СК. Скорости 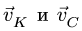
2. Определяем расстояния от МЦС звеньев до тех точек этих звеньев, скорости которых надо найти.
Звено BCD
Звено DEFG. Пользуясь подобием 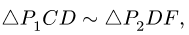
Звено ЕН (рис. 90). Находим расстояния до МЦС:
8.1.Скорости точек многозвенного механизма
3. Записываем систему уравнений для скоростей трех точек звена BCD, включая точку В с известной скоростью:
Решаем эту систему. Находим
Система уравнений для скоростей точек звена DEFG имеет вид
Из первого уравнения вычисляем угловую скорость:
Получаем скорости точек:
Система уравнений для скоростей точек звена ЕН имеет вид
Отсюда
Звено СК совершает мгновенно-поступательное движение. Следовательно, скорости точек С я К равны: 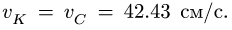
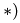
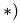
Частично проверить решение можно графически. Известно, что концы векторов скоростей точек неизменяемого отрезка лежат на одной прямой. Убеждаемся в этом, проводя прямую через концы векторов 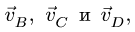
Аналогично, проверяем скорости 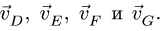
Результаты расчетов помещаем в таблицы. Скорости даны в см/с, угловые скорости — в рад/с.
2-й способ. План скоростей
1. Построение начинаем с вектора, величина и направление которого известны или легко вычисляются. В нашем случае это 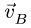
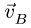
8.1.Скорости точек многозвенного механизма
Точки плана скоростей (концы векторов) отмечаем соответствующими строчными буквами. Таким образом, положение точки b на плане скоростей известно.
2. Рассматриваем звено BCD (рис. 90), на котором имеется точка В с известной скоростью. Неизменяемые отрезки механизма, обозначенные прописными буквами, перпендикулярны отрезкам плана скоростей, обозначенными теми же строчными буквами,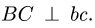
Следовательно, точка с плана скоростей лежит на одной вертикали с точкой b. Известно направление скорости ползуна С. Точку с находим на пересечении двух прямых. Вектор 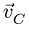
Так получаем точку d плана скоростей и, следовательно, величину и направление вектора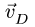
Определяем скорость 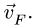
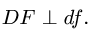
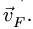
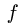
Из соотношения подобия 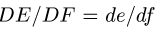
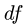
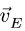
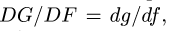
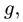
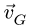
Аналогично, определяем скорость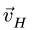
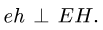
3. Угловые скорости звеньев определяем по простым формулам:
Ускорения точек многозвенного механизма
Постановка Задачи. Плоский шарнирно-стержневой механизм состоит из шарнирно соединенных стержней и ползунов. Механизм приводится в движение кривошипом, который вращается с заданной угловой скоростью. В указанном положении механизма найти ускорения всех его шарниров.
*) Существует еще несколько способов проверки вычисления скоростей точек многозвенного механизма.
8.2. Ускорения точек многозвенного механизма
План решения
1. Определяем угловые скорости звеньев и скорости точек механизма (см. § 8.1).
2. Определяем ускорение шарнира, принадлежащего звену с известным законом движения:
где R — длина звена. Если задан закон изменения утла поворота 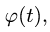
Если угловая скорость звена постоянна, 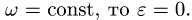
3. Для определения ускорения точки В тела, совершающего плоское движение, воспользуемся векторной формулой
Здесь 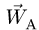
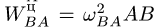
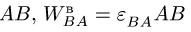
Возможны три случая определения ускорения по формуле (1). А. Точка В является ползуном, или направление ее вектора ускорения по каким-либо другим причинам известно. В этом случае формула (1) в проекциях на оси координат представляет собой систему двух линейных уравнений для неизвестного модуля ускорения ав и неизвестного углового ускорения звена
Б. В точке В шарнирно соединены звено АВ и звено ВС, где С — неподвижный шарнир. Таким образом, точка В движется по окружности с центром в С, и ее ускорение можно представить в виде векторной суммы нормального и тангенциального ускорения:
Величину нормального ускорения 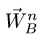
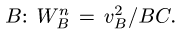
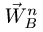
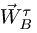
В результате, система уравнений (1-2), записанная в проекциях, дает четыре уравнения для четырех неизвестных 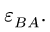
В. Точка В не удовлетворяет случаям А и Б. В этом случае либо она не является шарниром, либо к ней шарнирно присоединено тело, совершающее плоское (не вращательное и не поступательное) движение. Для решения задачи должны быть известны угловая скорость и угловое ускорение звена, на котором находится точка В. Они могут быть найдены при вычислении скорости и ускорения других точек этого звена. При этих условиях уравнение (1) является векторным уравнением для одной неизвестной 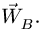
Этот пункт плана выполняем последовательно для всех звеньев механизма. Очередное звено должно иметь общую точку (шарнир) с предыдущим.
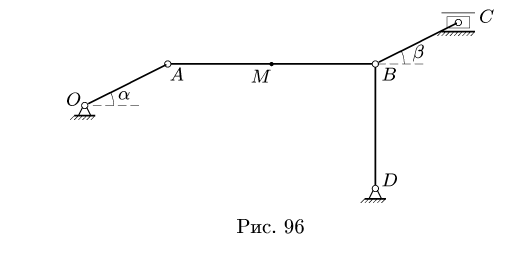
Задача №2
Плоский шарнирно-стержневой механизм состоит из четырех шарнирно соединенных стержней и горизонтально движущегося ползуна С (рис. 96). Механизм приводится в движение кривошипом OA, который вращается с постоянной угловой скоростью 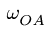
Решение
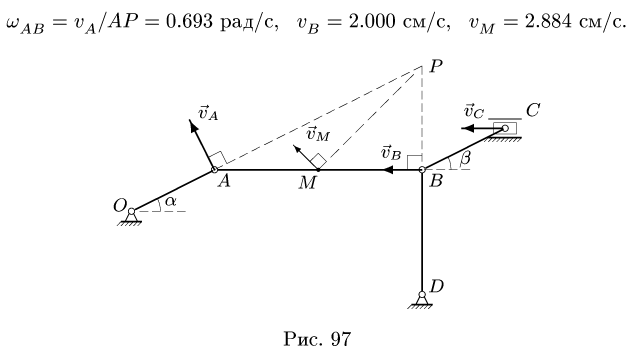
1. Определяем угловые скорости звеньев и скорости точек механизма. Находим величину скорости точки А:
Вектор 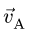
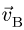
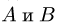
8.2. Ускорены точек многозвенного механизма
от точек А, В, М до МЦС:
Скорости точек находим из системы уравнений
В результате решения получаем
Найти скорость точки С не составит труда. Векторы 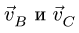
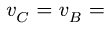
2. Определяем ускорение шарнира А, принадлежащего звену OA с известной постоянной угловой скоростью 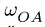
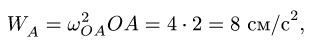
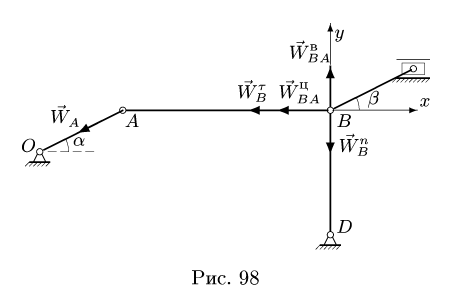
3. Находим ускорение точки В. Точка В движется по окружности с центром в неподвижном шарнире D, и ее ускорение можно представить в виде векторной суммы нормального и тангенциального ускорений:
С другой стороны, ускорение точки В выражается через ускорение точки А, лежащей на том же звене АВ. Рассматривая А в качестве полюса, имеем
Сравнивая (3) и (4), получаем, что
В проекциях на оси х, у (рис. 98) векторное уравнение (3) дает систем}’ двух уравнений относительно неизвестных
где
Решаем систему (5):
Окончательно, величина ускорения точки В
8.2. Ускорены точек многозвенного механизма
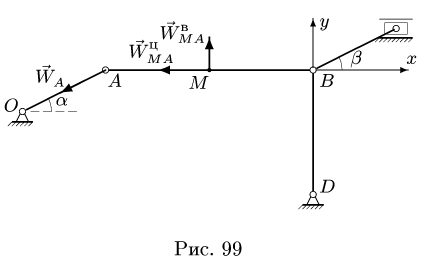
Вычисление ускорения точки М выполняем по п.ЗВ плана решения. Действительно, угловая скорость и угловое ускорение звена А В уже известны:
Рассматривая А в качестве полюса (рис. 99), записываем векторное уравнение
где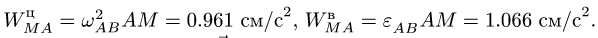
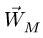
Величина ускорения точки M
Находим ускорение точки С. Скорости точек В я С звена ВС, совершающего мгновенно — поступательное движение, равны, однако, их ускорения различны.
Для определения 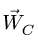
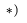
где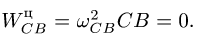
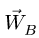
Векторное уравнение (7) содержит две неизвестных величины: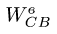
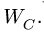
Спроецируем (7) на ось 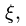
Находим
Результаты расчетов помещаем в таблицу (скорости в см/с, ускорения в см/
8.3. Уравнение трех угловых скоростей
Постановка задачи. Подобрать длины звеньев шарнирного четырехзвенника так, чтобы в некоторый момент движения угловые скорости его звеньев были бы равны заданным. Положение опорных шарниров четырехзвенника известно.
План решения:
Под угловыми скоростями будем понимать проекции соответствующих векторов на ось 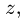
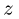
1. Последовательно нумеруем шарниры и звенья механизма. Выбираем систему координат, помещая ее начало в один из шарниров механизма. Определяем координаты шарниров.
2. Записываем уравнения трех угловых скоростей
где 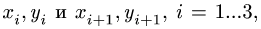
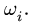
3. Решаем систему (1) относительно неизвестных координат. Определяем длины звеньев механизма (расстояния между шарнирами) по формулам
Задача №3
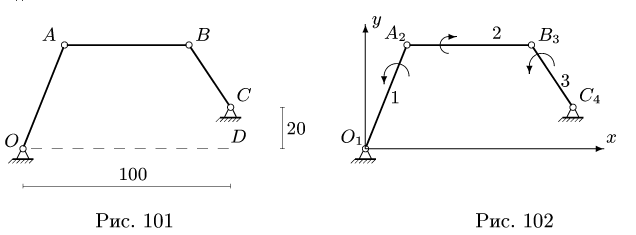
В положении, изображенном на рис. 101, известны угловые скорости шарнирного четырехзвенника О ABC: 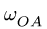
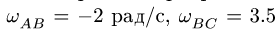
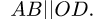
Решение
1. Последовательно нумеруем шарниры и звенья механизма. Номера шарниров указываем индексами у соответствующих букв. Выбираем систему координат, помещая ее начало в шарнир О. Определяем координаты шарниров (рис. 102):
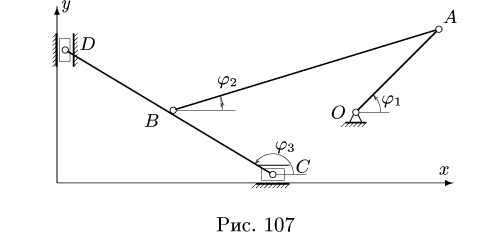
2. Записываем уравнения трех угловых скоростей (1), где по условию
8.3. Уравнение трех угловых скоростей
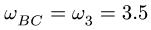
3. Решаем систему (2) относительно 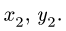
Кроме того, 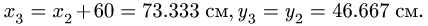
Уравнение трех угловых ускорений
Постановка задачи. Многозвенный механизм приводится в движение кривошипом, вращающимся с известной угловой скоростью и известным угловым ускорением. Найти угловые скорости и угловые ускорения звеньев механизма.
План решения:
Под угловыми скоростями и ускорениями будем понимать проекции соответствующих векторов на ось 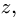
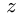
1. Нумеруем шарниры и звенья механизма. Выбираем систему координат, помещая ее начато в один из шарниров механизма. Определяем координаты шарниров.
2. Выделяем из механизма шарнирные четырехзвенники. Рассмотрим четырехзвенник, шарниры которого последовательно обозначены номерами 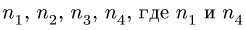
Гл. 8. Плоское движение тела
шарниров. Стержни четырехзвенника имеют номера 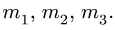
где 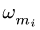
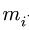
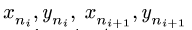
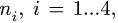
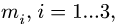
3. Из решения (1) получаем все угловые скорости механизма.
4. Записываем уравнения трех угловых ускорений для каждого четырехзвенника *) :
где 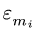
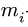
5. Решаем (2) относительно неизвестных угловых ускорений.
Задача №4
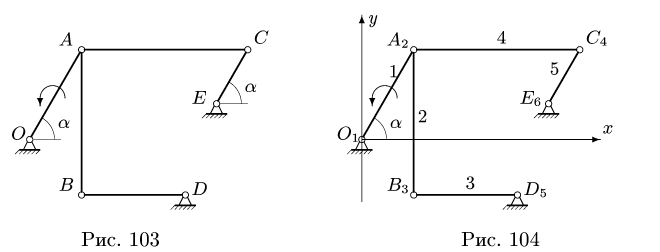
Многозвенный механизм приводится в движение кривошипом OA, вращающимся с угловой скоростью 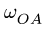
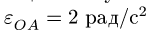
Дано: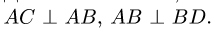
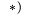
8.4. Уравнение трех угловых ускорений
Решение
1. Нумеруем шарниры и звенья механизма (рис. 104). Выбираем систему координат, помещая ее начало в шарнир О. Определяем координаты шарниров:
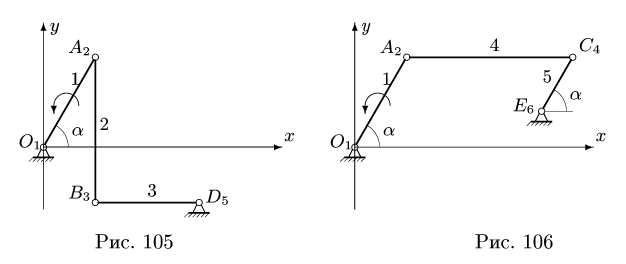
2. Выделяем из механизма шарнирные четырехзвенники (рис. 105, 106). Записываем уравнения трех угловых скоростей для четырехзвенника OABD (рис. 105),
и для четырехзвенника О АСЕ (рис. 106),
(4)
3. Решаем систему четырех линейных уравнений (3), (4). Получаем угловые скорости звеньев: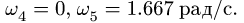
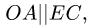
параллельны и но перпендикулярны АС. Мгновенного центра скоростей звена АС не существует (расположен в «бесконечности»), что соответствует
4. Записываем уравнения трех угловых ускорений для четырех-звенника OABD (рис. 105),
и для четырехзвенника ОАСЕ (рис. 106),
5. Из решения (5,6) получаем угловые ускорения:
Кинематические уравнения плоского движения
Постановка задачи. Составить кинематические уравнения плоского многозвенного механизма.
План решения:
1. Составляем кинематические графы механизма, выбирая наиболее короткие маршруты. Началом и концом графа должна быть точка с известной скоростью. Кинематические графы должны включать в себя все звенья механизма. Некоторые звенья могут входить в разные графы. Обозначения для графов приведены на с. 130.
8.5. Кинематические уравнения плоского движения
2. Записываем по два кинематических уравнения в проекциях на оси координат для каждого графа. Получаем систему дифференциальных уравнений.
3. Упрощаем систему уравнений, используя уравнения связей и тригонометрические формулы приведения.
Задача №5
Механизм состоит из стержней OA, АВ, CD и ползунов С и D. Ползун D движется вверх со скоростью 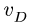
Решение
1. Составляем кинематические графы:
2. Записываем для каждого графа (1), (2) по два кинематических уравнения в проекциях на оси координат:
3. Упрощаем систему (3), используя уравнения связей,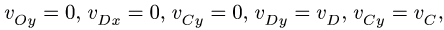
Гл. 8. Плоское движение тела
формулы приведения:
Задача №6
Плоский манипулятор состоит из жесткой детали ОАВ, стержней ВС, AM, колеса С и захвата М. Даны длины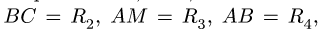
Составить кинематические уравнения манипулятора . Решение
1. Составляем кинематические графы:
2. Записываем по два кинематических уравнения в проекциях на оси координат для каждого графа (5):
8.5. Кинематические уравнения плоского движения
3. Упрощаем систему (6), используя уравнения связей,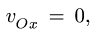
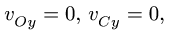
Замечание 1. В данной задаче скорости точек механизма можно найти для некоторого промежутка времени, а не для фиксированного момента времени, как в аналогичных задачах § 8.1, § 8.3. Решая нелинейную систему дифференциальных уравнений (4), получаем полную картину движения механизма . Для решения системы (4) необходимо дополнить ее начальными условиями:
где константы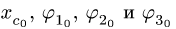
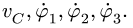
Замечание 2. В решении задачи следует использовать наиболее короткие графы. В данном случае вместо графа (2) можно было бы выбрать граф
Система дифференциальных уравнений изменится, однако в форме Коши ее вид останется прежним.
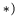
Замечание 3. Метод графов широко используется для решения задач кинематики и динамики. Примеры составления графов представлены также на с. 243, 244 310, 313, 316, 327, 329.
Замечание 4. Для того, чтобы проинтегрировать полученные кинематические уравнения, необходимо скорости ползунов выразить через соответствующие координаты, например, 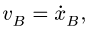
Предупреждение типичных ошибок:
- Кинематические графы являются ориентированными графами. Меняя направление маршрута, меняйте и угол. Следующие два графа
- эквивалентны:
- Угловая скорость звена, которому принадлежат точки А и В графа
, не обязательно равна
см., например, с. 243.
- Принцип виртуальных перемещений
- Аксиомы и теоремы статики
- Система сходящихся сил
- Моменты силы относительно точки и оси
- Равновесие вала
- Определение усилий в стержнях, поддерживающих плиту
- Тело на сферической и стержневых опорах
- Приведение системы сил к простейшему виду
Содержание:
- Плоское движение тела
- Определение скоростей точек тела
- Уравнения плоского движения
- Скорости точек фигуры. Мгновенный центр скоростей
- Определение положения мгновенного центра скоростей
- Порядок решения задач на тему: Определение скоростей точек тела
- Примеры решения задач на тему: Определение скоростей точек тела
- Решение задачи графоаналитическим способом
- Решение задачи с помощью мгновенного центра скоростей
- Определение ускорений точек тела
- Ускорения точек плоской фигуры
- Порядок решения задач на тему: Определение ускорений точек тела
- Примеры решения задач на тему: Определение ускорений точек тела
- План скоростей
- Порядок решения задач на тему: План скоростей
- Примеры решения задач на тему: План скоростей
- План ускорений
- Примеры решения задач на тему: План ускорений
Плоское движение тела — это такое движение, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Плоское движение тела
Плоскопараллельное движение (плоское движение) — вид движения абсолютно твёрдого тела, при котором траектории всех точек тела располагаются в плоскостях, параллельных заданной плоскости. Примером плоскопараллельного движения по отношению к вертикальной плоскости, относительно которой тело движется в параллельном направлении, является качение колеса по горизонтальной дороге
Определение скоростей точек тела
Скорости точек тела пропорциональны их расстояниям до мгновенного центра скоростей, и это отношение определяет угловую скорость тела в данный момент времени: Частные случаи определения положения мгновенного центра скоростей. Если плоскопараллельное движение осуществляется путем качения без скольжения одного цилиндрического тела по поверхности другого, то точка касания Р имеет в данный момент времени скорость равную нулю, и, следовательно является мгновенным центром скоростей .
Уравнения плоского движения
Плоским называется такое движение тела, при котором траектории всех его точек лежат в плоскостях, параллельных данной неподвижной плоскости.
При таком движении все точки твердого тела, лежащих на перпендикуляре к этой плоскости, имеют одинаковые траектории, скорости и ускорения.
Плоское движение фигуры можно рассматривать как сложное (то есть, абсолютное) движение, которое включает поступательное движение вместе с произвольно выбранной точкой 
На рис.4.1 с телом 





Уравнения (4.1) называются уравнениями плоского движения твердого тела.
При этом, поступательная часть плоского движения описывается двумя уравнениями:
а относительная вращательная вокруг полюса — третьим уравнением:
Координаты любой точки 



Скорости точек фигуры. Мгновенный центр скоростей
Поскольку плоское движение тела состоит из поступательного вместе с полюсом и вращательного вокруг него, то скорость любой точки тела 





Вектор относительной скорости 



Модуль и направление абсолютной скорости 


Относительная скорость 


где 
Найти скорость любой точки тела можно также на основе теоремы, которая гласит:
Проекции скоростей двух точек фигуры на прямую, что соединяет эти точки, равны между собой.
Согласно этой теореме (рис.4.3) :
или
Если известна скорость 

При плоском движении тела в каждый момент времени существует точка тела, скорость которой равна нулю. Эта точка называется мгновенным центром скоростей и, как правило, обозначается буквой 
Если мгновенный центр скоростей известен, то легко можно найти мгновенное распределение скоростей всех точек тела (рис.4.4).
Выберем за полюс поступательного движения мгновенный центр скоростей 


где 









Поскольку скорость выбранного полюса 

По модулю скорости вращения точек 


Разделив 

Таким образом, мгновенное распределение скоростей точек тела при его плоском движении, такое же, какое было бы при его вращательном движении вокруг мгновенного центра скоростей.
Определение положения мгновенного центра скоростей
Существует несколько способов нахождения положения мгновенного центра скоростей.
Случай 1. Известна скорость 


Мгновенный центр скоростей 


Для нахождения направления перпендикуляра надо повернуть вектор 


Случай 2. Известны направления скоростей 



Мгновенный центр скоростей должен лежать как на перпендикуляре к вектору 


Случай 3. Скорости двух точек 

Говорят, что в этом случае мгновенный центр скоростей лежит на бесконечности. Угловая скорость вращения равна нулю, а скорости всех точек тела геометрически равны, то есть в данный момент времени тело выполняет поступательное движение.
Случай 4. Скорости двух точек 




Мгновенный центр скоростей находится на продолжении отрезка 
Решив это уравнение относительно 
Таким образом, для определения положения мгновенного центра скоростей надо знать не только направления скоростей, но и их величину.
Случай 5. Скорости двух точек 


Мгновенный центр скоростей лежит на отрезке 

Решив уравнение относительно 
Таким образом, для нахождения положения мгновенного центра скоростей надо знать величины и направления скоростей обеих точек.
Случай 6. Тело катится без проскальзывания по неподвижной поверхности (рис.4.10).
В этом случае мгновенный центр скоростей находится в точке 

Тогда и скорость точки 
Порядок решения задач на тему: Определение скоростей точек тела
а) решение графоаналитическим методом:
- выбрать за полюс ту точку тела, скорость которой известна по величине и направлению или легко определяется из условий задачи;
- найти точку тела, направление скорости которой известно;
- пользуясь формулами плоского движения найти скорость этой точки;
- определить угловую скорость тела в данный момент времени;
- по известной угловой скорости и скорости полюса, пользуясь формулами плоского движения найти скорости других точек тела.
б) решение с помощью мгновенного центра скоростей:
- определить положение мгновенного центра скоростей одним из известных способов;
- определить значение мгновенного радиуса той точки тела, скорость которой известна, и найти угловую скорость тела;
- найти скорости других точек тела.
Примеры решения задач на тему: Определение скоростей точек тела
Задача №1
Стержень 






Определить величину скорости точки 

Решение задачи графоаналитическим способом
1. Выберем за полюс точку 
2. Используя формулу распределения скоростей при плоском движении, запишем векторное уравнение для определения скорости точки 
где 




Данное векторное уравнение можно решить построением векторного треугольника скоростей (рис.4.12). Для этого из произвольной точки плоскости 
При построении правой части уравнения (1) из точки 









Теперь из точки 



Точка 


В результате построения получили замкнутый треугольник скоростей, стороны которого в выбранном масштабе определяют искомую скорость точки 

В этом треугольнике известны все углы и одна сторона 

3. Определим угловую скорость вращения стержня 

4. Найдем скорость точки 



где 




Скорость 

Отложив от точки 







Поскольку стороны 




Решение задачи с помощью мгновенного центра скоростей
1. Определим положение мгновенного центра скоростей. Для этого с точек 




2. Определим мгновенные радиусы. Поскольку треугольник 
3. Вычислим угловую скорость вращения фигуры вокруг мгновенного центра скоростей:
4. Найдем скорости точек 

где 




Если надо было бы определить только величину скорости 
Тогда:
Ответ:
Задача №2
Колесо радиусом 


Определить: скорости точек 


Решение.
1. В качестве полюса выберем точку 
2.Используя формулу распределения скоростей точек тела при плоском движении определяем скорости других точек колеса.
Для точки 
где 


По модулю 
Скорость 



Из точки 


Тогда:
Векторное уравнение для определения скорости точки 
где 


Эта скорость параллельна скорости 
Из точки 


Поскольку векторы коллинеарны, то:
Таким образом, скорость точки 


Составляем векторное уравнение для определения скорости точки 
где 


По модулю 
Скорость 


Из точки 






Поскольку векторы 


Ответ:
Задача №3
Колесо радиусом 
Определить: скорости точек 


Решение. Решим задачу с помощью мгновенного центра скоростей.
1. Определим положение мгновенного центра скоростей. Поскольку колесо катится по неподвижной поверхности, то мгновенный центр скоростей находится в точке 
2. Мгновенный радиус для точки 


Направлена угловая скорость по ходу часовой стрелки.
3. Определим величину и направление скоростей точек 


Соединим точки 








По модулю скорости будут равны:
где
Ответ:
Задачи, которые рекомендуются для самостоятельной работы: 16.2; 16.4; 16.11; 16.12 [2]
Определение ускорений точек тела
Теорема: ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки во вращательном движении фигуры вокруг полюса.
Ускорения точек плоской фигуры
Формула распределения ускорений при плоском движении тела имеет вид:
где 






Ускорение любой точки 

Графическое определение ускорения точки 
Вычисление величины ускорения точки 


Учитывая, что 


где
Вектор 




Тогда уравнение (4.10) примет вид:
Если точка 


Порядок решения задач на тему: Определение ускорений точек тела
1. Выбрать точку, которая будет полюсом при записи уравнения плоского движения (как правило выбирают точку, ускорение которой известно).
2. Записать векторное уравнение распределения ускорений.
3. Спроектировать уравнение распределения ускорений на две взаимно перпендикулярные оси, одна из которых совпадает с нормальным ускорением, а вторая – с тангенциальным.
4. Определить мгновенное угловое ускорение плоской фигуры.
5. Найти искомые ускорения точек с помощью уравнения распределения ускорений.
Примеры решения задач на тему: Определение ускорений точек тела
Задача №1
Прямоугольная (рис.4.18, а) пластина 




Ускорение точки 



Определить мгновенную угловую скорость и мгновенное угловое ускорение пластины, и ускорение точки 
Решение.
1. Выберем за полюс точку 
2. Составим векторное уравнение для ускорения точки 
где 









Поскольку направление углового ускорения неизвестное, то направлением 
3. Спроектируем составленное уравнение (1) на оси 

В проекции на ось 
В проекции на ось 
4. Из уравнения (2) получим величину нормального ускорения:
Найдем мгновенную угловую скорость фигуры:
5. Из уравнения (3) получим величину тангенциального ускорения:
Угловое ускорение фигуры:
Поскольку величина 
6. Определим ускорение точки 
Для вычисления ускорения точки 


Направление векторов 

Спроектируем записанное уравнение на оси 

где
Полное ускорение точки 
Ответ: 
Задача №2
Равносторонний треугольник 



Определить ускорение вершины 
Решение. Если известны ускорения двух точек плоской фигуры, например 

1. Рассматривая первую точку 


2. Из уравнения проекций определить величину нормального ускорения 

3. Спроектировать векторное уравнение распределения ускорений при плоском движении на прямую, которая перпендикулярна 


4. Если нужно, то, используя формулу распределения ускорений при плоском движении, определить ускорение любой другой точки плоской фигуры.
Решим задачу, придерживаясь приведенной последовательности.
1. Выберем за полюс точку 

где 









Спроектируем записанное равенство (1) на прямую 
2. Откуда:
Поскольку 
3. Спроектируем векторное уравнение на прямую, которая перпендикулярна 
Откуда:
Учитывая то, что 
Поскольку величина тангенциального ускорения 
4. Определим ускорение точки 

где 










Учитывая, что 
От точки 
Выберем систему координат 


Спроектируем равенство (2) на оси выбранной системы координат:
Подставляя числовые данные, получим:
Таким образом, ускорение вершины 
Поскольку проекция ускорения 






Ответ:
Задача № 3
В шарнирном механизме (рис.4.21) в данный момент времени угловая скорость и угловое ускорение кривошипа 




Найти ускорение точки 


Решение. Скорость точки 

Направлена скорость 


Точка 


Поскольку скорости точек 

Ускорение точки 
где
Направления ускорений 

Выберем точку 


или
где 









Свяжем с точкой 


С другой стороны, при движении точки 


где 






По величине нормальное 

Спроектируем уравнение (4) на оси выбранной системы координат:
Подставим в (3) все рассчитанные величины:
Поскольку
то
Положительное значение величины 

Угловое ускорение тела 
Угловое ускорение 

Для определения тангенциального ускорения 

Откуда
Поскольку величина 

Полное ускорение точки 
Ответ:
Задачи, которые рекомендуются для самостоятельной работы: 18.12; 18.14; 18.22 [2].
План скоростей
План скоростей и план ускорений – физическое изображение векторных уравнений, связывающих скорости и ускорения точек механизма. Изображение механизма, выполненное с помощью условных обозначений (см. выше) называется структурной схемой механизма.
Определение скоростей различных точек движущейся плоской фигуры легко может быть выполнено графически с помощью построения плана скоростей.
План скоростей – это графическое изображение из единого центра (полюса) векторов абсолютных скоростей точек фигуры в фиксированный момент ее движения.
План скоростей может быть построен, если:
- известная скорость одной точки плоской фигуры и направление скорости другой точки;
- известная скорость одной точки плоской фигуры и мгновенная угловая скорость фигуры
Пусть известные скорости 













Установим свойства и правила построения плана скоростей.
По уравнению распределения скоростей при плоском движении фигуры, если за полюс принять точку 

где 





С другой стороны для векторов треугольника 
Учитывая, что векторы 





Таким образом, отрезок 

где 
Аналогично:
Отсюда мгновенная скорость вращения плоской фигуры:
Вектор 






Из рассматриваемого вытекает:
Порядок решения задач на тему: План скоростей
1. Изображают на чертеже в выбранном масштабе плоскую фигуру и вектор скорости той точки, скорость которой известна.
2. Определяют направление скорости второй точки плоской фигуры.
3. Записывают векторное уравнение распределения скоростей при плоском движении, принимая за полюс точку, скорость которой известна, а за искомую ту точку, направление скорости которой известно.
4. Решают записанное векторное уравнение графически путем построения в выбранном масштабе плана скоростей.
5. Определяют мгновенную угловую скорость вращения плоской фигуры.
6. Определяют скорость других точек плоской фигуры.
Примеры решения задач на тему: План скоростей
Задача №1
Найти угловую скорость 

Решение.
1. Согласно исходным данным в произвольном масштабе строим схему механизма (рис.4.25, а).
2. Учитывая, что кривошип 1 вращается вокруг неподвижной точки 


Направлена скорость 


3. Следующей точкой шатуна, скорость которого можно определить, является точка 
Для определения скорости точки 

где 





4. Решим уравнение (1) графически (рис.4.25, б). Для этого с произвольной точки 







Вектор который будет на плане скоростей изображать абсолютную скорость точки 




Определим направление отрезка 







Полученный векторный треугольник 








Перенесем из плана скоростей в точку 


Поскольку скорость 








Аналогично, 



Таким образом, и угол при вершине 



5. Определяем мгновенную угловую скорость шатуна 2. Поскольку 
где 

Направление угловой скорости 


Ответ:
Задача №2
Найти угловые скорости шатуна 2 и коромысла 3 и абсолютные скорости точек 



Угловая скорость кривошипа 1 — 
Решение.
1. В соответствии с исходными данными в произвольном масштабе строим схему механизма (рис.4.27, а).
2. Так как точка 


Вектор скорости 

2. Шатун 2 механизма движется плоскопараллельно. Скорость точки 






3. Для определения скорости точки 
где 









4. Решаем записанное уравнение графически. Для этого из произвольной точки 



Через конец вектора 




Скорость точки 




Полученный на рис. 4.27, б векторный треугольник 










Перенесем направления скоростей 


Поскольку 






Таким образом
Угол при вершине 






Тогда угол при вершине 
Для определения сторон 
Из уравнения (1) получим:
Таким образом:
5. Определим мгновенные угловые скорости шатуна 2 и коромысла 3. Поскольку 
Направление угловой скорости 


Угловая скорость коромысла 3 равна:
где
Направление 

6. Определить величины скоростей 

Поскольку вектор 

Скорости 



Тогда:
7. Для определения скорости точки 
Поскольку фигура 

В левой части пропорции (2) отношение отрезков на схеме механизма, а в правой — на плане скоростей.
Из уравнения (2) получим расстояние от точки 

Поскольку на схеме механизма отрезок 









Вектор скорости 



Ответ: 


Задача №3
В состав рычажного механизма (рис.4.29) входят два кривошипа 1 и 4, и два шатуна 2 и 3. Кривошип 1 вращается с угловой скоростью 

Найти угловые скорости шатунов 2 и 3 и абсолютные скорости точек 



Решение. Особенность этой задачи заключается в том, что определить сразу направление скорости точки 





1. В соответствии с исходными данными в произвольном масштабе строим схему механизма (рис.4.30, а).
2. Так как точка 


Вектор скорости 

Шатун 2 механизма движется плоскопараллельно. Скорость точки 

Для определения скорости точки 
где 








В уравнении (1) три неизвестных: величина и направление скорости точки 

для плоскости позволяет определить только две неизвестных, то решить уравнение (1) невозможно.
3. Рассмотрим определение скорости точки 

Скорость точки 
Вектор скорости 

Учитывая, что шатун 3 механизма движется плоскопараллельно, то для определения скорости точки 
где 






В записанной системе векторных уравнений (1,2) четыре неизвестных: величина и направление скорости точки 


4. Решаем записанную систему векторных уравнений (1) и (2) графически. Для этого из произвольной точки 
Согласно уравнению (1) из произвольной точки 





Тогда масштабный коэффициент плана скоростей будет равен:
Через конец вектора 




Теперь построим из того же самого полюса 




Через конец вектора 




Точка пересечения 





Полученный на рис. 4.30,б четырехугольник 






Перенесем направления скоростей 

5. Определим мгновенные угловые скорости шатунов.
Поскольку 
Направление угловой скорости 


Аналогично, угловая скорость шатуна 3 равна:
Направление 

Для определения скорости точки 



Вектор скорости 



Ответ: 
План ускорений
План ускорений – построенный в определенном масштабе векторный график, характеризующие ускорения всех точек и звеньев механизма. Произвольная точка ра, из которой производится построение плана ускорений, называется полюсом плана ускорений.
Рассмотрим графический способ определения ускорений точек плоской фигуры (тела) с помощью плана ускорений.
Планом ускорений плоской фигуры является геометрическое место концов векторов ускорений любых точек фигуры, что отложены из одной произвольной точки, которую называют полюсом плана ускорений.
Построение плана ускорений основано на представлении ускорения 

где 











Поскольку для определения величины 

Для того, чтобы уравнение (4.18) можно было решить, должно быть известно ускорение 

Кроме того, должно быть известно:
Рассмотрим определение ускорений точек 





Для ускорения точки 

Решим уравнение (4.18) графически. Для этого (рис.4.31, б) из произвольной точки 





Величину ускорения 
а направлен этот вектор вдоль 


К нормальному ускорению добавим, согласно уравнению (4.18), тангенциальное ускорение 





Направление абсолютного ускорения 









Для определения ускорения точки 


Запишем векторные уравнения для ускорения точки 


где 









Первым решаем уравнение (4.19). Поскольку ускорение 






Через конец вектора 



Следующим построим уравнение (4.20). Поскольку ускорение 






Через конец вектора 



Таким образом, конец вектора 




Векторы 







Кроме абсолютных и относительных ускорений точек фигуры 



Для определения же направления углового ускорения 



Треугольник 

Таким образом, для плана ускорений справедливо
правило подобия: фигура, которую образуют концы векторов абсолютных ускорений точек тела на плане ускорений подобная фигуре, которую одноименные точки образуют на теле.
Примеры решения задач на тему: План ускорений
Задача №1
Найти ускорение точки 


Решение. План скоростей для этого механизма был построен в задаче № 1 занятия № 7 (рис.4.25,б) и была определена угловая скорость шатуна 2 
1.Построим схему механизма (рис. 4.32, а).
2. Сначала найдем ускорение точки 

Учитывая, что угловая скорость кривошипа постоянная 





По модулю:
Направлено ускорение 



3. Для определения ускорения точки 

где 













Поскольку направление ускорения точки 

4. Решим уравнение (1) графически путем построения плана ускорений.
Из произвольной точки 

















Поскольку ускорение 








4. Из построенного плана ускорений определим абсолютные величины ускорений 







Из векторного четырехугольника 
Спроектируем векторное уравнение (2) на прямую 
Учитывая, что 


Откуда:
Теперь спроектируем уравнение (2) на прямую 
Учитывая, что 

Откуда:
Поскольку 
Из полученного результата следует, что в данный момент времени шатун механизма вращается равномерно 
Ответ:
Если построение плана ускорений выполнять с соблюдением масштаба, то ускорения характерных точек можно определить непосредственно измерением соответствующих отрезков на плане ускорений.
Задача №2
Найти абсолютное ускорение точек 




Решение. План скоростей механизма для положения, что рассматривается, был построен в задаче № 2 занятие № 7 (рис.4.27, б) и определены мгновенные угловые скорости шатуна 2 и коромысла 3:
Решим задачу путем построения в масштабе плана ускорений.
1. Сначала в произвольном масштабе строим схему механизма (рис.4.34, а).
2.Определим ускорение точки 
Поскольку кривошип 1 вращается вокруг неподвижной точки 





По модулю 
Направлено ускорение 


3.Запишем векторные уравнения для определения ускорения точки 
Точка 







где 



















4.Решим графически систему векторных уравнений (1,2).
Сначала построим уравнение (1). Для этого из произвольной точки 







От конца вектора 






Через конец вектора 




Следующим построим уравнение (2).
Поскольку 


От точки 






Через конец вектора 


Решением системы (1,2) будет точка 




Вектор абсолютного ускорения 



Величины тангенциальных ускорений 

Поскольку 



где 
Для определения направления углового ускорения 




Аналогично, для определения направления 



5.Для определения ускорения точки 



В левой части пропорции (3) отношение отрезков на схеме механизма, а в правой — на плане ускорений.
Из уравнения (3) получим расстояние от точки 

Поскольку на схеме механизма отрезок 









Вектор абсолютного ускорения 



Ответ: 
Задача №3
В состав рычажного механизма (рис.4.35) входят два кривошипа 1 и 4, и два шатуна 2 и 3. Кривошип 1 в настоящий момент времени вращается равномерно с угловой скоростью 

Найти угловые ускорения шатунов 2 и 3 и абсолютные ускорения точек 



Решение. План скоростей механизма для положения, что рассматривается, был построен в задаче №3 занятия №7 (рис.4.30, б) и определены мгновенные угловые скорости шатуна 2 и шатуна 3:
1. В произвольном масштабе построим схему механизма (рис. 4.36, а).
2.Сначала определим абсолютные ускорения точек 

Поскольку кривошип 1 вращается вокруг неподвижной точки 


Направлено ускорение 



Кривошип 4 вращается вокруг неподвижной точки 


Абсолютное ускорение точки 
Нормальная составляющая ускорения точки 



а тангенциальная — перпендикулярно 

3. Запишем векторные уравнения для определения ускорения точки 
Точка 





В уравнении (2):






В уравнении (3):






4. Решим графически систему векторных уравнений (2,3).
Сначала построим уравнение (2). Для этого из произвольной точки 







От конца вектора 






Через конец вектора 




Следующим построим уравнение (3).
Для построения вектора 






Длины векторов 

Абсолютное ускорение 


От точки 






Через конец вектора 


Решением системы (2,3) будет точка 




Вектор абсолютного ускорения 



Величины тангенциальных ускорений 

Поскольку 



Направления угловых ускорений 






5. Для определения ускорения точки 







Ответ: 
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки



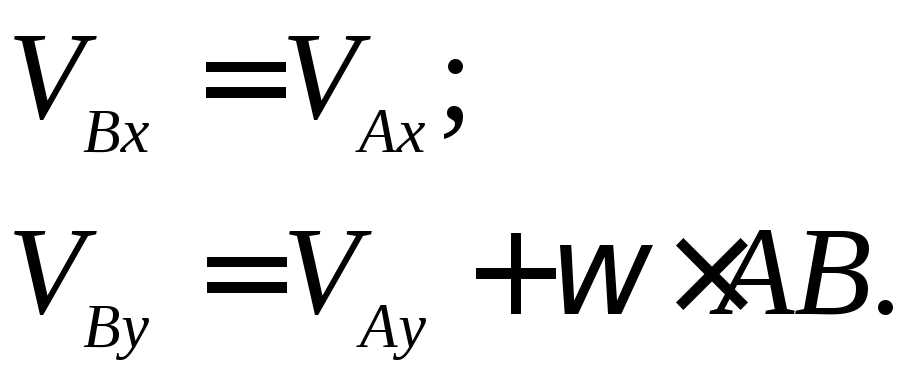

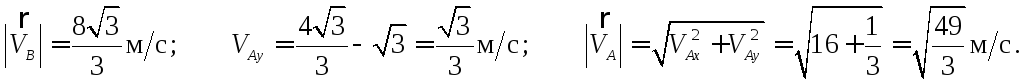




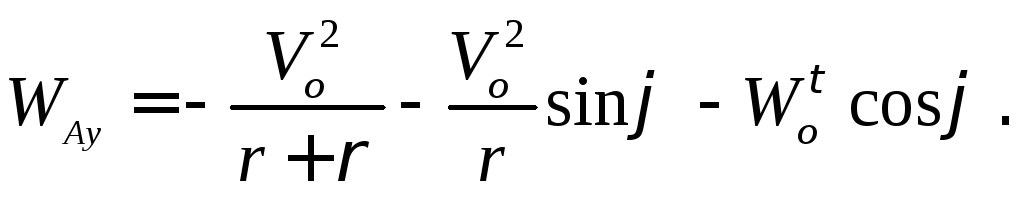
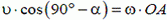
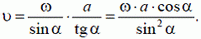
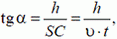
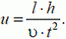
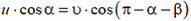
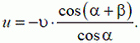
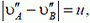
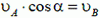
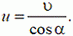
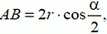
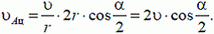
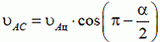
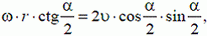
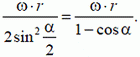
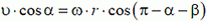
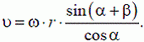
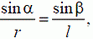
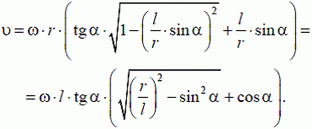
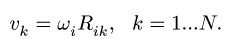
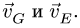
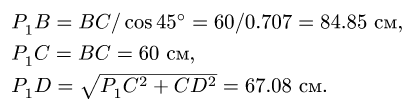
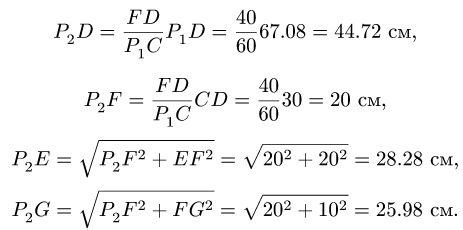
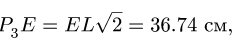
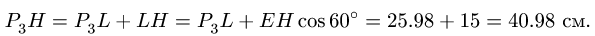
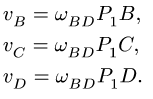
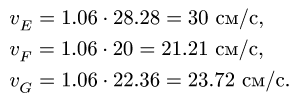
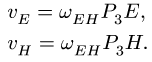

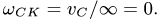
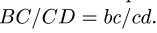
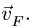
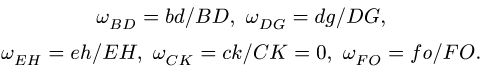
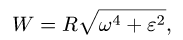
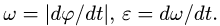
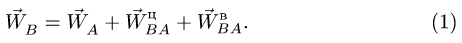
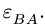

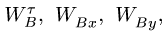
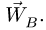
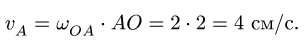
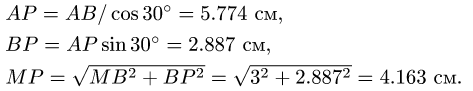
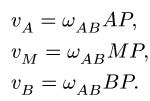

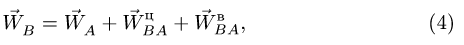
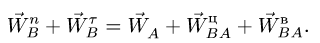
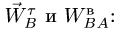
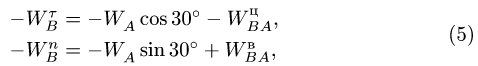
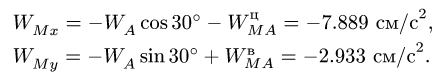
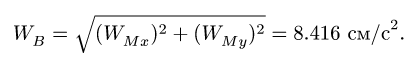
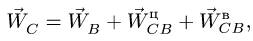
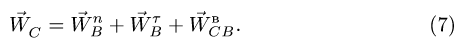
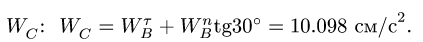
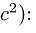

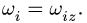
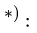
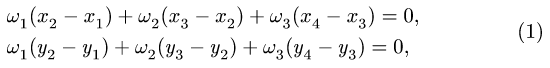
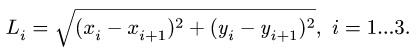
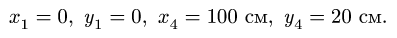
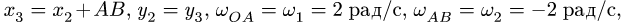

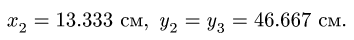
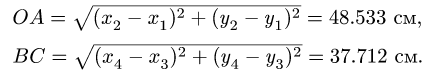
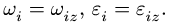
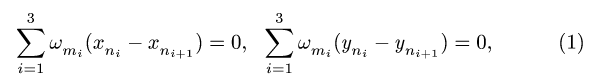
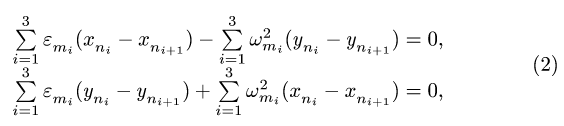
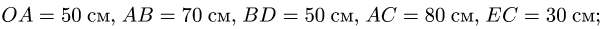
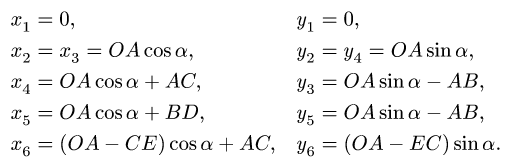
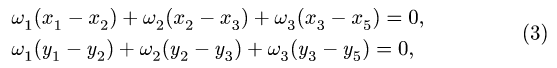
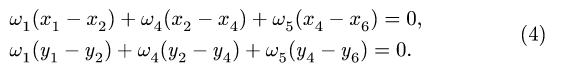
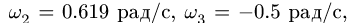
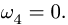
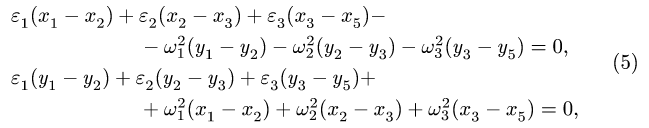
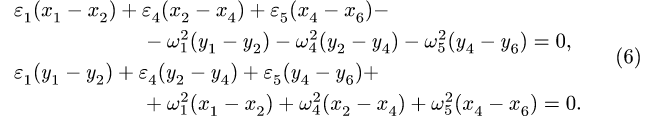
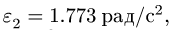
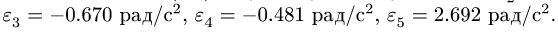
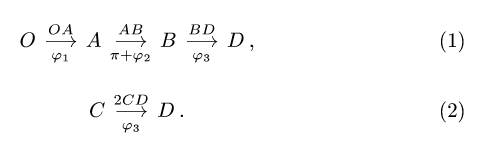
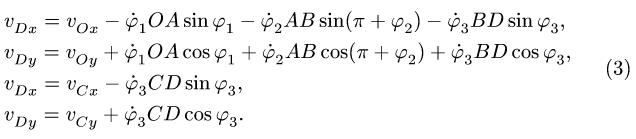
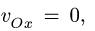
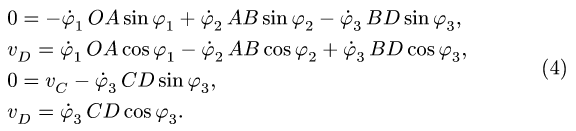
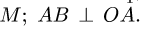
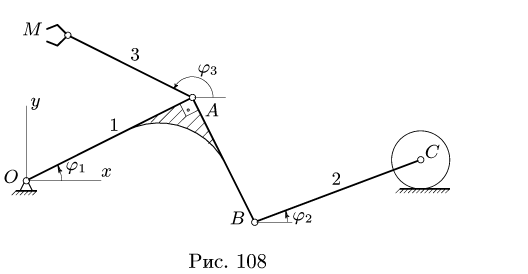
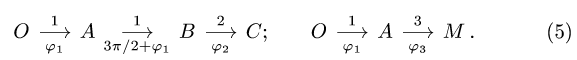
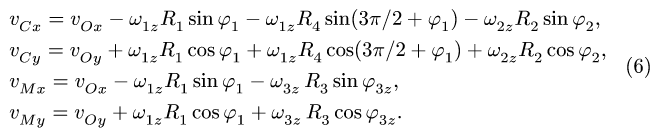
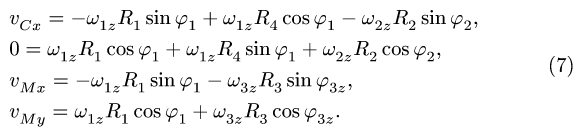
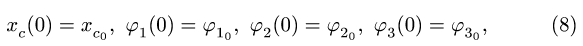
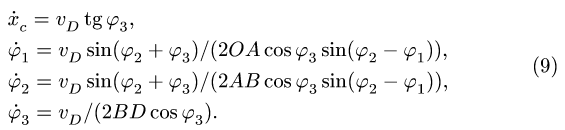
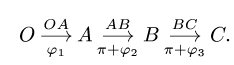
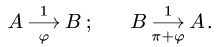
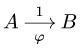 , не обязательно равна
, не обязательно равна 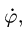 см., например, с. 243.
см., например, с. 243.














































































































































































































































