Решение.
Для решения задачи используем закон сохранения энергии. Потенциальная энергия переходит в кинетическую энергию. Кинетическая энергия состоит из энергии поступательного движения и энергии вращательного движения.
[ mcdot gcdot h=frac{mcdot {{upsilon }^{2}}}{2}+frac{Jcdot {{omega }^{2}}}{2} (1). ]
m – масса сплошного цилиндра, h – высота с которой спускается тело (см. рис.), υ – линейная скорость тела в конце спуска, J – момент инерции сплошного цилиндра, ω – угловая скорость вращения тела.
В конце спуска угловая скорость связана с линейной скоростью:
[ omega =frac{upsilon }{R} (2). ]
Определим скорость центра масс поступательного движения сплошного цилиндра. Момент инерции сплошного цилиндра определяется как момент инерции диска по формуле:
[ J=frac{mcdot {{R}^{2}}}{2} (3). ]
Подставим (3) и (2) в (1):
[ begin{align}
& mcdot gcdot h=frac{mcdot {{upsilon }^{2}}}{2}+frac{mcdot {{R}^{2}}cdot {{upsilon }^{2}}}{4cdot {{R}^{2}}}, gcdot h=frac{mcdot {{upsilon }^{2}}}{2}+frac{mcdot {{upsilon }^{2}}}{4}, gcdot h=frac{3cdot mcdot {{upsilon }^{2}}}{4}, \
& {{upsilon }^{2}}=frac{4cdot gcdot h}{3}, upsilon =sqrt{frac{4cdot gcdot h}{3}} (4). \
end{align} ]
υ = 1,63 м/с.
2021-02-12
На шероховатой доске на расстоянии $l$ от ее конца находится сплошной цилиндр (рис.). Доску начинают двигать с ускорением $vec{a}_{0}$ влево. С какой скоростью относительно доски будет двигаться центр масс цилиндра в тот момент, когда он будет находиться над краем доски? Движение цилиндра относительно доски происходит без скольжения.
Решение:
Введем неинерциальную систему координат OXY, связанную с доской. В неинерциальной системе координат OXY к цилиндру необходимо приложить силу инерции $m vec{a}_{0}$, $m$ — масса цилиндра.
Рассчитаем работу силы инерции на перемещении $l$: $A_{ин} = ma_{0}l$
По закону сохранения энергии для цилиндра:
$E_{кин} = A_{ин}$
$E_{кин} = ma_{0}l$. (1)
$E_{кин}$ — кинетическая энергия цилиндра в момент, когда он находится под краем доски
$E_{кин} = E_{пост} + E_{вр} = frac{mv^{2} }{2} + frac{I omega^{2} }{2}$ (2)
$v$ — скорость центра масс цилиндра в системе координат, т.е. скорость центра масс цилиндра относительно доски.
$omega = frac{v}{R}$ — угловая скорость вращения цилиндра
$I = frac{mR^{2} }{2}$ — момент инерции цилиндра.
Из (1) и (2) получаем:
$frac{mv^{2} }{2} + frac{1}{2} frac{mR^{2} }{2} frac{v^{2} }{R^{2} } = ma_{0}l$
$frac{mv^{2} }{2} + frac{mv^{2} }{4} = ma_{0};$
$frac{3}{4}v^{2} = a_{0}l; v^{2} = frac{4a_{0} l}{3}; v = 2 sqrt{ frac{a_{0}l }{3} }$.
Определение центра масс, теория и онлайн калькуляторы
Определение центра масс
При исследовании поведения систем частиц, часто удобно использовать для описания движения такую точку, которая характеризует положение и движение рассматриваемой системы как единого целого. Такой точкой служит центр масс.
Для однородных тел обладающих симметрией центр масс часто совпадает с геометрическим центром тела. В однородном изотропном теле одной выделенной точке найдется симметричная ей точка.
Радиус-вектор и координаты центра масс
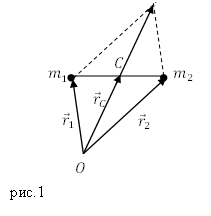
Предположим, что у нас имеются две частицы с равными массами, им соответствуют радиус-векторы: ${overline{r}}_1 и {overline{r}}_2$ . В этом случае центр масс расположен посередине между частицами. Центр масс (точка C) определён радиус-вектором ${overline{r}}_C$ (рис.1).
Из рис.1 видно, что:
[{overline{r}}_C=frac{{overline{r}}_1+ {overline{r}}_2}{2}left(1right).]
Можно ожидать, что вместе с геометрическим центром системы радиус-вектор, которого равен ${overline{r}}_C,$ играет роль точка, положение которой определяет распределение массы. Ее определяют так, чтобы вклад каждой частицы был пропорционален ее массе:
[{overline{r}}_C=frac{{overline{r}}_1m_1+ {overline{r}}_2m_2}{m_1+m_2}left(2right).]
Радиус -вектор ${overline{r}}_C$, определенный выражением (2) — средне взвешенная величина радиус-векторов частиц ${overline{r}}_1$ и ${overline{r}}_2$. Это становится очевидным, если формулу (2) представить в виде:
[{overline{r}}_C=frac{m_1}{m_1+m_2}{overline{r}}_1+frac{m_2}{m_1+m_2}{overline{r}}_2left(3right).]
Выражение (3) показывает, что радиус-вектор каждой частицы входит в ${overline{r}}_C$ с весом, который пропорционален его массе.
Выражение (3) легко обобщается для множества материальных точек, которые расположены произвольным образом.
Если положения N материальных точек системы задано при помощи их радиус-векторов, то радиус — вектор, определяющий положение центра масс находим как:
[{overline{r}}_c=frac{sumlimits^N_{i=1}{m_i{overline{r}}_i}}{sumlimits^N_{i=1}{m_i}}left(4right).]
Выражение (4) считают определением центра масс системы.
При этом абсцисса центра масс равна:
[x_c=frac{sumlimits^N_{i=1}{m_ix_i}}{sumlimits^N_{i=1}{m_i}}left(5right).]
Ордината ($y_c$) центра масс и его аппликата ($z_c$):
[y_c=frac{sumlimits^N_{i=1}{m_iy_i}}{sumlimits^N_{i=1}{m_i}}left(6right).]
[z_c=frac{sumlimits^N_{i=1}{m_iz_i}}{sumlimits^N_{i=1}{m_i}}left(7right).]
Формулы (4-7) совпадают с формулами, которые используют для определения тяжести тела. В том случае, если размеры тела малы в сравнении с расстоянием до центра Земли, центр тяжести считают совпадающим с центром масс тела. В большинстве задач центр тяжести совпадает с центром масс тела.
Скорость центра масс
Выражение для скорости центра масс (${overline{v}}_c=frac{d{overline{r}}_c}{dt}$) запишем как:
[{overline{v}}_c=frac{m_1{overline{v}}_1+m_2{overline{v}}_2+dots +m_n{overline{v}}_n}{m_1+m_2+dots +m_n}=frac{overline{P}}{M}left(8right),]
где $overline{P}$ — суммарный импульс системы частиц; $M$ масса системы. Выражение (8) справедливо при движениях со скоростями которые существенно меньше скорости света.
Если система частиц является замкнутой, то сумма импульсов ее частей не изменяется. Следовательно, скорость центра масс при этом величина постоянная. Говорят, что центр масс замкнутой системы перемещается по инерции, то есть прямолинейно и равномерно, и это движение не зависимо от движения составных частей системы. В замкнутой системе могут действовать внутренние силы, в результате их действия части системы могут иметь ускорения. Но это не оказывает влияния на движение центра масс. Под действием внутренних сил скорость центра масс не изменяется.
Примеры задач на определение центра масс
Пример 2
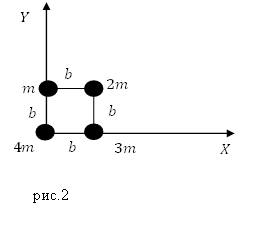
Задание. Система составлена из материальных точек (рис.2), запишите координаты ее центра масс?
Решение. Рассмотрим рис.2. Центр масс системы лежит на плоскости, значит, у него две координаты ($x_c,y_c$). Найдем их используя формулы:
[left{ begin{array}{c}
x_c=frac{sumlimits_i{Delta m_ix_i}}{m};; \
y_с=frac{sumlimits_i{Delta m_iy_i}}{m}. end{array}
right.]
Вычислим массу рассматриваемой системы точек:
[m=m+2m+3m+4m=10 m.]
Тогда абсцисса центра масс $x_{c } $равна:
[x_c=frac{0cdot 4m+3mcdot b+2mcdot b}{10m}=0,5 b.]
Ордината $y_с$:
[y_с=frac{0cdot m+mcdot b+2mcdot b}{10m}=0,3 b.]
Ответ. $x_c=0,5 b$; $y_с=0,3 b$
Пример 2
Задание. Космонавт, имеющий массу $m$, неподвижен относительно корабля массы $M$. Двигатель космического аппарата выключен. Человек начинает подтягиваться к кораблю при помощи легкого троса. Какое расстояние пройдет космонавт ($s_1$), какое корабль ($s_2$) до точки встречи? В начальный момент расстояние между ними равно $s$.
Решение. Центр масс корабля и космонавта лежит на прямой, соединяющей эти объекты.
В космосе, где внешние силы отсутствуют, центр масс замкнутой системы (корабль-космонавт) либо покоится, либо движется с постоянной скоростью. В избранной нами (инерциальной) системе отсчета он покоится. При этом:
[frac{s_1}{s_2}=frac{m_2}{m_1}left(2.1right).]
По условию:
[s=s_1+s_2left(2.2right).]
Из уравнений (2.1) и (2.2) получаем:
[s_1=sfrac{m_2}{m_1+m_2};; s_2=sfrac{m_1}{m_1+m_2}.]
Ответ. $s_1=sfrac{m_2}{m_1+m_2};; s_2=sfrac{m_1}{m_1+m_2}$
Читать дальше: период и частота колебаний.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,662 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,978 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Содержание:
- Динамика плоского движения твердого тела
- Дифференциальные уравнения плоского движения твердого тела
- Порядок решения задач динамики плоского движения твердого тела
- Примеры решения задач на тему: динамика плоского движения твердого тела
Плоское движение твердого тела определяют как движение, при котором скорости всех точек тела параллельны некоторой плоскости. Если с любой точкой тела (или его мысленного продолжения) связать поступательно движущуюся систему координат, то относительное движение будет чистым вращением вокруг неподвижной оси, перпендикулярной плоскости движения.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Динамика плоского движения твердого тела
Плоским движением твердого тела называется такое его движение, при котором каждая точка тела движется в плоскости, параллельной некоторой неподвижной плоскости.
Момент количества движения тела (главный момент количества движения твердого тела), вращающегося вокруг неподвижной оси, относительно этой оси равен произведению момента инерции тела относительно той же оси на угловую скорость вращения.
Дифференциальные уравнения плоского движения твердого тела
Из кинематики известно, что для определения положения твердого тела, которое совершает плоское движение, достаточно задать положение любой ее точки, которая принимается за полюс, и угол поворота вокруг мгновенной оси вращения, проходящей через полюс перпендикулярно плоскости движения.
Задачи динамики будут решаться проще всего, если за полюс выбрать центр масс 



Таким образом, для изучения плоского движения твердого тела достаточно составить три дифференциальных уравнения, которые связывают величины 


Для определения движения центра масс используется теорема о движении центра масс системы:
где 


Уравнение, определяющее вращательное движение тела, получается из теоремы об изменении момента количества движения относительно оси, которая проходит через точку 
где 

Проектируя уравнение (11.1) на неподвижные оси координат 



или
С помощью этих уравнений можно решать как прямую, так и обратную задачи динамики.
При несвободном движении, когда траектория центра масс известна, уравнение движения точки 



Порядок решения задач динамики плоского движения твердого тела
Выбрать неподвижную систему координат, относительно которой рассматривается движение тела.
Изобразить твердое тело в текущем положении и показать все внешние силы, которые приложены к нему.
Составить дифференциальные уравнения плоского движения твердого тела в форме уравнений (11.4).
Если известна траектория центра масс твердого тела, то удобнее применить уравнение (11.5).
В случае решения прямой задачи искомые внешние силы и их моменты определяются из систем дифференциальных уравнений (11.4) и (11.5).
В случае решения обратной задачи путем интегрирования систем (11.4) или (11,5) определяют кинематические уравнения движения центра масс твердого тела.
Примеры решения задач на тему: динамика плоского движения твердого тела
Задача №1
Однородный прямой круглый цилиндр радиусом 


Определить движение цилиндра (рис. 11.2) и давление его на наклонную поверхность.
Решение. Изобразим цилиндр в среднем положении на наклонной плоскости и покажем внешние силы, которые действуют на него: 

Дифференциальные уравнения плоского движения круглого цилиндра в данном случае имеют вид:
где 

Поскольку во время движения 
Из третьего уравнения системы находим:
Поскольку

Поскольку в начальный момент времени 

Решая первое уравнение, находим закон изменения координаты 
Разделим переменные и проинтегрируем:
Отсюда
Окончательно,
Следовательно, цилиндр совершает поступательное движение.
Ответ:
Задача № 2
Однородный круглый цилиндр с радиусом 



Определить уравнение движения цилиндра и его давление на наклонную поверхность.
Решение. К цилиндру приложены внешние силы: 


Дифференциальные уравнения движения цилиндра в этом случае запишутся в виде:
Поскольку во время движения 

Уравнения (1) и (3) имеют три неизвестных: 


Найдем еще одно дополнительное уравнение. Поскольку точка 
Тогда, с учетом уравнения (4), а также значения 
Окончательно
Поскольку левые части этих уравнений одинаковы, тогда равны и их правые части. Поэтому

По закону Кулона

Итак,
откуда
Это и есть условие качения цилиндра по шероховатой поверхности без проскальзывания.
Определим ускорение центра масс цилиндра при таком качении. Для этого в уравнение (1)
подставим значение силы трения
Поскольку 
Проинтегрируем это выражение:
Поскольку 
Определим закон вращения цилиндра вокруг оси. Для этого воспользуемся уравнением (3):
Поскольку
то

откуда
Разделим переменные и проинтегрируем:
Закон изменения угловой скорости имеет вид:
Определим закон изменения угла вращения:

и тогда
Видно, что закон вращения цилиндра вокруг его оси не зависит от движения центра масс.
Ответ:
Задача № 3
Тяжелый круглый цилиндр 



Определить скорость оси цилиндра 


Решение. К цилиндру 


За начало координат примем положение центра масс цилиндра 


Дифференциальные уравнения плоского движения в данном случае имеют вид:
Угол поворота цилиндра отсчитываем по направлению по часовой стрелке.
Поскольку
то из уравнения (2) имеем:

Следовательно, скорость центра масс будет иметь только одну составляющую — 

Уравнение (1) запишем в виде:
В этом уравнении две неизвестных величины — 

или
где 
Между угловой скоростью 


Подставим значение 
Левые части уравнений (4) и (6) равны, следовательно, равны и правые части:
Откуда:
Откуда получим:
Подставим в уравнение (4) значение 
Поскольку необходимо определить скорость центра масс 


Разделим переменные и проинтегрируем:
и
Окончательно,
Ответ:
Задача № 4
Однородный стержень 






Определить, как изменится давление стержня на шарнир 

Решение. Сначала определим реакции в шарнире 












Составим уравнение равновесия плоской системы сил, приложенной к стержню 
Из уравнения (3) находим натяжение нити 
Подставляя значения 


Если нить оборвется, то стержень начнет совершать вращательное движение вокруг шарнира 
Дифференциальные уравнения такого движения, учитывая, что точка 
где 







С рис.11.5 вытекает:
Продифференцируем эти выражения дважды, учитывая, что угол 

Поскольку в момент разрыва нити 
Подставив найденные значения 

Для определения неизвестного значения 
откуда
Момент инерции однородного стержня относительно оси, которая проходит через его конец:
Тогда
Подставив значение 
Следовательно, изменение реакций после обрыва нити будет равно:
Ответ:
Задача № 5
Тяжелое тело состоит из стержня 







Определить следующее движение тела, принимая во внимание только действие сил тяжести.
Решение. Сначала определим положение центра масс тела. Для этого с точкой 

Как видно из рисунка, вследствие симметрии тела относительно оси 


Для рассматриваемого случая эта формула принимает вид:
где 





С учетом приведенных соотношений формула (1) примет вид:
или
Таким образом, центр масс тела находится в точке с координатами 


Для определения движения тела, изобразим его в промежуточном положении на траектории (рис.11.6, б) и покажем действующие на тело силы: 

Принимаем за полюс центр масс 

Дифференциальные уравнения плоского движения (11.4) в данном случае примут вид
Из уравнения (2) вытекает:
Итак, проекция скорости центра масс на ось 
Определим величину 






или
Таким образом,
Определим закон движения центра масс по направлению оси 
Поскольку при 
Таким образом,
Центр масс в направлении оси 
Из дифференциального уравнения (3) определим закон движения центра масс тела по направлению оси 
Запишем уравнение (3) в виде:
Поскольку 
Разделяя переменные и интегрируя, находим зависимость скорости центра масс тела по направлению оси 
Постоянную интегрирования 

Таким образом,
то есть по направлению оси в центр масс движется равноускорено.
Находим закон движения центра масс:
Разделим переменные и проинтегрируем:
Постоянную интегрирования 

Следовательно, закон движения центра имеет тела по направлению оси 
Решая вместе зависимости (5) и (6), находим уравнение траектории центра масс.
Из выражения (5) вытекает, что
Подставив значение 
Таким образом, центр масс тела (точка 
Определим закон вращательного движения тела вокруг оси, которая проходит через центр масс тела. Для этого уравнения (4) запишем в виде (рис.11.6, б):
где 





С рис. 11.6,б найдем:
Подставляя в выражение (7) значения 

откуда, при 

Таким образом, при движении в плоскости 

По условиям задачи, при 



откуда
Ответ:
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки