Как найти скорость центра катящегося колеса - Autoru.top

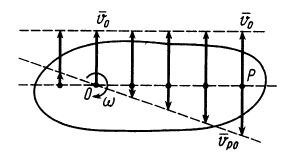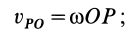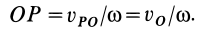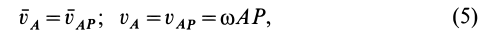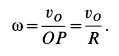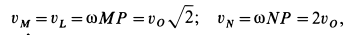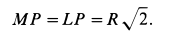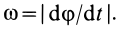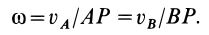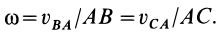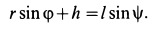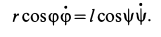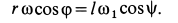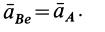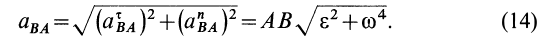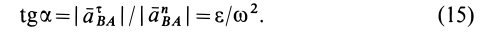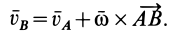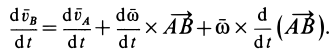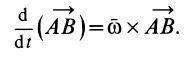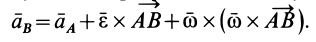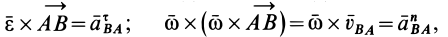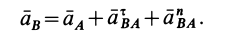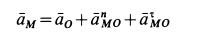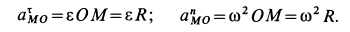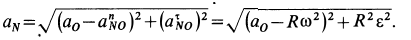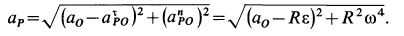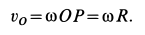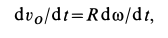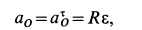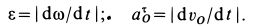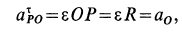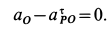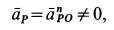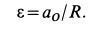
Рис.12

Способы нахождения мгновенного центра скоростей

Для определения положения мгновенного центра скоростей плоской фигуры необходимо знать только направления скоростей двух ее точек.

Указанные свойства позволяют определить положение мгновенного центра скоростей плоской фигуры в различных случаях.

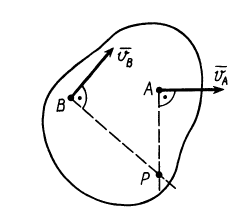
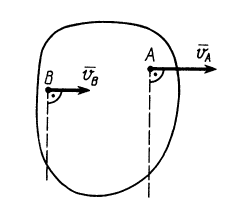
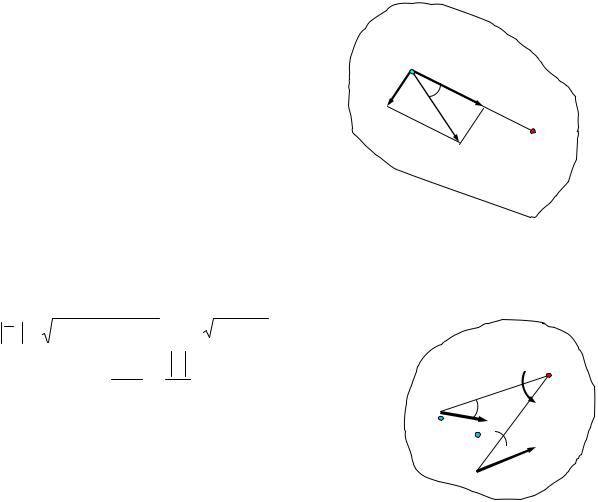
	VA		1. Если скорости двух точек не параллельны,
А	В	VB	то мгновенный центр скоростей лежит в точке
900	пересечения перпендикуляров к ним, что следует из
	900
			теоремы о существовании мгновенного центра ско-

Рростей (рис.12).

2. Если плоское движение осуществляется

качением без скольжения одного твердого тела по неподвижной поверхности другого, то точка их контакта Р имеет в данный момент скорость, равную нулю, и, следовательно, будет мгновен-

ным центром скоростей (рис.13).

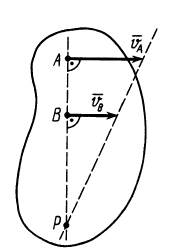
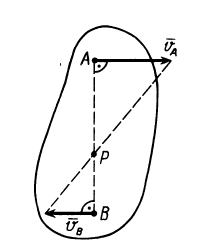
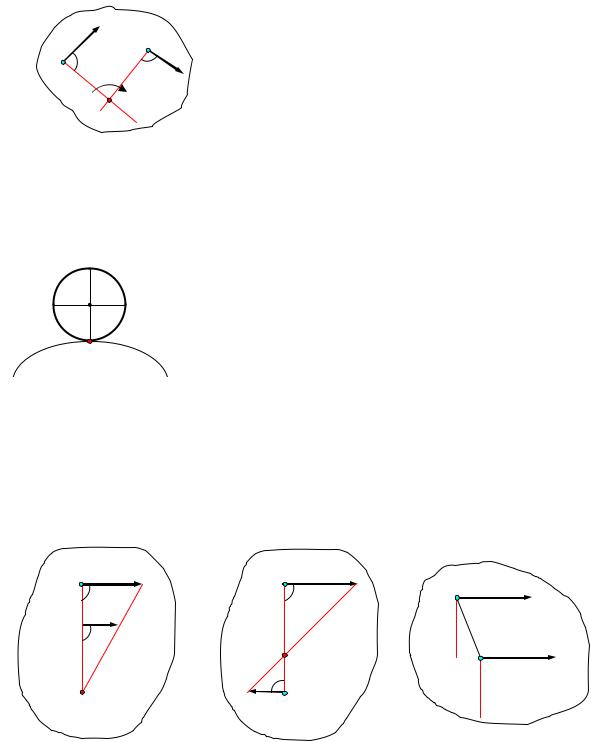
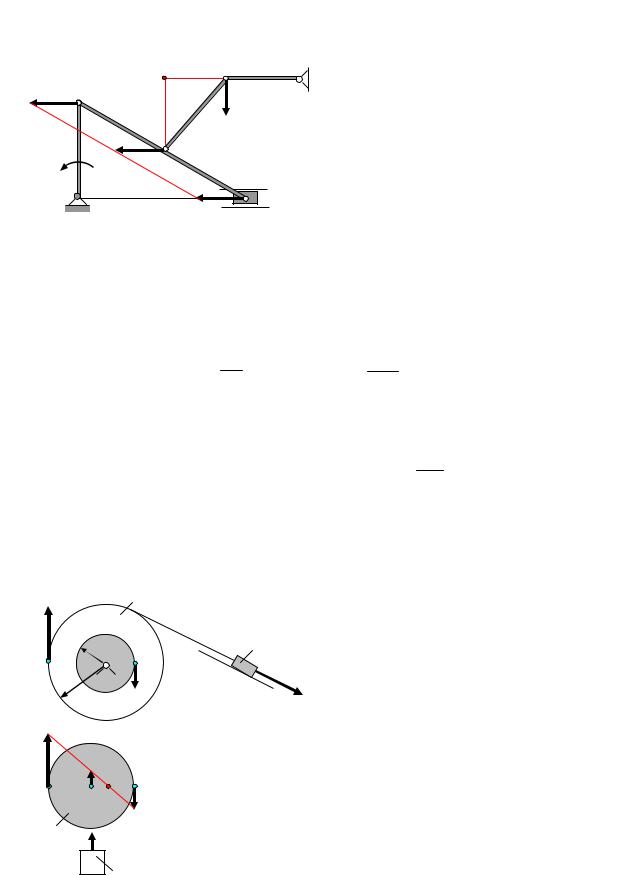
3. Если скорости двух точек А и В плоской фигуры параллельны и с прямой, соединяющей эти точки, составляют прямые углы, то мгновенный центр скоростей Р находится как точка пересечения об-

Рщего перпендикуляра, восстановленного к скоро-

Рис.13	стям в данных точках, и прямой, проходящей через
концы векторов скоростей (рис.14 и рис.15).

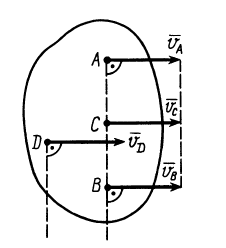
4. Если скорости двух точек параллельны и с прямой, соединяющей точки образуют острые углы, то мгновенный центр скоростей не суще-

ствует (находится в бесконечности). В этом случае скорости всех точек плоской фигуры равны, а угловая скорость равна нулю (рис. 16).

А	VA	А		VA	А	VA
90	0	90	0

В 90V0B

Р VB

Р	900
В
	VB
Рис. 14	Рис. 15	Рис. 16

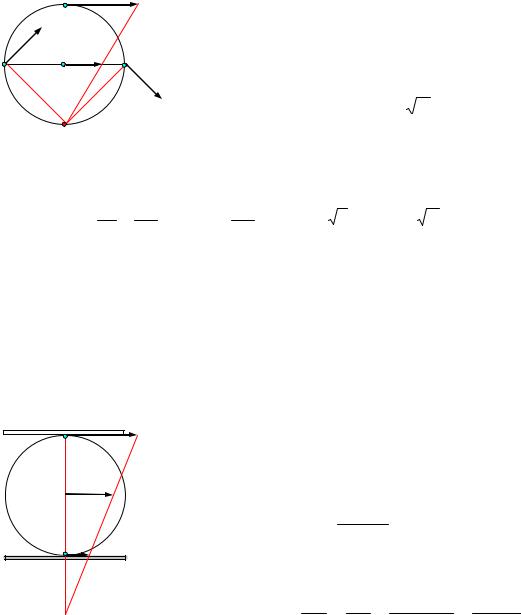
Решение задач с помощью мгновенного центра скоростей.

Задача 1. Найти скорости точек А, В и D обода колеса, катящегося по прямолинейному рельсу без скольжения, если скорость центра колеса С равна VC.

Определить скорости точек А, В, D и угловую скорость колеса.

Решение. Мгновенный центр скоростей

Р колеса находится (рис.177) в

точке контакта колеса с неподвижной плоскостью. Скорости точек А, В, D

перпендикулярны к отрезкам, соединяющим эти

точки с точкой Р, модули скоростей пропорцио-

нальны их длинам:

Расстояния точек А и В до мгновенного цен-

тра скоростей одинаковы,

следовательно, скоро-

сти этих точек равны

VA =VB =VC

Скорость точки D равна 2VC , так как рас-

стояние точки D

до мгновенного центра скоро-

Рис.17

VA =

стей в два раза больше расстояния СР .

; V

=V AP ;

AP = R 2, V

=V 2.

C CP

Угловая скорость колеса равна

ω =

Задача.2. Диск зажат между двумя рейками, (рис.18) которые движутся со скоростями V1 и V2 (V1 > V2).

Определить угловую скорость диска и скорость его центра, если его радиус равен R.

АVAa

С VC с

ВVB

Рис.18

Решение. Скорость точки А диска равна скорости верхней рейки, а скорость точки В – скорости нижней рейки. Мгновенный центр скоростей находится в точке Р (рис.16). Скорость точки С является средней линией трапеции ВАав:

VC = V1 +2V2 .

Угловая скорость

ω = VAPA = VBPB = APVA −−VBPB = V12−RV2 .

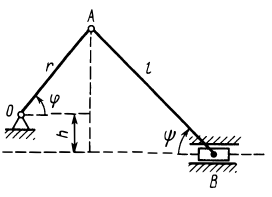
Задача 3. Кривошипно-шатунный механизм

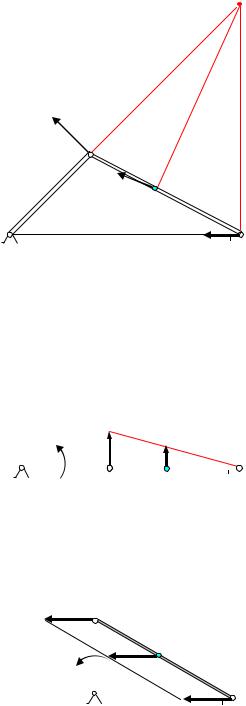
Угловая скорость кривошипа равна ωОА. Определить угловую скорость шатуна и скорости точек А,В, и С для трех положений механизма.

Кривошип ОА вращается вокруг точки О, шатун АВ совершает плоское движение в плоскости чертежа. Во всех случаях скорость точки А перпендикулярна кривошипу и равна VA =ωOA OA. , а скорость точки В направлена по

горизонтальной прямой.

1. Кривошип ОА образует острый угол с горизонтальной прямой

(рис.19). В этом случае мгновенный

центр скоростей шатуна находится в

точке Р, где пересекаются восстановлен-

ные в точках А и В перпендикуляры к

скоростям в этих точках.

= BP

VB =VA AP .

Скорость точки С направлена перпенди-

кулярно отрезку РС и находится из про-

порции:

CP .

Угловая скорость шатуна равна

Pис.19

ωAB =

2. Кривошип и шатун расположены на одной прямой (рис.20).

В этом положении мгновенный центр скоростей находится в точке В,

поэтому скорость VB

равна нулю. Ско-

рость точки С находится из пропорции:

V =V

Угловая скорость шатуна равна

Рис.20

ωAB =

VA A

Кривошип

занимает

вертикальное положение (рис.21). В

этом случае мгновенный центр скоростей

шатуна находится в бесконечности, скоро-

VВ

сти всех его точек равны, угловая скорость

шатуна равна нулю.

Рис. 21

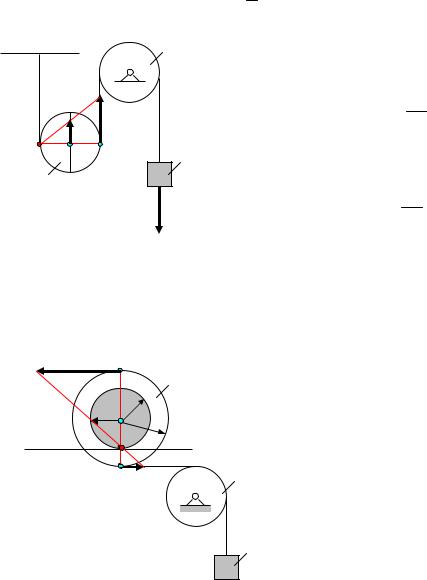
Задача 4. Определить скорости точек А, В, Р подвижного блока 3 (рис.22) и его угловую скорость, если скорость тела 1 равна V1

Решение. Подвижный блок совершает плоское движение. Скорость точки контакта Р подвижного блока с неподвижной нитью равна нулю: VР = 0, т.е. точка Р – мгновенный центр скоростей подвижного блока.

Скорость точки С перпендикулярна отрезку, соединяющему ее с мгновенный центром скоростей: VC CP .

			2
		О
	VС	VА

Р С	А	1

3	B

	Рис.22	V1

Скорости точек при плоском движении пропорциональны расстояниям до мгновенного центра скоростей

VC = CP .

VA AP

VA = V1, так как точка А и тело 1 связаны нерастяжимой нитью, тогда

VC = 0,5R .

V1 R

Следовательно, VC = 0,5 VA = 0,5 V1.

Задача 5. Определить угловую скорость и скорости точек А, В, С и Р катушки 3 (рис.23), если скорость груза 1 равна V1.

VA	A	3

VC	С	R
r
	P	B VB	2

		O

Рис.23

Решение. Скорость точки В катушки равна скорость груза 1, так как они связаны нерастяжимой нитью: VВ = V1.

При качении без скольжения в точке контакта катушки с рельсом находится мгновенный центр скоростей Р. Скорости точек А и С перпендикулярны отрезкам, соединяющим эти точки с мгновенным центром скоростей и пропорциональны их расстояниям до мгновенного центра скоростей, поэтому

	VC	=	CP	;	VC	=	r	.
V	BP	V	R −r

	B				B

Отсюда			VC	= VB	r	= V1	r
		R − r	R

Аналогично определим скорость точки А.
VA =	AP	;	VA =	r +R	.
BP
V		V		R −r
B			B

Следовательно,

V		=V	r +R	=V	r +R	.
	B R −r
	A		B R −r

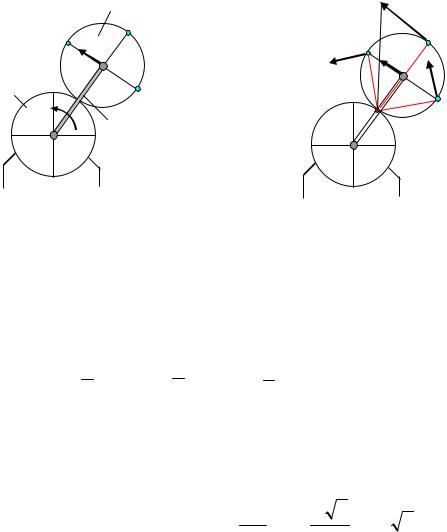
Задача 6. Определить угловую скорость и скорости точек А, В, D, E шестерни 3 (рис.24), которую приводит в движение кривошип ОА, вращающийся вокруг оси О неподвижной шестерни 1 с угловой скоростью ωОА.

	3			VD
	D
В VA		В		D
А	VВ	VA
		VE
1	Е
		А	Е
ωАВ			P
2

Решение. Скорость точки А, принадлежащей кривошипу ОА, перпендикулярна кривошипу и равна VA = ωAB AB.

Шестерня 3 совершает плоское движение, ее мгновенный центр скоростей находится в точке зацепления Р с неподвижной шестерней 1 (рис. 24а). Скорости точек В, Е и D перпендикулярны отрезкам, соединяющим их с мгновенным центром скоростей.

VB BP , VD DP , VE EP .

Скорости точек пропорциональны отрезкам, соединяющим эти точки с мгновенным центром скоростей Р.

VB =VE , так как расстояния этих точек до мгновенного центра скоростей равны: ВР = ЕР.

		VA	= AP ; откуда VB =VA BP	=VA	R	2	=VA 2.
	V		R
	BP	AP
			B
Аналогично определяем скорость точки D.
	VA	=	AP ;	откуда VD =VA DP =VA 2R	= 2VA.

V	DP	AP	R
	D

Задача 7. Определить скорости точек А, В, С, D и угловые скорости звеньев механизма, изображенного на рис. 25, если угловая скорость криво-

шипа ОА равна ωОА.

Решение. Во всех вариантах скорость точки А, являющейся концом кривошипа ОА, равна VA = ωОА OA и перпендикулярна кривошипу.

Звенья ОА и ОВ механизма (рис.25) совершают вращательное движение. Скорость точки А, являющейся концом кривошипа ОА, равна VA = ωОА OA и перпендикулярна кривошипу.

Скорость VB OB .Звенья АС и ВD совершают плоское движение. Звено

Р2

СD движется

поступательно, по-

этому скорости точек C и D равны:

VC = VD .

Мгновенный

центр

скоростей

звена АС лежит в точке Р1 пересе-

ωOA O

чения перпендикуляров к скоростям

в точках А и С.

VC С

1 .

A AP

Угловая скорость звена АС равна

ωAC =

Рис.25

Р1

AP1

Проведем

перпендикуляры к

скоростям VВ

и VD , точка их пересечения Р2

— мгновенный центр скоростей

VB	BP2			BP
звена ВD. V	= DP , откуда	2
VB =VD DP .
D	2			2
Угловая скорость звена ВD равна
	ωBD =	VB	.

		BP2

Задача 8. Определить скорости точек А, D и угловые скорости звеньев механизма, изображенного на рис. 26, если угловая скорость кривошипа ОА

равна ωОА.

Скорость точки А равна VA = ωОА OA и перпендикулярна кривошипу ОА. Звено АВ совершается плоское движение, скорость точки В направлена вертикально вниз. Мгновенный центр в данный момент находится в бесконечности, поэтому скорости всех его точек равны, а угловая скорость ωAB = 0 .

Скорость точки D перпендикулярна кривошипу О2D, следовательно, мгновенный центр скоростей звена ВD совпадает с точкой О2.

					Тогда	VD =	DO2 ;	откуда
О1	А			D			VB	BO2
				DO2 .
	ωОА	VD	90	0	V	=V
		D	B	BO2
	VA	В		О2					BD
		Угловая скорость	звена

					равна ωBD =	VB	= VD .
		VB					BO2	DO2

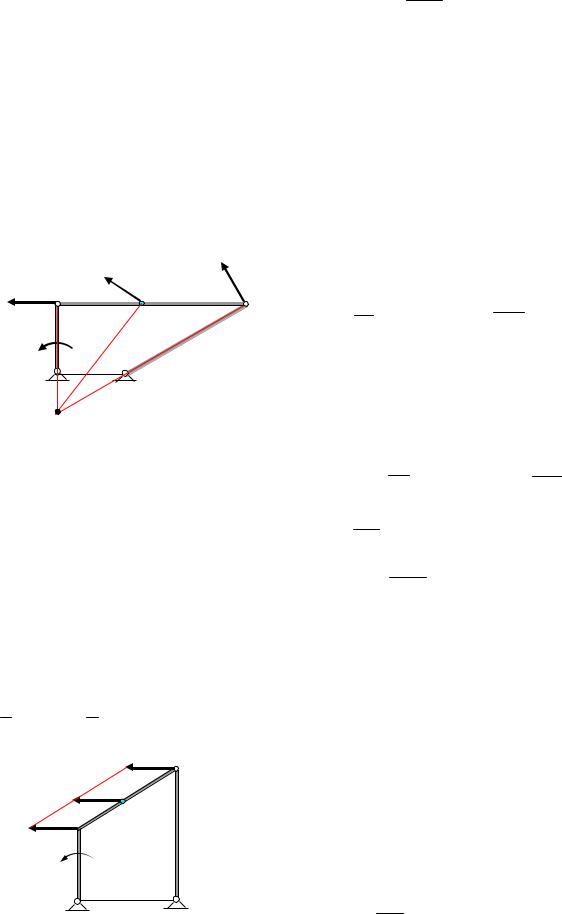
	Угловая скорость кривошипа O2D равна ωBD	= VD .
								DO2
	Задача 9. Определить скорости точек А, С, D и угловые скорости звень-
ев механизма, изображенного на рис. 25,	если угловая скорость кривошипа
ОА равна ωОА (рис.27).
	Решение. Звенья О1А и О2В совершают вращательные движения, поэто-
му скорость точки А направлена перпендикулярно кривошипу О1А и равна
	VA = ωОА· OA.
	Скорость точки D перпендикулярна звену О2D.
	Звено АD совершает плоское движение, мгновенный центр скоростей
этого звена лежит в точке Р пересечения перпендикуляров, проведенных в
			VD	точках А и D к скоростям VA и VD.
		VC	Скорость точки D находим из про-
VA	А	D
С	порции	VD		DP	. VD	=VA DP .
				=
ωОА					VA		AP		AP
		Соединим	точек	С с мгновенным
	О1
	О2		центром скоростей Р, скорость точки С

				будет направлена перпендикулярно от-
	Р			резку СР.
	Рис.27			Модуль этой скорости найдем из
			пропорции		VC	= CP	, VC =VA CP .

								VA	AP	AP
	Угловая скорость звена АD равна ωAD =	VA .
						AP	VD .
	Угловая скорость кривошипа равна	ω		=
	O2D		O2 D

Задача 10. Определить скорости точек А, В, С, и угловые скорости звеньев механизма, изображенного на рис. 28, если угловая скорость криво-

шипа ОА равна ωОА.

Решение. Звенья ОА и DB совершают вращательные движения, поэтому

VA OA , VB

ωОА А

BD . Скорость точки А равна VA = ωОА· OA. Звено совершает

VВ	плоское движение, так как скорости точек А и В
		В	параллельны, то мгновенный центр скоростей

С	этого звена находится в бесконечности, поэтому
скорости всех его точек геометрически равны

	VA = VB = VC.
	Угловая скорость звена AВ равна нулю. Уг-
D	ловая скорость кривошипа ВD равна
	ωBD = VB .
	BD

Рис.28

	Задача 11. Определить скорости точек А, В, С, D и угловые скорости
звеньев механизма, изображенного на рис. 29,	если угловая скорость криво-
	Р	D		шипа ОА равна ωОА.
	О2	Решение.	Скорость точки А
VA	А
VD		перпендикулярна	кривошипу	и
			равна VA = ωОА· OA. Звено АВ со-

	VC	С		вершает	плоское	движение,	ско-
ωОА		рость VВ точки В направлена гори-

	О1	VВ	В	зонтально влево. В данном положе-
			нии	мгновенный	центр скоростей
		Рис.29		звена АВ находится в бесконечно-
			сти, поэтому скоростей всех	его
точек геометрически равны: VA = VB = VC.
	Звено CD совершает плоское движение, мгновенный центр скоростей
этого звена лежит в точке Р пересечения перпендикуляров, проведенных к
	скоростям в точках С и D. Скорость точки D найдем из пропорции
		VC =	CP	, VD =VC	DP .
		V	DP		CP
		D
Угловая скорость звена СD равна ωCD = VC .
				CP	= VD .
Угловая скорость кривошипа О D равна	ω
			2		O2D	DP

Задача 12. Определить скорость точки С и угловую скорость подвижного блока 3 (рис.30), если скорость тела 1 равна V1, r = 0,5R.

Решение. Блок 2 вращается вокруг точки О, скорость его точки В по ве-

личине равна скорости тела 1, так

как они связаны нерастяжимой ни-

r O

тью: VB = V1.Скорость

точек

при

вращательном

движении пропор-

циональны

их

радиусам

вращения,

поэтому

0,5R

= 0,5 .

Сле-

довательно, VA = 0,5 VB.

Подвижный

блок 3 совершает

плоское движение,

при этом

VD =

VB, VК = VA, так как соответствую-

щие точки связаны нерастяжимыми

нитями.

Рассмотрим движение блока 3.

	Рис.30	Мгновенный центр скоростей нахо-
	дится в точке пересечения Р общего

		17

перпендикуляра, проведенного к скоростям VD и VК , и прямой, проходящей через концы этих векторов. Конец вектора скорости VС точки С лежит на прямой, соединяющей концы векторов скоростей VD и VК .

VК = VA = 0,5VB, VD = VB , тогда VК = 0,5VD.

Составим пропорцию:

VK = KP

VD DP .

Обозначив СР = х, тогда KP = R — x, DP = R + x. Подставив эти значения в пропорцию, получим

0,5 V	R − x		R
V	D =	,	откуда x =	.
R + x
3
D

Тогда расстояние точки К до мгновенного центра скоростей Р равно KP = R – x = 2/3 R, т.е. расстояние точки С до мгновенного центра скоростей в два раза меньше, чем то же расстояние до точки К, поэтому скорость точки будет в два раза меньше скорости точки К. VC = 0,5· VK = 0,5 VA = 0,25 V1.

Угловая скорость блока 3 равна ω3 = CPVC = 0,25RV1 3 = 0,75VR1 .

Скорость груза 4, подвешенного на нити в точке С, равна скорости точки С.

V4 = VC = 0,25 V1.

Задача 13. Определить скорость точки С и угловую скорость кривошипа ОС указанного на рис.31 механизма, если скорость тела 1 равна V1 (радиусы тел 3 и 5 заданы).

Решение. Данный механизм со-

стоит из пяти, соединенных между

собой тел.

1. Тело 1, двигаясь вниз по на-

клонной плоскости, сообщает телу 3

вращательное движение вокруг точ-

ки О.

Рис.31

В свою очередь тело 3, находясь

в зацеплении с телом 5, сообщает

ему плоское движение.

Точка С тела 5 приводит в движение кривошип ОС, кото-

рый вращается вокруг точки О.

2. Рассмотрим движение тела 3 (рис.31а). Скорость

точки А равна скорости груза 1, так как они связаны не-

растяжимой нитью. Определим скорость точки К.

Скорости точек вращающегося тела относятся как

их радиусы вращения:

Рис. 31 а

Отсюда скорость

VC	P	VK =VA	R	=V1	R	.
r
	5			r
K	C	3. Рассмотрим движение тела 5 (рис.31
б).	Точка Р является мгновенным центром

скоростей, так как в этой точке тело 5 находится в зацеплении с неподвижной шестер-

3ней 2. Скорость точки находим из пропорции

Рис. 31 б

=VK

=V1 R .

VC =VK

C 5

2r3

2 r

4. Кривошип вращается (рис.31в) вокруг точки О

определим по форму-

с угловой скоростью, которую

ле

ωOC =

Рис. 31 в

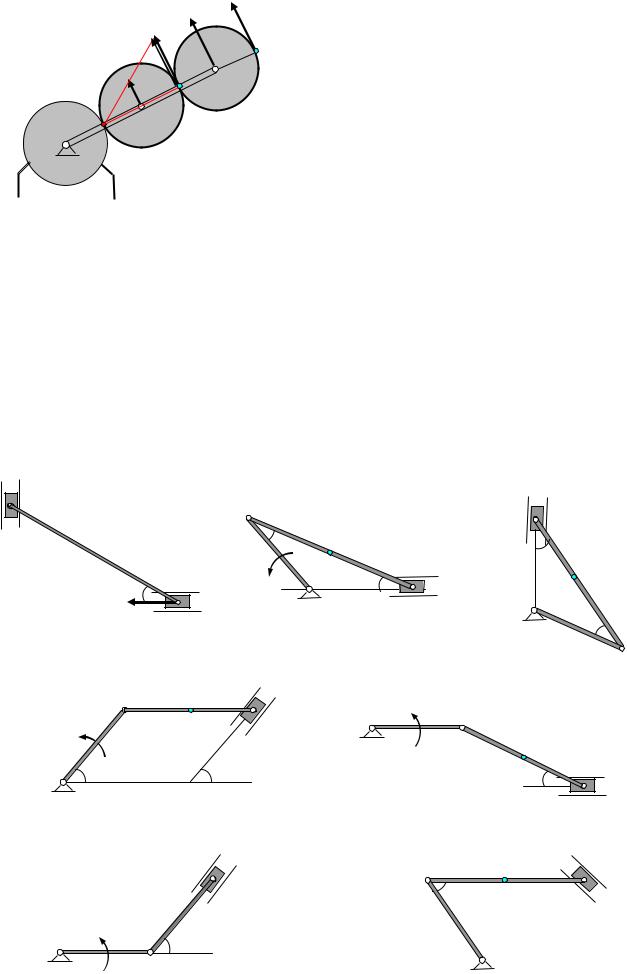
Задача 14. Кривошип ОС соединяющий центры трех шестерен одинакового радиуса R (рис.32), вращается вокруг точки О с угловой скоростью ω.

			VС	Шестерня	1 закреплена	неподвижно,
			шестерни 2 и 3 приводятся в движение
			D
			кривошипом. Определить скорости точек
		VA	С	контакта	между шестернями, скорость
		точки D и угловые скорости подвижных
ω
	А	3	шестерен.
О			2	Решение.
		1. Рассмотрим движение кривошипа.
	1
		Скорости точек А и С (рис.32) на-

				правлены	перпендикулярно	кривошипу

	Рис.32		ОС и равны

VA = ω·OA = 2 ω R, VC = ω·OC = 4 ω R.

2. Рассмотрим движение шестерни 2.

Шестерня 2 совершает плоское движение, (рис.32 а) скорость точки А известна. В точке контакта с неподвижной шестерней 1 находится мгновенный центр скоростей Р.

Скорость VK направлена перпендику-

лярно отрезку КР,

модуль ее определяет-

VК

VС

ся из пропорции

= 2 ,

откуда VK = 2 VA = 4ω R.

О Р

Угловая скорость шестерни 2 равна

ω2

2ω R

= 2ω .

Рис.32 а

3. Определим характер движения шес-

терни 3.

Скорости точек С и D шестерни 3 равны по модулю и параллельны, следовательно, шестерня 3 совершает поступательное движение, угловая скорость такого движения равна нулю.

Упражнения.

Определить с помощью мгновенного центра скоростей скорости точек А, В и С в механизмах, представленных на чертежах

А									В
				А

				300	C					300

	30	0	В	ωОА	О	300	В			C
					О
	VВ
Рис.1			Рис.2				300

											А
				В						Рис. 3
	A		C			ωОА
				O	A
ωОА
									C
O	450			450					30	0	В
							Рис.5

	Рис.4

				B			А	C		В

								600
O	ωОА		450					О
		A								20

Ускорения точек плоской фигуры.

Движение плоской фигуры в своей плоскости можно разложить на поступательное движение вместе с произвольно выбранной точкой, принимаемой за полюс, и вращательное движение вокруг этого полюса.

Следовательно, ускорение любой точки при плоском движении равно

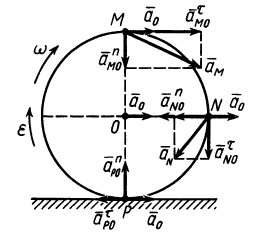
геометрической сумме двух ускорений: ускорения выбранного полюса, и ускорения, полученного данной точкой при ее вращательном движении вокруг полюса.

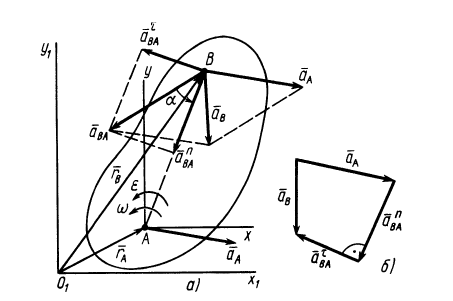
Пусть известно ускорение точки А плоской фигуры, тогда ускорение другой точки этой фигуры будет равно (рис.33).

aB = aA + aBA ,

где ускорение вращательного движения точки А вокруг точки В раскладывается на нормальное и касательное ускорения:

aBA = aBAτ + aBAn .

a BA a n a BAτ

BA B

Рис.33

Касательное ускорение вращательного движения точки вокруг полюса направлено перпендикулярно отрезку АВ, соединяющему точку В с полюсом А, и равно

aτBA = ε BA.

Нормальное ускорение направлено по отрезку ВА к полюсу А и равно

aBAn =ω2 BA.

Окончательно, полное ускорение точки В равно геометрической сумме трех ускорений: ускорения выбранного полюса А, нормального и касательного ускорений вращательного движения точки В вокруг этого полюса:

aB = aA +aBAn +aBAτ .

Мгновенным центром ускорений называется точка, принадлежащая связанной с плоской фигурой плоскости, ускорение которой в данный момент равно нулю.

Если за полюс выбрать мгновенный центр ускорений, то ускорение произвольной точки плоской фигуры определяется как ускорение вращательного движения вокруг мгновенного центра ускорений (рис.34).

	aA = aAL = aALn + aALτ ,
где L –мгновенный	центр ускорений, aALn	—
нормальное		τ	касательное ус-	А
ускорение, aAL —	aALτ	ε aALn
корение точки А вращательного движения пло-
ской фигуры вокруг мгновенного центра уско-		L
рений.	aALn =ω2 AL,	aτAL =ε AL.		aA

Ускорение aALn	— направлено по AL , уско-
рение aALτ	— перпендикулярно AL. Ускорение		Рис.34
aA точки А образует угол α с отрезком AL со-

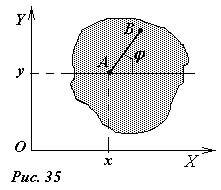
единяющим точку А с мгновенным центром ускорений и равно (рис.35)

aA = (aALn )2 +(aτAL )2 = AL ω4 +ε2 ,
tgα = aτAL	=	ε	.	L
aALn		ω2	А	ε

Таким образом, если известно ускорение точки А плоской фигуры, то, чтобы найти положение мгновенного центра ускорений, следует это ускорение повернуть вокруг точки А на угол α в сторону вращения фигуры и на полученной прямой отложить расстояние

Если известны направления ускорений двух точек плоской фигуры, то мгновенный центр ускорений определяется как точка пересечения получен-

ных поворотом этих ускорений на один и тот же угол α = arctq ωε2 в сторону вращения.

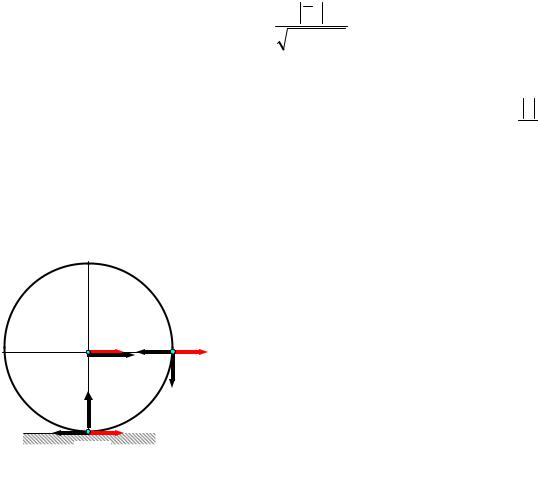
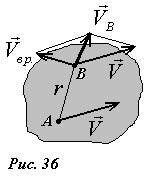
Задача1. Центр колеса, катящегося без скольжения по горизонтальной плоскости, в данный момент имеет скорость VC = 2 м/c и ускорение аC = 1,6 м/c. Радиус колеса R = 0,4 м. Определить точек В и Р (рис. 36).

Решение. Так как скорость и ускорение точки С известны, то принимаем точку С за полюс.

	С	aC	В	aC	Тогда aB = aC +aBCn +aBCτ
	aP = aC +aPCn +aPCτ ,
			VC
aPCn			a n	где
					BC
τ						aBCn = ω2 BC = ω2 R,	aPCn = ω2 PC = ω2 R,

aPC	Р	aC		τ	= ε BC = ε R,	τ
Рис. 36				aBC	aPC = ε BC = ε R.

Мгновенный центр скоростей колеса находится в точке Р – точке каса-

ния колеса с неподвижной плоскостью, поэтому

VC = ωCP =ω R, откуда ω =

, при t = 1c, ω =ω =

=5 (1/ c).

0,4

Угловое ускорение колеса

ε =

dω

dVC

, при t =1 c, ε =

1,6

= 4 (1/ c2 )

0,4

Тогда

aτBC = ε R =

R = aC ,

aτPC = ε R =

R = aC .

Ускорение точки Р будет направлено к центру колеса точке С и равно

aP = aBCn =ω2 R = 52 0,4 =10 (м/ c2 ) .

Для определения ускорения в точке В спроектируем векторное равенство aB = aC +aBCn +aBCτ на горизонтальную ось x и вертикальную ось у:

aBx	= aC − aBCn = aC −ω2 R =1,6 −52 0,4 = −8,4 ( м/ с2 )
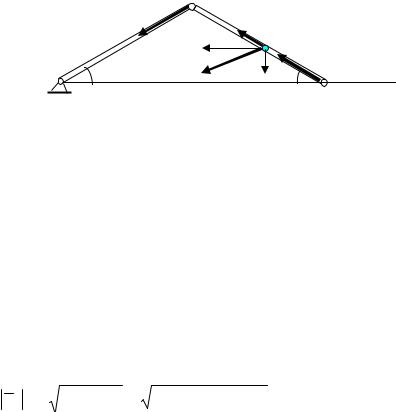
aBy	= −aτDC = −aC = −1,6 ( м/ c2 )
aB =	aBx2 + aBy2 = (−8,4)2 +(−1,6)2 ≈ 8,55 ( м/ c).

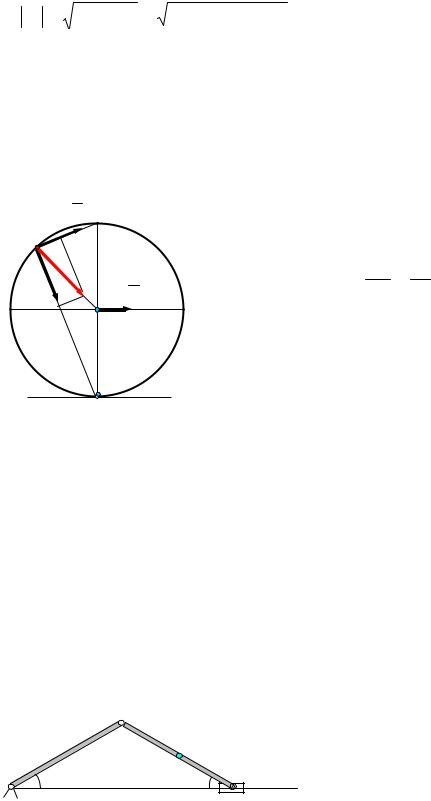
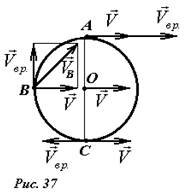
Задача 2. Колесо радиуса R = 0,4 м катится без скольжения так, что центр колеса имеет постоянную скорость VC =2 м/c. Определить ускорения точек Р и М обода колеса(рис.37)

Решение. Так как скорость центра колеса является постоянной, то его

ускорение рений.

aMτ

aMn

aC = 0 , следовательно, точка С будет мгновенным центром уско-

aMC VC

Мгновенный центр скоростей находится в точке Р – точке контакта с неподвижной плоскостью. Значит

ω = CPVC = VRC = const.

Отсюда следует,

&	tgα =	ε	= 0, α = 0.

чтоε =ω = 0,	ω	2

Следовательно, ускорения всех точек колеса будут направлены к центру колеса и равны

	aM =ω2	2
Рис.37	CM = ω2 R = VC .

			R

Ускорение точки М, находящейся на ободе колеса, являясь полным ускорением криволинейного движения, раскладывается на касательное, направленное по скорости в этой точке, и нормальное ускорение, направленное по перпендикуляру к скорости, т.е. по прямой, соединяющей точку М с мгновенным центром скоростей. (рис.37.).

aM = aMn + aMτ ; aMn = aM cosα, aτM = aM sin α.

Задача 3. Определить скорости точек А, В, С и ускорения точек А и В кри- вошипно-шатунного механизма (рис.38), если кривошип вращается с посто-

y							янной угловой скоростью ωОА = 2
	А					1/с, ОА = АВ = 0,6 м, МВ = 0,3 м, ϕ

				C				=300.

О		ϕ	ϕ			В x	Решение. Скорость точки А
					(рис. 39) перпендикулярна криво-


			Рис.38					шипу ОА и равна
								VA =ωOA OA =1,2 м/c.

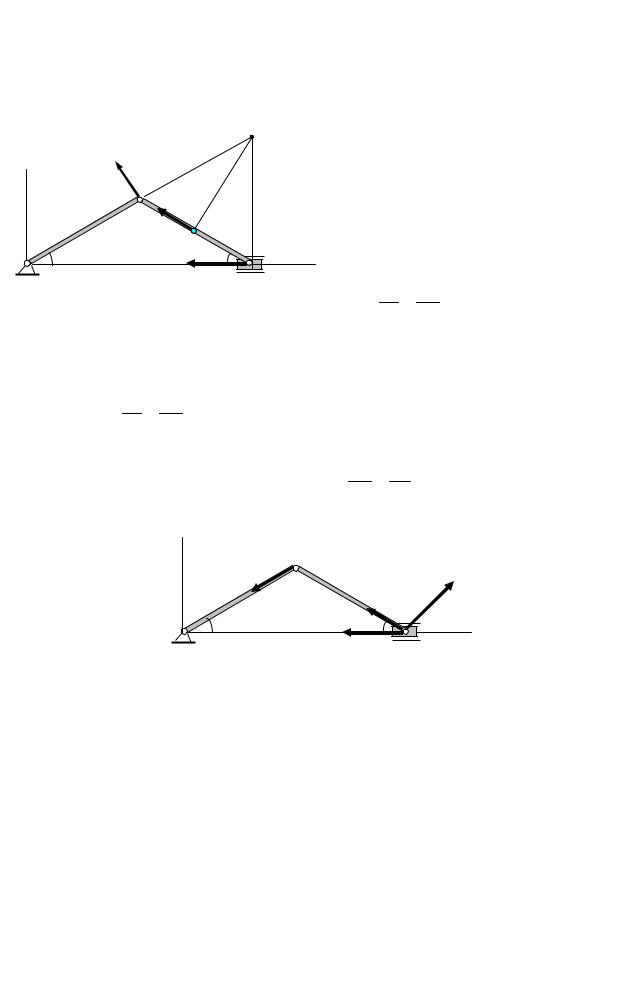
	Звено АВ совершает плоское движение/ Скорость точки В направлена
горизонтально, что обусловлено направляющими, вдоль которых движется
ползун В.
	Для определения скоростей точек А и В, принадлежащих шатуну АВ, оп-
ределим положение мгновенного центра скоростей этого звена. Проведем
			P		перпендикуляры	к	скоростям	в
				точках А и В, мгновенный центр

y	VA				скоростей Р находится в точке их
	A			пересечения.

		VC				Скорости точек при плоском
			C		движении пропорциональны рас-
О	300	300	x	стояниями до мгновенного центра
			В		скоростей.
		VB			VB =	AP
	Рис.39				. В треугольнике АВР:
АР = ВР, следовательно, VB=VA=1,2 м/с.	VA	BP

	Скорость VC	точки С направлена перпендикулярно отрезку СР, соеди-
няющему точку С с мгновенным скоростей. Значение скорости VC находим
из пропорции: VC	= CP . Из треугольника АСР:	СР =AP sin 60.
	VA	AP
	Следовательно, VC= VA sin 600 = 1,03 м/с.
	Угловая скорость шатуна равна	ωAB = VA	= 1,2	= 2	м/c.
					AP	0,6
		y		А
			aAn
				аВАn		aBAτ
		О	300
			aB		В	x


			Рис.40
	Ускорение точки А представляет собой нормальное ускорение аАn , на-
правленное по кривошипу (рис. 40)
	aAn =ωOA2	OA =2,4 м/c.
Ускорение точки В направлено по оси х и определяется векторным равенст-
вом:		aB = aAn +aBA = aAn +aBAn +aBAτ ,
					(а)
где векторы aBAn	и aBAτ	представляют собой составляющие ускорения вра-
щательного движения звена АВ вокруг точки А. Вектор	aBAn	направлен по
радиусу вращения ВА , ускорение aBAτ	— перпендикулярно АВ.
									25

Нормальное ускорение

aBAn =ωAB2 AB =2,4 м/с.

Таким образом, в уравнении (а) неизвестными являются ускорения aB и aBAτ . Для их определения спроектируем равенство (а) на оси х и у.

На ось х:

−aB

= −aAn cos 300

−aBAn cos 300

+ aτBA sin 300 .

(б)

На ось у:

0 = −aAn sin 300

+aBAn

sin 300 +aτBA cos300 .

(в)

Из уравнения (в) находим aτBA = aAn tg300 −aBAn

tg300 =0.

Угловое ускорение шатуна равно нулю.

Из уравнения (б) получаем aB =2,06 м/с.

Определим ускорение точки С (рис.41 ).

aC = aAn +aCA = aAn +aCAn +aCAτ

(г)

аАn

аCx

аCА

аn

300

аC

аCy

ВА В

Рис.41

Касательное ускорение

aCAτ = 0

Нормальное ускорение

aCAn =ω2 AC = 22 0,6 =1,2 (м/ c2 ).

Находим проекции уравнения (г)на оси Ох и Оу:

aCx = −aAn cos300 −aCAn cos300	= −1,82 (м/ c2 ).
aC y = −aAn sin 302 +aCAn sin 300 = −2,4 0,5 +1,2 0,5 = −0,6( м/ c2 ).
Ускорение точки С равно
aC = aCx2 +aCy2 = (1,82)2 +(−0,6)2	=1,91 ( м/ c2 )

Контрольрые вопросы

1.Определение плоскопараллельного движения.

2.Уравнения движения плоской фигуры.

3.Определение скоростей точек плоской фигуры.

4.Теорема Жуковского.

5.Мгновенный центр скоростей. Свойства м.ц.с.

6.Способы нахождения мгновенного центра скоростей.

7.Решение задач с помощью мгновенного центра скоростей.

8.Ускорения точек плоской фигуры.

Библиографический список

1.Бутенин Н.В и др. Курс теоретической механики.

Лань, 2002.- 736 стр.

2.Тарг С.М. Краткий курс теоретической механики. Высшая школа, 2004. – 416 стр.

3.Яблонский А.А., Никифорова В.М. Курс теоретической механики. Интеграл-Пресс, 2004. – 608 стр.

4.Яблонский А.А. Сборник заданий для курсовых работ по теоретической механике. Интеграл-Пресс, 2004. – 384 стр.

Соседние файлы в папке Термех

Источник

Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.

поделиться знаниями или
запомнить страничку

Все категории
экономические
43,662
гуманитарные
33,654
юридические
17,917
школьный раздел
611,985
разное
16,906

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Источник

Содержание:

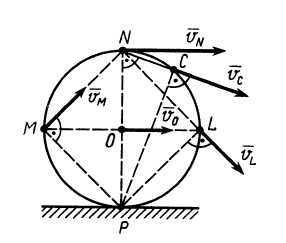
Мгновенный центр скоростей:

В каждый момент времени при плоском движении фигуры в ее плоскости, если Обозначим ее

Для доказательства этой теоремы достаточно указать способ нахождения мгновенного центра скоростей, если известны по модулю и направлению скорость какой-либо точки плоской фигуры и угловая скорость этой фигуры в рассматриваемый момент времени. Пусть вращение происходит по часовой стрелке ( и ) (рис. 46). Скорость точки плоской фигуры равна нулю, если скорость полюса и скорость от вращения вокруг полюса в этой точке равны по модулю, но противоположны по направлению. Эти точки лежат на перпендикуляре к скорости в точке . В других точках векторная сумма двух векторов не может быть равна нулю.

Рис. 46

Итак, если , то .

следовательно,

Таким образом, мгновенный центр скоростей находится на перпендикуляре к скорости , проведенном из точки , на расстоянии .

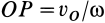
Мгновенный центр скоростей является единственной точкой плоской фигуры для данного момента времени. В другой момент времени мгновенным центром является уже другая точка плоской фигуры.

Если мгновенный центр известен, то, приняв его за полюс и учитывая, что скорость его в этом случае равна нулю, согласно (3) и (4), для точки фигуры имеем

где —расстояние от точки до мгновенного центра скоростей.

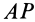
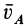
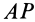
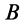
По направлению скорость в этом случае перпендикулярна отрезку . Для точки , аналогично,

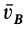
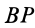
причем скорость перпендикулярна отрезку .

Из (5) и (6) имеем

Следовательно, если мгновенный центр скоростей известен, то скорости точек плоской фигуры при ее движении в своей плоскости вычисляют так же, как и в случае вращения фигуры в рассматриваемый момент вокруг своего мгновенного центра скоростей с угловой скоростью .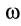

Для нахождения скоростей точек тела при его плоском движении обычно предварительно находят мгновенный центр скоростей. Но можно применить формулу, выражающую зависимость между скоростями двух точек тела.

Рассмотрим способы нахождения мгновенного центра скоростей. Существует два основных способа его нахождения: из механических условий задачи и по скоростям точек плоской фигуры.

В некоторых случаях удается сразу указать точку плоской фигуры, скорость которой в рассматриваемый момент равна нулю. Эти точки в таких задачах и являются мгновенными центрами скоростей. Так, в случае качения без скольжения одного тела по поверхности другого неподвижного тела точка соприкосновения поверхностей тел и является мгновенным центром скоростей.

Рис. 47

Рис. 48

Например, при качении без скольжения колеса по неподвижной прямой линии (см. рис. 52) и одного колеса по неподвижному другому колесу (см. рис. 61) мгновенный центр скоростей находится в точках соприкосновения колеса с прямой и соответственно колеса с колесом. В общем случае, если известны скорости двух точек плоской фигуры (рис. 47), мгновенный центр скоростей находится на пересечении перпендикуляров к скоростям этих точек.

В том случае, когда точки лежат на общем перпендикуляре к скоростям этих точек, скорости точек параллельны и концы их лежат на одной прямой, проведенной через мгновенный центр скоростей (рис. 48 и 49), так как скорости точек пропорциональны расстояниям от этих точек до мгновенного центра скоростей. Если скорости двух точек, расположенных на общем перпендикуляре к этим скоростям, еще и равны (рис. 50), то имеем мгновенное поступательное движение плоской фигуры, при котором скорости всех точек фигуры одинаковы по модулю и направлению. Угловая скорость плоской фигуры при мгновенном поступательном движении равна нулю, и в этом случае, согласно формуле (7), мгновенный центр скоростей находится в бесконечности.

Рис. 49

Рис. 50

Рис. 51

Рис. 52

Заметим, что при мгновенном поступательном движении только скорости точек одинаковы, а их ускорения в общем случае различны. Невозможен случай, когда скорости двух точек, не лежащих на общем перпендикуляре к скоростям, не равны друг другу по модулю, но параллельны (рис. 51), так как для него не выполняется теорема о проекциях скоростей двух точек тела на прямую, соединяющую эти точки.

Пример:

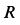
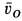
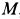
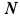
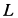
Колесо радиусом (рис. 52) катится без скольжения по неподвижной прямой, имея скорость центра . Определить скорости точек , и обода колеса в данный момент времени.

Решение. Мгновенный центр скоростей в этом случае находится в точке 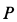соприкосновения колеса с прямой. Угловая скорость колеса определяется по формуле (7):

По формуле (5) для скоростей указанных точек имеем

так как

Скорости точек колеса направлены по перпендикулярам к отрезкам прямых, соединяющих мгновенный центр скоростей с рассматриваемыми точками.

Вычисление угловой скорости при плоском движении

Угловую скорость плоской фигуры при плоском движении можно вычислить, согласно ее определению, как

Затем ее можно определить по формуле (7):

Чтобы определить угловую скорость, надо скорость какой-либо точки плоской фигуры разделить на расстояние от этой точки до мгновенного центра скоростей. Направление вращения определяем по направлению скорости какой-либо точки, считая, что плоская фигура в данный момент вращается вокруг мгновенного центра скоростей с угловой скоростью .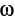

Рис. 53

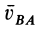
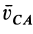
Угловую скорость при плоском движении можно вычислить путем предварительного нахождения скорости какой-либо точки плоской фигуры от вращения фигуры вокруг другой ее точки, принятой за полюс, например или . Тогда угловая скорость, согласно формуле (4),

Знак угловой скорости определяют по направлению относительной скорости какой-либо точки фигуры от вращения фигуры вокруг другой ее точки, выбранной за полюс.

Применяют и другие способы определения угловой скорости. Так, если предварительно установить зависимость угла поворота плоской фигуры от линейных и угловых величин других плоских фигур тождественным соотношением, то, дифференцируя его по времени, получаем соотношение, из которого иногда удается определить искомую угловую скорость. Этот способ используют часто для нахождения зависимости угловых скоростей отдельных звеньев плоских механизмов.

Пример:

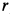
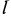
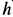
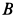
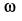
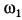
В кривошипно-шатунном механизме (рис. 53) даны длины кривошипа , шатуна и расстояние от оси вращения кривошипа до направляющей ползуна . Установить зависимость между угловыми скоростями кривошипа и шатуна при любом положении механизма.

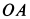
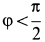
Решение. Положение кривошипа определяется углом , а шатуна — углом . До тех пор пока , справедливо тождество

Дифференцируя это тождество по времени, получим

Но ; следовательно,

Полученное соотношение и является искомой зависимостью между угловыми скоростями кривошипа и шатуна. При имеем частный случай кривошипно-шатунного механизма. Если дополнительно , то и .

Направления вращений кривошипа и шатуна противоположны. При вращении кривошипа против часовой стрелки шатун вращается по часовой стрелке.

Ускорения точек тела при плоском движении

Рассматривая плоское движение плоской фигуры как сложное, состоящее из переносного поступательного вместе с полюсом и относительного вращательного вокруг , по теореме о сложении ускорений для точки имеем

Рис. 54

Так как переносное движение является поступательным вместе с точкой фигуры, то переносное ускорение

Относительное ускорение точки от вращения вокруг полюса обозначим . После этого формула (9) принимает вид

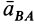
т. е. ускорение какой-либо точки плоской фигуры при плоском движении равно векторной сумме ускорения полюса и ускорения этой точки от вращательного движения плоской фигуры вокруг полюса.

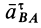
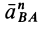
Ускорение от относительного вращательного движения вокруг полюса, как и в случае вращения тела вокруг неподвижной оси, состоит из касательной и нормальной составляющих и :

причем

и _________

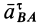
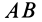
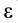
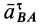
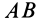
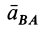
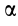
Касательное относительное ускорение направлено по перпендикуляру к отрезку в сторону дуговой стрелки углового ускорения (рис. 54, а). Нормальное относительное ускорение соответственно направлено по линии от точки к полюсу . Наконец, полное относительное ускорение составляет с отрезком угол , тангенс которого можно определить по формуле

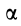
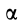
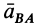
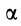
Из формулы (15) следует, что угол для всех точек плоской фигуры одинаков. При угол от ускорения к отрезку надо откладывать против часовой стрелки. При его надо откладывать по часовой стрелке, т. е. во всех случаях, независимо от направления вращения фигуры, угол всегда надо откладывать в направлении дуговой стрелки углового ускорения. В соответствии с (10) и (11) можно построить в выбранном масштабе многоугольник ускорений для точки (рис. 54, б).

Формулу (10), определяющую зависимость ускорений двух точек плоской фигуры, можно получить непосредственным дифференцированием векторного равенства для скоростей, справедливого в любой момент времени. Имеем

Продифференцируем по времени обе части этого равенства, учитывая изменения векторных величин относительно неподвижной системы координат (полные производные). Получаем

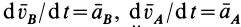
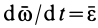
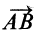
Здесь — ускорения точек и относительно неподвижной системы координат; — угловое ускорение плоской фигуры. У вектора постоянный модуль; следовательно, его производная по времени выражается в форме

Объединяя полученные результаты, получаем

Рассуждения, аналогичные тем, которые проведены для скорости 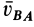, позволяют сделать вывод о том, что

т. е. 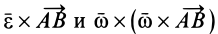являются соответственно касательным и нормальным ускорениями от вращения плоской фигуры вокруг точки . Следовательно,

Заказать решение задач по теоретической механике

Пример:

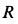
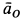
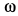
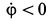
Колесо радиусом катится со скольжением по неподвижной прямой, совершая плоское движение (рис. 55). Ускорение центра колеса в рассматриваемый момент времени , а угловая скорость и угловое ускорение колеса и . Дуговые стрелки для и направлены по часовой стрелке, т. е. и . Определить в этот момент времени ускорения точек , и , расположенных на концах вертикального и горизонтального диаметров обода колеса.

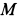
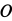
Решение. Ускорение точки , приняв за полюс точку , определим по формуле

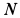
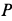
и аналогичным формулам для точек и . Для касательного и нормального ускорений точки от вращения колеса вокруг точки имеем

Рис. 55

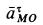
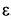
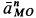
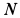
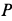
Ускорение перпендикулярно отрезку и направлено в сторону, указываемую дуговой стрелкой , а ускорение направлено от точки к точке , принятой за полюс. Аналогично направлены ускорения для точек и .

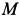
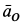
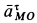
Так как для точки ускорения и направлены по одной прямой, то, предварительно их сложив, получим две перпендикулярные составляющие ускорения и, следовательно,

Для точки

так как

Окончательно для точки 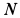имеем

Для точки 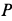соответственно

В том случае, когда колесо катится без скольжения, точка 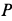является мгновенным центром скоростей и скорость точки в любой момент времени равна нулю. Скорость точки в этом случае можно определить по формуле

Дифференцируя по времени обе части этого тождества и приравнивая результат дифференцирования, получим

или

так как точка движется прямолинейно, и

Учитывая, что

имеем

Следовательно, при качении колеса по прямой без скольжения

т. е. ускорение мгновенного центра скоростей, скорость которого равна нулю, не равно нулю.

Если угловое ускорение не задано, то при отсутствии скольжения колеса по прямой его можно определить по формуле

Мгновенный центр ускорений
Мгновенный центр вращения
Вращение твердого тела вокруг неподвижной точки
Сложное движение точки
Пространственная система сил
Центр тяжести
Кинематика точки
Плоское движение твердого тела

Источник

Содержание книги

Предыдующая страница

§3. Криволинейное движение. Плоскопараллельное движение твердого тела

3.6 Плоскопараллельное движение

Движение твердого тела называется плоскопараллельным, если траектории движения всех его точек являются плоскими кривыми, лежащими в параллельных плоскостях.

Плоскопараллельное движение твердого тела можно представить как суперпозицию поступательного движения и вращения вокруг оси, направление которой не изменяется. Наглядными примерами такого движения являются качение колеса, движение книги без отрыва от стола и т.д.

Для описания положения абсолютно твердого тела при плоскопараллельном движении необходимо задать две декартовые координаты какой-либо точки тела ^[1] и угол его поворота, то есть плоскопараллельное движение обладает тремя степенями свободы.

Выберем внутри тела две точки A, B; зададим координаты x_A, y_A точки A и угол φ, который образует отрезок AB с направлением оси X. Три числа x_A, y_A и φ однозначно определяют положение тела на плоскости, следовательно, являются его координатами. Зная эти координаты, можно определить положение в пространстве любой другой точки твердого тела путем геометрических построений.

Покажем теперь, как можно найти скорость любой точки твердого тела при плоскопараллельном движении (рис. 36).

Разложим движение на две составляющих — поступательное движение, скорость которого обозначим (~vec V) , и вращение вокруг оси, проходящей через точку A, с угловой скоростью (~omega = frac{Delta varphi}{Delta t}) . Тогда скорость любой другой точки тела (например, B) является векторной суммой скоростей поступательного и вращательного движений —

(~vec V_B = vec V + vec V_{BP}) , (1)

причем вектор скорости вращательного движения направлен перпендикулярно отрезку AB и равен по абсолютной величине V_BP = ωr, где r расстояние от точки B до оси вращения.

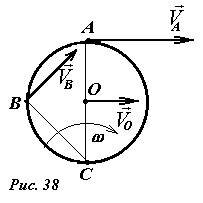
Рассмотрим катящееся без проскальзывания колесо радиуса R (рис. 37).

Пусть его центр движется со скоростью (~vec V). Найдем скорости некоторых других точек колеса. Для этого представим движение колеса как сумму поступательного движения его центра и вращения вокруг его оси. Так как движение происходит без проскальзывания, то угловая скорость вращения определяется формулой (~omega = frac{upsilon}{R}). Для точек, находящихся на ободе колеса линейная скорость вращательного движения равна по модулю скорости поступательного движения, так как для них расстояние до оси вращения равно радиусу колеса, поэтому (~V_{BP} = omega r = frac{V}{R} R = V) . Однако, направление этой скорости различно для разных точек. Так, для точки A скорость вращательного движения направлена горизонтально, также как и скорость поступательного движения. Поэтому суммарная скорость точки A равна 2V и направлена горизонтально. Скорость вращательного движения точки B направлена вертикально вверх, поэтому ее полная скорость направлена под углом 45° к горизонту, а ее модуль (~V_B = V sqrt{2}) . Очень интересна точка касания с поверхностью C : скорость ее вращательного движения направлена горизонтально в сторону противоположную скорости поступательного движения, поэтому ее полная скорость равна нулю.

Так как разложение движения на составляющие не является однозначным, можно теперь представить качение колеса как сумму движения точки C и вращения вокруг оси, проходящей через эту точку. Мы показали, что скорость точки C равна нулю, поэтому появляется возможность рассматривать движение колеса как чистый поворот вокруг точки C. Правда, это возможно в течение только бесконечно малого промежутка времени, потому, что в следующий момент точкой касания будет другая точка колеса. Множество точек твердого тела, скорости которых в данный момент равны нулю, образуют мгновенную ось вращения тела. Такая ось существует при любом движении твердого тела. Правда положение этой оси постоянно изменяется, поэтому для вычисления координат точек такое представление движения не дает особых преимуществ. Но для вычисления скоростей точек, рассматривать плоскопараллельное движение как чистый поворот очень удобно.

Легко доказать, что угол поворота тела не зависит от того, относительно какой оси мы его рассматриваем, следовательно, и угловая скорость не зависит от оси. С этой точки зрения, скорость любой точки колеса определяется формулой V = ωr’ , где r’ — расстояние от данной точки до мгновенной оси вращения.

Рассмотренная задача об определении скоростей точек катящегося колеса может быть легко решена, если рассматривать его движение как поворот вокруг точки C (рис. 38): точка A находится на расстоянии 2R от мгновенной оси вращения, поэтому ее скорость равна V_A = 2Rω = 2V; точка B находится на расстоянии (~R sqrt{2}) от оси, ее скорость (~V sqrt{2}). Направления векторов скоростей также совпадают с полученными ранее.

Таким образом, мы имеем два примерно одинаковых по сложности способа описания движения твердого тела: первый — суперпозиция поступательного и вращательного движений: второй — поворот вокруг мгновенной оси.

Примечания

↑ С точки зрения кинематического описания выбор этой точки произволен — только следует стремиться к тому, чтобы траектория этой точки была попроще. Далее мы укажем как можно легко найти такую точку.

Следующая страница

Источник

Содержание:

Плоское движение тела
Определение скоростей точек тела
Уравнения плоского движения
Скорости точек фигуры. Мгновенный центр скоростей
Определение положения мгновенного центра скоростей
Порядок решения задач на тему: Определение скоростей точек тела
Примеры решения задач на тему: Определение скоростей точек тела
Решение задачи графоаналитическим способом
Решение задачи с помощью мгновенного центра скоростей
Определение ускорений точек тела
Ускорения точек плоской фигуры
Порядок решения задач на тему: Определение ускорений точек тела
Примеры решения задач на тему: Определение ускорений точек тела
План скоростей
Порядок решения задач на тему: План скоростей
Примеры решения задач на тему: План скоростей
План ускорений
Примеры решения задач на тему: План ускорений

Плоское движение тела — это такое движение, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Плоское движение тела

Плоскопараллельное движение (плоское движение) — вид движения абсолютно твёрдого тела, при котором траектории всех точек тела располагаются в плоскостях, параллельных заданной плоскости. Примером плоскопараллельного движения по отношению к вертикальной плоскости, относительно которой тело движется в параллельном направлении, является качение колеса по горизонтальной дороге

Определение скоростей точек тела

Скорости точек тела пропорциональны их расстояниям до мгновенного центра скоростей, и это отношение определяет угловую скорость тела в данный момент времени: Частные случаи определения положения мгновенного центра скоростей. Если плоскопараллельное движение осуществляется путем качения без скольжения одного цилиндрического тела по поверхности другого, то точка касания Р имеет в данный момент времени скорость равную нулю, и, следовательно является мгновенным центром скоростей .

Уравнения плоского движения

Плоским называется такое движение тела, при котором траектории всех его точек лежат в плоскостях, параллельных данной неподвижной плоскости.

При таком движении все точки твердого тела, лежащих на перпендикуляре к этой плоскости, имеют одинаковые траектории, скорости и ускорения.

Плоское движение фигуры можно рассматривать как сложное (то есть, абсолютное) движение, которое включает поступательное движение вместе с произвольно выбранной точкой , что называется полюсом (переносное движение), и на вращательное движение фигуры вокруг этой точки (относительное движение).

На рис.4.1 с телом связана подвижная система координат . При движении тела начало координат и угол поворота подвижной системы координат относительно неподвижной системы со временем меняются. Таким образом, чтобы однозначно задать положение тела при плоском движении нужно задать закон движения начала подвижной системы координат (полюса ) и угол поворота подвижной системы относительно неподвижной системы координат, то есть:

Уравнения (4.1) называются уравнениями плоского движения твердого тела.

При этом, поступательная часть плоского движения описывается двумя уравнениями:

а относительная вращательная вокруг полюса — третьим уравнением:

Координаты любой точки плоской фигуры (рис.4.1), если за полюс выбрана точка и задан угол , определяются по уравнениям:

Скорости точек фигуры. Мгновенный центр скоростей

Поскольку плоское движение тела состоит из поступательного вместе с полюсом и вращательного вокруг него, то скорость любой точки тела (рис.4.2) геометрически состоит из абсолютной скорости точки , которую принято за полюс, и относительной скорости в относительном вращательном движении точки вместе с телом вокруг полюса :

Вектор относительной скорости точки в относительном вращательном движении вместе с телом вокруг полюса направлен перпендикулярно в сторону угловой скорости.

Модуль и направление абсолютной скорости находится построением соответствующего параллелограмма на векторах и (рис.4.2). Таков путь решения векторного уравнения, когда по записанному уравнению строят векторную фигуру, называется графоаналитическим.

Относительная скорость в относительном вращательном движении точки вместе с телом вокруг полюса по модулю равна:

где — угловая скорость вращения тела вокруг полюса.

Найти скорость любой точки тела можно также на основе теоремы, которая гласит:

Проекции скоростей двух точек фигуры на прямую, что соединяет эти точки, равны между собой.

Согласно этой теореме (рис.4.3) :

или

Если известна скорость точки тела, то:

При плоском движении тела в каждый момент времени существует точка тела, скорость которой равна нулю. Эта точка называется мгновенным центром скоростей и, как правило, обозначается буквой .

Если мгновенный центр скоростей известен, то легко можно найти мгновенное распределение скоростей всех точек тела (рис.4.4).

Выберем за полюс поступательного движения мгновенный центр скоростей . Тогда для точек и тела можно записать векторные уравнения (4.3):

где — вектор абсолютной скорости полюса ;

— вектор относительной скорости точки в относительном вращательном движении вместе с телом вокруг полюса , направлен перпендикулярно ;

— вектор относительной скорости точки в относительном вращательном движении вместе с телом вокруг полюса , направлен перпендикулярно .

Поскольку скорость выбранного полюса равна нулю , то:

По модулю скорости вращения точек и вокруг полюса равны:

Разделив на получим:

Таким образом, мгновенное распределение скоростей точек тела при его плоском движении, такое же, какое было бы при его вращательном движении вокруг мгновенного центра скоростей.

Определение положения мгновенного центра скоростей

Существует несколько способов нахождения положения мгновенного центра скоростей.

Случай 1. Известна скорость одной точки тела и угловая скорость его вращения (рис.4.5).

Мгновенный центр скоростей лежит на перпендикуляре к скорости точки , на расстоянии:

Для нахождения направления перпендикуляра надо повернуть вектор относительно точки на угол в сторону угловой скорости.

Случай 2. Известны направления скоростей и двух точек и тела (рис.4.6).

Мгновенный центр скоростей должен лежать как на перпендикуляре к вектору , так и на перпендикуляре к вектору , то есть мгновенный центр скоростей лежит в точке пересечения этих перпендикуляров.

Случай 3. Скорости двух точек и тела параллельны между собой, а перпендикуляры к ним не совпадают (рис.4.7).

Говорят, что в этом случае мгновенный центр скоростей лежит на бесконечности. Угловая скорость вращения равна нулю, а скорости всех точек тела геометрически равны, то есть в данный момент времени тело выполняет поступательное движение.

Случай 4. Скорости двух точек и параллельны, направлены в одну сторону и не равны по модулю. Кроме того, и перпендикулярны отрезку (рис.4.8).

Мгновенный центр скоростей находится на продолжении отрезка той точки, скорость которой меньше. Расстояние от точки к мгновенному центру скоростей можно найти из пропорции (4.6):

Решив это уравнение относительно , получим:

Таким образом, для определения положения мгновенного центра скоростей надо знать не только направления скоростей, но и их величину.

Случай 5. Скорости двух точек и тела параллельны друг другу, перпендикулярны отрезку , но направлены в разные стороны (рис.4.9).

Мгновенный центр скоростей лежит на отрезке и делит его на части пропорциональные скоростям. Поскольку , то по формуле (4.6) можно записать:

Решив уравнение относительно , получим:

Таким образом, для нахождения положения мгновенного центра скоростей надо знать величины и направления скоростей обеих точек.

Случай 6. Тело катится без проскальзывания по неподвижной поверхности (рис.4.10).

В этом случае мгновенный центр скоростей находится в точке прикосновения тела к поверхности. Действительно, если отсутствует скольжение тела относительно поверхности, то скорости точек прикосновения тела и поверхности должны быть одинаковыми. Но скорости точки , принадлежащей неподвижной поверхности, равна нулю.

Тогда и скорость точки , которой в данный момент времени движущееся тело прикасается к неподвижной поверхности, тоже равна нулю.

Порядок решения задач на тему: Определение скоростей точек тела

а) решение графоаналитическим методом:

выбрать за полюс ту точку тела, скорость которой известна по величине и направлению или легко определяется из условий задачи;
найти точку тела, направление скорости которой известно;
пользуясь формулами плоского движения найти скорость этой точки;
определить угловую скорость тела в данный момент времени;
по известной угловой скорости и скорости полюса, пользуясь формулами плоского движения найти скорости других точек тела.

б) решение с помощью мгновенного центра скоростей:

определить положение мгновенного центра скоростей одним из известных способов;
определить значение мгновенного радиуса той точки тела, скорость которой известна, и найти угловую скорость тела;
найти скорости других точек тела.

Примеры решения задач на тему: Определение скоростей точек тела

Задача №1

Стержень (рис.4.11) длиной выполняет плоское движение. Вектор скорости точки образует угол с осью стержня и в данный момент времени равен . Вектор скорости точки в этот же момент времени образует угол с осью стержня.

Определить величину скорости точки , положение мгновенного центра скоростей, угловую скорость стержня и скорость точки , которая лежит на середине стержня.

Решение задачи графоаналитическим способом

1. Выберем за полюс точку (рис.4.11), поскольку известны направление и величина скорости этой точки.

2. Используя формулу распределения скоростей при плоском движении, запишем векторное уравнение для определения скорости точки :

где — скорость полюса точки ;

— относительная скорость точки в ее относительном вращательном движении вместе с телом вокруг полюса .

Данное векторное уравнение можно решить построением векторного треугольника скоростей (рис.4.12). Для этого из произвольной точки плоскости надо построить правую и левую часть векторного уравнения (1).

При построении правой части уравнения (1) из точки в произвольном масштабе отложим вектор скорости , который является известным и по величине и по направлению. К вектору надо добавить вектор относительной скорости , направление которого является известным, поскольку скорость точки у ее относительном вращательном движении вокруг полюса перпендикулярна радиусу вращения, в данном случае радиус вращения — отрезок . Величина вектора неизвестна и поэтому через точку проводится только его направление (прямая рис.4.12).

Теперь из точки построим левую часть уравнения (1). Направление скорости точки является известным (по условию задачи), но неизвестна ее величина, и потому, из точки проводим линию параллельную .

Точка пересечения прямых, параллельных и , и будет решением данного векторного уравнения.

В результате построения получили замкнутый треугольник скоростей, стороны которого в выбранном масштабе определяют искомую скорость точки и относительную скорость этой же точки при ее вращении вместе с телом вокруг полюса .

В этом треугольнике известны все углы и одна сторона . С треугольника находим:

3. Определим угловую скорость вращения стержня . Поскольку , то :

4. Найдем скорость точки , лежащей посередине отрезка . Для этого запишем формулу для скорости точки относительно того же самого полюса точки :

где — скорость полюса точки ;

— относительная скорость точки в ее относительном вращательном движении вместе с телом вокруг полюса .

Скорость имеет то же направление, что и , а по модулю равна:

Отложив от точки (рис.4.12) вектор , равный половине вектора , получим точку . Вектор, проведенный из точки начала построения (точки ) в точку изображает скорость точки .

Поскольку стороны и треугольника равны между собой и угол между ними , то треугольник равносторонний. Таким образом:

Решение задачи с помощью мгновенного центра скоростей

1. Определим положение мгновенного центра скоростей. Для этого с точек и (рис.4.13) проведем перпендикуляры к скоростям и . Пересечение этих перпендикуляров (точка ) будет мгновенным центром скоростей.

2. Определим мгновенные радиусы. Поскольку треугольник прямоугольный, то:

3. Вычислим угловую скорость вращения фигуры вокруг мгновенного центра скоростей:

4. Найдем скорости точек и :

где — мгновенный радиус точки , поскольку треугольник равносторонний ( угол между ними ), то

Если надо было бы определить только величину скорости , то можно было бы воспользоваться теоремой о равенстве проекций двух точек плоской фигуры на прямую, соединяющую эти точки:

Тогда:

Ответ:

Задача №2

Колесо радиусом катится по горизонтальной поверхности. В момент рассматриваемого времени скорость центра и угловая скорость колеса (рис.4.14).

Определить: скорости точек , и , которые лежат на концах вертикального и горизонтального диаметров.

Решение.

1. В качестве полюса выберем точку , направление и величина скорости которой известны.

2.Используя формулу распределения скоростей точек тела при плоском движении определяем скорости других точек колеса.

Для точки колеса:

где — относительная скорость точки в ее относительном вращательном движении вокруг полюса .

По модулю равна:

Скорость направлена перпендикулярно в сторону угловой скорости, то есть по направлению и будут совпадать.

Из точки (рис.4.14) строим уравнение (1): откладываем вектор , а с его конца по тому же направлению .

Тогда:

Векторное уравнение для определения скорости точки , будет иметь вид:

где — скорость точки в ее вращательном движении вокруг полюса .

Эта скорость параллельна скорости , но будет направлена в противоположную сторону и по модулю равна:

Из точки (рис.4.14) строим векторное уравнение (2): откладываем вектор , а с его конца в противоположную сторону .

Поскольку векторы коллинеарны, то:

Таким образом, скорость точки равна и направлена в противоположную сторону от . Колесо катится со скольжением по поверхности.

Составляем векторное уравнение для определения скорости точки :

где — относительная скорость точки в ее относительном вращательном движении вокруг полюса .

По модулю равна:

Скорость направлена перпендикулярно в сторону угловой скорости , то есть вертикально вниз.

Из точки (рис.4.14) строим уравнение (3): откладываем вектор , а с его конца вектор вертикально вниз. Соединив точку с концом вектора получим вектор скорости точки .

Поскольку векторы и между собой перпендикулярны, то вектор является гипотенузой прямоугольного треугольника:

Ответ:

Задача №3

Колесо радиусом катится без проскальзывания по горизонтальной поверхности со скоростью центра колеса

Определить: скорости точек , , (рис.4.15).

Решение. Решим задачу с помощью мгновенного центра скоростей.

1. Определим положение мгновенного центра скоростей. Поскольку колесо катится по неподвижной поверхности, то мгновенный центр скоростей находится в точке прикосновения колеса к неподвижной поверхности.

2. Мгновенный радиус для точки равен . Тогда с формулы (4.4) получим угловую скорость колеса:

Направлена угловая скорость по ходу часовой стрелки.

3. Определим величину и направление скоростей точек , , .

Соединим точки , , с мгновенным центром скоростей . Векторы скоростей , и будут направлены перпендикулярно мгновенным радиусам и , соответственно.

По модулю скорости будут равны:

где

Ответ:

Задачи, которые рекомендуются для самостоятельной работы: 16.2; 16.4; 16.11; 16.12 [2]

Определение ускорений точек тела

Теорема: ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки во вращательном движении фигуры вокруг полюса.

Ускорения точек плоской фигуры

Формула распределения ускорений при плоском движении тела имеет вид:

где — ускорение полюса, точки , в поступательном движении;

— относительное ускорение точки в ее вращательном движении вместе с телом вокруг полюса ;

— ускорение любой точки тела.

Ускорение любой точки плоской фигуры равно геометрической сумме ускорения точки, которую выбрано за полюс, и ускорения точки при его вращении вместе с телом вокруг этого полюса.

Графическое определение ускорения точки выполняется следующим образом (рис.4.16):

Вычисление величины ускорения точки с помощью рассматриваемого параллелограмма затрудняет расчеты, поскольку предварительно надо определить угол между векторами и .

Учитывая, что представляет собой относительное ускорение точки в ее относительном вращательном движении вокруг полюса , то это ускорение можно разложить на относительную тангенциальную (касательную) и относительную нормальную (центростремительную) составляющие:

где

Вектор направлен перпендикулярно в сторону углового ускорения, а вектор всегда направлен от точки к выбранному полюсу (рис.4.17).

Тогда уравнение (4.10) примет вид:

Если точка , которая выбрана за полюс поступательного движения, движется не прямолинейно, то ее ускорение, в свою очередь, тоже можно разложить на тангенциальную и нормальную составляющие:

Порядок решения задач на тему: Определение ускорений точек тела

1. Выбрать точку, которая будет полюсом при записи уравнения плоского движения (как правило выбирают точку, ускорение которой известно).

2. Записать векторное уравнение распределения ускорений.

3. Спроектировать уравнение распределения ускорений на две взаимно перпендикулярные оси, одна из которых совпадает с нормальным ускорением, а вторая – с тангенциальным.

4. Определить мгновенное угловое ускорение плоской фигуры.

5. Найти искомые ускорения точек с помощью уравнения распределения ускорений.

Примеры решения задач на тему: Определение ускорений точек тела

Задача №1

Прямоугольная (рис.4.18, а) пластина движется в плоскости чертежа. Ускорение точки в данный момент времени равно и образует с прямой угол .

Ускорение точки составляет и образует угол с прямой .

Определить мгновенную угловую скорость и мгновенное угловое ускорение пластины, и ускорение точки , если

Решение.

1. Выберем за полюс точку , поскольку ее ускорение известно (задано в исходных данных).

2. Составим векторное уравнение для ускорения точки пластины:

где — относительное нормальное ускорение точки в ее вращательном движении вместе с телом вокруг точки . Вектор этого ускорения направлен от точки к точке и по модулю равен:

— относительное тангенциальное (касательное) ускорение точки в ее вращении вместе с телом вокруг точки . Направлен вектор этого ускорения перпендикулярно в сторону углового ускорения и по модулю равен .

Поскольку направление углового ускорения неизвестное, то направлением на рис. 4.18,а задаемся.

3. Спроектируем составленное уравнение (1) на оси и .

В проекции на ось получим:

В проекции на ось :

4. Из уравнения (2) получим величину нормального ускорения:

Найдем мгновенную угловую скорость фигуры:

5. Из уравнения (3) получим величину тангенциального ускорения:

Угловое ускорение фигуры:

Поскольку величина положительная, то направление тангенциального, а соответственно и углового ускорений выбрано верно.

6. Определим ускорение точки .

Для вычисления ускорения точки лучше за полюс выбрать точку , поскольку ускорение этой точки уже известно и задана сторона прямоугольника:

Направление векторов и показано на рис. 4.18,б.

Спроектируем записанное уравнение на оси и :

где

Полное ускорение точки :

Ответ:

Задача №2

Равносторонний треугольник движется в плоскости чертежа. Ускорение вершин и в данный момент времени равны и направлены вдоль сторон треугольника (рис.4.19).

Определить ускорение вершины .

Решение. Если известны ускорения двух точек плоской фигуры, например и , то задачу рекомендуется решать в следующей последовательности:

1. Рассматривая первую точку как полюс поступательного движения, записать векторное уравнение распределения ускорений при плоском движении для точки и спроектировать это уравнение на прямую , соединяющую обе точки.

2. Из уравнения проекций определить величину нормального ускорения и значение угловой скорости фигуры .

3. Спроектировать векторное уравнение распределения ускорений при плоском движении на прямую, которая перпендикулярна , и определить из уравнения проекций величину тангенциального ускорения и значение углового ускорения фигуры .

4. Если нужно, то, используя формулу распределения ускорений при плоском движении, определить ускорение любой другой точки плоской фигуры.

Решим задачу, придерживаясь приведенной последовательности.

1. Выберем за полюс точку . Для точки треугольника можно записать:

где — относительное нормальное ускорение точки в ее относительном вращательном движении вокруг точки , направлено вдоль от точки к точке ;

— относительное тангенциальное ускорение точки в ее относительном вращательном движении вокруг точки , направлено перпендикулярно , направлением задаемся (рис.4.19).

Спроектируем записанное равенство (1) на прямую :

2. Откуда:

Поскольку то:

3. Спроектируем векторное уравнение на прямую, которая перпендикулярна :

Откуда:

Учитывая то, что , получим:

Поскольку величина тангенциального ускорения положительная, то его направление на рис. 4.19 выбрано верно. Отсюда следует, что угловое ускорение направлено против хода часовой стрелки.

4. Определим ускорение точки , приняв за полюс точку :

— относительное тангенциальное ускорение точки в ее относительном вращательном движении вокруг точки , направлено перпендикулярно в сторону углового ускорение фигуры .

Учитывая, что , определим модули относительного нормального и тангенциального ускорений:

От точки (рис.4.20) отложим векторы ускорений, которые составляют правую часть уравнения (2).

Выберем систему координат , причем ось направим вдоль стороны треугольника.

Спроектируем равенство (2) на оси выбранной системы координат:

Подставляя числовые данные, получим:

Таким образом, ускорение вершины треугольника равно:

Поскольку проекция ускорения на ось равна нулю и величина проекции на ось положительная, то вектор ускорения точки будет направлен вдоль стороны треугольника от точки к точке .

Ответ:

Задача № 3

В шарнирном механизме (рис.4.21) в данный момент времени угловая скорость и угловое ускорение кривошипа равны Точка механизма движется по дуге окружности радиусом и в момент времени, что рассматривается, лежит на прямой .

Найти ускорение точки и мгновенное угловое ускорение шатуна , если

Решение. Скорость точки кривошипа, который вращается вокруг точки равен:

Направлена скорость перпендикулярно в сторону угловой скорости (рис.4.21).

Точка шатуна вращается вокруг центра и ее линейная скорость направлена перпендикулярно .

Поскольку скорости точек и шатуна параллельны, то мгновенный центр скоростей шатуна лежит в бесконечности и мгновенное движение шатуна является поступательным, то есть

Ускорение точки равно геометрической сумме нормального и тангенциального ускорений:

где

Направления ускорений и показаны на рис.4.21.

Выберем точку за полюс для шатуна . Тогда для точки шатуна:

или

где — относительное нормальное ускорение точки в ее относительном вращательном движении вокруг точки , направлено вдоль от точки к точке ,

— относительное тангенциальное ускорение точки в ее относительном вращательном движении вокруг точки , направлено перпендикулярно , направлением задаемся (рис.4.22),

Свяжем с точкой прямоугольную систему координат (рис.4.22) и спроектируем уравнение (1), помня, что , на оси выбранной системы координат:

С другой стороны, при движении точки по дуге окружности радиуса , точка приобретет ускорения :

где — нормальное ускорение точки в ее вращательном движении вокруг точки направлено к центру вращения;

— тангенциальное ускорение точки в ее вращательном движении вокруг точки , направлено перпендикулярно , задаемся направлением (рис.4.22).

По величине нормальное и тангенциальное ускорения соответственно равны:

Спроектируем уравнение (4) на оси выбранной системы координат:

Подставим в (3) все рассчитанные величины:

Поскольку

то

Положительное значение величины указывает на то, что направление было выбрано верно.

Угловое ускорение тела равно:

Угловое ускорение направлено в сторону , то есть против хода часовой стрелки.

Для определения тангенциального ускорения в уравнение (2) подставим из (5):

Откуда

Поскольку величина отрицательная, то направление тангенциального ускорения выбрано не в ту сторону.

Полное ускорение точки :

Ответ:

Задачи, которые рекомендуются для самостоятельной работы: 18.12; 18.14; 18.22 [2].

План скоростей

План скоростей и план ускорений – физическое изображение векторных уравнений, связывающих скорости и ускорения точек механизма. Изображение механизма, выполненное с помощью условных обозначений (см. выше) называется структурной схемой механизма.

Определение скоростей различных точек движущейся плоской фигуры легко может быть выполнено графически с помощью построения плана скоростей.

План скоростей – это графическое изображение из единого центра (полюса) векторов абсолютных скоростей точек фигуры в фиксированный момент ее движения.

План скоростей может быть построен, если:

известная скорость одной точки плоской фигуры и направление скорости другой точки;
известная скорость одной точки плоской фигуры и мгновенная угловая скорость фигуры

Пусть известные скорости , , и , вершин прямоугольника (рис. 4.23, а). Для построения плана скоростей с произвольной точки (рис.4.23,б), которая называется полюсом плана скоростей, отложим направленные отрезки и , которые в выбранном масштабе будут изображать скорости , , и . Полученные точки и , которые называются вершинами плана скоростей, соединим между собой прямыми линиями.

Установим свойства и правила построения плана скоростей.

По уравнению распределения скоростей при плоском движении фигуры, если за полюс принять точку , то для точки получим:

где — вектор абсолютной скорости точки ;

— вектор относительной скорости точки в относительном вращательном движении вместе с телом вокруг точки , направлена перпендикулярно и по модулю равна

С другой стороны для векторов треугольника плана скоростей (рис.4.23,б) можно записать:

Учитывая, что векторы и изображают в выбранном масштабе абсолютные скорости и и, сравнивая уравнения (4.14) и (4.15), можно сделать вывод, что отрезок изображает в масштабе скорость .

Таким образом, отрезок плана скоростей направлен перпендикулярно стороне фигуры и по модулю равен:

где — масштабный коэффициент, который принят при построении плана скоростей.

Аналогично:

Отсюда мгновенная скорость вращения плоской фигуры:

Вектор согласно уравнению (4.14) направлен на плане скоростей от точки к точке . Если этот вектор перенести в точку фигуры, то можно определить направление вращения точки вокруг точки вместе с фигурой (в данном случае, по ходу часовой стрелки). Направление же мгновенной угловой скорости плоской фигуры будет совпадать с направлением ее вращения.

Из рассматриваемого вытекает:

Порядок решения задач на тему: План скоростей

1. Изображают на чертеже в выбранном масштабе плоскую фигуру и вектор скорости той точки, скорость которой известна.

2. Определяют направление скорости второй точки плоской фигуры.

3. Записывают векторное уравнение распределения скоростей при плоском движении, принимая за полюс точку, скорость которой известна, а за искомую ту точку, направление скорости которой известно.

4. Решают записанное векторное уравнение графически путем построения в выбранном масштабе плана скоростей.

5. Определяют мгновенную угловую скорость вращения плоской фигуры.

6. Определяют скорость других точек плоской фигуры.

Примеры решения задач на тему: План скоростей

Задача №1

Найти угловую скорость шатуна 2 и скорость точки ползуна 3 кривошипно-шатунного механизма (рис. 4.24), если :

Решение.

1. Согласно исходным данным в произвольном масштабе строим схему механизма (рис.4.25, а).

2. Учитывая, что кривошип 1 вращается вокруг неподвижной точки с угловой скоростью определяем скорость точки кривошипа 1 и шатуна 2:

Направлена скорость перпендикулярно в сторону угловой скорости .

3. Следующей точкой шатуна, скорость которого можно определить, является точка , поскольку она, кроме шатуна, одновременно принадлежит и ползуну 3, что движется поступательно в горизонтальных направляющих. То есть направление этой скорости известно.

Для определения скорости точки запишем уравнение распределения скоростей при плоскопараллельном движении, принимая за полюс точку , скорость которой известна:

где — относительная скорость точки в ее относительном вращательном движении вместе с шатуном 2 вокруг точки . Вектор направлен перпендикулярно ;

— абсолютная скорость точки , которая движется прямолинейно вместе с ползуном 3 в горизонтальных направляющих.

4. Решим уравнение (1) графически (рис.4.25, б). Для этого с произвольной точки (полюса плана скоростей) отложим направленный отрезок , который в определенном масштабе будет изображать вектор скорости . Через точку этого отрезка проведем линию перпендикулярно , вдоль которой от точки будет направлен вектор скорости , длина и направление которого неизвестны.

Вектор который будет на плане скоростей изображать абсолютную скорость точки , выходит из полюса параллельно к пересечению с линией в точке .

Определим направление отрезка , который на плане скоростей изображает относительную скорость . Поскольку, согласно уравнению (1), вектор надо прибавить к вектору , который на плане скоростей изображается вектором , то вектор будет направлен от точки к точке .

Полученный векторный треугольник представляет собой план скоростей для кривошипно-шатунного механизма в положении, что рассматривается. Стороны этого треугольника в определенном масштабе изображают: — абсолютную скорость точки ; — относительную скорость точки в ее относительном вращательном движении вместе с шатуном вокруг точки ; — абсолютную скорость точки .

Перенесем из плана скоростей в точку на рис.4.25, а найденные направления скоростей и .

Поскольку скорость на плане изображается вектором , а — вектором , то угол при вершине равен углу между этими двумя векторами скоростей. Если на рис.4.25, а перенести и в точку , то угол между ними будет составлять , то есть

Аналогично, равен углу между векторами и . Учитывая, что , с рис.4.25, а получим:

Таким образом, и угол при вершине тоже будет равняться , а треугольник будет равносторонним, то есть:

, или

5. Определяем мгновенную угловую скорость шатуна 2. Поскольку , то:

где , исходя из того, что треугольник (рис.4.25,а) равнобедренный.

Направление угловой скорости определяется вектором . В данном случае направлена против хода часовой стрелки.

Ответ:

Задача №2

Найти угловые скорости шатуна 2 и коромысла 3 и абсолютные скорости точек и рычажного механизма (рис.4.26), если:

Угловая скорость кривошипа 1 —

Решение.

1. В соответствии с исходными данными в произвольном масштабе строим схему механизма (рис.4.27, а).

2. Так как точка принадлежит кривошипу 1, который вращается вокруг шарнира с угловой скоростью , то:

Вектор скорости направлен перпендикулярно в сторону вращения кривошипа (рис.4.27, а).

2. Шатун 2 механизма движется плоскопараллельно. Скорость точки шатуна 2 равна скорости точки кривошипа 1. Второй точкой шатуна, направление скорости которой известно, есть точка . Точка , кроме шатуна, принадлежит и коромыслу 3, которое вращается вокруг центра . Таким образом, скорость точки направлена перпендикулярно радиусу вращения .

3. Для определения скорости точки запишем формулу распределение скоростей:

где — абсолютная скорость точки , которая направлена перпендикулярно ;

— абсолютная скорость точки ;

— относительная скорость точки в ее относительном вращательном движении вместе с шатуном 2 вокруг полюса . Направлен вектор перпендикулярно .

4. Решаем записанное уравнение графически. Для этого из произвольной точки (полюса плана скоростей) (рис.4.27,б) проводим вектор параллельно , который в определенном масштабе будет изображать скорость точки .

Через конец вектора проводим линию перпендикулярно , вдоль которой от точки будет направлен вектор относительной скорости . Длина и направление этого вектора неизвестны.

Скорость точки направлена перпендикулярно и, по правилу, должна проходить через полюс плана скоростей. Исходя из этого, через точку проводим линию перпендикулярную коромыслу 3 к пересечению в точке с линией .

Полученный на рис. 4.27, б векторный треугольник являет собой план скоростей механизма в данном положении. В этом треугольнике вектор изображает абсолютную скорость точки , вектор направлен от полюса к точке — абсолютную скорость точки , а вектор направлен от точки к точке — относительную скорость , поскольку, согласно уравнению (2), эта скорость прибавляется к .

Перенесем направления скоростей и в точку на рис. 4.27, а.

Поскольку , а , то угол при вершине равен углу при вершине треугольника на схеме механизма (рис. 4.28), который образован путем продолжения кривошипа и коромысла к пересечению.

Таким образом

Угол при вершине будет равняться углу между продолжением прямой (рис.4.28) и прямой , поскольку сторона , а прямая . Учитывая, что , то:

Тогда угол при вершине :

Для определения сторон плана скоростей воспользуемся теоремой синусов:

Из уравнения (1) получим:

Таким образом:

5. Определим мгновенные угловые скорости шатуна 2 и коромысла 3. Поскольку , то:

Направление угловой скорости определяется направлением относительной скорости . С рис.4.27,а видно, что угловая скорость будет направлена против хода часовой стрелки.

Угловая скорость коромысла 3 равна:

где

Направление определяет скорость . Направлена угловая скорость коромысла 3 (рис.4.27,а) по ходу часовой стрелки.

6. Определить величины скоростей и можно непосредственно и путем измерения соответствующих отрезков на построенном плане скоростей.

Поскольку вектор на плане скоростей изображается отрезком , то масштабный коэффициент плана скоростей будет равен:

Скорости на плане скоростей соответствует отрезок , а скорости – .

Тогда:

7. Для определения скорости точки воспользуемся теоремой подобия.

Поскольку фигура на схеме механизма и фигура на плане скоростей должны быть подобными, то можно составить пропорцию:

В левой части пропорции (2) отношение отрезков на схеме механизма, а в правой — на плане скоростей.

Из уравнения (2) получим расстояние от точки к точке на плане скоростей:

Поскольку на схеме механизма отрезок перпендикулярен , то и на плане скоростей отрезок надо провести перпендикулярно , причем в ту сторону, чтобы обход точек , и на плане скоростей должен был быть против хода часовой стрелки, как и для точек , и на схеме механизма.

Вектор скорости точки на плане скоростей в масштабе будет изображаться вектором , а величина скорости точки равна:

Ответ:

Задача №3

В состав рычажного механизма (рис.4.29) входят два кривошипа 1 и 4, и два шатуна 2 и 3. Кривошип 1 вращается с угловой скоростью , а кривошип 4 с угловой скоростью .

Найти угловые скорости шатунов 2 и 3 и абсолютные скорости точек и , если: В данном положении механизма кривошип 1 расположен вертикально, а кривошип 2 – горизонтально.

Решение. Особенность этой задачи заключается в том, что определить сразу направление скорости точки невозможно. Но точка одновременно принадлежит к двум телам (шатуну и шатуну ), и для нее можно записать два векторных уравнения распределения скоростей при плоском движении (относительно точек и ), что позволяет решить задачу.

1. В соответствии с исходными данными в произвольном масштабе строим схему механизма (рис.4.30, а).

2. Так как точка принадлежит кривошипу 1, который вращается вокруг шарнира с угловой скоростью , то:

Вектор скорости направлен перпендикулярно в сторону вращения кривошипа 1 (рис.4.30, а).

Шатун 2 механизма движется плоскопараллельно. Скорость точки шатуна 2 равна скорости точки кривошипа 1.

Для определения скорости точки шатуна 2 запишем формулу распределения скоростей при плоском движении:

где — абсолютная скорость точки , величина и направление которой является неизвестным;

— абсолютная скорость точки ;

— относительная скорость точки при ее вращении вместе с шатуном 2 вокруг полюса . Направлен вектор перпендикулярно .

В уравнении (1) три неизвестных: величина и направление скорости точки ; величина скорости . Поскольку векторное уравнение

для плоскости позволяет определить только две неизвестных, то решить уравнение (1) невозможно.

3. Рассмотрим определение скорости точки шатуна 3 относительно точки .

Скорость точки кривошипа 4 равна:

Вектор скорости направлен перпендикулярно в сторону вращения кривошипа 4 (рис.4.30, а).

Учитывая, что шатун 3 механизма движется плоскопараллельно, то для определения скорости точки шатуна 3 запишем формулу распределения скоростей при плоском движении:

где — абсолютная скорость точки ;

— относительная скорость точки в ее относительном вращательном движении вместе с шатуном 3 вокруг полюса . Направлен вектор перпендикулярно .

В записанной системе векторных уравнений (1,2) четыре неизвестных: величина и направление скорости точки ; величина скорости ; величина скорости . Поскольку из каждого уравнения можно определить две неизвестных, то записанная система является определенной и ее можно решить.

4. Решаем записанную систему векторных уравнений (1) и (2) графически. Для этого из произвольной точки построим сначала уравнение (1), а затем (2) (рис.4.30, б).

Согласно уравнению (1) из произвольной точки проводим вектор параллельно , который будет изображать скорость точки . Длину отрезка выберем .

Тогда масштабный коэффициент плана скоростей будет равен:

Теперь построим из того же самого полюса уравнение (2). Сначала отложим вектор параллельно , который в масштабе будет изображать скорость точки . Длина этого вектора соответственно равна:

Через конец вектора проводим линию перпендикулярно , вдоль которой от точки будет направлен вектор относительной скорости .

Точка пересечения прямых и , которая одновременно удовлетворяет векторным уравнением (1) и (2), и будет решением системы, а вектор который на плане скоростей изображает будет направлен от полюса к точке .

Полученный на рис. 4.30,б четырехугольник представляет собой план скоростей механизма в данном положении. В этом четырехугольнике: вектор определяет относительную скорость ; вектор — относительную скорость ; — абсолютную скорость точки .

Перенесем направления скоростей и на рис. 4.30,а и, померив длины соответствующих отрезков, определим величины этих скоростей:

5. Определим мгновенные угловые скорости шатунов.

Поскольку , то:

Направление угловой скорости определяется направлением относительной скорости . С рис.4.30, а видно, что будет направлена против хода часовой стрелки.

Аналогично, угловая скорость шатуна 3 равна:

Направление определяется относительной скоростью . Направлена угловая скорость шатуна 3 по ходу часовой стрелки.

Для определения скорости точки воспользуемся теоремой подобия. Поскольку точка на схеме механизма лежит посередине шатуна , то и на плане скоростей она должна лежать посередине отрезка .

Ответ:

План ускорений

План ускорений – построенный в определенном масштабе векторный график, характеризующие ускорения всех точек и звеньев механизма. Произвольная точка ра, из которой производится построение плана ускорений, называется полюсом плана ускорений.

Рассмотрим графический способ определения ускорений точек плоской фигуры (тела) с помощью плана ускорений.

Планом ускорений плоской фигуры является геометрическое место концов векторов ускорений любых точек фигуры, что отложены из одной произвольной точки, которую называют полюсом плана ускорений.

Построение плана ускорений основано на представлении ускорения любой точки фигуры в виде суммы трех векторов:

где — ускорение точки фигуры, которую принято за полюс поступательного движения;

— относительное нормальное (центростремительное) ускорение точки в ее относительном вращательном движении вместе с телом вокруг полюса . Направлено это ускорение от точки к точке и по модулю равно

— относительное тангенциальное (касательное) ускорение точки в ее относительном вращательном движении вместе с телом вокруг полюса . Направлено это ускорение перпендикулярно (отрезка ) в сторону углового ускорения тела и по модулю равно

Поскольку для определения величины надо знать угловую скорость плоской фигуры, то, если она не задана, предварительно надо построить план скоростей. Из плана скоростей определить относительную скорость вращения одной точки фигуры относительно второй и найти угловую скорость относительного вращательного движения (занятие 7).

Для того, чтобы уравнение (4.18) можно было решить, должно быть известно ускорение любой точки фигуры, которую выбирают за полюс поступательного движения.

Кроме того, должно быть известно:

Рассмотрим определение ускорений точек и треугольника (рис.4.31, а). Известными являются ускорение точки , направление ускорения точки и угловая скорость треугольника , то есть случай 1.

Для ускорения точки , если за полюс выбрать точку , будет справедливым векторное уравнение (4.18).

Решим уравнение (4.18) графически. Для этого (рис.4.31, б) из произвольной точки (полюса плана ускорений) построим вектор , который в масштабе будет изображать ускорение . С конца построенного вектора (точки ) построим вектор , который в том же масштабе будет изображать ускорение .

Величину ускорения определим из формулы:

а направлен этот вектор вдоль от точки к точке .

К нормальному ускорению добавим, согласно уравнению (4.18), тангенциальное ускорение . Поскольку величина этого ускорения неизвестна, то через точку (конец вектора ) проведем линию перпендикулярно , вдоль которой и будет направлен вектор .

Направление абсолютного ускорения точки известно из условия задачи. Поскольку все абсолютные ускорения точек на плане откладываются от полюса , то через полюс проведем прямую, параллельную направлению ускорения точки . Точка пересечения линий и будет решением уравнения (4.18), а вектор будет в выбранном масштабе изображать ускорение точки .

Для определения ускорения точки воспользуемся тем, что известными уже являются ускорения двух точек фигуры и (случай 2).

Запишем векторные уравнения для ускорения точки относительно полюсов и :

где и — относительные нормальные ускорения точки в ее относительном вращательном движении соответственно вокруг точек и ;

и — относительные тангенциальные ускорения точки в ее относительном вращательном движении вокруг точек и , соответственно.

Первым решаем уравнение (4.19). Поскольку ускорение точки на плане (рис.4.31, б) уже построено, то с его конца (точки ) строим вектор , который направлен от точки к точке и по модулю в масштабе равен :

Через конец вектора проводим прямую, перпендикулярную , вдоль которой будет направлено ускорение и на которой будет лежать точка конца вектора .

Следующим построим уравнение (4.20). Поскольку ускорение точки на плане уже построено, то с его конца, точки , строим вектор , который направлен от к и по модулю в масштабе равен :

Таким образом, конец вектора будет лежать на пересечении линий, вдоль которых будут направлены тангенциальные ускорения и . Вектор на плане ускорений будет в масштабе изображать абсолютное ускорение точки .

Векторы , и , выходящие из полюса плана ускорений, определяют абсолютные ускорения точек , и . Отрезки же, соединяющие концы векторов абсолютных ускорений и определяют относительные ускорения одних точек при их вращении вокруг других

Кроме абсолютных и относительных ускорений точек фигуры , определяется величина ее углового ускорения :

или или

Для определения же направления углового ускорения надо перенести в точку вектор тангенциального ускорения и направление этого вектора укажет направление углового ускорения. В данном случае, угловое ускорение направлено по ходу часовой стрелки.

Треугольник , который образовался на плане ускорений будет подобно треугольнику .

Таким образом, для плана ускорений справедливо

правило подобия: фигура, которую образуют концы векторов абсолютных ускорений точек тела на плане ускорений подобная фигуре, которую одноименные точки образуют на теле.

Примеры решения задач на тему: План ускорений

Задача №1

Найти ускорение точки ползуна 3 и угловое ускорение шатуна 2 механизма, изображенном на рис.4.24. Выходные данные: , кривошип 1 вращается равномерно

Решение. План скоростей для этого механизма был построен в задаче № 1 занятия № 7 (рис.4.25,б) и была определена угловая скорость шатуна 2

1.Построим схему механизма (рис. 4.32, а).

2. Сначала найдем ускорение точки механизме, поскольку она принадлежит кривошипу 1, который вращается вокруг точки с известной угловой скоростью.

Учитывая, что угловая скорость кривошипа постоянная то и полное ускорение будет равняться нормальному ускорению точки в ее вращательном движении вокруг :

По модулю:

Направлено ускорение от точки к точке по линии .

3. Для определения ускорения точки запишем формулу распределения ускорений при плоском движении, приняв за полюс точку , ускорение которой уже известно:

где — абсолютное ускорение точки , которое направлено по направлению движения ползуна 3 в горизонтальных направляющих;

— ускорение точки , известное по величине и по направлению;

— относительное нормальное ускорение точки в ее относительном вращательном движении вокруг точки , направлено по шатуну от точки к точке и по модулю равно:

— тангенциальное ускорение точки при ее вращении вокруг точки , направлено перпендикулярно шатуну и по модулю равно:

Поскольку направление ускорения точки известно, то уравнение (1) достаточно для определения .

4. Решим уравнение (1) графически путем построения плана ускорений.

Из произвольной точки полюса плана ускорений (рис.4.32,б) отложим вектор , который будет изображать ускорение , и который направлен параллельно линии от точки к точке . От конца этого вектора отложим вектор , что будет изображать , и который направлен параллельно от точки к точке . Через конец вектора , точку , проведем линию , перпендикулярную , вдоль которой будет направлено тангенциальное ускорение и на этой линии будет лежать точка — конец вектора абсолютного ускорения точки механизма.

Поскольку ускорение направлено по оси движения ползуна 3, то с полюса проводим горизонтальную прямую. Точка пересечения этой прямой с линией , проведенная перпендикулярно , будет концом вектора ускорения точки , а вектор будет изображать на плане ускорений .

4. Из построенного плана ускорений определим абсолютные величины ускорений и . Для этого с полюса опустим перпендикуляр на продолжение линии . Угол равен углу и составляет .

Из векторного четырехугольника (рис. 4.32, б) вытекает:

Спроектируем векторное уравнение (2) на прямую :

Учитывая, что изображает на плане ускорений , , уравнение (3) можно переписать следующим образом:

Откуда:

Теперь спроектируем уравнение (2) на прямую :

Учитывая, что на плане ускорений изображает , получим:

Откуда:

Поскольку , то:

Из полученного результата следует, что в данный момент времени шатун механизма вращается равномерно и план ускорений будет иметь вид как на рис.4.33.

Ответ:

Если построение плана ускорений выполнять с соблюдением масштаба, то ускорения характерных точек можно определить непосредственно измерением соответствующих отрезков на плане ускорений.

Задача №2

Найти абсолютное ускорение точек и на угловые ускорения шатуна 2 и коромысла 3 шарнирного механизма, схема которого изображена на рис.4.26, если: . Кривошип 1 механизма вращается с постоянной угловой скоростью

Решение. План скоростей механизма для положения, что рассматривается, был построен в задаче № 2 занятие № 7 (рис.4.27, б) и определены мгновенные угловые скорости шатуна 2 и коромысла 3:

Решим задачу путем построения в масштабе плана ускорений.

1. Сначала в произвольном масштабе строим схему механизма (рис.4.34, а).

2.Определим ускорение точки кривошипа.

Поскольку кривошип 1 вращается вокруг неподвижной точки с постоянной угловой скоростью (то есть и соответственно ), то ускорение точки :

По модулю равно:

Направлено ускорение от точки к точке .

3.Запишем векторные уравнения для определения ускорения точки .

Точка принадлежит одновременно шатуну 2 и коромыслу 3 (случай 3). У шатуна 2 известно уже определенное ускорение точки , а в коромысла 3 ускорение точки (точка неподвижная, то есть ). Таким образом, можно записать формулы распределения ускорений для точки , взяв за полюс точку для шатуна 2 в первом уравнении и точку для коромысла 3 во втором уравнении:

где — относительное нормальное ускорение точки в ее относительном вращательном движении вокруг точки , направлено вдоль от точки к точке и по модулю равно:

— относительное тангенциальное ускорение точки в ее относительном вращательном движении вокруг точки , направлено перпендикулярно и по модулю равно:

— относительное нормальное ускорение точки в ее относительном вращательном движении вокруг точки , направлено вдоль от точки к точке и по модулю равно:

4.Решим графически систему векторных уравнений (1,2).

Сначала построим уравнение (1). Для этого из произвольной точки полюса плана ускорений (рис.4.34,б) отложим вектор , который будет изображать ускорение . Направлен вектор параллельно линии от точки к точке . Длину этого вектора выберем . Тогда масштабный коэффициент плана ускорений будет равняться:

От конца вектора отложим вектор , который будет изображать . Направлен вектор параллельно от точки к точке , а длина этого вектора равна:

Через конец вектора проведем линию перпендикулярную , вдоль которой будет направлено тангенциальное ускорение и на этой линии будет лежать точка — конец вектора абсолютного ускорения точки механизма.

Следующим построим уравнение (2).

Поскольку , то точка будет лежать в полюсе плана ускорений.

От точки отложим вектор , который будет изображать . Направлен вектор параллельно от точки к точке , а длина этого вектора соответственно равна:

Через конец вектора проведем линию перпендикулярную , вдоль которой будет направлено тангенциальное ускорение .

Решением системы (1,2) будет точка , в которой пересекаются линии, проведенные перпендикулярно и , вдоль которых направлены соответственно тангенциальные ускорения и .

Вектор абсолютного ускорения точки на плане ускорений в масштабе будет изображаться вектором , а величина ускорения точки равна:

Величины тангенциальных ускорений и найдем путем измерения соответствующих отрезков на плане ускорений:

Поскольку и , то мгновенные угловые ускорения шатуна 2 и коромысла 3 соответственно равны:

где — длина коромысла 3, которая была определена в задаче №2 занятия №7.

Для определения направления углового ускорения перенесем мысленно в точку относительное тангенциальное ускорение . Направление указывает на то, что будет направлено по ходу часовой стрелки.

Аналогично, для определения направления в точку перенесем . Угловое ускорение будет направлено против хода часовой стрелки.

5.Для определения ускорения точки воспользуемся теоремой подобия. Для этого сначала построим прямую на плане ускорений (рис.4.34, б). Поскольку фигура на схеме механизма и фигура на плане ускорений должны быть подобными, то можно составить пропорцию:

В левой части пропорции (3) отношение отрезков на схеме механизма, а в правой — на плане ускорений.

Из уравнения (3) получим расстояние от точки к точке на плане ускорений:

Поскольку на схеме механизма отрезок перпендикулярен , то и на плане ускорений отрезок надо провести перпендикулярно , причем в ту сторону, чтобы расположение точек , и на плане ускорений было против хода часовой стрелки, как и точки , и на схеме механизма.

Ответ:

Задача №3

В состав рычажного механизма (рис.4.35) входят два кривошипа 1 и 4, и два шатуна 2 и 3. Кривошип 1 в настоящий момент времени вращается равномерно с угловой скоростью , а кривошип 4 – замедленно с угловой скоростью и угловым ускорением

Найти угловые ускорения шатунов 2 и 3 и абсолютные ускорения точек и , если: . В данном положении механизма кривошип 1 расположен вертикально, а кривошип 4 — горизонтально.

Решение. План скоростей механизма для положения, что рассматривается, был построен в задаче №3 занятия №7 (рис.4.30, б) и определены мгновенные угловые скорости шатуна 2 и шатуна 3:

1. В произвольном масштабе построим схему механизма (рис. 4.36, а).

2.Сначала определим абсолютные ускорения точек и , принадлежащие соответственно кривошипам 1 и 4, угловые скорости которых известны.

Поскольку кривошип 1 вращается вокруг неподвижной точки с постоянной угловой скоростью то есть , то:

Направлено ускорение вдоль кривошипа от точки к точке .

Кривошип 4 вращается вокруг неподвижной точки с угловой скоростью и угловым ускорением . Поскольку кривошип 4 вращается замедленно, то угловое ускорение направлено противоположно угловой скорости (рис.4.35.)

Абсолютное ускорение точки кривошипа 4 представляет собой векторную сумму нормальной и тангенциальной составляющих:

Нормальная составляющая ускорения точки направлена вдоль от точки к точке и по модулю равна:

а тангенциальная — перпендикулярно в сторону углового ускорения и по модулю равна:

3. Запишем векторные уравнения для определения ускорения точки .

Точка принадлежит одновременно шатуну 2 и шатуну 3. У шатуна 2 известно ускорение точки , а у шатуна 3 — точки . Таким образом, можно записать формулы распределения ускорений для точки , взяв за полюс точку для шатуна 2 в первом уравнении и точку шатуна 3 во втором:

В уравнении (2):

— направлено вдоль от точки к точке и по модулю равно:

— направлено перпендикулярно , величина и направление этого ускорения неизвестны.

В уравнении (3):

— направлено вдоль от точки к точке и по модулю равно:

— направлено перпендикулярно , величина и направление этого ускорения неизвестны.

4. Решим графически систему векторных уравнений (2,3).

Сначала построим уравнение (2). Для этого из произвольной точки полюса плана ускорений (рис.4.36,б) отложим вектор , который будет изображать ускорение . Направлен вектор параллельно линии от точки к точке . Длину этого вектора выберем . Тогда масштабный коэффициент плана ускорений будет равняться:

Следующим построим уравнение (3).

Для построения вектора от полюса согласно уравнению (1) отложим вектор , а с его конца . Эти векторы в масштабе будут изображать ускорения и и будут направлены им параллельно (рис. 4.36, а).

Длины векторов и соответственно равны:

Абсолютное ускорение точки на плане ускорений будет изображаться вектором .

От точки отложим вектор , который будет изображать. Направлен вектор параллельно от точки к точке , а длина этого вектора равна:

Решением системы (2,3) будет точка , в которой пересекаются линии, проведенные перпендикулярно и , вдоль которых направлены соответственно тангенциальные ускорения и .

Величины тангенциальных ускорений и найдем путем измерения соответствующих отрезков на плане ускорений:

Поскольку и , то мгновенные угловые ускорение шатуна 2 и шатуна 3 соответственно равны:

Направления угловых ускорений и определяем путем перенесения мысленно в точку относительных тангенциальных ускорений и (аналогично задаче №2). Угловое ускорение направлено по ходу часовой стрелки, а — против хода часовой стрелки.

5. Для определения ускорения точки воспользуемся теоремой подобия. Поскольку точка на схеме механизма лежит посередине шатуна , то и на плане ускорений она должна лежать посередине отрезка . Вектор ускорения точки плане ускорений в масштабе будет изображаться вектором , а величина абсолютного ускорения точки равна:

Ответ:

Услуги по теоретической механике:

Заказать теоретическую механику
Помощь по теоретической механике
Заказать контрольную работу по теоретической механике

Учебные лекции:

Статика
Система сходящихся сил
Момент силы
Пара сил
Произвольная система сил
Плоская произвольная система сил
Трение
Расчет ферм
Расчет усилий в стержнях фермы
Пространственная система сил
Произвольная пространственная система сил
Плоская система сходящихся сил
Пространственная система сходящихся сил
Равновесие тела под действием пространственной системы сил
Естественный способ задания движения точки
Центр параллельных сил
Параллельные силы
Система произвольно расположенных сил
Сосредоточенные силы и распределенные нагрузки
Кинематика
Кинематика твердого тела
Движения твердого тела
Динамика материальной точки
Динамика механической системы
Динамика плоского движения твердого тела
Динамика относительного движения материальной точки
Динамика твердого тела
Кинематика простейших движений твердого тела
Общее уравнение динамики
Работа и мощность силы
Обратная задача динамики
Поступательное и вращательное движение твердого тела
Плоскопараллельное (плоское) движение твёрдого тела
Сферическое движение твёрдого тела
Движение свободного твердого тела
Сложное движение твердого тела
Сложное движение точки
Статика твердого тела
Равновесие составной конструкции
Равновесие с учетом сил трения
Центр масс
Колебания материальной точки
Относительное движение материальной точки
Статические инварианты
Дифференциальные уравнения движения точки под действием центральной силы и их анализ
Динамика системы материальных точек
Общие теоремы динамики
Теорема об изменении кинетической энергии
Теорема о конечном перемещении плоской фигуры
Потенциальное силовое поле
Метод кинетостатики
Вращения твердого тела вокруг неподвижной точки

Источник

Способы нахождения мгновенного центра скоростей

Вычисление угловой скорости при плоском движении

Ускорения точек тела при плоском движении

§3. Криволинейное движение. Плоскопараллельное движение твердого тела

3.6 Плоскопараллельное движение

Примечания

Плоское движение тела

Определение скоростей точек тела

Уравнения плоского движения

Скорости точек фигуры. Мгновенный центр скоростей

Определение положения мгновенного центра скоростей

Порядок решения задач на тему: Определение скоростей точек тела

Примеры решения задач на тему: Определение скоростей точек тела

Решение задачи графоаналитическим способом

Решение задачи с помощью мгновенного центра скоростей

Определение ускорений точек тела

Ускорения точек плоской фигуры

Порядок решения задач на тему: Определение ускорений точек тела

Примеры решения задач на тему: Определение ускорений точек тела

План скоростей

Порядок решения задач на тему: План скоростей

Примеры решения задач на тему: План скоростей

План ускорений

Примеры решения задач на тему: План ускорений

Не пропустите также: