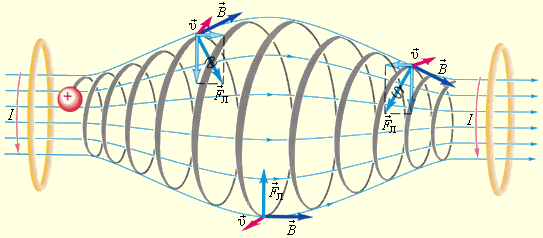
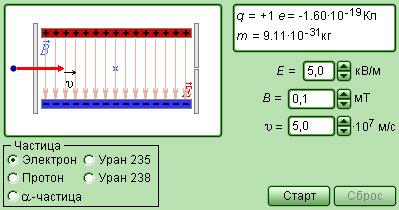
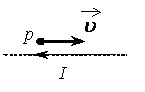Пусть в однородном магнитном поле, индукция которого , движется частица со скоростью
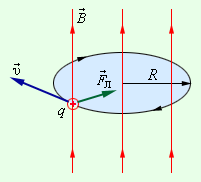
, направленной перпендикулярно линиям индукции. Масса частицы m и заряд q. Так как сила Лоренца
перпендикулярна скорости
движения частицы (см. рис. 170), то эта сила изменяет только направление скорости, сообщая частице центростремительное ускорение, модуль которого согласно второму закону Ньютона:
В результате частица движется по окружности, радиус которой можно определить из формулы :
Период Т обращения частицы, движущейся по окружности в однородном магнитном поле:
(30.2)
Как следует из выражения (30.2), период обращения частицы не зависит от модуля скорости её движения и радиуса траектории, а определяется только модулем заряда частицы, её массой и значением индукции магнитного поля.
От теории к практике
В однородном магнитном поле, модуль индукции которого В = 4,0 мТл, перпендикулярно линиям индукции поля движется электрон. Чему равен модуль ускорения электрона, если модуль скорости его движения ? Масса и модуль заряда электрона mе = 9,1 · 10–31 кг и е = 1,6 · 10–19 Кл соответственно.
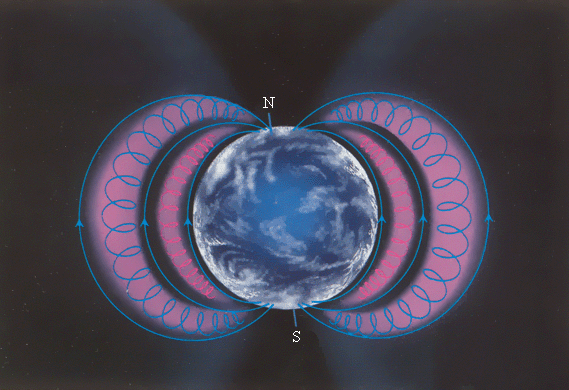
Подобное явление происходит в магнитном поле Земли, которое является защитой для всего живого от потоков заряженных частиц из космического пространства. Движущиеся с огромными скоростями заряженные частицы из космоса захватываются магнитным полем Земли и образуют так называемые радиационные пояса (рис. 170.2), в которых частицы перемещаются по винтообразным траекториям между северным и южным магнитными полюсами туда и обратно за промежуток времени порядка долей секунды. Лишь в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные сияния (рис. 170.3).
Если заряженная частица в момент возникновения внешнего электрического поля покоилась, то , где U — напряжение между точками, в которых находилась частица в моменты возникновения внешнего электрического поля и выхода из него, q — модуль заряда частицы. Поэтому модуль скорости частицы при выходе из электрического поля:
Если после этого частица попадает в однородное магнитное поле, индукция которого перпендикулярна направлению её скорости, то радиус окружности, по дуге которой будет двигаться частица,
, откуда
Величину называют удельным зарядом частицы. Поэтому если опытным путём определить радиус траектории движения частицы в магнитном поле, то, зная индукцию магнитного поля и ускоряющее напряжение электрического поля, можно рассчитать удельный заряд частицы. Этот метод используют при конструировании приборов, которые называют масс–спектрометрами.
Интересно знать
Поскольку сила Лоренца направлена под углом 90° к скорости движения заряженной частицы в каждой точке траектории (рис. 171), то работа этой силы при движении заряженной частицы в магнитном поле равна нулю. Поэтому кинетическая энергия частицы, движущейся в стационарном (не изменяющемся во времени) магнитном поле, не изменяется, т. е. стационарное магнитное поле нельзя использовать для ускорения заряженных частиц.
Увеличение кинетической энергии частицы, т. е. её разгон, возможно под действием электрического поля (в этом случае изменение кинетической энергии частицы равно работе силы поля). Поэтому в современных ускорителях (рис. 172) заряженных частиц электрическое поле используют для ускорения, а магнитное — для «формирования» траектории движения заряженных частиц.
1. Как определить модуль силы, действующей со стороны магнитного поля на движущуюся в нём заряженную частицу?
2. Как определяют направление силы Лоренца?
3. Заряженная частица движется в однородном магнитном поле со скоростью, направленной перпендикулярно линиям индукции. По какой траектории движется частица?
4. От чего зависит период обращения заряженной частицы в однородном магнитном поле?
5. Почему сила Лоренца изменяет направление скорости движения частицы, но не влияет на её модуль?
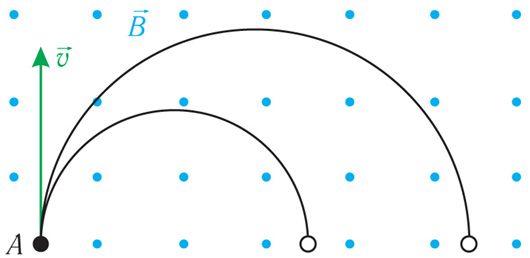
6. На рисунке 172.1 представлены траектории движения двух частиц, имеющих одинаковые заряды. Частицы влетают в однородное магнитное поле из одной точки А с одинаковыми скоростями. Определите знак заряда частиц. Объясните причину несовпадения траекторий их движения.
Сила Лоренца
теория по физике 🧲 магнетизм
Сила Лоренца — сила, действующая на движущуюся заряженную частицу со стороны магнитного поля.
Модуль силы Лоренца обозначается как FЛ. Единица измерения — Ньютон (Н).
Модуль силы Лоренца численно равен отношению модуля силы F, действующий на участок проводника длиной l, к числу N заряженных частиц, упорядоченно движущихся на этом участке проводника:
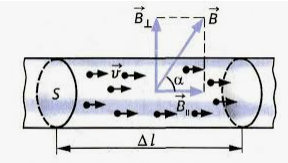
Рассмотрим отрезок тонкого прямого проводника с током. Пусть длина отрезка ∆l и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля → B можно считать неизменным в пределах этого отрезка проводника.
Сила тока I в проводнике связана с зарядом частиц q, концентрацией заряженных частиц (число зарядов в единице объема) и скоростью их упорядоченного движения v следующей формулой:
Модуль силы, действующей со стороны магнитного поля на выбранные элемент тока, равен:
F = | I | Δ l B sin . α
Подставляя сюда выражение, полученное для силы тока, получим:
F = | q n v S | Δ l B sin . α = | q | n v S Δ l B sin . α
Учтем, что число заряженных частиц в рассматриваемом объеме равно произведению величины этого объема на концентрацию самих частиц:
F = | q | v N B sin . α
Следовательно, на каждый движущийся заряд действует сила Лоренца, равная:
F Л = F N . . = | q | v N B sin . α N . . = | q | v B sin . α
α — угол между вектором скорости движущегося заряда и вектором магнитной индукции.
Пример №1. Определить силу, действующую на заряд 0,005 Кл, движущийся в магнитном поле с индукцией 0,3 Тл со скоростью 200 м/с под углом 45 o к вектору магнитной индукции.
F Л = | q | v B sin . α = 0 , 005 · 200 · 0 , 3 · √ 2 2 . . ≈ 0 , 2 ( Н )
Направление силы Лоренца
Сила Лоренца перпендикулярна вектору магнитной индукции и вектору скорости движущегося заряда. Ее направление определяется с помощью правила левой руки:
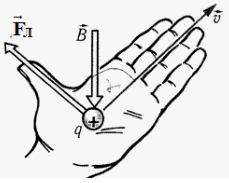
Если левую руку расположить так, чтобы составляющая магнитной индукции → B , перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца.
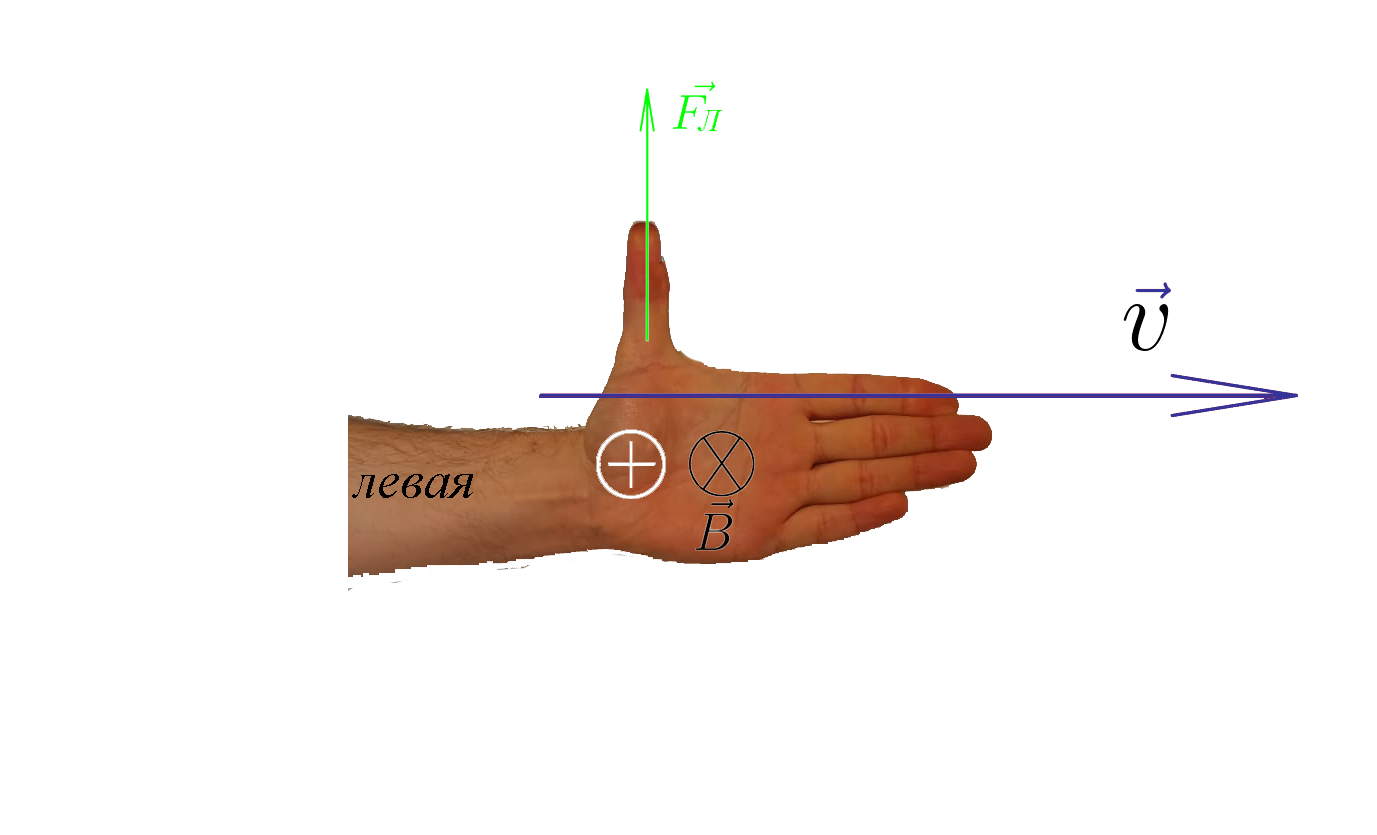
Пример №2. Протон p имеет скорость → v , направленную горизонтально вдоль прямого длинного проводника с током I (см. рисунок). Куда направлена действующая на протон сила Лоренца?
В точке, в которой находится протон, вектор магнитной индукции направлен в сторону от наблюдателя. Это следует из правила буравчика. Теперь применим правило левой руки. Для этого четыре пальца левой руки направим в сторону движения протона — вправо. Ладонь развернем в сторону наблюдателя, чтобы линии магнитной индукции входили в нее перпендикулярно. Теперь отставим на 90 градусов большой палец. Он показывает вверх. Следовательно, сила Лоренца, действующая на протон, направлена вверх.
Работа силы Лоренца
Поскольку вектор силы Лоренца направлен перпендикулярно скорости движения заряда, угол между перемещением этого заряда и этой силы равен 90 о . Работа любой силы определяется формулой:
Но так как косинус 90 о равен 0, сила Лоренца не совершает работу. Это значит, что сила Лоренца не влияет на модуль скорости перемещения заряда. Но она может менять вектора его скорости.
Полная сила, действующая на заряд
При решении задач, в которых заряженная частица находится одновременно в электрическом и магнитном полях, нужно учитывать, что не нее действует сразу две силы. Со стороны магнитного поля — сила Лоренца. Со стороны электрического поля — сила → F э л , действующая на неподвижный заряд, помещенный в данную точку поля. Она равна произведению этого заряда на напряженность электрического поля:
Следовательно, полная сила, действующая на заряд, равна:
→ F = → F э л + → F л = q → E + | q | → v → B sin . α
Пример №3. В пространстве, где существует одновременно однородное и постоянное электрическое и магнитное поля, по прямолинейной траектории движется протон. Известно, что напряженность электрического поля равна → E . Какова индукция → B магнитного поля?
Прямолинейное движение протона возможно в двух случаях:
- Вектор → E направлен вдоль траектории движения протона. Тогда вектор → B также должен быть направлен вдоль этой траектории, и его модуль может быть любым, так как магнитное поле на частицу действовать не будет.
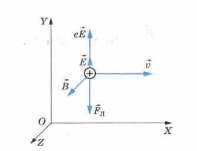
- Векторы → E , → B и → v взаимно перпендикулярны, и сила, действующая на протон со стороны электрического поля, равна по модулю и противоположна по направлению силе Лоренца, действующей на протон со стороны магнитного поля (см. рисунок).
Заряд протона равен модулю заряда электрона — e . Сложим силы, действующие на протон по оси ОУ:
В скалярной форме:
Протон ускоряется постоянным электрическим полем конденсатора, напряжение на обкладках которого 2160 В. Затем он влетает в однородное магнитное поле и движется по дуге окружности радиуса 20 см в плоскости, перпендикулярной линиям магнитной индукции. Каков модуль вектора индукции магнитного поля? Начальной скоростью протона в электрическом поле пренебречь. Ответ выразить в мТл, округлив до десятых.
Формула силы Лоренца
Определение и формула силы Лоренца
Сила $bar$ , действующая на движущуюся заряженную частицу в магнитном поле, равная:
называется силой Лоренца (магнитной силой).
Исходя из определения (1) модуль рассматриваемой силы:
$$F=q v B sin alpha(2)$$
где $bar$ – вектор скорости частицы, q – заряд частицы, $bar$ – вектор магнитной индукции поля в точке нахождения заряда, $alpha$ – угол между векторами $bar$ и $bar$. Из выражения (2) следует, что если заряд движется параллельно силовым линиям магнитного поля,то сила Лоренца равна нулю. Иногда силу Лоренца стараясь выделить, обозначают, используя индекс: $bar_L$
Направление силы Лоренца
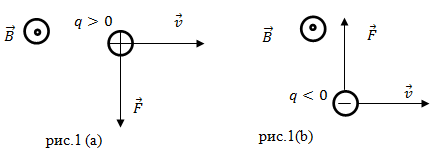
Сила Лоренца (как и всякая сила) – это вектор. Ее направление перпендикулярно вектору скорости $bar$ и вектору $bar$ (то есть перпендикулярно плоскости, в которой находятся векторы скорости и магнитной индукции) и определяется правилом правого буравчика (правого винта) рис.1 (a). Если мы имеем дело с отрицательным зарядом, тонаправление силы Лоренца противоположно результату векторного произведения 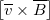
вектор $bar$ направлен перпендикулярно плоскости рисунков на нас.
Следствия свойств силы Лоренца
Так как сила Лоренца направлена всегда перпендикулярно направлению скорости заряда, то ее работа над частицей равна нулю. Получается, что воздействуя на заряженную частицу при помощи постоянного магнитного поля нельзя изменить ее энергию.
Если магнитное поле однородно и направлено перпендикулярно скорости движения заряженной частицы, то заряд под воздействием силы Лоренца будет перемещаться по окружности радиуса R=const в плоскости, которая перпендикулярна вектору магнитной индукции. При этом радиус окружности равен:
где m – масса частицы,|q|- модуль заряда частицы, $gamma=frac<1><sqrt<1-frac>>>>$ – релятивистский множитель Лоренца, c – скорость света в вакууме.
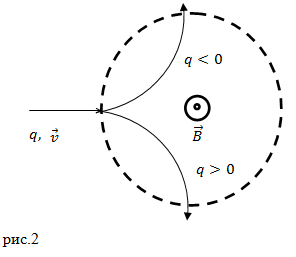
Сила Лоренца — это центростремительная сила. По направлению отклонения элементарной заряженной частицы в магнитном поле делают вывод о ее знаке (рис.2).
Формула силы Лоренца при наличии магнитного и электрического полей
Если заряженная частица перемещается в пространстве, в котором находятся одновременно два поля (магнитное и электрическое), то сила, которая действует на нее, равна:
где $bar$ – вектор напряженности электрического поля в точке, в которой находится заряд. Выражение (4) было эмпирически получено Лоренцем. Сила $bar$, которая входит в формулу (4) так же называется силой Лоренца (лоренцевой силой). Деление лоренцевой силы на составляющие: электрическую $(bar = q bar)$ и магнитную $(bar=q[bar times bar])$ относительно, так как связано с выбором инерциальной системы отсчета. Так, если система отсчета будет двигаться с такой же скоростью $bar$, как и заряд, то в такой системе сила Лоренца, действующая на частицу, будет равна нулю.
Единицы измерения силы Лоренца
Основной единицей измерения силы Лоренца (как и любой другой силы) в системе СИ является: [F]=H
Примеры решения задач
Задание. Какова угловая скорость электрона, который движется по окружности в магнитном поле с индукцией B?
Решение. Так как электрон (частица имеющая заряд) совершает перемещение в магнитном поле, то на него действует сила Лоренца вида:
где q=qe – заряд электрона. Так как в условии сказано, что электрон движется по окружности, то это означает, что $bar perp bar$, следовательно, выражение для модуля силы Лоренца примет вид:
Сила Лоренцаявляется центростремительной и кроме того, по второму закону Ньютона будет в нашем случае равна:
Приравняем правые части выражений (1.2) и (1.3), имеем:
Из выражения (1.3) получим скорость:
Период обращения электрона по окружности можно найти как:
Зная период, можно найти угловую скорость как:
Ответ. $omega=frac B>$
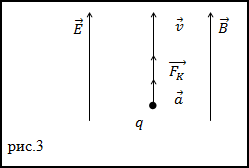
Задание. Заряженная частица (заряд q, масса m) со скоростью vвлетает в область, где имеется электрическое поле напряженностью E и магнитное поле с индукцией B. Векторы $bar$ и $bar$ совпадают по направлению. Каково ускорение частицы в моментначалаперемещения в полях, если $bar uparrow bar uparrow bar$?
Решение. Сделаем рисунок.
На заряженную частицу действует сила Лоренца:
Магнитная составляющая имеет направление перпендикулярное вектору скорости ($bar$) и вектору магнитной индукции ($bar$). Электрическая составляющая сонаправлена с вектором напряжённости ($bar$) электрического поля. В соответствии со вторым законом Ньютона имеем:
Получаем, что ускорение равно:
Если скорость заряда параллельна векторам $bar$ и $bar$, тогда $[bar times bar]=0$, получим:
Сила Лоренца
Сила Лоренца. Определение и формула
Сила Ампера, воздействующая на часть проводника длиной Δ l с некоторой силой тока I , находящийся в магнитном поле B , F = I · B · Δ l · sin α может выражаться через действующие на конкретные носители заряда силы.
Пускай заряд носителя обозначается как q , а n является значением концентрации носителей свободного заряда в проводнике. В этом случае произведение n · q · υ · S , в котором S представляет собой площадь поперечного сечения проводника, эквивалентно току, протекающему в проводнике, а υ – это модуль скорости упорядоченного движения носителей в проводнике:
Формула силы Ампера может записываться в следующем виде:
F = q · n · S · Δ l · υ · B · sin α .
По причине того, что полное число N носителей свободного заряда в проводнике сечением S и длиной Δ l равняется произведению n · S · Δ l , действующая на одну заряженную частицу сила равняется выражению: F Л = q · υ · B · sin α .
Найденная сила носит название силы Лоренца. Угол α в приведенной формуле эквивалентен углу между вектором магнитной индукции B → и скоростью ν → .
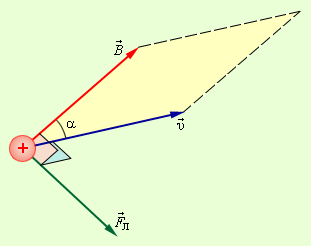
Направление силы Лоренца, которая воздействует частицу с положительным зарядом, таким же образом, как и направление силы Ампера, находится по правилу буравчика или же с помощью правила левой руки. Взаимное расположение векторов ν → , B → и F Л → для частицы, несущей положительный заряд, проиллюстрировано на рис. 1 . 18 . 1 .
Рисунок 1 . 18 . 1 . Взаимное расположение векторов ν → , B → и F Л → . Модуль силы Лоренца F Л → численно эквивалентен произведению площади параллелограмма, построенного на векторах ν → и B → и заряда q .
Сила Лоренца направлена нормально, то есть перпендикулярно, векторам ν → и B → .
Сила Лоренца не совершает работы при движении несущей заряд частицы в магнитном поле. Данный факт приводит к тому, что модуль вектора скорости в условиях движения частицы так же не меняет своего значения.
Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость ν → лежит в плоскости, которая направлена нормально по отношению к вектору B → , то частица будет совершать движение по окружности некоторого радиуса, рассчитывающегося с помощью следующей формулы:
Сила Лоренца в данном случае применяется в качестве центростремительной силы (рис. 1 . 18 . 2 ).
Рисунок 1 . 18 . 2 . Круговое движение заряженной частицы в однородном магнитном поле.
Для периода обращения частицы в однородном магнитном поле будет справедливо следующее выражение:
T = 2 π R υ = 2 π m q B .
Данная формула наглядно демонстрирует отсутствие зависимости заряженных частиц заданной массы m от скорости υ и радиуса траектории R .
Применение силы Лоренца
Приведенное снизу соотношение представляет собой формулу угловой скорости движения заряженной частицы, происходящего по круговой траектории:
ω = υ R = υ q B m υ = q B m .
Оно носит название циклотронной частоты. Данная физическая величина не имеет зависимости от скорости частицы, из чего можно сделать вывод, что и от ее кинетической энергии она не зависит.
Данное обстоятельство находит свое применение в циклотронах, а именно в ускорителях тяжелых частиц (протонов, ионов).
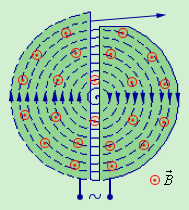
На рисунке 1 . 18 . 3 приводится принципиальная схема циклотрона.
Рисунок 1 . 18 . 3 . Движение заряженных частиц в вакуумной камере циклотрона.
Дуант – это полый металлический полуцилиндр, помещенный в вакуумную камеру между полюсами электромагнита в качестве одного из двух ускоряющих D -образного электрода в циклотроне.
К дуантам приложено переменное электрическое напряжение, чья частота эквивалентна циклотронной частоте. Частицы, несущие некоторый заряд, инжектируются в центре вакуумной камеры. В промежутке между дуантами они испытывают ускорение, вызываемое электрическим полем. Частицы, находящиеся внутри дуантов, в процессе движения по полуокружностям испытывают на себе действие силы Лоренца. Радиус полуокружностей возрастает с увеличением энергии частиц. Как и во всех других ускорителях, в циклотронах ускорение заряженной частицы достигается путем применения электрического поля, а ее удержание на траектории с помощью магнитного поля. Циклотроны дают возможность ускорять протоны до энергии, приближенной к 20 М э В .
Однородные магнитные поля используются во многих устройствах самых разных типов назначений. В частности, они нашли свое применение так называемых масс-спектрометрах.
Масс-спектрометры – это такие устройства, использование которых позволяет нам измерять массы заряженных частиц, то есть ионов или ядер различных атомов.
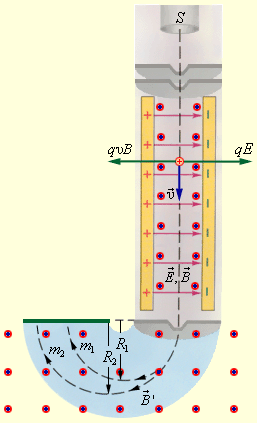
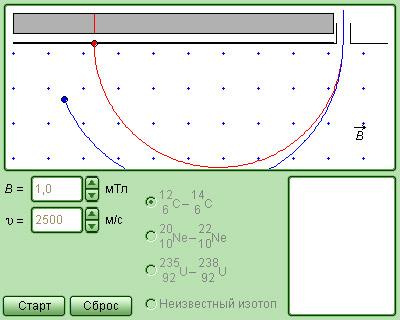
Данные приборы используются для разделения изотопов (ядер атомов с одинаковым зарядом, но разными массами, к примеру, Ne 20 и Ne 22 ). На рис. 1 . 18 . 4 изображен простейшая версия масс-спектрометра. Вылетающие из источника S ионы проходят через несколько малых отверстий, которые в совокупности формируют узкий пучок. После этого они попадают в селектор скоростей, где частицы движутся в скрещенных однородных электрическом, создающимся между пластинами плоского конденсатора, и магнитном, возникающим в зазоре между полюсами электромагнита, полях. Начальная скорость υ → заряженных частиц направлена перпендикулярно векторам E → и B → .
Частица, которая движется в скрещенных магнитном и электрическом полях, испытывает на себе воздействия электрической силы q E → и магнитной силы Лоренца. В условиях, когда выполняется E = υ B , данные силы полностью компенсируют воздействие друг друга. В таком случае частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, которые движутся со скоростью υ = E B .
После данных процессов частицы с одинаковыми значениями скорости попадают в однородное магнитное поле B → камеры масс-спектрометра. Частицы под действием силы Лоренца движутся в камере перпендикулярной магнитному полю плоскости. Их траектории представляют собой окружности с радиусами R = m υ q B ‘ . В процессе измерения радиусов траекторий при известных значениях υ и B ‘ , мы имеем возможность определить отношение q m . В случае изотопов, то есть при условии q 1 = q 2 , масс-спектрометр может разделить частицы с разными массами.
С помощью современных масс-спектрометров мы имеем возможность измерять массы заряженных частиц с точностью, превышающей 10 – 4 .
Рисунок 1 . 18 . 4 . Селектор скоростей и масс-спектрометр.
Магнитное поле
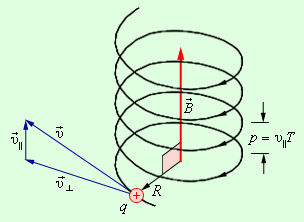
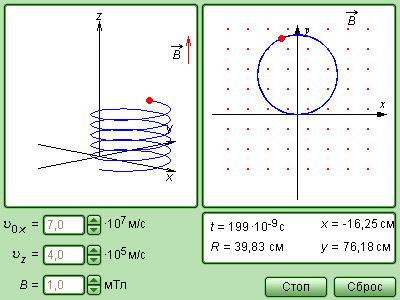
В случае, когда скорость частицы υ → имеет составляющую υ ∥ → вдоль направления магнитного поля, подобная частица в однородном магнитном поле будет совершать спиралевидное движение. Радиус такой спирали R зависит от модуля перпендикулярной магнитному полю составляющей υ ┴ вектор υ → , а шаг спирали p – от модуля продольной составляющей υ ∥ (рис. 1 . 18 . 5 ).
Рисунок 1 . 18 . 5 . Движение заряженной частицы по спирали в однородном магнитном поле.
Исходя из этого, можно сказать, что траектория заряженной частицы в каком-то смысле «навивается» на линии магнитной индукции. Данное явление используется в технике для магнитной термоизоляции высокотемпературной плазмы — полностью ионизированного газа при температуре порядка 10 6 K . При изучении управляемых термоядерных реакций вещество в подобном состоянии получают в установках типа «Токамак». Плазма не должна касаться стенок камеры. Термоизоляция достигается путем создания магнитного поля специальной конфигурации. На рисунке 1 . 18 . 6 в качестве примера проиллюстрирована траектория движения несущей заряд частицы в магнитной «бутылке» (или ловушке).
Рисунок 1 . 18 . 6 . Магнитная «бутылка». Заряженные частицы не выходят за ее пределы. Необходимое магнитное поле может быть создано с помощью двух круглых катушек с током.
Такое же явление происходит в магнитном поле Земли, которое защищает все живое от потока несущих заряд частиц из космического пространства.
Быстрые заряженные частицы из космоса, по большей степени от Солнца, «перехватываются» магнитным полем Земли, вследствие чего образуются радиационные пояса (рис. 1 . 18 . 7 ), в которых частицы, будто в магнитных ловушках, перемещаются туда и обратно по спиралеобразным траекториям между северным и южным магнитными полюсами за доли секунды.
Исключением являются полярные области, в которых часть частиц прорывается в верхние слои атмосферы, что может приводить к возникновению таких явлений, как «полярные сияния». Радиационные пояса Земли простираются от расстояний около 500 к м до десятков радиусов нашей планеты. Стоит вспомнить, что южный магнитный полюс Земли находится поблизости с северным географическим полюсом на северо-западе Гренландии. Природа земного магнетизма до сих пор не изучена.
Рисунок 1 . 18 . 7 . Радиационные пояса Земли. Быстрые заряженные частицы от Солнца, в основном электроны и протоны, попадают в магнитные ловушки радиационных поясов.
Возможно их вторжение в верхние слои атмосферы, служащее причиной возникновения «северных сияний».
Рисунок 1 . 18 . 8 . Модель движения заряда в магнитном поле.
Рисунок 1 . 18 . 9 . Модель Масс-спектрометра.
Рисунок 1 . 18 . 10 . Модель селектора скоростей.
http://www.webmath.ru/poleznoe/formules_21_29_sila_lorenca.php
http://zaochnik.com/spravochnik/fizika/magnitnoe-pole/sila-lorentsa/
Как найти скорость частицы
Часто при изучении школьного курса электромагнетизма или при научных исследованиях возникает необходимость установить скорость, с которой двигалась какая-нибудь элементарная частица, например, электрон или протон.

Инструкция
Допустим, дана следующая задача: электрическое поле с напряженностью Е и магнитное поле с индукцией В, возбуждены перпендикулярно друг другу. Перпендикулярно им, равномерно и прямолинейно движется заряженная частица с зарядом q и скоростью v. Требуется определить ее скорость.
Решение очень простое. Если частица по условиям задачи движется равномерно и прямолинейно, значит, ее скорость v постоянная. Таким образом, в соответствии с первым законом Ньютона, величины действующих на нее сил взаимно уравновешены, то есть в сумме они равны нулю.
Какие силы действуют на частицу? Во-первых, электрическая составляющая силы Лоренца, которая вычисляется по формуле: Fэл = qE. Во-вторых, магнитная составляющая силы Лоренца, которую вычисляют по формуле: Fм = qvBSinα. Поскольку по условиям задачи частица движется перпендикулярно магнитному полю, угол α = 90 градусам, и соответственно, Sinα = 1. Тогда магнитная составляющая силы Лоренца Fм = qvB.
Электрическая и магнитная составляющие уравновешивают друг друга. Следовательно, величины qE и qvB численно равны. То есть Е = vB. Следовательно, скорость частицы вычисляется по такой формуле: v = E/B. Подставив в формулу значения Е и В, вы вычислите искомую скорость.
Или, например, у вас такая задача: частица с массой m и зарядом q, двигаясь со скоростью v, влетела в электромагнитное поле. Его силовые линии (как электрические, так и магнитные) параллельны. Частица влетала под углом α к направлению силовых линий и после этого началась двигаться с ускорением а. Требуется вычислить, с какой скоростью она двигалась первоначально. Согласно второму закону Ньютона, ускорение тела с массой m вычисляется по формуле: a = F/m.
Массу частицы вы знаете по условиям задачи, а F – результирующая (суммарная) величина сил, действующих на нее. В данном случае на частицу действуют электрическая и магнитная оставляющие силы Лоренца: F = qE + qBvSinα.
Но поскольку силовые линии полей (по условию задачи) параллельны, то вектор электрической силы перпендикулярен вектору магнитной индукции. Следовательно, суммарная сила F вычисляется по теореме Пифагора: F = [(qE)^2 + (qvBSinα)^2]^1/2
Преобразуя, получите: am = q[E^2 +B^2v^2Sin^2α]^1/2. Откуда: v^2 = (a^2m^2 – q^2E^2)/(q^2B^2Sin^2α). После вычисления и извлечения квадратного корня, получите искомую величину v.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Сила Лоренца .
Сила Лоренца действует на заряженную частицу, движущуюся в магнитном поле.
( F_л=Bqv cdot sin alpha )
(B) -магнитная индукция, единица измерения Тесла [Тл]
(q) — заряд частицы, единица измерения Кулон [Кл] )
(v) — скорость частицы
( alpha )- угол между вектором магнитной индукции ( vec{B} ) и вектором скорости частицы ( vec{v} )
Направление силы Лоренца, действующей на положительно заряженную частицу .
Если вектор магнитной индукциии входит в ладонь левой руки, а четыре пальца сонаправлены с
направлением вектора скорости положительно заряженной частицы, то отогнутый на ( 90^0 )
большой палец показывает направление силы Лоренца действующей на эту частицу.
Задача 1. (Сила Лоренца)
Пылинка, имеющая заряд (q=10^{-6} Кл) движется в магнитном поле с индукцией
(B=20 Тл) . Скорость пылинки перпендикулярна линиям магнитной индукции и равна
(100 м/с )
Вычислить значение силы Лоренца, действующей на пылинку со стороны магнитного поля.
Дать ответ в миллиньютонах.
Показать ответ
Показать решение
Видеорешение
Задача 2.
Шарик с зарядом (q=100 мкКл) влетает в магнитное поле с
индукцией (B=100 Тл) со скоростью (v=30 м/с .)
Угол между вектором магнитной индукции ( vec{B} ) и вектором скорости частицы
( vec{v} ) составляет ( alpha=30^0 . )
Найти значение силы Лоренца, действующей на шарик со стороны поля.
Показать ответ
Показать решение
Видеорешение
Задача 3. (Сила Лоренца)
Электрон движется в магнитном поле с индукцией
(B=1 Тл) перпендикулярно линиям магнитного поля со скоростью (v=10^8 м/с . )
Вычислить значение силы Лоренца, действующей на электрон со стороны магнитного поля.
Заряд электрона ( q=1,6 cdot 10^{-19} Кл . )
Дать ответ в пиконьютонах.
1 пН ( = 10^{-12} Н . )
Показать ответ
Показать решение
Видеорешение
Задача 4. (Сила Лоренца)
С какой скоростью двигался протон в магнитном поле с индукцией (B=10^{-2} Тл) перпендикулярно линиям поля,
если на него действовала сила Лоренца (F_л=3,2 cdot 10^{-17 } Н ? )
Заряд протона ( q=1,6 cdot 10^{-19} Кл . )
Дать ответ в километрах в секунду.
Показать ответ
Показать решение
Видеорешение
Задача 5. (Сила Лоренца)
Альфа-частица движется в магнитном поле с индукцией (B=10^{-3} Тл) перпендикулярно линиям поля, при этом на нее действует сила Лоренца (F_л=6,4 cdot 10^{-15 } Н . )
Вычислить скорость альфа-частицы, если ее заряд (q=3,2 cdot 10^{-19} Кл . )
Дать ответ в километрах в секунду.
Показать ответ
Показать решение
Видеорешение
Задача 8. (Сила Лоренца)
Протон влетает в магнитное поле со скоростью (v= 10^{5} м/с ) перпендикулярно линиям индукции,
после чего он движется по окружности.Найти радиус этой окружности, если индукция поля
(B=0,01 Тл . )
Заряд протона (q=1,6 cdot 10^{-19} Кл )
Масса протона (m=1,6 cdot 10^{-27} кг )
Показать ответ
Показать решение
Видеорешение
Содержание:
- Определение и формула силы Лоренца
- Направление силы Лоренца
- Следствия свойств силы Лоренца
- Формула силы Лоренца при наличии магнитного и электрического полей
- Единицы измерения силы Лоренца
- Примеры решения задач
Определение и формула силы Лоренца
Определение
Сила $bar{F}$ , действующая на движущуюся заряженную частицу в магнитном поле, равная:
$$bar{F}=q[bar{v} times bar{B}](1)$$
называется силой Лоренца (магнитной силой).
Исходя из определения (1) модуль рассматриваемой силы:
$$F=q v B sin alpha(2)$$
где $bar{v}$ – вектор скорости частицы, q – заряд частицы,
$bar{B}$ – вектор магнитной индукции поля в точке нахождения заряда,
$alpha$ – угол между векторами
$bar{v}$ и
$bar{B}$. Из выражения (2) следует, что если заряд движется параллельно
силовым линиям магнитного поля,то сила Лоренца равна нулю. Иногда силу Лоренца стараясь выделить, обозначают, используя индекс:
$bar{F}_L$
Направление силы Лоренца
Сила Лоренца (как и всякая сила) – это вектор. Ее направление перпендикулярно вектору скорости
$bar{v}$ и вектору
$bar{B}$ (то есть перпендикулярно плоскости, в которой находятся векторы скорости и магнитной
индукции) и определяется правилом правого буравчика (правого винта) рис.1 (a). Если мы имеем дело с отрицательным зарядом,
тонаправление силы Лоренца противоположно результату векторного произведения
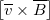
вектор $bar{B}$ направлен перпендикулярно плоскости рисунков на нас.
Следствия свойств силы Лоренца
Так как сила Лоренца направлена всегда перпендикулярно направлению скорости заряда, то ее работа над частицей равна нулю. Получается,
что воздействуя на заряженную частицу при помощи постоянного магнитного поля нельзя изменить ее энергию.
Если магнитное поле однородно и направлено перпендикулярно скорости движения заряженной частицы, то заряд под воздействием
силы Лоренца будет перемещаться по окружности радиуса R=const в плоскости, которая перпендикулярна вектору магнитной индукции.
При этом радиус окружности равен:
$$R=frac{m gamma v}{|q| B}(3)$$
где m – масса частицы,|q|- модуль заряда частицы,
$gamma=frac{1}{sqrt{1-frac{v^{2}}{c^{2}}}}$ – релятивистский множитель Лоренца, c – скорость света в вакууме.
Сила Лоренца — это центростремительная сила. По направлению отклонения элементарной заряженной частицы в магнитном поле делают вывод о ее знаке (рис.2).
Формула силы Лоренца при наличии магнитного и электрического полей
Если заряженная частица перемещается в пространстве, в котором находятся одновременно два поля (магнитное и
электрическое), то сила, которая действует на нее, равна:
$$bar{F}=q bar{E}+q[bar{v} times bar{B}](4)$$
где $bar{E}$ – вектор напряженности электрического поля в точке, в которой находится заряд.
Выражение (4) было эмпирически получено Лоренцем. Сила
$bar{F}$, которая входит в формулу (4) так же называется силой Лоренца
(лоренцевой силой). Деление лоренцевой силы на составляющие: электрическую
$(bar{F} = q bar{E})$ и магнитную
$(bar{F}=q[bar{v} times bar{B}])$ относительно, так как связано с выбором инерциальной системы отсчета.
Так, если система отсчета будет двигаться с такой же скоростью
$bar{v}$, как и заряд, то в такой системе сила Лоренца, действующая на частицу, будет равна нулю.
Единицы измерения силы Лоренца
Основной единицей измерения силы Лоренца (как и любой другой силы) в системе СИ является: [F]=H
В СГС: [F]=дин
Примеры решения задач
Пример
Задание. Какова угловая скорость электрона, который движется по окружности в магнитном поле с индукцией B?
Решение. Так как электрон (частица имеющая заряд) совершает перемещение в магнитном поле, то на
него действует сила Лоренца вида:
$$bar{F}=q[bar{v} times bar{B}](1.1)$$
где q=qe – заряд электрона. Так как в условии сказано, что электрон движется по окружности, то это означает, что
$bar{v} perp bar{B}$, следовательно, выражение для модуля силы Лоренца примет вид:
$$F=q v B(1.2)$$
Сила Лоренцаявляется центростремительной и кроме того, по второму закону Ньютона будет в нашем случае равна:
$$F=m a_{n}=m frac{v^{2}}{R}(1.3)$$
Приравняем правые части выражений (1.2) и (1.3), имеем:
$$q v B=m frac{v^{2}}{R}(1.4)$$
Из выражения (1.3) получим скорость:
$$v=frac{q B R}{m}(1.5)$$
Период обращения электрона по окружности можно найти как:
$$T=frac{2 pi R}{v}=frac{2 pi m}{q B}(1.6)$$
Зная период, можно найти угловую скорость как:
$$omega=frac{2 pi}{T}=frac{q_{e} B}{m}$$
Ответ. $omega=frac{q_{e} B}{m}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Заряженная частица (заряд q, масса m) со скоростью vвлетает в область, где имеется электрическое поле
напряженностью E и магнитное поле с индукцией B. Векторы $bar{E}$ и
$bar{B}$ совпадают по направлению. Каково ускорение частицы в моментначалаперемещения в полях, если
$bar{v} uparrow bar{B} uparrow bar{E}$?
Решение. Сделаем рисунок.
На заряженную частицу действует сила Лоренца:
$$bar{F}=q bar{E}+q[bar{v} times bar{B}](2.1)$$
Магнитная составляющая имеет направление перпендикулярное вектору скорости ($bar{v}$) и вектору
магнитной индукции ($bar{B}$).
Электрическая составляющая сонаправлена с вектором напряжённости ($bar{E}$) электрического поля.
В соответствии со вторым законом Ньютона имеем:
$$bar{F}=q bar{E}+q[bar{v} times bar{B}]=m bar{a}(2.2)$$
Получаем, что ускорение равно:
$$frac{q bar{E}+q[bar{v} times bar{B}]}{m}=bar{a}(2.3)$$
Если скорость заряда параллельна векторам $bar{E}$ и
$bar{B}$, тогда $[bar{v} times bar{B}]=0$, получим:
$$bar{a}=frac{q bar{E}}{m}$$
Ответ. $bar{a}=frac{q bar{E}}{m}$
Читать дальше: Формула силы натяжения нити.