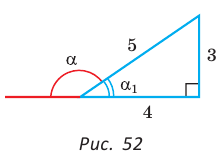
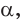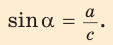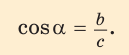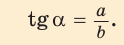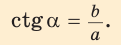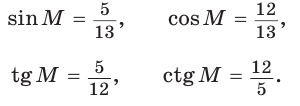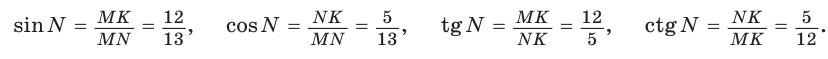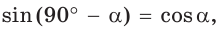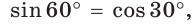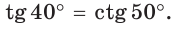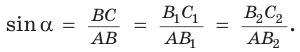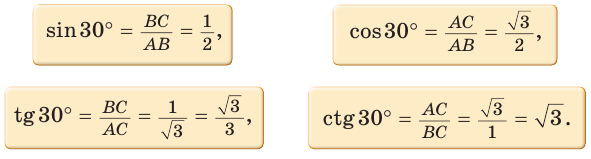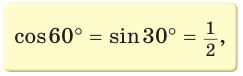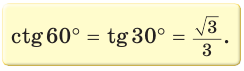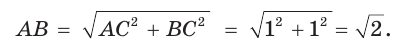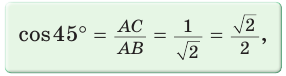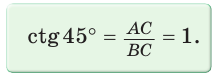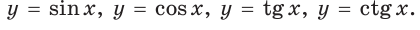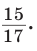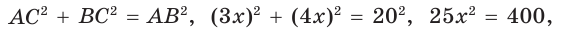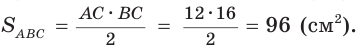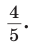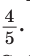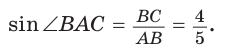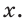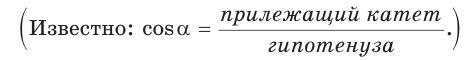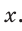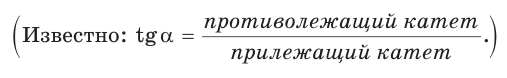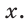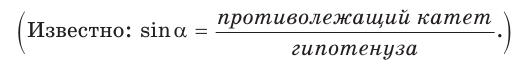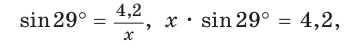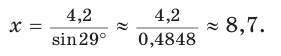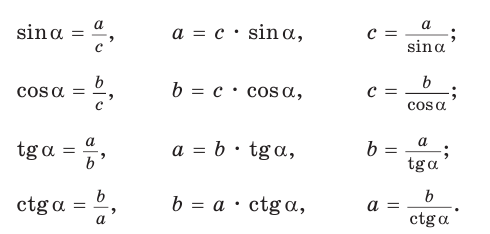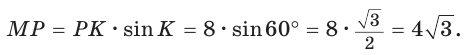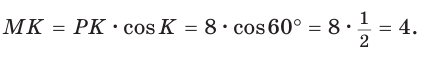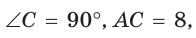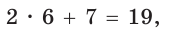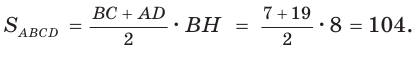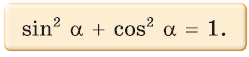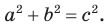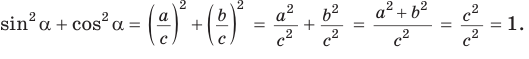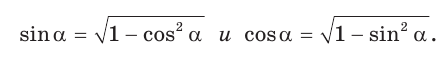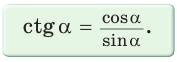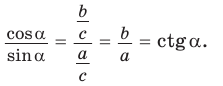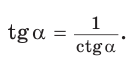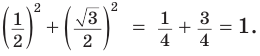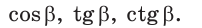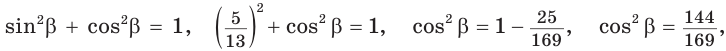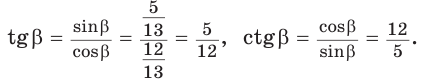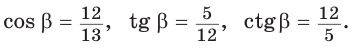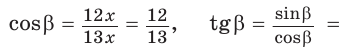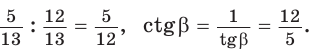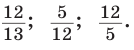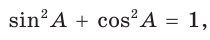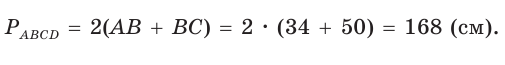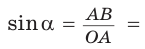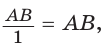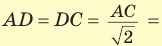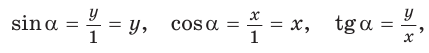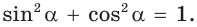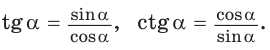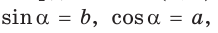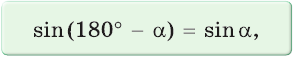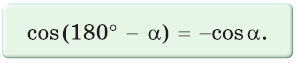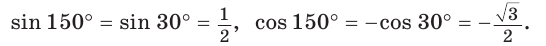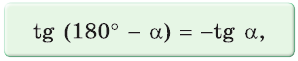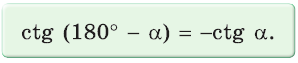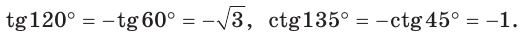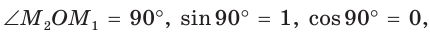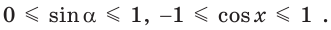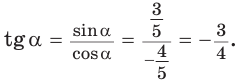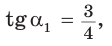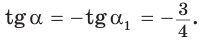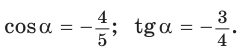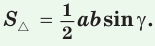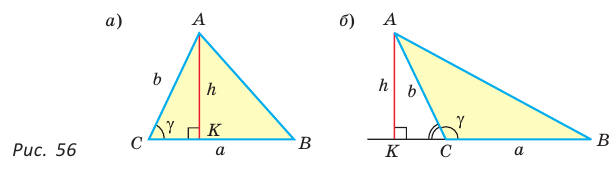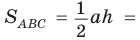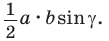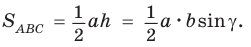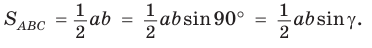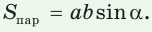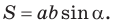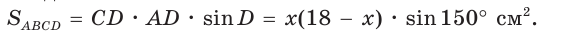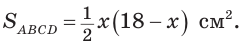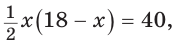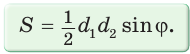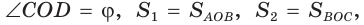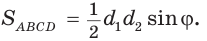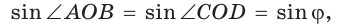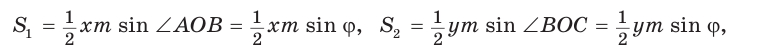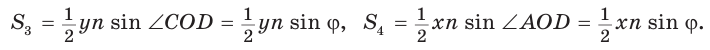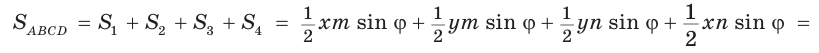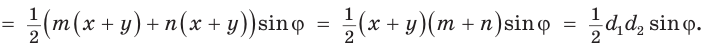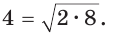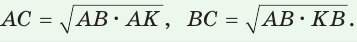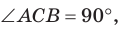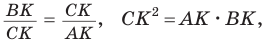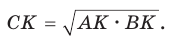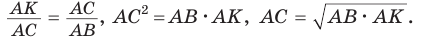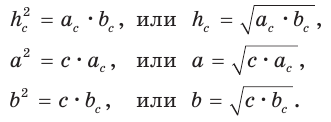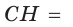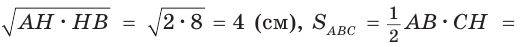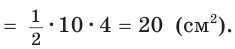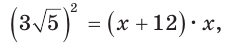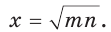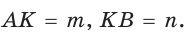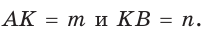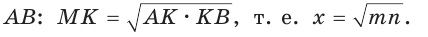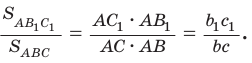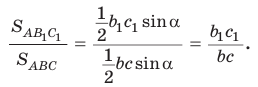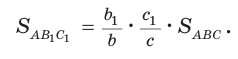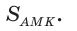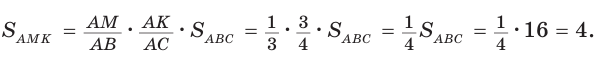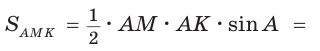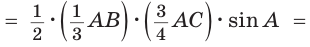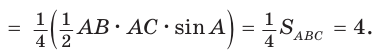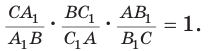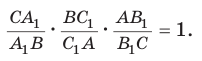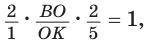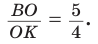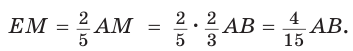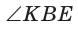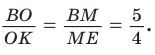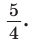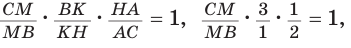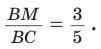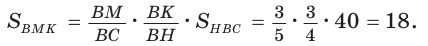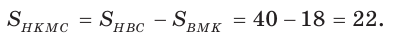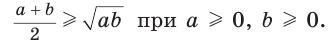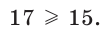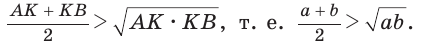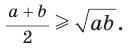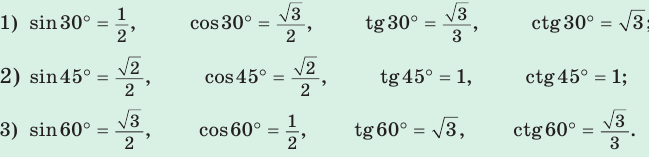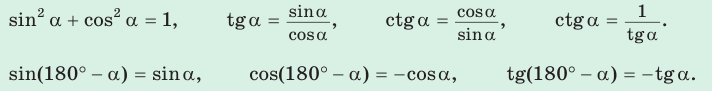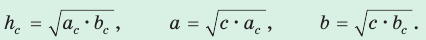Во-первых, что такое смежный угол? Это угол, который в сумме с заданным углом даёт 180 градусов. Приведём чертёж для пояснения вычислений.
Пусть дан угол ?0, смежный с углом α0 будет угол α1, причём α0 + α1 = 180°.
Если известен синус угла ?0, то по формулам приведения находим синус смежного угла ?1.
sin (а1) = sin (а0)= sin (180° — а1).
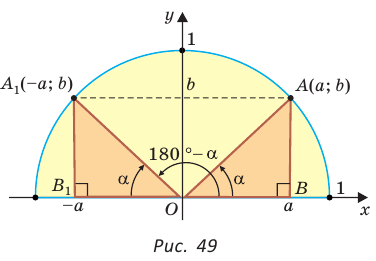
Если начертить угол а0 в системе координат, и синус углов а0 и а1 представляет в системе координат одну и ту же ординату у, равную синусу угла.
Здесь угол а0 = углу а, а угол а1 = (180° — а).
И sin (а) = MD = у = sin (180° — а).
Здесь ОМ — единичный вектор, у — ордината точки М и также синус угла ?.
Работа с внешними углами многоугольника с помощью тригонометрии
Определение
Смежные углы – это два угла, у которых общая вершина и сторона, а другие стороны образуют прямую.
Внешний угол многоугольника – это угол, смежный с каким-нибудь внутренним углом многоугольника.
Утверждение
Для любого действительного (alpha) верно, что
(sinleft(pi — alpharight) = sinalpha),
(cosleft(pi — alpharight) = -cosalpha).
Следствия
Синусы смежных углов равны.
Косинусы смежных углов противоположны.
Следствия
Тангенсы смежных углов либо противоположны, либо оба не существуют (когда смежные углы равны (90^circ)).
Котангенсы смежных углов либо противоположны, либо оба не существуют (когда один из смежных углов развёрнутый).
Содержание:
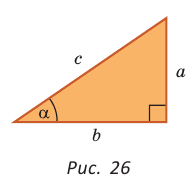
Пусть в прямоугольном треугольнике гипотенуза равна с, один из острых углов равен
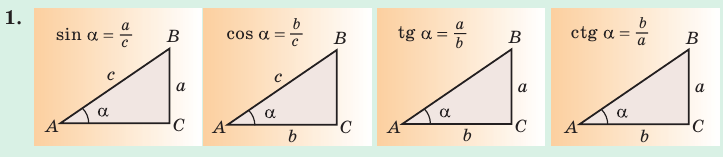
Определения синуса, косинуса, тангенса и котангенса острого угла
Определение. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе:
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе:
Определение. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему:
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему:
Пример:
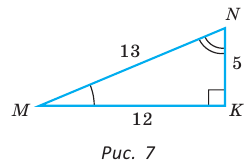
Угол К в 
Тогда:
Для угла N катет МК — противолежащий, а катет NK — прилежащий (см. рис. 7, с. 11). Поэтому согласно определениям получаем:
Можно заметить, что синус острого угла а прямоугольного треугольника и косинус другого острого угла этого треугольника, содержащего 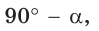
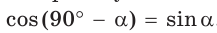
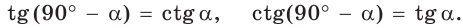
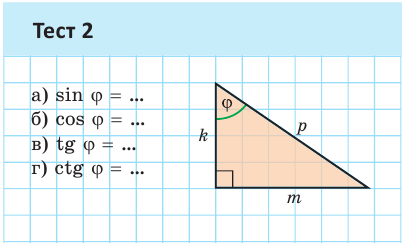
А теперь выполните Тест 1 и Тест 2.
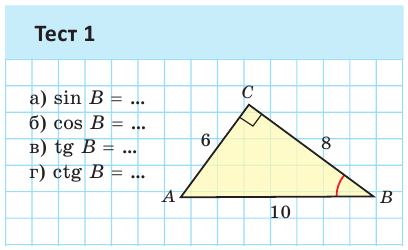
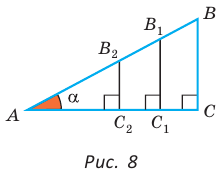
Значение синуса острого угла, а также косинуса, тангенса и котангенса зависит только от величины угла и не зависит от размеров и расположения прямоугольного треугольника с указанным острым углом.
Это следует из того, что прямоугольные треугольники с равным острым углом подобны, а у подобных треугольников соответствующие стороны пропорциональны. Так, в 

Значения синуса, косинуса, тангенса и котангенса углов 30°, 45°, 60°
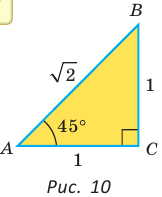
Рассмотрим прямоугольный треугольник АВС, у которого 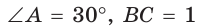
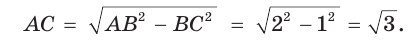
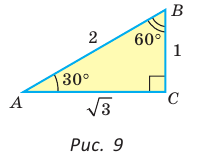
Так как 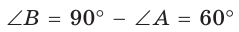

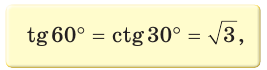
Рассмотрим равнобедренный прямоугольный треугольник АВС, у которого 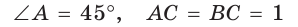
Тогда:
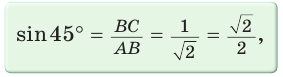
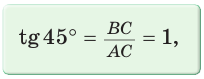
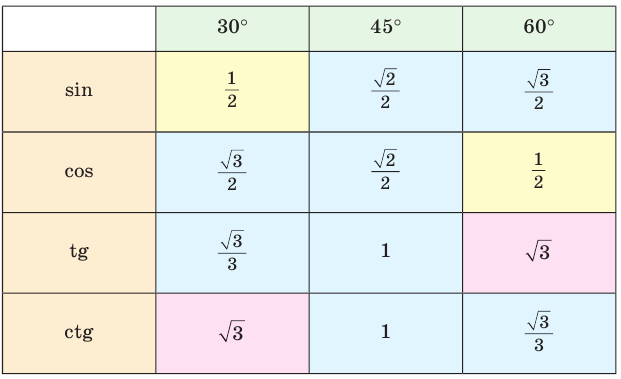
Составим таблицу значений синусов, косинусов, тангенсов и котангенсов для углов 30°, 45° и 60°.
Нахождение значений тригонометрических функций
Значения синуса, косинуса, тангенса и котангенса данного угла можно приближенно находить при помощи специальных тригонометрических таблиц* либо калькулятора.
Например, с помощью калькулятора, компьютера или мобильного телефона (смартфона) находим: sin45° = 0,707106… . Приближенное значение тригонометрических функций при решении задач будем брать с округлением до четырех знаков после запятой: sin45° = 0,7071.
Итак, точное значение sin 45° равно 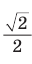
Таблицы и калькулятор также позволяют находить величину острого угла по значению синуса, косинуса или тангенса. Например, найдем острый угол, синус которого равен 0,4175. Выбрав на компьютере вид калькулятора «инженерный», далее «градусы», нужно ввести последовательно 
А теперь выполните Тест 3.
Тригонометрические функции острого угла
Синус, косинус, тангенс и котангенс являются функциями угла, так как каждому острому углу 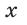
Поскольку в прямоугольном треугольнике катет меньше гипотенузы, то для острого угла 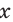
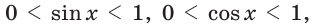
Тангенс и котангенс острого угла могут принимать любое положительное значение. Например, tg85° ~ 11,4.
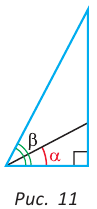
С увеличением острого угла синус и тангенс возрастают, а косинус и котангенс убывают (рис. 11), то есть если 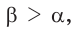
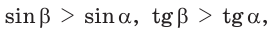
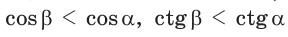
Пример №1
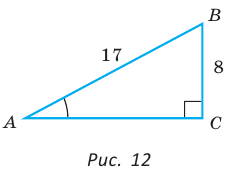
В прямоугольном треугольнике АВС, где 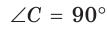
Решение:
По теореме Пифагора найдем катет 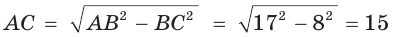
Ответ:
Пример №2
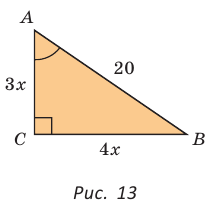
Гипотенуза АВ прямоугольного треугольника АВС равна 20 см, 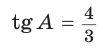
Решение:
Так как 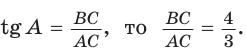
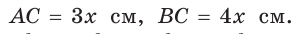
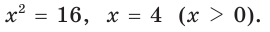
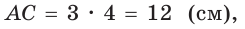
Ответ: 96
Пример №3
При помощи циркуля и линейки построить угол, синус которого равен
Решение:
Идея решения. Построим прямоугольный треугольник с катетом, равным 4 единицы, и гипотенузой, равной 5 единиц. Синус угла, противолежащего указанному катету, будет равен
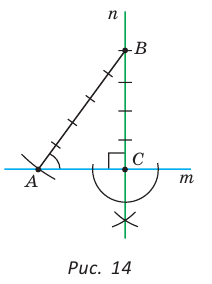
Построение. 1) Строим прямой угол С (рис. 14), для чего проводим произвольную прямую 
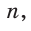
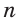
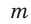
Угол ВАС — искомый.
Доказательство:
Из 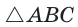
Алгоритм решения прямоугольного треугольника
Под решением прямоугольного треугольника понимают нахождение его неизвестных сторон и углов по некоторым элементам, определяющим этот треугольник. Рассмотрим три задачи:
- нахождение катета по гипотенузе и острому углу;
- нахождение катета по другому катету и острому углу;
- нахождение гипотенузы по катету и острому углу.
Пример №4
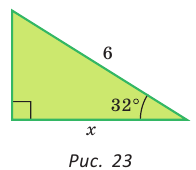
Гипотенуза прямоугольного треугольника равна 6, острый угол равен 32° (рис. 23). Найти катет, прилежащий к данному углу. Ответ округлить до 0,1.
Решение:
Примем длину искомого катета за
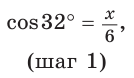

Ответ: 5,1.
Пример №5
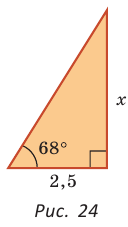
Катет прямоугольного треугольника равен 2,5, а прилежащий к нему угол равен 68° (рис. 24). Найти другой катет. Ответ округлить до 0,1.
Решение:
Примем длину неизвестного катета за
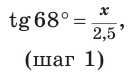
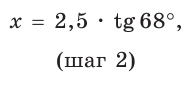
Ответ: 6,2.
Пример №6
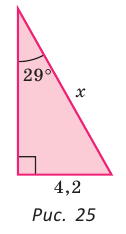
Катет прямоугольного треугольника равен 4,2, противолежащий ему угол равен 29° (рис. 25). Найти гипотенузу треугольника. Ответ округлить до 0,1.
Решение:
Примем длину гипотенузы за
Ответ: 8,7.
Правила решения прямоугольного треугольника
Преобразуем формулы синуса, косинуса, тангенса и котангенса и запишем результаты для треугольника на рисунке 26:
Удобно пользоваться следующими правилами:
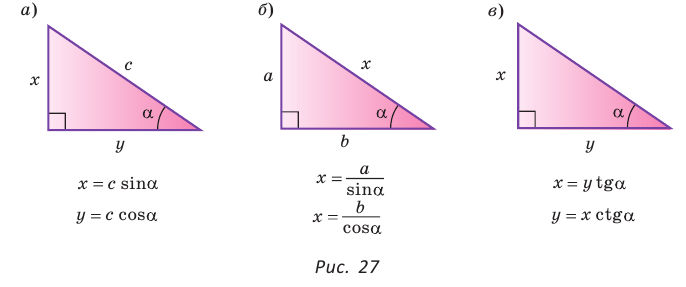
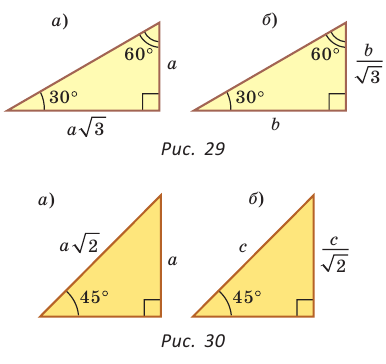
- Катет равен гипотенузе, умноженной на синус противолежащего или на косинус прилежащего угла (рис. 27, а).
- Гипотенуза равна катету, деленному на синус противолежащего или на косинус прилежащего угла (рис. 27, б).
- Катет равен другому катету, умноженному на тангенс противолежащего или на котангенс прилежащего к первому катету угла (рис. 27, в).
Пример №7
В 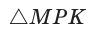
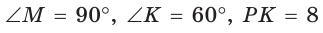
Полезно запомнить!
Если в прямоугольном треугольнике с углом 30° (или 60°) дан меньший катет а, то больший
катет 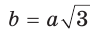
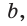
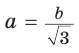
Если в прямоугольном треугольнике с углом 45° дан катет а,
то гипотенуза 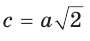
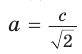
Пример №8
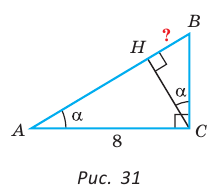
В прямоугольном треугольнике АВС известно: 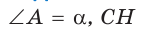
Решение:
Заметим, что 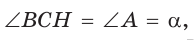
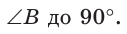
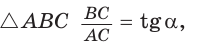
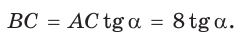
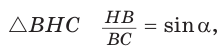
Ответ:
Пример №9
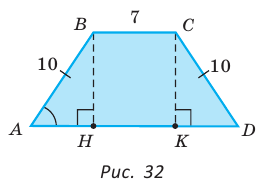
В равнобедренной трапеции ABCD меньшее основание ВС равно 7, боковая сторона АВ равна 10, sinA = 0,8. Найти площадь трапеции.
Решение:
Площадь трапеции находится по формуле 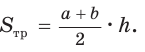
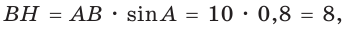
Ответ: 104.
Тригонометрические формулы
Используя формулы 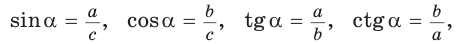
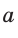
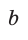
1. Основное тригонометрическое тождество
Доказательство:
По теореме Пифагора
Тогда
Следствие:
Так как синус и косинус острого угла а положительны, то
2. Выражение тангенса и котангенса через синус и косинус
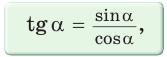
Доказательство:
a)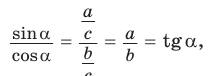
Следствие:
Проверим справедливость основного тригонометрического тождества.
Верно ли, например, что 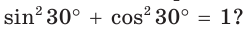
3. Основная задача
Дано: 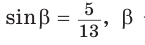
Найти:
Решение:
Способ 1. Используем основное тригонометрическое тождество: 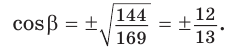
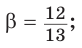
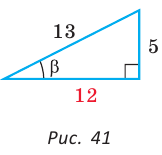
Способ 2. Изобразим прямоугольный треугольник с катетом 5 и гипотенузой 13 (рис. 41). Синус угла, противолежащего данному катету, равен 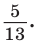
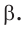
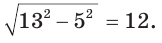
Способ 3. Пусть катет, противолежащий углу 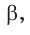
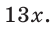
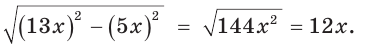
Ответ:
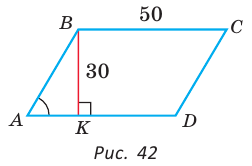
Пример №10
В параллелограмме ABCD (рис. 42) сторона ВС = 50 см, высота ВК = 30 см, 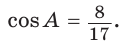
Решение:
Из треугольника АВК находим: 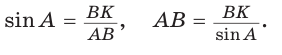
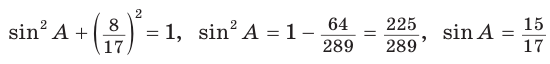
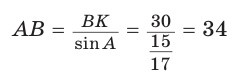
Ответ: 168 см.
Пример №11
Доказать, что при увеличении угла от 0° до 90°:
а) синус угла увеличивается от 0 до 1, а косинус — уменьшается от 1 до 0;
б) тангенс угла увеличивается от О до бесконечности.
Решение:
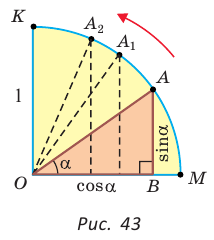
а) Рассмотрим прямоугольные треугольники с гипотенузой, равной 1. Для этого опишем радиусом ОМ, равным 1, четверть окружности — дугу МК (рис. 43). Пусть 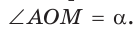
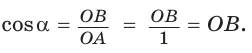
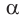
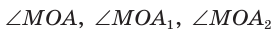
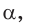
Из формулы 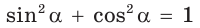
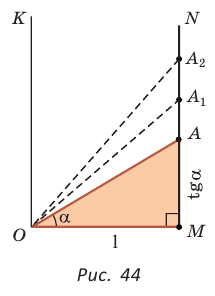
б) Для определения изменения тангенса угла удобно рассматривать треугольники, у которых прилежащий катет не изменяется и остается равным 1, а противолежащий катет изменяется. Рассмотрим прямоугольный треугольник АОМ, у которого отрезок ОМ = 1, 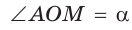
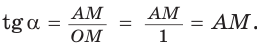
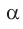
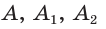
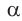
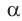
К такому же выводу можно прийти, рассматривая формулу 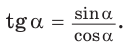
Пример №12
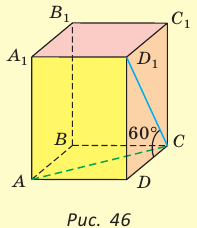
В основании прямоугольного параллелепипеда 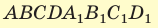
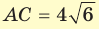
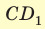
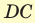

Решение:
Объем прямоугольного параллелепипеда находится по формуле 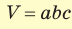
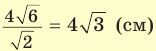
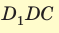
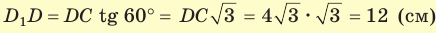
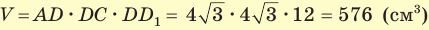
Ответ: 576 см3.
Синус, косинус, тангенс и котангенс тупого угла
1. Определение значений 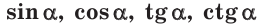
Ранее мы дали определения синуса, косинуса, тангенса и котангенса острого угла через отношение сторон прямоугольного треугольника. Сделаем теперь это для углов от 0° до 180°.
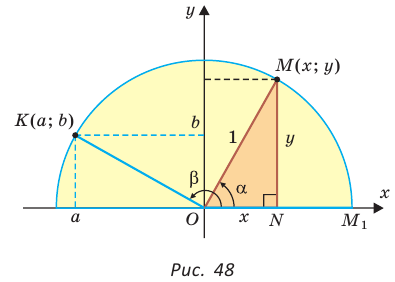
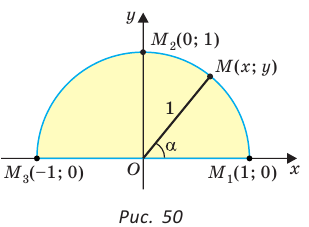
Рассмотрим полуокружность с центром в начале координат и радиусом, равным 1 (рис. 48). От положительной полуоси 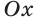
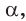
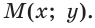
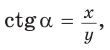
тангенс и котангенс острого угла а выражаются через координаты 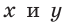
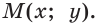
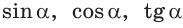
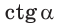
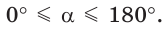
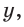
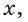
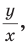
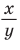
Например, для тупого 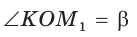
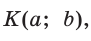
Для любого положения точки 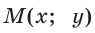
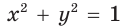
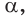

Также верны тождества:
Нахождение синуса, косинуса, тангенса и котангенса тупых углов
Пусть 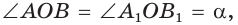
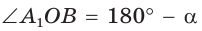
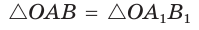
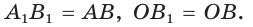
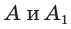
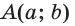
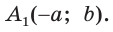
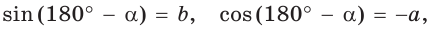
Можно пользоваться следующим правилом:
Синус тупого угла равен синусу смежного с ним острого угла.
Косинус тупого угла равен косинусу смежного с ним острого угла, взятому со знаком «минус».
Пример 1.
Разделив почленно равенство 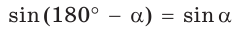
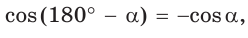
Можно пользоваться следующим правилом:
Тангенс (котангенс) тупого угла равен тангенсу (котангенсу) смежного с ним острого угла, взятому со знаком «минус».
Пример 2.
Указанные формулы и правила позволяют находить значения тригонометрических функций тупого угла через значения тригонометрических функций острого угла, который дополняет данный тупой угол до 180°: синусы углов, дополняющих друг друга до 180°, равны между собой, а косинусы, тангенсы и котангенсы — противоположны. Так как синус, косинус, тангенс и котангенс острого угла положительные, то синус тупого угла положительный, а косинус, тангенс и котангенс — отрицательные.
Значения тригонометрических функций для углов 0°, 90°, 180°
Если луч ОМ совпадет с лучом 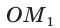
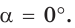
а) 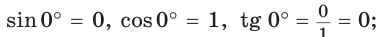
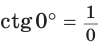
б) 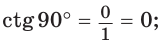
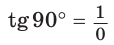
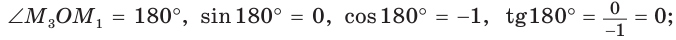
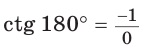
Поскольку проекции радиуса, равного 1, на оси координат меньше либо равны 1, то для углов 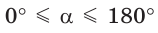
Пример №13
Найти 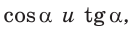
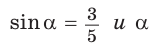
Решение:
Способ 1. Так как 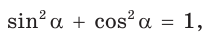
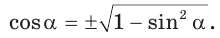
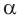
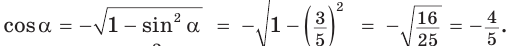
Способ 2. Синус острого угла 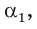
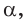
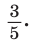
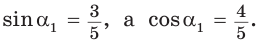
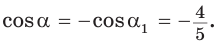
Ответ:
Формулы площади треугольника и площади параллелограмма
Тригонометрические функции позволяют получить формулы для вычисления площади треугольника и площади параллелограмма. Сформулируем их в виде двух теорем.
Теорема. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними, т. е.
Доказательство:
Пусть в треугольнике 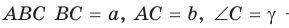
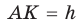
Из прямоугольного треугольника 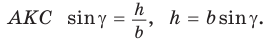
Если угол 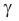
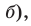
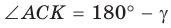
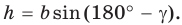
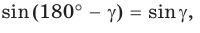
Если 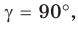
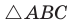
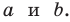

Теорема доказана.
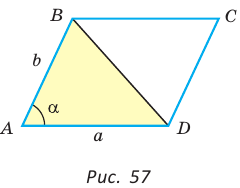
Теорема. Площадь параллелограмма равна произведению двух его соседних сторон на синус угла между ними, т. е.
Используя рисунок 57, докажите эту теорему самостоятельно.
Замечание. Если 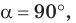
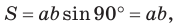

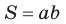
Известно, что слово «синус» в переводе с латинского имеет множество значений: изгиб, дуга, пазуха, бухта, впадина, залив, хорда, забота и нежная любовь. При помощи Интернета выясните:
а) какое из значений подходит к математическому понятию «синуса»;
б) какие из значений относятся к медицине и почему насморк врачи иногда называют синуситом.
Пример №14
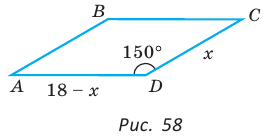
Дан параллелограмм ABCD, площадь которого 40 см2, а периметр 36 см. Найти стороны параллелограмма, если его угол D равен 150° (рис. 58).
Решение:
Полупериметр параллелограмма равен 18 см. Если 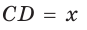
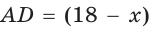
Тогда
Так как 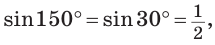
По условию 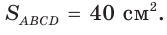
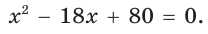
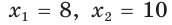
Если CD = 8 см, то AD = 10 см, если CD = 10 см, то AD = 8 см.
Ответ: 8 см, 10 см.
Пример №15
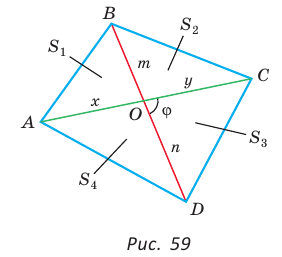
Доказать, что площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними, т.е.
Доказательство:
Пусть диагонали 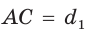
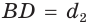
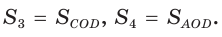
Обозначим 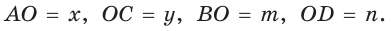
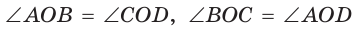
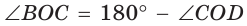
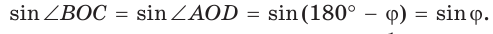
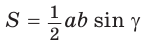
Утверждение доказано
Среднее пропорциональное (среднее геометрическое) в прямоугольном треугольнике
Если для положительных чисел 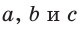
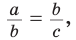
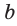
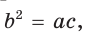
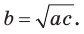
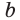
Пример №16
Число 4 является средним пропорциональным, или средним геометрическим чисел 2 и 8, так как = 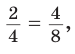
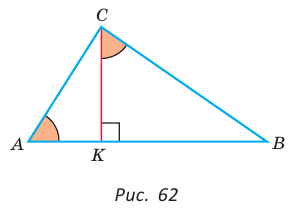
В прямоугольном треугольнике АВС, где 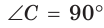
Теорема (о среднем пропорциональном в прямоугольном треугольнике).
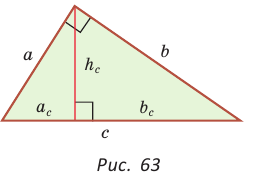
а) Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу, т. е. 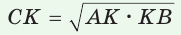
б) Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу, т. е.
Доказательство:
а)3аметим, что если 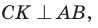
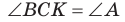
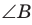
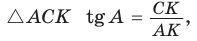
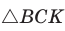
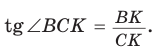
б) Из 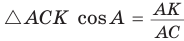
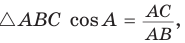
Аналогично доказывается, что 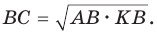
Обозначив катеты 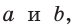
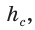
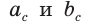
Пример №17
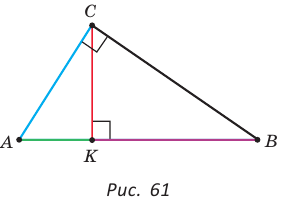
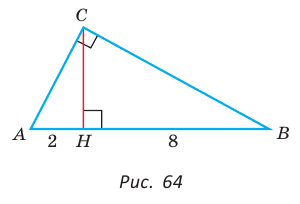
Найти площадь прямоугольного треугольника, если проекции катетов на гипотенузу равны 2 см и 8 см.
Решение:
Пусть СН — высота прямоугольного треугольника АВС 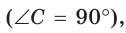
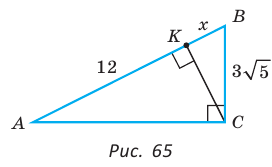
проекция катета СВ на гипотенузу (рис. 64). Так как высота СН есть среднее геометрическое между проекциями катетов на гипотенузу, то
Ответ: 20 см2.
Пример №18
В прямоугольном треугольнике АВС из вершины прямого угла С проведена высота 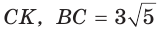
Решение:
Пусть 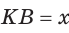
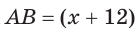
Катет есть среднее пропорциональное между гипотенузой и проекцией катета на гипотенузу. Поэтому 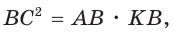
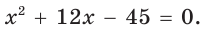
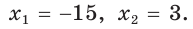
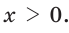
Ответ: 15 см.
Пример №19
При помощи циркуля и линейки построить отрезок, равный среднему геометрическому отрезков т и п .
Решение:
Пусть даны отрезки т и п . Необходимо построить отрезок
Построение.
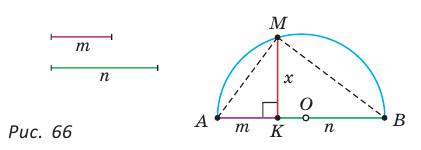
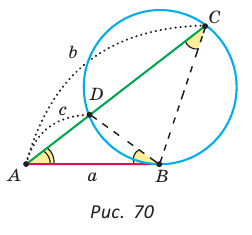
1) На произвольной прямой откладываем данные отрезки:
2) На отрезке АВ как на диаметре строим полуокружность, для чего находим середину О отрезка АВ, откуда ОА — радиус данной окружности.
3) Из точки К восстанавливаем перпендикуляр к прямой АВ до пересечения с полуокружностью в точке М (рис. 66).
Отрезок 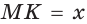
Доказательство:
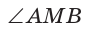
Повторение*
В 8-м классе мы доказали следующую теорему:
Теорема (о касательной и секущей). Если из одной точки к окружности проведены касательная и секущая, то квадрат отрезка касательной, соединяющего данную точку и точку касания, равен произведению отрезков се кущей, соединяющих данную точку и точки пересечения секущей с окружностью, т. е. 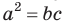
Как видим, отрезок 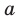
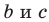
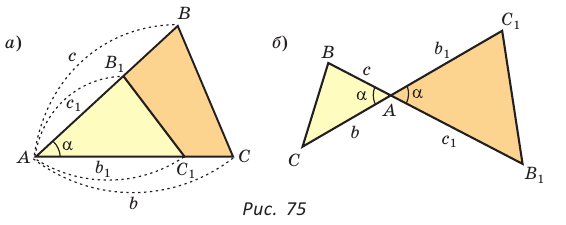
Теорема о площадях треугольников с общим (равным) углом
Площади треугольников, имеющих общий угол (или равный угол), относятся как произведения сторон, заключающих этот угол (рис. 75),
т.е.
Доказательство:
Следствие: Верно:
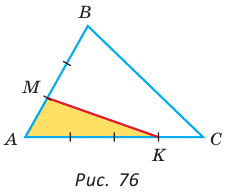
Пример №20
Площадь треугольника АВС равна 16, АК : КС = 3 :1 , AM : МВ = 1 :2 (рис. 76). Найти
Решение:
Способ 1. По следствию из теоремы о площадях треугольников с общим углом получаем:
Способ 2.
Ответ: 4.
Теорема Менелая
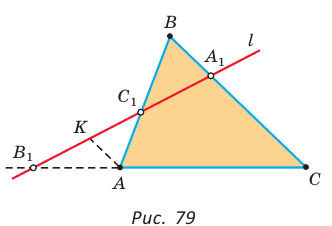
Если дан треугольник АВС и прямая 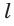
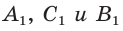
Доказательство:
Проведем отрезок 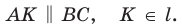
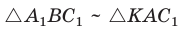

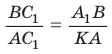
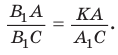
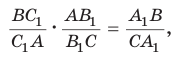
Замечание. При составлении произведения трех отношений теоремы Менелая можно начинать с любой из шести точек (трех вершин треугольника и трех точек пересечения прямой 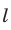
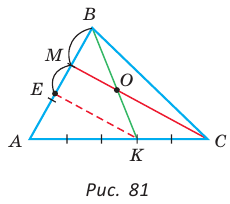
Пример №21
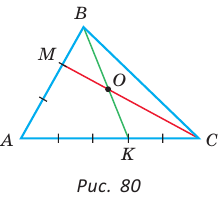
В треугольнике АВС на сторонах АВ и АС взяты соответственно точки М и К, такие, что AM : МВ = 2 :1 , АК : КС = 3 :2 . Отрезки СМ и ВК пересекаются в точке О. Найти ВО : ОК.
Решение:
Способ 1 (теорема Менелая). Рассмотрим 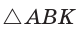
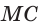
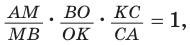
Способ 2 (теорема Фалеса обобщенная). Проведем 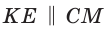
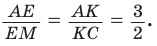
Но 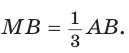
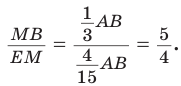
по теореме Фалеса
Ответ:
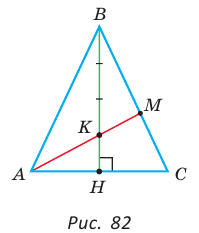
Пример №22
Дан равнобедренный треугольник АВС (АВ = ВС), площадь которого равна 80. Точка К делит высоту ВН в отношении 1 : 3, считая от основания. Прямая АК пересекает сторону ВС в точке М. Найти площадь четырехугольника НКМС (рис. 82).
Решение:
1) 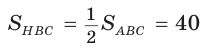
2) Применим теорему Менелая к треугольнику НВС.
Прямая AM пересекает его стороны ВН и ВС соответственно в точках К и М и продолжение стороны НС в точке 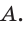
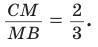
3)
4)
Ответ: 22.
Неравенство Коши
Среднее арифметическое двух неотрицательных чисел больше либо равно их среднему геометрическому, т. е.
Например, 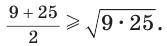
Алгебраическое доказательство указанного неравенства таково. Рассмотрим разность левой и правой частей неравенства 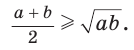
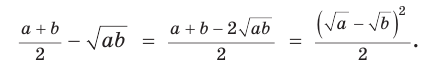
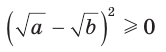
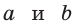
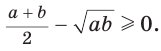
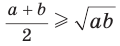
Неравенство 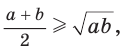
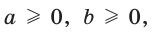
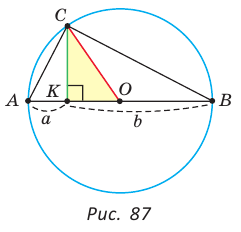
Приведем геометрическое доказательство указанного неравенства. Изобразим окружность с диаметром АВ и центром в точке О (рис. 87). На диаметре возьмем точку К (для определенности левее центра О). Пусть 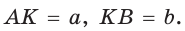

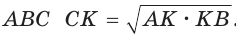
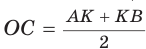
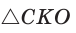
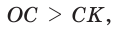
Равенство левой и правой частей неравенства достигается, когда точка К совпадает с точкой О и 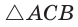
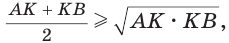
ЗАПОМИНАЕМ
2. Значения тригонометрических функций углов 30 45°, 60°:
3. Тригонометрические формулы (тождества):
Примеры:
4. Формулы площади треугольника и параллелограмма:
5. Среднее пропорциональное в прямоугольном треугольнике:
- Сумма углов треугольника
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Угол — определение, виды, как обозначают с примерами
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
Содержание
Общее определение синуса
-
Синус острого угла равен отношению перпендикуляра к наклонной.
-
Синус тупого угла равен синусу смежного острого угла.
-
Синус прямого угла равен единице.
-
Синус развернутого угла равен нулю.
Корректность определения синуса
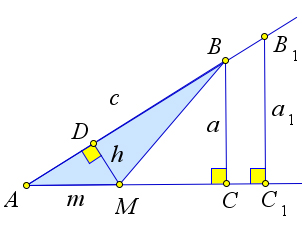
Пусть из точки $B$, лежащей на стороне $p$ острого угла $A$, опущен
перпендикуляр $BC$ на сторону $q$ этого угла. Тогда отношение
перпендикуляра $BC$ к наклонной $BA$ не зависит от выбора точки $B$.
Доказательство
Первый способ (не использует подобия).
На стороне $q$ выберем любую точку $M$.
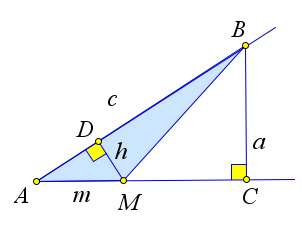
Выразим площадь $S$ треугольника $ABM$ двумя способами.
С одной стороны, $S=dfrac{1}{2}ma$, где $a=BC, m=AM$.
C другой стороны, $S=dfrac{1}{2}ch$, где $h=MD$ – высота треугольника $ABM$ и $c=BA$.
Поэтому $ma=ch$ или $dfrac{a}{c}=dfrac{h}{m}$.
Если на стороне $p$ взять другую точку $B_1$ и повторить проведенные рассуждения, то снова получим, что $dfrac{a_1}{c_1}=dfrac{h}{m}$, где $a_1=B_1C, c_1=AB_1$.
Поэтому $dfrac{a_1}{c_1}=dfrac{a}{c}$.
Отношение перпендикуляра к наклонной не зависит от того, на какую
сторону угла опущен перпендикуляр.
Действительно, пусть, как и раньше, $M$ – точка на стороне $q$ угла $A$ и $MDperp p$.
Вернемся к равенству $dfrac{a}{c}=dfrac{h}{m}$
В правой части этого равенства стоит отношение перпендикуляра к наклонной, которое с
выбором точки $M$ не связано.
Значит правая часть этого равенства от выбора точки $M$ не зависит.
Второй способ (использует подобие).
Если на стороне $p$ взять точки $B$ и $B_1$ и опустить из них
перпендикуляры $BC$ и $B_1C_1$ к стороне $q$ угла $A$, то
треугольники $ABC$ и $AB_1C_1$ будут подобны по двум углам.
Следовательно, $dfrac{BC}{AB}=dfrac{B_1C_1}{AB_1}$.
Отношение перпендикуляра к наклонной не зависит от того, на какую сторону угла опущен
перпендикуляр.
Действительно, пусть, как и раньше, $M$ – точка на стороне $q$ угла $A$ и $MDperp p$.
Треугольники $ADM$ и $ABC$ подобны по двум углам ($angle A$ – общий).
Следовательно, $dfrac{MD}{AM}=dfrac{BC}{AB}$, а отношение, стоящее в правой части
этого равенства не зависит от выбора точки $M$.
Теорема
Синусы углов, имеющих равные величины, равны.
Доказательство
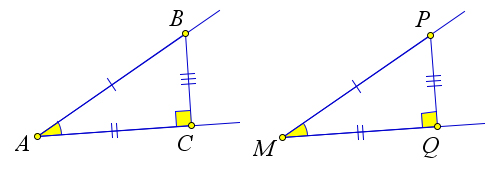
Возьмем два равных острых угла: $angle A$ и $angle M$.
Из некоторой точки $B$ на стороне угла $A$ опустим перпендикуляр
$BC$ на другую сторону угла $A$.
Получим прямоугольный треугольник $ABC$.
Отложим на сторонах угла $M$ отрезки $MP=AB$ и $MQ=AC$.
Тогда $triangle MPQ=triangle ABC$ по первому признаку равенства.
Поэтому $angle Q=angle C=90^circ$.
Итак $PQ$ – перпендикуляр, опущенный из точки $P$ одной стороны угла $M$ на другую его сторону.
Но тогда $sin{angle A}=dfrac{BC}{AB}=dfrac{PQ}{PM}=sin{angle M}$.
Смежные углы. Свойства смежных углов
Определение 1. Смежными называются два угла, у которых одна сторона общая, а другие стороны являются продолжениями друг друга.
На Рис.1 углы AOB и BOC смежные, так как сторона OB общая для этих углов, а стороны OA и OC являются продолжениями друг друга. Поскольку угол AOC является развернутым углом, то сумма смежных углов равна 180°:
Свойства смежных углов
1. Сумма смежных углов равна 180°
2. Если оба смежных угла равны между собой, то они являются прямыми.
3. В паре смежных углов всегда один острый, а другой тупой, или оба угла прямые.
4. Синусы смежных углов равны.
5. Косинусы, тангенсы и котангенсы смежгых углов равны, но имеют противоположный знак.
Справедливость пунктов 2 и 3 очевидны и следуют из (1).
Доказательство пункта 4. Обозначим через α один из смежных углов. Тогда величина другого угла будет равна 180°−α. Но (см. статью Формулы приведения тригонометрических функций онлайн)
То есть синусы смежных углов равны.
Доказательство пункта 5. Обозначим через α один из смежных углов. Тогда величина другого угла будет равна 180°−α. Но
То есть косинусы, тангенсы и котангенсы смежных углов равны, но имеют противоположный знак.