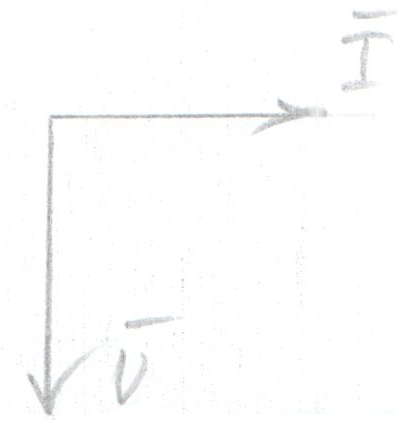
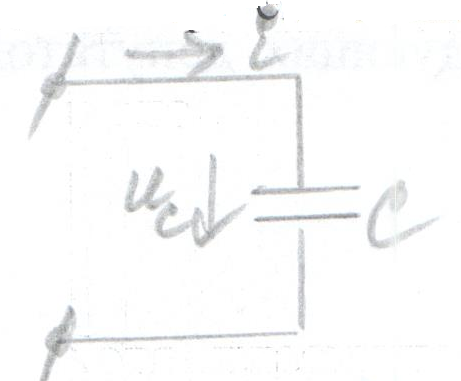Многие потребители электроэнергии не подозревают того, что часть учтённого электричества расходуется бесполезно. В зависимости от вида нагрузки уровень потерь электроэнергии может достигать от 12 до 50%. При этом счетчики электроэнергии засчитывают эти потери, относя их к полезной работе, за что приходится платить. Виной завышения оплаты за потребление электроэнергии, не выполняющей полезной работы, является реактивная мощность, присутствующая в сетях переменных токов.
Чтобы понять, за что мы переплачиваем и как компенсировать влияние реактивных мощностей на работу электрических установок, рассмотрим причину появления реактивной составляющей при передаче электроэнергии. Для этого придётся разобраться в физике процесса, связанного с переменным напряжением.
Что такое реактивная мощность?
Для начала рассмотрим понятие электрической мощности. В широком смысле слова, этот термин означает работу, выполненную за единицу времени. По отношению к электрической энергии, понятие мощности немного откорректируем: под электрической мощностью будем понимать физическую величину, реально характеризующую скорость генерации тока или количество переданной либо потреблённой электроэнергии в единицу времени.
Понятно, что работа электричества в единицу времени определяется электрической мощностью, измеряемой в ваттах. Мгновенную мощность на участке цепи находят по формуле: P = U×I, где U и I – мгновенные значения показателей параметров напряжения и силы тока на данном участке.
Строго говоря, приведённая выше формула справедлива только для постоянного тока. Однако, в цепях синусоидального тока формула работает лишь тогда, когда нагрузка потребителей чисто активная. При резистивной нагрузке вся электрическая энергия расходуется на выполнение полезной работы. Примерами активных нагрузок являются резистивные приборы, такие как кипятильник или лампа накаливания.
При наличии в электрической цепи ёмкостных или индуктивных нагрузок, появляются паразитные токи, не участвующие в выполнении полезной работы. Мощность этих токов называют реактивной.
На индуктивных и ёмкостных нагрузках часть электроэнергии рассеивается в виде тепла, а часть препятствует выполнению полезной работы.
К устройствам с индуктивными нагрузками относятся:
- электромоторы;
- дроссели;
- трансформаторы;
- электромагнитные
реле и другие устройства, содержащие обмотки.
Ёмкостными сопротивлениями обладают конденсаторы.
Физика процесса
Когда мы имеем дело с цепями постоянного тока, то говорить о реактивной мощности не приходится. В таких цепях значения мгновенной и полной мощности совпадают. Исключением являются моменты включения и отключения ёмкостных и индуктивных нагрузок.
Похожая ситуация происходит при наличии чисто активных сопротивлений в синусоидальных цепях. Однако если в такую электрическую цепь включены устройства с индуктивными или ёмкостными сопротивлениями, происходит сдвиг фаз по току и напряжению (см. рис.1).
При этом на индуктивностях наблюдается отставание тока по фазе, а на ёмкостных элементах фаза тока сдвигается так, что ток опережает напряжение. В связи с нарушением гармоники тока, полная мощность разлагается на две составляющие. Ёмкостные и индуктивные составляющие называют реактивными, бесполезными. Вторая составляющая состоит из активных мощностей.
Угол сдвига фаз используется при вычислениях значений активных и реактивных ёмкостных либо индуктивных мощностей. Если угол φ = 0, что имеет место при резистивных нагрузках, то реактивная составляющая отсутствует.
Важно запомнить:
- резистор потребляет исключительно активную мощность, которая выделяется в виде тепла и света;
- катушки индуктивности провоцируют образование реактивной составляющей и возвращают её в виде магнитных полей;
- Ёмкостные элементы (конденсаторы) являются причиной появления реактивных сопротивлений.
Треугольник мощностей и cos φ
Для наглядности изобразим полную мощность и её составляющие в виде векторов (см. рис. 2). Обозначим вектор полной мощности символом S, а векторам активной и реактивной составляющей присвоим символы P и Q, соответственно. Поскольку вектор S является суммой составляющих тока, то, по правилу сложения векторов, образуется треугольник мощностей.
Применяя теорему Пифагора, вычислим модуль вектора S:
Отсюда можно найти реактивную составляющую:
Выше мы уже упоминали, что реактивная мощность зависит от сдвига фаз, а значит и от угла этого сдвига. Эту зависимость удобно выражать через cos φ. По определению cos φ = P/S. Данную величину называют коэффициентом мощности и обозначают Pf. Таким образом, Pf = cos φ = P/S.
Коэффициент мощности, то есть cos φ, является очень важной характеристикой, позволяющей оценить эффективность работы тока. Данная величина находится в промежутке от 0 до 1.
Если угол сдвига фаз принимает нулевое значение, то cos φ = 1, а это значит что P = S, то есть полная мощность состоит только из активной мощности, а реактивность отсутствует. При сдвиге фаз на угол π/2 , cos φ = 0, откуда следует, что в цепи господствуют только реактивные токи (на практике такая ситуация не возникает).
Из этого можно сделать вывод: чем ближе к 1 коэффициент Pf , тем эффективнее используется ток. Например, для синхронных генераторов приемлемым считается коэффициент от 0,75 до 0,85.
Формулы
Поскольку реактивная мощность зависит от угла φ, то для её вычисления применяется формула: Q = UI×sin φ. Единицей измерения реактивной составляющей является вар или кратная ей величина – квар.
Активную составляющую находят по формуле: P = U*I×cosφ. Тогда
Зная коэффициент Pf (cos φ), мы можем рассчитать номинальную мощность потребителя тока по его номинальному напряжению, умноженному на значение силы потребляемого тока.
Способы компенсации
Мы уже выяснили, как влияют реактивные токи на работу устройств и оборудования с индуктивными или ёмкостными нагрузками. Для уменьшения потерь в электрических сетях с синусоидальным током их оборудуют дополнительными устройствами компенсации.
Принцип действия установок компенсации основан на свойствах индуктивностей и ёмкостей по сдвигу фаз в противоположные стороны. Например, если обмотка электромотора сдвигает фазу на угол φ, то этот сдвиг можно компенсировать конденсатором соответствующей ёмкости, который сдвигает фазу на величину – φ. Тогда результирующий сдвиг будет равняться нулю.
На практике компенсирующие устройства подключают параллельно нагрузкам. Чаще всего они состоят из блоков конденсаторов большой ёмкости, расположенных в отдельных шкафах. Одна из таких конденсаторных установок изображена на рисунке 3. На картинке видно группы конденсаторов, используемых для компенсации сдвигов напряжений в различных устройствах с индуктивными обмотками.
Компенсацию реактивной мощности ёмкостными нагрузками хорошо иллюстрируют графики на рисунке 4. Обратите внимание на то, как эффективность компенсации зависит от напряжения сети. Чем выше сетевое напряжение, тем сложнее компенсировать паразитные токи (график 3).
Устройства компенсации часто устанавливаются в производственных цехах, где работает много устройств на электроприводах. Потери электричества при этом довольно ощутимы, а качество тока сильно ухудшается. Конденсаторные установки успешно решают подобные проблемы.
Нужны ли устройства компенсации в быту?
На первый взгляд в домашней сети не должно быть больших
реактивных токов. В стандартном наборе бытовых потребителей преобладают
электрическая техника с резистивными нагрузками:
- электрочайник (Pf = 1);
- лампы накаливания
(Pf = 1); - электроплита (Pf =
1) и другие нагревательные приборы;
Коэффициенты
мощности современной бытовой техники, такой как телевизор, компьютер и т.п.
близки к 1. Ими можно пренебречь.
Но если речь идёт о холодильнике (Pf = 0,65), стиральной машине и микроволновой печи, то уже стоит задуматься об установке синхронных компенсаторов. Если вы часто пользуетесь электроинструментом, сварочным аппаратом или у вас дома работает электронасос, тогда установка устройства компенсации более чем желательна.
Экономический эффект от установки таких устройств
ощутимо скажется на вашем семейном бюджете. Вы сможете экономить около 15%
средств ежемесячно. Согласитесь, это не так уж мало, учитывая тарифы не
электроэнергию.
Попутно вы решите следующие вопросы:
- уменьшение нагрузок на индуктивные элементы и на проводку;
- улучшение качества тока, способствующего стабильной работе электронных устройств;
- понижение уровня высших гармоник в бытовой сети.
Для того чтобы ток и напряжение работали синфазно, устройства компенсации следует размещать как можно ближе к потребителям тока. Тогда реальная отдача индуктивных электроприёмников будет принимать максимальные значения.
Видео в тему
Реактивная мощность
Реактивная мощность обусловлена способностью реактивных элементов накапливать и отдавать электрическую или магнитную энергию.
Eмкостная нагрузка в цепи переменного тока за время половины периода накапливает заряд в обкладках конденсаторов и отдаёт его обратно в источник.
Индуктивная нагрузка накапливает магнитную энергию в катушках и возвращает её в источник питания в виде электрической энергии.
Напряжение на выводах реактивного элемента будет достигать максимального значения во время смены направления тока, следовательно,
расхождение во времени между напряжением и током в пределах элемента составит четверть периода (сдвиг фаз 90°).
Угол сдвига фаз φ в цепи нагрузки определяется соотношением активного и реактивного сопротивлений нагрузки.
Реактивная мощность характеризует потери, созданные реактивными элементами в цепи переменного тока, и выражается формулой
Q = UIsinφ.
Природу потерь в цепи с реактивными элементами можно рассмотреть с помощью графиков на рисунках.
φ = 90° sin90° = 1 cos90° = 0
При отсутствии активной составляющей в нагрузке, сдвиг фаз между напряжением и током составит 90°.
В начале периода, когда напряжение максимально – ток будет равен нулю, следовательно, мгновенное значение мощности UI в это время будет равно нулю.
В течении первой четверти периода, мощность можно видеть на графике, как произведение UI,
которое станет равным нулю при максимуме тока и нулевом значении напряжения.
В следующую четверть периода на графике UI принимает отрицательное значение, следовательно, мощность возвращается обратно в источник питания.
То же самое произойдёт и в отрицательном полупериоде тока. В результате средняя (активная) потребляемая мощность P avg за период будет равна нулю.
В таком случае:
Реактивная мощность Q = UIsin90° = UI
Потребляемая мощность P = UIcos90° = 0
Полная мощность S = UI = √(P² + Q²) будет равна реактивной мощности
Коэффициент мощности P/S = 0
При отсутствии реактивных элементов и сдвига фаз в нагрузках, мгновенная мощность в полупериоде Umax*Imax будет максимальной,
и в следующем полупериоде произведение отрицательного напряжения с отрицательным током дадут положительный результат – полезную мощность в нагрузке.
φ = 0° sin90° = 0 cos90° = 1
В этом случае:
Реактивная мощность Q = UIsin0 = 0
Потребляемая мощность P = UIcos0 = UI
Полная мощность S = UI = √(P² + Q²) будет равна потребляемой мощности
Коэффициент мощности P/S = 1
Ниже представлен рисунок графиков со сдвигом фаз 45°, для случая равенства активного и реактивного сопротивлений в нагрузке.
φ = 45° sin45° = cos45° = √2/2 ≈ 0.71
Здесь:
Реактивная мощность Q = UIsin45° = 0.71UI
Потребляемая мощность P = UIcos45° = 0.71UI
Полная мощность S = √(P² + Q²) = UI
Коэффициент мощности P/S = 0.71
В примерах рассмотрены случаи с индуктивной нагрузкой, когда ток отстаёт от напряжения (положительный сдвиг фаз).
В случаях с ёмкостной нагрузкой, процессы и расчёты аналогичны,
только напряжение будет отставать от тока (отрицательный сдвиг фаз).
Угол сдвига фаз в сети определится соотношением активного и реактивного сопротивлений нагрузок в
параллельном соединении следующим образом:
XL и XС соответственно индуктивное и ёмкостное сопротивление нагрузок.
Преобладание индуктивных нагрузок будет уменьшать общее индуктивное сопротивление.
Из выражения видно, что угол в этом случае будет принимать положительный знак,
а преобладание ёмкостных нагрузок будет уменьшать ёмкостное сопротивление и вызывать отрицательный сдвиг.
При равенстве индуктивного и ёмкостного сопротивлений, угол сдвига будет равен нулю.
В бытовых и производственных потребителях индуктивное сопротивление обычно существенно преобладает над ёмкостным.
Подробнее о вычислениях общего угла сдвига φ для вариантов соединений активного и
реактивного сопротивлений в нагрузках можно ознакомиться на страничке электрический импеданс.
Компенсация реактивной мощности
Огромное количество индуктивных нагрузок в сети суммарно обладает колоссальной реактивной мощностью,
которая возвращается в генераторы и не совершает никакой полезной работы, расходуя энергию на нагрев кабелей и проводов ЛЭП,
перегружает трансформаторы, снижая их КПД, тем самым уменьшая пропускную способность активных токов.
Если параллельно индуктивной нагрузке подключить конденсатор,
фаза тока в цепи источника будет смещаться в противоположную сторону, компенсируя угол, созданный индуктивностью нагрузки.
При определённом соотношении номиналов,
можно добиться отсутствия сдвига фаз, следовательно, и отсутствия реактивных токов в цепи источника питания.
Ёмкость конденсатора определяется реактивным (индуктивным) сопротивлением нагрузки, которое необходимо компенсировать:
C = 1/(2πƒX),
X = U²/Q — реактивное сопротивление нагрузки,
Q — реактивная мощность нагрузки.
Компенсация реактивных токов в сети позволяет значительно уменьшить потери на активном сопротивлении проводов ЛЭП, кабелей и обмоток трансформаторов питающей сети.
В целях компенсации реактивной мощности на производственных предприятиях, где основными потребителями энергии являются асинхронные электродвигатели,
индукционные печи, люминесцентное освещение, которые обладают индуктивным сопротивлением, часто применяют специальные конденсаторные
установки, способные в ручном или автоматическом режиме поддерживать нулевой сдвиг фаз, тем самым минимизировать реактивные потери.
В масштабах энергосистемы компенсация происходит непосредственно на электростанциях путём контроля сдвига фаз и обеспечения соответствующего тока
подмагничивания роторных обмоток синхронных генераторов станций.
Компенсация реактивной мощности — одна из составляющих комплекса мер по Коррекции Коэффициента Мощности (ККМ) в электросети
(Power Factor Correction — PFC в англоязычной литературе). Применяется в целях уменьшения потерь электроэнергии, как на паразитную реактивную, так и нелинейную составляющую искажений тока в энергосистеме. Более подробно с материалом о ККМ (PFC) можно ознакомиться на странице — коэффициент мощности.
Онлайн-калькулятор расчёта реактивной мощности и её компенсации.
Достаточно вписать значения и кликнуть мышкой в таблице.
|
Реактивная мощность Q = √((UI)²-P²) |
Похожие страницы с расчётами:
Рассчитать импеданс.
Рассчитать частоту резонанса колебательного контура LC.
Рассчитать реактивное сопротивление катушки индуктивности L и конденсатора C.
Альтернативные статьи:
Дизель-генератор.
Мгновенная мощность
т.к.
,
то
.
Из формулы видно,
что мощность на индуктивности колеблется
с удвоенной частотой и принимает как
положительные, так и отрицательные
значения (см. временную диаграмму для
мощности).
Активная мощность
За период изменения
тока в цепи поступление и возврат энергии
в индуктивности равны друг другу. Энергия
поступает от источника и временно
запасается в магнитном поле индуктивности,
а затем возвращается источнику при
исчезновении магнитного поля. Т.о,
происходит колебание энергии между
источником и индуктивностью. В среднем
катушка не потребляет энергии и
следовательно, активная мощность равна
нулю: Р
= 0.
Такой режим работы
электрической цепи является вредным,
поскольку существуют встречные потоки
энергии, бесполезно загружаются провода,
и в результате снижается пропускная
способность линии.
Реактивная мощность
Для количественной
характеристики интенсивности обмена
энергией между источником и катушкой
служит реактивная мощность
,
Реактивная мощность
обозначается [Q].
Единицей реактивной мощности является
вольт-ампер реактивный (Вар).
8. Электрическая цепь с емкостью
Конденсатор –
элемент цепи, обладающий значительной
емкостью.
Конструктивно
конденсатор представляет собой две
пластины с большой поверхностью;
выполнены они из проводящего материала
и разделены слоем диэлектрика.
Конденсатор
характеризуется емкостью С. Емкость
определяет величину заряда, который
накапливается на пластинах при разности
потенциалов 1 В:
С=
Хотя пластины
конденсатора и разделены слоем
диэлектрика, при переменном напряжении
ток в цепи с конденсатором существует.
Это связано с тем, что синусоидальное
напряжение непрерывно меняется по
значению и направлению, =>но, и заряд
на пластинах конденсатора непрерывно
меняется.
Это изменение
заряда и связанное с ним движение
электронов и есть электрический ток в
цепи.
Рассмотрим электрическую цепь, состоящую
из источника питания и конденсатора
емкостью С.
|
|
Пусть в цепи с |
Так как
,
а q=C∙uC,
то
,
и следовательно,
В результате
интегрирования получаем
,
где
– амплитуда напряжения на емкости.
Таким образом, ток
в цепи с емкостью опережает по фазе
напряжение на
(или, что то же самое, напряжение отстает
по фазе от тока на
).

|
|
Векторная |
Это объясняется
тем, что напряжение на обкладках
конденсатора появляется только после
возникновения тока.
Емкость запасает
внутри себя энергию электрического
поля.
Обозначим
,
ХС
– емкостное сопротивление цепи.
Из формулы видно,
что с увеличением частоты емкость
уменьшается.
Закон Ома для цепи
с емкостью
– закон Ома для
амплитудных значений;
– закон Ома для
действующих значений;
– закон Ома в
комплексной форме.
Множитель (–j)
перед емкостным сопротивлением ХС
необходим для обеспечения сдвига фаз
между током и напряжением.
9. Мощность в цепи с емкостью
Мгновенная мощность
(см. график на
временной диаграмме)
Из графика и формулы
для мгновенной мощности следует, что в
цепи с емкостью, так же, как и в цепи с
индуктивностью, происходит переход
энергии от источника к нагрузке, и
наоборот. В данном случае энергия
источника преобразуется в энергию
электрического поля конденсатора.
Мощность колеблется
с удвоенной частотой. За период изменения
тока, поступление и возврат энергии в
емкостном элементе равны друг другу.
Это значит, что, сколько энергии поступает
в нагрузку, столько же возвращается
обратно в генератор. Энергия здесь не
тратится, а колеблется между нагрузкой
и генератором. В результате этого
снижается пропускная способность линии.
Средняя мощность
в цепи с емкостью Р = 0.
Реактивная мощность
Для количественной
характеристики интенсивности обмена
энергией между источником и конденсатором
служит реактивная мощность:
Реактивная мощность
Что такое реактивная мощность?
Для начала рассмотрим понятие электрической мощности. В широком смысле слова, этот термин означает работу, выполненную за единицу времени. По отношению к электрической энергии, понятие мощности немного откорректируем: под электрической мощностью будем понимать физическую величину, реально характеризующую скорость генерации тока или количество переданной либо потреблённой электроэнергии в единицу времени.
Понятно, что работа электричества в единицу времени определяется электрической мощностью, измеряемой в ваттах. Мгновенную мощность на участке цепи находят по формуле: P = U×I, где U и I – мгновенные значения показателей параметров напряжения и силы тока на данном участке.
Строго говоря, приведённая выше формула справедлива только для постоянного тока. Однако, в цепях синусоидального тока формула работает лишь тогда, когда нагрузка потребителей чисто активная. При резистивной нагрузке вся электрическая энергия расходуется на выполнение полезной работы. Примерами активных нагрузок являются резистивные приборы, такие как кипятильник или лампа накаливания.
При наличии в электрической цепи ёмкостных или индуктивных нагрузок, появляются паразитные токи, не участвующие в выполнении полезной работы. Мощность этих токов называют реактивной.
На индуктивных и ёмкостных нагрузках часть электроэнергии рассеивается в виде тепла, а часть препятствует выполнению полезной работы.
К устройствам с индуктивными нагрузками относятся:
- электромоторы;
- дроссели;
- трансформаторы;
- электромагнитные реле и другие устройства, содержащие обмотки.
Ёмкостными сопротивлениями обладают конденсаторы.
Физика процесса
Когда мы имеем дело с цепями постоянного тока, то говорить о реактивной мощности не приходится. В таких цепях значения мгновенной и полной мощности совпадают. Исключением являются моменты включения и отключения ёмкостных и индуктивных нагрузок.
Похожая ситуация происходит при наличии чисто активных сопротивлений в синусоидальных цепях. Однако если в такую электрическую цепь включены устройства с индуктивными или ёмкостными сопротивлениями, происходит сдвиг фаз по току и напряжению.
При этом на индуктивностях наблюдается отставание тока по фазе, а на ёмкостных элементах фаза тока сдвигается так, что ток опережает напряжение. В связи с нарушением гармоники тока, полная мощность разлагается на две составляющие. Ёмкостные и индуктивные составляющие называют реактивными, бесполезными. Вторая составляющая состоит из активных мощностей.
Угол сдвига фаз используется при вычислениях значений активных и реактивных ёмкостных либо индуктивных мощностей. Если угол φ = 0, что имеет место при резистивных нагрузках, то реактивная составляющая отсутствует.
Важно запомнить:
- резистор потребляет исключительно активную мощность, которая выделяется в виде тепла и света;
- катушки индуктивности провоцируют образование реактивной составляющей и возвращают её в виде магнитных полей;
- Ёмкостные элементы (конденсаторы) являются причиной появления реактивных сопротивлений.
Возникновение реактивная мощность
Допустим, цепь содержит источник питания постоянного тока и идеальную индуктивность. Включение цепи порождает переходный процесс. Напряжение стремится достичь номинального значения, росту активно мешает собственное потокосцепление индуктивности. Каждый виток провода согнут круговой траекторией. Образуемое магнитное поле будет пересекать соседствующий сегмент. Если витки расположены один за другим, характер взаимодействия усилится. Рассмотренное называется собственным потокосцеплением.
Характер процесса таков: наводимая ЭДС препятствует изменениям поля. Ток пытается стремительно вырасти, потокосцепление тянет обратно. Вместо ступеньки видим сглаженный выступ. Энергия магнитного поля потрачена, чтобы воспрепятствовать процессу создавшему. Случай возникновения реактивной мощности. Фазой отличается от полезной, вредит. Идеально: направление вектора перпендикулярно активной составляющей. Подразумевается, сопротивление провода нулевое (фантастический расклад).
При выключении цепи процесс повторится обратным порядком. Ток стремится мгновенно упасть до нуля, в магнитном поле запасена энергия. Пропади индуктивность, переход пройдет внезапно, потокосцепление придает процессу иную окраску:
- Уменьшение тока вызывает снижение напряженности магнитного поля.
- Произведенный эффект наводит противо-ЭДС витков.
- В результате после отключения источника питания ток продолжает существовать, понемногу затухая.
Реактивная мощность некое звено инерции, постоянно запаздывающее, мешающее. Первый вопрос: зачем тогда нужны индуктивности? О, у них хватает полезных качеств. Польза заставляет мириться с реактивной мощностью. Распространенным положительным эффектом назовем работу электрических двигателей. Передача энергии идет через магнитный поток. Меж витками одной катушки, как было показано выше. Взаимодействию подвержены постоянный магнит, дроссель, все, способное захватить вектором индукции.
Случаи нельзя назвать в смысле описательном всеобъемлющими. Иногда применяется поток сцепления в виде, показанном для примера. Принцип используют пускорегулирующие аппараты газоразрядных ламп. Дроссель снабжен несметным количеством витков: отключение напряжения вызывает не плавное снижение тока, но выброс большой амплитуды противоположной полярности. Индуктивность велика: отклик поистине потрясающий. Превышает исходные 230 вольт на порядок. Достаточно, чтобы возникла искра, лампочка зажглась.
Реактивная мощность и конденсаторы
Реактивная мощность запасается энергией магнитного поля индуктивностями. А конденсатор? Выступает источником возникновения реактивной составляющей. Дополним обзор теорией сложения векторов. Поймет рядовой читатель. В физике электрических сетей часто используются колебательные процессы. Всем известные 220 вольт (теперь принятые 230) в розетке частотой 50 Гц. Синусоида, амплитуда которой равна 315 вольт. Анализируя цепи, удобно представить вращающимся по часовой стрелке вектором.
Анализ цепей графическим методом
Упрощается расчет, можно пояснить инженерное представление реактивной мощности. Угол фазы тока считают равным нулю, откладывается вправо по оси абсцисс. Реактивная энергия индуктивности совпадает фазой с напряжением UL, опережает на 90 градусов ток. Идеальный случай. Практикам приходится учитывать сопротивление обмотки. Реактивной на индуктивности будет часть мощности.Угол меж проекциями важен. Величина называется коэффициентом мощности. Что означает на практике? Перед ответом на вопрос рассмотрим понятие треугольника сопротивлений.
Треугольник мощностей и cos φ
Для наглядности изобразим полную мощность и её составляющие в виде векторов. Обозначим вектор полной мощности символом S, а векторам активной и реактивной составляющей присвоим символы P и Q, соответственно. Поскольку вектор S является суммой составляющих тока, то, по правилу сложения векторов, образуется треугольник мощностей.
Коэффициент мощности
Применяя теорему Пифагора, вычислим модуль вектора S:
Отсюда можно найти реактивную составляющую:
Реактивная составляющая
Выше мы уже упоминали, что реактивная мощность зависит от сдвига фаз, а значит и от угла этого сдвига. Эту зависимость удобно выражать через cos φ. По определению cos φ = P/S. Данную величину называют коэффициентом мощности и обозначают Pf. Таким образом, Pf = cos φ = P/S.
Коэффициент мощности, то есть cos φ, является очень важной характеристикой, позволяющей оценить эффективность работы тока. Данная величина находится в промежутке от 0 до 1.
Если угол сдвига фаз принимает нулевое значение, то cos φ = 1, а это значит что P = S, то есть полная мощность состоит только из активной мощности, а реактивность отсутствует. При сдвиге фаз на угол π/2 , cos φ = 0, откуда следует, что в цепи господствуют только реактивные токи (на практике такая ситуация не возникает).
Из этого можно сделать вывод: чем ближе к 1 коэффициент Pf , тем эффективнее используется ток. Например, для синхронных генераторов приемлемым считается коэффициент от 0,75 до 0,85.
Формулы
Поскольку реактивная мощность зависит от угла φ, то для её вычисления применяется формула: Q = UI×sin φ. Единицей измерения реактивной составляющей является вар или кратная ей величина – квар.
Активную составляющую находят по формуле: P = U*I×cosφ. Тогда
Зная коэффициент Pf (cos φ), мы можем рассчитать номинальную мощность потребителя тока по его номинальному напряжению, умноженному на значение силы потребляемого тока.
Полная мощность
По сложившейся практике потребители оплачивают не полезную мощность, которая непосредственно используется в хозяйстве, а полную, которую отпускает предприятие-поставщик. Различают эти показатели по единицам измерения – полная мощность измеряется в вольт-амперах (ВА), а полезная – в киловаттах. Активная и реактивная электроэнергия используется всеми запитанными от сети электроприборами.
Понятие реактивной электроэнергии
Этот вид электроэнергии присущ цепям, в составе которых имеются реактивные элементы. Реактивная электроэнергия — это часть полной поступаемой мощности, которая не расходуется на полезную работу.
В электроцепях постоянного тока понятие реактивной мощности отсутствует. В цепях переменного тока реактивная составляющая возникает только в том случае, когда присутствует индуктивная или емкостная нагрузка. В таком случае наблюдается несоответствие фазы тока с фазой напряжения. Данный сдвиг фаз между напряжением и током обозначается символом «φ».
При индуктивной нагрузке в цепи наблюдается отставание фазы, при емкостной – ее опережение. Поэтому потребителю приходит только часть полной мощности, а основные потери происходят из-за бесполезного нагревания устройств и приборов в процессе эксплуатации.
Потери мощности происходят из-за наличия в электрических устройствах индуктивных катушек и конденсаторов. Из-за них в цепи в течение некоторого времени происходит накопление электроэнергии. После этого запасенная энергия поступает обратно в цепь. К приборам, в составе потребляемой мощности которых имеется реактивная составляющая электроэнергии, относятся переносные электроинструменты, электродвигатели и различная бытовая техника. Эта величина рассчитывается с учетом особого коэффициента мощности, который обозначается как cos φ.
Активная электроэнергия
Активная составляющая полной мощности совершает полезную работу и преобразовывается в те виды энергии, которые нужны потребителю. У части бытовых и промышленных электроприборов в расчетах активная и полная мощность совпадают. Среди таких устройств – электроплиты, лампы накаливания, электропечи, обогреватели, утюги и гладильные прессы и прочее.
Если в паспорте указана активная мощность 1 кВт, то полная мощность такого прибора будет составлять 1 кВА.
Расчет реактивной электроэнергии
Коэффициент мощности лежит в пределах от 0,5 до 0,9; точное значение этого параметра можно узнать из паспорта электроприбора. Полная мощность должна быть определена как частное от деления активной мощности на коэффициент.
Например, если в паспорте электрической дрели указана мощность в 600 Вт и значение 0,6, тогда потребляемая устройством полная мощность будет равна 600/06, то есть 1000 ВА. При отсутствии паспортов для вычисления полной мощности прибора коэффициент можно брать равным 0,7.
Поскольку одной из основных задач действующих систем электроснабжения является доставка полезной мощности конечному потребителю, реактивные потери электроэнергии считаются негативным фактором, и возрастание этого показателя ставит под сомнение эффективность электроцепи в целом. Баланс активной и реактивной мощности в цепи может быть наглядно представлен в виде этого забавного рисунка:
Мощность активная, реактивная и полная
Перечисленные понятия рассматривают с учетом особенностей нагрузки. Активная мощность потребляется обычным проводником. При увеличении силы тока энергия расходуется на повышение температуры (ТЭН чайника) или световое излучение (нить лампы накаливания).
Индуктивная нагрузка и конденсатор потребляют реактивную мощность. Энергия в этих вариантах преобразуется в магнитное (электрическое) поле, соответственно. Суммарная величина – полная мощность.
Различия
Разница между величинами в том, что активно действующая мощностная характеристика показывает КПД устройств, а реактивная является передачей этого КПД. Разница также наблюдается в определении, символе, формуле и значимости.
Вам это будет интересно Особенности единиц измерения кВТ и кВА
Обратите внимание! Что касается значения, то вторая нужна лишь для того, чтобы управлять создавшимся напряжением от первой величины и преодолевать мощностные колебания.
Смысл реактивной нагрузки
Любая реактивная нагрузка создает временной сдвиг между фазами тока и напряжения. Эту величину измеряют в градусах. Наиболее наглядным является векторное представление электрических параметров. Если подключить индуктивность, напряжение будет опережать ток. Угол между ними обозначают в формулах буквой «ϕ» («Фи» греч.).
Временные и векторные диаграммы показывают, как изменяются основные параметры при подключении индуктивных (емкостных) элементов
На картинке показано, что при подключении емкостной нагрузки вектора «меняются» местами. В идеальных условиях сдвиг между векторами равен 90°. В действительности следует учитывать влияние электрического сопротивления цепи, несовершенство конструкций. С учетом особенностей элементов следует напомнить, что в индуктивности (емкости) при сохранении параметров источника питания плавно изменяется ток (напряжение), соответственно.
Почему в сети напряжение переменное
Для объяснения настоящей ситуации надо сделать краткий экскурс в историю. Электричество известно человеку сотни (по некоторым данным, тысячи лет). Однако действительно массовое использование этой энергии началось сравнительно недавно – в конце 19 века. Именно тогда (1879 г.) Эдисон запатентовал первый функциональный прибор, который помогал решать проблемы освещения. Для питания лампочек он стал монтировать сети постоянного тока.
Через десять лет Тесла создал генераторы переменного тока. После ожесточенной конкурентной борьбы именно его способ передачи энергии на расстояния одержал победу. Этот результат был обеспечен скорее рыночными методами, чем внимательным сравнением потребительских характеристик.
К сведению. Метрополитен Нью-Йорка до сих пор функционирует с подключением к сети постоянного тока.
Источники
- https://www.asutpp.ru/reaktivnaya-moschnost.html
- https://VashTehnik.ru/enciklopediya/reaktivnaya-moshhnost.html
- https://FB.ru/article/191380/chto-takoe-aktivnaya-i-reaktivnaya-elektroenergiya
- https://amperof.ru/teoriya/reaktivnaya-moshhnost.html
- https://rusenergetics.ru/ustroistvo/reaktivnaya-moschnost
Все мы ежедневно сталкиваемся с электроприборами, кажется, без них наша жизнь останавливается. И у каждого из них в технической инструкции указана мощность. Сегодня мы разберемся что же это такое, узнаем виды и способы расчета.
Содержание
- 1 Мощность в цепи переменного электрического тока
- 1.1 Понятие активной мощности
- 1.2 Понятие реактивной мощности
- 1.2.1 Емкостные и индуктивные нагрузки
- 1.2.2 Коэффициент мощности cosφ
- 1.3 Понятие полной мощности. Треугольник мощностей
- 2
- 3 Как измеряют cosφ на практике
Мощность в цепи переменного электрического тока
Электроприборы, подключаемые к электросети работают в цепи переменного тока, поэтому мы будем рассматривать мощность именно в этих условиях. Однако, сначала, дадим общее определение понятию.
Мощность — физическая величина, отражающая скорость преобразования или передачи электрической энергии.
В более узком смысле, говорят, что электрическая мощность – это отношение работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
Если перефразировать данное определение менее научно, то получается, что мощность – это некое количество энергии, которое расходуется потребителем за определенный промежуток времени. Самый простой пример – это обычная лампа накаливания. Скорость, с которой лампочка превращает потребляемую электроэнергию в тепло и свет, и будет ее мощностью. Соответственно, чем выше изначально этот показатель у лампочки, тем больше она будет потреблять энергии, и тем больше отдаст света.
Поскольку в данном случае происходит не только процесс преобразования электроэнергии в некоторую другую (световую, тепловую и т.д.), но и процесс колебания электрического и магнитного поля, появляется сдвиг фазы между силой тока и напряжением, и это следует учитывать при дальнейших расчетах.
При расчете мощности в цепи переменного тока принято выделять активную, реактивную и полную составляющие.
Понятие активной мощности
Активная «полезная» мощность — это та часть мощности, которая характеризует непосредственно процесс преобразования электрической энергии в некую другую энергию. Обозначается латинской буквой P и измеряется в ваттах (Вт).
Рассчитывается по формуле: P = U⋅I⋅cosφ,
где U и I – среднеквадратичное значение напряжения и силы тока цепи соответственно, cos φ – косинус угла сдвига фазы между напряжением и током.
ВАЖНО! Описанная ранее формула подходит для расчета цепей с напряжением 220В, однако, мощные агрегаты обычно используют сеть с напряжением 380В. В таком случае выражение следует умножить на корень из трех или 1.73
Понятие реактивной мощности
Реактивная «вредная» мощность — это мощность, которая образуется в процессе работы электроприборов с индуктивной или емкостной нагрузкой, и отражает происходящие электромагнитные колебания. Проще говоря, это энергия, которая переходит от источника питания к потребителю, а потом возвращается обратно в сеть.
Использовать в дело данную составляющую естественно нельзя, мало того, она во многом вредит сети питания, потому обычно его пытаются компенсировать.
Обозначается эта величина латинской буквой Q.
ЗАПОМНИТЕ! Реактивная мощность измеряется не в привычных ваттах (Вт), а в вольт-амперах реактивных (Вар).
Рассчитывается по формуле:
Q = U⋅I⋅sinφ,
где U и I – среднеквадратичное значение напряжения и силы тока цепи соответственно, sinφ – синус угла сдвига фазы между напряжением и током.
ВАЖНО! При расчете данная величина может быть как положительной, так и отрицательной – в зависимости от движения фазы.
Емкостные и индуктивные нагрузки
Главным отличием реактивной (емкостной и индуктивной) нагрузки – наличие, собственно, емкости и индуктивности, которые имеют свойство запасать энергию и позже отдавать ее в сеть.
Индуктивная нагрузка преобразует энергию электрического тока сначала в магнитное поле (в течение половины полупериода), а далее преобразует энергию магнитного поля в электрический ток и передает в сеть. Примером могут служить асинхронные двигатели, выпрямители, трансформаторы, электромагниты.
ВАЖНО! При работе индуктивной нагрузки кривая тока всегда отстает от кривой напряжения на половину полупериода.
Емкостная нагрузка преобразует энергию электрического тока в электрическое поле, а затем преобразует энергию полученного поля обратно в электрический ток. Оба процесса опять же протекают в течение половины полупериода каждый. Примерами являются конденсаторы, батареи, синхронные двигатели.
ВАЖНО! Во время работы емкостной нагрузки кривая тока опережает кривую напряжения на половину полупериода.
Коэффициент мощности cosφ
Коэффициент мощности cosφ (читается косинус фи)– это скалярная физическая величина, отражающая эффективность потребления электрической энергии. Проще говоря, коэффициент cosφ показывает наличие реактивной части и величину получаемой активной части относительно всей мощности.
Коэффициент cosφ находится через отношение активной электрической мощности к полной электрической мощности.
ОБРАТИТЕ ВНИМАНИЕ! При более точном расчете следует учитывать нелинейные искажения синусоиды, однако, в обычных расчетах ими пренебрегают.
Значение данного коэффициента может изменяться от 0 до 1 (если расчет ведется в процентах, то от 0% до 100%). Из расчетной формулы не сложно понять, что, чем больше его значение, тем больше активная составляющая, а значит лучше показатели прибора.
Понятие полной мощности. Треугольник мощностей
Полная мощность – это геометрически вычисляемая величина, равная корню из суммы квадратов активной и реактивной мощностей соответственно. Обозначается латинской буквой S.
Также рассчитать полную мощность можно путем перемножения напряжения и силы тока соответственно.
S = U⋅I
ВАЖНО! Полная мощность измеряется в вольт-амперах (ВА).
Треугольник мощностей – это удобное представление всех ранее описанных вычислений и соотношений между активной, реактивной и полной мощностей.
Катеты отражают реактивную и активную составляющие, гипотенуза – полную мощность. Согласно законам геометрии, косинус угла φ равен отношению активной и полной составляющих, то есть он является коэффициентом мощности.
Как найти активную, реактивную и полную мощности. Пример расчета
Все расчеты строятся на указанных ранее формулах и треугольнике мощностей. Давайте рассмотрим задачу, наиболее часто встречающуюся на практике.
Обычно на электроприборах указана активная мощность и значение коэффициента cosφ. Имея эти данные несложно рассчитать реактивную и полную составляющие.
Для этого разделим активную мощность на коэффициент cosφ и получим произведение тока и напряжения. Это и будет полной мощностью.
Далее, исходя из треугольника мощностей, найдем реактивную мощность равную квадрату из разности квадратов полной и активной мощностей.
Как измеряют cosφ на практике
Значение коэффициента cosφ обычно указано на бирках электроприборов, однако, если необходимо измерить его на практике пользуются специализированным прибором – фазометром. Также с этой задачей легко справится цифровой ваттметр.
Если полученный коэффициент cosφ достаточно низок, то его можно компенсировать практически. Осуществляется это в основном путем включения в цепь дополнительных приборов.
- Если необходимо скорректировать реактивную составляющую, то следует включить в цепь реактивный элемент, действующий противоположно уже функционирующему прибору. Для компенсации работы асинхронного двигателя, для примера индуктивной нагрузки, в параллель включается конденсатор. Для компенсации синхронного двигателя подключается электромагнит.
- Если необходимо скорректировать проблемы нелинейности в схему вводят пассивный корректор коэффициента cosφ, к примеру, это может быть дроссель с высокой индуктивностью, подключаемый последовательно с нагрузкой.
Мощность – это один из важнейших показателей электроприборов, поэтому знать какой она бывает и как рассчитывается, полезно не только школьникам и людям, специализирующимся в области техники, но и каждому из нас.