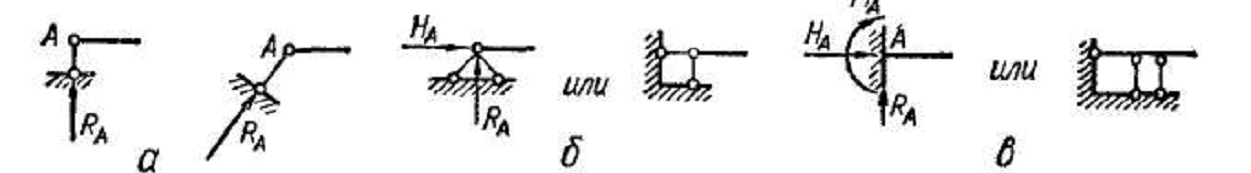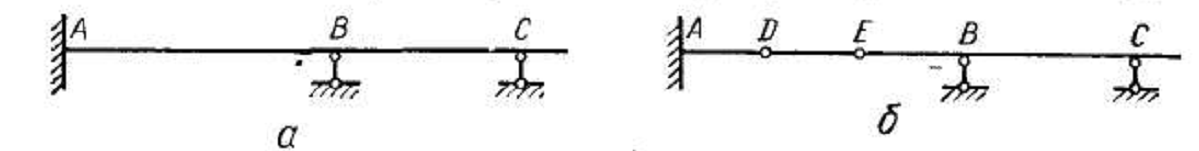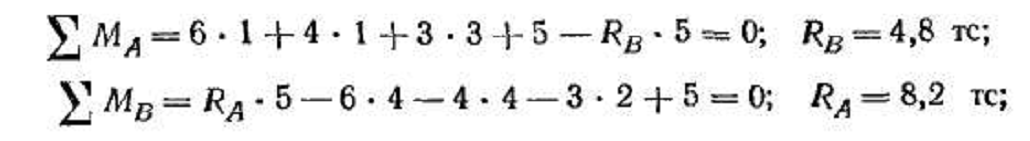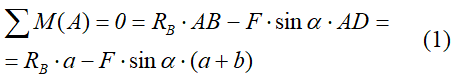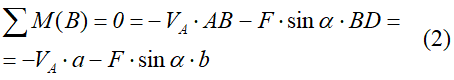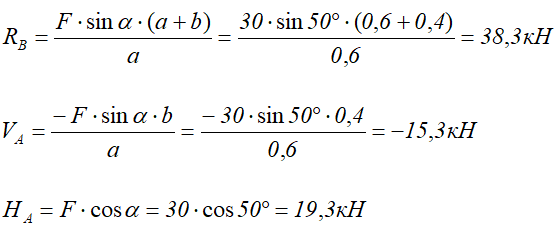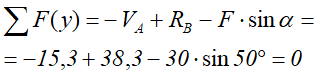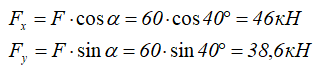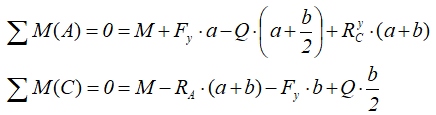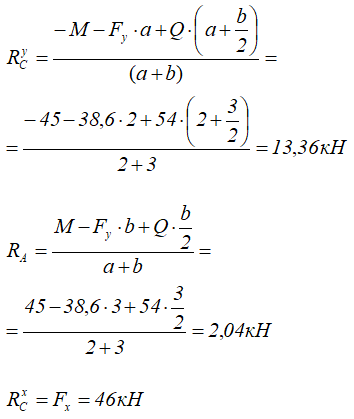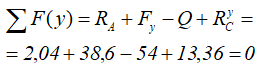Привет! В этой статье предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции опор, чему учат еще в рамках дисциплины — «теоретическая механика». Но для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.
Так как этот урок для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику.
В рамках статьи рассмотрим 4 примера: двухопорная балка, загруженная посередине пролёта сосредоточенной силой, такая же балка, но загруженная распределённой нагрузкой, консольная балка и плоская рама.
Что такое реакция опоры?
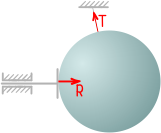
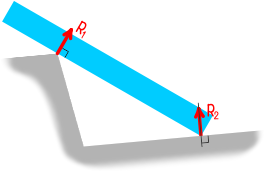
Чтобы лучше понять, что такое реакция опоры (опорная реакция), давай рассмотрим следующий пример — балку (стержень) лежащую на опорах:

На балку давит нагрузка – сила, в свою очередь, балка давит на опоры. И чтобы балка лежала на опорах (никуда не проваливалась), опоры выполняют свою основную функцию — удерживают балку. А чтобы удерживать балку, опоры должны компенсировать тот вес, с которым балка давит на них. Соответственно, действие опор можно представить в виде некоторых сил, так называемых — реакций опор.

Для балки, и нагрузка, и реакции опор, будут являться внешними силами, которые нужно обязательно учитывать при расчёте балки. А чтобы учесть опорные реакции, сначала нужно научиться определять их, чем, собственно, и займёмся на этом уроке.
Виды связей и их реакции
Связи – это способы закрепления элементов конструкций. Опоры, которые я уже показывал ранее – это тоже связи.
В этой статье будем рассматривать три вида связей: жёсткая заделка, шарнирно-подвижная и шарнирно-неподвижная опора.
Жёсткая заделка

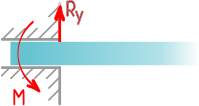
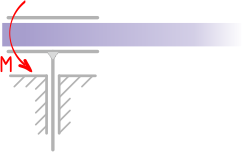
Жёсткая заделка — это один из вариантов закрепления элементов конструкций. Этот тип связи препятствует любым перемещениям, тем самым для плоской задачи, может возникать три реакции: вертикальная (RA), горизонтальная (HA) и момент (MA).

Шарнирно-подвижная и шарнирно-неподвижная опора
В этой статье будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

В шарнирно-неподвижной опоре возникает две реакции: вертикальная и горизонтальная. Так как опора препятствует перемещению в этих двух направлениях. В шарнирно-подвижной опоре возникает только вертикальная реакция.

Однако, видов связей и их условных обозначений достаточно много, но в рамках этой статьи их все рассматривать не будем. Так как, изученные ранее виды связей, являются основными и практически всегда, при решении задач по сопромату, ты будешь сталкиваться именно с ними.
Что такое момент силы?
Также необходимо разобраться с понятием момент силы.
Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр.
Проиллюстрирую написанное:

Правило знаков для моментов
Также для моментов, нужно задаться каким-то правилом знаков. Я в своих уроках буду придерживаться такого правила:
- если сила относительно точки стремится повернуть ПРОТИВ часовой стрелки, то момент положительный;
- если она стремится повернуть ПО часовой стрелке, то момент отрицательный.

Всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнём с простейшей расчётной схемы балки.
Определение реакций для двухопорной балки
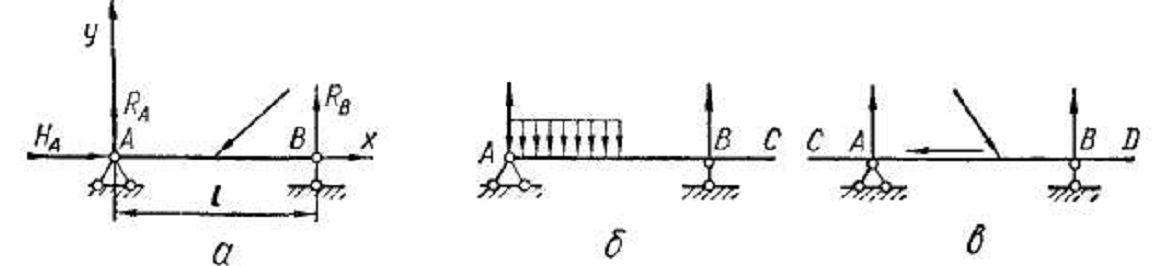
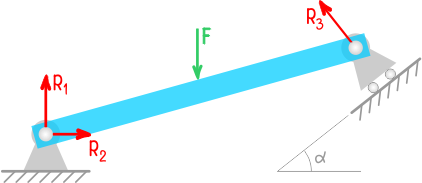
Возьмём балку, загруженную посередине сосредоточенной силой и опирающейся на шарнирно-неподвижную и шарнирно-подвижную опору:

Введём систему координат: направим ось x вдоль балки, а ось y вертикально. Обозначим реакции в опорах как HA, RA и RB:

Для тех, кто пришёл сюда, ещё будучи на этапе изучения теоретической механики, а я знаю, таких будет много, важно отметить, что в сопромате не принято указывать знаки векторов над силами.
В термехе же, в обязательном порядке, преподаватель от тебя настойчиво будет требовать указывать знак вектора над всеми силами, вот так:

Условия равновесия системы
Чтобы найти все реакции, нужно составить и решить три уравнения — уравнения равновесия:

Данные уравнения являются условиями равновесия системы. А так как мы предполагаем, что опоры обеспечивают это состояние равновесия (удерживают балку). То составив и решив уравнения равновесия — найдём значения опорных реакций.
Первое уравнение называется уравнением проекций — суммой проекций всех сил на координатную ось, которая должна быть равна нулю. Два других уравнения называются уравнениями моментов — суммами моментов всех сил относительно точек, которые должны быть равны нулю.
Уравнения равновесия
Как видишь, чтобы научиться находить реакции опор, главное — научиться правильно составлять уравнения равновесия.

Уравнение проекций
Запишем первое уравнение — уравнение проекций для оси x.
В уравнении будут участвовать только те силы, которые параллельны оси x. Такая сила у нас только одна — HA. Так как HA направлена против положительного направления оси x, в уравнение её нужно записать с минусом:
Тогда HA будет равна:
Поздравляю, первая реакция найдена!
Уравнения моментов
А теперь самое интересное…запишем уравнение моментов, относительно точки A, с учётом ранее рассмотренного правила знаков для моментов.
Так как сила F поворачивает ПО часовой стрелке, записываем её со знаком «МИНУС» и умножаем на плечо.
Так как сила RB поворачивает ПРОТИВ часовой стрелки, пишем её со знаком «ПЛЮС» и умножаем на плечо. И, наконец, всё это приравниваем к нулю:
Из полученного уравнения выражаем реакцию RB:

Вторая реакция найдена! Третья реакция находится аналогично, но только теперь уравнение моментов записываем относительно другой точки:

Проверка правильности найденных опорных реакций
Чем хороши задачи на определение реакций, так это тем, что правильность расчёта реакций легко проверить. Для этого достаточно составить дополнительное уравнение равновесия, подставить все численные значения и если сумма проекций сил или сумма моментов будет равна нулю, то и реакции, значит, найдены — верно, а если нет, то ищем ошибку.
Составим дополнительное уравнение проекций для оси y и подставим все численные значения:
Как видишь, реакции опор найдены правильно.
Определение реакций опор для балки с распределенной нагрузкой
Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно «свернуть» до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:


Расчёт реакций для консольной балки
Давай рассмотрим теперь пример с жёсткой заделкой – консольную балку. Заодно посмотрим, как учесть силу, приложенную под углом (α = 30°).

Силу, направленную под определённым углом, нужно разложить на две составляющие – горизонтальную и вертикальную. А их значения найти из силового треугольника:


Покажем реакции в заделке и выполним расчёт:

Для этой задачи выгоднее использовать другую форму условий равновесия:

А выгодна она тем, что из каждого записанного уравнения будем сразу находить реакцию:
Не пугайся отрицательного значения реакции! Это значит, что при указании реакции, мы не угадали с её направлением. Расчёт же показал, что MA, направлена не по часовой стрелке, а против.
В теоретической механике, когда реакции получают с «минусом» обычно не заморачиваются и не меняют их направление на схеме, так и оставляют в ответе отрицательное значение, оговаривая, что да реакция найдена, но с учётом знака, на самом деле направлена в другую сторону. Потому что найденные реакции в задачах на статику, являются конечной точкой расчёта.
У нас же, в сопромате после нахождения опорных реакций, всё только начинается. Найдя реакции, мы всего лишь находим ВСЕ силы действующие на элемент конструкции, а дальше по сценарию стоит задача определить внутренние усилия, возникающие в этом элементе, расчёты на прочность и т. д. Поэтому на схеме, обязательно следует указывать истинное направление реакций. Чтобы потом, когда будут рассчитываться внутренние усилия ничего не напутать со знаками.
Если получили отрицательное значение, нужно отразить это на схеме:

С учётом изменений на схеме реакция будет равна:
Сделаем проверку, составив уравнение равновесие, ещё не использованное – сумму моментов относительно, скажем, точки B, которая, при правильном расчёте, конечно, должна быть равна нулю:
Если не менять направление реакции, то в проверочном уравнении нужно учесть этот «минус»:
Можешь посмотреть еще один пример, с похожей схемой, для закрепления материала, так сказать.
Реакции опор для плоской рамы
Теперь предлагаю выполнить расчёт плоской рамы. Для примера возьмём расчётную схему, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:
- заменяем опоры на реакции;
- сворачиваем распределенную нагрузку до сосредоточенной силы;
- вводим систему координат x и y.

Выполняем расчёт реакций опор:

Меняем направление реакции RA:

В итоге получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумма будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!
Балками
будем
называть прямолинейные стержни,
работающие на изгиб. В сопротивлении
материалов термин «балка» значительно
шире, чем в обычном употреблении этого
слова: с точки зрения расчета на прочность,
жесткость и устойчивость балкой является
не только строительная балка, но также
и вал, болт, ось железнодорожного
вагона, зуб шестерни и т. д.
Вначале
ограничимся построением эпюр для
простейшего случая изгиба балок, при
котором все заданные нагрузки лежат в
одной плоскости, называемой силовой
(на
рис. 4, а
—
плоскость П), причем эта плоскость
совпадает с одной из главных плоскостей
балки. Такой случай будем называть
плоским
изгибом.
На
расчетной схеме балку принято заменять
ее осью (рис. 4, б). При этом все нагрузки,
естественно, должны
Рис
4 быть приведены к оси
балки и силовая плоскость будет
совпадать с плоскостью чертежа.
Как
правило, балки имеют опорные устройства
— опоры. Для расчета же их схематизируют
в виде трех основных типов опор:
а)
шарнирно-подвижная
опора (рис.
5, а), в которой может возникать только
одна составляющая реакции — ,
направленная
вдоль опорного стерженька;
б)
шарнирно-неподвижная
опора (рис.
5, б), в которой могут возникать две
составляющие — вертикальная реакция
и
горизонтальная
реакция
в)
защемление
(иначе
жесткое
защемление или заделка), где
могут быть три составляющие — вертикальная
и
горизонтальная
реакции
и опорный момент Ма
(рис.
5, в).
Рис
5
Все
реакции и моменты считаются приложенными
в точке А
—
центре тяжести опорного сечения.
Балка,
показанная на рис. 6, с, называется
простой,
или
однопролетной
, или
двухопорной,
а
расстояние l
между опорами — пролетом.
Рис
6
Консолью
называется
балка, защемленная одним концом и не
имеющая других опор (рис. 4, б), или часть
балки, свешивающаяся за опоры (часть ВС
на
рис. 6, б; части АС
и
BD
на
рис. 6, е). Банки, имеющие свешивающиеся
части, называют консольными (рис. 6, б,
в).
Для
плоской системы сил можно составить
три уравнения статики для определения
неизвестных реакций.
Поэтому
балка будет статически определимой,
если число неизвестных опорных
реакций не превышает трех; в противном
случае балка статически неопределима.
Очевидно, что балки, изображенные на
рис. 4 и 6,
статически определимы.
Рис
7
Балка,
изображенная на рис. 7, а,
называется неразрезной
и
является статически
неопределимой, поскольку
имеет пять неизвестных опорных реакций:
три в опоре А
и
по одной в опорах В
и С.
Поставив
в сечениях балки шарниры, например в
точках D
и
Е
(рис.
7, б), получим статически определимую
шарнирную балку, ибо каждый такой
промежуточный шарнир к трем основным
уравнениям статики прибавляет одно
дополнительное уравнение: сумма
моментов относительно центра шарнира
от всех сил, расположенных по одну
сторону от него, равна нулю.
Построение
эпюр для статически неопределимых балок
требует умения вычислять деформации,
а поэтому ограничимся пока исключительно
статически определимыми балками.
Способы
определения опорных реакций изучают в
курсе теоретической механики. Поэтому
здесь остановимся только на некоторых
практических вопросах. Для этого
рассмотрим простую балку (рис. 6,
а).
1.
Опоры
обычно обозначают буквами А
и
В.
Три
неизвестные реакции находят из следующих
уравнений равновесия:
а)
сумма проекций всех сил на ось балки
равна нулю:
откуда находят
б)
сумма моментов всех сил относительно
опорного шарнира А
равна
нулю:
откуда находят .
в)
сумма моментов всех сил относительно
опорного шарнира В
равна
нулю:
откуда
находят .
2.
Для
контроля можно использовать или условие
равенства нулю суммы проекций на
вертикаль:
или
условие равенства нулю суммы моментов
относительно какой-либо точки С, отличной
от А
и
В,
т.
е.
У
Условием
пользоваться
проще, но оно дает надежную проверку
только в тех случаях, когда к балке не
приложены сосредоточенные моменты.
3.
Перед
составлением уравнений равновесия
нужно выбрать (вообще говоря, произвольно)
направления реакций и изобразить их на
рисунке. Если в результате вычислений
какая-либо реакция получается
отрицательной, нужно изменить на рисунке
ее направление на обратное и в
дальнейшем считать эту реакцию
положительной,
5.
Если
на балку действует распре
деленная
нагрузка, то для определения реакций
ее заменяют равнодействующей, которая
равна площади эпюры нагрузки и приложена
в центре тяжести этой эпюры.
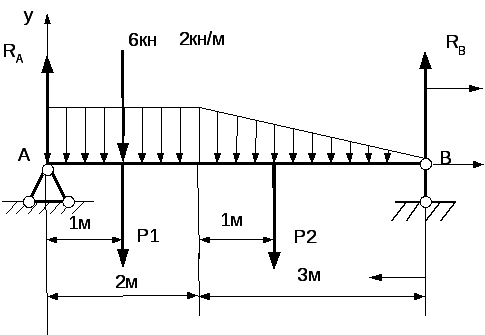
Пример
5. Вычислить
опорные реакции для балки, показанной
на рис. 8.
Прежде
всего находим равнодействующие Р1
и
Р2
нагрузок,
распределенных на участках АС
н
СВ:
;
.
Сила
Р1
приложена
в центре тяжести прямоугольника, а Р2
—
в центре тяжести треугольника. Находим
реакции:
Рис
8
Проверка:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определением реакций опор называют расчет величины и направления реактивных (т.е. ответных) сил и моментов, возникающих в опорах конструкций под действием системы заданных внешних нагрузок.
В рассмотренных ниже примерах, для наглядности, заданные внешние нагрузки показаны синим или зеленым цветом, а реакции опор — красным или оранжевым.
При решении задач, определяемые реакции опор могут обозначаться по разному:
- буквой R (от англ. Reaction). В этом случае, для уточнения точки приложения и направления силы могут добавляться соответствующие индексы (например, RAy — это реакция в точке A направленная вдоль оси Y);
- буквами V (Vertical) и H (Horizontal) обозначаются соответственно вертикальная и горизонтальная составляющие полной реакции (например, HB — это реакция в точке B направленная вдоль оси балки);
- Также возможно обозначение реакций по осям координат — YA, XB и т.д.
Сохранить или поделиться с друзьями
Рассмотрим решение всех типов задач по расчету величины и направления опорных реакций в заделках, шарнирных опорах и стержнях:
Примеры нахождения реакций опор
Примеры нахождения реакций опор для различных способов закрепления и нагружения бруса, балок, рам и других элементов конструкций.
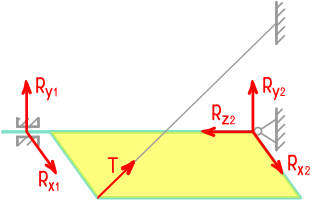
Реакции опоры и стержня системы
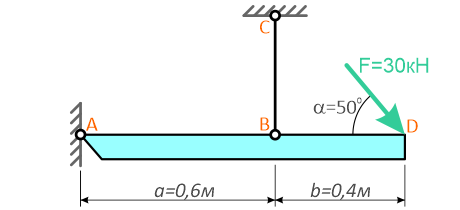
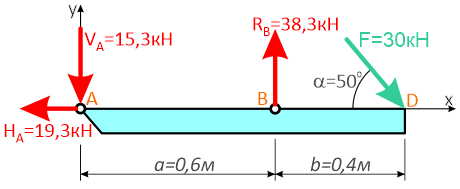
Невесомая балка удерживается в горизонтальном положении шарнирно-неподвижной опорой в т. A и вертикальным стержнем BC.
В точке D к балке приложена сосредоточенная сила F=30кН под углом 50°.
Требуется найти реакции, возникающие в опоре A и стержне BC.
Решение
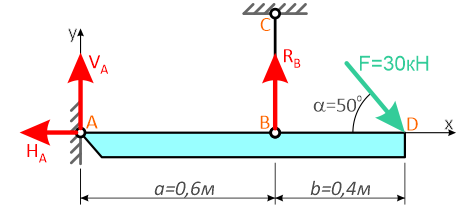
Для решения задачи, покажем систему координат x-y и зададим произвольное направление реакций.
В точке A реакция в опоре раскладывается на две составляющие — вертикальную VA и горизонтальную HA.
Реакция в стержне (RB) всегда направлена вдоль самого стержня.
Для определения трех реакций требуется три уравнения равновесия.
Это будут два уравнения суммы моментов относительно точек в опорах и сумма проекций всех сил на ось x равные нулю.
Составим их:
Из полученных уравнений выражаем и находим искомые реакции опор
Вертикальная реакция в опоре A получилась отрицательной, это значит что она направлена в противоположную сторону.
Направляем ее вниз, изменив знак на «плюс».
Выполним проверку найденных реакций, проецируя все силы на ось y.
Равенство нулю суммы проекций всех сил и реакций показывает то, что реакции опор найдены верно.
Таким образом, заданная балка удерживается в равновесии под действием одной активной и трех реактивных сил.
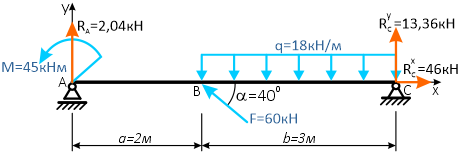
Расчет реакций опор балки
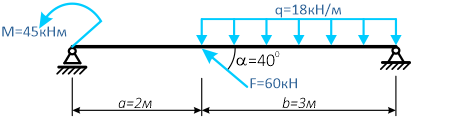
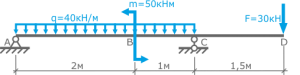
Простая балка на двух шарнирных опорах нагружена системой усилий, включающей силу F=60кН, приложенную под углом 40°, момент M=45кНм и равномерно распределенную нагрузку q=18кН/м.
Требуется определить реакции в опорах A и C.
Решение
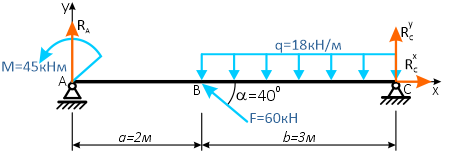
Вычерчиваем заданную схему в масштабе, показываем численные значения нагрузок, систему координат x-y и задаем произвольное направление реакций.
Здесь, в шарнирно-подвижной опоре будет только одна составляющая реакции.
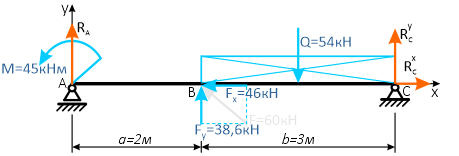
Для упрощения решения, распределенную нагрузку можно заменить её равнодействующей, которая при равномерном распределении q будет приложена по её центру
а силу F можно разложить на составляющие, спроецировав её на оси x и y.
В следющих примерах эти действия выполнять не будем, проводя вычисления напрямую со значениями q и F.
Аналогично тому, как это делалось при решении предыдущей задачи, записываем уравнения равновесия балки: нулевые суммы моментов всех нагрузок и искомых реакций относительно опор
и проекций сил на ось балки
Откуда находим все три опорные реакции
Все результаты положительны, следовательно, направление реакций было выбрано верно.
Проверяем найденные значения.
Величина реакций рассчитана правильно.
Подробное решение данного типа задач
Остальные задачи по определению опорных реакций с детальным разбором выполняемых действий:
При растяжении-сжатии стержней
Определение реакций в опорах стержней и стержневых систем при действии продольных сил.
- Расчет опорной реакции при растяжении-сжатии
- Расчет опорной реакции ступенчатого бруса
- Опорная реакция в заделке стержня с продольно распределенной нагрузкой
При кручении
Примеры расчета опорных моментов и реакций в подшипниках вала при кручении.
- Определение неизвестного крутящего момента вала
- Определение реакций подшипников пространственно нагруженного вала
- Расчет уравновешивающего момента вала
При изгибе балок и рам
Определение реакций в шарнирных опорах и заделках консольных балок и рам при действии систем внешних сил, моментов и распределенных нагрузок.
- Определение реакций в опорах двухопорной балки
- Расчет опорных реакций консольной балки
- Определение опорных реакций в жесткой заделке при изгибе
- Определение реакций опор балки, когда сила приложена под углом
- Проверка опорных реакций балки
- Расчет реакций в опорах рамы
- Определение опорных реакций балки (Видео)
Наш короткий видеоурок по расчету реакций опор балки:
Другие видео
Другие примеры определения реакций опор
Расчет реакций в опорах нестандартных систем.
- Определение реакции шарнира и опоры
- Реакции в шарнирах
- Реакции опор и шарнира
- Расчет веса противовеса и реакций в шарнирах
- Величина груза обеспечивающая равновесие и реакции в подшипниках
- Определение усилий в стержнях
- Натяжение троса и реакция опоры
- Реакции опор в точках системы
- Опорные реакции невесомой конструкции
- Опорные реакции в скользящей заделке
- Давление в шарнире и реакции в бискользящей заделке
- Реакции в скользящей заделке
- Расчет усилия в стержне
Типы опор и их реакции
В механике различают тела свободные: возможность перемещения, которых в любом направлении ничем не ограничена, и несвободные, когда перемещение данного тела ограничивают другие тела.
Сами тела ограничивающие свободу перемещения данного тела называют опорами (связями), а силы, с которыми опоры удерживают данное тело в равновесии, называют реакциями опор.
Направление реакций зависит от вида опор и схемы нагружения.
При решении задач очень важно правильно заменить опоры их реакциями, иначе записанные уравнения равновесия окажутся неверными.
И здесь важно помнить о том, что реакции могут появляться только по тем направлениям, в которых перемещение невозможно.
Рассмотрим определение реакций в основных типах опор:
Другие видео
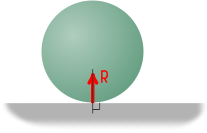
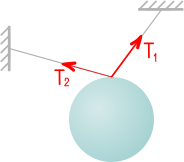
Реакция гладкой поверхности
Пусть некоторое тело опирается на гладкую поверхность.
Здесь перемещение тела возможно только вдоль поверхности.
Движение перпендикулярно ей исключено.
Потому что перемещению в сторону поверхности препятствует сама поверхность, а при движении от нее нарушится сама связь.
Таким образом, гладкая поверхность препятствует перемещению тела только в направлении нормали, поэтому реакция гладкой поверхности всегда направлена по нормали к этой поверхности.
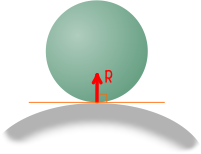
При взаимодействии криволинейных поверхностей аналогично, реакция направлена нормально к касательной в точке контакта тел.
То же самое будет при контакте в двух точках.
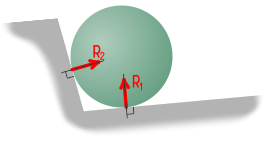
Реакция ребра
В случае, когда прямая балка опирается на ребро, реакции будут направлены перпендикулярно опираемой или опирающейся плоскости в точке их касания.
При повороте балки реакция всегда будет оставаться нормальной к соответствующей поверхности.
Гибкая связь
Для тела, подвешенного на нерастяжимой нити или тросе, связь не позволяет телу удаляться от точки подвеса в направлении самой нити.
Поэтому реакция гибкий связи будет направлена всегда только вдоль самой нити.
Реакции в стержнях
Как и в предыдущем пункте, в стержнях, которые с помощью шарниров соединяют какие-либо элементы с опорами, реакции направлены вдоль самих стержней.
Но в отличие от нитей, здесь может быть одно из двух направлений: растягивающее стержень или сжимающее его.
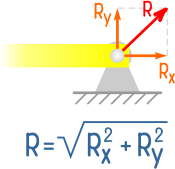
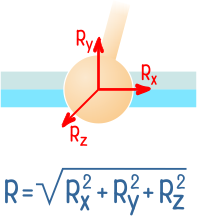
Реакции в шарнирных опорах
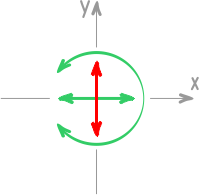
На плоскости возможны только три направления перемещения:
Линейные — вдоль осей x и y, и вращение относительно оси Z.
Поэтому в двумерных системах каждая опора может давать не более трех реакций.
Если свободное тело закрепить шарнирно-неподвижной опорой, которая допускает вращение, но исключает любые линейные перемещения, то в такой опоре могут возникать две реакции.
Они являются осевыми проекциями полной реакции опоры, которая может быть найдена как корень из суммы квадратов её составляющих.
Направление вектора полной реакции зависит от схемы нагружения элемента.
Встречаются разные способы изображения шарнирно-неподвижных опор в расчетных схемах.
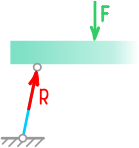
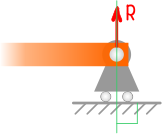
В шарнирно-подвижных опорах, помимо вращения возможно линейное перемещение вдоль поверхности, поэтому здесь будет только одна, нормальная к поверхности, составляющая реакции, которая по направлению и величине будет совпадать с полной.
У таких опор так же существуют дополнительные варианты схематичного изображения.
Пример направления реакций опор для балки на двух шарнирных опорах.
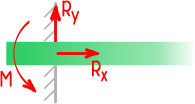
Реакции в заделках
Вид связи, при котором брус жестко закреплен в опоре называется глухой заделкой.
В этом случае исключены любые перемещения элемента.
Поэтому в плоских заделках может возникать до трех реакций: горизонтальная и вертикальная составляющие полной реакции, а также момент.
Скользящая заделка допускает линейное перемещение вдоль одной из осей.
Следовательно, по этой оси реакции не будет.
В бискользящей заделке исключается только угловое перемещение элемента.
Здесь из реакций будет один момент.
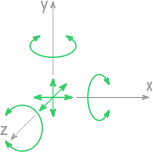
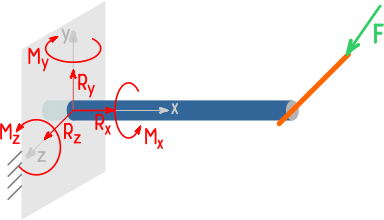
Реакции опор в трехмерных системах
В пространстве возможно уже шесть направлений движения:
Поступательные вдоль каждой из осей и вращение относительно них.
Поэтому в трехмерных системах опоры могут давать до шести реакций.
Шкив на валу, закрепленном подшипниками, может вращаться относительно продольной оси вала.
Любые другие перемещения невозможны.
В силу конструктивных особенностей подшипников моментов в них не возникает.
Здесь имеют место только реактивные силы.
В радиальном подшипнике (который справа) все реакции поперечны оси вала.
В радиально-упорном (который слева) добавляется еще и продольная.
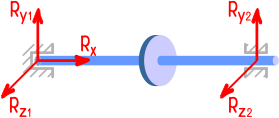
В трехмерном шарнире исключены любые линейные перемещения и возможны только повороты относительно трех осей, что дает до трех составляющих полной реакции R.
В жесткой заделке при общем случае нагружения может возникать до шести реакций: трёх сил и трех моментов.
Пример замены опор их реакциями для трехмерной системы:
Порядок расчета опорных реакций
В рассмотренных выше примерах при определении реакций в опорах выполняется следующая последовательность действий:
- Вычерчивается (в масштабе) расчетная схема элемента с указанием всех размеров и приложенных внешних нагрузок;
Расчетная схема балки - Выбирается система координат и обозначаются характерные сечения бруса;
Система координат для балки - Определяется количество и возможное направление связей;
Направление опорных реакций балки - Записываются уравнения статики (по количеству неизвестных реакций);
- Из уравнений равновесия находим величину и направление (по знаку) опорных реакций.
Опорные реакции балки
После расчетов выполняется проверка найденных значений.
Более подробно порядок расчета опорных реакций рассматривается в разделе «Статика» теоретической механики.
Другие примеры решения задач >
государственное
автономное профессиональное образовательное учреждение
Челябинской области
«Политехнический колледж»
ГАПОУ ЧО ПК
Методическая разработка
практического занятия
ОП 07 Техническая механика
Для специальности «22.02.06 Сварочное производство»
Тема 1.1 Основы
статики
Урок 15-16 «Определение опорных реакций
балок»
Разработал: преподаватель
Смородина Н. В.
Практическое
занятие
Тема: «Определение опорных реакций
балок»
Цель занятия: закрепить
теоретические знания и умения определять реакции в опорах балочных
систем
Краткие теоретические сведения
Очень часто в машинах и
конструкциях встречаются тела удлиненной формы, называемые балками (или
балочными системами). Балки в основном предназначены для восприятия поперечных
нагрузок. Балки имеют специальные опорные устройства для сопряжения их с
другими элементами и передачи на них усилий.
По способу приложения нагрузки делятся на:
· сосредоточенные – если реально
передача нагрузки происходит на пренебрежимо малой площадке (в точке);
· распределенные – если нагрузка распределена
по значительной площадке или линии (давление воды на плотину, давление снега
на крышу и т.п.).
В задачах статики для абсолютно твердых тел
распределенную нагрузку можно заменить равнодействующей сосредоточенной силой (рис. 1).
|
Рис. 1 |
q I — длина стержня; G |
Жесткая заделка (защемление) (рис. 2)
|
|
Опора не допускает перемещений и поворотов. Для определения этих неизвестных удобно Каждое уравнение имеет одну неизвестную |
Для контроля правильности решений используют дополнительное уравнение моментов
относительно любой точки на балке, например
Шарнирно-подвижная опора (рис. 3)
|
|
Опора Шарнирно-неподвижная опора (рис. 4) Опора допускает поворот вокруг шарнира и может быть |
Балка на двух шарнирных опорах (рис. 5)
Не
известны три силы, две из них — вертикальные, следовательно, удобнее для
определения неизвестных использовать систему уравнений во второй форме:
Составляются
уравнения моментов относительно точек крепления балки. Поскольку момент силы,
проходящей через точку крепления, равен 0, в уравнении останется одна неизвестная
сила.
Для контроля правильности решения используется дополнительное
уравнение
Упражнения при подготовке к
самостоятельной работе
1.
Привести систему сил к точке В, определить главный вектор и главный
момент системы сил (рис. 6). АВ = 2м; ВС = 1,5м; CD = 1м. F1 = 18кН; F2 = 10кН; F3 = 30кН; т = 36кН-м.
Рис. 6
2. Система сил находится в равновесии. Определить величину момента пары
т (рис. 7).
F1 = F1’ = 10
кН; F2 = F2’ = 20кН.
Рис. 7
3.
Нанести реакции в опорах
балок 1 и 2 (рис. 8).
Рис. 8
4. Определить величину реакции в опоре А. Приложена распределенная
нагрузка интенсивностью q = 5кН/м (рис. 9).
Рис. 9
5. Записать систему уравнений равновесия для
определения реакций в опоре защемленной балки.
6.
Записать систему уравнений
равновесия для определения реакций в опорах двухопорной балки, закрепленной на
двух шарнирах.
Примеры решения задач
Пример№1. Одноопорная (защемленная)
балка нагружена сосредоточенными силами и парой сил (рис. 10). Определить
реакции заделки.
Рис. 10
Решение
1.
В заделке
может возникнуть реакция, представляемая двум: составляющими (RAy, RAx), и реактивный момент МA. Наносим на схему балки возможные
направления реакций.
Замечание. Если направления выбраны
неверно, при расчетах получим отрицательные значения реакций. В этом случае
реакции на схеме следует направить в противоположную сторону, не повторяя
расчета.
В силу малой высоты считают, что все точки балки
находятся на одной прямой; все три неизвестные реакции приложены в одной точке.
Для решения удобно использовать систему уравнений равновесия в первой форме.
Каждое уравнение будет содержать одну неизвестную.
2.
Используем
систему уравнений:
Знаки полученных реакций (+), следовательно,
направления реакций выбраны верно.
3. Для проверки правильности решения составляем
уравнение моментов относительно точки В.
Подставляем значения полученных реакций:
Решение выполнено верно.
Пример №2. Двухопорная балка с шарнирными опорами А и В
нагружена сосредоточенной силой F, распределенной нагрузкой с интенсивностью q и парой сил с моментом т
(рис. 11). Определить реакции опор.
Рис. 11
Решение
1.
Левая
опора (точка А) — подвижный шарнир, здесь реакция направлена
перпендикулярно опорной поверхности.
Правая опора (точка В) — неподвижный шарнир, здесь
наносим две составляющие реакции вдоль осей координат. Ось Ох совмещаем
с продольной осью балки.
2.
Поскольку
на схеме возникнут две неизвестные вертикальные реакции, использовать первую
форму уравнений равновесия нецелесообразно.
3.
Заменяем
распределенную нагрузку сосредоточенной:
G = ql; G = 2*6 = 12 кН.
Сосредоточенную силу помещаем в середине пролета,
далее задача решается с сосредоточенными силами (рис. 2б).
4.
Наносим
возможные реакции в опорах (направление произвольное).
5.
Для
решения выбираем уравнение равновесия в виде
6. Составляем уравнения моментов
относительно точек крепления:
Реакция отрицательная, следовательно, RАy нужно направить н противоположную
сторону.
7.
Используя
уравнение проекций, получим:
RBx — горизонтальная реакция в опоре В.
Реакция отрицательна, следовательно, на схеме ее
направление будет противоположно выбранному.
8.
Проверка
правильности решения. Для этого используем четвертое уравнение равновесия
Подставим полученные значения реакций. Если условие
выполнено, решение верно:
-5,1 — 12 + 34,6 – 25 -0,7 =
0.
Решение выполнено верно.
Порядок выполнения работы:
1.
Заменить распределенную нагрузку ее равнодействующей и указать
точку ее приложения (если действует на балку).
2.
Освободить балку от связей, заменив их реакциями.
3.
Выбрать систему уравнений равновесия.
4.
Решить уравнения равновесия.
5.
Выполнить проверку решения.
Задания для самостоятельной
работы:
Задание №1: Определить величины реакций в опоре защемленной
балки. Провести проверку правильности решения.
 |
Задание №2: Определить величины реакций в
шарнирных опорах балки. Провести проверку правильности решения.
Контрольные вопросы
1. Какую из форм уравнений равновесия
целесообразно использовать при определении реакций в заделке?
2. Какую форму системы уравнений равновесия
целесообразно использовать при определении реакций в опорах двухопорной балки и
почему?
3. Сколько уравнений равновесия необходимо
составить при параллельных внешних силах?
4. Как определить равнодействующую силу
равномерно распределённой нагрузки?
5. Назовите формулу для определения момента силы
относительно точки.
6. Сформулируйте правила знаков для определения
моментов сил.
7. Как проверить правильность определения реакций
опор балочных систем?
8. В каком случае момент силы равен 0?
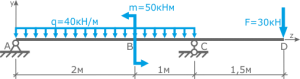
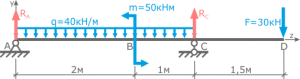
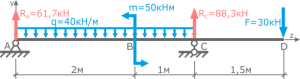
Определить опорные реакции в балке с жесткой заделкой.
В жесткой заделке три опорные реакции — вертикальная, горизонтальная и опорный момент. Так как горизонтальные нагрузки отсутствуют, горизонтальная реакция равна 0. Обозначим опору (жесткую заделку) буквой В. Задаемся (произвольно) направлениями вертикальной реакции В и реактивного момента МВ в заделке.
Составляем два уравнения статики:
(1),
откуда
Далее определяем опорный момент в заделке

откуда
Чтобы проверить правильность определения реакций, следует выбрать любую точку на балке и составить уравнение равновесия моментов относительно этой точки (сумма моментов относительно любой точки должна равняться 0).
Если реакции определены верно, записываем их значения на расчетную схему.