Как найти расстояние между параболами

Recently, a problem asked me to find the minimum distance between the parabolas $y=x^2$ and $y=-x^2-16x-65$.

I proceeded with the problem as thus.

Let $P(a,a^2), Q(b, -b^2-16b-65), a-b=x$.

$therefore PQ^2=x^2+(2a^2+2ax+16a+x^2+16x+65)^2$.

$PQ^2=x^2+(2(a+frac{x+8}{2})^2+frac{(x+8)^2+2}{2})^2 ge (x^2+(frac{(x+8)^2+2}{2})^2)(1+frac{1}{4}) times frac{4}{5}$

Applying Cauchy gives us that

$PQ^2 ge (frac{1}{4}x^2+3x+frac{33}{2})^2 times frac{4}{5} ge (frac{15}{2})^2 times frac{4}{5}=75$

This implies that the answer is $sqrt{75}$.

However, it took me a long time to find the values for Cauchy, and the calculations proved tedious.

What are other approaches to this problem?

EDIT: $(frac{15}{2})^2 times frac{4}{5} neq 75$, it`s $45$ actually!

Scientific journal PHYSICAL AND MATHEMATICAL EDUCATION

Has been issued since 2013.

Науковий журнал Ф1ЗИКО-МАТЕМАТИЧНА ОСВ1ТА

Видасться з 2013.

http://fmo-journal.fizmatsspu.sumy.ua/

Тургунбаев Р.М., Шарипова Л.Д. Об одной занимательной задаче на расстояние между кривыми. Фiзико-математична осв’та. 2018. Випуск 2(16). С. 130-135.

Turgunbaev R., Sharipova L. On An Entertaining Problem Of The Distance Between The Curves. Physical and Mathematical Education. 2018. Issue 2(16). Р. 130-135.

УДК 514.11

Р.М. Тургунбаев1, Л.Д. Шарипова2

Ташкентский государственный педагогический университет имени Низами, Узбекистан

musamat1@yan dex.ru

2Ташкентский институт инженеров железнодорожного транспорта, Узбекистан

slola@mail.ru

DOI 10.31110/2413-1571-2018-016-2-025 ОБ ОДНОЙ ЗАНИМАТЕЛЬНОЙ ЗАДАЧЕ НА РАССТОЯНИЕ МЕЖДУ КРИВЫМИ

Аннотация. В школьном курсе геометрии расстояние от точки А до прямой I определяется как длина перпендикуляра, опущенного из точки А на прямую I. А формулы расстояния как между точкой и прямой, так и между параллельными прямыми выводятся уже в вузовском курсе аналитической геометрии. Прямая как график линейной функции определяется в школьном курсе алгебры, где общий вид линейной функции рассматривается как общее уравнение прямой. В курсе алгебры и начал анализа определяется касательная и приводится ее уравнение. Но ни уравнения прямой, проходящей через заданные две точки, ни условия перпендикулярности прямых в общеобразовательном курсе математики не изучаются. Однако эти факты можно вполне доступно изложить как учащимся старших классов средних школ, так и академических лицеев. Вместе с тем можно рассматривать задачи на расстояние между кривыми, в частности, между прямой и параболой, а также между параболами. Эти задачи можно изучать на факультативных занятиях по математике со школьниками, проявляющими повышенный интерес к изучаемому предмету.

В данной статье расстояние между точкой и кривой определяется как наименьшее расстояние от данной точки до точек кривых, а расстояние между кривыми определяется как наименьшее расстояние между точками данных кривых. В случае, когда кривые являются графиками некоторых дифференцируемых функций, используя методы дифференциального исчисления и обобщения доказаны следующие факты: расстояние между точкой и прямой равно длине перпендикуляра, опущенного из данной точки на данную прямую; в случае параболы расстояние от точки до кривой равно длине перпендикуляра, проведенного к касательной в точке касания; расстояние между параболой и прямой равно расстоянию между прямой и касательной к параболе, параллельной данной прямой; расстояние между двумя параболами равно расстоянию между параллельными касательными к этим параболам. Приводится пример решения задачи на нахождение расстояние между параболами. При этом предварительно выводится уравнение прямой, проходящей через две заданные точки, доказывается критерий перпендикулярности прямых, заданных уравнениями с угловыми коэффициентами.

Ключевые слова: точка, прямая, перпендикуляр, кривая, парабола, расстояние, производная

Из школьного курса геометрии известно, что если точки А и В заданы своими координатами: А(х1,у1) и В(х2,у2), то расстояние между этими точками вычисляется по формуле d = ^(х2 — х1)2 + (у2 — у1)2. Расстояние между прямой и точкой определяется как длина перпендикуляра, опущенного из заданной точки на эту прямую. Уравнение прямой, понятия углового коэффициента, касательной и геометрический смысл производной вводятся в курсах алгебры, алгебры и начал анализа [1].

При изучении расстояния между точкой и линией было бы полезным рассмотреть следующую задачу: если прямая задана уравнением у = kx + т, как можно найти расстояние между произвольной точкой М0(х0,у0) и этой прямой. Далее можно рассмотреть обобщения этой задачи: как найти расстояние между точкой и кривой (в нашем случае графиком некоторой функции), как найти расстояние между прямой и кривой, между кривыми? Отметим, что приведенные задачи вполне доступны учащимся старших классов средних школ и академических лицеев.

В данной статье приведено решение этих задач в случае, когда кривой является парабола. Для этого предварительно выведены вспомогательные формулы и утверждения. Задачи решены методами дифференциального исчисления и обобщения.

ISSN 2413-158X (online) ISSN 2413-1571 (print)

Известно, что через две данные точки можно провести единственную прямую. Это означает, что уравнение прямой можно выразить (получить), используя координаты заданных точек. Будем считать, что уравнение прямой имеет вид у = кх + т, где к ф 0. Пусть точки М1(х1,у1) и М2(х2,у2) принадлежат прямой у = кх + т. Тогда их координаты удовлетворяют уравнению прямой, и мы получаем систему

(у1 = кх1 + т, у2 = кх2 + т.

Из системы находим к = :

Откуда имеем

1. Подставляя выражение для к в первое уравнения системы, получим

1

У2 — У1 УЛ — У2*1 т = у1—х1 =

хг — Х-1 У2-У1

У =

Х2 — Xi

х +

х2 — Х1

У1Х2 — У2Х1 х2 — Х1

(1)

Это и есть уравнение прямой, проходящей через точки М1(х1,у1) и М2(х2,у2), при х1 ф х2, у1 Ф у2. Если х1 ф х2, У1 = У2> то из (1) имеем у = у1. Это уравнение прямой, параллельной оси Ох. Если х1 = х2, у1 Ф у2, то выражая в (1) х через у:

х2 Х1 ‘ У 2—У1

■у —

У1Х2 — У2Х1

У 2 —У1 ‘

(2)

получим, что уравнение прямой имеет вид х = х1. Это уравнение прямой, параллельной оси 0у. Таким образом, если даны две точки М1(х1,у1) и М2(х2,у2), то уравнение прямой проходящей через эти точки имеет вид (1) или (2). Частными случаями этих уравнений являются уравнения горизонтальных прямых вида у = у1 или вертикальных прямых вида х = х1.

Из уравнения (1) с помощью несложных преобразований можно получить следующий вид уравнения прямой проходящей через точки М1(х1,у1) и М2(х2,у2):

Х — Х1 у —у 1

Х2 —Х1 У 2 У1

(3)

Имеет место следующая

Теорема 1. Прямые у = к1х + т1 и у = к2х + т2 перпендикулярны тогда и только тогда, когда к1к2 = —1. Доказательство. Необходимость. Пусть прямые у = к1х + т1 и у = к2х + т2, где к1 = ¡да, к2 = ¡дР (рис.1), перпендикулярны. Очевидно, что р = 900 + а. Используя известные тригонометрические формулы, получим

к1к2 = ¡да • ¡д@ = ¡да • ¡д(90 + а) = ¡да • (—ида) = —1.

Рис. 1

Достаточность. Пусть кхк2 = —1. Тогда

.л . г, г, г* sina , cosfí п sinasinfí+cosacosfí ~ cos(fí-a) —

¡да • ¡gB = —1 о ¡да = —c¡gB о ¡да + c¡gB = 0 о-+ —- = 0 о —- = 0 о —-—- = 0 о

& «Г а а cosa sin/3 cosasin/3 cosasin/3

cos(/3 — а)=0о p — a = 90o.

Отсюда следует, что угол между прямыми равен 90o, т.е. данные прямые перпендикулярны. Теорема доказана. Определение 1. Расстоянием между точкой А и прямой I называется наименьшее расстояние между точкой А и точками прямой I.

Теорема 2. Пусть даны точка М0(х0,у0) и прямая у = кх + т. Тогда расстояние d между ними определяется по формуле

d =

кХо + т — уо

(4)

Vк2 + 1 ‘

Если М1(х1,у1) — точка прямой такая, что расстояние между точками М0 и М1 равно d, то прямая М0М1 перпендикулярна прямой у = кх + т.

Доказательство. Пусть точка М(х,у) принадлежит прямой у = кх + т. Тогда ее координаты удовлетворяют уравнению прямой, т.е. у = кх + т, и квадрат расстояния между точками М0 и М d2 = (у — у0)2 + (х — х0)2. Учитывая это, имеем d2 = (кх + т — у0)2 + (х — х0)2. Как видно, d2 является функцией от х, для удобства обозначим эту функцию через [(х):

[(х) = (кх + т — у0)2+(х — х0)2. (5)

Таким образом, нахождение расстояния между точкой М0(х0,у0) и прямой у = кх + т сводится к отысканию наименьшего значения функции (5).

Находим производную функции [(х):

/'(х) = 2(кх + т — у0)(кх + т — у0)’ + 2(х — х0)(х — х0)’ = 2к(кх + т — у0) + 2(х — х0).

Из уравнения /'(х) = 0 находим стационарную точку: 2к(кх + т — у0~) + 2(х — х0~) = 0,

к(кх + т — у0) + (х — х0) = 0, (6)

откуда

(к2 + 1)х + к(т — у0) — х0 = 0,

х = —

х0 — к(т — Уо)

(к2 + 1) ‘

Очевидно, что эта точка является точкой минимума функции (5). Вычислим значение функции в этой точке:

,, , , Хо—к(т — уо)

/(х) = (к—т^—.-+ т — у0

к2 + 1

(х0— к(т — у о) + —=

+

х0 — к(т — у0) — х0к2 — х0

к^Л

кхо — к2(т — уо) + к2(т — у0) + (т — у0) к2 + 1 —к(кх0 +т — у0) к2 + 1

+

(кх0+т—у0)2^к2(кх0+т—у0)2 (кх0+т — у0)2(1 + к2) (кх0+т — у0)2

(к2 + 1)2

к2 + 1

(к2 + 1)2 (к2 + 1)2 откуда получаем формулу (4).

Пусть точка М1(х1,у1) — точка прямой, для которой расстояние между М0 и М1 равно расстоянию между точкой М0 и заданной прямой. Тогда она удовлетворяет равенству (6): к(у1 — у0) + (х1 — х0) = 0, откуда

Х1 — хо

к = —-

к = —-.

У1—У0 1

(7)

У1—У0′ Х1 — хо

Введем обозначение У1 Уо = к1. Число к1 равно угловому коэффициенту прямой М1М0. Из (7) имеем к • к1 = —1.

Х1~Х0

А это означает перпендикулярность прямых М1М0 и у = кх + т. Теорема доказана.

Из этой теоремы следует, что расстояние от точки до прямой равно длине перпендикуляра, опущенного из точки на прямую.

Определение 2. Расстоянием между параллельными прямыми называется наименьшее расстояние между точками этих прямых.

Теорема 3. Пусть прямые у = кх + т1 и у = кх + т2 параллельны. Тогда расстояние между ними определяется по формуле

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Ы2—т11

й=-

(8)

Vк2 + 1 ‘

Доказательство. Возьмем на прямой у = кх + т1 точку М0(х0,у0). Тогда расстояние от этой точки до прямой у = кх + т2 равно

1кХо+т.2—уо1

й=-

Но по выбору точки М0(х0,у0) имеем у0 = кх0 + т1 или кх0 — у0 = т1. Учитывая это получим (8). Формулу (8) можно получить, используя графическое представление прямых (рис. 2).

Рис. 2

Очевидно, что 1т2 — т11 будет равно длине отрезка АВ. В прямоугольном треугольнике АСВ угол ¿А равен углу

между прямой и положительным направлением оси Ох, поэтому Ьд(^А) = к. Тогда длина перпендикуляра АС =

АВ

при этом cos2(¿A) = ■

— Поэтому АС =

т2~т1

соз(^А)

1д2(±А)+1 к2 + 1…….’ «»

Определение 3. Расстоянием между заданной точкой и параболой называется наименьшее расстояние между этой точкой и точками параболы.

Теорема 4. Если точка М1(х1,у1) принадлежит параболе у = ах2 + Ьх + с, расстояние между этой параболой и точкой М0(х0,у0) равно длине отрезка МоМ^ то прямая М0М1 перпендикулярна касательной, проведенной к данной параболе в точке М1(х1,у1).

Доказательство. Нахождение расстояния между параболой у = ах2 + Ьх + с и точкой М0(х0,у0) сводится к нахождению наименьшего значения функции [(х) = (ах2 + Ьх + с — у0)2 + (х — х0)2. Найдем стационарные точки

2

2

1

1

этой функции. Так как f(x) = 2(ах2 + bx + с — у0) • (2ах + Ь) + 2(х — х0), то стационарные точки являются корнями уравнения

(2ах + Ь) • (ах2 +Ьх + с — у0) + (х — х0) = 0. (9)

Это кубическое уравнение имеет хотя бы один действительный корень. Пусть х1 — действительный корень уравнения (6). Тогда число 2ах1 + b равно угловому коэффициенту касательной, проведенной к параболе у = ах2 +Ьх + с в точке с абсциссой х1 . Обозначим этот угловой коэффициент через к1. Учитывая вышесказанное и то, что ах2 + Ьх1 + с = у1, из (9) имеем:

_ 11

к1 = —~К-Ж = —к2′ Х1 — Х0

где У1 Уо = к2 — угловой коэффициент прямой, проходящей через точки М1(х1,у1) и М0(х0,у0). Отсюда следует, что

Х1~Х0

касательная и прямая М0М1 взаимно перпендикулярны.

Определение 4. Расстоянием между параболой и прямой называется наименьшее расстояние между точками параболы и прямой.

Очевидно, что если парабола и прямая имеют общую точку, то расстояние между ними равно нулю. Теорема 5. Пусть даны парабола у = ах2 +Ьх + с и прямая у = кх + т. Тогда расстояние между ними

1(к — Ь)2 + 4а(т — с)1

d=-

(10)

4а^к2 + 1 ‘

Доказательство. Пусть точка М0(х0,у0) принадлежит прямой у = кх + т, а точка М1(х1,у1) принадлежит параболе у = ах2 +Ьх + с. Расстояние между этими точками равно длине отрезка М0М1. По доказанной теореме 2 прямая М0,М1 перпендикулярна прямой у = кх + т. Из теоремы 4 следует, что прямая М0,М1 перпендикулярна касательной к параболе, проведенной в точке М1(х1,у1). Значит, прямая у = кх + т и эта касательная параллельны, откуда 2ах1 + Ь = к. Из этого равенства следует, что х1 = . Вычислим у1:

(k — b2 k — b (k — b)2 b(k — b) (к — b)2 + 2b(k — b) + 4ас

2а 4а 2а

(к — b)(k — b + 2b) + 4ас (к — b)(k + b) + 4ас

4а

4а

4а

Расстояние от точки М1(х1,у1) до прямой у = кх + т равно d = Подставляя значения х1 и у1 в

числитель последнего равенства имеем:

1кх1 +т — у11 =

к — b (к — b)(k + Ь)+ 4ас к •——+т—

2а

4а

2к(к — b)+ 4ат — (к — b)(k + Ь) — 4ас

(к — b)(2k— к — Ь)+ 4а(т — с)

4а

(к — Ь)2 + 4а (т — с)

4а 4а

откуда следует (9). Теорема доказана.

Нетрудно заметить, что выражение под модулем числителя формулы (9) есть дискриминант квадратного трехчлена ах2 + (Ь — к)х + с — т. Если дискриминант неотрицателен, то парабола и прямая имеют общую точку, и расстояние между ними равно нулю.

Таким образом, для того чтобы найти расстояние между параболой у = ах2 +Ьх + с и прямой у = кх + т, достаточно составить квадратный трехчлен ах2 + (Ь — к)х + с — т и вычислить его дискриминант й = (Ь — к)2 + 4а(т — с). В случае й > 0 расстояние между параболой и прямой равно 0; а в случае й <0 расстояние определяется по формуле

d =

4Wk2 + 1

Расстояние между параболой у = ах2 +Ьх + с и прямой у = кх + т можно найти и следующим способом

(рис. 3).

Рис. 3

Функция f(x) = ах2 + Ьх + с — (кх + т) (а > 0) выражает длину отрезка, параллельного оси Оу, соединяющего точки параболы у = ах2+Ьх + с и прямой у = кх + т (длина отрезка FE). Очевидно, что длина этого отрезка пропорциональна длине перпендикуляра, опущенного из точки параболы на прямую. Поэтому, если функция f(x)=ax2 + bx + c — (kx + m) принимает наименьшее значение (длина отрезка AB), то соответствующая длина перпендикуляра (AC) равна расстоянию между параболой и прямой. Из прямоугольного треугольника ABC имеем

AC=^h ■

<Jk2 + 1

Таким образом, для того чтобы найти расстояние между параболой у = ах2 + Ьх + с (а > 0) и прямой у = кх + т, надо найти наименьшее значение функции f(x) = ах2 + Ьх + с — (кх + т) и разделить полученное число на VF- + 1. В случае, когда а < 0 достаточно рассмотреть функцию f(x) = —ах2 — Ьх — с + (кх + т)■

Теперь рассмотрим две параболы у = а1х2 + bj^x + с1 и у = а2х2 + Ь2х + с2. Предположим, что они не имеют общих точек. Аналогично, наименьшее расстояние между точками этих парабол назовем расстоянием между параболами. Абсциссы этих парабол меняются независимо друг от друга. Поэтому абсциссу первой параболы обозначим через х, а вторую — через z. Тогда квадрат расстояния между точками парабол

d2 = (у(х) — y(z))2 + (х — z)2

или

d2 = (а1х2 + b-^x + с1 — a2z2 — b2z — с2)2 + (х — z)2. (11)

Имеет место

Теорема 6. Если параболы у = а1х2 + Ь1х + с1 и у = а2х2 + Ь2х + с2 не пересекаются, то расстояние между ними равно расстоянию между параллельными касательными, проведенными к этим параболам.

Доказательство. Допустим, что искомое расстояние равно расстоянию между точками М1(х0,у(х0)) и M2(z0,y(z0)). Подставим значение z0 в (11). Тогда получим функцию

f(x) = (а-х2 + Ъ-х + с-— a2Z¡2 — b2Z0 — С2)2 + (х — Zo)2. (12)

Точка х0 является стационарной точкой этой функции, т.е. она удовлетворяет уравнению

(2а-х + b-)(y(x) — y(Zo)) + х — Zo = 0. (13)

Отсюда имеем

(2a-Xo + b1)—= —1. (14)

х0 ¿0

Первый множитель левой части равенства (11) является угловым коэффициентом касательной, проведенной к параболе у = а1х2 + Ь1х + с1 в точке с абсциссой х0. Второй множитель — это угловой коэффициент прямой, проходящей через точки М1(х0,у(х0)) и M2(z0,y(z0)). Равенство (14) выражает перпендикулярность этих прямых.

Аналогично, подставляя значение х0 в (11), можно доказать перпендикулярность прямой М1М2 и касательной, проведенной к параболе у = а2х2 + Ь2х + с2 в точке M2(z0,y(z0)). Отсюда следует доказательство теоремы.

Задача. Найти расстояние между параболами у = —3х2 +8х — 9 и у = х2 + 8х + 13.

Решение. Используем теорему 6. Аргумент первой параболы обозначим через х, второй — через z. Тогда квадрат расстояния между точками парабол выражается формулой:

d2 = (—3х2 +8x — 9 — z2—8z — 13)2 + (х — z)2. (15)

Из параллельности касательных имеем —6х + 8 = 2z + 8, откуда z = —3х. Т.е., если М1(х0,у(х0)) — искомая точка первой параболы, то М2(—3х0,у • (—3х0)) есть искомая точка второй параболы. Эти точки должны удовлетворять условию (14). Имеем:

. £ —3х02 + 8X0 — 9 — ((—3Xo)2 + 8(—3Xo) + 13)

(—6Х° + 8)—Ъ—РЬо)-= —1

(—6х0 + 8)(—12х0 + 32х0 — 22) + 4х0 = 0, (6×2 — 16х0 + 11)(—3х0 +4)+х0 = 0, —18×3 + 12×2 — 98х0 +44 = 0, 9×3 — 36×2 + 49х0 — 22 = 0.

Нетрудно проверить, что х0 = 1 является единственным действительным корнем последнего уравнения, отсюда находим z0 = —3. Подставляя полученные значения х0 и z0 в (15) получаем d = 2^5.

Замечание 1. Из доказанной теоремы следует, что если у = С1х + С2 — уравнение общего перпендикуляра к касательным, который проходит через точки касания, то неизвестные коэффициенты С1 и С2 , а также расстояние между параболами можно найти из системы:

а1х3 + b1x0 + с1 = С^а + D, a2z3 + b2Zo + с- = C-Zo + D,

2a1x0 +b1 = С-1, (16)

2a2Zo + b2 = С-1, d2 = (a1x2 + Ь^_х + c1 — a2z2 — b2z — c2)2 + (x — z)2.

Замечание 2. Обычно расстояние между гладкими кривыми находят методами вариационного исчисления. Решение нашей задачи сводится к нахождению экстремального значения функционала

V(y) = j ^1 + y’2dx (17)

при условии, что х0 принадлежит параболе (р(х) = х2 + 8х + 13, а х1 — параболе ф(х~) = —3х2 + 8х — 9. Известно [3], что для функционала (17) экстремальными кривыми являются у = С1х + С2, где С1 и С2 — произвольные постоянные, которые предстоит определить. Из условия трансверсальности и пересечения экстремали с параболами имеем:

х

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

(—6×0 + 8)C1 + 1 = 0, (2×1 + 8)C1 + 1 = 0, C1X0 + C2 = Xq + 8×0 + 13

2

(18)

{С1х1 + С2= —3×2 + 8х1 + 9.

1 7

Из этой системы находим: ^ =~’,С2 = —-;х0 = —3;х1 = 1.

Значит, экстремалью является прямая у = -х — 1-, а расстояние между данными параболами

2 2

1

d =

-3N

I

1 J5

1+—dx =^-х 42

1 J5 r-

= — •4 = 2^5. -3 2

Нетрудно заметить, что систему (18) можно получить из системы (14).

В общем случае теоремы, аналогичные теоремам 4, 5 и 6, можно сформулировать и для других гладких кривых. Суть метода доказательства не меняется.

В рассмотренных задачах (теоремах) нахождение расстояния между кривыми приводит к неожиданному решению — нахождению расстояния между параллельными прямыми, что подчеркивает занимательность данных задач. Эти задачи можно использовать на факультативных занятиях для приобщения учащихся к творческому поиску, активизации их к самостоятельной исследовательской деятельности.

Список использованных источников

1. Алгебра и начала анализа: Учебник для 10-11 кл. общеобразоват. учреждений/ Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. и др. 15-е изд. М.: Просвещение, 2007. 384 с.

2. Тракимус Ю.В. Основы вариационного исчисления. Новосибирск: Изд-во НГТУ, 2016. 73 с.

References

1. Algebra i nachala analiza: Uchebnik dlya 10-11 klassa obsheobrazovat. uchrezhdenij/ Alimov Sh.A., Kolyagin Ju.M., Sidorov Ju.V. i dr. 15-e izd. M.: Prosveshhenie, 2007. 384 p.

2. Trakimus Ju.V. Osnovy variatsionnogo ischisleniya. Novosibirsk: Izd-vo NGTU, 2016. 73 p.

ON AN ENTERTAINING PROBLEM OF THE DISTANCE BETWEEN THE CURVES Riskeldi Turgunbaev

TSPU named after Nizami, Tashkent, Uzbekistan Lola Sharipova TIRE, Tashkent, Uzbekistan

Abstract. In the school course of geometry, the distance from the point A to the straight line l is defined as the length of the perpendicular dropped from the point A to the line l. And the formulas of the distance both between a point and a straight line, and between parallel straight lines are deduced already in a high school course of the analytical geometry. The straight line as a graph of a linear function is defined in the school course of algebra, where the general form of a linear function is considered as the general equation of a straight line. The tangent is determined and its equation is given in the course of algebra and the beginnings of analysis. But neither the equation of a straight line passing through given two points nor the conditions of perpendicularity of straight lines are studied in the school course of mathematics. However, these facts can be fully explained to both high school students of secondary schools and academic lyceums. At the same time, one can consider problems on the distance between curves, in particular, between a straight line and a parabola, and also between parabolas. These problems can be studied in facultative classes in mathematics with students who show increased interest in the subject.

In the present paper, the distance between a point and a curve is defined as the smallest distance from the given point to the points of the curves, and the distance between the curves is defined as the smallest distance between the points of these curves. In the case when the curves are graphs of certain differentiable functions, the following facts are proved with the help of the derivative: the distance between a point and a straight line is equal to the length of the perpendicular dropped from the point to the line; in the case of a parabola, the distance from a point to a curve is equal to the length of the perpendicular drawn to the tangent at the point of tangency; the distance between the parabola and the straight line is equal to the distance between the line and the tangent to the parabola parallel to this straight line; the distance between two parabolas is equal to the distance between the parallel tangents to these parabolas. An example of a solution to the problem on finding the distance between the parabolas is given. In this connection, the equation of a straight line passing through two given points is preliminarily derived, and a criterion for the perpendicularity of lines given by slope-intercept forms is proved.

Keywords: point, straight line, perpendicular, curve, parabola, distance, derivative

Пятый тип задач на касательную — уравнение общей касательной нескольких кривых

Говорят, что прямая
y=kx
+ b
является общей касательной графиков
функций y=f₁(x)
и y=f₂(x),
если она касается как одного, так и
другого графиков, но не обязательно в
одной и той же точке.

Правило.

Функции y=f₁(x)
и y=f₂(x)
имеют в точке пересечения M(x₀;y₀)
общую невертикальную касательную, если

f₁’(x_0)
= f₂^’(x₀)

ЗАДАЧА. Докажите,
что параболы y₁=3x²-5x-2
и y₂=2x²-x-6
имеют в их общей точке общую касательную.
Найти уравнение этой общей касательной.

1. Найдем точку
   пересечения парабол

3x²-5x-2
= 2x²-x-6

x²-4x+4
= 0

(x-2)²
= 0

x
= 2

y(2)=
2·4-2-6=0 y(2)=3·4-5·2-2=0

значит, у парабол
одна точка пересечения (2;0)

1. Теперь перейдем
   к составлению уравнений касательных

y₍₁₎=6x
-5 y₍₁₎(2)
= 12-5=7

y₍₂₎=4x-1
y₍₂₎(2)
= 8-1=7

Получим уравнение
касательной

y=0+7(x-2)

y=7x-14

Ответ: y=7x-14

ЗАДАЧА. Найти
уравнение всех общих касательных к
графикам функции y=x²+1
и y=4x²-2

1. Составим уравнение
   касательной в точке x₀
   = a
   к графику

y=x²+1

y(a)=a²+1

y^’=2x

y^’(a)=2a

Получим уравнение
касательной

y=a²+1+2a(x-a)

y=a²+1+2ax-2a²

y=2ax-a²+1

1. Составим уравнение
   касательной в точке с абсциссой x₀=b
   к графику y=4x²-2

y(b)=4b²-2

y^’=8x

y’(b)=8b

Получим уравнение
касательной

y=4b²-2+8b(x-b)

y= 4b²-2+8bx-8b²

y=8bx-4b²-2

1. Уравнения прямых
   совпадают, если угловые коэффициенты
   и свободные члены равны, т.е.

Подставим a=4b
во второе уравнение, получим

-16b²
+1 = -4b²
-2

12b²
= 3

b²
=

Получим уравнения
касательных

y=4x-3 y=-4x-3

Ответ: y=4x-3 y=-4x-3

Шестой тип задач на касательную – расстояние между кривыми.

Пусть дана функция
y
= f(x)
и прямая y
= kx
+b,
тогда можно составить уравнение
касательной, параллельной данной прямой.
Проведенная касательная разделит
плоскость на две части: в одной из них
будет находиться заданная прямая, а в
другой график функции y
= f(x).

Кратчайшее
расстояние между кривой y
= f(x)
и прямой y
= kx
+b
можно посчитать по формуле :

=

Задача. Найти
кратчайшее расстояние между параболой
y
= x²
и прямой y
=

1. Убедимся,
   что графики не имеют общих точек, для
   этого решим уравнение:

x²
=
,

3x²
– 4x
+6 = 0,

D
= 16-72< 0.

Нет корней, нет
общих точек.

1. Найдем
   точку, в которой касательная параллельна
   прямой y
   =
   

y = x²,

y^’
= 2x,

2x =
,

x=
,

x₀
=
,

y₀
=
.

1. Получим касательную
   y
   =
   

y
=

Прямая y
=

и парабола y
= x²
лежат по разные стороны от касательной
y
=
,
тогда расстояние от прямой y
=

до параболы y
= x²,
это расстояние от точки M
(x₀;y₀),
лежащей на параболе, до прямой y
=
,
находим его по формуле

=


=
.

Ответ:

Задача. Найти
расстояние между касательными к графику
функции
,
образующими с положительным направлением
оси Ох угол 45⁰.

1. y^’
   =
   
   =
   

2. y₀^’
   = tg 45⁰

3. 
   
   = 1

x= 3 x= 1

x₀=
3 x₀=
1

1. Составим
   уравнение касательной в точке x₀=
   3

2. y(3)
   = 0

y = 0 +
1
(x-3)

y = x-3

1. Составим уравнение
   касательной в точке x₀=
   1

2. y(1)
   = 2

y = 2 +
1
(x-3)

y = x+1

1. Пусть
   y
   = x
   +1 – данная прямая,

— данная кривая,

y
= x-3
— данная касательная,

=

Ответ :

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

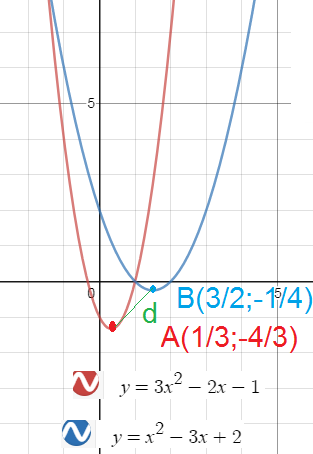
Задача 45639 Найти расстояние между вершинами парабол.

Условие

Найти расстояние между вершинами парабол y1=3x^2-2x-1 и y2=x^2+px+q, если квадратичная функция, соответствующая второй параболе, имеет корни 1 и 2.

Решение

по условию:
x^2+px+q =0
x_(1)=1; x_(2)=2

Абсцисса вершины параболы y=ax^2+bx+c
[b]x_(o)=-b/2a[/b]

Для параболы y_(1)=3x^2–2x–1
абсцисса вершины[b] x_(o)[/b]=2/6=[b]1/3[/b]

Находим ординату, подставив х=1/3 в выражение:
y(1/3)=3*(1/3)^2-2*(1/3)-1
y(1/3)=-4/3

Для параболы y_(3)=x^2–3x+2
абсцисса вершины[b] x_(o)[/b]=[b]3/2[/b]

Находим ординату, подставив х=3/2 в выражение:
y(3/2)=(3/2)^2-3*(3/2)+2
y(1/3)=-1/4

Находим расстояние между двумя точками
A(1/3; -4/3) и В (3/2;(-1/4))

Рисунок для наглядности.

Кривые второго порядка — определение и построение с примерами решения

Содержание:

Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде

1. Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
2. если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.

Это определение в более компактной записи выглядит следующим образом. Уравнение называется уравнением фигуры, если , то есть (а, b) — решение уравнения F(x,y) = 0.

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения , т.е. уравнение фигуры задает эту фигуру.

Возможны два вида задач:

1. дано уравнение и надо построить фигуру Ф, уравнением которой является ;
2. дана фигура Ф и надо найти уравнение этой фигуры.

Первая задача сводится к построению графика уравнения и решается, чаще всего, методами математического анализа.

Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:

1. Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
2. Записать в координатах условие, сформулированное в первом пункте.

Эллипс

Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек , есть величина постоянная (большая, чем расстояние между ).

Точки называются фокусами эллипса. Обозначив расстояние между фокусами через 2с, а сумму расстояний от точек эллипса до фокусов через 2а, имеем с b. В этом случае а называется большой полуосью, a b — малой.

Если а =Ь, то уравнение (7.3) можно переписать в виде:

(7.5)

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку координаты которой задаются формулами будет окружность (4) переводить в эллипс, заданный соотношением

Число называется эксцентриситетом эллипса. Эксцентриситет характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении становится более вытянутым

Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами . Их длины и задаются формулами Прямые называются директрисами эллипса. Директриса называется левой, а — правой. Так как для эллипса и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая — правее правой вершины.

Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.

Гипербола

Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек есть величина постоянная (не равная нулю и меньшая, чем расстояние между ).

Точки называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 2с. Модуль расстояний от точек гиперболы до фокусов обозначим через а. По условию, а 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А — произвольная точка плоскости с координатами (х, у) и пусть . Тогда точка А будет лежать на параболе, если r=d, где d- расстояние от точки А до директрисы. Фокус F имеет координаты .

Тогда А расстояние Подставив в формулу r=d, будем иметь. Возведя обе части равенства в квадрат, получим

или

(9.4.1)

Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения также определяют параболы.

Легко показать, что уравнение , определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а О. Для этого выделим полный квадрат:

и сделаем параллельный перенос по формулам

В новых координатах преобразуемое уравнение примет вид: где р — положительное число, определяется равенством .

Пример:

Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию, называется параболой. Прямая у = -1 называется директрисой параболы, а точка F — фокусом параболы. Чтобы выяснить, как располагаются точки Р, удовлетворяющие условию, запишем это равенство с помощью координат: , или после упрощения . Это уравнение геометрического места точек, образующих параболу (рис. 9.8).

Кривые второго порядка на плоскости

Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:

где коэффициенты А, В и С не равны одновременно нулю

Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.

Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.

Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

которое называют каноническим уравнением эллипса.

Число а называют большей полуосью эллипса, число — мень-

шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки называют вершинами эллипса, а — его фокусами (рис. 12).

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.

Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.

В случае а=b каноническое уравнение эллипса принимает вид и определяет окружность радиуса а с центром в начале координат.

Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.

Так, в случае а>b эксцентриситет эллипса выражается формулой:

Эксцентриситет изменяется от нуля до единицы и характеризует форму эллипса. Для окружности Чем больше эксцентриситет, тем более вытянут эллипс.

Пример:

Показать, что уравнение

является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.

Решение:

Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:

— каноническое уравнение эллипса с центром в точке большей полуосью а=3 и меньшей полуосью

Найдем эксцентриситет эллипса:

Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке а оси параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е.

В новой системе координат координаты вершин и фокусов гиперболы будут следующими:

Переходя к старым координатам, получим:

Построим график эллипса.

Задача решена.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.

Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Найти расстояние между вершинами параболы и центром окружности

Ах 2 + 2Вху + Су 2 + 2 Dx + 2 Ey + F = 0.

Существует система координат (не обязательно декартова прямоугольная), в которой данное уравнение может быть представлено в одном из видов, приведенных ниже.

1) — уравнение эллипса.

2) — уравнение “мнимого” эллипса.

3) — уравнение гиперболы.

4) a 2 x 2 – c 2 y 2 = 0 – уравнение двух пересекающихся прямых.

5) y 2 = 2 px – уравнение параболы.

6) y 2 – a 2 = 0 – уравнение двух параллельных прямых.

7) y 2 + a 2 = 0 – уравнение двух “мнимых” параллельных прямых.

y 2 = 0 – пара совпадающих прямых.

9) ( x – a ) 2 + ( y – b ) 2 = R 2 – уравнение окружности.

В окружности ( x – a ) 2 + ( y – b ) 2 = R 2 центр имеет координаты ( a ; b ).

Пример. Найти координаты центра и радиус окружности, если ее уравнение задано в виде:

2 x 2 + 2 y 2 – 8 x + 5 y – 4 = 0.

Для нахождения координат центра и радиуса окружности данное уравнение необходимо привести к виду, указанному выше в п.9. Для этого выделим полные квадраты:

x 2 + y 2 – 4 x + 2,5 y – 2 = 0

x 2 – 4 x + 4 –4 + y 2 + 2,5 y + 25/16 – 25/16 – 2 = 0

( x – 2) 2 + ( y + 5/4) 2 – 25/16 – 6 = 0

( x – 2) 2 + ( y + 5/4) 2 = 121/16

Отсюда находим О (2; -5/4); R = 11/4.

Определение. Эллипсом называется линия, заданная уравнением .

О пределение. Фокусами называются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.

у

с – половина расстояния между фокусами;

a – большая полуось;

b – малая полуось.

Теорема. Фокусное расстояние и полуоси эллипса связаны соотношением:

Доказательство: В случае , если точка М находится на пересечении эллипса с вертикальной осью, r ₁ + r ₂ = 2 (по теореме Пифагора). В случае , если точка М находится на пересечении эллипса с горизонтальной осью, r ₁ + r ₂ = a – c + a + c . Т.к. по определению сумма r ₁ + r ₂ – постоянная величина, то , приравнивая, получаем:

a 2 = b 2 + c 2

Определение. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом.

Определение. Величина k = b / a называется коэффициентом сжатия эллипса, а величина 1 – k = ( a – b )/ a называется сжатием эллипса.

Коэффициент сжатия и эксцентриситет связаны соотношением: k 2 = 1 – e 2 .

Если a = b ( c = 0, e = 0, фокусы сливаются), то эллипс превращается в окружность.

Если для точки М( х₁, у₁) выполняется условие: , то она находится внутри эллипса, а если , то точка находится вне эллипса.

Теорема. Для произвольной точки М( х , у), принадлежащей эллипсу верны соотношения:

r ₁ = a – ex , r ₂ = a + ex .

Доказательство. Выше было показано, что r ₁ + r ₂ = 2 a . Кроме того, из геометрических соображений можно записать:

После возведения в квадрат и приведения подобных слагаемых:

Аналогично доказывается, что r ₂ = a + ex . Теорема доказана.

С эллипсом связаны две прямые, называемые директрисами. Их уравнения:

x = a / e ; x = — a / e .

Теорема. Для того , чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету е.

Пример. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса, заданного уравнением:

1) Координаты нижней вершины: x = 0; y 2 = 16; y = -4.

2) Координаты левого фокуса: c 2 = a 2 – b 2 = 25 – 16 = 9; c = 3; F ₂ (-3; 0).

3) Уравнение прямой, проходящей через две точки:

Пример. Составить уравнение эллипса, если его фокусы F ₁ (0; 0), F ₂ (1; 1), большая ось равна 2.

Уравнение эллипса имеет вид: . Расстояние между фокусами:

2 c = , таким образом, a 2 – b 2 = c 2 = ½

по условию 2а = 2, следовательно а = 1, b =

Итого: .

Определение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.

y

По определению ï r ₁ – r ₂ ï = 2 a . F ₁ , F ₂ – фокусы гиперболы. F ₁ F ₂ = 2 c .

Выберем на гиперболе произвольную точку М( х , у). Тогда :

обозначим с 2 – а 2 = b 2 (геометрически эта величина – меньшая полуось)

Получили каноническое уравнение гиперболы.

Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.

Ось 2а называется действительной осью гиперболы.

Ось 2 b называется мнимой осью гиперболы.

Гипербола имеет две асимптоты, уравнения которых

Определение. Отношение называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.

С учетом того, что с 2 – а 2 = b 2 :

Если а = b , e = , то гипербола называется равнобочной (равносторонней).

Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a / e от него, называются директрисами гиперболы. Их уравнения: .

Теорема. Если r – расстояние от произвольной точки М гиперболы до какого — либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r / d – величина постоянная, равная эксцентриситету.

Доказательство. Изобразим схематично гиперболу.

y