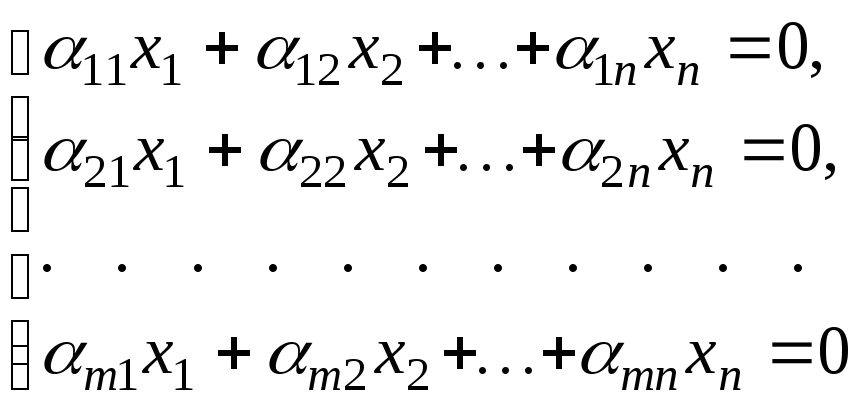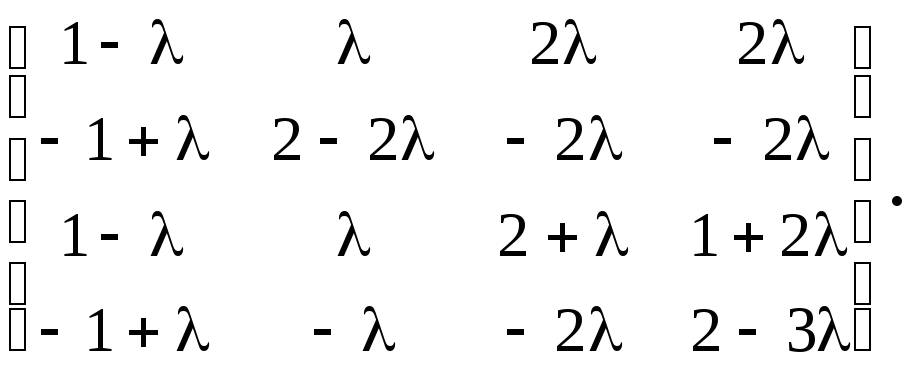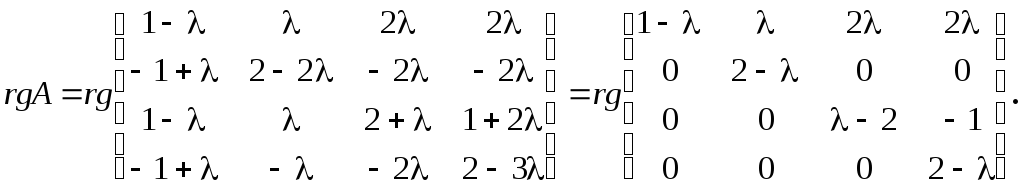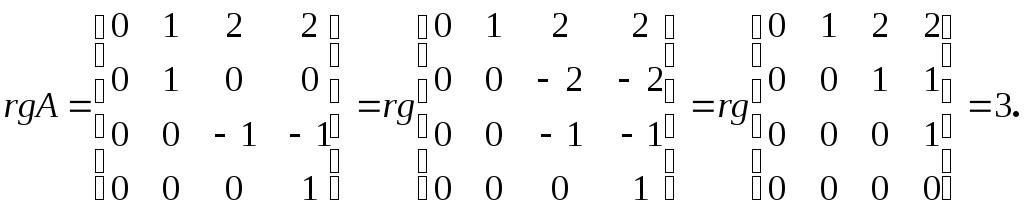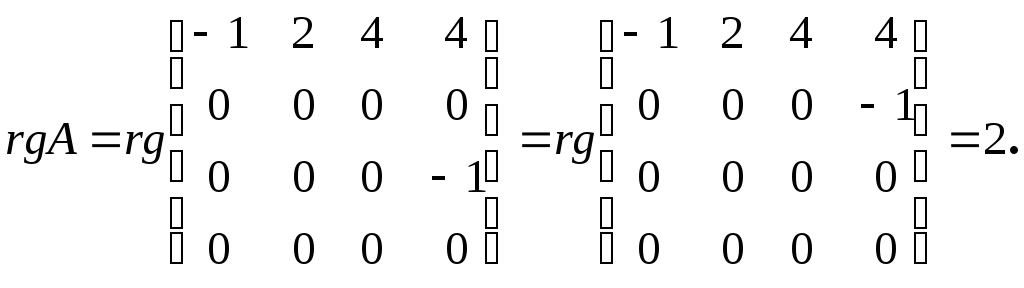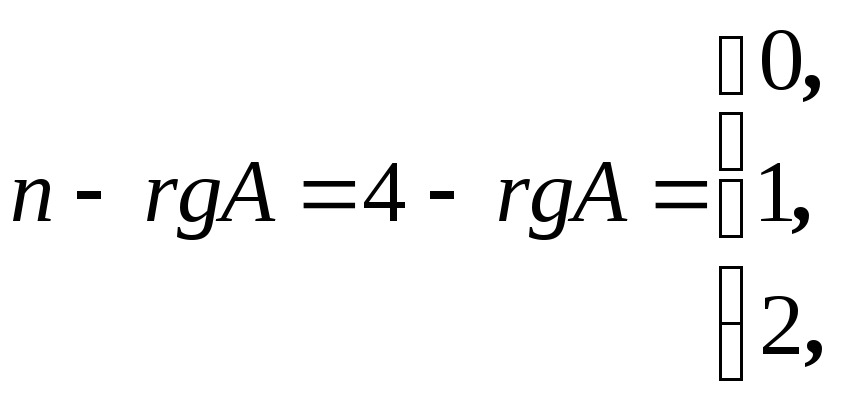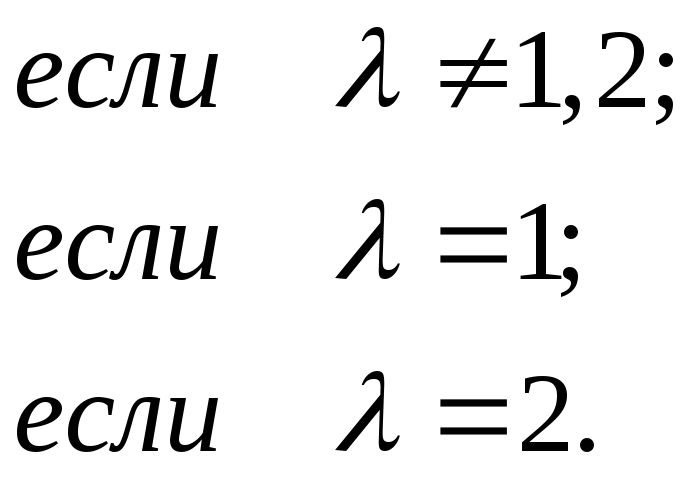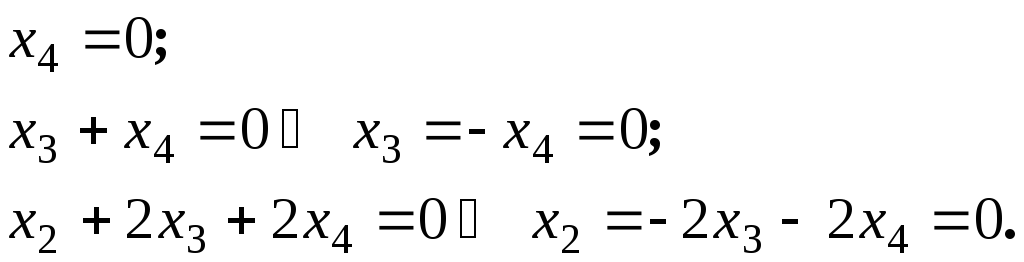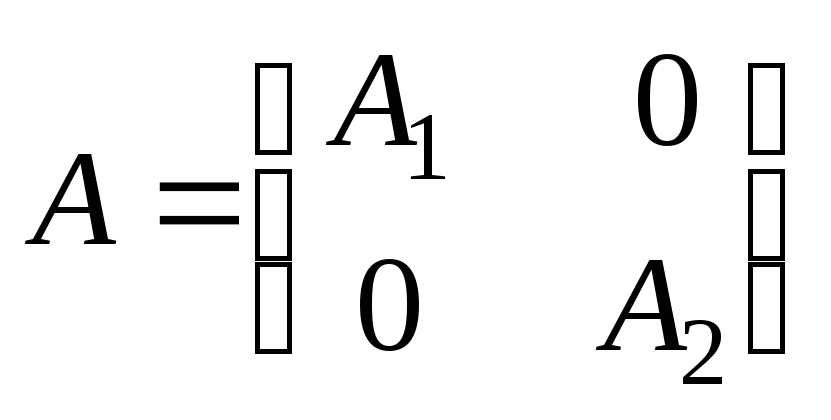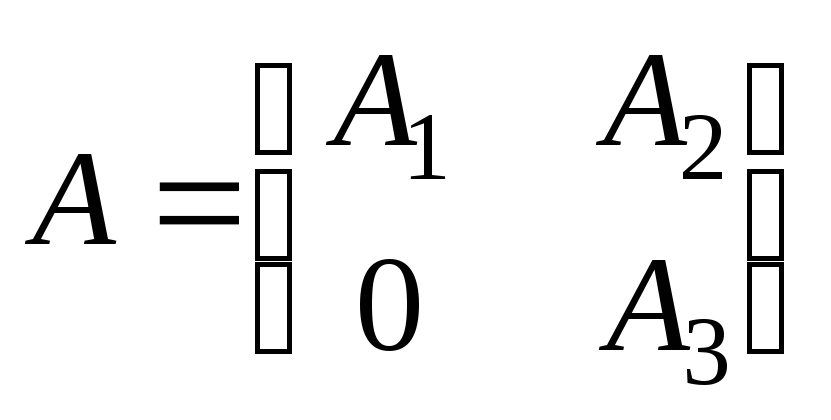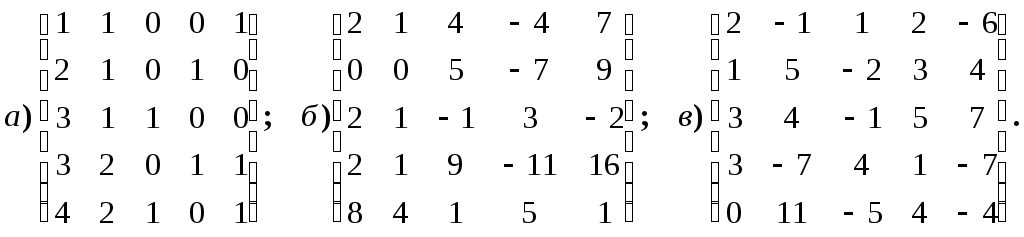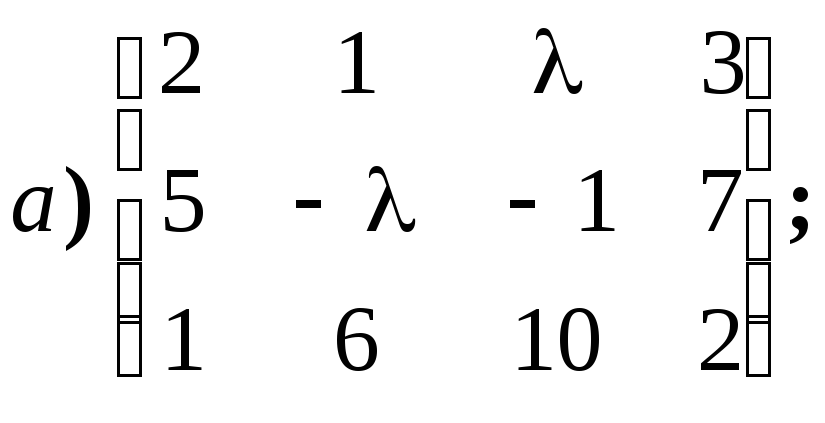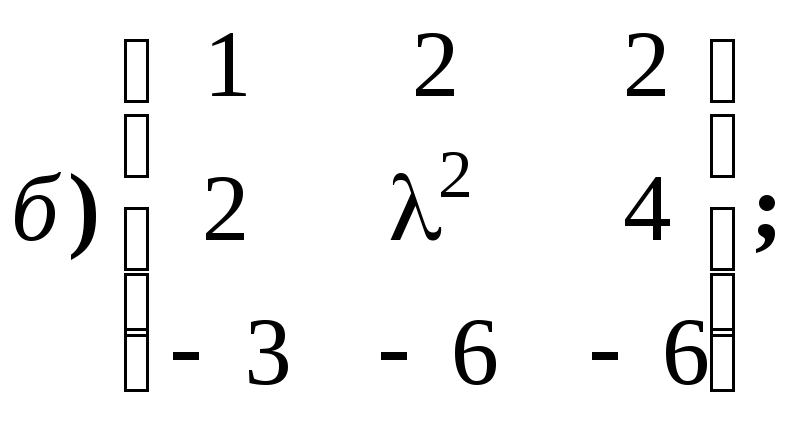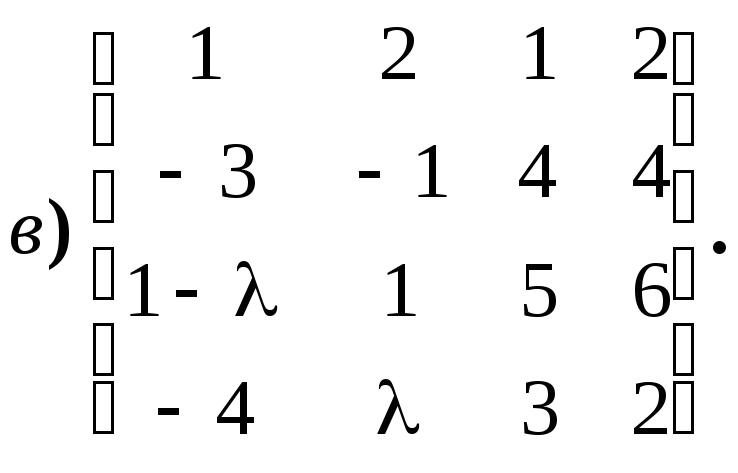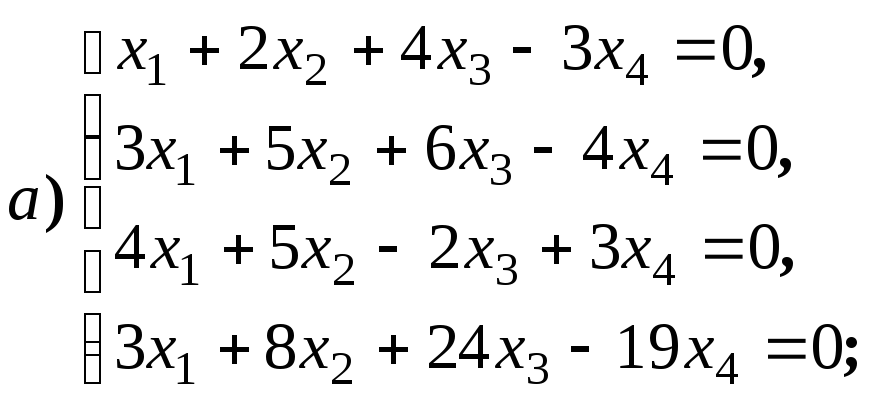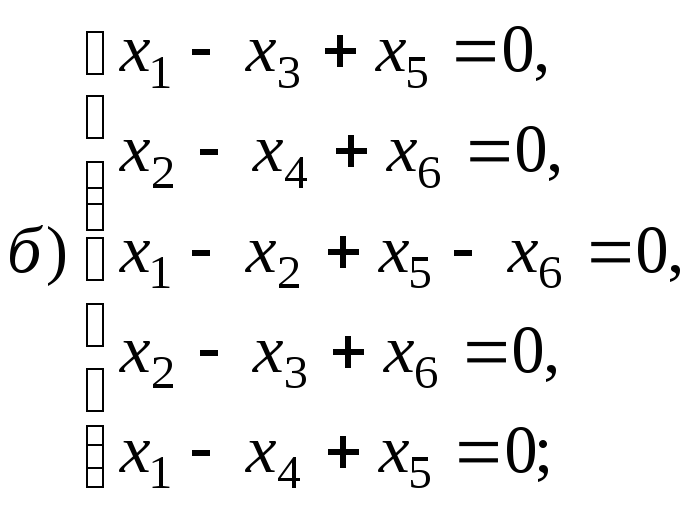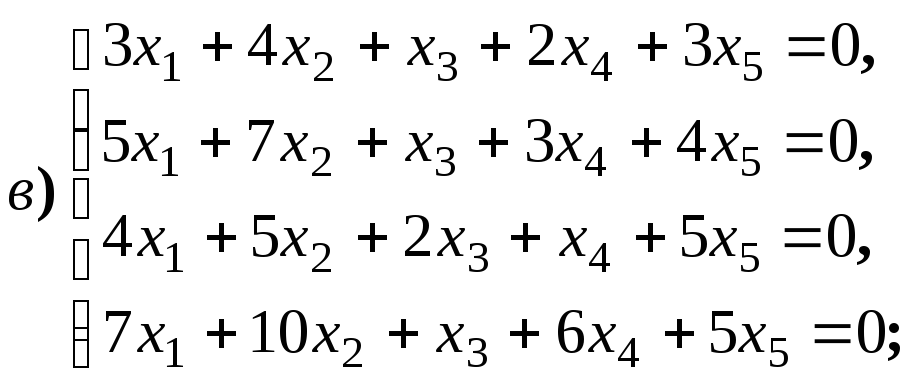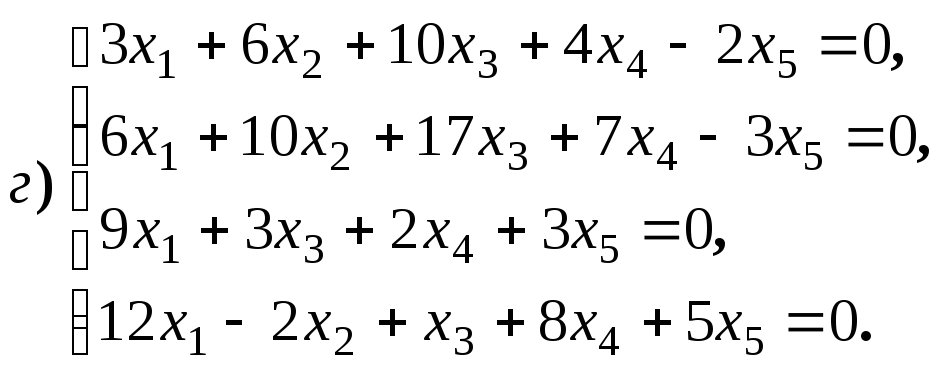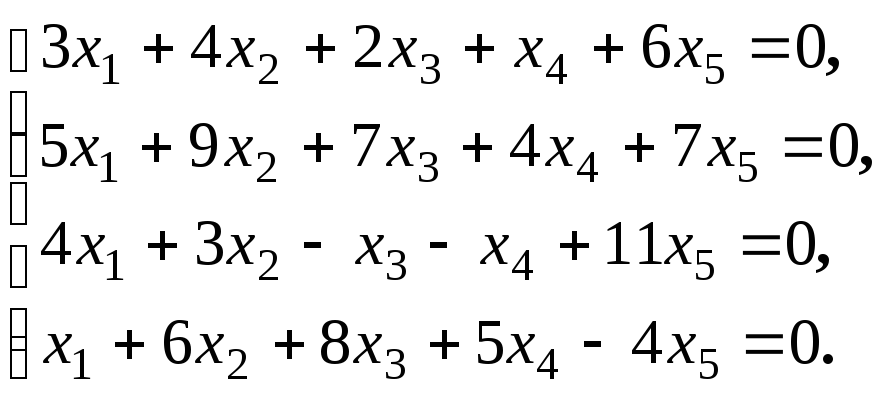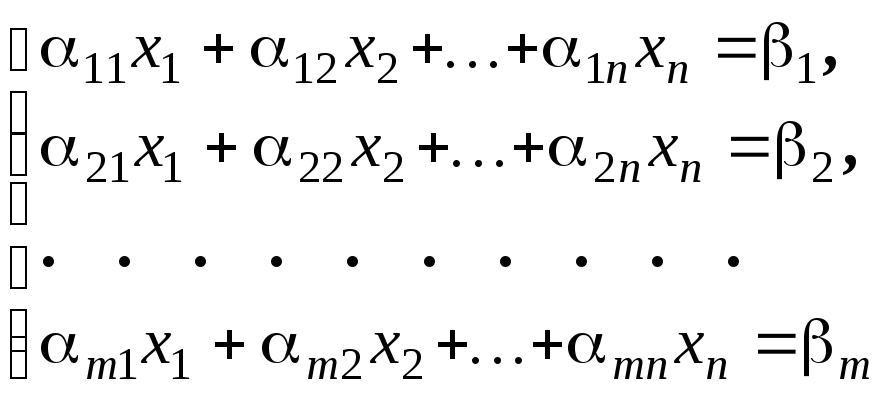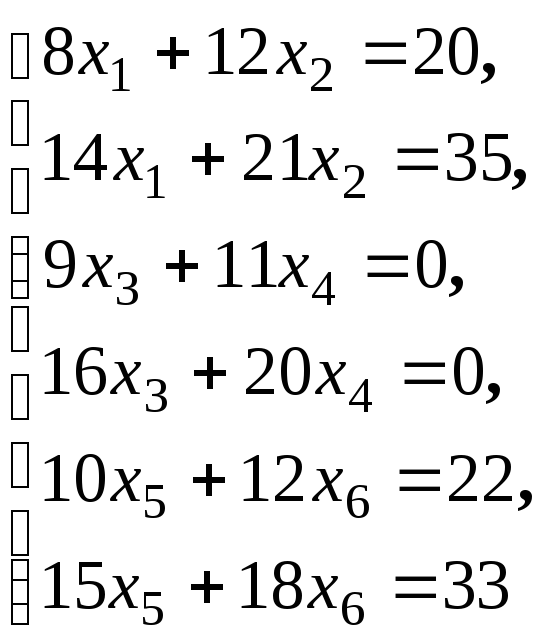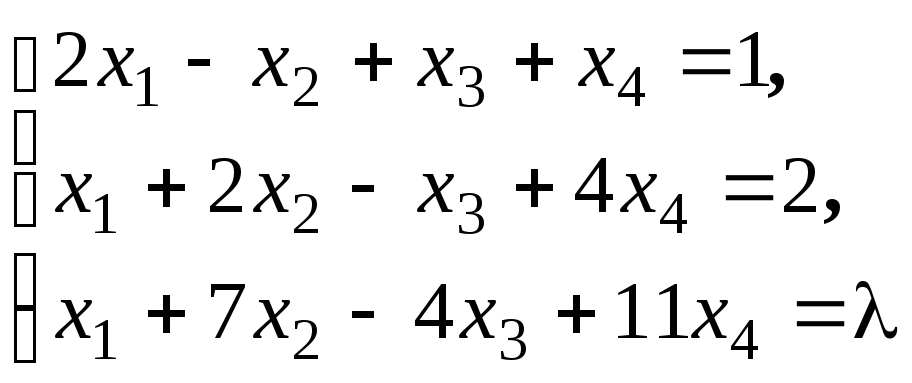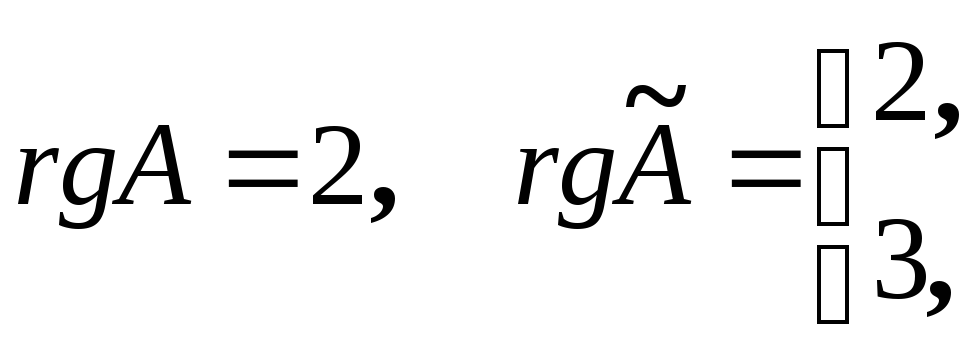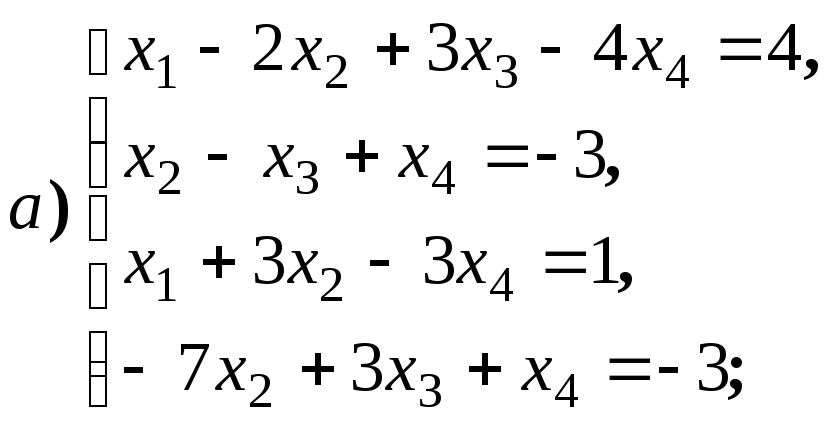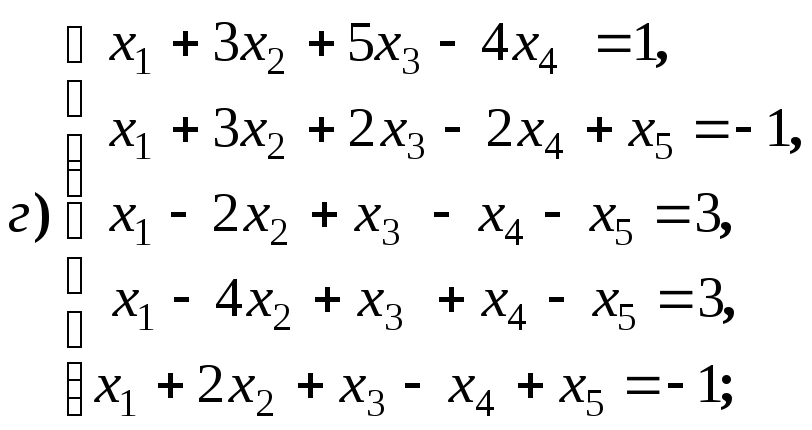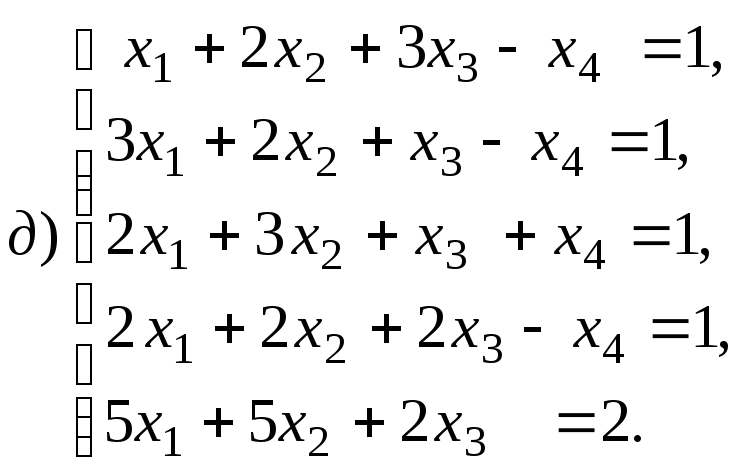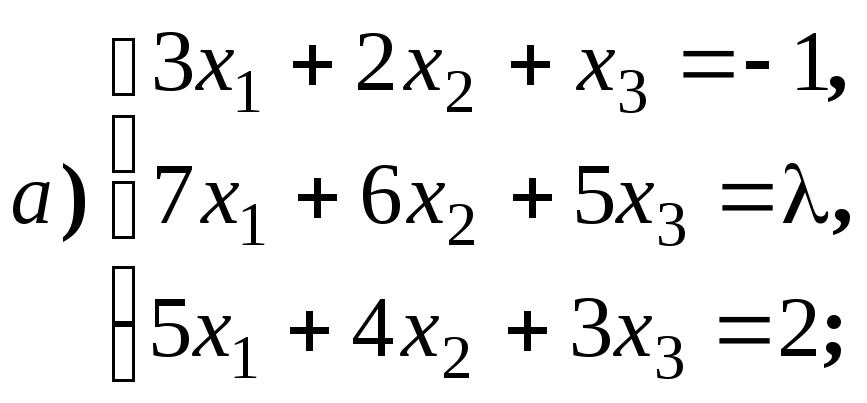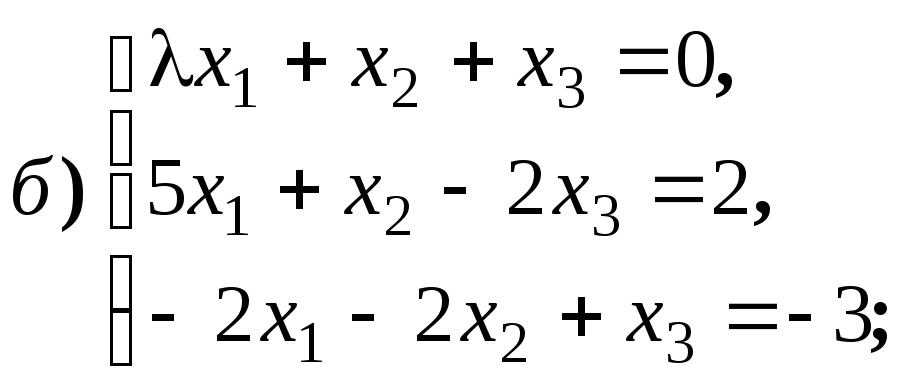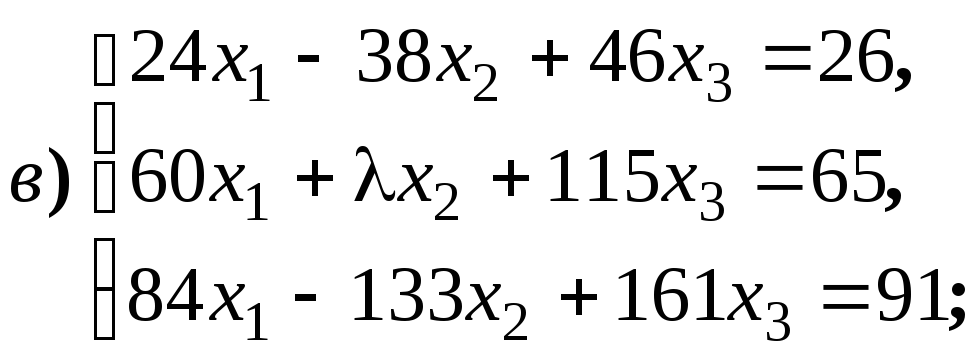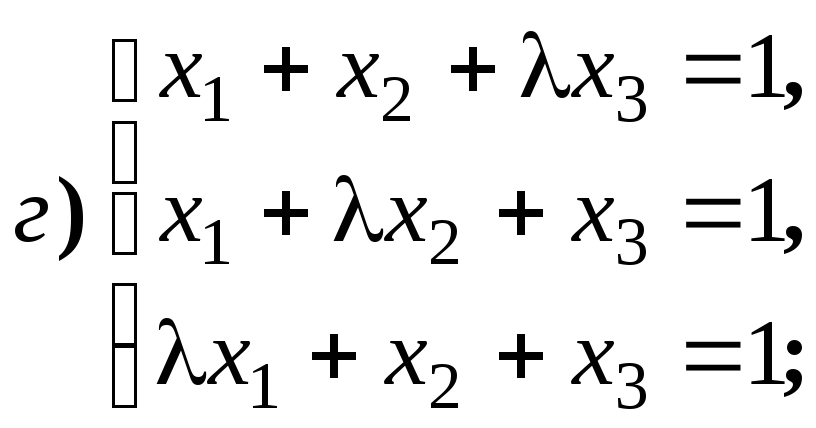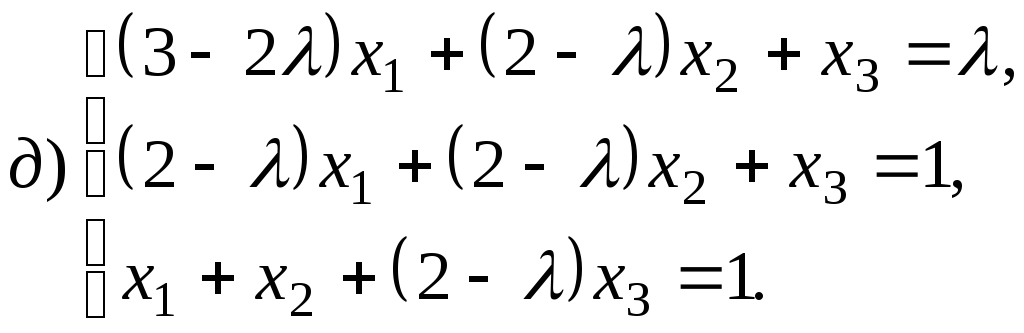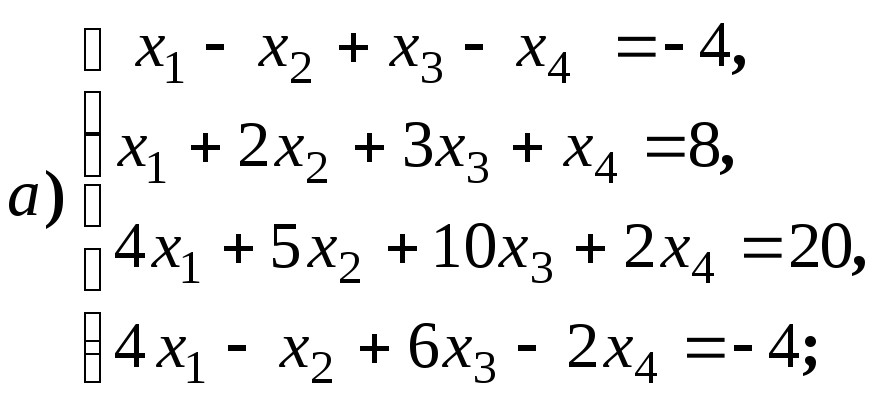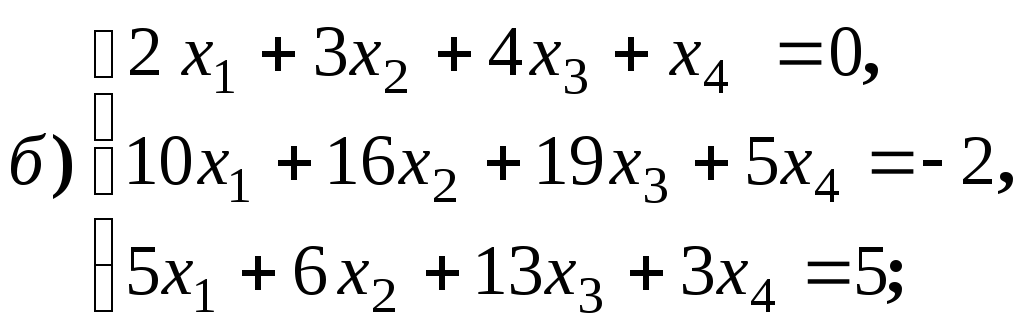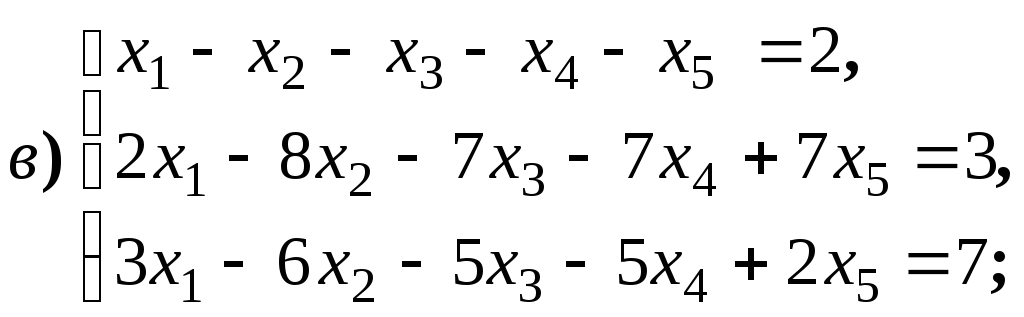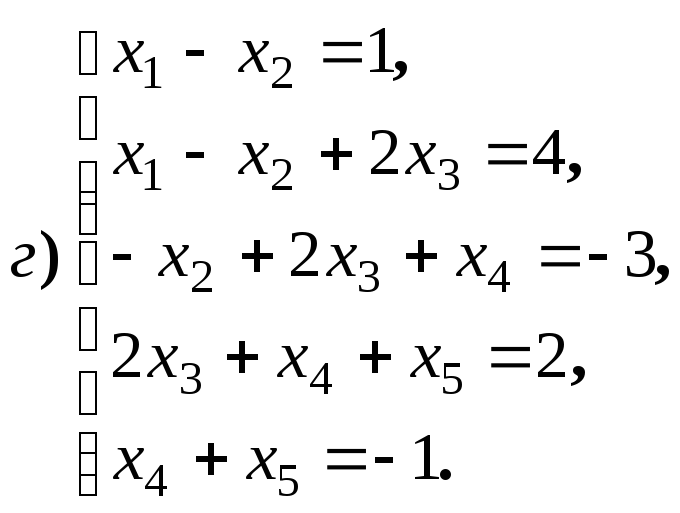Как найти ранг матрицы с лямбдой - Autoru.top - решение различных проблем

$begingroup$

Find the rank of the following matrix depending on $lambdainBbb R$.
$$A=begin{pmatrix}
1&2&3&4\
2&lambda&6&7\
3&6&8&9\
4&7&9&10
end{pmatrix}$$

My attempt:

$$begin{pmatrix}
1&2&3&4\
2&lambda&6&7\
3&6&8&9\
4&7&9&10
end{pmatrix}simbegin{pmatrix}
1&2&3&4\
0&lambda-4&0&-1\
0&0&-1&-3\
0&-1&-3&-6
end{pmatrix}simbegin{pmatrix}
1&0&-3&-8\
0&lambda-4&0&-1\
0&0&-1&-3\
0&-1&-3&-6\
end{pmatrix}$$
For $lambda=4$ we have:
$$begin{pmatrix}
1 &0&-3&-8\
0&0&0&-1\
0&0&-1&-3\
0&-1&-3&-6
end{pmatrix}simbegin{pmatrix}
1&0&0&1\
0&0&0&-1\
0&0&-1&-3\
0&-1&0&3end{pmatrix}simbegin{pmatrix}
1&0&0&0\
0&0&0&-1\
0&0&-1&0\
0&-1&0&0\
end{pmatrix}$$

$Rightarrow r(A)=4$

For $lambdaneq 4$ we have:

$$begin{pmatrix}
1&0&0&1\
0&lambda-4&0&-1\
0&0&-1&-3\
0&-1&0&3\
end{pmatrix}simbegin{pmatrix}
1&0&0&1\
0&0&0&3lambda-13\
0&0&-1&-3\
0&-1&0&3
end{pmatrix}$$

For$lambda=frac{13}{3}Rightarrow r(A)=3$ and for $lambdaneq frac{13}{3} Rightarrow r(A)=4$

Is this correct? Thanks!

asked Jan 31, 2017 at 13:08

$endgroup$

$begingroup$

It looks fine to me!! Or, we have $A=begin{pmatrix}
1&2&3&4\
2&lambda&6&7\
3&6&8&9\
4&7&9&10
end{pmatrix}$ with $lambda in Bbb{R}$ and we know: $$r(A) leq 4 text{ and } big[r(A)= 4 leftrightarrow det(A)neq 0big]$$

We have $displaystyledet(A)= 13 — 3 lambda$ therefore: $$ r(A) =4leftrightarrow bigg(det(A) neq 0 leftrightarrow 13 — 3 lambda neq 0 leftrightarrow 13 neq 3 lambda leftrightarrow lambda neq frac{13}{3}bigg)$$ $$4 neq r(A) < 4leftrightarrowbigg(det(A)=0 leftrightarrow 13 — 3 lambda = 0 leftrightarrow 13 = 3 leftrightarrow lambda=frac{13}{3} bigg) $$

But if $det(A)=0$ and exists a $T in M(A)_{3}$ with $det(T) neq 0$ and such that for all $Rin M(A)_{3+1=4}$ which contain $T$ we have $det(R)=0$ then $r(A)=3$
$(M(A)_{n}:={X| X text{ is minor of order }n text{ for }A})$

And, with $lambda=frac{13}{3}$, we have a $T in M(A)_{3}$ with $det(T) neq 0$: $$det(T)=detbegin{pmatrix}
2&frac{13}{3}&6\
3&6&8\
4&7&9
end{pmatrix}=frac{-1}{3}neq 0$$ and $M(A)_{3+1=4}={A}$ and $det(A)=0$ because $lambda=frac{13}{3}$ then $r(A)=3$

Summary:

$r(A)=4 leftrightarrow Bbb{R}nilambdaneq frac{13}{3}$

$r(A)=3 leftrightarrow Bbb{R}nilambda =frac{13}{3}$

answered Jan 31, 2017 at 14:22

mlemle

2,2771 gold badge19 silver badges35 bronze badges

$endgroup$

$begingroup$

I will point out that you can also check the result in Wolfram Alpha.

Here is my computation — rather similar to yours.

$$begin{pmatrix}
1 & 2 & 3 & 4\
2 &lambda& 6 & 7\
3 & 6 & 8 & 9\
4 & 7 & 9 &10
end{pmatrix}overset{(1)}sim
begin{pmatrix}
1 & 2 & 3 & 4\
2 &lambda& 6 & 7\
3 & 6 & 8 & 9\
1 & 1 & 1 & 1
end{pmatrix}sim
begin{pmatrix}
0 & 1 & 2 & 3\
0 &lambda-2& 4 & 5\
0 & 3 & 5 & 6\
1 & 1 & 1 & 1
end{pmatrix}overset{(2)}sim
begin{pmatrix}
0 & 1 & 2 & 3\
0 &lambda-2& 4 & 5\
0 & 1 & 1 & 0\
1 & 1 & 1 & 1
end{pmatrix}sim
begin{pmatrix}
0 & 1 & 2 & 3\
0 &lambda-2& 4 & 5\
0 & 1 & 1 & 0\
1 & 1 & 1 & 1
end{pmatrix}sim
begin{pmatrix}
0 & 0 & 1 & 3\
0 & 0 & 6-lambda & 5\
0 & 1 & 1 & 0\
1 & 1 & 1 & 1
end{pmatrix}sim
begin{pmatrix}
0 & 0 & 1 & 3\
0 & 0 & 0 & 3lambda-13\
0 & 1 & 1 & 0\
1 & 1 & 1 & 1
end{pmatrix}sim
begin{pmatrix}
1 & 1 & 1 & 1\
0 & 1 & 1 & 0\
0 & 0 & 1 & 3\
0 & 0 & 0 & 3lambda-13
end{pmatrix}$$

$(1)$: Subtracted third row from the last one.
$(2)$: Subtracted twice the first row from the last one.
In both cases I did so because the resulting row seemed to be simple (only zeroes and ones), which made further row operations a bit easier.

From the final matrix we see that rank is three if $3lambda-13=0$ and in all other cases rank in equal to four.

answered Jan 31, 2017 at 15:28

Martin SleziakMartin Sleziak

51.8k20 gold badges181 silver badges357 bronze badges

$endgroup$

You must log in to answer this question.

Not the answer you’re looking for? Browse other questions tagged

.

Источник

Задача 1.

Определить ранг матрицы

Указание

Единственным минором максимального (3-го) порядка для матрицы А является ее определитель. Если ΔА не равен нулю, R(A) = 3; если ΔА = 0, R(A) < 3.

Решение

Единственным минором максимального (3-го) порядка для матрицы А явля-ется ее определитель. Если ΔА не равен нулю, R(A) = 3; если ΔА = 0, R(A) < 3.

Найдем ΔА разложением по первой строке:

Следовательно, R(A) < 3. Поскольку матрица А содержит ненулевые элементы, R(A) > 0. Значит, R(A) = 1 или R(A) = 2. Если найдется минор 2-го порядка, не равный нулю, то R(A) = 2.

Вычислим минор из элементов, стоящих на пересечении двух первых строк и двух первых столбцов:

Ответ: R(A) = 2.

Если найден минор K-го порядка, не равный нулю, то можно утверждать, что R(A) ≥ K. Если же выбранный минор K-го порядка равен нулю, то из этого еще не следует, что R(A) < K, так как могут найтись миноры того же порядка, не равные нулю.

Задача 2.

Определить ранг матрицы

Указание

Используя элементарные преобразования, приведите матрицу А к треугольному виду.

Решение

У матрицы А существуют миноры до 4-го порядка включительно, поэтому

R(A) ≤ 4. Разумеется, непосредственное вычисление всех миноров 4-го, 3-го и т. д. порядка потребовало бы слишком много времени. Поэтому, используя элементарные преобразования, приведем матрицу А к треугольному виду. Поменяем местами 1-ю и 2-ю строки, чтобы элемент А11 стал равным 1:

Прибавим к третьей строке первую, ко второй – удвоенную первую, к четвертой – первую, умноженную на 3. Тогда все элементы 1-го столбца, кроме А11, окажутся равными нулю:

Вычтем вторую строку полученной матрицы из третьей и четвертой строк:

И вычеркнем нулевые строки:

Итак, ранг матрицы А равен рангу полученной матрицы размера , т. е.

R(A) < 2. Минор

Следовательно, R(A) = 2.

Ответ: R(A) = 2.

Задача 3.

Определить ранг матрицы

Указание

Используя элементарные преобразования, приведите матрицу А к треугольному виду.

Решение

Отметим, что минор, составленный из элементов матрицы, стоящих на пересечении первых трех строк и первых трех столбцов, не равен нулю:

Поэтому ранг данной матрицы не меньше трех.

Приведем матрицу к треугольному виду:

Вычеркивание нулевых строк приводит к тому, что

Размер полученной матрицы , поэтому ее ранг не более трех. Поскольку минор 3-го порядка, не равный нулю, существует, ранг исходной матрицы равен 3.

Ответ: R(A) = 3.

Задача 4.

Найти значения L, при которых матрица

Имеет наименьший ранг.

Указание

Приведите матрицу А к треугольному виду и найдите значения L, при которых с помощью элементарных преобразований вторую строку можно сделать нулевой.

Решение

Переставим столбцы матрицы А:

И приведем ее к треугольному виду с помощью элементарных преобразований:

Теперь видно, что при L = 0 вторая строка матрицы становится нулевой, и после ее вычеркивания получаем:

Минор его порядок равен 2, следовательно, при L = 0 R(A) = 2.

Если L ≠ 0, то минор, составленный из последних трех столбцов, имеет вид:

Значит, при L ≠ 0 R(A) = 3.

Итак, наименьший ранг, равный 2, матрица А имеет при L= 0.

Ответ: L = 0.

< Предыдущая		Следующая >

Источник

Ранг матрицы

Чему равен ранг матрицы при различных значениях $% lambda $%

задан
9 Мар ’15 22:33

Snaut
391●1●24●74

65% принятых

1 ответ

Нужно применить гауссовы преобразования. Третью строку не меняем, ставя её не первое место. Вместо второй строки получится $%(0;21;-lambda-12; 3)$%, вместо первой $%(0;lambda-10;5;1)$%. Если эти строки не пропорциональны, то ранг матрицы равен $%3$%, а если пропорциональны, то он равен $%2$%. В последнем случае коэффициент пропорциональности может быть равен только трём, и это имеет место при $%lambda=3$%. Получаются пропорциональные строки $%(0;21;-15;3)$% и $%(0;-7;5;1)$%.

Здравствуйте

Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.

Присоединяйтесь!

отмечен:

матрицы
×531

задан
9 Мар ’15 22:33

показан
4589 раз

обновлен
9 Мар ’15 22:50

Связанные вопросы

Отслеживать вопрос

по почте:

Зарегистрировавшись, вы сможете подписаться на любые обновления

по RSS:

Ответы

Ответы и Комментарии

Источник

вторник, 31 мая 2011

`((lambda 1 1 1 1),(1 lambda 1 1 1),(1 1 lambda 1 1),(1 1 1 lambda 1))`

помогите разобраться
сначала беру минор первого порядка-единичку
затем `|(lambda 1),(1 lambda)|`
получается что ранг равен единице при лямда +- 1
берем третий порядок минора
получается что лямда=1 и лямда =-2

как решать?
помогите
актуально до вечера сегодняшнего

@темы:

Линейная алгебра,
Матрицы

Источник

Глава
4

Системы
линейных уравнений

§
4.1. Ранг матрицы. Однородные системы.
Фундаментальная

система
решений

Рангом
матрицы

(обозначается

)
называется наивысший порядок
отличных
от нуля миноров этой матрицы.

Ранг
нулевой матрицы полагается равным нулю
по определению.

Для
любой прямоугольной матрицы ранги ее
систем векторов- строк и векторов-
столбцов совпадают и равны рангу матрицы.

Система
уравнений

называется
однородной.
Однородная система всегда совместна,
так как одним из ее частных решений
является нулевое решение.

Для
того, чтобы однородная система имела
ненулевое решение, необходимо и
достаточно, чтобы ранг матрицы системы
был меньше числа неизвестных.

Множество
решений однородной системы линейных
уравнений

образует линейное пространство
размерности
,
где
—
ранг матрицы системы. Любой базис
пространства решений однородной системы
называется фундаментальной
системой решений
этой системы.

Пример
1.
Найдите ранг матрицы в зависимости от
значения параметра

Решение.
При помощи элементарных преобразований,
не изменяющих ранг, приведем матрицу к
ступенчатому виду. Прибавив ко второй
строке первую, к третьей- первую,
умноженную на
,
к четвертой- первую, получим:

Если

,
то

Рассмотрим
теперь случай, когда
:

Очевидно,
что если
,
то
.

Пример
2.
Найдите размерность пространства
решений однородной системы линейных
уравнений с матрицей системы из примера
1.

Решение.
Размерность пространства решений равна

Пример
3.
Найдите общее решение и фундаментальную
систему решений однородной системы
линейных уравнений из примера 1.

Решение.
Если

система имеет только нулевое решение.

Пусть

.
Тогда, как было показано в примере 1,

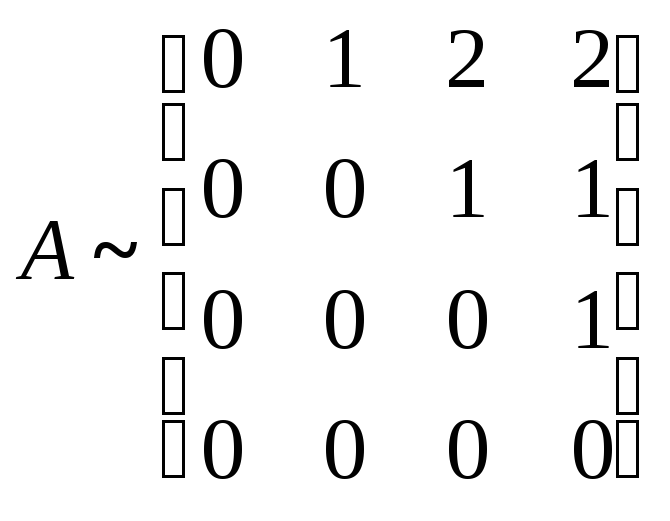
Пространство
решений одномерное и фундаментальная
система решений состоит из одного
вектора. Из

находим:

—
свободная переменная.

Общее
решение имеет вид:.
Фундаментальная система решений:.

Пусть
теперь
.
В этом случае

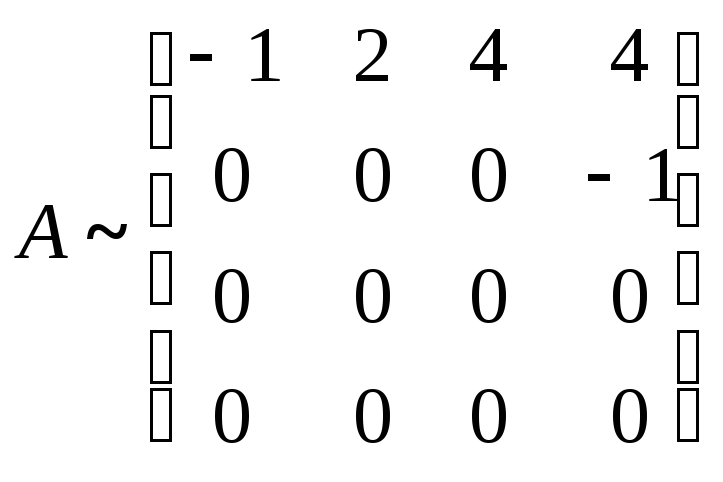
пространство
решений двумерное и фундаментальная
система решений состоит из двух векторов.
Из

получаем:

—
свободные переменные;

Общее
решение имеет вид:

Выбирая
значения свободных переменных в
соответствии с таблицей,

i
1	1	0
2	0	1

записываем
фундаментальную систему решений:

и
.

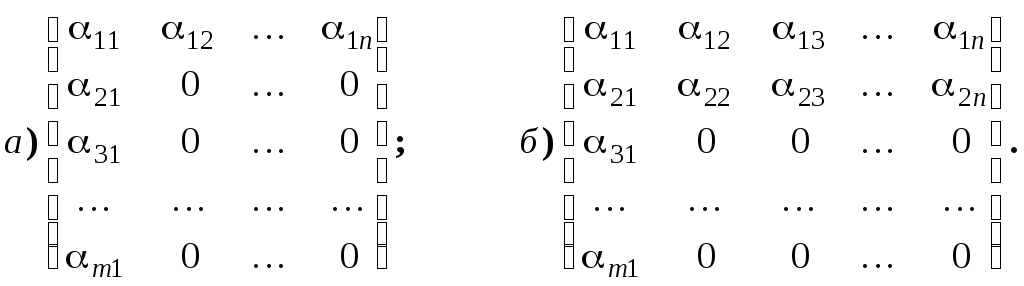
4.1.1.
Укажите всевозможные значения ранга
матриц вида:

4.1.2.Как
может измениться ранг матрицы, если
изменить значение одного ее элемента?

4.1.3.
Как может изменится ранг матрицы, при
изменении элементов лишь одной строки?

строк?

4.1.4.
Докажите, что ранг квазидиагональной
матрицы

равен сумме рангов матриц

и
.

4.1.5.
Верно ли следующее утверждение:
ранг квазитреугольной
матрицы

всегда равен сумме рангов матриц

и
?

Докажите,
что ранг суммы двух матриц не больше
суммы их рангов.

4.1.7.
Вычислите ранг матриц:

4.1.8.
Найдите ранг матриц в зависимости от
значений параметров:

4.1.9.
Найдите общее решение и фундаментальную
систему решений для систем уравнений:

4.1.10.
Образуют ли строки каждой из матриц

фундаментальную
систему решений для системы уравнений

§
4.2. Неоднородные системы. Теорема
Кронекера- Капелли

Согласно
теореме
Кронекера- Капелли неоднородная система
линейных уравнений

совместна
тогда и только тогда, когда ранг матрицы
этой системы

равен
рангу ее расширенной матрицы

т.е.
когда

Общее
решение

неоднородной системы представимо в
виде суммы общего решения

соответствующей однородной системы и
какого- либо частного решения

неоднородной системы.

Пример
1.
Исследуйте совместность и запишите
общее решение неоднородной системы
уравнений

в
виде суммы частного решения этой системы
и линейной комбинации базисных решений
соответствующей однородной системы.

Решение.
Запишем систему уравнений в матричном
виде. Используя элементарные преобразования
над строками полученной матрицы, приведем
ее к ступенчатому виду и проверим
выполнимость условия
:

т.е.
по теореме Кронекера- Капелли система
уравнений совместна. Запишем ее общее
решение. Поскольку

будем иметь две свободные переменные.

—
свободная переменная,

Таким
образом,

Заметим,
что
,
а векторы

и

образуют фундаментальную систему
решений соответствующей однородной
системы уравнений.

Пример
2.
Подберите

так, чтобы система уравнений

имела
решение.

Решение.
Нужно найти такое значение параметра

,
при котором выполняется условие
.

По
теореме Кронекера- Капелли система
уравнений совместна при

4.2.1.
Исследуйте совместность и найдите общее
решение систем уравнений

4.2.2.
Исследуйте систему и найдите общее
решение в зависимости от значения
параметра
:

4.2.3.
Исследуйте совместность и запишите
общее решение неоднородной системы
уравнений в виде суммы одного решения
этой системы и линейной комбинации
базисных решений соответствующей
однородной системы: