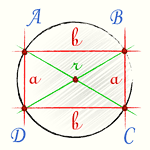
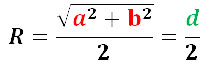Вокруг прямоугольника становится возможным описать окружность, так как сумма противоположных углов в нем равна 180°, а это обязательно условие для окружностей, описанных вокруг многоугольников. Такая окружность касается всех вершин прямоугольника, а ее центр находится в точке пересечения диагоналей прямоугольника. Если провести радиусы к вершинам прямоугольника, то станет очевидным, что они представляют собой половины диагоналей, а диагонали прямоугольника можно найти из теоремы Пифагора в прямоугольном треугольнике, стороны которого – это стороны прямоугольника.
Радиус описанной окружности прямоугольника, формула
Формула радиуса описанной окружности прямоугольника выходит из теоремы Пифагора поскольку диагональ прямоугольника является диаметром описанной окружности.
[R=frac{sqrt{a^2+b^2}}{2}]
(a,b — стороны прямоугольника; R — радиус описанной окружности прямоугольника)
Вычислить, найти радиус описанной окружности прямоугольника по формуле (1)
| a (сторона прямоугольника) |
| b (сторона прямоугольника) |
Вычислить
нажмите кнопку для расчета
Радиус описанной окружности прямоугольника |
стр. 249 |
|---|
Радиус описанной окружности прямоугольника
Радиус описанной окружности
Как известно, прямоугольником является четырехугольник с прямыми углами. Противоположные углы прямоугольника в сумме составляют 180°, соответственно, вокруг него можно описать одну окружность, при этом, вершины прямоугольника должны быть расположены на этой окружности. Центр прямоугольника и описанной вокруг него окружности размещен в месте пересечения диагоналей. Диагонали прямоугольника равны. Если известны стороны прямоугольника, можно рассчитать величину диагоналей по теореме Пифагора. Диагональ прямоугольника является в то же время и диаметром описанной окружности. R описанной окружности представляет половину диагонали прямоугольника и рассчитывается путем извлечения квадратного корня из суммы квадратов его сторон деленный на 2 или как половина его диагонали:

d — диагональ;
a, b — величины сторон прямоугольника.
Если известны стороны прямоугольника или диагонали, можно быстро найти R описанной окружности с помощью калькулятора.
Радиус описанной окружности прямоугольника
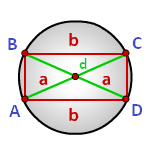
Радиус описанной окружности прямоугольника равен половине его диагонали
a, b — стороны прямоугольника
d — диагональ
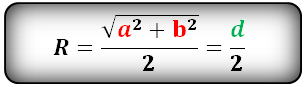
Формула радиуса описанной окружности прямоугольника (R):
Калькулятор — вычислить, найти радиус описанной окружности прямоугольника через стороны
- Подробности
-
Автор: Administrator
-
Опубликовано: 09 сентября 2011
-
Обновлено: 13 августа 2021
Прямоугольник — это четырёхугольник, у которого четыре прямых угла. Размеры прямоугольника задаются длиной его сторон, обозначаемых обычно a и b. Прямоугольник, все стороны которого равны (a=b) называется квадратом.
Свойства прямоугольника
- противолежащие стороны равны и параллельны друг другу;
- диагонали равны и в точке пересечения делятся пополам;
- сумма квадратов диагоналей равна сумме квадратов всех (четырех) сторон;
- прямогугольниками одного размера можно полностью замостить плоскость;
- прямоугольник можно двумя способами разделить на два равных между собой прямоугольника;
- прямоугольник можно разделить на два равных между собой прямогульных треугольника;
- вокруг прямоугольника можно описать окружность, диаметр которой равен диагонали прямоугольника;
- в прямогульник (кроме квадрата) нельзя вписать окружность так, чтобы она касалась всех его сторон.
Параллельность сторон, одинаковость углов и возможность замощения плоскости делают прямоугольник самой удобной геометрической фигурой при разбиении площади на участки будь то на местности, в помещении или внутри технического устройства. Участок можно считать прямоугольным, если его отклонения от идеального прямоугольника не превышают допустимой в расчетах погрешности. Тогда для периметр и площадь участка можно определять по формулам расчета периметра и площади прямоугольника.
Периметр P прямоугольника равен удвоенной сумме сторон, прилежащих к одному углу
P = 2(a + b).
Длина диагонали d прямоугольника вычисляется по теореме Пифагора:
d = √(a2 + b2).
Углы между диагоналями прямоугльника определяются соотношением сторон:
α = 2arctg(a/b),
β = 2arctg(b/a),
α + β = 180°.
Площадь S прямоугольника равна произведению сторон, прилежащих к одному углу (произведению длины на ширину):
S = a·b.
Также можно выразить площадь прямоугольника через длину диагоналей и угол между ними:
S = d2·sin(α/2)·cos(α/2).
Радиус описанной вокруг прямоугольника окружности равен половине длины диагонали:
R = √(a2 + b2)/2.
В прямоугольник (если он не квадрат) нельзя вписать окружность так, чтобы она касалась всех его сторон. Максимальный радиус окружности, которая может поместиться внутри прямоугольника, равен половине его меньшей стороны.
Источники:
- Прямоугольник — Википедия
- Четырехугольники — на сайте Омского университета
Дополнительно от Генона:
- Как найти площадь и периметр квадрата?
- Как найти площадь прямоугольного треугольника?
- У каких многоугольников все диагонали равны между собой?