ЛАБОРАТОРНАЯ
РАБОТА №13
ОПРЕДЕЛЕНИЕ РАДИУСА
КАПИЛЛЯРОВ
ОБОРУДОВАНИЕ:
капилляры, линейка, секундомер.
П
течении жидкости в трубке скорости
разных слоёв распределены так, как
показано на рис. 1. Длина стрелок
характеризует величину скорости.
Наибольшая скорость наблюдается на оси
трубки. По мере приближения к стенкам
скорость уменьшается, а слой, прилегающий
к стенкам, покоится. При таком течении
происходит перенос импульса молекулами
центрального слоя жидкости, где скорость
наибольшая, к слоям, движущимся с меньшей
скоростью. Это равносильно тому, что на
каждый из слоёв действует сила, равная
изменению импульса в ед. времени, т.е.
любой слой жидкости, движущиёся
относительно соседнего, испытывает
действие некоторой силы внутреннего
трения или вязкости. Величина этой силы
определяется законом Ньютона:
,
(1)
где S
– площадь трущихся слоёв;
– градиент скорости;
– коэффициент
внутреннего трения (коэффициент вязкости)
жидкости.
Коэффициент
вязкости численно равен силе трения,
действующей на слой единичной площади
при градиенте скорости, равном единице.
В системе СГС коэффициент вязкости
имеет размерность [г/(cмc)].
Эта единица называется Пуазом (Пз).
В системе СИ единица
вязкости определяется как коэффициент
вязкости такой жидкости, в которой при
единичном градиенте скорости на площадь
1 м2
действует сила, равная 1 Н, т.е. 1 кг/(мс);
размерность – [Пас].
Внутреннее трение
(вязкость) является причиной того, что
для протекания жидкости через трубку
требуется некоторая разность давлений
жидкости, тем больше, чем больше вязкость
жидкости.
При ламинарном,
установившемся течении жидкости
зависимость между объемом жидкости,
протекающей в единицу времени через
трубку радиуса R,
определяется формулой Пуазейля:
,
(2)
где l
– длина трубки,
Р
– разность давлений на концах трубки.
Пользуясь формулой
(2), следует учесть, что течение жидкости
должно быть ламинарным, т.е. скорость
движения жидкости в направлении,
перпендикулярном оси, во всех точках
должна быть равна нулю. Это значит, что
слои жидкости должны течь хотя и с
разными скоростями, но параллельно друг
другу. Для турбулентного течения формула
Пуазейля непригодна.
Из механики газов
и жидкостей известно, что переход от
ламинарного к турбулентному движению
происходит хотя и не скачком, но при
определенных условиях, связанных со
свойствами газа (жидкости) с размерами
трубы и скоростью движения.
Так, для движения
в цилиндрической трубе переход к
турбулентному движению происходит,
когда безразмерная величина
(3)
становится больше
критического значения порядка 103.
В формуле (3):
– плотность
газа (жидкости);
– средняя
скорость течения;
R
– радиус трубы (капилляра);
– вязкость газа
(жидкости).
Эта величина
называется числом Рейнольдса (Re).
В данной работе
формула Пуазейля используется для
определения радиуса капилляра:
,
где
.
(4)
Отсюда следует,
что для вычисления R
необходимо измерить l
– длину капилляра, V0
– объём жидкости, протекающий в единицу
времени через капилляр и P
– разность давлений на концах капилляра
(V
– объём жидкости, протекающий через
капилляр за время t).
ОПИСАНИЕ ПРИБОРА
Прибор,
используемый в работе, называется
горизонтальным капиллярным вискозиметром.
Он смонтирован на стойке, где имеются
пазы для сменных капилляров и которую
с помощью винтов можно установить строго
по отвесу и уровню. На стойке закреплен
сосуд, по шкале которого определяют
объем жидкости, протекающий через
капилляр за время t.
Рядом с мерной трубкой укреплена линейка
с визирным устройством, по которой можно
определить высоту столба жидкости. Зная
высоту столба жидкости, легко определить
создаваемое ею гидростатическое
давление.
В
процессе опыта высота столба жидкости
меняется, т.е. изменяется и P.
Считая, что P
изменяется равномерно, можно для расчета
использовать среднее значение P,
которое, очевидно, равно
,
(5)
где
h1
и h2
– высота жидкости в сосуде, до опыта и
после него, измеренные по вертикальной
линейке.
При
расчете радиуса капилляра по формуле
(4) следует учитывать зависимость
коэффициентов вязкости от температуры.
Эта зависимость дана в таблице 1.
Таблица
1 – Коэффициент внутреннего трения воды
при разных температурах
|
t, |
, |
t, |
, |
|
10 |
0,001307 |
20 |
0,001004 |
|
15 |
0,001140 |
21 |
0,000980 |
|
16 |
0,001110 |
22 |
0,000957 |
|
17 |
0,001083 |
23 |
0,000936 |
|
18 |
0,001055 |
24 |
0,000915 |
|
19 |
0,001029 |
30 |
0,000903 |
ВЫПОЛНЕНИЕ РАБОТЫ
-
Установить прибор
по уровню и отвесу. -
Измерить длину
капилляра. -
Налить воды в
мерный сосуд. -
Измерив
V,
t,
h1,
h2
3–5 раз вычислить среднее значение
радиус капилляра, погрешность измерений
и число Рейнольдса. -
Экспериментальные
данные занести в таблицу.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.
Из теоретических соображений постройте
качественный график зависимости высоты
в мерном сосуде от времени, при течении
жидкости через капилляр. Если теоретически
не получится, постройте его, проведя
соответствующий эксперимент.
2.
При каких значениях h1
и h2
можно пользоваться формулой (5)?
3. Выведите формулу
Пуазейля.
4. Какое течение
называется ламинарным?
5.
При каких значениях числа Рейнольдса
происходит переход ламинарного течения
в турбулентное?
3
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
svetlanaGB
5 лет назад
Светило науки — 24 ответа — 173 помощи
Из формулы высоты подъёма в капилляре
h=2*б / p*g*r . ( h-высота подъема=0,022м , б ( сигма) — коэффициент поверхностного натяжения (спирта)=22*10^(-3)Н/м, р(ро) — плотность спирта=800кг/куб.м , g -ускорение свободного падения=10м/c^2 , r -радиус капилляра) выразим радиус
r=2*б / p*g*h .
r=2*22*10^(-3) / 800*10*0,022=0,00025м. ( 0,25мм).
Формула нахождения радиуса капилляра.
Вы находитесь на странице вопроса Формула нахождения радиуса капилляра? из категории Физика.
Уровень сложности вопроса рассчитан на учащихся 5 — 9 классов. На странице
можно узнать правильный ответ, сверить его со своим вариантом и обсудить
возможные версии с другими пользователями сайта посредством обратной связи.
Если ответ вызывает сомнения или покажется вам неполным, для проверки
найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте
новый вопрос, используя ключевые слова: введите вопрос в поисковую строку,
нажав кнопку в верхней части страницы.
2017-11-29 19:46
Итак, высота
поднятия жидкости в капиллярных трубках зависит от радиуса
канала в трубке, поверхностного натяжения
и плотности
жидкости. Выведем формулу, связывающую эти величины. Наибольший интерес представляют случаи, когда жидкость хорошо смачивает стенки трубки, т. е. стремится растечься по поверхности стенок. Наш расчет будет относиться именно к этим случаям.
Примем, что поверхность жидкости внутри капиллярной трубки имеет строго сферическую форму, радиус которой равен радиусу капилляра (рис. 432). Согласно формуле (255.1) непосредственно под вогнутым мениском давление жидкости меньше атмосферного давления
на величину
, т. е. равно
. На глубине
, соответствующей уровню жидкости в широком сосуде, к этому давлению прибавляется гидростатическое давление
. В широком сосуде на том же уровне, т. е. непосредственно под плоской свободной поверхностью жидкости, давление равно атмосферному давлению
.
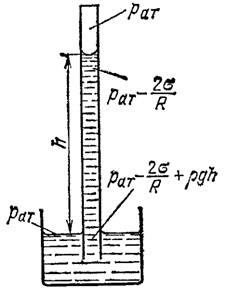
Рис. 432. К выводу формулы высоты поднятия жидкости в капилляре
Так как имеет место равновесие жидкости, то давления на одном и том же уровне равны. Следовательно,
;
отсюда
, (257.1)
т.е. высота поднятия жидкости в капилляре пропорциональна ее поверхностному натяжению и обратно пропорциональна радиусу канала капилляра и плотности жидкости.
Этой формулой можно воспользоваться для определения поверхностного натяжения
. Для этого надо только точно измерить высоту поднятия жидкости
и радиус трубки
. Зная ускорение свободного падения
и плотность жидкости
, найдем по формуле (257.1) значение
. Это один из употребительных способов определения
. Конечно, поверхность трубки и жидкость должны быть очень чисты.
257.1.
Вычислите высоту поднятия воды в капилляре радиуса
и спирта в капилляре диаметра
(см. табл. 11). Плотность спирта равна
.
257.2.
Определите поверхностное натяжение бензина, если в трубке радиуса
высота его поднятия равна
. Плотность бензина равна
.
257.3.
Подвесьте полоску
промокательной бумаги так, чтобы она своим нижним концом была опущена в воду, налитую в блюдце. Дождитесь, пока поднятие воды в промокательной бумаге прекратится (4-5 часов). Измерьте высоту поднятия и приблизительно оцените размеры каналов в волокнах бумаги.
