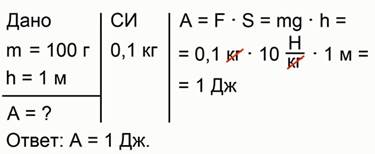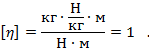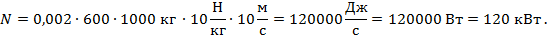Как найти работу через диаметр

Механическая работа – это одна из основных скалярных величин в физике. В рамках стандартной школьной программы она изучается в седьмом классе в разделе механики. Механическая работа – один из способов изменения внутренней энергии тела или субстанции (например, газа или жидкости) наряду с такими формами теплопередачи, как теплопроводность, конвекция и излучение, которые изучаются в разделе тепловых явлений.

Что такое работа в физике – определение и формула

Механическая работа – это количество энергии, которое нужно затратить для того, чтобы тело начало равномерно замедляющееся движение и прошло некоторую дистанцию. 

В физике механической работой называется произведение силы, которая действует на некоторое тело, на расстояние, которое оно проходит под ее воздействием:

A = F * S

В более сложных случаях в формуле появляется и третья величина – косинус угла, под которым друг к другу расположены векторы движения и приложенной силы. Найти ее значение можно по формуле:

A = F * S * cosA

В чем измеряется работа

Физические единицы, в которых выражается механическая работа, – Джоули. 

Существуют разные способы для ее практического измерения, которые зависят от типа произведенного движения. При этом в формулу работы подставляют значение силы в Ньютонах и расстояния в метрах. Угол между векторами измеряют в математических единицах – градусах. 

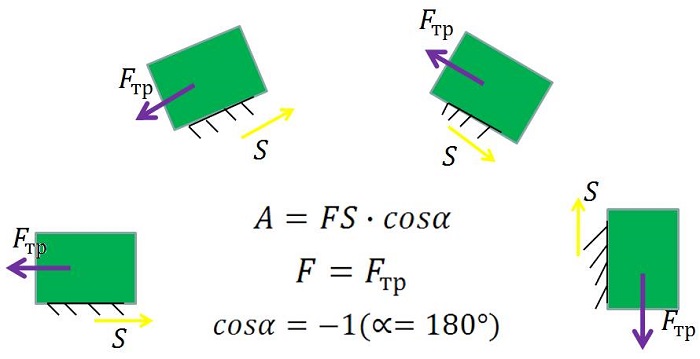
Работа силы трения

При условиях, существующих на Земле, на любое движущееся тело оказывает воздействие сила трения, замедляющая его движение. Чаще всего это трение поверхности, по которой движется объект. Это очевидно из того факта, что при воздействии постоянной силы на тело его скорость окажется переменной. 

Следовательно, должна быть и другая сила, противодействующая ей – и это сила трения. Если система координат выбрана по направлению движения тела, то ее числовое значение будет отрицательным.

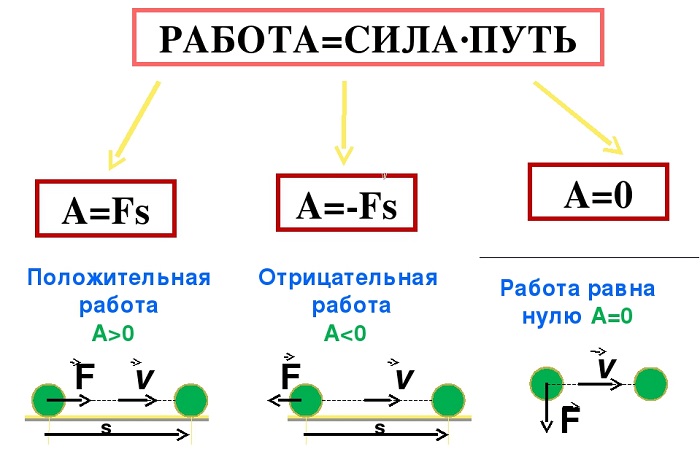
Положительная и отрицательная работа

Числовое значение работы, которую совершает сила, может становиться отрицательным в случае если ее вектор противоположен вектору скорости. 

Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае она будет называться противодействующей. 

Полезная или затраченная работа

У тела, совершающего одно и то же действие, есть два значения работы. Первая из них, полезная, вычисляется по обычной формуле. 

Вторая, затраченная, по своему понятию не имеет общей формулы для вычисления и измеряется практически. Эта разница между совершенной в реальности работой и той, которая должна была быть совершена в теории, равна коэффициенту полезного действия – КПД. Он вычисляется так:

КПД = А полезная / А затраченная,

и выражается в процентах. КПД всегда меньше 100.

Мощность

Среднее количество работы, совершаемой за единицу времени (секунду), характеризует такую величину, как мощность. Формула для ее вычисления выглядит так:

Р = A / t

В качестве работы можно подставить люблю известную формулу для ее вычисления в зависимости от ситуации. Ответ будет выражен в Ваттах.

Однако при равномерном движении можно использовать и другую формулу:

Р = F * v

Подставив вместо обычной скорости мгновенную, можно получить значение мгновенной мощности.

Примеры решения задач

Рассмотрим несколько простых задач на нахождение механической работы.

Задача 1

Какую работу совершает подъемный механизм, поднимающий десятикилограммовый блок на высоту 50 метров.

Решение:

Для того, чтобы поднять тело, необходимо преодолеть действующую на него силу тяжести. То есть F, с которой поднимают блок, равна той, с которой он притягивается к земле. Так как последняя равна m * g, то для нахождения конечного результата понадобится только одна измененная версия стандартной формулы, упомянутой выше: A = S * m * g.

При помощи простой математики найдем числовой ответ:

A = 50 м * 10 кг * 10 Н/кг;

A = 5000 Дж.

Ответ: 5000 Дж.

Впрочем, не всегда речь идет о силе тяжести.

Задача 2

Какая работа совершается силой упругости, когда пружина с жесткостью 10 Н/м, сжатая на 20 см, возвращается в исходное состояние? Система замкнута, нет никаких внешних сил, воздействующих на пружину.

Решение:

Для начала нужно найти саму F упругости, которая совершает работу. Ее формула – F = x * |k|, где x – это длина, на которую сжимается или растягивается пружина, а k – коэффициент ее жесткости. Перемещение пружины равно ее деформации, и следовательно, конечная формула в этом случае будет выглядеть так: A = S * x * k = x * x * k = x^2 * k.

Далее при помощи элементарных вычислений рассчитаем ответ:

A = (0,2 м)^2 * 10 Н/м = 0,04 * 10 = 0,4 Дж.

Ответ: 0,4 Дж.

Но во всех задачах по данной теме траектория движения тела прямая.

Задача 3

Рассчитайте, какова сила, действующая на колесо, если на то, чтобы совершить полный оборот, ему требуется 10 кДж. Диаметр диска равен 40 см, а толщина шины – 10 см.

Решение:

В этом случае нам нужно найти не А, а F, но сделать это можно при помощи все той же формулы. Возьмем точку на поверхности колеса. Предположим, что при вращательном движении ее вектор будет противоположен вектору приложения силы, а значит косинусом в формуле вновь можно пренебречь. Таким образом, за один оборот колеса точка пройдет расстояние, равное длине окружности, которую можно вычислить как 2πr или πd. Диаметр окружности можно найти из предоставленных данных: он равен сумме диаметра диска и удвоенной толщины шины, то есть 40 см + 2 * 10 см = 40 см + 20 см = 60 см = 0,6 м.

Теперь, когда мы можем вычислить расстояние, у нас есть все данные для того, чтобы приступить к нахождению силы.

Формула работы для этого случая будет такой: A = F * π * d, то силу, соответственно, можно будет выразить как F = A / (π * d).

В таком случае:

F = 10 кДж / (3,14 * 0,6 м) = 10000 Дж / 1,884 м = ~ 5308 Н.

Ответ: 5308 Н.

В завершение решим самый сложный вариант задачи, включающий в себя все, о чем говорилось выше.

Задача 4

Автомобиль Фольксваген весом 2500 кг заезжает на гору. Какова должна быть его минимальная скорость, чтобы удержаться на горе, если сила тяги равна 10 кН, время работы двигателя – 10 с, КПД – 30%, а угол наклона горы – 60 градусов. Трением и прочими силами пренебречь.

Решение:

На первый взгляд задача может показаться сложной, но для ее решения используются только простые известные формулы. 

Запишем условие в более наглядном виде.

Дано:

m = 2500 кг;

F = 10000 H;

t = 10 с;

КПД = 30%;

угол A = 150⁰ (60+90, т. к. сила тяжести приложена под углом 90 к горизонтали);

V – ?

Выведение формулы:

Шаг 1. По условию A1 (силы тяжести) = А2 (тяги).

A1 = mg;

A2 = P * t / КПД.

То есть mg = P * t / КПД.

Шаг 2. P = F * V * cosA.

Шаг 3. Общая формула: mg = F * V * cosA * t / КПД.

V = (m * g * КПД) / (F * t * cosA).

Числовое решение:

V = (2500 кг * 10 Н/кг * 30%) / (10000 H * 10 с * cos150);

V = (2500 кг * 10 Н/кг * 0,3) / (10000 H * 10 с * cos60);

V = 7500 / 50000;

V = 0,15 м/с.

Ответ: 0,15 м/с.

«Механическая работа. Механическая мощность»

Код ОГЭ 1.16. Механическая работа. Формула для вычисления работы силы. Механическая мощность.

Работа силы – физическая величина, характеризующая результат действия силы.

Механическая работа А постоянной силы  равна произведению модуля вектора силы на модуль вектора перемещения  и на косинус угла а между вектором силы и вектором перемещения: А = Fs cos а.

Единица измерения работы в СИ – джоуль: [А] = Дж = Н • м.
Механическая работа равна 1 Дж, если под действием силы в 1 Н тело перемещается на 1 м в направлении действия этой силы.

Анализ формулы для расчёта работы показывает, что механическая работа не совершается если:

• сила действует, а тело не перемещается;
• тело перемещается, а сила равна нулю;
• угол между векторами силы и перемещения равен 90° (cos a = 0).

Внимание! При движении тела по окружности под действием постоянной силы, направленной к центру окружности, работа равна нулю, так как в любой момент времени вектор силы перпендикулярен вектору мгновенной скорости.

Работа – скалярная величина, она может быть как положительной, так и отрицательной.

1. Если угол между векторами силы и перемещения 0° ≤ а < 90°, то работа положительна.
2. Если угол между векторами силы и перемещения 90° < a ≤ 180°, то работа отрицательна.

Работа обладает свойством аддитивности: если на тело действует несколько сил, то полная работа (работа всех сил) равна алгебраической сумме работ, совершаемых отдельными силами, что соответствует работе равнодействующей силы.

Примеры расчёта работы отдельных сил:

Работа силы тяжести: не зависит от формы траектории и определяется только начальным и конечным положением тела: A = mg(h₁ – h₂). По замкнутой траектории работа силы тяжести равна нулю.
Внимание! При движении вниз работа силы тяжести положительна, при движении вверх работа силы тяжести отрицательна.

Работа силы трения скольжения: всегда отрицательна и зависит от формы траектории. Если сила трения не изменяется по модулю, то её работа А = –F_тр l , где l – путь, пройденный телом (длина траектории). Очевидно, что чем больший путь проходит тело, тем большую по модулю работу совершает сила трения. Работа силы трения по замкнутой траектории не равна нулю!

Мощность N – физическая величина, характеризующая быстроту (скорость) совершения работы и равная отношению работы к промежутку времени, за который эта работа совершена: .

Мощность показывает, какая работа совершается за 1 с.
Единица измерения мощности в СИ – ватт: [ N ] = Дж/с = Вт.
Мощность равна одному ватту, если за 1 с совершается работа 1 Дж.

Может пригодиться! 1 л. с. (лошадиная сила) ~ 735 Вт.
Внимание! Для случая равномерного движения (равнодействующая сила равна нулю) при расчете мощности отдельных сил, действующих на тело, получим  .

Для равноускоренного движения (F = const)   где ʋ_ср– средняя скорость движения за расчётный промежуток времени.

Конспект урока «Механическая работа. Механическая мощность».

Следующая тема: «Кинетическая и потенциальная  энергия» (код ОГЭ 1.17)

Содержание:

1. Работа и мощность силы
2. Работа силы
3. Элементарная работа
4. Аналитическое выражение элементарной работы силы. Работа силы на конечном перемещении
5. Работы сил тяжести и упругости
6. Работа силы, приложенная к вращающемуся телу
7. Мощность силы
8. Порядок решения задач на определение работы и мощности силы
9. Примеры решения задач на тему: работа и мощность силы

Работа постоянной силы равна произведению модулей силы и перемещения точки приложения силы и косинуса угла между ними. Мощность – отношение работы к интервалу времени, за который эта работа совершена.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Работа и мощность силы

Мощностью называется величина, определяющая работу, совершаемую силой в единицу времени. Если работа совершается равномерно, то мощность N=A/t, где t — время, в течение которого произведена работа.

Работа силы

Работа силы на любом перемещении является одной из основных характеристик, которая оценивает действие силы на этом перемещении.

Работа постоянной силы (рис.9.1) на некотором прямолинейном перемещении точки приложения силы определяется по выражению:

Если угол острый, то работа — положительная, .

При работа равна:

Если угол — тупой, то работа отрицательная, .

При работа равна:

Если угол , то есть сила направлена перпендикулярно перемещению, то работа равна нулю: .

Знак работы имеет такой смысл: работа — положительная, когда сила ускоряет движение; работа — отрицательная, когда сила тормозит движение.

Выражение для вычисления работы можно представить как скалярное произведение векторов:

Работа постоянной по модулю и направлению силы при прямолинейном перемещении определяется скалярным произведением вектора силы на вектор перемещения точки ее приложения.

Элементарная работа

В общем случае, когда материальная точка движется по криволинейной траектории под действием переменной силы вводится понятие элементарной работы.

Элементарная работа силы на элементарном перемещении  (рис.9.2) определяется следующим образом:

где  — проекция силы на тангенциальную ось, которая направлена в сторону перемещения точки; — бесконечно малое перемещение точки.

Поскольку

то

Аналитическое выражение элементарной работы силы. Работа силы на конечном перемещении

Элементарную работу силы можно представить в виде скалярного произведения векторов и  (рис.9.3):

где  — вектор элементарного перемещения точки .

Выражение элементарной работы переменной силы через проекции силы на оси декартовых координат имеет вид:

где  — проекции силы на координатные оси, а — проекции вектора элементарного перемещения на координатные оси.

Работа силы на любом конечном перемещении определяется интегралом:

или

Работы сил тяжести и упругости

Работа силы тяжести равна взятому со знаком плюс или минус произведению силы тяжести на вертикальное перемещение точки ее приложения

где  — сила тяжести;

 — вертикальное перемещение точки приложения силы.

Из этой формулы вытекает, что работа силы тяжести не зависит от формы траектории между начальной и конечной точками движения, а зависит только от расстояния между горизонтальными плоскостями, которые проходят через исходное и конечное положение точки.

Если начальная точка расположена выше конечной, то работа силы тяжести положительная, в противном случае – отрицательная.

Работа силы упругости равна половине произведения коэффициента жесткости пружины на разность квадратов начального и конечного удлинений (или сжатий) пружины

Работа силы упругости отрицательна в том случае, когда деформация увеличивается, то есть когда . Это соответствует перемещению конца пружины от положения равновесия. Если , работа будет положительная. В этом случае конец пружины перемещается к положению равновесия.

Работа силы, приложенная к вращающемуся телу

Элементарная работа силы, приложенной к любой точке тела, которое вращается вокруг неподвижной оси, например , равна произведению момента силы относительно оси вращения на дифференциал угла поворота:

Для того, чтобы определить работу силы, которая действует на тело при его повороте на угол от к , необходимо проинтегрировать уравнение в этих пределах, выразив момент силы как функцию угла поворота:

В отдельном случае, когда момент силы является постоянным, то есть , работа равна произведению момента силы на угол поворота тела:

Единицей измерения работы в системе СИ является Джоуль (1), а в системе 

Мощность силы

Мощностью называется величина, определяющая работу, которую выполняет сила за единицу времени:

Это выражение справедливо, если работа выполняется равномерно.

В общем случае

Поскольку , то:

Таким образом, мощность равна произведению величины касательной составляющей силы на скорость движения.

При вращательном движении тела:

Тогда

Мощность выражается произведением вращательного момента на угловую скорость.

Единицей измерения мощности в системе СИ является Ватт в системе

Порядок решения задач на определение работы и мощности силы

При определении работы необходимо различать следующие случаи:

Прямолинейное движение под действием постоянной силы; в этом случае применяются формулы (9.2) и (9.3).

Прямолинейное движение под действием силы, которая является функцией расстояния; в этом случае используют формулу (9.5), которая, если направить ось по траектории точки, принимает вид:

Криволинейное движение под действием постоянной по модулю и направлению силы; в этом случае можно использовать формулу (9.4) или (9.5).

Криволинейное движение под действием силы, что определяется функцией координат точки приложения силы; в этом случае определение работы сводится к вычислению криволинейного интеграла по формуле (9.5).

Вращательное движение твердого тела под действием постоянного момента или момента, который является функцией угла поворота тела; в этом случае для вычисления работы используются формулы (9.8) или (9.9).

Для вычисления мощности в зависимости от характера движения пользуются формулой (9.11), если имеет место прямолинейное или криволинейное движение точки приложения силы, или формуле (9.12) – в случае вращательного движения твердого тела.

Во всех этих случаях перед вычислением работы или мощности необходимо изобразить все внешние силы, которые приложены к телу или рассматриваемой механической системе.

Примеры решения задач на тему: работа и мощность силы

Задача № 1

Определить наименьшую работу , которую необходимо выполнить, чтобы поднять на высоту груз передвигая его по наклонной плоскости, которая составляет с горизонтом угол ; коэффициент трения

Решение: Изобразим груз в произвольном положении на наклонной плоскости и покажем все действующие на него силы (рис.9.4): силу тяжести , силу трения и нормальную реакцию .

Работа, расходуемая на подъем груза на высоту , равна сумме работ силы трения вдоль длины  и силы тяжести на перемещении точки ее приложения. Нормальная реакция работы не выполняет, поскольку она перпендикулярна перемещению.

Вычислим работу силы трения:

Поскольку и то

Работа силы тяжести в нашем случае отрицательная, поскольку груз движется вверх, и равна:

Полная работа, затраченная на подъем груза, равна 

Ответ: 

Задача № 2

Тело (рис.9.5) удерживается в равновесии на гладкой наклонной поверхности, расположенной под углом к горизонту, с помощью пружины. Вследствие полученного толчка тело переместилось вниз по наклонной поверхности на расстояние .

Определить сумму работ всех сил, приложенных к телу на этом перемещении, если сила тяжести тела угол жесткость пружины

Решение. К телу приложены следующие силы: сила тяжести , нормальная реакция поверхности и сила упругости растянутой пружины (рис.9.5).

Ось направим параллельно наклонной поверхности, а начало отсчета совместим с концом недеформированной пружины.

Тогда тело под действием толчка начнет двигаться из положения , которое характеризуется координатой , что равно:

где  — статическое отклонение пружины.

Вычислим сумму работ сил , ,  на перемещении 

где  — работа силы тяжести на перепаде высот между точками  и ,

 — работа силы упругости пружины,

 — работа нормальной реакции.

Работа силы тяжести равна:

Работа силы упругости пружины определяется по формуле:

где 

Итак. 

Окончательно

Вычислим  — статическое отклонение пружины, которое имеет место в положении равновесия тела (точка ), когда пружина растянута постоянной силой тяжести. Для этого положения запишем в проекции на ось уравнение равновесия для сил тяжести и силы упругости пружины , которые действуют на тело:

Поскольку

Тогда

Окончательно,

Работа нормальной реакции равна нулю, так как эта сила перпендикулярна перемещению тела, то есть

Итак,

Ответ: 

Задача № 3

Материальная точка массой движется прямолинейно по горизонтальной плоскости по закону под действием силы (рис.9.6).

Определить работу этой силы при перемещении точки ее приложения из исходного положения ( ) в положение, где

Решение Сила, действующая на материальную точку , меняется с течением времени. Следовательно, для определения работы этой силы необходимо воспользоваться уравнением (9.4):

где — проекция силы на элементарное перемещение точки приложения силы.

В нашем случае заданная сила совпадает по направлению с перемещением точки , а работу необходимо высчитывать на перемещении от к .

Таким образом, уравнение (1) примет вид:

Найдем зависимость между силой и перемещением , исключив параметр , который входит в выражения для значения силы и перемещения:

Подставив новое выражение для силы в уравнение (2), получим:

Вычислим этот интеграл:

Ответ: 

Задача № 4

Шлифовальный камень радиусом делает об/мин. Потребляемая мощность равна коэффициент трения шлифовального камня равен

Определить, с какой силой прижимает камень деталь, которая шлифуется?

Решение. Деталь (рис.9.7) прижимается к шлифовальному камню с силой . Возникающая при этом сила трения развивает мощность , равную потребленной мощности 1,5 , то есть

где  — скорость точки на ободе камня, к которому приложена сила .

Сила трения между камнем и деталью будет составлять:

угловая скорость камня будет:

а скорость точки на ободе камня равна:

Тогда

Откуда: 

Ответ: 

Задача № 5

Для измерения мощности двигателя на его шкив надета лента с деревянными колодками (рис.9.8).

Правая часть ленты удерживается упругими весами силой , а левая ее часть  натягивается грузом .

Определить мощность двигателя , если его вал при равномерном вращении делает об/мин, при этом пружинные весы показывают натяжение ленты вес груза диаметр шкива

Примечание: разность натяжений частей  и ленты равна силе, которая тормозит шкив.

Решение. Поскольку шкив вращается равномерно, то сила трения, которая возникает между шкивом и деревянными колодками, вместе с силой уравновешивают силу (рис.9.8), следовательно

Мощность силы трения равна мощности двигателя при условии, что шкив вращается равномерно:

 — скорость точки обода шкива, на который действует сила трения и которая равна:

Ответ: 

Задача № 6

Груз весом , который опускается по наклонной плоскости, приводит к вращению барабана весом , на который намотана нить (рис.9.9). Принять за механическую систему совокупность тел  и , которые соединены между собой невесомой нитью, которая не растягивается.

Определить сумму работ всех сил, приложенных к этой системе за один оборот барабана , если — радиус барабана, — коэффициент трения скольжения груза по наклонной плоскости, которая составляет угол с горизонтом.

Решение. Данная механическая система является неизменной. На нее наложены следующие связи: наклонная плоскость и шарнирная опора барабана у точке .

Реакция наклонной плоскости состоит из нормальной реакции и силы трения , которая направлена в сторону, противоположную перемещению груза .

Реакция () шарнира лежит в плоскости, перпендикулярной оси шарнира, проходит через ось шарнира и может занимать в этой плоскости любое положение.

Поскольку данная система является неизменной, то работа всех сил, которые приложены к ней, определяется только работой внешних сил: силы тяжести  груза ; нормальной реакции наклонной плоскости; силы трения груза по наклонной плоскости; силы тяжести барабана ; реакции шарнира .

Вычислим элементарную работу внешних сил системы

где  — элементарные работы внешних сил, приложенных, соответственно, к телам  и .

Тело движется поступательно. Элементарная работа внешних сил, приложенных к этому телу, равна

где  — элементарные работы силы тяжести , нормальной реакции и силы трения .

Элементарная работа реакции равна нулю, поскольку  перпендикулярна  перемещению тела.

Элементарная работа силы тяжести равна

Элементарная работа силы трения  определяется из выражения:

Поскольку

то

Итак,

Тело вращается вокруг неподвижной оси, которая проходит через точку перпендикулярно плоскости рисунка. Элементарная работа внешних сил, приложенных к телу , определится из выражения:

где  — главный момент внешних сил ( и ) относительно оси вращения;

 — элементарное угловое перемещение тела относительно оси вращения.

Поскольку линии действия сил  и пересекают ось вращения, то и 

Подставляя (2) и (3) в (1), получим

Перемещение груза связано с углом поворота барабана равенством , тогда последнее уравнение дает выражение элементарной работе всех сил, приложенных к данной механической системе, на элементарном перемещении барабана :

Для определения работы сил за один оборот барабана возьмем определенный интеграл в пределах от к :

Ответ: 

Задача № 7

Колесо радиусом катится без скольжения по прямолинейной горизонтальной рейке (рис.9.10) под действием устойчивой силы , которая приложена в центре тяжести колеса и параллельна рельсу, и постоянного вращательного момента .

Определить сумму работ всех внешних сил, если ось колеса переместилась на расстояние . Трением качения пренебречь.

Решение. К колесу приложены внешние силы и момент: — сила тяжести колеса, — движущая сила, — вращательный момент, — нормальная реакция рейки, — сила трения.

Работы реакции и силы трения равны нулю, поскольку эти силы приложены в мгновенном центре вращения колеса , элементарное перемещение которого равно нулю. Работа силы тяжести колеса  тоже равна нулю, в связи с тем, что элементарное перемещение  точки перпендикулярно линии действия силы тяжести .

Следовательно необходимо вычислить только работу движущей силы и момента :

где 

Согласно условию задачи, колесо катится без скольжения, поэтому

Соответственно, уравнение (1) запишется следующим образом:

Для определения суммы работ всех сил на перемещении оси колеса на расстояние проинтегрируем последнее уравнение в пределах от к :

Ответ: 

Услуги по теоретической механике:

1. Заказать теоретическую механику
2. Помощь по теоретической механике
3. Заказать контрольную работу по теоретической механике

Учебные лекции:

1. Статика
2. Система сходящихся сил
3. Момент силы
4. Пара сил
5. Произвольная система сил
6. Плоская произвольная система сил
7. Трение
8. Расчет ферм
9. Расчет усилий в стержнях фермы
10. Пространственная система сил
11. Произвольная пространственная система сил
12. Плоская система сходящихся сил
13. Пространственная система сходящихся сил
14. Равновесие тела под действием пространственной системы сил
15. Естественный способ задания движения точки
16. Центр параллельных сил
17. Параллельные силы
18. Система произвольно расположенных сил
19. Сосредоточенные силы и распределенные нагрузки
20. Кинематика
21. Кинематика твердого тела
22. Движения твердого тела
23. Динамика материальной точки
24. Динамика механической системы
25. Динамика плоского движения твердого тела
26. Динамика относительного движения материальной точки
27. Динамика твердого тела
28. Кинематика простейших движений твердого тела
29. Общее уравнение динамики
30. Обратная задача динамики
31. Поступательное и вращательное движение твердого тела
32. Плоскопараллельное (плоское) движение твёрдого тела
33. Сферическое движение твёрдого тела
34. Движение свободного твердого тела
35. Сложное движение твердого тела
36. Сложное движение точки
37. Плоское движение тела
38. Статика твердого тела
39. Равновесие составной конструкции
40. Равновесие с учетом сил трения
41. Центр масс
42. Колебания материальной точки
43. Относительное движение материальной точки
44. Статические инварианты
45. Дифференциальные уравнения движения точки под действием центральной силы и их анализ
46. Динамика системы материальных точек
47. Общие теоремы динамики
48. Теорема об изменении кинетической энергии
49. Теорема о конечном перемещении плоской фигуры
50. Потенциальное силовое поле
51. Метод кинетостатики
52. Вращения твердого тела вокруг неподвижной точки

Задача №1

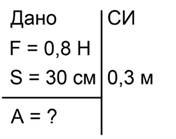
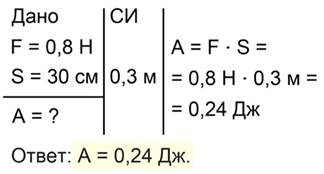
К брус­ку при­кре­пи­ли ди­на­мо­метр и пе­ре­ме­сти­ли бру­сок на рас­сто­я­ние 30 см. По­ка­за­ния ди­на­мо­мет­ра равны 0,8 Н. Найти ра­бо­ту силы тяги по пе­ре­ме­ще­нию брус­ка (рис. 1).

Рис 1. К за­да­че №1

Пре­жде всего за­пи­шем крат­кое усло­вие за­да­чи и по­за­бо­тим­ся, чтобы все дан­ные были вы­ра­же­ны в си­сте­ме СИ (рис. 2).

Рис 2. Крат­кое усло­вие за­да­чи №1

Для вы­чис­ле­ния ра­бо­ты вос­поль­зу­ем­ся фор­му­лой

Пол­ное ре­ше­ние за­да­чи вы­гля­дит так (рис. 3).

Рис 3. Пол­ное ре­ше­ние за­да­чи №1

Задача №2

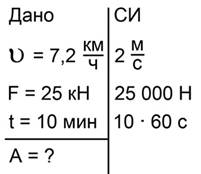
Трак­тор пе­ре­ме­ща­ет плат­фор­му со ско­ро­стью 7,2 км/ч, раз­ви­вая тя­го­вое уси­лие в 25 кН. Какую ра­бо­ту со­вер­шит трак­тор за 10 мин (рис. 4)?

Рис 4. К за­да­че №2

За­пи­шем крат­кое усло­вие за­да­чи и пе­ре­ве­дем все еди­ни­цы из­ме­ре­ния в си­сте­му СИ (рис. 5).

Рис 5. Крат­кое усло­вие за­да­чи №2

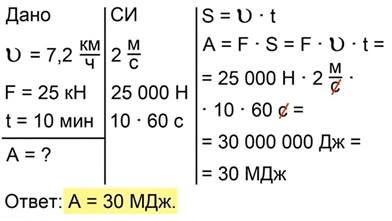
Для вы­чис­ле­ния ра­бо­ты необ­хо­ди­мо знать рас­сто­я­ние, прой­ден­ное телом. В усло­вии за­да­чи дана ско­рость дви­же­ния трак­то­ра и время дви­же­ния, по­это­му вос­поль­зу­ем­ся фор­му­лой

ко­то­рую под­ста­вим в вы­ра­же­ние для ра­бо­ты  и по­лу­чим ра­бо­чую фор­му­лу

Под­ста­нов­ка дан­ных из усло­вия за­да­чи дает

Рис 6. Пол­ное ре­ше­ние за­да­чи №2

Задача №3

Най­дем ра­бо­ту силы тя­же­сти при па­де­нии гру­зи­ка.

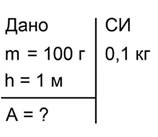
Для ре­ше­ния за­да­чи нам по­тре­бу­ет­ся ли­ней­ка и сам гру­зик. Из­ме­рим вы­со­ту, с ко­то­рой будет па­дать гру­зик. По­лу­ча­ем 1 м. Масса гру­зи­ка на­пи­са­на на нем самом и равна 100 г. Под­ни­мем гру­зик на ука­зан­ную вы­со­ту и от­пу­стим его.

Крат­кое усло­вие за­да­чи будет вы­гля­деть так (рис. 7):

Рис 7. Крат­кое усло­вие за­да­чи №3

Для на­хож­де­ния ра­бо­ты вы­ра­зим силу тя­же­сти через массу тела , и учтем, что рас­сто­я­ние, прой­ден­ное телом, равно вы­со­те, с ко­то­рой оно упало: .

Тогда

Под­ста­нов­ка чисел дает

Рис 8. Пол­ное ре­ше­ние за­да­чи №3

Те­перь у нас есть пред­став­ле­ние о том, на­сколь­ко ве­ли­ка ра­бо­та в 1 джо­уль. Такая ра­бо­та со­вер­ша­ет­ся при па­де­нии гру­зи­ка мас­сой 100 г со стола вы­со­той 1 м.

Пе­ре­хо­дим к ре­ше­нию более слож­ных задач.

Задача №4

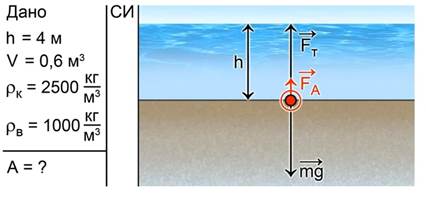
Со дна реки глу­би­ной 4 м под­ни­ма­ют ка­мень объ­е­мом 0,6 м³ на по­верх­ность. Плот­ность камня 2500 кг/м³, плот­ность воды 1000 кг/м³. Найти ра­бо­ту по подъ­ему камня.

Для ре­ше­ния за­да­чи необ­хо­ди­мо не толь­ко за­пи­сать крат­кое усло­вие за­да­чи, но и сде­лать схе­ма­ти­че­ский ри­су­нок и по­ка­зать силы, дей­ству­ю­щие на ка­мень. Это сила тяги F_т (ра­бо­ту имен­но этой силы мы будем на­хо­дить), сила тя­же­сти mg и сила Ар­хи­ме­да F_a. Кроме того, по­ка­жем вы­со­ту, на ко­то­рую сила тяги пе­ре­ме­ща­ет ка­мень (рис. 9).

Рис 9. К ре­ше­нию за­да­чи №4

Как видно из ри­сун­ка, ис­ко­мая ра­бо­та равна .

Для на­хож­де­ния силы тяги вос­поль­зу­ем­ся усло­ви­ем рав­но­ве­сия тела: если оно непо­движ­но или дви­жет­ся с по­сто­ян­ной ско­ро­стью, то рав­но­дей­ству­ю­щая всех сил, при­ло­жен­ных к нему, равна нулю.

, от­ку­да .

Массу камня вы­ра­зим через плот­ность камня и его объем, а силу Ар­хи­ме­да – через плот­ность воды и объем по­гру­жен­ной части камня (в этом за­да­че он равен объ­е­му всего камня). Объем камня и уско­ре­ние вы­но­сим за скоб­ки.

Оста­ет­ся под­ста­вить силу тяги в фор­му­лу для вы­чис­ле­ния ра­бо­ты

По­сколь­ку ра­бо­чая фор­му­ла по­лу­чи­лась более слож­ной, еди­ни­цы из­ме­ре­ния ре­зуль­та­та опре­де­лим от­дель­но от рас­че­та его чис­лен­но­го зна­че­ния.

Рис 10. Пол­ное ре­ше­ние за­да­чи №4

Задача №5

Пор­шень дви­га­те­ля пе­ре­ме­ща­ет­ся на 20 см под дав­ле­ни­ем 800 кПа. Опре­де­ли­те ра­бо­ту, со­вер­ша­е­мую дви­га­те­лем за один ход порш­ня, если пло­щадь порш­ня 150 см² (рис. 11).

Рис 11. К за­да­че №5

За­пи­шем крат­кое усло­вие и вы­ра­зим все еди­ни­цы в си­сте­ме СИ (рис. 12).

Рис. 12. Крат­кое усло­вие за­да­чи №5

В дан­ной за­да­че ра­бо­ту вы­пол­ня­ет сила дав­ле­ния газа в ци­лин­дре дви­га­те­ля. Для на­хож­де­ния этой силы необ­хо­ди­мо дав­ле­ние в ци­лин­дре умно­жить на пло­щадь порш­ня. Рас­сто­я­ние, прой­ден­ное порш­нем, мы обо­зна­чи­ли бук­вой l.

Еди­ни­цы из­ме­ре­ния ре­зуль­та­та:

Чис­лен­ное зна­че­ние ре­зуль­та­та:

Рис 13. Пол­ное ре­ше­ние за­да­чи №5

Задача №6

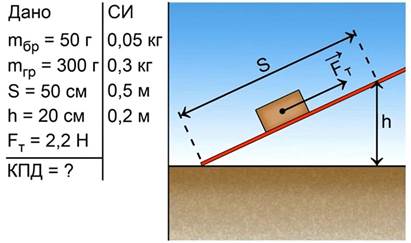
Найти КПД (ко­эф­фи­ци­ент по­лез­но­го дей­ствия) на­клон­ной плос­ко­сти (экс­пе­ри­мен­таль­ная) (рис. 14).

Рис. 14. Груз под­ни­ма­ют вверх по на­клон­ной плос­ко­сти

Под­ни­мая груз по на­клон­ной плос­ко­сти с по­мо­щью ди­на­мо­мет­ра, из­ме­рим силу, ко­то­рая для этого тре­бу­ет­ся. Она ока­зы­ва­ет­ся рав­ной 2,2 Н. Рас­сто­я­ние, прой­ден­ное гру­зом вдоль плос­ко­сти, из­ме­ря­ем ру­лет­кой. Оно со­ста­ви­ло 0,5 м. При этом груз под­нял­ся над сто­лом на вы­со­ту 20 см. Кроме того, из­вест­ны масса брус­ка, рав­ная 50 г, и общая масса трех под­ни­ма­е­мых гру­зов – 300 г.

По­лу­чен­ные опыт­ные дан­ные за­не­сем в крат­кое усло­вие за­да­чи, вы­ра­зим все ве­ли­чи­ны в еди­ни­цах си­сте­мы СИ и сде­ла­ем схе­ма­ти­че­ский ри­су­нок из­ме­ри­тель­ной уста­нов­ки (рис. 15).

Рис 15. Крат­кое усло­вие за­да­чи №6

Ко­эф­фи­ци­ен­том по­лез­но­го дей­ствия ме­ха­низ­ма на­зы­ва­ет­ся фи­зи­че­ская ве­ли­чи­на, рав­ная от­но­ше­нию по­лез­ной ра­бо­ты, со­вер­шен­ной ме­ха­низ­мом, к ра­бо­те, за­тра­чен­ной для при­ве­де­ния его в дей­ствие.

КПД также обо­зна­ча­ют гре­че­ской бук­вой η (эта) и часто вы­ра­жа­ют в про­цен­тах.

В нашем слу­чае ме­ха­низ­мом яв­ля­ет­ся на­клон­ная плос­кость.

По­лез­ная ра­бо­та – эта ра­бо­та, ко­то­рую нужно со­вер­шить, чтобы под­нять тело на вы­со­ту h.

За­тра­чен­ная ра­бо­та со­вер­ша­ет­ся силой тяги, то есть силой упру­го­сти пру­жи­ны ди­на­мо­мет­ра.

Тогда КПД равен

Опре­де­ля­ем еди­ни­цы из­ме­ре­ния КПД

Такой ре­зуль­тат озна­ча­ет, что КПД яв­ля­ет­ся без­раз­мер­ной ве­ли­чи­ной (про­сто число без еди­ниц из­ме­ре­ния).

Его чис­ло­вое зна­че­ние

Об­ра­ти­те вни­ма­ние, что ко­эф­фи­ци­ент по­лез­но­го дей­ствия не может быть боль­ше еди­ни­цы, по­сколь­ку по­лез­ная ра­бо­та все­гда мень­ше за­тра­чен­ной. Если у вас по­лу­чи­лось на­о­бо­рот, зна­чит, либо при из­ме­ре­ни­ях, либо в ходе вы­чис­ле­ний до­пу­ще­на ошиб­ка.

Рис 16. Пол­ное ре­ше­ние за­да­чи №6

Задача №7

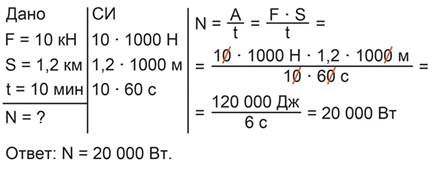
Трак­тор рав­но­мер­но тянет плуг, при­ла­гая силу в 10 кН. За 10 мин он про­хо­дит путь 1,2 км. Опре­де­лить мощ­ность, раз­ви­ва­е­мую трак­то­ром (рис. 17).

Рис 17. К усло­вию за­да­чи №7

За­пись крат­ко­го усло­вия и пе­ре­вод ве­ли­чин в си­сте­му СИ будет вы­гля­деть так (рис. 18):

Рис 18. Крат­кое усло­вие за­да­чи №7

Для на­хож­де­ния мощ­но­сти нужно ра­бо­ту, вы­пол­нен­ную трак­то­ром, раз­де­лить на время ее вы­пол­не­ния. Ра­бо­та вы­чис­ля­ет­ся как про­из­ве­де­ние силы тяги трак­то­ра на прой­ден­ное трак­то­ром рас­сто­я­ние. Таким об­ра­зом, по­лу­ча­ем:

Рис 19. Пол­ное ре­ше­ние за­да­чи №7

Задача №8

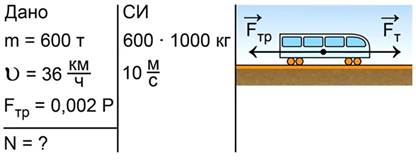
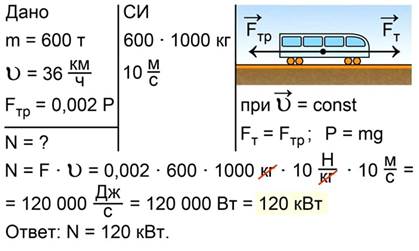
Поезд мас­сой 600 тонн рав­но­мер­но дви­жет­ся со ско­ро­стью 36 км/ч. Опре­де­лить раз­ви­ва­е­мую теп­ло­во­зом мощ­ность, если сила тре­ния со­став­ля­ет 0,002 веса по­ез­да.

Рис. 20. К усло­вию за­да­чи №8

За­пи­шем крат­кое усло­вие за­да­чи, вы­ра­зим ве­ли­чи­ны в еди­ни­цах си­сте­мы СИ, сде­ла­ем ри­су­нок, на ко­то­ром по­ка­жем силу тяги теп­ло­во­за и силу тре­ния (рис. 21).

Рис. 21. Крат­кое усло­вие за­да­чи №8

По­сколь­ку по усло­вию за­да­чи ско­рость по­ез­да не из­ме­ня­ет­ся и равна 36 км/ч, сила тяги равна силе тре­ния  Вес в слу­чае дви­же­ния с по­сто­ян­ной ско­ро­стью равен силе тя­же­сти  Тогда сила тяги равна

Для вы­чис­ле­ния мощ­но­сти вос­поль­зу­ем­ся фор­му­лой  от­ку­да

Под­ста­нов­ка дан­ных из усло­вия дает

Рис. 22. Пол­ное ре­ше­ние за­да­чи №8

Подборка задач «Механическая работа. Мощность» включает в себя задания разлиного уровня сложности, решение которых даст возможность учащимся закрепить теоретические  и практические навыки решения физических задач.