Данный материал представляет собой систему
задач по теме “Движение”.
Цель: помочь учащимся более полно овладеть
технологиями решения задач по данной теме.
Задачи на движение по воде.
Очень часто человеку приходится совершать
движения по воде: реке, озеру, морю.
Сначала он это делал сам, потом появились плоты,
лодки, парусные корабли. С развитием техники
пароходы, теплоходы, атомоходы пришли на помощь
человеку. И всегда его интересовали длина пути и
время, затраченное на его преодоление.
Представим себе, что на улице весна. Солнце
растопило снег. Появились лужицы и побежали
ручьи. Сделаем два бумажных кораблика и пустим
один из них в лужу, а второй — в ручей. Что же
произойдет с каждым из корабликов?
В луже кораблик будет стоять на месте, а в
ручейке — поплывет, так как вода в нем «бежит»
к более низкому месту и несет его с собой. То же
самое будет происходить с плотом или лодкой.
В озере они будут стоять на месте, а в реке –
плыть.
Рассмотрим первый вариант: лужа и озеро. Вода в
них не движется и называется стоячей.
Кораблик поплывет по луже только в том случае,
если мы его подтолкнем или если подует ветер. А
лодка начнет двигаться в озере при помощи весел
или если она оснащена мотором, то есть за счет
своей скорости. Такое движение называют движением
в стоячей воде.
Отличается ли оно от движения по дороге? Ответ:
нет. А это значит, что мы с вами знаем как
действовать в этом случае.
Задача 1. Скорость катера по озеру равна 16 км/ч.
Какой путь пройдет катер за 3 часа?
Ответ: 48 км.
Следует запомнить, что скорость катера в
стоячей воде называют собственной скоростью.
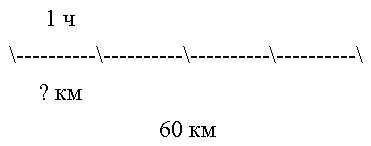
Задача 2. Моторная лодка за 4 часа проплыла по
озеру 60 км.
Найдите собственную скорость моторной лодки.
Ответ: 15 км/ч.
Задача 3. Сколько времени потребуется лодке,
собственная скорость которой
равна 28 км/ч, чтобы проплыть по озеру 84 км?
Ответ: 3 часа.
Итак, чтобы найти длину пройденного пути,
необходимо скорость умножить на время.
Чтобы найти скорость, необходимо длину пути
разделить на время.
Чтобы найти время, необходимо длину пути
разделить на скорость.
Чем же отличается движение по озеру от
движения по реке?
Вспомним бумажный кораблик в ручье. Он плыл,
потому что вода в нем движется.
Такое движение называют движением по течению.
А в обратную сторону – движением против
течения.
Итак, вода в реке движется, а значит имеет свою
скорость. И называют ее скоростью течения реки.
( Как ее измерить?)
Задача 4. Скорость течения реки равна 2 км/ч. На
сколько километров река относит
любой предмет (щепку, плот, лодку) за 1час, за 4
часа?
Ответ: 2 км/ч, 8 км/ч.
Каждый из вас плавал в реке и помнит, что по
течению плыть гораздо легче, чем против течения.
Почему? Потому, что в одну сторону река
«помогает» плыть, а в другую — «мешает».
Рис.1
Те же, кто не умеет плавать, могут представить
себе ситуацию, когда дует сильный ветер.
Рассмотрим два случая:
1) ветер дует в спину,
2) ветер дует в лицо.
И в том и в другом случае идти сложно. Ветер в
спину заставляет бежать, а значит, скорость
нашего движения увеличивается. Ветер в лицо
сбивает нас, притормаживает. Скорость при этом
уменьшается.
Остановимся на движении по течению реки. Мы уже
говорили о бумажном кораблике в весеннем ручье.
Вода понесет его вместе с собой. И лодка,
спущенная на воду, поплывет со скоростью течения.
Но если у нее есть собственная скорость, то она
поплывет еще быстрее.
Следовательно, чтобы найти скорость движения
по течению реки, необходимо сложить собственную
скорость лодки и скорость течения.
Задача 5. Собственная скорость катера равна 21
км/ч, а скорость течения реки 4 км/ч. Найдите
скорость катера по течению реки.
Ответ: 25км/ч.
Теперь представим себе, что лодка должна плыть
против течения реки. Без мотора или хотя бы весел,
течение отнесет ее в обратную сторону. Но, если
придать лодке собственную скорость ( завести
мотор или посадить гребца), течение будет
продолжать отталкивать ее назад и мешать
двигаться вперед со своей скоростью.
Поэтому, чтобы найти скорость лодки против
течения, необходимо из собственной скорости
вычесть скорость течения.
Задача 6. Скорость течения реки равна 3 км/ч, а
собственная скорость катера 17 км/ч.
Найдите скорость катера против течения.
Ответ: 14 км/ч.
Задача 7. Собственная скорость теплохода равна
47,2 км/ч, а скорость течения реки 4,7 км/ч. Найдите
скорость теплохода по течению и против течения.
Ответ: 51,9 км/ч; 42,5 км/ч.
Задача 8. Скорость моторной лодки по течению
равна12,4 км/ч. Найдите собственную скорость
лодки, если скорость течения реки 2,8 км/ч.
Ответ: 9,6 км/ч.
Задача 9. Скорость катера против течения равна
10,6 км/ч. Найдите собственную скорость катера и
скорость по течению, если скорость течения реки
2,7 км/ч.
Ответ: 13,3 км/ч; 16 км/ч.
Связь между скоростью по течению и
скоростью против течения.
Введем следующие обозначения:
Vс. — собственная скорость,
Vтеч. — скорость течения,
V по теч. — скорость по течению,
V пр.теч. — скорость против течения.
Тогда можно записать следующие формулы:
V no теч = Vc + Vтеч ;
V np. теч = Vc — V теч.;
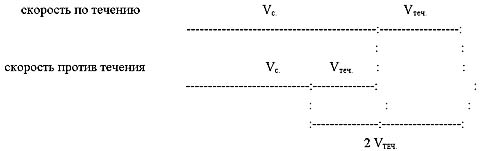
Попытаемся изобразить это графически:
Рис. 2
Вывод: разность скоростей по течению
и против течения равна удвоенной скорости
течения.
Vno теч — Vnp. теч = 2 Vтеч.
Vтеч = (V по теч — Vnp. теч ): 2
Задача.
1) Скорость катера против течения равна 23 км/ч, а
скорость течения 4 км/ч.
Найдите скорость катера по течению.
Ответ: 31 км/ч.
2) Скорость моторной лодки по течению реки равна
14 км/ч/ а скорость течения 3 км/ч. Найдите скорость
лодки против течения
Ответ: 8 км/ч.
Задача 10. Определите скорости и заполните
таблицу:
|
V С. |
Vтеч. |
Vпо теч. |
Vпр.теч. |
|
|
1 |
12 км/ч |
3 км/ч |
||
|
2 |
23 км/ч |
25 км/ч |
||
|
3 |
24 км/ч |
20 км/ч |
||
|
4 |
4 км/ч |
17 км/ч: |
||
|
5 |
5 км/ч |
18 км/ч |
||
|
6 |
42 км/ч |
34 км/ч |
* — при решении п.6 смотри рис.2.
Ответ: 1) 15 и 9; 2) 2 и 21; 3) 4 и 28; 4) 13 и 9; 5)23 и 28; 6) 38 и 4.
Задачи на движение по реке
Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.
Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.
Задача 1. Катер движется против течения реки. За сколько часов он преодолеет расстояние 112 км, если его собственная скорость 30 км/ч, а скорость течения реки 2 км/ч?
Решение: Сначала узнаем скорость движения катера против течения реки, для этого от его собственной скорости отнимем скорость течения:
30 — 2 = 28 (км/ч) — скорость движения катера против течения.
Теперь можно узнать за сколько часов катер преодолеет 112 км, разделив расстояние на скорость:
112 : 28 = 4 (ч).
Решение задачи по действиям можно записать так:
1) 30 — 2 = 28 (км/ч) — скорость движения катера против течения,
2) 112 : 28 = 4 (ч).
Ответ: За 4 часа катер преодолеет расстояние 112 км.
Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки.
Задача 2. Расстояние от пункта A до пункта B по реке равно 120 км. Сколько времени потратит моторная лодка на путь от пункта A до B, если её собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Рассмотрите два варианта:
1) лодка движется по течению реки;
2) лодка движется против течения реки.
Решение: Если моторная лодка будет двигаться по течению реки, то её скорость будет равна сумме собственной скорости со скоростью течения реки:
27 + 3 = 30 (км/ч).
Значит расстояние между пунктами лодка преодолеет за:
120 : 30 = 4 (ч).
Если лодка будет двигаться против течения реки, то её скорость будет равна разности собственной скорости и скорости течения реки:
27 — 3 = 24 (км/ч).
Значит, чтобы узнать сколько времени потратит лодка на путь от пункта A до пункта B, надо расстояние разделить на скорость:
120 : 24 = 5 (ч).
Решение задачи по действиям для движения по течению реки можно записать так:
1) 27 + 3 = 30 (км/ч) — скорость лодки,
2) 120 : 30 = 4 (ч).
Для движения против течения реки решение задачи по действиям можно записать так:
1) 27 — 3 = 24 (км/ч) — скорость лодки,
2) 120 : 24 = 5 (ч).
Ответ:
1) При движении по течению реки моторная лодка потратит 4 часа на путь от пункта A до пункта B.
2) При движении против течения реки моторная лодка потратит 5 часов на путь от пункта A до пункта B.
Решение задач с помощью уравнений.
Движение по воде.
ФОРМУЛЫ.
V
соб. – собственная скорость (скорость в стоячей
воде)
Vтеч.р.
– скорость течения реки
Vпо
теч. = V соб. + Vтеч.р.
Vпр.
теч. = V соб. — Vтеч.р.
Задача
1. Лодка
плыла 1,4
ч по течению реки и 1,7 ч против течения. Путь,
который проплыла лодка по течению, оказался на 2,2 км меньше пути, который она
проплыла против течения. Найдите скорость
течения реки, если скорость лодки в стоячей воде 28 км/ч.
 |
|||||
 |
|||||
|
V (км/ч) |
t (ч) |
S (км) |
|
|
По |
28 + |
1,4 |
1,4(28 + x) |
|
Против |
28 — |
1,7 |
1,7(28 – x) |
V соб. = 28 км/ч
Vтеч.р. = x км/ч
1)
1,7(28 – x) – 1,4(28 + x) = 2,2
47,6 — 1,7x – 39,2 – 1,4x = 2,2
-1,7x – 1,4x= 2,2 — 47,6 +39,2
-3,1x = -6,2
x = -6,2 : (-3,1)
x = 2
2)
2 км/ч – Vтеч.р.
Ответ. 2
Задача
2. Расстояние между двумя пунктами катер прошёл по течению реки за 7
часов, а против течения за 8 часов. Найдите расстояние
между этими пунктами, если скорость течение реки 3,5 км/ч
|
V (км/ч) |
t (ч) |
S (км) |
|
|
По |
x + |
7 |
|
|
Против |
x – |
8 |
8(x |
V соб. = x км/ч
Vтеч.р. = 3,5 км/ч
1)
7(x + 3,5) = 8(x – 3,5)
7x + 24,5 = 8x — 28
7x – 8x= -28 – 24,5

x = 52,5
2) 52,5 км/ч – V
соб.
3) 7(52,5 + 3,5) = 7 · 56 = 392 км –
расстояние
Ответ. 392
РЕШИ ЗАДАЧИ ПО ОБРАЗЦУ.
1) Туристы на байдарке плыли
2,4 ч по течению реки и 1,8 ч против течения. Путь, который байдарка проплыла
по течению, был на 14,1 км больше, чем путь, пройденный против течения. Найдите
скорость байдарки в стоячей воде, если скорость течения 2,5 км/ч.
2) Расстояние между двумя
пунктами катер прошел по течению реки за 5 часов, а против течения — за 6
часов. Найдите расстояние между этими пунктами, если скорость течения реки 3
км/ч.
3) Катер
проходит по течению реки за 5 ч такое же расстояние, как за 6 ч 15 мин против
течения. Найдите скорость катера в стоячей воде, если скорость течения реки
равна 2,4 км/ч.
4) Моторная
лодка прошла 7 ч по течению реки и 6 ч против течения. Определите скорость
течения реки, если скорость лодки в стоячей воде 10
км/ч и за все путешествие лодка прошла 132
км.
Задание 1017
На реке расположены пункты А и Б. Известно, что из А в Б баржа плывет 4 часа, а из Б в А – 6 часов. За какое время из пункта А в пункт Б доберется плот? Ответ дайте в часах.
Ответ: 24
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть x- скорость баржи в стоячей воде. у — скорость течения и s — расстояние между пунктами, примем его за 1. Тогда, $$t_1=frac{1}{x+y}=4 ; t_2=frac{1}{x-y}=6 Leftrightarrow x+y = 1/4 ; x-y=1/6$$
Вычтем из первого уравнения второе и получим: $$ 2y=1/12 Leftrightarrow y=1/24$$
То есть скорость течения составляет одну двадцать четвертую от расстояния, а плот двигается только со скоростью течения, значит расстояние пройдет за 24 часа
Задание 2354
Катер в 11:00 вышел из пункта А в пункт В, расположенный в 30 км от А. Пробыв в пункте В 2 часа 40 минут, катер отправился назад и вернулся в пункт А в 19:00 того же дня. Определите (в км/ч) собственную скорость катера, если известно, что скорость течения реки 3 км/ч.
Ответ: 12
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть х — скорость катера в стоячей воде, путь был с 1100 до 1900 (8 часов) и стоял 2 часа 40 минут ($$2frac{2}{3}$$), тогда: время по течению — $$frac{30}{x+3}$$;
время против течения — $$frac{30}{x-3}$$;
время в движении — $$8-2frac{2}{3}=5frac{1}{3}=frac{16}{3}$$
$$frac{30}{x+3}+frac{30}{x-3}=frac{16}{3}Leftrightarrow frac{30x-96+30x+90}{x^{2}-9}=frac{16}{3}$$
$$60xcdot 3=16x^{2}-144Leftrightarrow 16x^{2}-180x-144=0$$
$$4x^{2}-45x-36=0$$
D=$$2025+576=2601=51^{2}$$
$$x_{1}=frac{45+51}{8}=12$$
$$x_{2}=frac{45-51}{8}$$ — отрицательной скорость быть не может
Задание 2989
Расстояние между пристанями A и B равно 120км. Из A в B по течению реки отправляется плот, а через час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому моменту плот прошел 24км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.
Ответ: 22
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Плот затратил 24/2=12 часов. Лодка выплыла на час позже: 12-1=11 часов. Пусть x — скорость лодки в стоячей воде, тогда общее время движения вычисляется как: $$frac{120}{x+2}+frac{120}{x-2}=11$$ $$120(x-2)+120(x+2)=11(x^{2}-4)$$ $$11x^{2}-240x-44=0$$ $$D=57600+1936=59536=244^{2}$$ $$x_{1}=frac{240+244}{22}=22$$ $$x_{2}$$-меньше нуля
Задание 3246
Расстояние между пристанями A и B равно 105 км. Из A в B по течению реки отправился плот, а через 1 час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот проплыл 40 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч.
Ответ: 24
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
tплота$$=frac{40}{4}=10$$ (ч) — время плота
$$10-1=9$$ (ч) — время яхты
Пусть х — собственная скорость яхты
$$frac{105}{x+4}+frac{105}{x-4}=9$$
$$105x-420+105x+420=9(x^{2}-16)$$
$$9x^{2}-210x-144=0$$
$$3x^{2}-70x-48=0$$
$$D=4900+576=5476=74^{2}$$
$$x_{1}=frac{70+74}{6}=24$$
$$x_{2}<0$$
Задание 3659
Теплоход прошел путь от пункта А до пункта В за 6 часов. В некоторый момент плавания с борта теплохода на воду была спущена моторная шлюпка, которая вернулась в пункт А и без задержки направилась в пункт В, прибыв туда одновременно с теплоходом. Теплоход и шлюпка двигались равномерно и без остановок, причём скорость шлюпки вдвое превышала скорость теплохода. Определите, через какое время после отплытия теплохода из пункта А на воду была спущена шлюпка? Ответ дайте в часах.
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть $$S=1$$ — расстояние от А до В. Раз теплоход плыл 6 часов, то $$frac{1}{6}$$ — скорость теплохода. Тогда $$frac{2}{6}=frac{1}{3}$$ — скорость шлюпки. Пусть х — расстояние от места спуска до А; $$frac{1+x}{frac{1}{3}}$$ — время шлюпки; $$frac{1-x}{frac{1}{6}}$$ — время теплохода
$$3(1+x)=6(1-x)$$
$$3+3x=6-6x$$ $$Leftrightarrow$$
$$9x=3$$
$$x=frac{1}{3}$$
$$t=frac{1-frac{1}{3}}{frac{1}{6}}=frac{2}{3}cdotfrac{6}{1}=4$$ часа
$$Rightarrow$$ $$6-4=2$$
Задание 4860
По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй ‐ длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго сухогруза составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
Ответ: 6
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Необходимо понять, как протекает данный процесс. За точку, которая передвигается, принимается нос второго сухогруза. В таком случае он проходит сначала расстояние 400 метров, потом длину первого 120 метров, потом свою длину 80 метров, и только с этого момента начинает его опережать, то есть проходит еще 600 метров. В таком случае общий путь S=1200 метров = 1,2 км. Далее можно рассмотреть эту задачу немного иначе. Раз один догоняет другого, мы можем представить, что первый стоит, а второй двигается к нему со скоростью, равной разности их скоростей, то есть то, что мы ищем. Время представляем в часах: 0,2 часа. И далее применяем стандартную формулу нахождения скорости через расстояние и время. Получаем: $$v=frac{1,2}{0,2}=6$$
Задание 4911
Теплоход, скорость которого в неподвижной воде равна 24 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 2 км/ч, стоянка длится 4 часа, а в исходный пункт теплоход возвращается через 16 ч после отплытия из него. Сколько километров прошел теплоход за весь рейс?
Ответ: 286
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть х — расстояние в один конец. Скорость по течению составляет 24+2=26, против течения 24-2=22. Стоянка длилась 4 часа, следовательно само плавание составило 16-4=12. Данное время получается суммирование времени по течени и против течения:
$$frac{x}{26}+frac{x}{22}=12Leftrightarrow$$$$frac{24x}{11cdot13cdot2}=12Leftrightarrow $$$$x=frac{11cdot12cdot13cdot2}{24}=143$$
Тогда расстояние туда/обратно составило 143-143=286 км.
Задание 5054
От лесоповала вниз по течению реки движется плот. Плотовщик доплывает на моторной лодке из конца плота к его началу и обратно за 9 минут. Найдите длину плота, если собственная скорость лодки равна 16 км/ч. Ответ дайте в метрах.
Ответ: 1200
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть S — длина плота, x — скорость течения: $$frac{S}{16+x-x}+frac{S}{16-x+x}=frac{9}{60}=frac{3}{20}$$; $$frac{S}{8}=frac{3}{20}$$; $$S=frac{8cdot3}{20}=1,2$$ км
Задание 6566
По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй — длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
Ответ: 6
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть x кмч –разница скоростей сухогрузов. Тогда, точка на носу второго сухогруза пройдет расстояние : 400+120+80+600 метров=1,2 км.( нагнал(400), поравнялись носы (120), опередил (80), удалился (600) ) за 12 минут ($$frac{12}{60}*frac{1}{5}$$ часа ):$$frac{1,2}{frac{1}{5}}=6$$ кмч –разница
Задание 7016
Катер и плот одновременно отплыли вниз по реке. Пройдя 16 км, катер развернулся и пошел вверх по реке. Пройдя 12 км, он встретился с плотом. Какова собственная скорость катера, если скорость течения реки 4 км/ч? Ответ выразите в км/ч.
Ответ: 28
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Так как катер проплыл вниз по течению 16 км, а вверх -12 км, то они встретились с плотом в 4 км. от старта. Т.к. скорость плота равна скорости течения , то время плота : $$t=frac{4}{4}=1$$ час( как и время катера) .Пусть x кмч –собственная скорость катера, тогда:
$$frac{16}{x+4}+frac{12}{x-4}=1 Leftrightarrow$$ $$16x-64+12x+48=x^{2}-16Leftrightarrow$$ $$x^{2}-28x=0Leftrightarrow$$ $$left{begin{matrix}x=0\x=28end{matrix}right.$$
Скорость не может быть нулевой $$Rightarrow$$ 28 кмч
Задание 7197
От пристани одновременно отправились катер и плот. Через 9 км катер развернулся и, пройдя еще 13 км, догнал плот. Найдите скорость течения реки, если собственная скорость катера равна 22 км/ч. Ответ дайте в км/ч.
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Сначала катер поплыл вниз по течению. Пусть скорость течения составляет х кмч , тогда катер до момента разворота потратил $$frac{9}{22+x}$$ часов, затем $$frac{13}{22+x}$$ часов. При этом плот уплыл на 13-9=4 км от пристани и потратил $$frac{4}{x}$$ часа $$Rightarrow$$ $$frac{9}{22-x}+frac{13}{22+x}=frac{4}{x}Leftrightarrow$$ $$x(9(22+x)+13(22-x))=4(484-x^{2})Leftrightarrow$$ $$x(484-4x)=4(484-x^{2})|:4Leftrightarrow$$ $$121x-x^{2}=484-x^{2}Leftrightarrow$$ $$121x=484Leftrightarrow$$ $$x=4$$ кмч
Задание 7511
Собственная скорость теплохода равна 20 км/ч, скорость течения реки равна 4 км/ч. Теплоход проплыл от одной пристани до другой и вернулся обратно. Найдите среднюю скорость теплохода на протяжении всего пути. Ответ дайте в км/ч.
Ответ: 19,2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть S км — расстояние, пройденное в одну сторону, тогда время движения по течению: $$t_{1}=frac{S}{20+4}$$, против течения: $$t_{2}=frac{S}{20-4}$$. Тогда средняя скорость составит: $$v=frac{S+S}{t_{1}+t_{2}}=frac{2S}{frac{S}{24}+frac{S}{16}}=19,2$$
Задание 7632
На реке расположены пункты А и Б. Известно, что из А в Б баржа плывет 4 часа, а из Б в А – 6 часов. За какое время из пункта А в пункт Б доберется плот? Ответ дайте в часах
Ответ: 24
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 7875
Пароход, отчалив от пристани A, спустился вниз по течению реки на 60 км до устья впадающего в реку притока и поднялся вверх по притоку (против течения) на 20 км до пристани B. Весь путь от A до B пароход прошёл за 7 часов. Скорость течения реки и скорость течения притока равны 1 км/ч. Найти собственную скорость парохода в км/ч. (Собственная скорость – скорость в неподвижной воде.)
Ответ: 11
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 7940
Пункты A, B и C расположены на реке в указанном порядке вниз по течению реки. Расстояние между A и B равно 4 км, а между B и C – 14 км. В 12.00 из пункта B отплыла лодка и отправилась в A. Достигнув пункта A, она сразу же повернула и в 14.00 того же дня прибыла в пункт C. Скорость течения реки равна 5 км/ч. Найти скорость лодки в стоячей воде.
Ответ: 10
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

11. Сюжетные текстовые задачи
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на движение по воде
Верны те же формулы: [{large{S=vcdot t quad quad quad v=dfrac
St quad quad quad
t=dfrac Sv}}]
(blacktriangleright) Если тело движется по реке по течению:
(v_c) — собственная скорость тела (скорость в неподвижной воде);
(v_t) — скорость течения;
тогда скорость движения тела (v=v_c+v_t).
Значит, [{large{S=(v_c+v_t)cdot t}}]
(blacktriangleright) Если тело движется по реке против течения:
(v_c) — собственная скорость тела (скорость в неподвижной воде);
(v_t) — скорость течения;
тогда скорость движения тела (v=v_c-v_t).
Значит, [{large{S=(v_c-v_t)cdot t}}]
(blacktriangleright) Заметим, что плот — это тело, у которого собственная скорость (v_c=0). Значит, плот может плыть только по течению и со скоростью течения.
Задание
1
#2120
Уровень задания: Легче ЕГЭ
Антон знает, что собственная скорость его лодки равна (10, км/ч). При этом ему надо успеть проплыть (25, км) за (2) часа. Плыть он будет по течению. Какой должна быть скорость течения реки, чтобы Антон успел? Ответ дайте в км/ч. Если в задаче может быть более одного ответа – выберите наименьший.
Чтобы Антон успел, необходимо и достаточно, чтобы его лодка перемещалась со скоростью не меньше, чем (25 : 2 = 12,5, км/ч). То есть для того, чтобы Антон успел, необходимо и достаточно, чтобы скорость течения была не меньше, чем (2,5, км/ч).
Ответ: 2,5
Задание
2
#2124
Уровень задания: Легче ЕГЭ
Лодка прошла (10, км) по течению, а затем (5, км) против течения. На весь путь лодка затратила (3, часа). Найдите среднюю скорость лодки на описанном участке пути, если скорость течения равна (2, км/ч). Ответ дайте в км/ч.
Средняя скорость есть отношение всего пути ко времени, затраченному на этот путь. Независимо от скорости течения, средняя скорость лодки:[v_{ср} = dfrac{10 + 5}{3} = 5, км/ч,.]
Ответ: 5
Задание
3
#826
Уровень задания: Равен ЕГЭ
Катер береговой охраны прошёл по течению реки Конго 120 км и вернулся обратно. Известно, что обратный путь занял на 1 час больше времени, а скорость катера в неподвижной воде равна 27 км/ч. Найдите скорость течения. Ответ дайте в км/ч.
Пусть (v) км/ч – скорость течения, (v > 0), тогда
(27 + v) – скорость перемещения катера по течению,
(27 — v) – скорость перемещения катера против течения,
(dfrac{120}{27 + v}) – время, затраченное катером на перемещение по течению,
(dfrac{120}{27 — v}) – время, затраченное катером на перемещение против течения.
Так как время перемещения против течения на час больше, чем время по течению, то: [dfrac{120}{27 + v} + 1 = dfrac{120}{27 — v}qquadLeftrightarrowqquad v^2 + 240 v — 729 = 0] – при (v neq pm 27), что равносильно (v_1 = 3, v_2 = -243), откуда получаем, что (v = 3) км/ч, так как (v > 0).
Ответ: 3
Задание
4
#3075
Уровень задания: Равен ЕГЭ
Катер прошел 40 км по течению реки и 6 км против течения реки, затратив на весь путь 3 ч. Найдите скорость катера в стоячей воде, если известно, что скорость течения реки равна 2 км/ч.
Пусть (x) км/ч – скорость катера в стоячей воде. Тогда можно составить следующее уравнение: [dfrac{40}{x+2}+dfrac 6{x-2}=3 quadRightarrowquad
dfrac{46x-68}{x^2-4}=3 quadRightarrowquad 3x^2-46x+56=0] Дискриминант равен (D=4cdot 361=(38)^2), следовательно, корнями будут (x_1=dfrac43) и (x_2=14). Так как скорость катера не может быть меньше скорости течения, то (x_1) не подходит. Следовательно, (x=14).
Ответ: 14
Задание
5
#3864
Уровень задания: Равен ЕГЭ
Теплоход, скорость которого в неподвижной воде равна (24) км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна (3) км/ч, стоянка длится (2) часа, а в исходный пункт теплоход возвращается через (34) часа после отправления из него. Сколько километров прошёл теплоход за весь рейс?
Пусть (S) – расстояние в километрах, которое проходит теплоход, двигаясь в одну сторону. Тогда: [dfrac S{24+3}+dfrac S{24-3}+2=34quadLeftrightarrowquad S=378] Тогда за весь рейс теплоход прошел (2S=2cdot 378=756) километров.
Ответ: 756
Задание
6
#827
Уровень задания: Равен ЕГЭ
От пристани A в направлении пристани В с постоянной скоростью отправился первый теплоход. Через час после этого от пристани В в направлении пристани А отправился второй теплоход, причём скорость второго теплохода на 1 км/ч меньше, чем скорость первого. При этом скорость течения составляет 2 км/ч. Найдите скорость первого теплохода в неподвижной воде, если расстояние от А до В равно 120 км, а встретились теплоходы посередине между пристанями А и В. Ответ дайте в км/ч.
Так как теплоходы встретились посередине, а время, затраченное на это теплоходом с меньшей скоростью в неподвижной воде, меньше, чем время теплохода с большей скоростью в неподвижной воде, то теплоход с большей скоростью в неподвижной воде плыл против течения, то есть течение направлено от В к А.
Пусть (v) км/ч – скорость первого теплохода в неподвижной воде, (v > 0), тогда
(v — 2) км/ч – скорость перемещения первого теплохода,
((v — 1) + 2) км/ч – скорость перемещения второго теплохода,
(dfrac{60}{v — 2}) ч – время, затраченное первым теплоходом,
(dfrac{60}{v + 1}) ч – время, затраченное вторым теплоходом.
Так как время, затраченное первым теплоходом, на час больше, то: [dfrac{60}{v — 2} — dfrac{60}{v + 1} = 1qquadLeftrightarrowqquad v^2 — v — 182 = 0] – при (v neq 2, v neq -1), откуда находим (v_1 = 14, v_2 = -13), значит, (v = 14) км/ч (т.к. (v > 0)).
Ответ: 14
Задание
7
#828
Уровень задания: Равен ЕГЭ
На озере расположены пристани А и В. Расстояние между пристанями равно 90 км. Моторная лодка проплыла от А до В с постоянной скоростью, после чего сразу отправилась обратно со скоростью на 5 км/ч больше прежней. На середине пути из В в А лодка замедлилась и поплыла со скоростью на 2,5 км/ч меньшей, чем по дороге из А в В. В результате лодка затратила на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость лодки на пути из А в В. Ответ дайте в км/ч.
Пусть (v) км/ч – скорость лодки по пути от А до В, тогда
(dfrac{90}{v}) ч – время, затраченное лодкой на путь из А в В,
(dfrac{45}{v + 5}) ч – время, затраченное лодкой на первую половину пути из В в А,
(dfrac{45}{v — 2,5}) – время, затраченное лодкой на вторую половину пути из В в А.
Так как в итоге лодка проплыла из В в А за такое же время, как и из А в В, то: [dfrac{90}{v} = dfrac{45}{v + 5} + dfrac{45}{v — 2,5},] откуда (v = 10) км/ч.
Ответ: 10

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды